1 Introduction

The availability of highly accurate thermophysical properties is of enormous importance for the modernization of any process in energy and process engineering as well as for the design of new processes. In order to make these data available at any time and at any state point, equations of state are used. In the context of thermodynamic properties, the Helmholtz energy was established as the basic model from which any thermodynamic state property can be calculated. These equations are of an empirical nature and their parameters are adjusted in such a way that the available experimental data can ideally be reproduced within their experimental uncertainty. In the last decades, such highly accurate reference equations have been developed for most of the pure fluids (e.g., CO2 [1], water [2], and propane [3]) that are relevant in energy technology and are accordingly very well measured experimentally. With further developed fitting techniques, less well-measured substances that are important in the chemical industry (e.g., siloxanes [4,5,6,7], vinyl chloride [8], and propylene glycol [9]) are now also described in this form. These equations are not as accurate as the reference equations but follow the same mathematical concept. On the basis of this uniform mathematical structure, a mixture model was developed, which is also formulated in the form of the Helmholtz energy [10]. Due to its modular structure, it is fast and easily possible to add a new component to the mixture model as soon as a pure-fluid equation becomes available for the corresponding fluid. In this way, thermodynamic properties can nowadays be provided for many processes by means of highly accurate mixture models. The most prominent equations are the GERG-2008 [11] and EOS-LNG [12] for applications in the natural gas business, and the EOS-CG [13, 14], which was mainly developed for CO2-rich mixtures relevant for example in carbon, capture, and storage processes.

In the context of transport properties (e.g., viscosity or thermal conductivity), development has not yet progressed as far. Although there are also highly accurate equations available for transport properties for numerous pure fluids, they are not based on a uniform mathematical construct. Many equations are based on a physically founded model. The choice of a physically based model has the advantage that the basic mathematical structure is already defined and only a few experimental data for the respective fluid are required. On the other hand, such abstracted physical models can be quite complex and are usually not sufficiently accurate to reproduce the experimental data within their experimental uncertainties. Therefore, empirical corrections are also made here, so that most equations are ultimately semi-empirical models. The different mathematical functional forms of the available pure-fluid models make it quite difficult to develop a generally valid and easily extendable but also accurate mixture model. As a result, various mixing approaches can be found in the literature that have been optimized for a specific fluid group or specific applications, but are not generally valid. The commonly used all-encompassing approaches that are valid for any fluid/mixture and in all fluid states, as well as being easily extensible, are the extended corresponding states or the entropy scaling approach. However, due to their generalized nature, the description of fluid–mixtures is not as accurate as it is needed to be for many applications. Thol and Richter [15] have shown the limitations of such viscosity models with the example of CO2 and alkane mixtures. Deviations with respect to experimental data exceed more than 50 % for asymmetric mixtures. Therefore, it is desirable to have a concept for a model for the calculation of the dynamic viscosity of mixtures, which works in a similar manner as thermodynamic Helmholtz equations of state. The basic idea is to develop empirical pure-fluid equations, which all have the same mathematical functional form and, thus, can be easily and modularly combined in a mixture model. Hereby, the experimental data should ideally be reproduced within their experimental uncertainty and the physically correct behavior of the equation must be ensured outside the domain covered by experimental data. The second aspect plays a major role especially for the application in mixtures, since the pure-fluid equations must be evaluated in the mixture at points which are actually no longer within the range of validity.

First attempts to develop empirical equations for viscosities and thermal conductivities were made by Span and colleagues. Viscosity and thermal conductivity models for propane [16] and carbon dioxide [17] were developed using the fitting algorithms for the development of equations of state in terms of the Helmholtz energy that were state-of-the-art at that time [18]. This work was subsequently continued using hydrocarbons as examples [19,20,21].

In this work, a first pure-fluid equation for the application in a mixture model as described before is presented. Propane was chosen as an example, since an extensive experimental database is available and there is a highly accurate reference equation developed by Vogel and Herrmann [21] available, which can be used for comparison purposes. The equation of Vogel and Herrmann [21] is already an empirical model based on the concept of the thermodynamic Helmholtz equations and was developed using modern optimization techniques. However, it is only suitable for use in mixture models to a limited extent, since it contains modulus functions. These form poles, which can lead to numerical problems in mixture models. Therefore, the aim of this work is to develop an equation which is as accurate as the one of Vogel and Herrmann [21] without using term types which complicate the application of the equation in mixture models.

2 New Viscosity Equation

The equation for the dynamic viscosity \(\eta\) is separated into the temperature-dependent dilute-gas contribution \({\eta }^{0}\) and a residual part \({\eta }^{\mathrm{r}}\), depending on temperature and density:

$$\eta (T,\rho )={\eta }^{0}(T)+{\eta }^{\mathrm{r}}(T,\rho ).$$
(1)

In this work, the temperature is reduced with the critical temperature \({T}_{\mathrm{c}}\) = 369.89 K and the density is reduced with the critical density \({\rho }_{\mathrm{c}}\) = 5.0 mol·dm−3 of propane according to

$$\tau =T/{T}_{\mathrm{c}}$$
(2)

and

$${\delta =\rho /\rho }_{\mathrm{c}}.$$
(3)

2.1 Dilute-Gas Contribution

Vogel and Herrmann [21] developed the current reference equation for the viscosity of propane including an accurate correlation for the dilute-gas contribution, cf. Eq. 4. Assuming no interactions between molecules, the viscosity is described in the range of zero density. The parameters ni and ti according to Vogel and Herrmann [21] are listed in Table 1. This approach is adopted in this work.

Table 1 Parameters of the dilute-gas contribution \({\eta }^{\mathrm{r}}\) according to Vogel and Herrmann [21], cf. Eq. 4
Full size table
$${\eta }^{0}\left(\tau \right)=\sum_{i=1}^{4}{n}_{i}{\tau }^{{t}_{i}}$$
(4)

2.2 Residual Part

For the residual contribution \({\eta }^{\mathrm{r}}\), an approach commonly used for fundamental equations in terms of the Helmholtz energy is used. The equation consists of four polynomial, two exponential, and five Gaussian bell-shaped terms, cf. Eq. 5. The fitted parameters ni, ti, di, li, \(\zeta\) i, \(\beta\) i, \(\gamma\) i and \(\varepsilon\) i of Eq. 5 are listed in Table 2. Test values calculated with the present equation are given in Table 3 for a verification of a computer implementation.

Table 2 Parameters of the residual contribution \({\eta }^{\mathrm{r}}\), cf. Eq. 5
Full size table
Table 3 Test values for computer implementations
Full size table
$${\eta }^{\mathrm{r}}(\tau ,\delta )=\sum_{i=1}^{4}{n}_{i}{\tau }^{{t}_{i}}{\delta }^{{d}_{i}}+\sum_{i=5}^{6}{n}_{i}{\tau }^{{t}_{i}}{\delta }^{{d}_{i}}\mathrm{exp}\left(-{\delta }^{{l}_{i}}\right)+\sum_{i=7}^{11}{n}_{i}{\tau }^{{t}_{i}}{\delta }^{{d}_{i}}\mathrm{exp}\left({{\zeta }_{i}(\delta -{\varepsilon }_{i})}^{2}+{{\beta }_{i}(\tau -{\gamma }_{i})}^{2}\right)$$
(5)

For the development of the new equation, a fitting process based on a constrained nonlinear optimization problem was used [22, 23]. In order to ensure that the exponents of the reduced density are integer values only, a branch-and-bound algorithm is integrated [24]. As the present equation is intended to be empirically only, no theory for the critical enhancement such as the one of Bhattacharjee et al. [25] or Olchowy and Sengers [26] was used. Nevertheless, the critical contribution is represented by the residual contribution by means of the Gaussian bell-shaped terms. It was ensured that the behavior in the near-critical region is appropriately modeled by adjusting the equation parameters to experimental data. The data measured by Seibt et al. [27] and by Wilhelm and Vogel [28] are the most relevant near the critical point. These data will be further discussed in Sect. 4.

3 Experimental Viscosity Data

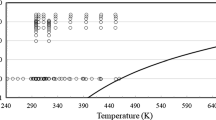
In total, 1759 experimental data points for the dynamic viscosity of propane were found in the literature. In Fig. 1, the distribution in relation to the vapor-pressure curve is shown in a p,T-diagram. A temperature range between 88 K and 626 K is covered with a maximum pressure of 145 MPa. However, the temperature range T > 525 K is only investigated at dilute-gas conditions.

Fig. 1
figure 1

p,T-diagram showing the distribution of the available experimental datasets in relation to the vapor-pressure curve. Datasets not used in the fitting procedure are marked with gray symbols. The vapor pressure pv was calculated with the current reference equation of state for propane of Lemmon et al. [3]

Full size image

An overview of all publications is given in Table 4 with further information about the measurement procedure, temperature, pressure, and density ranges, and an assumed expanded experimental uncertainty. For the determination of the expanded uncertainty reported in Table 4, information provided by the respective authors was used as well as publications on the measurement apparatus. As a consequence, for several experimental datasets no uncertainty is given due to lacking information. For the development of the present equation, only a subset of the available datasets was used, whereas all data were evaluated to assess the quality of the present equation.

Table 4 Overview of experimental datasets for the dynamic viscosity of propane
Full size table

For the comparison of the present equation as well as the reference equation of Vogel and Herrmann [21] to experimental data, the average absolute relative deviation (AARD) was used:

$$\mathrm{AARD}=\frac{1}{N}\sum_{i=1}^{N}\left|\Delta {\eta }_{i}\right|$$
(6)

with

$$\Delta {\eta }_{i}=100\frac{{\eta }_{\mathrm{DATA},i}-{\eta }_{\mathrm{EOS},i}}{{\eta }_{\mathrm{DATA},i}}.$$
(7)

\(\Delta {\eta }_{i}\) is defined as relative deviation of a data point \({\eta }_{\mathrm{DATA}}\) from the value calculated with the equation \({\eta }_{\mathrm{EOS}}\) and N describes the number of data points of one dataset. The AARD was calculated for the present equation and for the equation of Vogel and Herrmann [21]. The respective values of the datasets are tabulated in Table 4.

4 Comparison with Literature Data

Due to the large amount of data, only selected datasets used for fitting will be discussed in detail. However, for an overview, deviations of all data points from values calculated with the present equation are illustrated in Fig. 2. Deviations of available viscosity data measured at atmospheric pressure from values calculated with the present equation are separately illustrated in Fig. 3.

Fig. 2
figure 2

Percentage deviations of experimental viscosity data from values calculated with the present equation. Note that the scale of the y-axis is linear in the white area and logarithmic in the gray shaded area

Full size image
Fig. 3
figure 3

Percentage deviations of available viscosity data measured at atmospheric pressure from values calculated with the present equation. Note that the scale of the y-axis is linear in the white area and logarithmic in the gray shaded area

Full size image

4.1 Low-Density Viscosity Data

As the approach for the dilute-gas contribution is adopted from Vogel and Herrmann [21], calculated values from the present equation are the same as from their equation at \(\rho\) = 0 mol·dm−3. With higher density, the influence of the residual part increases, because every term of the residual part includes a contribution \({\delta }^{{d}_{i}}\) with \({d}_{i}\) > 0. In Fig. 4, the deviations of low-density viscosity data from values calculated with the present equation are shown. Deviations from Vogel and Herrmann [21] are included as dashed curves along different isochores. For \(\rho\) = 0.001 mol·dm−3, the equations are almost congruent; thus, the corresponding curve in Fig. 4 is almost unrecognizable. Deviations between both equations rise with increasing density.

Fig. 4
figure 4

Percentage deviations of low-density viscosity data (\(\rho\) < 0.05 mol·dm−3) from values calculated with the present equation and comparison with the equation from Vogel and Herrmann [21]. Note that the scale of the y-axis is linear in the white area and logarithmic in the gray shaded area. For data points marked in gray, a possible “influence of slip” was indicated by the corresponding authors

Full size image

Measurements at zero-density limit were carried out by Vogel [50], who investigated densities from 0.01 mol·dm−3 to 0.05 mol·dm−3 in a temperature range between 297 K and 626 K. The dataset was re-evaluated by Vogel and Herrmann [21], who specified a standard uncertainty of 0.3 % (0.6 % for k = 2). The percentage deviations of the re-evaluated data from the present equation do not exceed 0.14 %, so that the deviations are within the expanded uncertainty.

Other measurements at densities below 0.05 mol·dm−3 were reported by Kestin et al. [42, 43] and Abe et al. [34, 35]. The same oscillating disk viscometer was used, introduced by Dipippo et al. [51]. The first published measurements [42, 51] were reported with an accuracy of 0.1 %, whereas in later publications [34, 35, 43] an accuracy of 0.2 % is specified as well as an accuracy of 0.3 % for smoothed data. Both are assumed to be the standard uncertainty here. This leads to an expanded uncertainty of 0.6 % for smoothed data in the case of Abe et al. [34, 35] and Kestin et al. [43] as well as 0.4 % for Kestin et al. [42] with k = 2. The two data points of Kestin et al. [42] are reproduced with a maximum deviation of 0.2 %. For the other publications [34, 35, 43], experimental data deviate within 0.28 % to 0.37 % for a temperature range between 297 K and 299 K and within 0.55 % to 1.12 % for higher temperatures. Vogel and Herrmann [21] discussed that a shift of approximately 0.2 % is caused by outdated reference values used for evaluation. In addition, for higher temperatures, Vogel et al. [52] discussed an error of the temperature measurement, which leads to a systematic error between 0.5 % and 1 %. As a consequence, Vogel and Herrmann [21] assumed a standard uncertainty of 1 % (2 %, k = 2) for higher temperatures and 0.4 % (0.8 %, k = 2) at room temperature for the data points of Abe et al. [34, 35] and Kestin et al. [42, 43]. Thus, all data points from these publications are within the uncertainty assumed by Vogel and Herrmann [21]. Nevertheless, due to the possible measurement errors, the datasets were not considered for the fitting process.

Wilhelm and Vogel [28] as well as Seibt et al. [27] measured viscosity data with a vibrating-wire viscometer in the gaseous phase in a wide temperature range. Both datasets will be discussed in detail in Sect. 4.2. For experimental data measured at a density below 0.05 mol·dm−3, all data points are represented well within the expanded uncertainty of 0.25 % and 0.6 %, respectively. At T = 423.1 K and T = 373.1 K, data points of Seibt et al. [27] exhibit a small offset to the present equation as well as to the current reference equation [21]. At the same temperatures, data points of Wilhelm and Vogel [28] match well with both equations.

4.2 Gaseous Phase

In the gaseous and supercritical phases, eleven datasets are available. An overview of deviations of the viscosity data of selected datasets from values calculated with the present equation are shown in Figs. 5, 6, and 7. Not all available datasets in the gaseous and supercritical phase are illustrated due to large deviations from values calculated with the present equation as well as to other datasets. Data points in the critical region are illustrated in Fig. 5 as well, but are discussed in detail in Sect. 4.3. The boundaries of the critical region are defined in this work as 0.98 ≤ T/Tc ≤ 1.1 and 0.7 ≤ \(\rho\)/\(\rho\)c ≤ 1.4.

Fig. 5
figure 5

Percentage deviations of viscosity data of selected datasets measured in the gaseous and supercritical phases from values calculated with the present equation. The phase boundary is marked according to the lower temperature limit of a subplot. Note that the scale of the y-axis is linear in the white area and logarithmic in the gray shaded area. The pressure ranges on the x-axis are also different

Full size image
Fig. 6
figure 6

Percentage deviations of viscosity data of Wilhelm and Vogel [28] at T = 398 K and Starling et al. [33] at T = 394 K from values calculated with the present equation. The experimental uncertainties are shown with error bars for selected data points. The critical density is 5.0 mol·dm.−3

Full size image
Fig. 7
figure 7

Percentage deviations of viscosity data of selected datasets measured at temperatures T > 430 K from values calculated with the present equation. Note that the scale of the y-axis is linear in the white area and logarithmic in the gray shaded area

Full size image

The most consistent measurements in the vapor and supercritical regions were published by Wilhelm and Vogel [28] and Seibt et al. [27]. Both datasets were measured with a vibrating-wire viscometer. Seibt et al. [27] used a single-sinker densimeter for simultaneous density measurements. Wilhelm and Vogel [28] re-evaluated data from an earlier publication of themselves [53] and determined the density by using the current reference equation of state for propane of Lemmon et al. [3]. According to the authors, the estimated uncertainties (k = 2) in the reference equation of state for density are 0.03 % in the vapor phase for temperatures below 350 K and 0.1 % in the extended critical region. Uncertainties are higher close to the critical point [3]. The calculated density from the equation of state is expected to be more accurate than the density measurements of Seibt et al. [27]. Moreover, the dataset of Seibt et al. [27] exhibits an offset at low densities, described in Sect. 4.1, as well as a bump in the course of the near-critical isotherm, which will be discussed in Sect. 4.3. Therefore, the dataset of Wilhelm and Vogel [28] was preferred for the development of the present equation.

In the publication of Wilhelm and Vogel [53], a total uncertainty of 0.25 % for \(\rho\) < 2 mol·dm−3, 0.4 % for \(\rho\) > 8 mol·dm−3, and 3 % in the critical region is reported. Since there is no information whether the standard or the expanded uncertainty is meant, the given uncertainty is assumed to be the expanded uncertainty here. For densities between 2 mol·dm−3 and 8 mol·dm−3, no information about the uncertainty is given. Excluding data points in the critical region, the maximum deviation of values calculated with the present equation from these data is 0.27 % over the entire density range. Only 2 out of 541 data points exceed a deviation of 0.25 %. The AARD is 0.082 %, 0.073 %, and 0.055 % for low, medium, and high densities, respectively. Thus, the uncertainty of the present equation is estimated to 0.25 % for a temperature range from 300 K to 500 K.

Seibt et al. [27] state a maximum standard uncertainty of 0.3 % (0.6 % for k = 2), which increases to 0.34 % in the critical region. In the vapor phase, all data points can be reproduced with the present equation with an AARD of 0.12 % and a maximum deviation of 0.15 %. For the supercritical isotherm T = 423 K, all data points are well within the expanded uncertainty with a maximum deviation of 0.47 %. However, data points of the near-critical isotherm T = 373 K deviate by more than 0.6 % in a density range from 0.68 mol·dm−3 to 7.7 mol·dm−3. This deviation will be further discussed in Sect. 4.3. The dataset of Seibt et al. [27] was used for the fitting process for temperatures below 300 K. The corresponding data points are reproduced within 0.15 %, whereas the expanded uncertainty is 0.6 %. Thus, an assumption of 0.6 % for the uncertainty of the present equation in the gaseous phase below T = 300 K is too pessimistic. As a result, the uncertainty of the present equation in the gaseous phase of 0.25 %, described above, is extended to temperatures of 270 K. For temperatures below 270 K, no experimental data for the vapor phase of the dynamic viscosity is available.

Starling et al. [33] documented experimental data in the gaseous and supercritical phases in a temperature range between 311 K and 411 K. The measurements were conducted with a capillary viscometer with an estimated uncertainty of 0.5 % without further information whether the standard or the expanded uncertainty is meant. Starling et al. [33] also report extrapolated data to larger temperature and pressure ranges but only the originally measured data were considered in the present paper. In the gaseous phase, only 20 of 89 data points are reproduced within 0.5 %. The maximum deviation from values calculated with the present equation is 4.7 %. Moreover, a systematic shift in the dataset becomes obvious, when single isotherms are assessed. In Fig. 6, deviations of viscosity data of Wilhelm and Vogel [28] at T = 398 K and Starling et al. [33] at T = 394 K from values calculated with the present equation are illustrated. Data points of Starling et al. [33] below the critical density deviate by 2.3 % up to 3.4 % while data points above the critical density deviate by − 0.2 % up to 1.0 %. This jump in the course of isotherms of Starling et al. [33] is present in the whole temperature range. Meanwhile, data points of Wilhelm and Vogel [28] are consistently reproduced within 0.2 %. In addition, Vogel and Herrmann [21] reassessed the standard uncertainties for several datasets from the literature based on the measurement instruments. For Starling et al. [33], a standard uncertainty of 2.5 % was assumed. With the present equation, an expanded uncertainty of 5 % is not exceeded for all data points.

Carmichael et al. [29] conducted viscosity measurements with a rotating-cylinder viscometer in a temperature range from 278 K to 478 K. The author specified an absolute standard error of the data of 0.153 μPa·s. This results in low relative uncertainties for the liquid phase and supercritical liquid-like region and high relative uncertainties for the vapor phase and supercritical gas-like region. Data points in the vapor phase are reproduced within 2.7 % with an AARD = 1.3 %, whereas the experimental uncertainty is between 3.5 % and 4 % (k = 2). In the supercritical region, data deviate by up to 4.6 % from values calculated with the present equation, whereas the experimental uncertainty varies between 0.4 % and 3 %. 10 out of 32 points cannot be reproduced within the uncertainty specified by the authors. As for the dataset of Starling et al. [33], Vogel and Hermann [21] suggest a higher standard uncertainty of 2.5 % (5 % for k = 2) based on the measurement procedure. This uncertainty is not exceeded for the whole dataset.

For higher temperatures T ≥ 430 K, only a restricted database is available. The available datasets apart from the zero-density limit are illustrated in Fig. 7. Experimental measurements conducted of Carmichael et al. [29] at T = 478 K are reproduced within 4.3 %. This isotherm was used for the fitting process because the dataset of Carmichael et al. [29] matches well within the experimental uncertainty with the datasets of Wilhelm and Vogel [28] and Seibt et al. [27] at lower temperatures (see Fig. 2).

For temperatures above 500 K, viscosity data of Golubev [31] are the only ones available. The author measured with a capillary viscometer in a temperature range from 298 K to 523 K and does not provide any uncertainty specification. Therefore, these data were applied to the fit only with a small weight in order to model the high-temperature region. Excluding the critical regime, gaseous and supercritical data of Golubev [31] are reproduced within 7.4 % except for one outlier.

As a result, the uncertainty of values calculated with the present equation for temperatures above 423 K is higher as for lower temperatures. Since data of Carmichael et al. [29] deviate by up to 4.3 % at T = 478 K and data of Golubev [31] deviate by up to 6.4 % at T = 523 K, the uncertainty of the present equation is estimated to 6 % for temperatures above 423 K. For a reliable statement, additional measurements are required.

4.3 Critical Region

An overview of deviations of viscosity data in the critical region from values calculated with the present equation is illustrated in Fig. 8. The dataset of Wilhelm and Vogel [28] was chosen for the development of the present equation, see Sect. 4.2. The authors conducted measurements in the critical region at T = 373 K as well as T = 398 K, which are highlighted in green in Fig. 8. Both isotherms are reproduced within 0.25 % except for the data close to the critical pressure pc = 4.2512 MPa. Except for four of 40 data points, the data are well represented within the specified uncertainty of 3 % (AARD = 1.2 %).

Fig. 8
figure 8

Percentage deviations of selected viscosity data from values calculated with the present equation in the critical region (361 K < T < 405 K). The complete isotherms with near-critical densities (3.5 mol·dm−3 ≤ \(\rho\)  ≤ 7 mol·dm−3) are shown. Note that the scale of the y-axis is linear in the white area and logarithmic in the gray shaded area

Full size image

The stated experimental uncertainty of 3 % of the data of Wilhelm and Vogel [28] are assumed to be too pessimistic here. Therefore, the uncertainty of the present equation in the critical region is estimated to 0.5 % except at the critical pressure where deviations are higher.

Seibt et al. [27] measured viscosity at T = 373 K. The specified uncertainty in the near-critical region of 0.68 % given by the authors cannot be reflected by the present equation, because the data differ from those of Wilhelm and Vogel [28], which were used for the fit. The maximum deviation is 4.1 % and the AARD in the critical region is 2.9 %. Figure 8 shows a bump in the course of this isotherm. It has to be considered that the authors point out a possible error due to an influence of convection at T = 373 K in the critical region.

4.4 Liquid Phase

For the liquid phase, 13 datasets are observed. Percentage deviations of selected experimental datasets from values calculated with the present equation are illustrated in Fig. 9. To cover the whole temperature range in the liquid phase, the datasets of Diller [30], Huang et al. [32], and Starling et al. [33] were used for the development of the present equation. Other datasets were not included into the fitting process due to higher uncertainties when comparing with the aforementioned datasets.

Fig. 9
figure 9

Percentage deviations of selected viscosity data in the liquid phase from values calculated with the present equation. The phase boundary is marked according to the lower temperature limit of a subplot

Full size image

Diller [30] conducted measurements with an oscillating-quartz crystal viscometer in a temperature range from 90 K to 140 K as well as one isotherm at T = 299 K. The author reports an accuracy of 2 %, which is adopted as expanded uncertainty (k = 2) here. It is not possible to reproduce all data points within this uncertainty with the present equation. The data exhibit a significant scatter (see Fig. 9) and eight out of 84 data points exceed this uncertainty with a maximum deviation of 3.1 % resulting in an overall AARD of 0.9 %. However, there are some outliers in the dataset. For example, the measured viscosities at T = 90 K are only slightly different for 27.4 MPa and 24.9 MPa: 10 215 μPa·s vs. 10 121 μPa·s. A further reduction in pressure from 24.9 MPa to 24.6 MPa leads to a significant smaller viscosity: 10 121 μPa·s vs. 9866.9 μPa·s. This discrepancy cannot be explained by a experimental uncertainty of 2 %. Excluding such outliers from the datasets, most of the data are reproduced within the stated uncertainty. As for some other literature data, Vogel and Herrmann [21] re-evaluated the experimental uncertainty based on the measurement procedure and assume a standard uncertainty of 2.5 % for Diller [30]. With an expanded uncertainty of 5 % (k = 2), deviations from the present equation are well within this range.

Experimental measurements of Huang et al. [32] were carried out with a falling body viscometer in a temperature range from 173 K to 273 K. The dataset deviates by up to 1.5 % from the present equation with an AARD of 0.46 %. Since there is no information on the experimental uncertainty of the dataset in the publication of Huang et al. [32], no conclusions can be drawn about the uncertainty of the present equation in this region. Nevertheless, Vogel and Herrmann [21] also estimate an expanded uncertainty of 5 % for the data of Huang et al. [32]. The deviations from the present equation are well within this uncertainty.

Starling et al. [33] measured viscosity data in the liquid phase in a temperature range from 311 K to 361 K. The data points deviate by up to 1.6 % with an AARD of 0.43 %. Eleven out of 51 data points exceed an uncertainty of 0.5 % specified by the authors. However, the uncertainty of the dataset has to be higher than 0.5 % as discussed in Sect. 4.2. Since no better data are available, they were nevertheless included with a small weight in the fitting procedure.

In summary, the three datasets [30, 32, 33] cannot be reproduced within the uncertainty specified by the authors. However, an expanded uncertainty of 5 % adopted of Vogel and Hermann [21] is clearly too pessimistic. Therefore, uncertainties for the present equation in the liquid state are based on average deviations of the majority of experimental data from the present equation. It is estimated to 3 % for temperatures up to 170 K and 1.5 % for higher temperatures.

In the saturated liquid phase, two datasets are available, which are presented in Fig. 10. For the fitting procedure, the dataset of Diller [30] was chosen, who carried out measurements for temperatures between 90 K and 300 K. Here, all data points are reproduced within the uncertainty of 2 %. Lipkin et al. [44] also conducted experimental measurements with a capillary viscometer in a temperature range from 200 K to 289 K. The authors report an uncertainty of 2 %. However, the dataset deviates in a range from 4.3 % to 11 % from values calculated with the present equation. This systematic offset to the present equation as well as to the dataset of Diller [30] is visible in Fig. 10. In comparison to the dataset of Lipkin et al. [44], the experimental data of Diller [30] match well with the experimental data in the homogenous liquid phase. Thus, the uncertainty of the present equation in the saturated liquid phase is estimated to 2 % based on the data of Diller [30].

Fig. 10
figure 10

Percentage deviations of selected viscosity data at vapor pressure from values calculated with the present equation

Full size image

5 Uncertainty of the Present Equation

The expanded uncertainty (k = 2) of dynamic viscosity values calculated with the present equation is estimated in the liquid phase to 3 % for low temperatures up to 170 K and 1.5 % for higher temperatures as well as 2 % in the saturated liquid phase. In the gaseous and supercritical phases, the uncertainty is estimated to 0.25 % for a temperature range from 270 K to 420 K. For temperatures above 420 K, the uncertainty may increase up to 6 %. However, additional measurements are required for a reliable statement. For temperatures below 270 K in the gaseous phase, no uncertainty can be given due to missing experimental data. In the critical region, the uncertainty is estimated to 0.5 % except at the critical pressure where deviations are higher.

6 Extrapolation

In order to evaluate the quality of the present equation, the extrapolation behavior must be considered, in addition to the reproduction of experimental data. In Fig. 11, dynamic viscosity values calculated with the present equation along isotherms and isobars are illustrated over a wide density and temperature range, respectively. There is no overlapping of any isobar. Moreover, the course of the isotherms and isobars is smooth and no bumps occur. However, the course of the isotherms at very high densities (\(\rho\) > 3\({\rho }_{\mathrm{c}}\)) is striking. When evaluating other viscosity equations from the literature, different behaviors were found. For example, the equations for propane [21] and ethylene [54] show a monotonically increasing curve, while the equations for methane [55] and nitrogen [56] show a decreasing curve. The region in which this behavior occurs is already in the extrapolation range; under real conditions in the solid region. Therefore, no experimental data can be used to verify any course. Thus, this issue remains subject to future research.

Fig. 11
figure 11

\(\eta\),T-diagram along isobars up to 200 MPa (left), \(\eta\),\(\rho\)-diagram along isotherms up to 780 K (right) calculated with the present equation

Full size image

7 Conclusion

A new equation for the dynamic viscosity of propane as a function of temperature and density was developed. The dilute-gas contribution was adopted from Vogel and Herrmann [21]. The residual part is an empirical approach designed following the example of thermodynamic Helmholtz equations of state. It consists of four polynomial, two exponential, and five Gaussian bell-shaped terms. Special attention was paid to the ability of the mathematical structure to be easily applied in mixture models. Mathematical functions with poles were, therefore, avoided and proper extrapolation behavior was ensured. Based on the experimental datasets available in the literature, the equation is valid from 90 K to 525 K with a maximum pressure of 145 MPa. Most data are represented within the corresponding experimental uncertainties. The quality of the equation corresponds to that of the current reference equation of Vogel and Hermann [21] and could even be slightly improved in some places by a different selection of the data included in the fit.