Abstract
The present study provides a strategy for the determination of the viscosity and surface tension of high-viscosity fluids in the form of ionic liquids (ILs) at equilibrium conditions by combining surface light scattering (SLS) and the pendant-drop (PD) method within one experimental setup. Through the study of the same sample under identical conditions by both methods inside a closed system, the surface tension determined via the PD method can be directly used to evaluate the dynamics of surface fluctuations of ILs with an overdamped behavior probed by SLS for accessing their viscosity. In connection with the SLS experiments, variations in the applied detection geometries in reflection and transmission direction and in the probed wave vectors down to relatively small values were also addressed. The reliability and self-consistency of SLS and the PD method applied within the same sample cell has been proven by investigating the reference fluids tris(2-ethylhexyl) trimellitate (TOTM) and n-dodecane featuring relatively high and low viscosities. For the two studied model ILs of opaque to non-transparent color, i.e., the hydrophobic 1-methyl-3-octylimidazolium hexafluorophosphate ([OMIM][PF6]) and the hydrophilic 1,3-bis(2-(2-methoxyethoxy)ethyl)imidazolium iodide ([(mPEG2)2Im]I), the combination of PD measurements and SLS experiments in reflection direction performed at ambient pressure between (303 and 373) K allowed access to the viscosity and surface tension with typical relative expanded uncertainties of (4 and 2) %. These results agree well with own viscosity data from capillary viscometry and experimental data in the literature, demonstrating the performance of the novel approach for the contactless in-situ measurement of viscosity and surface tension of fluids with relatively high-viscosity such as ILs.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Ionic liquids (ILs) are molten salts with a melting point below 100 °C and are considered to be an interesting class of working fluids in chemistry as well as in chemical and energy engineering [1, 2]. Given the huge number of possible cation–anion combinations [3], ILs can be tailored to many different technological applications. Here, ILs can serve as, e.g., electrolytes [2, 4], fluids for heat transfer and energy storage [5, 6], gas separation media [7, 8], and solvents for catalytic processes [2, 9]. In the latter application, the concept of Supported Ionic Liquid Phase (SILP) catalysis has shown to be very promising [10]. In SILP catalysis, a thin IL film containing a dissolved catalyst – usually a metal coordination complex – is dispersed over a large inner surface area of porous solid support. By this, the SILP technology combines the advantages of homogeneous catalysis, such as uniformity of the catalytic sites and selectivity control, with the ease of use of heterogeneous catalysis.
To design and optimize processes and apparatuses involving ILs, accurate information on the thermophysical properties of ILs and their mixtures with other compounds is required. This holds especially for the two properties of interest in the present study, i.e., the dynamic shear viscosity of the liquid phase ηL and the surface tension between the liquid and the gas phase σ. In terms of the aforementioned SILP concept, the surface tension affects, e.g., wetting on the solid support and the size of dispersed gas bubbles, while the viscosity is a predominant parameter for the characterization of heat and mass transfer in the liquid layer. Besides their relevance in process design, reliable data for viscosity and surface tension are also needed to understand the characteristics of ILs from a physicochemical point of view and to develop corresponding fluid property models. The accurate measurement of viscosity and surface tension of ILs is a challenging task. Although considerable work has gone into the experimental investigation of ILs over the last few decades, a sound characterization of their properties including ηL and σ is often not fully given. Large discrepancies between published data for viscosity and surface tension, as observed in Refs. [11, 12], seem to be related to the improper use of experimental techniques and/or to the ill-defined sample preparation or characterization.
Among the conventional techniques for the measurement of surface tension [13], the pendant-drop method as a static technique is one of the most suitable ones and is commonly applied in literature for ILs; see, e.g., Refs. [14,15,16,17]. Here, the analysis of σ is based on the comparison between the recorded shape of an axisymmetric PD and its theoretical description by the Young–Laplace equation [13]. In our previous studies [14, 18, 19], the PD method was used to determine σ for ILs and IL mixtures as a function of temperature with typical expanded uncertainties (coverage factor k = 2) of 2 %. An alternative to conventional methods is surface light scattering (SLS). This technique probes the dynamics of thermal surface fluctuations at phase boundaries in a contactless way in macroscopic thermodynamic equilibrium and enables the absolute determination of viscosity and/or surface tension [20, 21]. Besides its use within thermophysical property research [21], SLS has been applied to characterize interfaces of complex fluids including IL-cosolvent mixtures [22], surfaces covered by adsorbed layers [20], and multiphase systems [23]. From the study of the dynamics of the surface fluctuations with a defined wave vector that is reflected by the temporal behavior of the scattered light intensity, viscosity or surface tension and – for ILs with relatively low-viscosity – both properties are accessible with typical uncertainties (k = 2) of 3 % and below; see, e.g., Refs. [16, 21, 23,24,25].
For fluids of relatively large viscosity, as is often the case for ILs, the determination of viscosity by SLS requires information about the surface tension as an input parameter. For this, surface tension measurements by another technique, e.g., the PD method, as used in our previous works, need to be performed. To accurately determine the viscosity by SLS, it has to be guaranteed that the fluid sample and, in particular, its surface probed during separate SLS and PD experiments are identical. If this is not valid, it may happen that the surface tension determined by the PD method is different from that present in the SLS experiment, which in turn would lead to systematically wrong values for the obtained viscosity of the bulk liquid phase. To suppress the possibility of such a scenario, it is the motivation for the present study to combine SLS and the PD method within a single setup by performing experiments on the same fluid sample within one sample cell under identical conditions, i.e., temperature, pressure, and surrounding gas atmosphere. For sufficiently low viscosities achievable by, e.g., studying ILs at higher temperatures, it is possible to simultaneously determine viscosity and surface tension by SLS. Thus, the new concept offers the opportunity to compare the SLS results for σ with those determined by the PD method, which will also be addressed in the current work.
In the following, our new approach of combining the two surface-analyzing techniques, i.e., the PD method and SLS studying the fluid surfaces on a macroscopic and microscopic scale, respectively, is shown, which has the objective of a quasi-simultaneous determination of viscosity and surface tension of high-viscosity ILs. In the first section, the experiments are described, which includes the sample preparation, a brief background on SLS and the PD method, details to the combined experimental setup and measurement procedure, and the data evaluation, in particular for the SLS experiments over a broad range of probed wave vectors. Due to the opaque or non-transparent color of the two studied ILs potentially relevant for SILP technology, the SLS measurements had to be performed in reflection direction. In the Results and Discussion section, the new methodology is validated by investigating ηL and σ of two reference fluids of relatively high- and low-viscosity, before the data for viscosity and surface tension of the two model ILs are shown as a function of temperature. Here, also a comparison with own viscosity results from capillary viscometry and available experimental data in the literature is carried out.
2 Experimental
2.1 Materials and Sample Preparation
The chemical structures of the two studied imidazolium-based ILs 1-methyl-3-octylimidazolium hexafluorophosphate ([OMIM][PF6], molar mass M = 340.29 g·mol−1) and 1,3-bis(2-(2-methoxyethoxy)ethyl)imidazolium iodide ([(mPEG2)2Im]I, M = 400.26 g·mol−1), which is based upon methylated polyethylene glycol chains (mPEGn) with a repeating unit n = 2, are shown in Fig. 1. While [OMIM][PF6] purchased from Iolitec showed a weak yellowish color, [(mPEG2)2Im]I was self-synthesized according to a procedure described in literature [19] and features an intense yellow to brown color. In addition, the four colorless reference liquids, namely, n-dodecane (n-C12H26) and toluene provided by Merck KGaA, tris(2-ethylhexyl) trimellitate (TOTM) purchased from Sigma-Aldrich, and deionized water (H2O) obtained from a Milli-Q system, were investigated by PD measurements and, in case of n-C12H26 and TOTM, additionally by SLS since they allow to cover a broad range of surface tensions and dynamic viscosities. Prior to this, the reference fluids n-dodecane, toluene, and TOTM were filtered with a polytetrafluoroethylene filter having pore sizes of (0.45 and 0.2) µm). In addition, samples of [OMIM][PF6], [(mPEG2)2Im]I, n-C12H26, and TOTM, which were investigated by combined SLS-PD measurements, were evacuated at a temperature T of about 295 K at a pressure p below 5 Pa over a period of at least 4 h via an oil-sealed vacuum pump. In case of the three high-viscosity liquids TOTM, [OMIM][PF6], and [(mPEG2)2Im]I, the water contents of the degassed samples were analyzed by Karl–Fischer coulometric titration before and after the experiments. Details to the used chemicals including their purities and the water contents for the IL and TOTM samples are given in Table S1 of the Supporting Information. After the purification treatment, all liquid samples were stored inside glass flasks under an argon (Ar) inert gas atmosphere. Ar was also used as inert atmosphere for the SLS and PD measurements within the newly designed sample cell and peripheral setup.
2.2 Experimental Methods and Setup
In the following, a brief description of the principles behind the PD method and SLS applied in the present work is provided. For more details on the techniques, the reader is referred to the corresponding literature cited. Then, the setup combining SLS and the PD method is explained and its features are elaborated. Finally, relevant details to the data evaluation, especially for the SLS experiments, are addressed. A description of the additional measurements by capillary viscometry (CV) on [OMIM][PF6] is given in section S2 of the Supporting Information.
2.2.1 Theoretical Background
The PD method was applied for the determination of the gas–liquid surface tension σ of the two ILs [OMIM][PF6] and [(mPEG2)2Im]I as well as of the reference fluids H2O, toluene, n-C12H26, and TOTM used for validation purposes. The principle of this static method is the evaluation of the axisymmetric shape of a liquid PD that is surrounded by a gas phase and exposed to the gravitational field [13]. Under equilibrium conditions, the shape is defined by the competition between the gravitational force acting in the same direction as the gravitational field, the buoyancy force, and the capillary force related to σ. The final working equation, also known as Young–Laplace (YL) equation [13], gives the theoretical description of the droplet profile, which is compared with the corresponding contour acquired experimentally from images of the droplet. Besides the geometry of the PD contour in the pixel scale evaluated by axisymmetric drop shape analysis (ADSA) [26] and conversion to the metric scale via a calibration procedure, further required input parameters in the YL equation are the densities of the liquid (ρL) and gas (ρG) phase. σ is then determined from the parameters used to represent the theoretical droplet contour with the lowest deviation to the experimental one. Specific details about the image processing and the evaluation of the YL equation are given later in Sect. 2.2.2.
Surface light scattering (SLS) was used for the determination of the liquid viscosity ηL of [OMIM][PF6], [(mPEG2)2Im]I, and TOTM as well as the simultaneous determination of ηL and σ of [(mPEG2)2Im]I at the largest studied T = 373 K and of n-C12H26. Fundamentals of the principles of the SLS method, which are only briefly summarized below, can be found in the literature [20, 21, 27, 28]. With SLS, the dynamics of thermally excited surface fluctuations at the phase boundary between two fluid phases is probed at macroscopic thermodynamic equilibrium, i.e., without applying any external gradient or force. The dynamics of these fluctuations, having typical wavelengths between (0.1 and 1000) µm as well as amplitudes on the range of nanometers [20], is imprinted in the light scattered from the interface and can be accessed by photon correlation spectroscopy. Here, the time-dependent intensity of the scattered light is recorded by photo-sensitive detectors and further processed in order to calculate the normalized correlation function (CF).
The temporal behavior of the probed surface fluctuation with a specified wavelength or wave vector q is characterized by its propagation frequency ωq and mean lifetime or decay time τC, which is the inverse of the damping Γ. Depending on the dimensionless capillary number Y = (σ·ρL)/(4 ηL2·q) for a fluid neglecting its gas or vapor properties, one can either find an overdamped or oscillatory behavior. The latter behavior (Y > 0.145) is associated with fluids of relatively small viscosities and/or large surface tensions, giving rise to a propagation of the surface fluctuations (ωq > 0). For fluids of relatively large viscosities and/or small surface tensions (Y < 0.145), the surface fluctuations are overdamped and do not propagate (ωq = 0). In either case, the dynamics of hydrodynamic surface fluctuations is described by their dispersion relation for the phase boundary between two fluid phases, showing no anomalous surface properties such as monolayers or viscoelastic effects [20, 28]. Besides the dynamics of the surface fluctuations probed by SLS, i.e., ωq and τC, this dispersion relation includes the thermophysical properties density of the liquid (ρL) and gas (ρG) phase, viscosity of the liquid (ηL) and gas (ηG) phase, and surface tension σ. For known values of ρL, ρG, and ηG, a simultaneous determination of ηL and σ is possible in the oscillatory case, while the overdamped case gives typically only access to the ratio of ηL to σ. In the present work, it is the main aim to determine σ via the PD method for evaluating ηL from overdamped SLS signals.
2.2.2 Description of the Combined SLS-PD Setup
In this subsection, our new setup and sample cell combining SLS and the PD method are described. Here, the SLS-related part is based on the setup that has been described in Ref. [29]. While this reference provides details on the different detection schemes for performing SLS in reflection direction as well as their advantages and drawbacks, only a brief recap is given in this work. Here, the focus lies on the new sample cell specifically designed for the combined SLS-PD experiments, the periphery, and the specific features of the updated apparatus which includes additional instrumentation for applying the PD method. Details to the latter method and its experimental realization adapted for the current setup are given by Jander et al. [30].
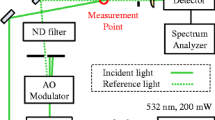
Figure 2 gives a schematic representation of the apparatus, which can be distinguished into two main parts. The left part represents the periphery enclosure with the gas-manifold required for preconditioning the sample, while the right part as measurement enclosure mainly consists of the sample cell for combined SLS-PD measurements including a connected sample vessel. The sample cell is made of hydrogen-resistant stainless-steel designed for pressures p up to 10 MPa and temperatures T up to 523 K, has a cylindrical cavity with an inner diameter of 70 mm and a depth of 40 mm (i.e., volume of about 150 cm3), and is equipped with six optical accesses. Two of them are placed longitudinally at the top or bottom, and the other four are positioned radially in pitch circles of 90°. These windows, which have a surface roughness smaller than λ/10 and are sealed via Kalrez o-rings against the ambience, serve as optical accesses to perform SLS measurements in transmission and reflection direction under different detections geometries as well as PD measurements; cf. discussion later in connection with Fig. 3. In addition, a stainless-steel capillary is inserted into the sample cell that provides the supply of the PDs formed at the tip of the capillary and observed in the horizontal plane of the cell. The inner and outer diameter of the used capillary is (1.00 and 1.59) mm according to specifications from the supplier VICI.
Optical and electronic arrangement used for the combined PD and SLS experiments in a reflection geometry using a perpendicular (blue color) or non-perpendicular (green color) detection scheme. The additional possibility for SLS experiments in transmission geometry is not shown in the figure. Details of the used abbreviations are given in the legend and/or in the text
To control the temperature of the sample cell, resistance heating is used by mounting a heating wire around the outer surface of the cell. Three calibrated Pt-100 Ω probes with expanded (k = 2) uncertainties of 0.02 K are inserted into the main body and the inner volume of the cell; see Fig. 3. One is placed close to the heating wire in the outer cell wall and serves as a regulation sensor, while the other two are located on the bottom close to the liquid sample and in close vicinity to the PD in the gas phase. These latter two sensors agreed within 0.02 K throughout all experiments. The T values reported in the present work correspond to the average of T measured by the probe inside the gas phase during the total measurement time. The T stability was better than ± 0.006 K in all cases. To prevent condensation at the two side windows used for the PD measurements and the SLS experiments under a non-perpendicular geometry, additional resistance heating was placed around cone-shaped aluminum tubes. Resistance heating was also used for an optionally employed stainless-steal sample vessel with an inner volume of about 150 cm3. This vessel placed above the cell contains the same liquid sample as used in the sample cell and can be connected via a tube and a dosing valve to the PD-related capillary for sample supply. It allows preconditioning of the liquid close to the measurement conditions inside the sample cell at comparable T and p and will be used for future experiments in the presence of pressurized gases. For the here-present measurements at p of about 0.1 MPa, the dosing of the PDs was realized by using a gas-tight glass syringe with a volume of 10 mL that was filled with the liquid sample under investigation.
The sample cell and, in case of future high-pressure applications above 0.1 MPa, also the sample vessel are connected to the gas-manifold system shown in the left part of Fig. 2. It comprises 1/4″ and 1/16″ tubes, connectors, several diaphragm and needle valves, and a further gas buffer for gas storage. The periphery enclosure allows for evacuating the entire system by application of a vacuum pump, flushing with inert gases such as Ar, and pressurizing with the gas of interest. Furthermore, the manifold contains four manometers, two of which refer to calibrated pressure transducers for measuring p in the sample cell and the sample vessel with an expanded (k = 2) uncertainty of 5 kPa. For all studied systems, the stability for p was better than ± 2 kPa. The entire apparatus is covered by a fume hood and ventilated permanently, which is necessary as a precaution for the future experiments with flammable gases such as hydrogen.
The optical and electronic arrangement for the SLS and PD experiments can be seen in Fig. 3. In connection with the PD method that probes the PDs hanging in the gas phase inside the sample cell, the image acquisition is realized though a monochromatic CMOS camera from IDS GmbH with a resolution of 2456 × 2054 pixels. Assisted with a fixed-focus objective, a final view field of (33 × 28) mm is achieved. A translational stage is used for fine adjustment of the camera position. The PDs are illuminated from the opposite side by using a narrow bandwidth monochromatic LED with a nominal wavelength of 530 nm that allows to suppress chromatic aberration effects. In order to obtain a collimated homogeneous light source, a ground glass diffuser (D) and two plano-convex lenses (L) are used in the optical path.
The used SLS setup for performing measurements in reflection direction is modified from the configuration which has been developed in our previous work [29]. The corresponding configuration for SLS experiments in transmission direction has been detailed in Refs. [21, 31, 32]. For experiments in reflection geometry on opaque or non-transparent ILs, the applied two cases in the form of a perpendicular (P, blue lines) or non-perpendicular (NP, green lines) detection of the scattered light relative to the gas–liquid interface of the fluid is shown in Fig. 3. For this, the main beam emitted from a Nd:YVO4 laser (Coherent, Verdi-V2, single-mode operation with a wavelength λ0 = 532 nm) and focused on the interface via one lens (focal length f = 4 m) or two lenses (f = 4 m and 2 m) is guided under a specific angle of incidence ε, relative to the normal of the surface, into the cell. This guidance is realized either through the upper window (P-case, ε between about 2.5° and 3.5°) or through the side window (NP-case, ε between about 65.6° and 67.5°) into the sample cell. In comparison to the previous version, where ε was limited to about 45° due to the sample cell available at that time, the new sample cell allows to probe a broader range of ε. This could be achieved by the installation of a 1.8 m long rail onto which a high-precision rotational table with mirror for the angle adjustment with an uncertainty (k = 2) of 0.005° can be moved laterally. The scattered light is collected in reflection direction around the reflected beam at a defined scattering angle ΘS = |δ – ε|, whereby δ represents the specific angle between the direction of the scattered light and the detection direction. Here, the scattered light passes the same window as the incident light in the P-geometry, whereas in the NP-geometry it is guided through the side window opposite to the one where the incident enters. Caused by geometrical boundary conditions, ΘS can be varied between 2.5° and 3.5° for the P-geometry (since δ = 0 and, thus, ΘS = ε), while smaller ΘS values below about 2.0° are accessible for the NP-geometry. Overall, based on the adjusted values for ε, δ, and ΘS, the wave vector q of the probed fluctuations can be varied over a broad range from about 7 × 105 m−1 down to about 0.5 × 105 m−1. Details on the calculation of q for the different scattering geometries can be found in Ref. [29].
The scattered light is mixed with a frequency-unshifted reference light of much stronger intensity in order to ensure heterodyne conditions, facilitating the signal development and analysis. In the P-case, the mixing is achieved by a beam splitter positioned above the sample cell, while such device is not needed for the NP-case. This is because here the reference beam is also guided through the sample cell, where it is reflected at the gas–liquid interface and superimposed to the scattered light. The detection direction is defined by two apertures in the form of pinholes (diameter 1 mm) that are placed about 4 m apart from each other. One pinhole is closely behind the sample cell and the other is integrated into the entrance of the detection system. The latter represent two independent photomultiplier tubes (PMTs) or Avalanche photodiodes (APDs). In either case, the scattered light is guided to the two detector units by using a splitter. The outputs of the two detector units were proceeded by a single-τ correlator (ALV-LinCorr) to calculate the second-order pseudo-cross CF of the scattered light intensity g(2)(τ). To control the power and polarization of both the incident beam and the reference light, a combination of a half-wave plate (λ/2) and a polarization beam splitter (PBS) are used. For further details to the alignment of the different beams, the reader is referred to Ref. [29].
2.2.3 Experimental Procedure and Data Evaluation
With respect to the experimental procedure, the two ILs [OMIM][PF6] and [(mPEG2)2Im]I as well as the two reference systems n-dodecane and TOTM were filled into the sample cell (SLS, around 30 mL) via a syringe and into a sealed glass syringe (PD method, around 5 mL) that substitutes the sample vessel in Fig. 2. The inner volume of the sample cell was evacuated shortly, before it was flushed several times with Ar via the connection to the peripheral manifold. After the equilibration of T and p inside the sample cell, first the PD measurements and subsequently the SLS experiments were performed under an inert Ar atmosphere at p close to 0.1 MPa. This low pressure in combination with the very low solubility of the gas in liquids including ILs [33] justifies to reliably neglect the influence of Ar on the viscosity and surface tension of the studied fluids.
Prior to the PD measurements, the outer diameter of the capillary was calibrated by using a calibration ball (PMT Präzisionsmesstechnik) made of Si3N4 with a diameter of 3.0000 mm and a sphericity of better than ± 0.09 µm. This allowed to convert the droplet profiles from the pixel scale related to the camera settings to the metric scale in order to evaluate σ from the ADSA analysis performed in the pixel domain. At each thermodynamic state studied, 5 drops were generated close to their rupture from the tip of the capillary, whereby 5 pictures were recorded for each of these droplets. Before their recording, the waiting time was about 10 min to ensure equilibrium conditions. The evaluation of σ on grounds of the YL equation was carried out with a self-developed algorithm described by Kerscher et al. [34]. The required sources for ρL and ρG of the studied fluids are provided in section S3 of the Supporting Information. The final values for σ refer to the mean averages of the σ values associated to the in total 25 pictures. In line with our previous works, the expanded (k = 2) uncertainty of the present surface tension data can be specified with 2 %. This value reasonably accounts for the uncertainties introduced by the calibration procedure and the input parameters as well as the reproducibility within the individual σ values. The stated uncertainty can be further rationalized by considering the agreement of our measurements results for the reference fluids water, toluene, and n-dodecane, which were obtained from sole PD measurements in the new sample cell at selected temperatures prior to the measurement procedure. The results from these investigations and those from the combined SLS-PD measurements are given later.
With respect to the SLS investigations, measurements were performed at equilibrium conditions in the reflection geometry in the perpendicular (R-P) and/or non-perpendicular (R-NP) configuration. The use of both configurations served not only to cover a broad range of wave vectors, but also to compare the signal qualities and corresponding measurements results for the dynamics of surface fluctuations as well as the thermophysical properties of interest. For an additional comparison, SLS has also been applied in transmission direction for the transparent reference fluids n-dodecane and TOTM. In this configuration detailed in Refs. [21, 31], the scattered light is detected in the forward direction near the refracted light and perpendicular to the fluid interface (T-P). Such a detection scheme is beneficial in consideration of stability issues and the increased light scattering intensity in comparison to a detection in the reflection direction, yet it is only applicable for transparent fluids. In all cases, a heterodyne detection scheme was applied, where reference light of much larger intensity was superimposed to the light scattered from the fluid interface. To suppress falsifying laser-heating and thermal-lensing effects on the studied IL samples, preliminary SLS investigations in R-P-geometry performed for [OMIM][PF6] at 333 K and q = 6.2 × 105 m−1 revealed agreement for the evaluated liquid viscosity ηL within combined uncertainties for applied powers of the incident laser light impinging the sample between (20 and 70) mW. The same statement can also be given for [(mPEG2)2Im]I in R-NP-geometry studied at 343 K and q = 0.95 × 105 m−1 varying the laser power from (15 to 40) mW. Above the maximum values for both cases, a weak decrease in ηL was found, which implies a locally larger T in the scattering volume at the interface than in the surrounding bulk liquid. As a precaution, the power of the incident light was kept always below 15 mW for the non-transparent [(mPEG2)2Im]I and below 45 mW for the weakly opaque IL [OMIM][PF6].
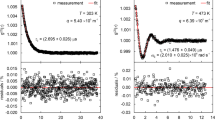
For comparison purposes, Fig. 4 shows two exemplary normalized CFs obtained from SLS experiments on the IL [OMIM][PF6] in reflection direction using a perpendicular (a) and non-perpendicular (b) detection geometry at 353.15 K. The contribution of a long-time signal, which originates from, e.g., mechanical vibrations, and was mainly found for signals covering a relatively large τ range, could be represented by a linear or quadratic term and is already subtracted from the CF in Fig. 4b. For a sufficiently low laser power of the incident beam of (45 and 12) mW employed for the R-P and R-NP-case, respectively, an about four times larger q of 5.8 × 105 m−1 was adjusted in Fig. 4a compared to Fig. 4b (q = 1.3 × 105 m−1). In both cases, an overdamped signal reflecting the overdamped behavior of the probed surface fluctuations on fluids with a relatively large viscosity was found, which could be described by the theoretical expression [20, 21]
with the experimental constants a and b. In the simplified version given by Eq. 1, only the slower mode of the theoretically two present, exponentially decaying modes was evaluated for the determination of the decay time τC. The faster mode with a smaller decay time than τC appears only for conditions close to the critical damping (Y ≈ 0.145) and was disregarded adequately by omitting the first few measured data channels of the CF based on an approach detailed in Ref. [35]. A nonlinear regression based on the Levenberg–Marquardt algorithm was carried out to represent the measured CFs in Fig. 4 and in all other cases by fit. Despite the relatively small laser power applied, a reasonable signal with an expanded (k = 2) uncertainty for τC of 0.9 % is obtained for the measurement in the R-P-geometry (ε = 2.8°) at a relatively large q after a measurement time of about 11 min.
To probe also distinctly smaller q, which are associated with an increase in the scattered light intensity according to a 1/q2 dependency [35], the R-NP detection scheme was used for the signal in Fig. 3b associated with ε = 66.5°. Here, for a comparable measurement time of 8 min, the signal quality is slightly improved compared to Fig. 4a, as can be deduced from the lower uncertainty (k = 2) for τC of 0.5 %. In both presented signals and for all other measurements in the overdamped case, the residual plots exemplarily shown in the lower part of Fig. 4 are free of systematics. The fact that the measurement signals recorded at relatively small q values on the order of 1 × 105 m−1, as given in Fig. 3b, are described adequately by the theory already indicates that the increasing relative spread in the wave vector with decreasing q [27, 29] appears to have no significant effect on overdamped SLS signals, which has also been stated, e.g., in literature [20, 36]. Further details to this issue will be given in the Results and Discussion section.
For all studied fluids, SLS measurements were performed in a stepwise manner from low to high T. While in case of the reference fluids n-dodecane and toluene only two selected temperatures of (323 and 373 K) were probed for validation purposes, a finer temperature variation from (303 to 373) K for [(mPEG2)2Im]I and from (303 to 353) K for [OMIM][PF6] was carried out regarding the two model ILs. Despite the generally slightly lower signal quality obtained from experiments with the R-P-geometry in contrast to the R-NP one, the former was used for the investigations on [(mPEG2)2Im]I from (303 to 353) K because the liquid level in the sample cell was not high enough to employ the non-perpendicular scheme. The latter could only be used at the largest T of (353 and 373) K due to the sufficiently large expansion of the liquid phase with increasing T. In the case of [OMIM][PF6], a larger amount of sample was available, which is why the R-NP-geometry was mainly applied here between (303 and 353) K. Only for comparison as shown in Fig. 3, the R-P-geometry was also applied at 353 K. For the overlapping T states, the evaluated viscosity results of both ILs agreed within the single uncertainty; cf. exemplarily the results shown in Fig. 4. The data for ηL from repetition measurements performed at 353 K for both ILs after investigations at the highest T agreed within combined uncertainties with the original data.
An overdamped behavior (Y > 0.145) associated with relatively large fluid viscosities was found for all measurements on TOTM and both ILs, with the exception of the highest studied T of 373 K for [(mPEG2)2Im]I. For this state and for all states investigated with the low-viscosity fluid n-dodecane, an oscillatory behavior of surface fluctuations (Y > 0.145) appeared, which is represented by the decay time τC and the frequency ωq. To access these two dynamical properties, the representation of the measured signals by a damped oscillation [20, 21] could be used at sufficiently large q values beyond (1.3 and 1.7)·105 m−1 for (323 and 373) K, respectively. Only for smaller q, the influence of line-broadening effects caused by the increasing relative spread in q was observed, which agrees well with the observations made by Koller et al. [29] on the reference fluid toluene. In the present work, these effects could be accounted for reasonably by inclusion of the commonly employed empirical fit parameter β in the damped-oscillator model. For a detailed discussion about line-broadening effects on SLS experiments in the oscillatory case, the reader is referred to Refs. [29, 37].
To determine ηL in the overdamped case or both ηL and σ in the oscillatory case by SLS in an accurate way, the full solution of the dispersion relation D(ηL, ηG, ρL, ρG, σ, τC = Γ−1, ωq, q) for hydrodynamic surface fluctuations at the interface between a liquid (Index L) and a gas (Index G) phase was considered [20, 28]. Information about the sources for ρL, ρG, and ηG for the studied fluids are provided in section S3 of the Supporting Information. For each thermodynamic state, between three and, in most cases, six individual experiments related to different q were conducted and used for the determination of ηL or ηL and σ by unweighted averaging of the different results. Since the overdamped case gives only access to the ratio ηL/σ, knowledge on σ is needed to access ηL. Therefore, the T-dependent correlation for σ, Eq. 2, obtained by the present PD measurements with a relative expanded (k = 2) uncertainty of 2 % served as an input. Error propagation schemes were applied to calculate the measurement uncertainties for ηL in the overdamped case, considering the uncertainties of Γ, q, σ, and ηL [35, 38], as well as for ηL and σ in the oscillatory case, accounting for the reproducibility of the individual measurements and the uncertainties of the input data for ρL, ρG, and ηG [31, 32]. For the investigated ILs, the relative expanded (k = 2) uncertainties for ηL range from (2.4 to 4.0) % for [OMIM][PF6] and from (4.6 to 9.7) % for [(mPEG2)2Im]I. The larger uncertainties for the latter non-transparent IL are mainly related to the larger uncertainties for Γ caused by the lower signal quality as a result of the application of distinctly lower laser powers as well as by the close vicinity to the critical damping at the largest T investigated.
Overall, the measurement time for the combined SLS-PD experiments is between about (90 and 120) min for a single thermodynamic state.
3 Results and Discussion
First, the PD and SLS measurement results for the reference fluids water, toluene, n-dodecane, and TOTM will be presented and discussed, with the intension of validating the feasibility of the new combined setup. Thereafter, for the two model ILs, the T-dependent experimental results for the surface tension obtained by the PD method and, in a single case, also from SLS as well as for the liquid dynamic viscosity determined by SLS are shown and discussed. For both the ILs and the reference fluids, a comparison is made between the results determined in this work from different measurement techniques and the recommended correlations or available data from literature.
3.1 Reference Fluids
3.1.1 Check of PD Method
In a first step, the functionality of the PD method integrated into the combined PD-SLS setup has been checked by studying the fluids H2O, toluene, and n-C12H26 at selected T between (303 and 373) K to cover a broad range for σ. The results measured solely via the PD method are compared with reference data for water [39], toluene [40], and n-dodecane [40] recommended by the REFPROP database [41] in the form of a deviation plot, as can be seen in Fig. S2 of the Supporting Information. The measured values show agreement with the reference data mostly within the experimental uncertainty of 2 % and always within combined uncertainties, which validates the PD tensiometer.
3.1.2 SLS – Hydrodynamic Theory
Before discussing the measurement results for ηL and σ, it is of importance to guarantee that the hydrodynamic theory is reflected by the SLS experiments for both the oscillatory case and, particularly relevant here, the overdamped case over the entire range of probed wave vectors q down to relatively small values that are often required for the study of non-transparent fluids. For this task, the dispersion relation [20, 28] was also applied in a reverse manner, where reference values for ηL and σ detailed in the captions of Figs. 5 and 6 were used to calculate the theoretical values for Γ in the overdamped case or Γ and ωq in the oscillatory case. The latter holds for n-dodecane, for which the theoretical values for damping and frequency (lines) are compared with the experimental results (markers) as a function of the adjusted q in Fig. 5. Here, SLS measurements were carried out in the R-P, R-NP, and T-P geometries. For a broad q range from (6.6 down to 0.84) × 105 m−1, the measured values for the dynamics of the surface fluctuations at (323 and 373) K agree with each other at overlapping q for the T-P and R-P cases and with the theory within the experimental uncertainties, resulting in an average absolute relative deviation (AARD) of 2.6 % for Γ and 1.5 % for ωq. The present results are in accordance with our findings from SLS measurements on toluene [29], featuring similar ηL and σ values as n-C12H26, and show that line-broadening effects on the SLS signals are not significant for q down to about (1.3 and 1.7) × 105 m−1 at (323 and 373) K, respectively. For smaller q down to about 0.9 × 105 m−1, these effects can be represented adequately by including the line-broadening parameter β in the fit model, even with respect to Γ that is much more sensitive than ωq.
Damping Γ (upper part) and frequency ωq (lower part) of surface fluctuations of n-dodecane as a function of the adjusted wave vector q obtained from SLS measurements with different detection geometries at (323 or 373) K (markers according to legend) in comparison with the theoretical calculations (lines) based on exact solution of dispersion relation [20, 28]. For the application of the latter, input values for ηL and σ were employed from the REFPROP database [41]
Damping Γ of surface fluctuations of TOTM as a function of the adjusted wave vector q obtained from SLS measurements with different detection geometries at (313 or 323) K (markers according to legend) in comparison with the theoretical calculations (lines) based on exact solution of dispersion relation [20, 28]. For the application of the latter, input values for ηL and σ were employed from the correlations developed from separate SLS and PD measurements in Ref. [35]
For the high-viscosity reference fluid TOTM, the variation of the measured damping values Γ at (313 and 323) K using the R-P, R-NP, and T-P configurations is illustrated is Fig. 6 in dependence on q and compared with the theoretical values based on the correlations for ηL and σ in Ref. [35]. In this overdamped case, the experimental results match for different scattering configurations and agree with the theory over the entire range of q between (0.70 and 7.0) × 105 m−1. This is reflected by the AARD of all measured data for Γ from the predictions with a value of 0.19 %. The results in Fig. 6 for TOTM suggest that line-broadening effects are insignificant for overdamped SLS signals in the range of relatively small q, a conclusion which was also observed by Byrne and Earnshaw [36] in their investigations on glycerol and has been stated by Langevin [20]. This means that probing of small wave vectors on the order of 1 × 10–5 m−1 still allows for an accurate determination of viscosity in the overdamped case, as it will be addressed in the following.
3.1.3 Viscosity and Surface Tension
Based on the results for the dynamics of the surface fluctuations in Figs. 5 and 6, the resulting SLS values for ηL and σ of n-dodecane and for ηL of TOTM are shown in left and right part of Fig. 7, respectively, together with the corresponding σ data obtained by the PD method in the combined SLS-PD setup and sample cell. In this bar diagram, the different bars represent the relative deviations of the experimental data at the two selected T from the same reference correlations that were used as input sources in the calculations of the theoretical lines in Figs. 5 and 6. For the SLS results, a categorization with respect to the three different configurations R-P, R-NP, and T-P applied for varying q ranges according to Figs. 5 and 6 is shown. Here, the individual data related to the measurements at different q are the unweighted averages, while the error bars display the corresponding average expanded (k = 2) uncertainties. In the case of n-dodecane in Fig. 7a, the SLS values for ηL and σ as well as the PD data for σ coincide with the references, mostly within combined uncertainties. Importantly, the good agreement of the σ values obtained independently from SLS and the PD method indicate that the fluid surfaces studied by the two techniques are the same. This is a necessary boundary condition for a reliable evaluation of ηL of high-viscosity fluids including ILs by SLS, as in this case the knowledge of σ determined by, e.g., the PD method in the present work, is inevitably required.
Relative deviations of the results for the surface tension (upper part) and viscosity (lower part) of n-C12H26 (a) and TOTM (b) at selected T obtained by the PD method and by SLS using different detection geometries from correlations for σref or ηL,ref for n-C12H26 [40, 42] implemented in REFPROP [41] and for TOTM developed in Ref. [35]. The expanded (k = 2) uncertainties are indicated by the error bars for the present data and by the dashed lines for the reference values
3.2 Ionic Liquids
3.2.1 SLS – Hydrodynamic Theory
In the following, the application of the developed combined SLS-PD setup is demonstrated for the investigation of the two high-viscosity ILs [OMIM][PF6] and [(mPEG2)2Im]I. First, similar to the analysis performed for the two reference fluids in Figs. 5 and 6, a check of the hydrodynamic theory in connection with the SLS experiments is carried out for both ILs at selected T. Figure 8 depicts the q-dependency of the measured values for Γ for the recorded overdamped signals applying the R-P and R-NP configurations, in comparison with theoretical dampings calculated from the hydrodynamic theory. For these, input quantities for ηL and σ are taken from the present CV and PD measurements in the case of [OMIM][PF6] as well as from the work of Seidl et al. [19] in the case of [(mPEG2)2Im]I. As can be observed from Fig. 8, for q between (0.83 and 6.6) × 105 m−1 the SLS results obtained at relatively large (R-P) and small (R-NP) values for q follow the theory well within the experimental uncertainties. These findings corroborate the conclusion drawn in connection with the results for TOTM in Fig. 6 that SLS experiments on liquids showing an overdamped behavior appear to be not influenced by disturbing line-broadening effects in the given range of q.
Damping Γ of surface fluctuations of [OMIM][PF6] and [(mPEG2)2Im]I as a function of the adjusted wave vector q obtained from SLS measurements with two different detection geometries in reflection direction at (333 or 353) K (markers according to legend) in comparison with the theoretical calculations (lines) based on exact solution of dispersion relation [20, 28]. For the latter, input values for η′ and σ were employed from literature sources as detailed in the text
3.2.2 Viscosity and Surface Tension
The final results for the surface tension σ and liquid viscosity ηL of [OMIM][PF6] and [(mPEG2)2Im]I obtained from combined SLS-PD measurements as a function of temperature between (303 and 373) K are summarized in Table 1. For T up to 353 K, the SLS signals showed an overdamped behavior, which required to employ the information about σ accessed by the PD method and correlated via Eq. 2 in order to determine ηL by SLS. At the largest T of 373 K studied exemplarily for [(mPEG2)2Im]I, it was possible to simultaneously determine ηL and σ via SLS from measurements in the R-NP-geometry at relatively small q.
The results for surface tension (a) and viscosity (b) are shown as a function of T in Fig. 9. For data representation, T-dependent correlations were developed according to the linear fit
Surface tension σ (a) and viscosity ηL (b) of [OMIM][PF6] and [(mPEG2)2Im]I obtained by combined PD (filled markers) and SLS (open markers) experiments close to 0.1 MPa in the presence of an Ar atmosphere as a function of temperature including the corresponding fit correlations according to Eqs. 2 and 3 (upper part) and the relative deviations of the experimental data from the fits (
 ) (lower part). A picture of the two IL samples is shown as inset of the left figure
) (lower part). A picture of the two IL samples is shown as inset of the left figure
for the surface tension based on the PD results as well as the Vogel-type equation
for the viscosity based on the SLS results. For the correlations in Eqs. 2 and 3 obtained by a least-squares minimization algorithm, the same statistical weight is considered for all data points. The fit parameters σ0 and σ1 in Eq. 2 as well as η0, B, and C in Eq. 3 are listed in Tables 2 and 3, together with the AARDs of the experimental data from the associated fit.
With respect to the surface tension, the relative deviations of the experimental PD data from Eq. 2 shown in the lower part of Fig. 9a are always clearly within the measurement uncertainty of 2 %, resulting in AARD values of (0.11 and 0.28) % for [OMIM][PF6] and [(mPEG2)2Im]I. This implies that σ of the studied ILs decreases linearly with respect to temperature within a limited T range, as it has also been found for many other ILs [14, 16, 17]. It should be mentioned that the single σ value for [(mPEG2)2Im]I at 373 K obtained by SLS simultaneously with ηL also agrees with the PD result within the uncertainty of the SLS experiment, which is somewhat larger with about 10 % due to the challenges in the evaluation of the signal close to the critical damping of surface fluctuations (Y about 0.145). This agreement between the PD method and SLS proves again the consistency of both surface-tension measurement techniques. The surface tensions for [(mPEG2)2Im]I are larger than those for [OMIM][PF6], with a relatively constant deviation about + 36 % for the entire T range studied. Considering the fact that only the outer region at the surface is responsible for surface tension according to Langmuir’s principle [43], the behavior for σ can be discussed in connection with the enrichment of the most surface-active groups of the two ILs, as revealed by angle-resolved X-ray photoelectron spectroscopy [15, 19]. While for [(mPEG2)2Im]I the surface shows a weak enrichment of the short-chained (n = 2) polar mPEGn side chains, the surface of [OMIM][PF6] is predominantly occupied by the long-chained non-polar octyl side chains of distinctly lower surface energy, resulting in a significantly lower value for σ.
According to Fig. 9b, the ηL data for the two ILs determined by SLS cover a broad range of viscosities between about (500 down to 40) mPa·s at T from (303 to 353) K, and can be described well by the Vogel-type equation, Eq. 3. For all states, the absolute relative deviations of the experimental data from ηL,calc are within their uncertainties and typically smaller than 2.5 %. A larger deviation of 4.4 % is only found at 373 K for the result for [(mPEG2)2Im]I, whose uncertainty is also elevated due to the same circumstance as aforementioned for σ. Despite the strongly different chemical and physical characteristics, both investigated ILs feature relatively similar viscosities. At 303 K, ηL of [(mPEG2)2Im]I is about 7 % larger than [OMIM][PF6], whilst the behavior turns between (313 and 323) K and [(mPEG2)2Im]I shows an about 9 % lower viscosity at 353 K compared to [OMIM][PF6]. Since the viscosity of ILs depends on various effects such as intermolecular interactions like van der Waals and Coulombic interactions as well as molecular entanglement, a physical interpretation for the viscosity behavior of the two studied ILs can hardly be drawn and is out of the scope of this work.
3.2.3 Data Comparison
To validate the present IL results from the combined SLS and PD measurements, a comparison with further available experimental data for viscosity and surface tension at or close to ambient pressure of about 0.1 MPa is carried out. Regarding [(mPEG2)2Im]I, there exist only two recent studies of Seidl et al. [19] and Paap et al. [44], both investigating a batch of sample synthesized in the same way as that used in this work. In the paper of Seidl et al. [19], experimental data were compiled for ηL between (293 and 393) K obtained by a rotational cone-plate viscometer as well as for σ between (303 and 363) K determined by the PD method in the same setup and sample cell as employed in the present work. For both properties, the results reported by Seidl et al. [19] are in agreement with the present work, given the AARDs of the ηL and σ data from Eqs. 2 and 3 of (1.4 and 0.3) % within the T range from (303 to 353) K. Also, the data measured by Paap et al. [44] using the PD method under high-vacuum conditions at p of about 5·10–4 Pa between (303 and 338) K match the present results with an AARD of 0.63 %.
In the case of the commercial IL [OMIM][PF6], a larger experimental database is available. These nine and seven data sets from literature for ηL [45,46,47,48,49,50,51,52] and σ [44, 45, 48, 53,54,55], respectively, which are differentiated with respect to the applied measurement principle by the used color of the markers, are shown in Fig. 10 as a function of T by plotting their relative deviations from the present results represented by Eqs. 2 and 3. As can be seen from Fig. 10a and b for ηL and σ, respectively, the literature data scatter around the present correlations. For the viscosity, the present data seem to form the center of the data sources. The deviations from ηL,calc range between (− 13 and + 13) % and are often within combined expanded uncertainties of the data sets if specified for the latter. It should be emphasized that our results determined by CV between (313 to 353) K and listed in section S5 of the Supporting Information coincide with the SLS data mostly within 3 %, i.e., within combined uncertainties. This agreement between the two viscometers applied to the same IL sample is a further indication for the performance of the developed SLS-PD apparatus. Discrepancies in the viscosity of ILs have also been observed in several studies, e.g., in Refs. [16, 18, 22] and can be related to the characteristics of the samples under investigation, especially the presence of air and/or impurities such as water, but also to the use of inadequate, often secondary measurement techniques.
Data comparison for the viscosity ηL (upper part) and surface tension (lower part) of [OMIM][PF6] at about 0.1 MPa as a function of temperature T, showing the relative deviation of the available experimental data from the correlations ηL,calc and σcalc(
 ), Eqs. 2 and 3, respectively, developed in this work based on the experimental data. The dashed lines indicate the average expanded (k = 2) uncertainty of the experimental data obtained in this work. In both figures, same measurement principles are indicated by the same color
), Eqs. 2 and 3, respectively, developed in this work based on the experimental data. The dashed lines indicate the average expanded (k = 2) uncertainty of the experimental data obtained in this work. In both figures, same measurement principles are indicated by the same color
For the surface tension of [OMIM][PF6], the majority of the literature data agree with the fit of the present PD data represented by Eq. 2 within absolute relative deviations of 3 %, i.e., within combined uncertainties [44, 53,54,55]. This also holds when considering the PD data obtained by Paap et al. [44] at a pressure of 0.1 MPa (shown as dashed-dotted line in the lower part of Fig. 10) or at high-vacuum conditions at p of about 3.3·10–4 Pa from (295 to 360) K. Only, the results reported by AlTuwaim et al. [48] and Pereiro et al. [45] are significantly larger than the other data sets, with deviations of about + 7 % relative to Eq. 2 that are clearly outside combined uncertainties. Such differences in published σ data for ILs are commonly found in the literature [15,16,17] and seem to be mainly related to a missing critical assessment of the reliability and uncertainty of the measurement technique and/or to the presence of surface-active impurities. In this context, water has shown to not significantly affect the surface tension of ILs up to relatively large H2O contents [22], in particular with respect to hydrophobic ILs including [OMIM][PF6] [54].
4 Conclusions
The present study has provided a proof of concept for the combination of the two well-established surface-sensitive measurement techniques given by SLS and the PD method, aiming at the determination of viscosity and surface tension of fluids with a relatively high-viscosity within one experimental setup. For an accurate determination of viscosity of such fluids by SLS experiments in the overdamped case, it is of importance that the sample surface investigated by SLS corresponds to that studied by the PD method. This can be ensured by the further optimized setup, where both methods are combined within the same sample cell, as outlined in the present work. Investigations of the high- and low-viscosity reference fluids TOTM and n-dodecane served for a mutual validation of the two techniques and also highlighted that small wave vectors, beneficial for the study of opaque to non-transparent fluids in reflection geometry, can be probed reliably in the case of overdamped SLS signals since line-broadening effects are negligible here. For the ILs [OMIM][PF6] and [(mPEG2)2Im]I investigated from (303 to 373) K under an Ar atmosphere of about 0.1 MPa, the application of the surface tension data obtained by the PD method with an expanded uncertainty of 2 % served as an input for the evaluation of the SLS experiments in order to access the viscosity with typical expanded uncertainties below 5 %. The agreement of these results with experimental data in literature including own values from capillary viscometry punctuates the capability of the presented strategy for the quasi-simultaneous measurement of viscosity and surface tension of highly viscous fluids at macroscopic thermodynamic equilibrium, as demonstrated for ILs in the present work. Considering that further improvements are still feasible by, e.g., using more sensitive light detection units, which helps reduce the uncertainties in SLS signals, one may take advantage of the present approach for future experiments on IL systems in the presence of dissolved metal complexes and reaction gases at elevated temperatures and pressures relevant for SILP technology.
Data Availability
Not applicable.
References
M. Śmiglak, A. Metlen, R.D. Rogers, Acc. Chem. Res. 40, 1182 (2007)
P. Wasserscheid, T. Welton, Ionic Liquids in Synthesis, 2nd edn. (WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim, 2007)
J.A.P. Coutinho, P.J. Carvalho, N.M.C. Oliveira, RSC Adv. 2, 7322 (2012)
D. Kuang, P. Wang, S. Ito, S.M. Zakeeruddin, M. Grätzel, J. Am. Chem. Soc 128, 7732 (2006)
L. Moens, D.M. Blake, D.L. Rudnicki, M.J. Hale, J. Sol. Energy Eng. 125, 112 (2003)
J.M.P. França, C.A. Nieto de Castro, M.M. Lopes, V.M.B. Nunes, J. Chem. Eng. Data 54, 2569 (2009)
D. Han, H.K.H. Row, Molecules 15, 2405 (2010)
S. Hanioka, T. Maruyama, T. Sotani, M. Teramoto, H. Matsuyama, K. Nakashima, M. Hanaki, F. Kubota, M. Goto, J. Membr. Sci. 314, 1 (2008)
S. Walter, M. Haumann, P. Wasserscheid, H. Hahn, R. Franke, AIChE J. 61, 893 (2015)
W.-M. Cheng, R. Shang, ACS Catal. 10, 9170 (2020)
A. Kazakov, J.W. Magee, R.D. Chirico, V.V. Diky, K. Kroenlein, C.D. Muzny, and M. Frenkel, NIST Standard Reference Database - (ILThermo), version 2.0, National Institute of Standards and Technology, Gaithersburg MD, United States, 20899, http://ilthermo.boulder.nist.gov).
Q. Dong, C.D. Muzny, A.F. Kazakov, V.V. Diky, J.W. Magee, J.A. Widegren, R.D. Chirico, K.N. Marsh, M. Frenkel, J. Chem. Eng. Data 52, 1151 (2007)
A.I. Rusanov, V.A. Prokhorov, Interfacial Tensiometry (Elsevier, Amsterdam, 1996)
T.M. Koller, M.H. Rausch, K. Põhako-Esko, P. Wasserscheid, A.P. Fröba, J. Chem. Eng. Data 60, 2665 (2015)
C. Kolbeck, J. Lehmann, K.R.J. Lovelock, T. Cremer, N. Paape, P. Wasserscheid, A.P. Fröba, F. Maier, H.-P. Steinrück, J. Phys. Chem. B 114, 17025 (2010)
A.P. Fröba, H. Kremer, A. Leipertz, J. Phys. Chem. B 112, 12420 (2008)
M.A. Tariq, M.G. Freire, B. Saramago, J.A.P. Coutinho, J.N. Canongia Lopes, L.P.N. Rebelo, Chem. Soc. Rev. 41, 829 (2012)
T.M. Koller, F.D. Lenahan, P.S. Schmidt, T. Klein, J. Mehler, F. Maier, M.H. Rausch, P. Wasserscheid, H.-P. Steinrück, A.P. Fröba, Int. J. Thermophys. 41, 144 (2020)
V. Seidl, M. Bosch, U. Paap, M. Livraghi, Z. Zhai, C.R. Wick, T.M. Koller, P. Wasserscheid, F. Maier, A.-S. Smith, J. Bachmann, H.-P. Steinrück, K. Meyer, J. Ionic Liq. 2, 100041 (2022)
D. Langevin, Light Scattering by Liquid Surfaces and Complementary Techniques (Dekker Marcel, New York, 1992)
A.P. Fröba, S. Will, Light Scattering by Surface Waves - Surface Light Scattering, in: Experimental Thermodynamics (The Royal Society of Chemistry, Cambridge, 2014).
A.P. Fröba, P. Wasserscheid, D. Gerhard, H. Kremer, A. Leipertz, J. Phys. Chem. B 111, 12817 (2007)
T.M. Koller, T. Prucker, J. Cui, T. Klein, A.P. Fröba, J. Colloid Interf. Sci. 538, 671 (2019)
T.M. Koller, M.H. Rausch, J. Ramos, P.S. Schulz, P. Wasserscheid, I.G. Economou, A.P. Fröba, J. Phys. Chem. B 117, 8512 (2013)
T. Klein, F.D. Lenahan, M. Kerscher, J.H. Jander, M.H. Rausch, T.M. Koller, A.P. Fröba, J. Chem. Eng. Data 66, 3205 (2021)
S.M.I. Saad, A.W. Neumann, J. Colloid Interf. Sci. 238, 62 (2016)
A.P. Fröba, Simultane Bestimmung von Viskosität und Oberflächenspannung transparenter Fluide mittels Oberflächenlichtstreuung, Dr.-Ing. Thesis, Friedrich-Alexander-Universität Erlangen-Nürnberg, 2002.
E.H. Lucassen-Reynders, J. Lucassen, Adv. Colloid Interf. Sci. 2, 347 (1970)
T.M. Koller, J. Cui, M. Schmidt, J. Knorr, A.P. Fröba, Appl. Opt. 60, 9042 (2021)
J.H. Jander, P.S. Schmidt, C. Giraudet, P. Wasserscheid, M.H. Rausch, A.P. Fröba, Int. J. Hydrog. Energy (2021).
T.M. Koller, T. Klein, C. Giraudet, J. Chen, A. Kalantar, G.P. van der Laan, M.H. Rausch, A.P. Fröba, J. Chem. Eng. Data 62, 3319 (2017)
A.P. Fröba, A. Leipertz, Int. J. Thermophys. 24, 895 (2003)
Z. Lei, C. Dai, B. Chen, Chem. Rev. 114, 1289 (2014)
M. Kerscher, J.H. Jander, J. Cui, M.M. Martin, M. Wolf, P. Preuster, M.H. Rausch, P. Wasserscheid, T.M. Koller, A.P. Fröba, Int. J. Hydrog. Energy 47, 15789 (2022)
J. Cui, J.H. Jander, T.M. Koller, A.P. Fröba, J. Chem. Eng. Data 67, 644 (2022)
D. Byrne, J.C. Earnshaw, J. Phys. D 12, 1133 (1979)
J. Knorr, J. Cui, T.M. Koller, A.P. Fröba, J. Colloid Interf. Sci. 623, 595 (2022)
A.P. Fröba, A. Leipertz, J. Chem. Eng. Data 52, 1803 (2007)
Revised Release on Surface Tension of Ordinary Water Substance, International Association for the Properties of Water and Steam, IAPWS R1-76 (2014), http://www.iapws.org/relguide/Surf-H2O.html
Á. Mulero, I. Cachadiña, M.I. Parra, J. Phys. Chem. Ref. Data 41, 43105 (2012)
E.W. Lemmon, M.L. Huber, M.O. McLinden, NIST Standard Reference Database 23: Reference Fluid Thermodynamic and Transport Properties (REFPROP), Version 10.0; National Institute of Standards and Technology, Standard Reference Data Program, 2018.
M. Huber, A. Laesecke, R.A. Perkins, Energy Fuels 18, 968 (2004)
I. Langmuir, Chem. Rev. 6, 451 (1930)
U. Paap, B. Kreß, H.-P. Steinrück, F. Maier, submitted to Int. J. Mol. Sci. (2022)
A.B. Pereiro, J.L. Legido, A. Rodriguez, J. Chem. Thermodyn. 39, 1168 (2007)
K.R. Seddon, A. Stark, M.-J. Torres, Viscosity and density of 1-alkyl-3-methylimidazolium ionic liquids, in Clean Solvents (ACS Symposium Series; American Chemical Society, Washington, DC, 2002, pp. 34–49).
J. Safarov, C. Bussemer, A. Aliyev, C. Lafuente, E. Hassel, I. Abdulagatov, J. Chem. Thermodyn. 124, 49 (2018)
M.S. AlTuwaim, K.H. Alkhaldi, A.S. Al-Jimaz, A.A. Mohammad, J. Chem. Eng. Data 59, 1955 (2014)
M.A. Rocha, F.M. Ribeiro, A.I.L. Ferreira, J.A. Coutinho, L.M. Santos, J. Mol. Liq. 188, 196 (2013)
L.C. Branco, J.N. Rosa, J.J. Moura Ramos, C.A.M. Afonso, Chem. Eur. J. 8, 3671 (2002)
D. Tomida, A. Kumagai, S. Kenmochi, K. Qiao, C. Yokoyama, J. Chem. Eng. Data 52, 577 (2007)
K.R. Harris, M. Kanakubo, L.A. Woolf, J. Chem. Eng. Data 51, 1161 (2006)
J. Klomfar, M. Soucková, J. Pátek, J. Chem. Eng. Data 54, 1389 (2009)
M.G. Freire, P.J. Carvalho, A.M. Fernandes, I.M. Marrucho, A.J. Queimada, J.A. Coutinho, J. Colloid Interf. Sci. 314, 621 (2007)
G. Law, P.R. Watson, Langmuir 17, 6138 (2001)
Acknowledgements
The authors gratefully acknowledge funding of the Erlangen Graduate School in Advanced Optical Technologies (SAOT) by the Bavarian State Ministry for Science and Art and funding by the Friedrich-Alexander-Universität Erlangen-Nürnberg (FAU). AB is grateful for a Ph.D. fellowship provided by the Studienstiftung des deutschen Volkes.
Funding
Open Access funding enabled and organized by Projekt DEAL. This work was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – Project-ID 431791331 – SFB 1452 (CLINT Catalysis at Liquid Interfaces).
Author information
Authors and Affiliations
Contributions
ZZ designed the optimized setup including the new sample cell, performed all measurements, and wrote the main manuscript text. JHJ developed the evaluation routine for the PD measurements and supported together with JC regarding the development of the setup and the data evaluation. AB synthesized the [(mPEG2)2Im]I sample under the supervision of KM. TMK supervised and coordinated all investigations and wrote the main manuscript text. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Conflict of interests
The authors have no competing interests as defined by Springer, or other interests that might be perceived to influence the results and/or discussion reported in this paper.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zhai, Z., Jander, J.H., Bergen, A. et al. Combined Surface Light Scattering and Pendant-Drop Experiments for the Determination of Viscosity and Surface Tension of High-Viscosity Fluids Demonstrated for Ionic Liquids. Int J Thermophys 43, 178 (2022). https://doi.org/10.1007/s10765-022-03103-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10765-022-03103-z