Framework for In Situ Measurements of Vapor–Liquid Equilibrium Using a Microwave Cavity Resonator

Abstract

The ability to accurately predict the behavior of multiphase fluid mixtures underpins a broad range of industrial and scientific activity. Expanding the scope and improving the performance of predictive thermodynamic models relies on the availability of accurate experimental data for the complete phase behavior of the corresponding fluid mixtures. Here, we present a novel approach to in situ measurements of heterogeneous two-phase behavior in binary fluid mixtures using a single apparatus. A modified microwave re-entrant cavity apparatus is employed to simultaneously measure the dielectric properties of the liquid and vapor as well as the quality of each phase, based on the frequency shifts caused by a heterogeneous fluid for three independent resonant modes. We report a so far unique mathematical framework to further characterize the thermophysical properties of each phase along tie lines, determining the compositions of the coexisting vapor and liquid phase as well as the vapor and liquid phase densities within the two-phase region based on the Clausius–Mossotti relation between phase dielectric properties, density, and molar polarizability. The framework was validated by comparison of the measured and predicted properties of a (0.35 propane + 0.65 carbon dioxide) mixture throughout the two-phase region along an isothermal pathway at T = 280 K. These proof-of-concept results demonstrate for the first time that thermophysical properties of a binary mixture with a known overall composition can be determined from experiments with a microwave cavity using a synthetic approach.

1 Introduction

The rising demand for energy brings with it a steady growth in potential carbon dioxide emissions. While carbon dioxide emissions have historically been associated with conventional burning of fossil fuel sources, generation and handling of carbon dioxide are increasingly important for net-zero carbon energy generation strategies [1]. Therefore, understanding the thermophysical behavior of carbon dioxide-rich mixtures is critical to ensure efficient and safe plant design and operation for industrial processes. However, the accuracy of widely used engineering models to predict fluid properties, such as the GERG-2008 equation of state (EOS) [2] and the multiparameter Helmholtz equation of state “EOS-CG” [3], is limited by the availability and quality of experimental data [4]. Data on phase transitions and the properties of binary mixtures in two-phase vapor–liquid equilibrium (VLE) are typically limited and exhibit a significant range of deviation from model predictions. For example, the data available for the (propane + carbon dioxide) system in two-phase VLE are confined to five sources with a deviation scatter of up to 20 % [5,6,7,8,9]. It is therefore crucial to generate high-quality VLE data to improve the interaction parameters for binary mixtures within the existing EOS, which in turn will improve the prediction of multicomponent mixture properties of industrial relevance [10]. Despite the improved availability of experimental data achieved in the last decades, industry frequently requires new reference data for fluid mixtures of specific interest, as a comprehensive study recently revealed [4].

A variety of apparatus have been developed to measure high-pressure two-phase systems at equilibrium, using either an analytical or a synthetic approach. Both the diversity of apparatuses and the advantages and disadvantages of each have been reported in great detail by Dohrn, Fonseca, and Peper in a series of publications [11,12,13]; only a brief summary of the key criteria is presented here in Table 1. The analytical approach provides compositional information about the heterogeneous two-phase region and comprehensive information about tie lines; however, the uncertainty introduced by sampling compounds with each measurement and the long equilibration times required after sampling lead to poor reproducibility [14]. Synthetic methods are not affected by the disadvantages of sampling; however, conventional VLE synthetic measurements are not able to resolve compositional information about the new phase or provide information on tie lines for multicomponent mixtures without complementary apparatus or measurements [12].

Table 1 Characteristics of analytical and synthetic methods for conventional VLE measurements

Microwave electromagnetic resonant techniques have proven to be a reliable method for synthetic measurements of phase transitions and fluid quality. First introduced by Rogers et al. [15] to investigate phase transitions, microwave re-entrant cavities were developed further by Goodwin et al. [16] and May et al. [17] to investigate molar polarizability, dielectric permittivity, and density and to detect dew points of mixtures [18,19,20,21,22]. May et al. [23] and later on Kandil et al. [24] employed microwave cavities for two-phase measurements of liquid volume fraction $\varLambda$ inside the resonator, introducing a normalized quantity, ${G}_{n}$, which relates $\varLambda$ with the dielectric properties of a two-phase fluid, thus, providing a measurement of quality but not composition.

In the present work, we present a novel approach of using microwave-based technology to describe the phase behavior of binary mixtures within a single measuring device that combines the advantages of analytical and synthetic methods (see Table 1). For this, an existing microwave resonator was modified by integrating a fluid recirculation pump in series with the resonator that allows for mixture homogenization, during or before a measurement. The method presented here simultaneously determines multiple thermophysical properties using a synthetic approach combined with in situ dielectric measurements. Figure 1 highlights the properties that can be determined with the new technique. For the first time, we present a mathematical framework for the characterization of binary mixture tie lines by determining the compositions of the coexisting vapor and liquid phase (x_i, y_i) and the vapor and liquid phase densities (ρ_vap, ρ_liq) within the heterogeneous two-phase region (Fig. 1, highlighted in red). The method of analysis builds on the approach introduced by May et al. [23] and Kandil et al. [24] by utilizing three resonant modes of the microwave cavity to uniquely determine the properties of the two phases.

Fig. 1

p, x diagram of the binary (C₃H₈ + CO₂) system illustrating the liquid and vapor phase composition (x_i, y_i) with an overall composition z_i. L liquid phase, V vapor phase, L + V coexisting liquid and vapor in the two-phase region. The phase boundaries were calculated with the GERG-2008 equation of state of Kunz and Wagner [2]

Finite element analysis (FEA) is used to characterize the normalized fluid response function (${G}_{n}$) of the microwave cavity to a two-phase binary mixture for each resonant mode n. Utilizing these ${G}_{n}$ model functions in conjunction with dielectric measurements, material balance, and the Clausius–Mossotti relationship, a mathematical approach to calculate the vapor and liquid phase compositions (x_i, y_i) and densities (ρ_vap, ρ_liq) is presented. As a demonstration of this method, measurements of a (0.35 C₃H₈ + 0.65 CO₂) mixture were conducted along an isotherm at T = 280 K from single-phase vapor, through the two-phase region, to single-phase liquid by incremental injection of the mixture. A total of 20 data points were collected throughout the two-phase region.

2 Theory and Modeling

2.1 Principle of a Microwave Re-entrant Cavity Resonator for Fluid Dielectric Permittivity Measurements

A detailed description of the overall measurement principle of a microwave re-entrant cavity system is given by several authors, e.g., Tsankova et al. [18], May [25], and Goodwin et al. [16] and only a brief description is provided below.

Complex dielectric permittivity, consisting of a real and an imaginary part, ${\varepsilon }_{\mathrm{r}}= {\varepsilon }{^{\prime}}$ + ${\varepsilon }{{^{\prime\prime}}}$, describes the amount of energy stored in an electric field within a material relative to the amount of energy stored within a vacuum and can be expressed using an implicit model developed by Hamelin et al. [26] (Eq. 1). The model relates the complex dielectric permittivity of a fluid with the complex electromagnetic resonant frequency of the system, whereby the latter can be determined experimentally. Here, f is the resonant frequency of the fluid contained inside the resonator, and g is the half-width of the resonant frequency, with the subscript n denoting the resonator’s mode number and the superscript 0 indicating vacuum conditions. For fluids with small dielectric losses and cavities with high quality factor $Q=\left(f/2g\right)$ (generally greater than 100 for microwave re-entrant cavities [18]), the imaginary component of Eq. 1 can be assumed negligible, and only the real component is taken into account, as presented in Eq. 2.

$${\varepsilon }_{\mathrm{r},n}={\left(\frac{{f}_{n}^{0}+\mathrm{i}{g}_{n}^{0}}{{f}_{n}+\mathrm{i}{g}_{n}}\right)}^{2}\cdot\frac{1+\left(-1+i\right){\left(\frac{{f}_{n}}{{f}_{n}^{0}}\right)}^{2}{\varepsilon }_{\mathrm{r},{n}}\left(\frac{2{g}_{n}^{0}}{{f}_{n}^{0}}\right)}{1+\left(-1+i\right)\left(\frac{2{g}_{n}^{0}}{{f}_{n}^{0}}\right)} ,$$

(1)

$${\varepsilon }_{\mathrm{meas},n}\approx {\left(\frac{{f}_{n}^{0}}{{f}_{n}}\right)}^{2}.$$

(2)

2.1.1 Single-Phase Fluid

The resonant modes of a typical microwave re-entrant cavity resonator are determined by the geometry of the cavity and the dielectric properties of the fluid contained inside the cavity (between the outer cylinder and the inner bulb). The former supports a number of resonant modes with different electric and magnetic field distributions. This is illustrated in the top panel of Fig. 2, where the spatial electric field distribution and intensity of the five lowest frequency resonant modes for the cavity (m = 0, 1) were modeled under vacuum conditions using FEA. The FEA presented in this work was performed using the commercially available software COMSOL Multiphysics (version 5.3) [27]. The system can be simplified for simulation purposes as being cylindrically symmetric, such that only one half of the cross-sectional plane needs to be defined. Variations in the relative magnitude of the electric field in the cross-sectional plane are represented by color with red indicating high intensity. Electric field variations in the azimuthal direction are defined by the azimuthal number m (where m = 0 indicates the field is constant magnitude around the cavity). As depicted in Fig. 2, the electric field of Mode 1 is concentrated in the narrow annular gap between the bulb and the outer cavity wall. Mode 2 resonates in the same region but with a different azimuthal mode number (m = 1). The electric field of Mode 3 is primarily concentrated between the lower surface of the bulb and the bottom of the cavity, with additional electric field focus near the top of the annular gap and a node in-between. The next higher order modes, Modes 4 and 5, exhibit additional variations between the base and top of the annular region compared to Mode 3. In the bottom panel of Fig. 2 the measured frequency spectrum for the microwave cavity under vacuum is shown with resonances assigned to the modeled electric field distributions. The resonator used for the simulations and measurements is described in more detail in Sect. 3.1. From these five resonant modes, three were selected for use in this work based on the contrast in their spatial distribution of electric field, to provide maximum information for heterogeneous fluid systems contained within the cavity.

Fig. 2

Top panel: Electric field distribution and intensity predicted with FEA for Modes 1, 2, 3, 4, and 5 for different azimuthal mode numbers (m = 0, 1) of the microwave re-entrant cavity resonator [19] used in the present work (see Sect. 3.1). Bottom panel: Corresponding measured resonant frequencies for Modes 1, 2, 3, 4, and 5 at vacuum conditions. The peak near 4 GHz is a higher azimuthal mode (m = 2), not considered in this work. Note the logarithmic amplitude scale; the scatter in |S₂₁| between resonance peaks is indicative of the measurement noise floor

2.1.2 Two-Phase Fluid

For a single-phase pure fluid or mixture, the overall dielectric permittivity at constant density and temperature is uniform throughout the entire sample space and can, hence, be determined from measurements of any cavity mode. This is not the case for a two-phase fluid, where the dielectric permittivity is no longer uniform throughout the cavity but instead depends on the dielectric properties of the two phases and the liquid volume fraction $\varLambda$. Since the resonant modes of the cavity exhibit different electric field spatial distributions, the liquid and vapor phase dielectric properties will affect the resonant frequency of each mode differently, correlated with the spatial overlap of each fluid phase and the electric field distribution. This results in a unique dependence on $\varLambda$ for each resonant mode. May et al. [23] established a method to link the dependence of $\varLambda$ with the dielectric properties of a fluid for each mode and thereby allowing for the determination of the liquid volume fraction (Eq. 3). May et al. [23] used the effective dielectric permittivity, ${\varepsilon }_{\mathrm{eff},{n}}$, calculated from measured resonant frequencies (e.g., using Eq. 2) and the corresponding single-phase vapor and liquid dielectric properties, ${\varepsilon }_{\mathrm{vap}}$ and ${\varepsilon }_{\mathrm{liq}}$, to generate a normalized quantity ${G}_{n}$, known as the mode-shape function:

$${G}_{n}\left(\varLambda \right)=\frac{{\varepsilon }_{\mathrm{eff},n}-{\varepsilon }_{\mathrm{vap}}}{{\varepsilon }_{\mathrm{liq}}-{\varepsilon }_{\mathrm{vap}}} ,$$

(3)

where ${\varepsilon }_{\mathrm{eff},n}= {\varepsilon }_{\mathrm{meas},n}$, ${\varepsilon }_{\mathrm{vap}}$ is the vapor phase dielectric permittivity, and ${\varepsilon }_{\mathrm{liq}}$ is the liquid phase dielectric permittivity. The mode-shape function reflects the electric field distribution for each mode and how the two fluid phases interact with it as the liquid level rises. May [25] further demonstrated that, to first approximation, the ${G}_{n}$ function can be assumed fluid independent for non-polar fluids by presenting measurements of n-decane and carbon dioxide. We recently drew similar conclusions for low frequency modes [28]. However, it has to be noted that for higher frequency modes (f $>$ 5 GHz) and modes with high electrical sensitivity, a small but measurable fluid dependence cannot be excluded, as discovered by Hopkins et al. [28]. This behavior arises from the impedance mismatch at the vapor–liquid interface that in turn depends on the dielectric properties of both phases. Using FEA, we have shown that the ratio of the liquid to vapor dielectric permittivity ($\gamma =({\varepsilon }_{\mathrm{liq}}/{\varepsilon }_{\mathrm{vap}}$)), can be utilized to relate the dependence of ${G}_{n}$ to the dielectric heterogeneity present in the cavity [28]. In this work, corrections for $\gamma$ were not required since the binary fluid system was known and the ${G}_{n}$ functions were evaluated from FEA simulations that incorporated predictions of phase properties at each $\gamma .$

For pure fluids in the two-phase region at constant temperature, ${\varepsilon }_{\mathrm{liq}}$ and ${\varepsilon }_{\mathrm{vap}}$ are constant through the two-phase region for all liquid volume fractions. Therefore, the ${G}_{n}$ function can be determined experimentally by measuring the dielectric permittivity of a reference pure fluid from just below the dew-point pressure through to when the resonator is filled with liquid. The initial and final measurements are measurements of ${\varepsilon }_{\mathrm{liq}}$ and ${\varepsilon }_{\mathrm{vap}}$, respectively, and ${\varepsilon }_{\mathrm{eff},n}$ is measured along an isotherm for increasing $\varLambda$. Experimentally characterized ${G}_{n}$ curves can be verified using FEA to simulate the mode-shape functions for the same reference fluid; i.e., the resonant frequencies and, thus, ${\varepsilon }_{\mathrm{eff},n}$ may be calculated for increasing heights of liquid by using the constant values of ${\varepsilon }_{\mathrm{liq}}$ and ${\varepsilon }_{\mathrm{vap}}$ for a reference fluid as input parameters to the simulation. The values of ${\varepsilon }_{\mathrm{liq}}$ and ${\varepsilon }_{\mathrm{vap}}$ are calculated at the experimental temperature and pressure using the correlation of Harvey and Lemmon [29] together with the reference EOS for the pure fluid as implemented, for example, in the database REFPROP (Reference Fluid Thermodynamic and Transport Properties, version 10.0) of the National Institute of Standards and Technology [30]. This procedure is described in more detail by Hopkins et al. [28]. A comparison between experimental and modeled results for pure propane and carbon dioxide is presented in Fig. 3. As described earlier in this section, only simulated values for Modes 1, 3, and 5 are shown along with experimental results for Modes 1 and 3. Comparing the ${G}_{n}$ functions to the simulated electrical field distribution presented in Fig. 2 (top panel) it can been observed that the gradient of the function (i.e., sensitivity to change in fluid property) is largest when the liquid level ($\varLambda$) is within the high electric field intensity region of each resonant mode. Taking ${G}_{1}$ as an example (Fig. 3, red line), its slope is the steepest at the annular gap (0.2 $<\varLambda <$ 0.25) which has the strongest electrical field intensity for Mode 1 within the same region of the cavity (Fig. 2, top panel). Comparing the electrical field intensity below the annular gap, $\varLambda <$ 0.2, and the slope of the corresponding ${G}_{1}$ curve, the behavior can be transferred: very low electric field intensity results in a small slope. Consequently, minimal change in ${G}_{1}$ can be observed at the region above the annular gap, $\varLambda >$ 0.25, where there is negligible electrical field intensity. The good agreement between experimental and modeled mode-shape functions establishes the foundation for a two-phase investigation of binary mixtures.

Fig. 3

Mode-shape functions ${G}_{n}$ for three spatially separated modes simulated using FEA and Eq. 3 for pure C₃H₈  are in excellent agreement with experimental values of ${G}_{n}$ measured with pure C₃H₈ and pure CO₂. , Mode 1 modeled; , Mode 3 modeled; , Mode 5 modeled; , Mode 1 exp. C₃H₈; , Mode 1 exp. CO₂; , Mode 3 exp. CO₂

2.2 Microwave Cavity Response for a Two-Phase Binary Fluid Mixture

For binary mixtures, the aforementioned process of measuring and modeling the frequency response of a two-phase fluid does not apply as the phase compositions of the coexisting vapor and liquid phase change throughout the two-phase region, resulting in varying vapor and liquid dielectric properties with increasing $\varLambda$. For the investigation of the frequency response via FEA simulation, this effect can be incorporated into the simulation inputs ${\varepsilon }_{\mathrm{liq}}$, ${\varepsilon }_{\mathrm{vap}}$, and $\varLambda$ by modeling an isothermal compression across the heterogeneous region. By specifying a known amount of liquid within the apparatus volume at constant temperature, the number of moles and overall composition of the system thermodynamically define the remaining properties of relevance for the mixture (here: p, ${\rho }_{\mathrm{vap}},$ ${\rho }_{\mathrm{liq}}$, ${x}_{\mathrm{vap}}$, ${x}_{\mathrm{liq}}$, ${y}_{\mathrm{vap}}$, ${y}_{\mathrm{liq}}$) at each $\varLambda$, predicted using existing equations of state (EOS). Based on these properties, the input parameters for the simulation, ε_vap and ε_liq, for each $\varLambda$ are then calculated with the correlation of Harvey and Lemmon [29]. This correlation links the mixture’s density, composition, polarizability, and dielectric permittivity using the polarizability mixing rule introduced by Harvey and Prausnitz [31]. Polarizabilities and dielectric permittivities are linked with either the Clausius–Mossotti or Kirkwood relation, for non-polar and polar fluids, respectively, while pure component polarizabilities are described by empirical equations with fluid-specific parameter sets. The fluid dependence on the ${G}_{n}$ curves is captured by re-calculating ${\varepsilon }_{\mathrm{liq}}$ and ${\varepsilon }_{\mathrm{vap}}$ at each $\varLambda$. The phase densities, fractions, and compositions of the (0.35 C₃H₈ + 0.65 CO₂) mixture investigated in this work are calculated with the GERG-2008 EOS of Kunz and Wagner [2]. The uncertainty for these values is up to 3 % and even higher for T = (90 to 450) K and p < MPa due to limited and poor data availability.

A graphical representation on how to numerically model the effect of liquid volume fractions is presented in Fig. 4, showing varying liquid volume levels. Here, the finite element (FE) model was split into two separate sections with the lower section representing the liquid phase and the upper section representing the vapor phase. The ${G}_{n}$ functions (Eq. 3) for each mode were calculated for increasing height of liquid, h_liq, which can be converted to $\varLambda$ based on the cavity geometry. The system was re-meshed using linear triangle elements for each liquid height and the vacuum frequency (used to calculate the effective dielectric permittivity according to Eq. 2) was recalculated at each h_liq to eliminate numerical errors associated with variations in the mesh. Similarly, different mesh sizes were examined. The results have shown that using varying mesh sizes does not affect the outcome of our model. Therefore, and because of low computation times of < 60 s, a fine mesh was utilized. Further details regarding the FE analysis are listed in Table 2.

Fig. 4

Schematic of the FE modeled cavity representing different liquid levels and the corresponding mesh. Highlighted in gray is the liquid fraction, white indicates the vapor phase. The dielectric properties of the liquid and vapor phase, respectively, change with varying liquid-vapor ratio due to changing liquid and vapor phase composition

Table 2 Configuration utilized within the FEA software COMSOL to numerically model the effect of liquid volume fractions inside a microwave resonator

Using these results, the simulated ${G}_{n}$ curves can be used as calibration curves for this fluid to interpret experimental two-phase measurements under similar conditions.

As was the case for the pure component modeling, no additional fluid dependency needs to be incorporated into the simulation, since the changing phase compositions and permittivities were accounted for in the property modeling. Nonetheless, it is envisaged that the analysis can be enhanced by incorporating this effect to provide a generalized set of calibration curves for unknown systems.

2.3 Framework for Complete Binary Phase Description from Measurements

Given at least three sufficiently distinct and calibrated (e.g., via FEA) mode-shape functions (G_n,cal), we outline a framework for the determination of the composition and density of the vapor and liquid phases of a binary mixture inside the two-phase region from microwave measurements of the cavity’s effective overall dielectric permittivity. State points in the two-phase region, along a tie line, can thus be characterized by solving two systems of equations consecutively. An overview of this procedure is presented in Fig. 5.

Fig. 5

Framework for the determination of the composition and density of the vapor and liquid phases of a binary mixture from microwave measurements of the effective dielectric permittivity ε_meas,n measured for at least three cavity modes, n. Two systems of equations are solved based on measured values at each liquid volume fraction ($\varLambda$). The frequency response equations (a) can be used to solve for ε_vap, ε_liq and $\varLambda$ using ε_meas,n measured by each mode and three sufficiently distinct and calibrated mode-shape functions G_n,cal as input values. The dielectric mixing equations (b) utilize the results of the first system as input values, together with known values of the overall binary mixture composition and density to solve for x₁, x₂, y₁, y₂, ρ_vap, ρ_liq

In the first stage (a), the optimum values for ${\varepsilon }_{\mathrm{vap}}$ and ${\varepsilon }_{\mathrm{liq}}$ at each liquid volume fraction ($\varLambda$) are determined based on the measured ${\varepsilon }_{\mathrm{meas},{n}}$ determined from the frequency response for each mode n using Eq. 2. If this information is available for at least three modes, Eq. 4 can be applied for each mode (re-arrangement of Eq. 3), to give a system of three equations. These three equations may then be regressed to minimize the deviation between the measured and calculated effective dielectric permittivity by fitting $\varLambda$, ${\varepsilon }_{\mathrm{vap}}$ , and ${\varepsilon }_{\mathrm{liq}}$.

$${\varepsilon }_{\mathrm{meas},n}={\varepsilon }_{\mathrm{vap}}\cdot \left(1-{G}_{n}\left(\varLambda \right)\right)+{\varepsilon }_{\mathrm{liq}}\cdot {G}_{n}\left(\varLambda \right).$$

(4)

In the second stage of analysis (b), the Clausius-Mossotti relationship (Eq. 5) is used to relate the phase dielectric permittivities (ε_vap, ε_liq) with the phase densities (ρ_vap, ρ_liq) and phase’s molar polarizabilities (P_vap, P_liq). Each phase’s polarizability is expressed as a function of composition for vapor (Eq. 6) and liquid (Eq. 7), respectively, using a linear mixing approach as a first approximation (components are denoted by i). This system of equations also includes material balance equations that link the overall composition of the binary mixture to the phase compositions via the vapor phase mole fraction (${X}$), and the volumetric balance equations which require the total volume, V_tot, occupied by the fluid to equal the sum of the liquid and vapor phase volumes. This gives a system of equations that allows the composition (x₁, x₂, y₁, y₂) and density (ρ_vap, ρ_liq) of each phase to be derived given the cavity volume V_tot and the total mass and fractions z_i of each component loaded in the cavity are known. The system of equations is solved by minimizing an objective function based on Eqs. 6–9 and letting it converge toward 0 by iteratively solving for the phase compositions and densities. Initial parameter estimates are based on the prediction of a suitable EOS (see Sect. 2.2).

$$\left(\frac{{\varepsilon }_{\mathrm{r}}-1}{{\varepsilon }_{\mathrm{r}}+2}\right)=\rho P,$$

(5)

$$\frac{{\varepsilon }_{\mathrm{vap}}-1}{{\varepsilon }_{\mathrm{vap}}+2}={\rho }_{\mathrm{vap}}\cdot \sum_{i=1}^{2}{y}_{i}\cdot {P}_{i,\mathrm{vap}},$$

(6)

$$\frac{{\varepsilon }_{\mathrm{liq}}-1}{{\varepsilon }_{\mathrm{liq}}+2}={\rho }_{\mathrm{liq}}\cdot \sum_{i=1}^{2}{x}_{i}\cdot {P}_{i,\mathrm{liq},}$$

(7)

$${X}=\frac{{V}_{\mathrm{vap}}\cdot {\rho }_{\mathrm{vap}}}{{V}_{\mathrm{tot}}\cdot {\rho }_{\mathrm{tot}}},$$

(8)

$${z}_{1}={X}{\cdot y}_{1}+\left(1-\mathrm{\rm X}\right)\cdot {x}_{1},$$

$${z}_{2}={X}\cdot {y}_{2}+\left(1-\mathrm{\rm X}\right)\cdot {x}_{2,}$$

(9)

$${x}_{1}+{x}_{2}= 1,$$

$${y}_{1}+{y}_{2}= 1,$$

(10)

$${V}_{\mathrm{tot}}={V}_{\mathrm{liq}}+{V}_{\mathrm{vap}}.$$

(11)

While a linear polarizability mixing rule is a reasonable approximation for many mixtures, the right-hand side of Eqs. 6 and 7 can be made more accurate by implementing a corresponding-states type mixing rule introduced by Harvey and Prausnitz [31]. This approach is based on mixing the pure component electric polarizations at constant temperature and reduced molar density and has been successfully applied to dielectric permittivity determinations by Tsankova et al. [21, 32]. Therefore, only a brief description is provided here. The mixing rule proposed by Harvey and Prausnitz can be expressed for vapor and liquid, respectively, as follows, represented by the vapor phase:

$${\rho }_{\mathrm{vap}}{P}_{\mathrm{vap}}=\sum_{i}{\Phi }_{i}\cdot \frac{{\rho }_{\mathrm{r},\mathrm{mix}}}{{\nu }_{i}^{*}}\cdot {P}_{i,\mathrm{vap}}\left(T,\frac{{\rho }_{\mathrm{r},\mathrm{mix}}}{{\nu }_{i}^{*}}\right).$$

(12)

Here, the volume fraction is defined as ${\Phi }_{i}={y}_{i}{\nu }_{i}^{*}/{\sum }_{j}{y}_{j}{\nu }_{j}^{*}$, the dimensionless reduced molar density is described as ${\rho }_{\mathrm{r},\mathrm{mix}}={\rho }_{\mathrm{mix}}{\sum }_{i}{y}_{i}{\nu }_{i}^{*}$ with ${\nu }_{i}^{*}$ being the critical volume and the quantity ${\rho }_{\mathrm{r},\mathrm{mix}}/{\nu }_{i}^{*}$ is the equivalent molar density of the pure component i at the same reduced density as the mixture. The pure component molar polarizabilities ${P}_{i,\mathrm{vap}/\mathrm{liq}}$ are calculated with the correlations of Harvey and Lemmon [29] using the experimental temperature and equivalent pure fluid densities corresponding to the same reduced mixture density. In this work, the equivalent pure fluid densities were calculated with the Helmholtz EOS for CO₂ of Span and Wagner [33] and the Helmholtz EOS for C₃H₈ of Lemmon et al. [34].

It is noted that the required operational assumptions are reasonable in that both accurate volume sizing and gravimetric loading of cavities can be routinely performed in thermodynamics laboratory environments.

3 Experimental

3.1 Apparatus Description

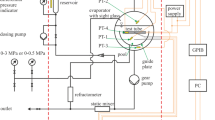
The experimental system used to demonstrate the suitability of microwave re-entrant cavities for full phase descriptions in this work is based on the microwave resonator built and described in great detail by Marsh and Kandil [19]. A cross-section of the resonator is presented by Sampson et al. [35]. The apparatus enables measurements over a temperature range from (243 to 373) K and pressures up to 10 MPa. A simplified schematic diagram of the setup is presented in Fig. 6. The sample fluid is transferred from the sample cylinder to a syringe pump (Teledyne ISCO 260D) used to control pressure throughout the experiment. From there on, the fluid is filled into the microwave re-entrant cavity system, which can be isolated from the syringe pump to achieve stable (p, T) conditions within the measuring system. The resonator is connected to a magnetically driven circulation pump (manufactured in-house at the University of Western Australia) withdrawing fluid from the top of the resonator and returning it to the bottom via an external flow loop. This ensures a uniform mixing of the sample contained within the cavity. All parts of the measuring cell containing sample fluid, i.e., the resonator itself, the circulation pump, and all tubing in between are immersed in a temperature-controlled bath to maintain homogenous (p, T) conditions.

Fig. 6

Schematic diagram of experimental setup for vapor-liquid equilibrium measurements using a microwave re-entrant cavity resonator

The temperature was monitored using three 100 Ω platinum resistance thermometers (PRT, Class-A, calibrated against a WIKA CTP5000 reference thermometer) placed in thermal-wells within the wall, base and bulb of the resonator with a combined expanded uncertainty (k = 2) of 0.1 K. For thermostatic control of the measuring system, a bath thermostat (Poly Science Model 9502A12E) filled with silicone oil was utilized. Pressure was measured with an OMEGA pressure transducer (Model MMA3.5KV10P3B6T3A6CE) located between the outlet of the circulation pump and bottom inlet of the resonator, with a maximum operating pressure of 34 MPa. The expanded uncertainty in pressure measurement, as specified by the manufacturer, was 0.08 % full scale. The resonant frequencies were determined from measurements of the complex transmission coefficient utilizing a vector network analyzer (Hewlett Packard Model 8719ET) with a frequency range of (0.05 to 12.7) GHz. The complex transmission coefficient S₂₁ was measured at 401 frequencies spanning an interval of 10–20 MHz (depending on the quality factor Q) and afterward fitted to a Q-circle algorithm based on the phase versus frequency approach described in Petersan and Anlage [36] to determine the resonant frequencies.

For the determination of the measuring system’s total volume and the volume of the circulation pump, volume sizing was performed by pressure and temperature expansion measurements of argon, a well-characterized gas. The precision syringe pump was used to vary the pressure and monitor the injected volume of argon. The molar density used for the volume determination was calculated with the Helmholtz EOS for argon by Tegeler et al. [37]. The total volume of the measuring system results in V_total = 64.35 cm³ and the volume of the circulation pump in V_pump = 8.64 cm³. The volume of the re-entrant cavity resonator is 54.94 cm³. A photograph of the resonator with the mounted circulation pump is presented in Fig. 7. The uncertainty of each of these volumes was roughly estimated to be less than or equal to 1 % (k = 1.73).

Fig. 7

Photograph of the modified re-entrant cavity resonator. A circulation pump is mounted onto the resonator creating the possibility of mixing the sample fluid contained inside the cavity. With the valve installed between the resonator and the circulation pump, the measuring system can be isolated from the rest of the apparatus

3.2 Materials

The binary mixture investigated in the present work was prepared gravimetrically using the procedure described by Schäfer [38]. The pure components used to prepare the mixture were supplied by Coregas and are listed in Table 3. The purities stated by the supplier were not further analyzed. The composition of the mixture was determined to be (0.348 C₃H₈ + 0.652 CO₂) mole fraction with an estimated expanded uncertainty (k = 2) in composition of 0.001 mol fraction; it was analytically verified by determining the dielectric permittivity according to Eq. 1 of the measured frequency at p = 1 MPa and T = 280 K and compared to the dielectric permittivity ε (p, T) calculated with the Harvey and Lemmon [29] correlation based on the density calculated with the GERG-2008 EOS of Kunz and Wagner [2]. The deviation in dielectric permittivity is 0.02 %, which is equivalent to a deviation in composition of 0.013 mol fraction.

Table 3 Molar purities of the pure substances used for the gravimetrical preparation of the (0.35 C₃H₈ + 0.65 CO₂) mixture investigated in this work

3.3 Measuring Procedure and Sample Handling

Based on the predicted mode-shape functions, liquid volume fraction measurements of the binary (0.35 C₃H₈ + 0.65 CO₂) mixture were conducted for an isotherm at T = 280 K. The liquid volume fractions were measured with respect to pressure increments of (0.01 to 0.40) MPa along an isothermal pathway, fully crossing the two-phase region. Figure 8 shows the experimental pathway of the isotherm measured.

Fig. 8

p, T diagram of the (0.35 C₃H₈ + 0.65 CO₂) mixture showing the experimental pathway. The phase boundary was calculated with the GERG-2008 EOS of Kunz and Wagner [2]; △, experimental pathway at T = 280 K

Before conducting the measurements, the apparatus was evacuated at T = 280 K using a rotary vane pump (1 Pa) and then flushed and filled with the mixture under investigation. The filling rate was kept to 10 ml·min⁻¹ to avoid demixing and stratification. Sample cylinder, syringe pump, and corresponding tubes were kept at ambient temperature, and prior to the filling process, the measuring cell was cooled to the target temperature. The gaseous fluid contained within the measuring system was then compressed isothermally up to saturation pressure using the syringe pump. Subsequently, the measuring system was isolated from the syringe pump, and the gaseous fluid inside the syringe pump was compressed until fully liquid. A pre-defined amount of liquid was then incrementally transferred to the microwave cavity via the syringe pump. The microwave cavity was isolated after each filling step and homogenized by mixing both phases over a period of 110 min using the circulation pump, after which time, the system was left to equilibrate until pressure and frequency response became constant over 60 min. In total, measurements were separated by approximately 3 h. Ultimately, the amount of liquid per injection was calculated based on the volume change of the syringe pump and accounted for temperature and density differences between the syringe pump and microwave cavity using the GERG-2008 EOS of Kunz and Wagner [2], as implemented in the REFPROP database [30]. The increment of sample injected was adjusted to match the sensitivity of the cavity modes at each liquid height to capture the sharp transitions in ${G}_{n}$, based on the simulated response curves. The volume of injected liquid was recorded at each equilibrium state and the pressure, temperature, and resonant frequencies were continuously logged using custom LabVIEW data acquisition software.

4 Results and Discussion

The resonant frequencies for Modes 1, 3, and 5 of a binary mixture with a composition of (0.35 C₃H₈ + 0.65 CO₂) were measured isothermally at T = 280 K across the two-phase region. The overall dielectric permittivities were calculated for each $\varLambda$ using Eq. 2 and compared to values simulated with FEA at the same conditions. Results are presented in Fig. 9. A good agreement can be observed between the experimental and FEA simulated mixture data for Modes 1 and 5 with only small differences at $\varLambda$< 0.1. These deviations may arise from the lower electric field intensity below the annular gap of Mode 5 compared to Mode 1 (see Figs. 2, 3). For Mode 3, however, a comparison between experimental and simulated dielectric permittivities shows good agreement at $\varLambda$> 0.2 but reveals larger discrepancies at $\varLambda$< 0.2.

Fig. 9

Comparison between measured and simulated (FEA) dielectric permittivity of the (0.35 C₃H₈ + 0.65 CO₂) mixture at T = 280 K. Lines indicate simulated values, symbols represent experimental values: Mode 1; Mode 3; Mode 5

These discrepancies may arise from the liquid volume fraction $\varLambda$ in the low volume region, either due to systematic errors in the experiment or fitting process. Experimentally, it may be possible that after mixing and for small liquid volumes, the liquid forms a thin film on the base surface of the cavity, resulting in a higher effective liquid level as probed by the cavity modes. In terms of fitting, errors in the $\varLambda$ determination and the associated allocation of the dielectric permittivity (see Sect. 2.3 and Fig. 5a) could also result in the observed deviations. Future work would aim to refine the cavity design to eliminate this possible experimental systematic error.

Utilizing the calculated dielectric permittivities for the three modes at each $\varLambda$, the corresponding compositions of the vapor and liquid phase for (x_i, y_i) as well as the vapor and liquid phase densities (ρ_vap, ρ_liq) were determined by solving the two systems of equations as described in Sect. 2.3. The results of the phase compositions are presented in Fig. 10 and compared to values predicted with the GERG-2008 equation of sate of Kunz and Wagner [2]. A good agreement can be observed for the vapor phase compositions (y_i) throughout the entire heterogeneous two-phase region with an average absolute deviation (AAD) of 6.8 %. In the same way, the liquid phase compositions (x_i) follow the trend predicted with the reference EOS, albeit to a lesser extent than the vapor phase values, with rather large differences around $\varLambda \ge$ 0.2 (annular gap). The AAD for the liquid phase compositions over the entire $\varLambda$-range is 8.6 %. A potential reason might be the uncertainty of the predicted phase boundary, which can be as large as 5 % (or even more) like reported for the GERG-2008 EOS by Kunz and Wagner [2]. Furthermore, the mixing rule introduced by Harvey and Prausnitz [31], and that is integrated in the Harvey and Lemmon [29] correlation to predict dielectric permittivities for mixtures, is used to calculate mixture molar polarizabilities (see Sect. 2.3). Here, the pure component values of the mixture’s compounds are combined using the Clausius–Mossotti relation for non-polar fluids. While pure component molar polarizabilities for the vapor phase have been measured with relatively low uncertainties for many natural gas fluids, the pure component molar polarizabilities for the liquid phase suffers from rather large uncertainties due to the absence of experimental data [29, 39] representing a potential weakness in the method’s ability to characterize two-phase properties.

Fig. 10

Comparison of experimental and calculated liquid and vapor phase compositions (x_i, y_i) of the (0.35 C₃H₈ + 0.75 CO₂) mixture at T = 280 K. The calculated phase compositions were determined with the GERG-2008 equation of state of Kunz and Wagner [2]. Data calculated with the EOS are indicated with lines, and experimental data are indicated with markers. , x_{C3H8, EOS}; , x_{CO2, EOS}; , y_C3H8, EOS; , y_{CO2, EOS}; , x_{C3H8, exp}; , x_{CO2, exp}; , y_{C3H8, exp}; , y_{CO2, exp}

The experimental phase densities of the vapor and liquid phase (ρ_vap/liq) in comparison with predicted values with the GERG-2008 EOS of Kunz and Wagner [2] are presented in Fig. 11. The predicted phase densities were calculated using the experimental phase compositions. The experimental vapor phase compositions and the vapor phase densities (ρ_vap) are in good agreement with the predicted values except for the highest liquid volume fraction measured ($\varLambda =$ 0.9454). This increased deviation is due to all three modes being almost identical in their ${G}_{n}$ response and insensitive to the diminishing vapor phase; the consequence is that the system of equations based on Eq. 4 for three modes no longer provides an independent basis for reliable inversion and parameter estimation. For $\varLambda$ < 0.9, the AAD of the experimental saturated vapor densities is 15.4 %. The liquid phase densities show larger differences in the range of small liquid volume fractions up to approximately $\varLambda =$ 0.2. In the case of liquids, the robustness of the inversion and solution for density improves as the liquid volume fraction increases, for complimentary reasons as described for the vapor phase. For $\varLambda$ > 0.1, the AAD of the experimental saturated liquid densities is 4.7 %.

Fig. 11

Comparison of experimental and calculated phase densities (ρ_liq, ρ_vap) of the (0.35 C₃H₈ + 0.75 CO₂) mixture at T = 280 K. The calculated phase densities were determined with the GERG-2008 equation of state of Kunz and Wagner [2] and the Harvey and Lemmon correlation [29]. Data calculated with the EOS are indicated with lines, and experimental data are indicated with markers. , ρ_{liq, EOS}; , ρ_{vap, EOS}; , ρ_{liq, exp}; , ρ_{vap, exp}

We note that the authors of the GERG-2008 EOS do not report an uncertainty for saturated vapor and liquid densities of the (C₃H₈ + CO₂) system studied in the present work. The overall VLE data situation (considered for the GERG-2008) for this binary system includes approximately 660 data points (published within the timeframe from 1951 to 2001) over almost the entire compositional range for temperatures between T = (211 and 361) K and pressures up to 6.9 MPa. Only 89 data points were used to fit the adjusted reducing functions (no departure function); for these data, the AAD ranges between (2.0 and 3.1) % while it goes up to 13.1 % when all data are considered.

Notwithstanding the limitations discussed for determining the liquid volume fraction and composition and densities of the two phases, the presented investigations serve as proof of concept, albeit with relatively large experimental uncertainties. Therefore, no detailed uncertainty analysis has been carried out; this is part of ongoing research, and improved results including a corresponding uncertainty analysis will be presented in future publications.

5 Conclusions and Outlook

In this work, we present a novel approach to fully describe the VLE phase behavior determination using a single measuring device, demonstrated through an examination of a selected binary mixture. An apparatus based on a microwave re-entrant cavity resonator was employed to characterize a binary mixture by investigating liquid volume fractions ($\varLambda$) throughout the two-phase region along a complete tie line. The experimental setup has been modified by installation of a circulation pump on the resonator to ensure uniform mixing throughout the sample. Liquid volume fraction measurements of a (0.348 C₃H₈ + 0.652 CO₂) mixture were carried out along an isothermal pathway at T = 280 K. The mixture was prepared gravimetrically with an expanded uncertainty (k = 2) in composition of 0.001 mol fraction. It has been shown that FEA provides a reliable path to characterize the frequency response of a cavity to $\varLambda$. The modeling was verified against pure fluid measurements with very good agreement between measured and modeled values. The results for pure fluids and the binary mixture validate that this method could reasonably be applied to measurements of binary mixtures where the properties of the components are not well known. Based on the FEA calibration curves and the measured frequency shift across the two-phase region, a two-stage mathematical framework was developed for the determination of the vapor and liquid phase compositions (x_i, y_i) and phase densities (ρ_vap/liq) within the heterogeneous region. The experimental vapor phase compositions (y_i) and densities (ρ_vap) are in good agreement with values predicted with the GERG-2008 EOS of Kunz and Wagner [2] throughout the two-phase region, with an average absolute deviation of 7.7 % for composition and 13.5 % for density. Compared to literature data based on analytical measurement techniques [5,6,7,8,9], the composition determination is in good order, demonstrating that this technique already provides useful information as is. With these findings, it has been demonstrated for the first time that thermophysical properties of a binary mixture with a known overall composition can be determined from experiments with a microwave cavity along tie lines using a synthetic approach.

We propose proceeding in two directions: (1) optimizing the apparatus and (2) refining the fitting process and mathematical framework. The former includes enhancements on the geometry of the cavity to improve the electromagnetic field distribution throughout sample space, i.e., by implementing multiple bulbs or other resonator geometries, as well as reducing the sample volume to minimize the quantity of sample needed. Hard transitions and sharp edges inside the resonator shall be softened to achieve better sample mixing. Similarly, an advanced mixture agitation system is needed to minimize the dead space and hence reduce uncertainties in measurements. For (2) we identify the quality and availability of molar polarizabilities for pure fluids in liquid conditions as one potential weak spot [29], as well as suitable mixing rules for polar fluids. For mixture calculations, the corresponding pure components molar polarizabilities are combined with the Clausius–Mossotti equation (see Eq. 7). They form the basis to link the mixture’s density with its molar polarizability and dielectric permittivity for both phases via the mixing rule introduced by Harvey and Prausnitz [31] that is integrated in the Harvey and Lemmon [29] correlation for the prediction of dielectric properties. It is therefore of particular importance to have good knowledge of the underlying pure component liquid molar polarizabilities.