Development of Numerical Model of the Thermal State of an Asteroid with Locally Rough Surface and Its Application

Abstract

We present a numerical method for simulating a disk-resolved thermal image of an asteroid with small-scale roughness. In our method, we carry out numerical thermal evolution model of a small but rough area taking into account its latitude, shadowing effect, and re-absorption of the thermal radiation by neighbor. By visualization of the resulting temperature distribution for an observation direction, we obtain the thermal flux from the area as a function of the observation direction. Then thermal image of an asteroid with random topography is constructed. The resulting daytime temperature evolution profile is different from the well-known parabolic shape due to the surface roughness, implying that the daytime temperature evolution profile is a diagnostic to evaluate the surface roughness. Although this model is inapplicable to a morphologically complex asteroid such as Itokawa, the target body of Hayabusa2, Ryugu is generally convex and suitable for application of our model. Furthermore, the study presents predictions of the location shift of Ryugu trajectory after one orbital rotation due to the thermal moment caused by the rebound force from thermally emitted photons known as the Yarkovsky effect. This model is thus verifiable by precise calculation of the ephemeris of Ryugu.

1 Introduction

The thermal evolution of asteroids is considered simple because they are so small that their internal heating and dynamic convection are negligible, and because they are airless bodies, meaning heat transfer above the surface via advection in a hydrosphere does not occur. Their thermal status changes by the balance between solar irradiation and thermal radiation into space. The typical thermal skin depth for the diurnal solar flux change is several 10 s of cm or less, which is much shorter than the observable asteroids. Thus in the previous studies the thermal evolution of an asteroid surface is simulated by a one-dimensional thermal conduction model in which the vertical direction is divided into layers and the boundary condition at the surface is given by the balance between the solar radiation and the thermal radiation (e.g., Fig. 1 in [1]). Received solar energy is partly transported to the subsurface by thermal conduction. After the meridian, part of the subsurface energy returns to the surface region, so the surface temperature does not decrease immediately with the solar incident angle. This effect is known as thermal effusivity (thermal inertia) and given by $\Gamma =\sqrt{k\rho {C}_{\mathrm{p}}}$ where $k$ is thermal conductivity, $\rho$ is density, and ${C}_{\mathrm{p}}$ is heat capacity. The thermophysical properties of the surface and subsurface layers are important for estimating the evolution of the surface temperature of an asteroid. Thermal inertia is a particularly good diagnostic parameter because it can be directly obtained from astronomical or spacecraft observations of surface brightness temperature. Note that the dimension of thermal inertia ($\mathrm{J}\cdot {\mathrm{m}}^{-2}\cdot {\mathrm{s}}^{-0.5}\cdot {\mathrm{K}}^{-1}$) contains the scale of time, meaning time-series observations or specific assumptions on time evolution are required to estimate thermal inertia. One way to estimate the thermal inertia from an observation data is parabolic fitting of the daytime surface temperature to obtain the peak position. The thermal inertia is estimated from the shift of the peak position from the noon [e.g. 2]. Once the thermal inertia is obtained, physical parameters such as grain size and porosity of the surface materials can be estimated (e.g., [3, 4]).

When the asteroid surface is rough, the relation between observed temperatures and thermophysical properties is not so straightforward. The parts of a boulder facing the sun would be heated to significantly higher temperatures compared to a flat surface, whereas parts of boulder pointing away from the sun would remain systematically. Consequently, the brightness temperature of a rough surface depends strongly on the observation angle and the phase angle between insolation and observation vectors. Concave structures such as impact craters can also change the bulk brightness temperature of a region. In this case, in addition to shadowing and slope effects, there is a reabsorption effect, by which thermal radiation from a distant position acts as an additional heat source that changes the temperature [5,6,7,8,9]. These effects should be treated as a bulk parameter when analyzing data obtained from astronomical or spacecraft observations. A series of studies by Hapke (e.g., [10]) considered the roughness effect by introducing a “roughness” parameter. By contrast, we characterize surface roughness using parameters used in the preparation of the rough surface, so the relation between the surface roughness and the parameters is straightforward.

Thus, in this study, we construct rough surfaces under simple assumptions that clarify the relation between parameters and surface morphology. We then simulate the thermal evolution of rough surfaces considering the shadowing effect, the slope effect, and reabsorption of thermal radiation. Finally, we visualize the temperature distribution for easier comparison of our results with actual observational data obtained in space missions.

The goal of this study is to clarify the relation between asteroid surface roughness and observed surface temperature distributions. We use the size, orbit, and spin rotation period and angle of the asteroid 162173 Ryugu, the target body of Hayabusa2, as an example. For simplicity, we assume a spherical target in this study. A separate paper [11] compares our numerical results with actual observation data acquired by TIR onboard Hayabusa2 [1, 12] which is a thermal imager at wavelengths in the 8–12 μm with FOV of $16^\circ \times 12^\circ$. The purpose of [11] was to obtain thermosphysical properties and roughness parameters of the surface of Ryugu from the comparison. However, this study did not describe the model precisely. Further studies [13, 14] applied this thermal model and data assimilation methods to in situ infrared data. On the other hand, this paper focus on the description of model development and its results regardless of Hayabusa2’s observation condition to clarify the relationship between the surface roughness and the thermal evolution.

2 Numerical Method

We numerically create rough surfaces containing $32\times 64$ triangle polygons and simulate the thermal evolution of each polygon, considering diurnal change of the solar incident angle and reabsorption of thermal radiation from other polygons. We then visualize the rough surface to evaluate thermal radiation from a small area as a function of the observation direction and the observation time. Finally, we numerically create a simulated TIR image by indicating the thermal radiation from each local point on a sphere. The total thermal moment from the sphere is also calculated by integration of the thermal moment to the whole direction.

2.1 Preparing a Rough Surface

Three parameters express the numerically created surface roughness: $\sigma$, $L$ and $D$. The initial surface shape is flat and covered with $32\times 32\times 2$ equatorial triangles (the factor of $2$ comes from a pair of normal and reverse triangles; see Fig. 1a). Then equatorial triangles with side length ${2}^{L}$ are selected and their vertices are moved perpendicular to the original level (Fig. 1b). The movement distance is randomly determined from a Gaussian distribution function with variance $\upsigma$ times the horizontal side length (${2}^{L}$). Next, we divide each triangle into four congruent triangles (Fig. 1c) and similarly move the three new vertices perpendicular to the original level. We iteratively divide triangles $\mathrm{D}$ times. Finally, the horizontal length of the smallest triangle becomes ${2}^{L-D}$ times the horizontal side length of the original unit triangle (Fig. 1d). The method above is following the Gaussian model in [8].

Fig. 1

Preparation of a rough surface. Starting with a flat surface, vertices move vertically. Each triangle polygons are divided into smaller triangles iteratively

2.2 Thermal Evolution of Each Polygon

We solve a one-dimensional thermal evolution equation for each polygon. The basic equation is

$$\rho {C}_{\mathrm{p}}\frac{\partial T}{\partial t}=\frac{\partial }{\partial z}\left(k\frac{\partial T}{\partial z}\right)+F$$

(1)

$$F=\left\{\begin{array}{cc}{F}_{\mathrm{S}}-{F}_{\mathrm{T}}+{F}_{\mathrm{R}}& \mathrm{for} z=0\\ 0& \mathrm{for} z\ne 0\end{array},\right.$$

(2)

where $T$ is temperature, $t$ is time, $z$ is depth from the surface, $F$ is flux at the surface, ${F}_{\mathrm{S}}$ is solar radiation, ${F}_{\mathrm{T}}$ is thermal flux from the surface, and ${F}_{\mathrm{R}}$ is thermal irradiation from other polygons. Solar radiation is calculated considering the solar distance and diurnal change of the incident angle. The shadowing effect [6, 15] is also considered. If solar light is blocked by other polygons, ${F}_{S}$ becomes $0$. Solar distance and diurnal trajectory of the sun from a latitude is calculated using the SPICE toolkit [16, 17]. Density, specific heat, and thermal conductivity are assumed homogeneous throughout the simulated area. We fix $\uprho {C}_{\mathrm{p}}=3\times {10}^{6} \text{J } \cdot {\text{m}}^{-3}\,\cdot {\text{K}}^{-1}$ regardless of temperature for simplification while changing the thermal conductivity as a function of thermal inertia $\Gamma$ as $k={\Gamma }^{2}/\rho {C}_{\mathrm{p}}$. This calculation is known to be mathematically equivalent to simultaneous arrangement of $\rho$, ${C}_{\mathrm{p}}$, and $k$. We fix the heliocentric location of Ryugu for a given day and time, then numerically simulate the thermal evolution by solving Eqs. 1 and 2 for at least $10$ spins to obtain the equilibrium state. $100$ layers are used in this numerical simulation. The thickness of the uppermost layer is $1/50$ that of the thermal skin depth for diurnal change and the thickness of each layer is $1.01$ times that of its upper layer, resulting in the simulated region having total thickness of about $3.4$ times the thermal skin depth.

2.3 Thermal Radiation and Its Reabsorption

The thermal radiation from the surface is

$${F}_{\mathrm{T}}=\varepsilon {\sigma }_{\mathrm{B}}{T}_{\mathrm{S}}^{4},$$

(3)

where $\varepsilon$ is emissivity, ${\sigma }_{\mathrm{B}}$ is the Stephan–Boltzmann constant, and ${T}_{\mathrm{S}}$ is surface temperature. We assume that the thermal radiation is emitted isotropic from each polygon and $\varepsilon =0.90$ for the thermal infrared range, a generally used value in the previous studies [2, 18]. Heat flux is assumed to be emitted isotropically. Thermal radiation partially irradiates and is absorbed by other polygons. To consider this reabsorption effect, we introduce a view factor

$${F}_{\mathrm{R},i}={\sum }_{j}{V}_{i,j}\cdot \varepsilon {F}_{\mathrm{T},j}$$

(4)

$${V}_{i,j}=\left\{\begin{array}{cc}2\mathrm{cos}{\theta }_{i,j}\left(1-\frac{1}{\sqrt{1+{S}_{j}\mathrm{cos}{\theta }_{j,i}/\pi {d}^{2}}}\right)& {\text{visible}}\\ 0& {\text{invisible}}\end{array}\right.,$$

(5)

where ${F}_{\mathrm{R},i}$ is thermal flux reabsorbed by the $i$th polygon, ${F}_{\mathrm{T},j}$ is thermal flux from the $j$th polygon, ${\theta }_{i,j}$ is the angle between the normal vector of the $i$th polygon and the vector from the $i$th polygon to the $j$th polygon, ${S}_{j}$ is the surface area of the $j$th polygon, and $d$ is the distance to the $j$th polygon from the $i$th polygon (see [7]). In this equation, the absorption coefficient is assumed to be same as the emissivity in Eq. 3, because they have the same target wavelength range.

2.4 Scattering Law

Previous studies of thermal evolution of the moon and asteroids assumed a Lambertian function for the scattering law of their surface, i.e., absorption efficiency of solar flux is independent on the solar incident angle (e.g., [2, 5]). The Lommel–Seeliger scattering law is widely used in analysis of visible wavelength images acquired by spacecraft and ground observatories (e.g., [19, 20]). The Lommel–Seeliger function assumes attenuation in the target surface layer and is adopted as a fundamental disk function (dependency on the incidence and emission angles) in a series of works by Hapke (e.g., [10, 21]).

Solar light is the heat source for thermal evolution of surface layers of the moon and asteroids, and its energy is mainly transferred as visible wavelength. We thus adopt the Lommel–Seeliger scattering law to simulate the absorption efficient of solar light at the surface being consistent with the albedo value obtained by camera observations [22]. The Lommel–Seeliger scattering law gives the radiance $I$ from a target as a function of not only the incident angle $i$, but also the emission angle $e$ as

$$\frac{I}{J}=\frac{w}{4\pi }\frac{\mathrm{cos}i}{\mathrm{cos}i+\mathrm{cos}e},$$

(6)

where $J$ is irradiance and $w$ is single-scattering albedo (e.g., [23]). Sugia et al. [22] derived the standard-condition reflectance ($I/J$ for $i=30^\circ$ and $e=0^\circ$) of Ryugu to be $0.016$ from the optical navigation cameras (ONC) on board Hayabusa2. Note that the reflectance is obtained as a bulk value of the surface. Thus, we arrange the $w$ value to achieve the same reflectance as the camera observation. See Appendix 1 for details.

2.5 Visualization

The brightness temperature of a rough surface is known to change with the observation direction. For example, the brightness temperature of a rough surface in the morning is higher in observations from the east than those from the west. Brightness temperature thus depends not only on latitude and local time, but also on the zenith and azimuth angle of the observation direction. We calculate the brightness temperature by rendering an observation of a rough surface whose temperature distribution is simulated as above, as a function of the observation direction.

We prepare a $256\times 256$ field of view and situate visible polygons from the far side to the near side to simulate the thermal image, so that the hiding effect is automatically satisfied. The pixel value is the brightness of each polygon, and does not need to be an integer value as in actual camera images. Note that the pixel value should not be the polygon temperature, but the intensity of thermal radiation from the polygon. If the purpose is to simulate Hayabusa2 TIR images, the intensity is the thermal radiation integrated within a wavelength range between $8$ μm and $12$ μm [11, 12, 15].

Once a simulated image is obtained, the averaged intensity of thermal radiation from the rough area is calculated as the averaged value of pixels occupied by polygons. The averaged brightness is converted to brightness temperature considering the emissivity. We then map the brightness temperature onto a sphere whose spin axis is the same as that of Ryugu, assuming the direction of the observer to be same as the earth direction, because the Hayabusa2 spacecraft stayed between Earth and Ryugu [2, 11]. The direction and spin axis in the J2000 frame and the directions to the Earth and the Sun are calculated using the SPICE toolkit.

3 Numerical Results

As a first step we carry out the numerical simulation of thermal evolution of a rough surface area at the latitude of 32 N, 0 N (equator), and 32S. Figure 2 represents the geometries of target areas described in Figs. 3, 4, and 5 below. Figure 3 shows the time series brightness temperature change of a rough surface. The latitude of the rough surface is assumed to be 32 N and the date is assumed to be 1 August 2018, resulting in the solar distance and subsolar latitude being $1.06\,{\text{AU}}$ and $8.36{\text{S}}$, respectively. Thermal inertia is assumed to be 200 in MKSA units. Roughness parameters are assumed as $\sigma =0.4$ and $L=D=2$ as a reference case. The observation directions are fixed to $30^\circ$ north from nadir (upper panel), nadir (middle panel), and 30° south from nadir (lower panel). As this figure shows, the brightness temperature of the rough surface is hotter in the observation from the south, because the rough surface is on the northern hemisphere and thus the sun goes through the southern sky.

Fig. 2

Geometric relationship of Figs. 3, 4, and 5. The location of target points are indicated as zig-zag lines and observation directions for each target are indicated by arrows

Fig. 3

Diurnal change of the brightness temperature distribution on 1 August 2018. The observer is at $e=30^\circ$ north (top panel), nadir (middle panel), and $e=30^\circ$ south (bottom panel). Each small panel shows the temperature distribution at local times of 7 h, 9 h, 12 h, 15 h, and 17 h. At the top panel, the sun rises from the left side, because the small area is observed from north to south

Fig. 4

Diurnal change in bulk brightness temperature of the rough surface shown in Fig. 3 for cases with the observer at the north, nadir, and south. Note that the temperature profile should be identical if the surface is flat. The separation comes from the surface roughness

Fig. 5

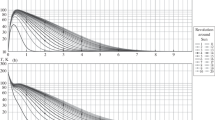
Diurnal change in the bulk brightness temperature of the rough surface on 1 August 2018 for various observation angles and local latitudes of the rough surface. Three curves in each panel represent the diurnal temperature change with the surface roughness $\sigma =0.0, 0.2, 0.4$. The thermal inertia is fixed to 200 in MKSA units

Figure 4 shows a time evolution of the averaged brightness temperature of the rough surface depending on the observation direction with the same parameters as in Fig. 3. The temperature reaches $346\,{\text{K}}$ for the observation from the south and becomes as low as $309\,{\text{K}}$ when the rough surface is observed from the north. These figures clearly show that the brightness temperature of the rough surface highly depends on the observation direction, even at nighttime.

The time evolution of the surface temperature changes smoothly and is convex, similar to the temperature profile discussed in previous studies (e.g., [2]). Figure 5 compares numerical results for rough and smooth surfaces. As this figure shows, the peak temperature decreases and its timing delays with roughness $\sigma$. This tendency is qualitatively similar to the delay of the peak temperature with the thermal inertia $\Gamma$. It is therefore not easy to distinguish effects from $\sigma$ and $\Gamma$ in observation data.

Hayabusa2 maintains its position along a line between Ryugu and Earth. The observation direction in the inertial coordinate system is thus fixed during at least the time scale of one spin rotation of Ryugu (7.63 h). In this case Hayabusa2 moves on the celestial sphere as seen from a standpoint fixed to a local area on Ryugu’s surface. Figure 6 shows the trajectory of Hayabusa2 and the sun on the celestial sphere from latitudes of 32N, 0N, and 32S. Black dots on those trajectories represent their celestial positions at local times of 9 h, 12 h, 15 h, and 17 h from west to east. As this figure shows, Hayabusa2 is near the sun in the celestial sphere. The apparent temperature distribution on the rough surface as observed from the satellite is then simulated using the time series of the observation angle as shown on the right of the trajectory map in Fig. 6.

Fig. 6

Change in the brightness temperature distributions of the rough surface at 32 N (top row), equator (middle row), and 32S (bottom row) at the local time of 9 h, 12 h, 15 h, and 17 h on 1 August 2018. The observer is assumed to be above the sub-Earth point. The leftmost panel shows the track of the sun and Earth from the small area. Numerals beside the track represent the local time. The top panel shows the same area as in Fig. 3, but the observation angle is different. The color scale is the same with Fig. 3

Figure 7 shows simulated TIR images with various thermal inertias and roughness parameters. The shape of target body is assumed to be a perfect sphere and the thermophysical properties are homogeneous throughout the surface and subsurface of the target. To create this figure, we followed the simulation method by Takita et al. [2]. Again, note that under the observation conditions on 1 August 2018, the Sun–Ryugu–Hayabusa2 angle was as small as 19°, so TIR onboard Hayabusa2 observed almost the entire dayside hemisphere. When the asteroid surface is flat ($\upsigma =0.0$), the highest temperature is achieved at the subsolar latitude, but its longitude moves westward with the thermal inertia. At the same time, the maximum temperature decreases with the thermal inertia. However, the brightness temperature distribution expands north and south with surface roughness, due to the local slope in each area. When $\upsigma$ is as large as $0.4$, the brightness temperature seems almost flat in the disk except for the rim.

Fig. 7

Simulated image of the spherical asteroid observed as from the earth direction on 1 August 2018 for various thermal inertia and surface roughness. North is upward. The center of each panel is the sub-earth point. A star symbol indicates the subsolar point. The color scale is the same with Fig. 3

Figure 8 shows the time evolution of the apparent temperatures at the latitude of $32{\text{N}}$, $0{\text{N}}$, and $32{\text{S}}$ for various thermal inertias, as a function of local time. The shape of the temperature evolution when $\sigma =0$ (flat) is the same as the temperature evolution for the nadir observation (Fig. 4). However, the daytime temperature profile for a rough surface flattens and the peak temperature is unclear. When $\sigma =0.4$, the temperature profile shows a double-peaked shape. This indicates that the effects of thermal inertia and roughness can be discerned according to the shape of the temperature profile [11] in Hayabusa2 data.

Fig. 8

Change in apparent brightness temperature at 32N, equator, and 32S positions as observed from the earth direction for various thermal inertia. The profile when σ = 0 is similar to that shown in Fig. 5, but the shape changes with surface roughness

Integration of pixel values in the simulated disk image gives the thermal moment to the observation direction. We vary the observation direction to obtain the distribution of the thermal moment on the sphere (Fig. 9). The peak thermal moment appears at the subsolar latitude but just after the meridian, because of the thermal inertia effect. The difference between the solar direction and the direction of maximum thermal moment causes a small acceleration or deceleration along the orbit due to the momentum exchange with solar radiation and thermally emitted photons, which is the well-known Yarkovsky effect [24,25,26].

Fig. 9

The thermal moment from the spherical asteroid as a function of longitude and the latitude on 1 August 2018 for various thermal inertia and surface roughnesses. Note that the thermal moment peak is obvious for smaller thermal inertia and larger surface roughness

We conducted numerical simulations in the same manner for days other than 1 August 2018. The next section presents and discusses the time evolution trend.

4 Discussion

The rough surface in this study was created by random dislocation of each vertex, resulting in a surface with an angular shape. We varied $\upsigma$ as a free parameter while fixing the division number $\mathrm{D}$ to $2$. Figure 10 shows the slope distribution of the rough surface with various values of $D$. As the figure shows, our rough surface contains hardly any horizontal areas. This causes differences in bulk brightness temperatures among flat and rough surfaces, especially in the morning and evening. When $D$ is nonzero, a peak value occurs in the slope distribution. The slope value of the peak increases with $\mathrm{D}$ and the slope distribution function widens with $D$. When $D=2$, the peak occurs at around $\mathrm{cos}\theta =0.56$ and FWHM of the distribution is about $0.55$. When the surface is covered by spheres, the angle distribution is

$$F\left(\mathrm{cos}\theta \right)=\mathrm{cos}\theta \sqrt{1-{\mathrm{cos}}^{2}\theta }d\left(\mathrm{cos}\theta \right),$$

(7)

which achieves a peak value at an angle of $\mathrm{cos}\theta =1/\sqrt{2}\approx 0.7$ and the FWHM of the distribution is $1/\sqrt{2}$. Thus, our model with $D=2$ represents a peakier slope distribution than when the surface is covered by spheres.

Fig. 10

Histograms of the cosine of the surface slope, where the slope is the angle between the normal and vertical vectors

Previous works showed that the thermal profile of a concave area like a crater is highly affected by the reabsorption effect [5, 7, 8]. If the shape of the target body of Hayabusa2 was complex like Itokawa (the target body of Hayabusa), our model could not be easily applied to the global temperature distribution, because thermal radiation from distant areas could work as an effective heat source. Fortunately, however, Ryugu has a double-topped and generally convex shape [27]. It is thus reasonable to apply our numerical results to Ryugu, except in the vicinity of small craters or boulders [11, 28]. Moreover, the reflectance of Ryugu is as small as $0.016$ [22], which allows omitting multiple scattering of solar light over the surface.

Our model shows that the daytime temperature profile as observed from a fixed direction flattens. This happens because the Sun–Ryugu–Hayabusa2 angle was as low as 19° on 1 August 2018, so Hayabusa2 preferentially observes the sunlit area even during morning and evening. In contrast, the temperature at noon becomes lower than the flat surface temperature. This is partly because of the increased surface area due to the roughness, which causes solar radiation to be shared over a wider area, decreasing the surface temperature. Note that bulk thermal radiation from a surface is unaffected by roughness as long as the surface temperature is uniform. Thermal radiation from a polygon is partially interrupted by other areas to keep the bulk thermal radiation the same as that from a flat surface (e.g., [7]). Thus, if the thermal inertia is negligible and the surface temperature can be considered uniform, the surface temperature can be estimated from $\upepsilon {\sigma }_{\mathrm{B}}{T}_{\mathrm{S}}^{4}=S/{f}_{\sigma }$, where ${f}_{\sigma }$ is the surface area enhancement due to surface roughness. In reality, however, the thermal inertia of an asteroid surface is ineligible, and the surface temperature is heterogeneous due to the roughness. In the case of a rough surface, convex parts are preferentially heated and then effectively cooled by radiation. This effectively disperses thermal energy into space, because thermal radiation works more effectively at higher temperatures. As a result, the peak temperature lowers for rougher surfaces and the temperature profile flattens with roughness. With $\upsigma \ge 0.4$, the temperature at noon could become colder than the apparently higher morning and evening temperatures, resulting in a double-peaked temperature profile (Fig. 8). The temperature profile thus cannot be expressed by a simple function like a parabolic function (e.g., [2]). In other words, the effect of thermal inertia (delayed and decreased peaks) and the surface roughness effect (enhanced morning and evening temperatures and decreased noontime temperatures) can be separated in the data analysis process [11]. On the other hand, Thermal Emission Spectrometer (OTES) on board Origins, Spectral Interpretation, Resource Identification and Security-Regolith Explorer (OSIRIS-Rex) observed the surface temperature of Bennu from nadir position [29]. As a result, the diurnal temperature pattern obtained by OTES did not show the flattened pattern like TIR result. Thus, the thermal inertia was estimated from the comparison between daytime and nighttime temperatures [30].

The thermal moment force on an asteroid is calculated as the thermal radiation energy divided by light speed $c$, which can be calculated from the simulated images. Assuming pixel value $T\left(x,y\right)$ represents the temperature at pixel $\left(x,y\right)$ and $T\left(x,y\right)=0$ in the background, the thermal moment $\mathrm{m}$ toward the observer is

$$m=-\frac{{\gamma }^{2}}{c}\sum_{x,y}\epsilon \sigma {T\left(x,y\right)}^{4},$$

(8)

where $\gamma$ is the pixel size at the asteroid center. We calculated the total thermal moment by omni-integration of the thermal moment on the first day of every month from 2018 to 2019. Figure 11 shows the time profile of the thermal moment along the orbital track for various thermal inertia and surface roughness. When the thermal inertia is as small as 10 in MKSA units, the thermal moment on the asteroid becomes positive from perihelion to aphelion, but negative from aphelion to perihelion. This is because the subsolar point is on the trailing hemisphere from perihelion to aphelion, but on the leading hemisphere from aphelion to perihelion. Thus, if thermal inertia is negligible or the spin rotation period is long, the thermal moment would elongate the elliptical orbit of an asteroid.

Fig. 11

Time-series thermal moments on the spherical asteroid going through Ryugu’s orbit. Orange vertical lines indicate perihelion, and cyan lines indicate aphelion (Color figure online)

However, when the effect of thermal inertia is non-negligible, the Yarkovsky effect acts as a deceleration through the orbit. This is because Ryugu has retrograde spin, so the maximum temperature is attained on the leading hemisphere. The deceleration maximizes at a thermal inertia around 200. When the thermal inertia exceeds 200, the diurnal temperature profile flattens with the thermal inertia (Fig. 6), decreasing the total thermal moment. Even with effective thermal inertia, the thermal moment along the orbit is larger in the season from perihelion to aphelion than in the other. The asteroid’s orbit should thus elongate with time.

Integration of the thermal moment estimates the dislocation after each revolution as around 200 m. This value is about a quarter of the size of Ryugu. Thus, ground observations in which the Ryugu image size is less than once pixel would be unable to detect the shift in location in the next orbit. Accumulating the shift over 10 orbits, which takes thirteen Earth years, the location shift would become 2.5 times the size of Ryugu. However, the Hayabusa2 mission measured the ephemeris of Ryugu. Thus, though beyond this paper’s scope, the Yarkovsky effect on Ryugu as estimated in this study might be verifiable by comparison with precise analysis of the Hayabusa2 orbit.

5 Summary

In this paper, we carried out the thermal evolution model of a small rough surface area on an asteroid with random topography. By using the numerical results, we derived (1) the apparent diurnal temperature change depending on the observational direction, (2) the disk-resolved temperature distribution of the target asteroid, and (3) the disk-integrated thermal radiation from the target asteroid. Results are summarized as followings:

The apparent temperature evolution of a rough area showed strong dependency on the observational direction (Fig. 3). Especially the apparent temperature changed whether the observer is on the sun-side or anti-sun-side. The difference was kept during the nighttime (Fig. 4). Although nighttime surface temperature had been thought to be a diagnostic parameter of the thermophysical properties regardless of surface morphology, our result showed that the apparent nighttime temperature is affected by the local roughness.

We found the flat structure in the disk-resolved temperature distribution (Fig. 7) as was observed by TIR onboard Hayabusa2 [11] could be reproduced by considering the surface roughness. This happened because the observation direction of Hayabusa2 on 1st Aug. 2018 was near the solar radiation direction (Fig. 6). This result indicated that the disk-resolved temperature distribution observation was suitable to estimate the thermal inertia and surface roughness independently. Otherwise if diurnal temperature change was observed only from nadir direction, the effects of thermal inertia was overlapped by the effect of surface roughness (Fig. 5; see also Fig. 1 in [1]).We also showed that the disk-integrated thermal radiation depends on not only the thermal inertia but also the surface roughness (Fig. 9). This result indicated that the surface roughness could be estimate from ground observations, but this topic is out of the scope of this paper. The availability of the roughness estimation from ground observation will be discussed in other papers. Disk-integrated thermal radiation was used to estimate Yarkovsky effect. We found that Ryugu would shift the location after one orbital rotation by around 200 m. The results of our model are verifiable by comparison with the thermal moment obtained from precise tracking of the asteroid Ryugu’s orbit.

Appendix 1: Bulk and Polygon Reflectance

The standard-condition reflectance (SCR) is the ratio of the radiance to irradiance at $i=30^\circ$ and $e=0^\circ$. If the surface is flat and has Lommel–Seeliger-type scattering, SCR can be calculated using Eq. (6) as.

$\mathrm{A}=\left(\frac{w}{4\pi }\frac{\mathrm{cos}{30}^{^\circ }}{\mathrm{cos}{30}^{^\circ }+\mathrm{cos}{0}^{^\circ }}\right)=\frac{w}{4\pi }\left(2\sqrt{3}-3\right)$. (A1).Thus, $\mathrm{w}$ is the tuning parameter for setting SCR to a value.

If the surface is rough, the relation between SCR and $\mathrm{w}$ becomes complicated, because the rough surface contains areas facing various directions. We numerically simulated the brightness of a rough surface as (1) a rough surface prepared in the same manner as the thermal model used in this study, (2) the direction of incoming light fixed to $30^\circ$ from normal and the brightness to the normal direction as calculated for each polygon, and (3) visualizing the brightness distribution and calculating the bulk brightness of the rough surface by averaging pixel values. Figure 

Fig. 12

Ratio of SCR of a rough surface to normal albedo values of a flat surface. The bulk SCR decreases with surface roughness so that the single scattering albedo of each polygon should be corrected according to the surface roughness to maintain the value of SCR

12 shows the numerical results. The bulk brightness decreases with $\upsigma$ if $\mathrm{w}$ is constant, meaning rougher surfaces require larger $\mathrm{w}$ for each polygon to maintain the bulk SCR. We use the inverse of the bulk brightness as a correction parameter for the single scattering albedo of each polygon.