1 Introduction

The first-principles prediction of thermophysical properties of molecular fluids requires detailed information on how the molecules in the fluid interact with each other. This information is contained in the potential energy surface (PES), which describes the potential energy of the fluid as a function of the positions, orientations, and internal degrees of freedom of the molecules. In a dilute gas consisting of molecules that are approximated as rigid rotors, the PES can be formulated as a sum over intermolecular pair PESs, with each pair PES depending only on the separation and mutual orientation of the two molecules that form the pair. For small molecules, accurate analytical pair PESs (see, for example, Refs. [1,2,3,4,5,6,7,8,9]) can be constructed by fitting suitable mathematical functions to interaction energies determined using high-level quantum-chemical ab initio methods such as coupled cluster with single, double, and perturbative triple excitations [CCSD(T)] [10]. Second virial coefficients can be extracted from pair potentials for rigid rotors in a straightforward manner either classically or semiclassically using standard expressions from statistical thermodynamics.

Recently, we reported cross second virial coefficients (often also referred to as interaction second virial coefficients) for the systems H2O–CO2 [7, 11], H2O–N2 [8, 12], H2O–O2 [9], and H2O–air [9] at temperatures up to 2000 K that we predicted using this proven first-principles methodology. In the present work, we extend the investigation to the H2O–CO system, which is of importance for many industrial applications, such as those involving the water-gas shift reaction. As in the mentioned previous studies, a new ab initio pair PES was developed instead of using an already existing one. We note that very recently two highly accurate H2O–CO ab initio PESs have been reported in the literature [5, 6], but the developers of these PESs did not calculate the H2O–CO cross second virial coefficient. The only first-principles values for this virial coefficient available in the literature are those of Wheatley and Harvey from 2009 [3]. They used their own ab initio PES for the calculations. Since the new PES of this work was developed at a higher level of theory than the PES of Wheatley and Harvey, the present virial coefficient values should be more accurate.

In Sect. 2, the new ab initio H2O–CO PES is presented, followed in Sect. 3 by the details of the calculation of the cross second virial coefficient. In Sect. 4, the results for the virial coefficient are presented both in the form of a table of discrete values and as a correlation fitted to these values; they are compared with experimental data and the calculated values of Wheatley and Harvey. Finally, conclusions are given in Sect. 5.

2 H2O–CO Pair Potential

2.1 Calculation of Interaction Energies

In this work, all H2O–CO interaction energies were obtained by treating the water and carbon monoxide molecules as rigid rotors to reduce the dimensionality of the pair PES from nine to five. The geometric parameters were fixed at their zero-point vibrationally averaged values. The respective H2O geometry is taken from Ref. [13]; it is characterized by an OH bond length of 0.9716257 Å (\(1 \, {\AA }=10^{-10}\; \mathrm {m}\)) and an HOH angle of 104.69°.

For CO, we obtained the zero-point vibrationally averaged bond length as part of this work using the CFOUR quantum chemistry code (version 2.1) [14]. First, we determined an accurate equilibrium bond length, starting with a geometry optimization at the all-electron (AE) CCSD(T) [10] level of theory with the cc-pCV6Z [15, 16] basis set. This yields a bond length of \(r_\mathrm {CO}=1.12796\) Å. The corresponding values for the smaller cc-pCV5Z and cc-pCVQZ [17] basis sets are 1.12821 Å and 1.12888 Å, respectively, indicating that the basis set incompleteness error for the cc-pCV6Z basis set is of the order of 0.0001 Å. In the next step, we calculated a correction for the higher CCSDT(Q) [18] level of theory by taking the difference between \(r_\mathrm {CO}\) values obtained at the AE-CCSDT(Q) and AE-CCSD(T) levels with the cc-pCVQZ basis set. The resulting correction is 0.00082 Å (0.00085 Å when the smaller cc-pCVTZ [17] basis set is used). In a similar manner, a correction for the even higher CCSDTQ [19, 20] level was calculated. This correction, at the AE level, amounts to \(-0.00021\) Å with the cc-pCVTZ basis set and to \(-0.00020\) Å with the smaller cc-pCVDZ [17] basis set. The last correction that we considered is that for scalar relativistic effects. It was determined by taking the difference between \(r_\mathrm {CO}\) values resulting from non-relativistic and scalar-relativistic AE-CCSD(T) calculations with the uncontracted cc-pV5Z [21] basis set. For the relativistic calculations, the spin-free exact two-component theory at the one-electron level [22] was chosen. The resulting correction is \(-0.00017\) Å (also when using the uncontracted cc-pVQZ [21] basis set). The final equilibrium bond length is 1.12840 Å, which is in perfect agreement with the value calculated by Heckert et al. of 1.1284 Å [23] and very close to the experimental value of 1.12832 Å [24]. In the last step, we performed a cubic force-constant calculation with CFOUR at the AE-CCSD(T)/cc-pCV5Z level with the respective equilibrium bond length to obtain the difference between the zero-point vibrationally averaged bond length and the equilibrium bond length. The resulting value of 0.00404 Å, which is also obtained when performing the calculations with the cc-pCVQZ basis set, was then added to our best estimate for the equilibrium bond length, yielding a final zero-point vibrationally averaged bond length of \(r_\mathrm {CO}=1.13244\) Å. This value is in excellent agreement with the experimental value of 1.1323 Å [25].

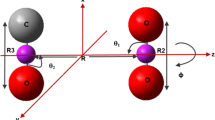
We describe each H2O–CO pair configuration by the separation between the centers of mass of the two molecules, R, and the four angles \(\theta _1\), \(\psi _1\), \(\theta _2\), and \(\phi\) as shown in Fig. 1. See also the Supplementary Information (SI) for further details. In total, 1978 symmetry-distinct angular configurations (\(\theta _1\), \(\psi _1\), \(\theta _2\), \(\phi\)) were considered for the new PES. They result from varying the angles \(\theta _1\) and \(\theta _2\) in steps of \(22.5^\circ\) starting with \(0^\circ\) and the angles \(\psi _1\) and \(\phi\) in steps of \(30^\circ\) starting with \(0^\circ\). For each of the 1978 angular configurations, 30 center-of-mass separations R in the range from 1.4 Å to 12.0 Å were considered, which results in a total of 59 340 H2O–CO configurations. We discarded some configurations with small R values for which the molecules exhibit unphysical overlap or for which severe numerical problems occurred in the quantum-chemical calculations, so that the final number of considered configurations is 57 992.

Fig. 1
figure 1

Visualization of the internal coordinates R, \(\theta _1\), \(\psi _1\), \(\theta _2\), and \(\phi\) used in this work to describe H2O–CO configurations. The center of mass of H2O is in the origin of the Cartesian coordinate system defined by the axes x, y, and z, with the latter axis passing through the center of mass of the CO molecule at the distance R from the origin in the positive direction. The molecule-fixed axes \(z_1\) and \(z_2\) are the symmetry axis of H2O and the bond axis of CO, respectively. The molecule-fixed axis \(y_1\) is in the molecular plane of H2O, is perpendicular to the axis \(z_1\), and crosses it in the center of mass of the molecule

Full size image

Interaction energies V were calculated for all configurations using the counterpoise-corrected [26] supermolecular approach at two different levels of theory. The lower level calculations were performed employing the resolution of identity second-order Møller–Plesset perturbation theory (RI-MP2) [27, 28] within the frozen-core (FC) approximation. To speed up the computations, the RI-JK approximation [29, 30] was applied in the Hartree–Fock (HF) step. All calculations were carried out using the aug-cc-pVXZ [21, 31] basis sets with \(X=4\) (Q) and \(X=5\) in conjunction with the auxiliary basis sets aug-cc-pV5Z-JKFIT [32] and aug-cc-pV5Z-MP2FIT [33] for both basis set levels. The basis sets were further enhanced by placing bond functions midway along the R axis of each H2O–CO configuration. These functions were chosen, as suggested by Patkowski [34], to be the hydrogenic functions of the respective basis set and auxiliary basis set levels used for the atoms. The correlation contributions to the calculated interaction energies, \(V_\text {RI-MP2 corr}^{X}\), were extrapolated to the complete basis set (CBS) limit employing the two-point scheme recommended by Halkier et al. [35]:

$$\begin{aligned} V_\text {RI-MP2 corr}^\text {CBS} = \frac{5^3 V_\text {RI-MP2 corr}^{X=5}-4^3 V_\text {RI-MP2 corr}^{X=4}}{5^3-4^3}. \end{aligned}$$
(1)

The total RI-MP2 interaction energies result from adding the HF interaction energies obtained at the \(X=5\) basis set level to the extrapolated correlation energies.

The higher level supermolecular calculations were performed at the CCSD(T) level of theory within the FC approximation using the aug-cc-pVXZ basis sets with \(X=3\) (T) and \(X=4\) (Q). Bond functions were not added. The differences between the CCSD(T) and the standard MP2 interaction energies, which we denote as \(\Delta V_\text {CCSD(T)}^{X}\), were extrapolated to the CBS limit in the same way as the correlation contributions to the RI-MP2 interaction energies:

$$\begin{aligned} \Delta V_\text {CCSD(T)}^\text {CBS} = \frac{4^3 \Delta V_\text {CCSD(T)}^{X=4}-3^3 \Delta V_\text {CCSD(T)}^{X=3}}{4^3-3^3}. \end{aligned}$$
(2)

By adding the \(\Delta V_\text {CCSD(T)}^\text {CBS}\) values to the total RI-MP2 interaction energies, we obtained our final interaction energies V, which we expect to be very close to the true CBS limit of the FC-CCSD(T) interaction energies. The errors with respect to this limit should be smaller than \(1 \%\) for most configurations in the well region of the PES.

The ab initio calculated interaction energies for the different levels of theory and basis sets are provided for all 57 992 investigated H2O–CO configurations in the SI. The RI-MP2 calculations were performed with the ORCA program (version 3.0.3) [36], while CFOUR (version 2.1) [14] was again used to perform the CCSD(T) calculations.

2.2 Analytical Potential Function

To represent the PES analytically, we use a site–site interaction model. As in our previous works [7,8,9], the H2O molecule has nine sites, all of which are in the molecular plane and three of which are on the symmetry axis. This arrangement results in six different types of sites. For CO, we use five sites, all of which are distinct. Thus, we have 30 distinct types of site–site combinations and altogether 45 site–site interactions. Each of them is represented by a function that depends only on the site–site separation:

$$\begin{aligned} V_{ij}(R_{ij}) = A_{ij}\exp (-\alpha _{ij}R_{ij}) - f_6(b_{ij},R_{ij})\frac{C_{6\,ij}}{R_{ij}^6} + \frac{q_{i} q_{j}}{R_{ij}}, \end{aligned}$$
(3)

where \(R_{ij}=R_{ij}(R,\theta _1,\psi _1,\theta _2,\phi )\) is the separation between site i in H2O and site j in CO, and \(f_6\) is a Tang–Toennies damping function [37],

$$\begin{aligned} f_6(b_{ij},R_{ij}) = 1 - \exp (-b_{ij}R_{ij})\sum _{k=0}^{6}\frac{(b_{ij}R_{ij})^k}{k!}. \end{aligned}$$
(4)

The total pair potential is simply the sum of the individual site–site interactions,

$$\begin{aligned} V(R,\theta _1,\psi _1,\theta _2,\phi ) = \sum _{i=1}^{9}\sum _{j=1}^{5}V_{ij}(R_{ij}). \end{aligned}$$
(5)

The site–site interaction parameters A, \(\alpha\), b, and \(C_6\) as well as the exact positions of the sites within the molecules and their partial charges q (set to zero for one of the sites in H2O) were optimized by means of a non-linear least-squares fit to the 57 992 ab initio interaction energies. The fit was constrained by enforcing that the partial charges yield neutral molecules and reproduce ab initio calculated values for the multipole moments of H2O and CO up to the octupole level. The multipole moment calculations were performed at the FC-CCSD(T)/aug-cc-pV6Z level using CFOUR [14]. The numerical values are given for CO in the SI of this work and for H2O in the SI of our work on the H2O–CO2 system [7]. In addition to including these constraints, the ab initio interaction energies were weighted by the following function:

$$\begin{aligned} w(V,R) = \frac{\exp \left[ 0.003\left( R/{\AA {}}\right) ^3\right] }{\left[ 1 + 5\times 10^{-7} \left( V/\mathrm {K}+850\right) ^2\right] ^2}, \end{aligned}$$
(6)

where the denominator has the effect that the weight increases as the interaction energy becomes more negative (\(V>-850\) K for all 57 992 configurations), while the numerator ensures that the PES is also represented accurately at the largest considered R values. We used weighting functions of similar form already in several previous works (e.g., in Ref. [9]). Note that in this work interaction energies V are quoted in units of kelvin, i.e., they were divided by Boltzmann’s constant \(k_\mathrm {B}\), but \(k_\mathrm {B}\) is omitted from the notation for brevity.

Figure 2 visualizes the optimized positions of the interaction sites in the two molecules. In Fig. 3, the deviations of the fitted interaction energies from the ab initio calculated ones are shown. It can be seen that the relative deviations are mostly within \(\pm \, 2\%\), which is sufficient for our purposes because the effects of positive and negative fitting errors on thermophysical properties calculated with the analytical PES should cancel out to a large extent. Figure 3 is restricted to interaction energies smaller than 12 000 K, but we note that the full range of interaction energies used for the PES fit extends up to almost 240 000 K for some angular configurations. The very high number of interaction energies used in the fit (57 992) in relation to the number of fit parameters (144) results in a very smooth potential function. At very small intermolecular separations R, spurious maxima of V with respect to R can be found on the analytical PES. The lowest of these points has an interaction energy of about 79 000 K, which is unproblematic for the thermophysical property calculations for which this PES was developed.

Fig. 2
figure 2

Optimized positions of the nine interaction sites for H2O (all of which are in the molecular plane) and the five interaction sites for CO

Full size image
Fig. 3
figure 3

Deviations of interaction energies calculated with the new H2O–CO potential function from the corresponding ab initio values used in the fit as a function of the latter. The dashed lines indicate relative deviations of \(\pm \, 2\%\)

Full size image

Figure 4 shows the separation dependence of the analytical potential function in the well region for 12 of the 1978 considered angular configurations. Also shown in the figure are the corresponding ab initio calculated interaction energies.

Fig. 4
figure 4

H2O–CO intermolecular PES as a function of the center-of-mass separation R for 12 of the 1978 investigated angular orientations. The discrete ab initio interaction energies are indicated by symbols, while the solid lines indicate the interaction energies obtained with the fitted PES for these orientations

Full size image

The PES features three minima, which correspond to planar H2O–CO geometries. The interaction energy of the global minimum is \(-914\) K, which is in good agreement with the respective values for the PESs of Wheatley and Harvey [3] (\(-904\) K), Kalugina et al. [5] (\(-930\) K), and Liu and Li [6] (\(-925\) K). While Wheatley and Harvey also found three planar minima, Kalugina et al. and Liu and Li found only two. However, the interaction energy difference between the saddle point separating the two secondary minima of our PES and the higher secondary minimum is only about 17 K, which is within the uncertainty of the PES due to the fit and due to the level of the ab initio calculations. Figure 5 illustrates this in the form of a contour plot of V as a function of \(\theta _1\) and \(\theta _2\), with the remaining three variables chosen such that V is minimized for each (\(\theta _1,\theta _2\)) combination. Further details regarding the minima of our PES are given in the SI. A Fortran 90 program that computes the PES is provided in the SI as well.

Fig. 5
figure 5

Contour plot of V (in kelvin) as a function of \(\theta _1\) and \(\theta _2\), with the variables R, \(\psi _1\), and \(\phi\) chosen such that V is minimized for each (\(\theta _1,\theta _2\)) combination. The contour spacing is 10 K, and contours are only shown for \(V\leqslant 0\) K because in parts of the omitted regions a minimum of V with respect to R, \(\psi _1\), and \(\phi\) does not exist. The three minima of the PES are marked (+)

Full size image

3 Calculation of the Cross Second Virial Coefficient

In the classical-mechanical approximation, the cross second virial coefficient for a pair of rigid molecules is given from statistical thermodynamics as

$$\begin{aligned} B_{12}^{\mathrm {cl}} = -\frac{N_{\mathrm {A}}}{2} \int \left\langle \exp \left[ -\frac{V(\mathbf {R},\Omega _1,\Omega _2)}{k_\mathrm {B}T}\right] -1\right\rangle _{\Omega _1,\Omega _2} \mathrm {d} \mathbf {R}, \end{aligned}$$
(7)

where \(N_{\mathrm {A}}\) is Avogadro’s constant, T is the temperature, \(\mathbf {R}\) is the separation vector between the molecules, the variables \(\Omega _1\) and \(\Omega _2\) represent the angular orientations of molecules 1 and 2, respectively, and the angle brackets indicate an orientational average. To account for nuclear quantum effects, we use the semiclassical Feynman–Hibbs approach, in which the pair potential V in the classical expression has to be replaced by the quadratic Feynman–Hibbs (QFH) effective pair potential [38]. For the H2O–CO system, the QFH potential takes the form

$$\begin{aligned} V_{\mathrm {QFH}} ={}&V + \frac{\hbar ^2}{24k_\mathrm {B} T}\Bigg [ \frac{1}{\mu }\Bigg (\frac{\partial ^2 V}{\partial x^2}+\frac{\partial ^2 V}{\partial y^2}+\frac{\partial ^2 V}{\partial z^2}\Bigg ) \nonumber \\&+ \frac{1}{I_{1\mathrm {a}}} \frac{\partial ^2 V}{\partial \psi _{1\mathrm {a}}^{2}} + \frac{1}{I_{1\mathrm {b}}} \frac{\partial ^2 V}{\partial \psi _{1\mathrm {b}}^{2}} + \frac{1}{I_{1\mathrm {c}}} \frac{\partial ^2 V}{\partial \psi _{1\mathrm {c}}^{2}} + \frac{1}{I_2} \Bigg (\frac{\partial ^2 V}{\partial \psi _{2\mathrm {a}}^{2}}+\frac{\partial ^2 V}{\partial \psi _{2\mathrm {b}}^{2}}\Bigg ) \Bigg ], \end{aligned}$$
(8)

where \(\hbar\) is Planck’s constant h divided by \(2\pi\); \(\mu\) is the reduced mass of the H2O–CO system; x, y, and z are the Cartesian components of \(\mathbf {R}\); \(I_{1\mathrm {a}}\), \(I_{1\mathrm {b}}\), and \(I_{1\mathrm {c}}\) are the three principal moments of inertia of molecule 1 (H2O); \(I_2\) is the moment of inertia of molecule 2 (CO) perpendicular to the bond axis; and the angles \(\psi _{1\mathrm {a}}\), \(\psi _{1\mathrm {b}}\), \(\psi _{1\mathrm {c}}\), \(\psi _{2\mathrm {a}}\), and \(\psi _{2\mathrm {b}}\) correspond to rotations around the principal axes of the two molecules except for the bond axis of CO. The two principal axes for CO can be chosen arbitrarily as long as they are perpendicular to the bond axis and to each other.

We evaluated the cross second virial coefficient of the H2O–CO system both semiclassically and, for comparison, classically at 99 temperatures from 200 K to 2000 K applying the Mayer-sampling Monte Carlo method devised by Singh and Kofke [39]. The details of these calculations, which we carried out using an in-house code, are mostly identical to those of the respective calculations performed in our work on the H2O–N2 system [8, 12]. Therefore, we omit the details here. The expanded uncertainty (coverage factor \(k=2\), corresponding approximately to a 95% confidence level) of our final semiclassical values due to the Monte Carlo integration is smaller than \(0.01\; \mathrm {cm}^3 \!\cdot\! \mathrm {mol}^{-1}\) at all temperatures.

4 Results and Discussion

Table 1 lists both the classical (\(B_{12}^{\mathrm {cl}}\)) and semiclassical (\(B_{12}^{\mathrm {scl}}\)) values for the H2O–CO cross second virial coefficient at 40 selected temperatures together with the estimated combined expanded (\(k=2\)) uncertainty. For the latter, we adopted the uncertainty statement from our previous work on the H2O–N2 system [8, 12], i.e., the combined expanded (\(k=2\)) uncertainty is 4% of the absolute value of \(B_{12}^{\mathrm {scl}}\) or \(2\; \mathrm {cm}^3 \!\cdot\! \mathrm {mol}^{-1}\), whichever value is larger. This approach to quantifying the uncertainty for the H2O–CO system is justified because of the similarity of the N2 and CO molecules. For the H2O–N2 system, our uncertainty estimate is supported by the agreement of the calculated \(B_{12}^{\mathrm {scl}}\) values with the best available experimental data.

Table 1 Classical values, \(B_{12}^{\mathrm {cl}}\), and semiclassical values, \(B_{12}^{\mathrm {scl}}\), for the cross second virial coefficient (in \(\mathrm {cm}^3 \!\cdot\! \mathrm {mol}^{-1}\)) of the H2O–CO system and the combined expanded (\(k=2\)) uncertainty of the semiclassical values, \(U\left( B_{12}^{\mathrm {scl}}\right)\) (in \(\mathrm {cm}^3 \!\cdot\! \mathrm {mol}^{-1}\)), at selected temperatures T
Full size table

We fitted a polynomial in \((T^*)^{-1/2}\) with \(T^* = T / (100 \, \mathrm {K})\) to the 99 calculated values for \(B_{12}^{\mathrm {scl}}\). The polynomial structure was optimized employing the symbolic regression software Eureqa (version 1.24.0) [40]. The resulting correlation is given as

$$\begin{aligned} \frac{B_{12}}{ \mathrm {cm}^3 \!\cdot\! \mathrm {mol}^{-1}} = 13.304 + \frac{113.21}{(T^*)^{1/2}} - \frac{333.09}{T^*} - \frac{261.86}{(T^*)^{3}} - \frac{165.91}{(T^*)^{9/2}}, \end{aligned}$$
(9)

which reproduces the \(B_{12}^{\mathrm {scl}}\) values within \(\pm 0.01 \, \mathrm {cm}^3 \!\cdot\! \mathrm {mol}^{-1}\). As shown in Fig. 6, the correlation extrapolates in a physically reasonable manner to temperatures below 200 K and above 2000 K.

Fig. 6
figure 6

Correlation for the cross second virial coefficient \(B_{12}\) of the H2O–CO system as given as a function of temperature T by Eq. 9, displayed in the figure as absolute values, \(\vert B_{12} \vert\). The correlation is depicted by a solid line within the range of validity and by a dotted line outside of this range

Full size image

In Fig. 7, the \(B_{12}^{\mathrm {scl}}\) values of the present work are compared with those of Wheatley and Harvey [3] (provided in the form of a correlation) and with the available experimental data [41, 42]. The \(B_{12}\) data of Gillespie and Wilson were not given in the original publication [41]; they were extracted by Wheatley and Harvey [3] from the measured solubility data. The figure shows that the values of the present work lie somewhat below those of Wheatley and Harvey and agree on average slightly better with the experimental data. Our estimated uncertainties are also significantly smaller for most temperatures than those given by Wheatley and Harvey. Unfortunately, the large uncertainties of the experimental data do not allow for a more stringent test of the uncertainty of the calculated values.

Fig. 7
figure 7

Semiclassically calculated values of this work and of Wheatley and Harvey [3] and the available experimental data [41, 42] for the cross second virial coefficient \(B_{12}\) as a function of temperature T. The shaded area indicates the combined expanded (\(k=2\)) uncertainty of the present values. The error bars for the values of Wheatley and Harvey correspond to \(k=2\) as well

Full size image

The \(B_{12}\) data of Wormald and Lancaster [42] shown in Fig. 7 were derived from measurements of the enthalpy of mixing of the two gases. A quantity that is more directly related to these measurements is the dilute gas cross isothermal Joule–Thomson coefficient, \(\phi _{12}=B_{12}-T(\mathrm {d}B_{12}/\mathrm {d}T)\), for which Wormald and Lancaster also provided values. In addition, \(\phi _{12}\) values were extracted by Wheatley and Harvey [3] from the enthalpy of mixing data of Wilson and Brady [43] and of Lancaster and Wormald [44]. Figure 8 displays the \(\phi _{12}\) values obtained with the \(B_{12}\) correlations of this work and of Wheatley and Harvey [3] as well as the experimental data for \(\phi _{12}\). Both sets of calculated values are consistent with most of the data, but, as in the case of the cross second virial coefficient, the data are fraught with relatively large uncertainties.

Fig. 8
figure 8

Semiclassically calculated values of this work and of Wheatley and Harvey [3] and the available experimental data [42,43,44] for the dilute gas cross isothermal Joule–Thomson coefficient \(\phi _{12}\) as a function of temperature T

Full size image

5 Conclusions

A proven first-principles approach was applied to predict the cross second virial coefficient of the H2O–CO system at temperatures from 200 K to 2000 K. For this purpose, a new site–site PES for the H2O–CO interaction was developed, which is based on quantum-chemical ab initio calculations at levels up to CCSD(T). A Fortran 90 implementation of the new PES is provided in the SI.

The cross second virial coefficient was computed from the PES in a semiclassical manner. We provide the calculated values in the form of a table of discrete values and as a correlation. Our PES was developed at a higher level of theory than the PES of Wheatley and Harvey from 2009 [3] and yields values for the cross second virial coefficient that are somewhat more negative than those reported by Wheatley and Harvey for their PES. Unfortunately, the available experimental data for the cross second virial coefficient and the related dilute gas cross isothermal Joule–Thomson coefficient are not accurate enough for a stringent test of either set of first-principles values. However, based on the findings from our studies of the systems H2O–CO2 [7, 11], H2O–O2 [9], H2O–air [9], and particularly H2O–N2 [8, 12], we were able to assign relatively small uncertainties to the new calculated values, making them the most accurate estimates for the H2O–CO cross second virial coefficient to date. A significant further reduction of the uncertainty would require a very large effort. It would certainly be necessary to go beyond the CCSD(T) level of theory and fully include the effects of molecular flexibility. In addition, it would be advisable to calculate corrections that account for relativistic effects and for the inclusion of the core electrons of the carbon and oxygen atoms in the correlation treatment.