Abstract
The homogeneous density of the liquid phase is experimentally investigated for methyl diethanolamine. Data are obtained along five isotherms in a temperature range between 300 K and 360 K for pressures up to 95 MPa. Two different apparatuses are used to measure the speed of sound for the temperatures between 322 K and 450 K with a maximum pressure of 95 MPa. These measurements and literature data are used to develop a fundamental equation of state for methyl diethanolamine. The model is formulated in terms of the Helmholtz energy and allows for the calculation of all thermodynamic properties in gaseous, liquid, supercritical, and saturation states. The experimental data are represented within their uncertainties. The physical and extrapolation behavior is validated qualitatively to ensure reasonable calculations outside of the range of validity. Based on the experimental datasets, the equation of state is valid for temperatures from 250 K to 750 K and pressures up to 100 MPa.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Global warming caused by greenhouse gases like carbon dioxide (CO2) has to be decelerated and ultimately terminated. The IPCC report [1] suggests four pathways of actions to limit the temperature rise of 1.5 °C. Three out of four include the reduction of CO2 emissions by a largescale deployment of “carbon capture and storage” (CCS) technologies. Several technologies can be applied to capture CO2. On an industrial scale, chemisorption is a feasible solution due to its comparably high efficiency and relatively low costs to separate CO2, e.g., from power plants burning fossil fuels. The benchmark sorbent is aqueous monoethanolamine (MEA), which is a so-called primary amine. However, academia and industry are constantly searching for new sorbents with better properties in order to make the capture process more efficient and economical.
Methyl diethanolamine (MDEA, CAS: 105-59-9, chemical formula CH3N(C2H4OH)2) is a promising candidate. It is mainly used as a solvent for hydrogen sulfide removal, but it also reacts with CO2. Thus, two separation purposes could be combined. Although the reaction rate with CO2 is slower compared to MEA, MDEA offers various advantages for CO2 capture (cf. Bullin et al. [2]). The heats of reaction and of regeneration are smaller, which directly leads to lower operation costs. Since MDEA is a tertiary amine, it needs to be in aqueous solution to react with CO2. However, MDEA allows for high solute mass fractions of up to 55 wt%, whereas the solute mass fraction of MEA in water is typically around 15 wt% to 30 wt%. Although MDEA enables a high acid loading, the corrosion effects are lower than with MEA. Moreover, the degradation rates are slower, which results in a reduced solvent loss. Taking all these technical aspects into account, economic feasibility still has to be proven because the fluid is more expensive than MEA.
Operating costs can be reduced by a well-designed and efficient process. For this purpose, the accurate knowledge of thermodynamic properties, e.g., vapor pressure, density, or heat capacity of MDEA, is necessary. These properties are nowadays calculated with equations of state (EOS). The model presented in this work is based on the reduced Helmholtz energy with temperature and density as independent variables. Since the Helmholtz energy is a fundamental property, the EOS allows for the calculation of all thermodynamic properties in the entire fluid region including saturation states. In return, the EOS was also adjusted to various thermodynamic properties. The essential basis were the density and speed of sound measurements presented in this work. For these measurements, two apparatuses were used. One is a combination of an Anton Paar densimeter connected to a pulse-echo apparatus measuring the speed of sound as described by Javed et al. [3] for temperatures from 283 K to 363 K with a maximum pressure of 100 MPa. The second pulse-echo apparatus can be used for speed of sound measurements up to 500 K and 190 MPa [4, 5].
Most of the available literature data were measured at atmospheric pressure and fairly low temperatures. However, it is of importance to expand the range of validity of the EOS to high temperature and pressure, in particular when the fluid is part of a mixture. MDEA as a solvent to capture CO2 will be used in solution with, e.g., water or glycols to absorb CO2. Moreover, after the regeneration process, some of the MDEA will remain as an impurity in the CO2-rich mixture. Since the common Helmholtz-energy-based mixture models use corresponding states approaches, thermodynamic properties are needed at elevated temperatures and pressures when the EOS is used in multicomponent mixture models to calculate properties in the transportation part of the CCS chain at high reduced temperatures.
2 Density Measurements in the Liquid State
The density of MDEA was measured with an Anton Paar densimeter (DMA-HPM with mPDS 5 evaluation unit). Therein, the oscillation period of a U-shaped metallic vibrating tube filled with the sample is a function of the sample density, pressure, and temperature of the device. To accurately determine the density of the sample, the densimeter was calibrated with propane and water on the basis of reference quality Helmholtz energy equations of state by Lemmon et al. [6] and Wagner and Pruß [7]. The calibration fit was described by Javed et al. [3] and it reflects the calibration data within \(0.2 \:\text{kg}\cdot {\text{m}}^{-3}\) as shown in Fig. 1.
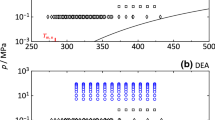
The device was connected to a thermostat (Huber CC415) and the temperature was determined by the built-in sensor of the densimeter. The density was measured along five isotherms, cf. Figure 2. Zuniga-Morena et al. [8] measured data at similar temperatures, which are included in Fig. 2 for comparison. The data points of this work are listed in Table 1 together with their expanded experimental uncertainties (Fig. 3).
Density of MDEA as a function of pressure. The data of Zuniga-Morena et al. [8] are included for comparison (Color figure online)
The uncertainty of the density was calculated according to Eq. 1.
Here, \({U}_{\rho }\) is the expanded uncertainty of the density at a confidence level of 95 % (k = 2), composed of standard uncertainties of temperature \({u}_{T}=0.1 \:\text{K}\), pressure \({u}_{p}=0.02 \:\text{MPa}\), oscillation period \({u}_{s}=0.015 \:\mu\text{s}\), calibration \({u}_{\text{cal}}=0.6 \:\text{kg}\cdot {\text{m}}^{-3}\), and impurities \({u}_{\text{imp}}= 0.2 \:\text{kg}\cdot {\text{m}}^{-3}\). A more detailed description of the uncertainty budget is given in Table 2.
The uncertainty resulting from impurities in the sample has the second largest contribution, as listed in Table 3.
3 Speed of Sound Measurements
Speed of sound measurements were performed with the pulse-echo technique by determining the propagation time difference Δt of an acoustic wave burst, which propagates over known distances in the fluid sample between two reflectors [3]. The experimental speed of sound is given by the ratio of propagation length and time. The path length was calibrated to water at 300 K and pressures from 0.1 MPa to 1 MPa and the change of path length due to temperature and pressure was calculated according to Javed et al. [3] based on the work of Meier [9].
An 8 MHz gold plated piezoelectric quartz crystal was built into the acoustic cell in a pressure vessel and used as a transducer, which was linked successively via a switch to the Arbitrary Waveform Generator and the Acquisition system of a USB-oscilloscope (TiePie HS5-540). The signal processing was done according to Dubberke et al. [10].
Two of these measuring setups were used. One of them was connected with the densimeter (see Javed et al. [3]) and the temperature of both parts was controlled in combination with the same bath circulation thermostat Huber CC-415 for measurements from 283 K to 363 K. Further measurements were performed with the standard setup, which allowed measurements between 200 K and 500 K with a vacuum-insulated thermostat [4] and with a higher accuracy of temperature and pressure measurement using a standard platinum resistance thermometer Pt25 (Rosemount 162CE) and an additional pressure sensor for pressures up to 10 MPa (Keller-PAA-33X).
The measurements were subject to some limitations. Because of the high sound absorption of MDEA at low temperatures, the signal amplitude of the echoes below 320 K was too weak to be evaluated and no speed of sound measurements could be performed below this temperature. Furthermore, the pressure vessel of the second setup was leaking at high pressure, limiting the 400 K isotherm to 80 MPa and the 450 K isotherm to 70 MPa.
Additionally, MDEA started to decompose at 500 K and elevated pressure. This was noticed during the experiment because the trend of these data deviated from the previous measurements. Decomposition became obvious when the substance was drained off the apparatus. Instead of a clear liquid, a dark brown liquid was found. Therefore, the entire isotherm was discarded. An overview of the data measured with the combined and standard apparatus is given in Fig. 4. Table 4 lists the values of the data, measured with the combined apparatus including their expanded experimental uncertainty, which was determined according to Eq. 2. Table 5 lists the data measured with the standard apparatus.
Percentage deviations of the isobaric heat capacity data of the ideal-gas calculated according to Joback and Reid [12] from the present EOS
\({U}_{w}\) is the expanded uncertainty of the speed of sound at a confidence level of 95 % (k = 2), composed of standard uncertainties of temperature \({u}_{T}=0.05 \:\text{K}\), pressure \({u}_{p}=0.02 \:\text{MPa}\), delay in time of flight \({u}_{\Delta t}=0.002 \:\upmu \text{s}\), path length difference \({u}_{\Delta L}=8 \:\upmu \text{m}\), and uncertainty caused by impurities \({u}_{\text{imp}}=0.2 \:\text{m}\cdot {\text{s}}^{-1}\). The specific contributions to the calculated uncertainty are shown in Table 6 for the combined apparatus and in Table 7 for the standard apparatus.
4 Equation of State
The thermodynamic properties of MDEA are described with an equation of state formulated in terms of the reduced Helmholtz energy. The Helmholtz energy is reduced by the universal gas constant R = 8.314 462 618 J mol−1 K−1 [11] and the temperature
The independent variables are density and temperature, which are reduced with their critical values according to
In Eq. 3, the Helmholtz energy is separated into an ideal part \({\alpha }^{\text{o}}\) and a residual part \({\alpha }^{\text{r}}\). The ideal part describes the fluid in a hypothetical ideal-gas state. Based on the principle of a static rotator and a harmonic oscillator, energetic contributions of translation, rotation, and internal molecular vibrations describe the ideal part. Assuming that translation and rotation are always fully excited, except for very low temperatures (\(T\to 0\:\text{K}\)), simplifies the approach in terms of the isobaric heat capacity to a temperature dependent formulation of the vibration modes by Planck-terms
Since MDEA is a non-linear molecule, three degrees of freedom resulting from translation and rotation each contribute to the isochoric heat capacity. With \({c}_{p}^{\text{o}}={c}_{v}^{\text{o}}+R\), the temperature independent parameter \({n}_{0}\) is 4. The ideal part of the reduced Helmholtz energy can be obtained by two-fold integration of Eq. 5, which yields
The integration constants cI and cII (see Table 8) were determined such that the enthalpy and entropy are zero at the normal boiling point.
The parameters mi and \({\theta }_{i}\) are commonly adjusted to isobaric ideal-gas heat capacity data, which are derived from experiments or statistical mechanics. However, no data of this kind were found for MDEA in the literature. Therefore, the method by Joback and Reid [12] was used to determine the isobaric ideal-gas heat capacity over a wide temperature range. According to Kleiber and Joh [13] the expected deviations are approximately 1 % to 2 % and may rise with increasing complexity of the molecule. However, to enhance the ideal part of the Helmholtz energy, experimental speed of sound and isobaric heat capacity data beyond ideal-gas states were used for the adjustment of the ideal part as done previously, see Thol et al. [14]. In addition, boundary conditions to fulfill the temperature independent contribution \({c}_{p}^{\text{o}}=4R\) for \(T \to 0 \:\text{K}\) and to achieve an asymptotic course of \({c}_{p}^{\text{o}}\) at high temperatures (\({c}_{p}^{\text{o}}=66R\) for fully exited vibrational modes) were applied. As shown in Fig. 4, the ideal-gas isobaric heat capacity calculated with the method by Joback and Reid [12] deviates by 27 %. Such large deviations are most likely due to limitations of the method to predict the properties of the quite complex molecule MDEA. Similar deviations are present for propylene glycol (see Eisenbach et al. [15]). Therefore, a reliable statement about the uncertainty of the EOS is not possible for this property.
The residual part of Eq. 3 comprises three different term types. In Eq. 7, the functional form is shown, where the five polynomial terms are labeled with \({\alpha }_{\text{Pol}}^{\text{r}}\), the five exponential terms with \({\alpha }_{\text{Exp}}^{\text{r}}\), and the five Gaussian bell-shaped terms with \({\alpha }_{\text{GBS}}^{\text{r}}\)
A description of the entire fluid region except for the critical regime is possible using only polynomial and exponential terms. Gaussian bell-shaped terms are applied to model the vicinity of the critical point. A summary of all parameters is given in Table 9.
The parameters were adjusted to experimental data by means of a non-linear fitting algorithm developed at the National Institute of Standards and Technology [16, 17]. This algorithm minimizes the deviations between the EOS and the data and applies constraints to ensure a correct physical and extrapolation behavior in the entire fluid region. More detailed information can be found in references [18,19,20].
For the development of EOS, several thermodynamic properties are of special interest. A summary is given in Table 10.
VonNiederhausern et al. [23] measured the critical temperature (\({T}_{\text{c}}=741.9 \:\text{K}\)), which was used as a starting point for the development of the presented EOS. However, the authors reported an uncertainty of ± 5 K. During the fitting process, the critical temperature was slightly adjusted in order to match the thermodynamic properties more accurately. Three values for the critical density were published by Yaws [24] (\({\rho }_{\text{c}}=2.494 \:\text{mol}\cdot {\text{dm}}^{-3}\)), Bishnoi and Rochelle [25] (\({\rho }_{\text{c}}=2.564 \:\text{mol}\cdot {\text{dm}}^{-3}\)), and Pourmohammadbagher and Shaw [26] (\({\rho }_{\text{c}}=2.494 \:\text{mol}\cdot {\text{dm}}^{-3}\)). An uncertainty was not reported for any of these values. Moreover, the three references measured the corresponding critical temperature with a value of approximately 678 K, which is more than 60 K lower than the value reported by VonNiederhausern et al. [23]. Since VonNiederhausern et al. [23] used a measurement technique to avoid the decomposition at elevated temperatures (see Sect. 5.1 for more details), the other authors most likely measured the critical point of decomposed MDEA. Therefore, the measured critical density values were only used as a starting point and the critical density was adjusted in the present fitting process. The critical pressure was calculated with the final critical density and temperature of the EOS. It is 13 % higher than the measured value by VonNiederhausern et al. [23] (\({p}_{\text{c}} = 4.16 \:\text{MPa}\), \(\Delta {p}_{\text{c}} = \pm 2 \:\%\)). Since there are no other data available, a reliable statement on which value is correct cannot be made.
No experimental triple point data are reported in the literature. Thus, the melting point temperature \({T}_{\text{melt}}=251.85 \:\text{K}\) at \(p=1 \:\text{atm}\) (cf. Table 10) was chosen as the lower temperature limit of the EOS. The upper temperature (\({T}_{\text{max}}=750 \:\text{K}\)) and pressure (\({p}_{\text{max}}=100 \:\text{MPa}\)) limits are based on the available experimental data.
To validate a correct implementation of the presented EOS, test values are given in Table 11.
The calculation of vapor–liquid-equilibrium properties can be significantly sped up when suitable initial values for vapor pressure as well as saturated liquid and vapor densities are available. The functional forms of the corresponding equations are given by Eqs. 8–10 and the respective parameters are listed in Table 5
Except for the critical region, the ancillary equations deviate from the fundamental EOS within 0.04 %, see Fig. 5. Close to the critical temperature, the deviations increase up to 0.08 % and 0.12 % for the saturated liquid and vapor densities, respectively.
5 Comparison with Literature Data
An overview of the available experimental literature data are given in Fig. 6. In general, the data were only measured in the liquid phase and mostly at atmospheric pressure, motivated by the use of MDEA in amine scrubbing processes. These processes operate typically at atmospheric pressure in a temperature range from 273 K to 373 K. With the data presented in this work, the data situation in particular for the speed of sound above atmospheric pressure was significantly improved (see Table 12).
To compare the data and the EOS, percentage deviations were calculated according to
where x is any thermodynamic property. Additionally, the average absolute relative deviation was calculated for complete datasets
where N corresponds to the number of data points in the dataset. Table 13 summarizes the experimental data for all available properties.
The performance of the EOS in terms of maintaining experimental uncertainties and a qualitatively correct physical description of the complete fluid region as well as the extrapolation behavior are discussed in the following.
5.1 Vapor Pressure
The EOS was adjusted to the vapor pressure data reported by VonNiederhausern et al. [23] and Daubert and Hutchison [27]. VonNiederhausern et al. [23] measured nine vapor pressure points in the temperature range from 519 to 738 K as shown in the deviation plot in Fig. 7.
The authors used a flow method with short residence times to avoid the decomposition of MDEA. The sample was flown through a capillary immersed in a molten salt bath to ensure a homogeneous temperature distribution. The temperature in the bath was increased until boiling of the sample ensued. Since the sample quantity was small, the heating up occurred in a fraction of a second, which reduced the time for decomposition. The pressure in the capillary was kept constant. The authors state an uncertainty of 2 %. The EOS represents the measured data with an AARD of 8.8 % and increasing deviations of up to 13 % close to the critical point. This difference might be an issue of the present EOS. VonNiederhausern et al. [23] measured vapor pressure data of toluene and ethyl benzene with the same method. These measurements are reproduced within 2 % and prove the measurement principle to be suitable. However, both of these molecules are thermally stable under the investigated conditions. Therefore, measurements of fluids which decompose might be more uncertain. However, a final conclusion can only be made with additional measurements. Because of the potential decomposition of MDEA, all other authors measured at temperatures below 500 K. The data of Daubert [28] and of Daubert and Hutchison [27] were measured with the same apparatus, but deviate significantly (see Fig. 7). For increasing temperatures, not only an offset but also a contrary trend is apparent. A possible explanation for this behavior could be different purities of the samples. Daubert [28] used 97 % pure MDEA, whereas Daubert and Hutchison [27] measured with a purity of better than 99 %. Because of the higher purity and the matching trend with the data of VonNiederhausern et al. [23], the data of Daubert and Hutchison [27] were included in the present fitting process. They are represented within 8 % and an AARD of 6.3 %. However, the authors did not report any uncertainties. For temperatures below 400 K, the only available dataset was published by Noll et al. [30]. These data scatter within 14 % and no clear trend is visible. The authors state uncertainties in terms of pressure (0.01 \(\cdot \:p\)) and temperature (\(0.05 \:\text{K}\)). According to the error propagation law, this results in a maximum combined expanded uncertainty of 2 % (k = 2) at the lowest temperature. This is not in accordance with the deviations shown in Fig. 7. However, the authors did not report the purity of their sample, which can have a significant influence as discussed above. Therefore, the data can only be taken as an indicator of the course of the vapor pressure curve. The present EOS reproduces the data with an AARD of 5.8 %. The data by Skylogianni et al. [31] deviate within 5 %. The authors do not state any uncertainty estimates, but their data match the data of Noll et al. [30] and Daubert and Hutchison [27] well. Kim et al. [29] measured the vapor pressure with the same Swietoslawski ebulliometer as Skylogianni et al. [31]. However, the data exhibit a significant offset in the same temperature range (cf. Figure 7). Therefore, they were excluded from the present fit. The data of Daubert [28] cover similar temperature ranges as Daubert and Hutchison [27] but exhibit an offset. A similar trend as for Daubert [28] and Daubert and Hutchison [27] is apparent for the data of Kim et al. [29]. Therefore, they were also discarded from the present fit. Soames et al. [32] and Yang et al. [33] used both samples with a high purity of 99 % and measured the vapor pressure with comparable rotary evaporators. The data confirm each other and deviate within a maximum of 8 %. Both groups do not state any uncertainty estimates. Since the deviations have a similar absolute value as the data of Daubert and Hutchison [27] in the same temperature range, the representation is reasonable.
Based on these data no reliable uncertainty estimate for the present EOS in terms of vapor pressure is possible.
5.2 Density
All density data were obtained in the liquid phase, where the majority of the sources reports measurements at atmospheric pressure. There is only a single publication, which contains data at significantly elevated pressures. The maximum pressure of the dataset of Zuniga-Morena et al. [8] is 21 MPa, covering temperatures from 313 K to 363 K. Therefore, new density measurements were carried out in this work, which extend the temperature range down to 300 K and the maximum pressure up to 95 MPa. This dataset was measured along six isotherms and it was the basis for the fitting process in terms of density. Deviations of less than 0.13 % were achieved (see Fig. 8), which is well within the experimental uncertainty.
Percentage deviations of experimental density data [8, 26, 30, 34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70, 72,73,74,75,76,77] from values calculated with the present EOS as a function of pressure along selected isotherms. The experimental uncertainty of the data measured in this work is shown with error bars
Furthermore, the new measurements agree well with the data of Zuniga-Morena et al. [8] in overlapping temperature and pressure ranges. Zuniga-Morena et al. [8] used an Anton Paar tube densimeter (model 60/512P) to measure 120 data points. The reported uncertainties are ± 0.03 K, ± 0.008 MPa, and ± \(0.2 \:\text{kg}\cdot {\text{m}}^{-3}\), which corresponds to 0.04 % in relative terms for k = 2. This is more than three times smaller than the uncertainty reported in this work although the measurement principle is similar. Zuniga-Morena et al. [8] probably reported the density specification provided by manufacturer. These are typically estimated under ideal conditions of atmospheric pressure, ambient temperature, and a sample of high purity. However, different temperatures, less pure samples, and calibration do have a significant influence on the uncertainty (see Prokopova et al. [84], Fortin et al. [85], and Gonzalez et al. [86]). Therefore, the estimated uncertainty is probably too optimistic. The maximum deviations are 0.14 % with an AARD of 0.072 %.
The other datasets were measured at atmospheric pressure, except for the data of Jayarathna et al. [53] and Han et al. [50] who measured also at 0.8 MPa and 0.7 MPa, respectively. The representation of experimental density data for pressures below 1 MPa is illustrated in Fig. 9.
Percentage deviations of experimental density data [26, 30, 34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70, 72,73,74,75,76,77] for \(p<1 \:\text{MPa}\) from values calculated with the present EOS as a function of temperature. The data presented in this work are highlighted in red (Color figure online)
The dataset of DiGuillo et al. [46] covers the widest temperature range, 293 K to 470 K. They used a pycnometer, which is a mass-based measurement principle and, therefore, independent to a tube densimeter employed by all other authors. A sample with 99 % purity was used and an experimental uncertainty of 0.25 % was stated. Figure 9 shows that all data are reproduced within that experimental uncertainty (AARD = 0.10 %) (Fig. 10).
The other two datasets, which report densities at elevated temperatures, are from Jayarathna et al. [53] and Han et al. [50]. Both used an Anton Paar tube densimeter with a low-pressure (model DMA 4500) and a high-pressure (model DMA HP) cell. Jayarathna et al. [53] measured 13 data points at 0.1 MPa and 0.8 MPa and covered several temperatures. The stated uncertainties are in absolute terms \(\pm 2.68 \:\text{kg}\cdot{\text{m}}^{-3}\), which corresponds to 0.29 %. All data deviate within the reported uncertainty. However, the data exhibit a trend of increasing negative deviations for rising temperature, which is contradictory to the data of DiGuillo et al. [46]. Although the trend is within the experimental uncertainty, a probable explanation is the low purity of 98 % stated by Jayarathna et al. [53]. The data of Han et al. [50] are in good agreement with the data of Jayarathna et al. [53]. Han et al. [50] stated an uncertainty of \(\pm 0.1 \:\text{kg}\cdot{\text{m}}^{-3}\), which is most likely the value given by the manufacturer. This corresponds to an uncertainty in relative terms of 0.01 %. As discussed above, this uncertainty is too optimistic because no comprehensive uncertainty analysis (cf. Prokopova et al. [84], Fortin et al. [85], and Gonzalez et al. [86]) was applied. Since the impurity content is similar to the one of the data of Jayarathna et al. [53], a similar experimental uncertainty has to be expected. Therefore, it seems reasonable that the data are described by the EOS within 0.2 %.
In Fig. 9, it is quite striking that most of the data exhibit positive deviations with respect to the present EOS. There is a visual impression that the EOS has a systematic offset to the majority of the data. However, the state points at the lowest pressure of each isotherm of the measurements presented in this work are included in the plot for comparison. It shows that they agree with the present EOS and also with other measurements, e.g., Han et al. [50], Noll et al. [30], and Jayarathna et al. [53], within their experimental uncertainty.
Therefore, the uncertainty of the EOS is 0.13 % for temperatures from 280 K to 360 K for pressures up to 95 MPa. For temperatures from 360 K to 470 K at atmospheric pressure, the uncertainty is 0.25 % based on the data of DiGuillo et al. [46].
5.3 Speed of Sound
There are five datasets available for the speed of sound, which were all measured in the liquid phase. The most comprehensive one with 44 data points was measured in this work. The other datasets comprise less than ten data points and are limited to atmospheric pressure and a rather limited temperature range from 298 K to 318 K. However, in the deviation plot in Fig. 11, opposite trends become apparent.
The data of Alvarez et al. [40] and Hawrylak et al. [51] exhibit increasing deviations for rising temperature. The data of Alvarez et al. [39] and Garica-Abuin et al. [47] deviate negatively from the present EOS. Moreover, the data of Alvarez et al. [39] have an opposite trend to the data of Alvarez et al. [40] although it is the same group of authors and the same apparatus (Anton Paar DSA 5000) was used to measure the speed of sound. The reported uncertainties are \(\pm 0.08 \:\text{m}\cdot {\text{s}}^{-1}\) [39] and \(\pm 0.05 \:\text{m}\cdot {\text{s}}^{-1}\) [40], which correspond to relative uncertainties of 0.0053 % and 0.0047 %, respectively. It is unclear why the uncertainty changed. However, these values are most likely specifications given by the manufacturer under ideal conditions, similar to the density measurements with vibrating tube densimeters (see Sect. 5.2). Moreover, the uncertainty must be at least as high as the deviation between the two datasets deviate because the same experimental setup was used. Due to the rather poor sample purity of 98 %, the combined expanded uncertainty of these measurements alone must be higher in both publications. Even the most accurate speed of sound measurements of water were not measured with such an accuracy (see Wagner and Thol [87]). Therefore, no clear statement can be made whether a representation of the data within 0.4 % for both publications is reasonable. The same conclusion applies to the data of Garcia-Abuin et al. [47]. These data were also measured with an Anton Paar DSA 5000 vibrating tube densimeter and a sample purity of 98 % and confirm the data of Alvarez et al. [39].
Because of the different trends and unclear uncertainty estimates of the literature data, the EOS was solely adjusted to the speed of sound data measured in this work. All data are represented within the experimental uncertainty of 0.09 %, see Fig. 11. This is likewise the uncertainty in terms of the speed of sound for temperatures from 320 K to 450 K with a maximum pressure of 95 MPa.
5.4 Isobaric Heat Capacity
The literature for the isobaric heat capacity is limited to seven publications reporting data in the liquid phase exclusively at atmospheric pressure. Although the temperature range (278 K to 398 K) is quite similar, all datasets exhibit different trends as illustrated in Fig. 12.
Therefore, it is not clear which one is the right dataset for the fitting process. The present EOS was adjusted to the data of Zhang et al. [83] because they cover the largest temperature range (see Fig. 12) with the lowest stated experimental uncertainty of 2 %. They used a heat flux differential scanning calorimeter (model CSC 4100) to measure the isobaric heat capacity of a MDEA sample with 99 % purity. The present EOS deviates from the data within the experimental uncertainty, except for a single state point.
The data measured by Chiu et al. [79] exhibit an offset to the data of Zhang et al. [83], which becomes smaller with increasing temperature. The work of Chiu et al. [79] is of special interest because it also reports isobaric heat capacity data for monoethanolamine (MEA). The corresponding EOS developed by Herrig [88] was fitted to the data of Chiu et al. [79] and represents them within 3 %, which is the experimental uncertainty estimated by the authors for both fluids. However, the MEA sample was 99 % pure, whereas MDEA had a purity of 98.5 %. This should result in a slightly larger experimental uncertainty for the MDEA measurements. Chen et al. [78] measured the isobaric heat capacity of MDEA with the same differential scanning calorimeter (DSC-2010) as Chiu et al. [79], but used a sample of 99 % purity. However, both datasets systematically differ by approximately 3 % from each other. The data of Chen et al. [78] confirm the data of Zhang et al. [83] at lower temperatures. For higher temperatures, deviations increase. Mundhwa and Henni [81] and Rayer et al. [82] are from the same group of authors and measured isobaric heat capacity in complementing temperature ranges with the same C80 heat flow calorimeter. The samples had similar purities of 99 % but no uncertainty estimates are given. Their data match within 2 %. Since this is within the uncertainty estimate of Zhang et al. [83], the data are described reasonably with the present EOS. The five datapoints measured by Maham et al. [80] are mostly in accordance with the data of Zhang et al. [83]. The AARD calculated with the presented EOS is 1.0 % with a maximum deviation of 1.5 %. Yusoff et al. [75] used a Mettler Toledo differential scanning calorimeter for the isobaric heat capacity measurement. However, their sample purity was only 98 %, which explains the high deviations similar to the ones of the data of Chiu et al. [79]. The overall trend for increasing negative deviations with decreasing temperature resulted from a compromise during the fitting process favoring the adjustment of the speed of sound data.
A reliable statement on the uncertainty of isobaric heat capacity calculated with the present EOS at atmospheric pressure cannot be made. However, the deviation of 4 % of the data from the present EOS can be used as guideline.
6 Extrapolation Behavior
In particular for fluids with a limited database, the correct and reasonable physical behavior is of great importance in order to ensure reliable extrapolations into regions where no data are available. Moreover, the use of pure-fluid EOS in mixture models may lead to calculations at state points outside of the range of validity. Since MDEA is usually used as a component in mixtures, the extrapolation behavior was carefully monitored during the fitting procedure. Typically, the thermal behavior including ideal curves and p-ρ-T relations under extreme conditions are evaluated. In recent years, also caloric properties, e.g., speed of sound and isochoric heat capacity, as well as lesser known properties, such as the phase identification parameter [89] and Grüneisen parameter [90], are used to analyze the EOS. Especially the latter properties are very useful for evaluation because they comprise various derivatives of the Helmholtz energy. In Figs. 13, 14, 15 and 16, exemplary diagrams are shown, which were part of a comprehensive analysis of the physical behavior of the present EOS.
In the double logarithmic p,\(\rho\)-diagram in Fig. 13a the course of the isotherms up to 106 K with pressures up to 107 MPa is shown. The converging behavior without intersections of the isotherms is demonstrated in the complete fluid region. No unreasonable sudden slope or curvature changes are visible. A similar convergence of the isobars can be seen in the T,\(\rho\)-diagram in Fig. 13b. The rectilinear diameter defined by the arithmetic mean of the saturated vapor and liquid densities at the same temperature, \({\rho }_{\text{RD}}=\left({\rho }_{\text{sat}.\text{ vap}.}+{\rho }_{\text{sat}.\text{ liq}.}\right)/2\), is included. According to Zollweg and Mullholland [91], it has to be a linear function in the vicinity of the critical point. The present EOS exhibits this behavior. The rectilinear diameter is of particular importance because no experimental data were available in the gaseous phase to properly shape the saturated vapor line. Another criterion for a reasonable extrapolation behavior is the saddle point of the critical isobar at the critical point defined by the vanishing derivatives \({\left(\partial T/\partial \rho \right)}_{{p}_{\text{c}}}\) and \({\left({\partial }^{2}T/\partial {\rho }^{2} \right)}_{{p}_{\text{c}}}\). The detailed inset in Fig. 13 confirms the correct course of the critical isobar.
Evaluating the isochoric heat capacity and speed of sound in terms of the extrapolation behavior focuses mostly on the critical region. Since the calculation of the isochoric heat capacity is related to the derivative \({\left(\partial p/\partial T\right)}_{\rho }\) (cf. Span [92]), which diverges towards infinity at the critical point, the same peak should be apparent in this property. However, the use of non-analytical terms as in the reference EOS for water [7] and CO2 [93] requires accurate data in the critical regime. This is not the case for MDEA. Moreover, numerical problems are likely to occur when such terms are used in mixture models. Therefore, the non-analytical behavior was only approximated with a GBS term with the extreme parameter \({\beta }_{12}=1000\), resulting in a distinct maximum (see Fig. 14a). The speed of sound becomes zero at the critical point because the derivative \({\left(\partial p/\partial \rho \right)}_{{T}_{\text{c}}}\) vanishes, see Span [92]. This behavior was approximated with a minimum, where the saturated liquid and vapor line meet at the critical point (see Fig. 14b).
The phase identification parameter (PIP), as defined by Venkatarathnam and Oellrich [61], is a valuable property for the evaluation of the extrapolation behavior because it consists of first and second order pressure derivatives with respect to temperature and density. Next to smooth slopes as well as curvature changes without unreasonable bumps, the characteristic maximum of the saturated liquid line and the minimum of the saturated vapor line at the critical point must be present. The maximum and minimum are clearly visible in Fig. 15a. However, at low temperatures, an unexpected change of the curvature in the liquid phase is visible. This behavior could not be corrected during the fitting process without distorting other properties. The same curvature change is apparent for the Grüneisen parameter [90] in Fig. 15b. The Grüneisen parameter connects thermal and caloric properties and is, therefore, an important indicator for a good extrapolation behavior. The overall shape as a function of temperature is similar to the speed of sound. The saturated liquid line should have a negative slope until it meets the saturated vapor line in a minimum at the critical point. This behavior can be observed in Fig. 15b.
Another important criterion are the so-called “ideal curves” (cf. Span and Wagner [94]). Along these curves, a real-fluid property, typically the compressibility factor, is equal to the corresponding one of a hypothetical ideal-gas at the same state point defined by temperature and pressure. The ideal curves calculated with the present EOS are shown in Fig. 16 in terms of the reduced pressure as a function of the reduced temperature. The ideal curves exhibit an excellent behavior because no bumps, discontinuities, or sudden changes of slope or curvature are apparent.
In summary, the analyzed diagrams indicate a good extrapolation behavior, except for the small bump at low temperatures seen for the PIP and Grüneisen parameter.
7 Conclusion
The liquid density and speed of sound of methyl diethanolamine were measured over wide ranges of pressure (0.1–95 MPa) and temperature (300–360 K for density and 322–450 K for speed of sound) ranges with two apparatuses. The uncertainties of these measurements are 0.13 % and 0.09 % for density and speed of sound, respectively.
An equation of state in terms of the Helmholtz energy was fitted to and validated with the presented data as well as all thermodynamic properties available in the literature. Since the Helmholtz energy is a fundamental property, combinations of its derivatives allow for the calculation of all time-independent thermodynamic properties. Its range of validity comprises temperatures from the melting point (\({T}_{\text{melt}}=251.85 \:\text{K}\)) to approximately the critical temperature (Tmax = 750 K) and pressures up to 100 MPa.
The expected uncertainties of the liquid density calculated with the present EOS (k = 2) are 0.13 % and liquid speed of sound are 0.09 % for the temperature and pressure ranges measured in this work. For temperatures from 360 to 470 K at atmospheric pressure, the uncertainty of the liquid density is 0.25 %. The accuracy of other properties cannot be assessed due to the limited database. In addition to the representation of all available experimental data, special attention was paid to a reasonable physical and extrapolation behavior of the model. This behavior was continuously monitored during the development of the equation of state and ensured by considering several thermodynamic properties, such as ideal curves, extreme values of thermal properties, heat capacities, speed of sound, etc.
The Supplementary Material includes a fluid file for the use in the software packages TREND [95] and REFPROP [96].
References
IPCC, Global Warming of 1.5 °C, https://www.Ipcc.Ch/Sr15/ (2019).
J. A. Bullin, J. C. Polasek, and S. T. Donnelly, Proceedings, Annu. Conv. - Gas Process. Assoc. 135 (1984).
M.A. Javed, M. Rüther, E. Baumhögger, J. Vrabec, J. Chem. Eng. Data 65, 2495 (2020). https://doi.org/10.1021/acs.jced.9b01133
M.A. Javed, E. Baumhögger, J. Vrabec, J. Chem. Thermodyn. 141, 105933 (2020). https://doi.org/10.1016/j.jct.2019.105933
F.H. Dubberke, D.B. Rasche, E. Baumhögger, J. Vrabec, Rev. Sci. Instrum. 85, 084901 (2014). https://doi.org/10.1063/1.4891795
E.W. Lemmon, M.O. McLinden, W. Wagner, J. Chem. Eng. Data 54, 3141 (2009). https://doi.org/10.1021/je900217v
W. Wagner, A. Pruß, J. Phys. Chem. Ref. Data 31, 387 (2002). https://doi.org/10.1063/1.1461829
A. Zúñiga-Moreno, L.A. Galicia-Luna, J.M. Bernal-García, G.A. Iglesias-Silva, J. Chem. Eng. Data 52, 1988 (2007). https://doi.org/10.1021/je700287u
K. Meier, The Pulse-Echo Method for High Precision Measurements of the Speed of Sound in Fluids, HelmutSchmidt-Universitat/Universitat der Bundeswehr Hamburg (2006).
F.H. Dubberke, E. Baumhögger, J. Vrabec, Rev. Sci. Instrum. 86, 054903 (2015). https://doi.org/10.1063/1.4921478
D.B. Newell, F. Cabiati, J. Fischer, K. Fujii, S.G. Karshenboim, H.S. Margolis, E. de Mirandés, P.J. Mohr, F. Nez, K. Pachucki, T.J. Quinn, B.N. Taylor, M. Wang, B.M. Wood, Z. Zhang, Metrologia 55, L13 (2018). https://doi.org/10.1088/1681-7575/aa950a
K.G. Joback, R.C. Reid, Chem. Eng. Commun. 57, 233 (1987). https://doi.org/10.1080/00986448708960487
M. Kleiber, R. Joh, In VDI-Wärmeatlas (Springer, Berlin, 2013)
M. Thol, G. Rutkai, A. Köster, F.H. Dubberke, T. Windmann, R. Span, J. Vrabec, J. Chem. Eng. Data 61, 2580 (2016). https://doi.org/10.1021/acs.jced.6b00261
T. Eisenbach, C. Scholz, R. Span, D. Cristancho, E.W. Lemmon, M. Thol, J. Phys. Chem. Ref. Data 50, 023105 (2021). https://doi.org/10.1063/5.0050021
E. W. Lemmon, Numerical Fitting Algorithm for the Development of Equations of State (Personal Communication) (2021).
E.W. Lemmon, R.T. Jacobsen, J. Phys. Chem. Ref. Data 34, 69 (2005). https://doi.org/10.1063/1.1797813
M. Thol, G. Rutkai, A. Köster, R. Lustig, R. Span, J. Vrabec, J. Phys. Chem. Ref. Data 45, 023101 (2016). https://doi.org/10.1063/1.4945000
K. Gao, J. Wu, P. Zhang, E.W. Lemmon, J. Chem. Eng. Data 61, 2859 (2016). https://doi.org/10.1021/acs.jced.6b00195
M. Thol, E.W. Lemmon, Int. J. Thermophys. 37, 1 (2016). https://doi.org/10.1007/s10765-016-2040-6
Sigma-Aldrich, Safety Data Sheet (2021).
M. Berglund, M.E. Wieser, Pure Appl. Chem. 83, 397 (2011). https://doi.org/10.1351/PAC-REP-10-06-02
D.M. VonNiederhausern, G.M. Wilson, N.F. Giles, J. Chem. Eng. Data 51, 1986 (2006). https://doi.org/10.1021/je0602465
C. L. Yaws, Chemical Properties Handbook (ISBN: 0070734011, 1999).
S. Bishnoi, G.T. Rochelle, Ind. Eng. Chem. Res. 41, 604 (2002). https://doi.org/10.1021/ie0103106
A. Pourmohammadbagher, J.M. Shaw, J. Chem. Eng. Data 58, 2202 (2013). https://doi.org/10.1021/je400184t
T.E. Daubert, G. Hutchison, AIChE Symp., Ser. 86, 93 (1990)
T.E. Daubert, DIPPR Data Ser. 2, 143 (1994)
I. Kim, H.F. Svendsen, E. Børresen, J. Chem. Eng. Data 53, 2521 (2008). https://doi.org/10.1021/je800290k
O. Noll, A. Valtz, D. Richon, T. Getachew-Sawaya, I. Mokbel, and J. Jose, Int. Elec. Journ. Phys.Chem. Data1 4, 105 (1998).
E. Skylogianni, I. Mundal, D.D.D. Pinto, C. Coquelet, H.K. Knuutila, Fluid Phase Equilib. 511, 112498 (2020). https://doi.org/10.1016/j.fluid.2020.112498
A. Soames, A. Al Helal, S. Iglauer, A. Barifcani, and R. Gubner, J. Chem. Eng. Data 63, 1752 (2018) . https://doi.org/10.1021/acs.jced.8b00054.
C. Yang, Y. Feng, B. Cheng, P. Zhang, Z. Qin, H. Zeng, F. Sun, J. Chem. Eng. Data 58, 2272 (2013). https://doi.org/10.1021/je400373d
M. Afkhamipour, M. Mofarahi, Fluid Phase Equilib. 457, 38 (2018). https://doi.org/10.1016/j.fluid.2017.09.019
J. Aguila-Hernández, R. Gómez-Quintana, F. Murrieta-Guevara, A. Romero-Martínez, A. Trejo, J. Chem. Eng. Data 46, 861 (2001). https://doi.org/10.1021/je0002944
M.M. Akbar, T. Murugesan, J. Mol. Liq. 169, 95 (2013). https://doi.org/10.1016/j.molliq.2012.02.014
M.M. Akbar, F. Chemat, A. Arunagiri, T. Murugesan, J. Therm. Anal. Calorim. 123, 785 (2016). https://doi.org/10.1007/s10973-015-4957-6
H.A. Al-Ghawas, D.P. Hagewiesche, G. Ruiz-Ibanez, O.C. Sandall, J. Chem. Eng. Data 34, 385 (1989). https://doi.org/10.1021/je00058a004
E. Álvarez, D. Gómez-Díaz, M.D. La Rubia, J.M. Navaza, R. Pacheco, S. Sánchez, J. Chem. Eng. Data 52, 2059 (2007). https://doi.org/10.1021/je700245a
E. Álvarez, F. Cerdeira, D. Gómez-Diaz, J.M. Navaza, J. Chem. Eng. Data 55, 994 (2010). https://doi.org/10.1021/je900437b
J.I. Baek, J.H. Yoon, H.M. Eum, Int. J. Thermophys. 21, 1175 (2000). https://doi.org/10.1023/A:1026454206200
J.M. Bernal-García, M. Ramos-Estrada, G.A. Iglesias-Silva, K.R. Hall, J. Chem. Eng. Data 48, 1442 (2003). https://doi.org/10.1021/je030120x
F.I. Chowdhury, S. Akhtar, M.A. Saleh, Phys. Chem. Liq. 47, 638 (2009). https://doi.org/10.1080/00319100802620538
M. Damanafshan, B. Mokhtarani, M. Mirzaei, M. Mafi, A. Sharifi, A.H. Jalili, J. Chem. Eng. Data 63, 2135 (2018). https://doi.org/10.1021/acs.jced.8b00142
B. Das, B. Deogam, Y. Agrawal, B. Mandal, J. Chem. Eng. Data 61, 2226 (2016). https://doi.org/10.1021/acs.jced.5b00922
R.M. DiGuillo, R.J. Lee, S.T. Schaeffer, L.L. Brasher, A.S. Teja, J. Chem. Eng. Data 37, 239 (1992). https://doi.org/10.1021/je00006a028
A. García-Abuín, D. Gómez-Díaz, M.D. La Rubia, J.M. Navaza, R. Pacheco, J. Chem. Eng. Data 54, 3114 (2009). https://doi.org/10.1021/je900064e
H. Ghaedi, M. Zhao, M. Ayoub, D. Zahraa, A.M. Shariff, A. Inayat, J. Chem. Thermodyn. 137, 108 (2019). https://doi.org/10.1016/j.jct.2018.12.014
A. Haghtalab, A. Shojaeian, J. Chem. Thermodyn. 68, 128 (2014). https://doi.org/10.1016/j.jct.2013.09.001
J. Han, J. Jin, D.A. Eimer, M.C. Melaaen, J. Chem. Eng. Data 57, 1843 (2012). https://doi.org/10.1021/je300345m
B. Hawrylak, S.E. Burke, R. Palepu, J. Solut. Chem. 29, 575 (2000). https://doi.org/10.1023/A:1005198230692
A. Henni, Y. Maham, P. Tontiwachwuthikul, A. Chakma, A.E. Mather, J. Chem. Eng. Data 45, 247 (2000). https://doi.org/10.1021/je9902140
S.A. Jayarathna, D.A. Kottage, D.A. Eimer, M.C. Melaaen, J. Chem. Eng. Data 57, 2975 (2012). https://doi.org/10.1021/je300530z
N.A. Kartikawati, R. Safdar, B. Lal, M.I.B.A. Mutalib, A.M. Shariff, J. Mol. Liq. 253, 250 (2018). https://doi.org/10.1016/j.molliq.2018.01.040
S.N. Khan, S.M. Hailegiorgis, Z. Man, A.M. Shariff, S. Garg, J. Mol. Liq. 229, 221 (2017). https://doi.org/10.1016/j.molliq.2016.12.056
M.H. Li, K.P. Shen, J. Chem. Eng. Data 37, 288 (1992). https://doi.org/10.1021/je00007a002
D. Ma, C. Zhu, T. Fu, X. Yuan, Y. Ma, J. Chem. Thermodyn. 138, 350 (2019). https://doi.org/10.1016/j.jct.2019.06.032
Y. Maham, T.T. Teng, A.E. Mather, L.G. Hepler, Can. J. Chem. 73, 1514 (1995). https://doi.org/10.1139/v95-187
A. Muhammad, M.I.A. Mutalib, T. Murugesan, A. Shafeeq, J. Chem. Eng. Data 53, 2217 (2008). https://doi.org/10.1021/je800416y
S. Paul, B. Mandal, J. Chem. Eng. Data 51, 1808 (2006). https://doi.org/10.1021/je060195b
F.A. Philip, D. Nath, K. Sibilla, A. Henni, J. Chem. Thermodyn. 142, 105978 (2020). https://doi.org/10.1016/j.jct.2019.105978
D.D.D. Pinto, J.G.M.S. Monteiro, B. Johnsen, H.F. Svendsen, H. Knuutila, Int. J. Greenh. Gas Control 25, 173 (2014). https://doi.org/10.1016/j.ijggc.2014.04.017
S. A. Razavizdeh, S. Sheikh, Z. N. Gerowgi, S. A. Razavizadeh, S. Sheikh, and Z. N. Gerowgi, Phys. Chem. Res. 5, 269 (2017). https://doi.org/10.22036/pcr.2017.41046.
M.E. Rebolledo-Libreros, A. Trejo, J. Chem. Eng. Data 51, 702 (2006). https://doi.org/10.1021/je050462y
N.A. Sairi, N.A. Ghani, M.K. Aroua, R. Yusoff, Y. Alias, Fluid Phase Equilib. 385, 79 (2015). https://doi.org/10.1016/j.fluid.2014.11.009
H.A. Shirazizadeh, A. Haghtalab, J. Chem. Thermodyn. 133, 111 (2019). https://doi.org/10.1016/j.jct.2019.02.003
A. Shojaeian, A. Haghtalab, J. Mol. Liq. 187, 218 (2013). https://doi.org/10.1016/j.molliq.2013.07.016
E. Skylogianni, R.R. Wanderley, S.S. Austad, H.K. Knuutila, J. Chem. Eng. Data 64, 5415 (2019). https://doi.org/10.1021/acs.jced.9b00607
F.J. Tamajón, F. Cerdeira, E. Álvarez, J. Chem. Eng. Data 65, 4417 (2020). https://doi.org/10.1021/acs.jced.0c00272
M. Vahidi, B. Moshtari, Thermochim. Acta 551, 1 (2013). https://doi.org/10.1016/j.tca.2012.10.004
X. Wang, F. Yang, Y. Gao, Z. Liu, J. Chem. Thermodyn. 57, 145 (2013). https://doi.org/10.1016/j.jct.2012.08.021
X. Wang, K. Kang, W. Wang, Y. Tian, J. Chem. Eng. Data 58, 3430 (2013). https://doi.org/10.1021/je400679k
X. Wang, J. Chen, X. Wang, Phys. Chem. Liq. 54, 499 (2016). https://doi.org/10.1080/00319104.2015.1115324
Y. Yin, T. Fu, C. Zhu, Y. Ma, J. Mol. Liq. 243, 664 (2017). https://doi.org/10.1016/j.molliq.2017.08.088
R. Yusoff, M.K. Aroua, A. Shamiri, A. Ahmady, N.S. Jusoh, N.F. Asmuni, L.C. Bong, S.H. Thee, J. Chem. Eng. Data 58, 240 (2013). https://doi.org/10.1021/je300628e
Q. Zhang, S. Cai, W. Zhang, Y. Lan, X. Zhang, J. Mol. Liq. 233, 471 (2017). https://doi.org/10.1016/j.molliq.2017.03.036
Y. Zhao, X. Zhang, S. Zeng, Q. Zhou, H. Dong, X. Tian, S. Zhang, J. Chem. Eng. Data 55, 3513 (2010). https://doi.org/10.1021/je100078w
Y.-J.J. Chen, T.-W.W. Shih, M.-H.H. Li, J. Chem. Eng. Data 46, 51 (2001). https://doi.org/10.1021/je0000367
L.F. Chiu, H.F. Liu, M.H. Li, J. Chem. Eng. Data 44, 631 (1999). https://doi.org/10.1021/je980217x
Y. Maham, L.G. Hepler, A.E. Mather, A.W. Hakin, R.A. Marriott, J. Chem. Soc. - Faraday Trans. 93, 1747 (1997). https://doi.org/10.1039/a607568a
M. Mundhwa, A. Henni, J. Chem. Eng. Data 52, 491 (2007). https://doi.org/10.1021/je0604232
A.V. Rayer, A. Henni, P. Tontiwachwuthikul, Can. J. Chem. Eng. 90, 367 (2012). https://doi.org/10.1002/cjce.20646
K. Zhang, B. Hawrylak, R. Palepu, P.R. Tremaine, J. Chem. Thermodyn. 34, 679 (2002). https://doi.org/10.1006/jcht.2002.0937
O. Prokopova, A. Blahut, M. Censky, M. Souckova, and V. Vins, Water & Air Calibration of Vibrating-Tube Densimeter at Temperatures from 0 to 90 °C and Atmospheric Pressure, Talk at 21th Symposium on Thermophysical Properties (2021)
T.J. Fortin, A. Laesecke, M. Freund, S. Outcalt, J. Chem. Thermodyn. 57, 276 (2013). https://doi.org/10.1016/j.jct.2012.09.009
D. González-Salgado, J. Troncoso, and L. Romani, Vol. Prop. 100 (2014). https://doi.org/10.1039/9781782627043-00100.
W. Wagner, M. Thol, J. Phys. Chem. Ref. Data 44, 043102 (2015). https://doi.org/10.1063/1.4931475
S. Herrig, New Helmholtz-Energy Equations of State for Pure Fluids and CCS-Relevant Mixtures, Ph.D. Thesis, Ruhr-Universität Bochum, 2018.
G. Venkatarathnam, L.R. Oellrich, Fluid Phase Equilib. 301, 225 (2011). https://doi.org/10.1016/j.fluid.2010.12.001
V. Arp, J.M. Persichetti, G. Chen, J. Fluids Eng. 106, 193 (1984). https://doi.org/10.1115/1.3243100
J.A. Zollweg, G.W. Mulholland, J. Chem. Phys. 57, 1021 (1972). https://doi.org/10.1063/1.1678352
R. Span, Multiparameter Equations of State - An Accurate Source of Thermodynamic Property Data, 1st edn. (Springer, Berlin, 2000)
R. Span, W. Wagner, J. Phys. Chem. Ref. Data 25, 1509 (1996). https://doi.org/10.1063/1.555991
R. Span, W. Wagner, Int. J. Thermophys. 18, 1415 (1997). https://doi.org/10.1007/BF02575343
R. Span, R. Beckmüller, S. Hielscher, A. Jäger, E. Mickoleit, T. Neumann, S. Pohl, B. Semrau, and M. Thol, (2020).
E. W. Lemmon, I. H. Bell, M. L. Huber, and M. O. McLinden, NIST Standard Reference Database 23: Reference Fluid Thermodynamic and Transport Properties-REFPROP, 10.0 (Gaithersburg, USA, 2018).
Acknowledgements
This publication has been produced with support from the NCCS Centre, performed under the Norwegian research program Centres for Environment-friendly Energy Research (FME). The authors acknowledge the following partners for their contributions: Aker Solutions, Ansaldo Energia, CoorsTek Membrane Sciences, EMGS, Equinor, Gassco, Krohne, Larvik Shipping, Lundin, Norcem, Norwegian Oil and Gas, Quad Geometrics, Total, Vår Energi, and the Research Council of Norway (257579/E20). The authors thank Dr. E. W. Lemmon for his support during the development of the equation of state.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Neumann, T., Baumhögger, E., Span, R. et al. Thermodynamic Properties of Methyl Diethanolamine. Int J Thermophys 43, 10 (2022). https://doi.org/10.1007/s10765-021-02933-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10765-021-02933-7