The Thermal Diffusivity of Glass Sieves: I. Liquid Saturated Frits

Abstract

The thermal diffusivity of evacuated and liquid-saturated borosilicate glass sieves (frits) of porosities between 20 % and 48 % is presented as measured at room temperature. The saturants cover a range in thermal diffusivity from 0.091 mm²·s⁻¹ to 0.143 mm²·s⁻¹. The runs were carried out using a transient hot bridge (THB) measuring instrument of an expanded uncertainty of 5 % to 10 %. The experimental results are successfully fitted to a novel transient parallel-serial (TPSC) conduction model for the time-dependent composite heat transfer in porous media. The TPSC-model is an extension of the steady-state parallel-serial conduction (PSC) model to predict the thermal conductivity. The TPSC model confirms the so-called thermal porosity of the frits under test, a term that has been introduced in a former report on the thermal conductivity of the matrices (Hammerschmidt and Abid, Int J Thermophys 42:40, 2021). The experimental findings on the conductive transport of heat by glass sieves and their accurate mathematical description in the framework of the PSC and TPSC models might effectively support improving the thermal management of electronic devices and lithium-ion batteries.

1 Introduction

In two previous papers [1, 2], the authors presented the thermal conductivities of nine different liquid and gas saturated glass sieves, so-called frits, as functions of porosity and saturant thermal conductivity, respectively. The frits range in porosity between 20 % and 48 %; the saturants cover thermal conductivities from 0.018 W·m⁻¹·K⁻¹ to 0.598 W·m⁻¹·K⁻¹ at room temperature.

Here again, we deal with these saturated frits, but now, the measurand of interest is their thermal diffusivity. When applying liquids as saturants, the accessible interval in thermal diffusivity naturally is relatively small. Here, only those liquids were selected that are readily available and non-hazardous. Their thermal diffusivities range from 0.091 mm²·s⁻¹ to 0.143 mm²·s⁻¹ at room temperature.

In [1, 2], it is demonstrated that fluid filled frits can serve as a favourable model substance for analysing the often-complex combination of solid and fluid conduction of heat in a porous medium. For steady-state conditions, the key transport property of a saturated porous medium, of course, is thermal conductivity. But, whenever conduction of heat becomes time-dependent, the further knowledge of thermal diffusivity is a must require thermal property. For porous media in nature and technique, transient transfer of heat is more the rule rather than the exception: just thinking of melting and solidification of wet soil as well as of latent heat thermal storage devices; thermal processing of food as well as thermal management of electronic devices, internally cooled lithium-ion batteries, and fuel cells. Last but not least, assessing evaporation and solidification of moisture in building envelopes, calculating the onset of convection within a pore or cavity, or investigating magneto-hydrodynamic nanofluids largely depend on the thermal diffusivities of the solids and fluids involved.

Relevant textbooks on heat transfer in porous media (e.g., [3,4,5,6,7,8]) almost exclusively deal with the thermal conductivity of this class of materials rather than with their thermal diffusivity. Generally, the (overall, apparent or effective) thermal conductivity, $\lambda^{*}$, of these solid–fluid media is mathematically represented by the steady-state ‘equations of composite walls’. These expressions are known well for combined heat transport of any number of series and parallel thermal conductors. The two basic relations are analogues to those derived for parallel and series circuits in electrical engineering [9, 10]. Obviously, there are no such equations for an overall thermal diffusivity, $a^{*}$. If this ‘dynamic property’ (unit: m²·s⁻¹) is concerned, in most cases, it is derived from $\lambda^{*}$ and the combined volumetric specific heat,¹$\left( {\rho c_{p} } \right)^{*}$, according to $a^{*} = {{\lambda^{*} } \mathord{\left/ {\vphantom {{\lambda^{*} } {\left( {\rho c_{p} } \right)^{*} }}} \right. \kern-\nulldelimiterspace} {\left( {\rho c_{p} } \right)^{*} }}$. This approach might furnish correct results in various uncomplicated cases of application but does not hold for the vast majority of more complex scenarios. The latter class of the challenging situations already includes the fluid saturated frits under test here [1, 2]. Suitable mathematical ways of looking at such a dynamic problem are, e.g., FEM calculations, Monte-Carlo, Fast Fourier Transform and inverse methods or numerical solutions of partial differential equations. Here, instead, transient equations of composite walls were derived. These were coupled with the so-called Parallel-Serial Conduction (PSC) model that proved effective and accurate in predicting the thermal conductivities of fluid saturated frits [1, 2]. The deviations of the PSC and the TPSC models from the actual data are well within the expanded ISO uncertainties of thermal conductivity and thermal diffusivity, respectively, of the measuring instrument.

All above-mentioned tests on the thermal conductivity and the thermal diffusivity of saturated frits were carried out at room temperature using a transient hot bridge (THB-)instrument [1, 2, 11,12,13]. On each run, this instrument simultaneously measures both above mentioned thermal transport properties.

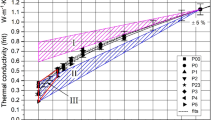
The complete experimental data set on thermal diffusivity comprises the data on liquid saturated frits (LSFs) as well as those on gas saturated frits (GSFs). The total number of data points are: [6 (liquid saturants) + 5 (gas saturants) + 1(evacuated state)] × 8 frits = 96. The entire range in thermal diffusivity covers almost four orders of magnitude from 9.1 × 10^–8 m²·s⁻¹ to 1.72 × 10^–4 m²·s⁻¹ (at room temperature and atmospheric pressure). Figure 1 presents the complete experimental outcome in one diagram that, only for reason of clarity, is a log-representation. Obviously, the LSFs (family of curves on the left-hand side of the diagram) behave completely different from the GSFs (family of curves on the right-hand side). At first sight, this global finding corresponds in some way with the related results on the thermal conductivity of fluid saturated frits (Fig. 2).

Fig. 1

Experimental thermal diffusivity of fluid saturated frits P000 to P5 vs. thermal diffusivity of saturating fluid. The horizontal logarithmic scale was chosen because it enables to compare both groups of liquid and gas saturated frits in one diagram

Fig. 2

Thermal conductivity of evacuated and fluid saturated frits P000 to P5 vs. thermal conductivity of gaseous, λ_G, and liquid, λ_L, saturants: 0.018 W·m⁻¹·K⁻¹ ≤ λ_G ≤ 0.15 W·m⁻¹·K⁻¹; 0.135 W·m⁻¹·K⁻¹ ≤ λ_L ≤ 0.6 W·m⁻¹·K⁻¹

Owing to the vast number of data and the distinct physical behavior they describe for liquids and gases as saturants, this report is divided into two parts: this first part deals with the LSFs whereas the second part will contain the presentation of results on the GSFs. Moreover, here, the novel TPSC equation is described in detail, its derivation, and its application to the thermal diffusivity data of liquid saturated frits (LSFs).

2 Materials and Methods

2.1 Glass Sieves

The nine frits under test were provided by the manufacturer “ROBU Glasfilter GmbH”, Hattert, Germany [14]. The specimens are made of borosilicate glass 3.3 (Table 1). Of each frit class, here termed “P000” to “P5”, two identical plates (“specimen halves”), each of size $80\, \times\,50 \,\times\, 10{\text{ mm}}^{{3}}$, were obtained (Table 2). During a run, the sensor of the transient hot-bridge (THB) instrument is clamped between two halves furnishing a specimen of overall thickness 20 mm.

Table 1 Thermophysical properties of borosilicate glass 3.3 at 20 °C [14]. The volumetric specific heat, $\left( {\rho c_{p} } \right)$, is defined by the arithmetic product of density, r, and specific heat, c_p

Table 2 Pore sizes, grain sizes and porosities of classes “Pxxx” of frits [14,15,16]

2.2 Saturants

Three pure liquids (toluene, alcohol, and water) and three well-defined mixtures of alcohol and water were taken to cover the broadest available range in thermal diffusivity with liquids that are easy to handle and non-hazardous: [0.091 mm²·s⁻¹ ≤ a ≤ 0.143 mm²·s⁻¹ at room temperature (23 °C)] (Table 3).

Table 3 Relevant transport properties and volumetric specific heat capacities (VSHC) of selected saturating fluids (tabulated values for room temperature (23 °C) [17, 18]

2.3 Transient Hot Bridge Setup

The transient hot bridge instrument to simultaneously measure thermal conductivity and thermal diffusivity of solids and liquids has already been described in detail in, e.g., [1, 2, 11,12,13]. The expanded ISO uncertainties ($k = 2$) are ${{3{{ \% }} \le \Delta \lambda } \mathord{\left/ {\vphantom {{3{\text{ \% }} \le \Delta \lambda } {\lambda \le 5\,\% }}} \right. \kern-\nulldelimiterspace} {\lambda \le 5\,\% }}$ and ${{5\,\% \le \Delta a} \mathord{\left/ {\vphantom {{5\,\% \le \Delta a} {a \le 10\,\% }}} \right. \kern-\nulldelimiterspace} {a \le 10\,\% }}$, respectively.

For a liquid saturated frit, a run takes less than one minute to reach the maximum probing depth of 8.8 mm [1, 2]. The temperature rise does not exceed 1.5 K. The short measuring time and the maximum increase in temperature prevent from any significant radiative and/or convective heat transfer inside the porous medium. A detailed analysis on the potential onset of convection $\left( {t_{\text{crit}} = 6.5{\text{ h}}} \right)$ can be found in [1, 2].

The THB instrument consists of the sensor and a field-programmable system source-meter “Keithley 2602”. The latter device provides a voltmeter and a constant current source to operate as a line recorder. The source-meter is programmed to automatically conduct a run and to simultaneously evaluate both measurands according to working equations that are given in [12]. The data reduction algorithm, the instrument applies to evaluate the measurands, is based on the transient line-heat source solution to Fourier’s second law, Eq. 2 [1].

3 Theory

Both transport properties of heat conduction, thermal conductivity, $\lambda$, and thermal diffusivity, $a: = {\lambda \mathord{\left/ {\vphantom {\lambda {\left( {\rho c_{p} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {\rho c_{p} } \right)}}$, are (intensive) material properties, i.e., for liquids, they only depend on temperature. The arithmetic product of density, ρ, and specific heat capacity, $c_{p}$, is called volumetric specific heat. Solved for λ, Fourier’s first law in scalar form and rectangular coordinates reads [18, 19]:

$$\lambda \left( {T,p} \right) = \frac{\phi }{{A_{0} }}\left( {\frac{{{\text{d}}T}}{{{\text{d}}x}}} \right)^{ - 1} \quad \to \quad \lambda \left( {T,p} \right) = \frac{\phi }{L \cdot W}\frac{H}{{T_{2} - T_{1} }}.$$

(1)

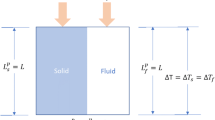
Here, the areic rate of heat flow is given by ${\phi \mathord{\left/ {\vphantom {\phi {A_{0} }}} \right. \kern-\nulldelimiterspace} {A_{0} }}$. The term ${{{\text{d}}T} \mathord{\left/ {\vphantom {{{\text{d}}T} {{\text{d}}x}}} \right. \kern-\nulldelimiterspace} {{\text{d}}x}}$ denotes the (microscopic) temperature gradient. The two geometrical quantities, $A_{0}$ and ${\text{d}}x$, indicate the cross-section area of the heat path and an infinitesimal part of its pathlength, respectively. In practice, the temperature gradient is determined macroscopically from the temperature difference, ${\Delta }T = T_{2} - T_{1}$, across a specimen of thickness H. The cross-section area, $A = L \cdot W$, is calculated from the length, L, and width, W, of the specimen. If the latter macroscopic measures are identical to the microscopic ones, the result of a measurement is a ‘material property’. If not, i.e., for a porous medium, a thermal transport property is determined that is sometimes termed overall, effective, or apparent because its numerical value further depends on geometrical quantities. A specimen of $L \cdot W > A_{0}$ is referred to as porous. If $H < H_{0}$, i.e., the heat path length, $H_{0}$, is greater than the thickness, the specimen is characterized as (thermally) tortuous (cf. Sect. 3.1).

A location and time dependent temperature profile of, e.g., a line heat source within an unbounded homogeneous and isotropic medium, is expressed as [18, 19]:

$${\Delta }T\left( {r,t} \right) = \frac{ - \phi }{{4{\pi }L\lambda }}{\text{Ei}}\left( {\frac{{ - r^{2} }}{4at}} \right) \approx \frac{\phi }{{4{\pi }L\lambda }}\ln \left( {\frac{4at}{{Cr^{2} }}} \right).$$

(2)

For arguments ${{r^{2} } \mathord{\left/ {\vphantom {{r^{2} } {\left( {4at} \right) < < 1}}} \right. \kern-\nulldelimiterspace} {\left( {4a t} \right) < < 1}}$, the exponential integral function $- {\text{Ei}}\left( { - x} \right)$ can be approximated as is already given above. Here, $C = \exp \left( \gamma \right)$ where $\gamma = 0.577...$ denotes Euler’s constant.

3.1 Porosity and Thermal Tortuosity

The conduction heat-path of a non-porous solid generally is characterized by thermal conductivity and thermal diffusivity as well as by the uniform cross-section area, $A_{0}$, and the (linear) length, $H_{0}$. When instead dealing with a porous medium, the latter geometrical properties generally are altered by (1) porosity and/or by (2) tortuosity.

• (1) Any cross-section area, $A_{0} = A_{M} + A_{V}$, of a porous medium can be composed of two distinct partial areas, a solid one, $A_{M}$, as part of the matrix and an empty or fluid filled one, $A_{V}$, as part of the void space. The latter space either is evacuated or fluid filled. In case of a matrix, the relevant transition is given by $A_{0} \to A_{M}$ where $A_{M} = \left( {1 - \phi_{A} } \right)A_{0}$. The areal porosity is given by $\phi_{A} = {{A_{V} } \mathord{\left/ {\vphantom {{A_{V} } {A_{0} }}} \right. \kern-\nulldelimiterspace} {A_{0} }} \le 1$. In measurement practice, commonly, the latter property is not at hand when required to calculate, e.g., the thermal conductivity of a specimen from an appropriate working equation. Hence, the (volumetric) porosity, $\phi = {{V_{V} } \mathord{\left/ {\vphantom {{V_{V} } {V_{0} }}} \right. \kern-\nulldelimiterspace} {V_{0} }}$ is applied instead. For the complementary porosity, it follows $\left( {1 - \phi } \right) = 1 - {{V_{V} } \mathord{\left/ {\vphantom {{V_{V} } {V_{0} = {{V_{M} } \mathord{\left/ {\vphantom {{V_{M} } {V_{0} }}} \right. \kern-\nulldelimiterspace} {V_{0} }}}}} \right. \kern-\nulldelimiterspace} {V_{0} = {{V_{M} } \mathord{\left/ {\vphantom {{V_{M} } {V_{0} }}} \right. \kern-\nulldelimiterspace} {V_{0} }}}}$ where $V_{M}$ and $V_{V}$ are the volume-shares of the matrix and the void space, respectively, as the two parts of the bulk volume $V_{0}$. To simplify matters, the bulk volume is normalized here, $V_{0} = 1{\text{ arb}}{\text{. unit}}$.

• (2) The heat path from source to sink through a porous medium can be tortuous (winding) rather than linear. The actual extension in length is corrected by $H_{0} \to H$ where $H = \tau_{\text{therm}} H_{0}$. For a heat transport scenario, the latter coefficient is termed thermal tortuosity and defined as $\tau_{\text{therm}} = {H \mathord{\left/ {\vphantom {H {H_{0} }}} \right. \kern-\nulldelimiterspace} {H_{0} }} \ge 1$. Since thermal tortuosity generally is a function of porosity, both these latter phenomena often appear concurrently.

Any above-mentioned changeover from inner to outer measurands requires the additional knowledge of $\phi_{A}$ or $\phi$ and/or $\tau_{\text{therm}}$. While the porosity of a specimen is often known from specifications or can be determined (by, e.g., Hg-porosimetry), commonly, any potential thermal tortuosity has to be tested for in situ.

3.1.1 Measuring Thermal Tortuosity of Porous Media

When solving Eq. 2 for the two transport properties concerned, initially, the location and time-dependences of temperature have to be separated from each other. These variables are additively associated to each other, ${\Delta }T\left( {r,t} \right) = {\Delta }T\left( t \right) + {\Delta }T\left( r \right)$, so that:

$$(1)\;{\Delta }T\left( t \right) = \frac{\phi }{{4{\pi }L\lambda }}\ln \left( t \right)\;{\text{and}}\;(2)\;{\Delta }T\left( r \right) = \frac{\phi }{{4{\pi }L\lambda }}\ln \left( {\frac{4a}{{Cr^{2} }}} \right).$$

(3)

• (1) In Eq. 3, any potential location dependence of an overall thermal conductivity is separated away. Together with ${{{\text{d}}T} \mathord{\left/ {\vphantom {{{\text{d}}T} {{\text{d}}\left( {\ln \left( t \right)} \right)}}} \right. \kern-\nulldelimiterspace} {{\text{d}}\left( {\ln \left( t \right)} \right)}} = m_{t} \left( t \right) = {\phi \mathord{\left/ {\vphantom {\phi {\left( {4{\pi }L\lambda } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {4{\pi }L\lambda } \right)}}$ and slope $m_{t} = {\text{const}}{.}$, for ${{r^{2} } \mathord{\left/ {\vphantom {{r^{2} } {\left( {4a t} \right) < < 1}}} \right. \kern-\nulldelimiterspace} {\left( {4a t} \right) < < 1}}$ the remaining time-dependence also vanishes as expected. Hence, any thermal tortuosity of the specimen cannot be determined by a transient technique based on the working equation, Eq. 3.

  When applying instead a steady-state technique, i.e., the guarded hot plate method [Eq. 1], thermal tortuosity can be measured provided the (inherent) thermal conductivity of the specimen and the porosity are known. From Eq. 1, one gets for the thermal conductivity of the matrix:

  $$\lambda_{M} = \frac{{\left( {1 - \phi_{A} } \right)}}{{\tau_{\text{therm}}^{\left( M \right)} }}\lambda_{1} \;{\text{and}}\;\lambda_{LG} = \frac{{\phi_{A} }}{{\tau_{\text{therm}}^{{\left( {LG} \right)}} }}\lambda_{1}.$$

  (4)

  Solving for $\tau_{\text{therm}}^{\left( M \right)}$ yields

  $$\tau_{\text{therm}}^{\left( M \right)} = \left( {1 - \phi_{A} } \right)\frac{{\lambda_{1} }}{{\lambda_{M} }}.$$

  (5)

  The latter three relations correspondingly apply to the void space if filled with a fluid.

• (2) With ${\Delta }T\left( {t = 0} \right) = m_{t} \ln \left( {{{4a} \mathord{\left/ {\vphantom {{4a} {\left( {Cr^{2} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {Cr^{2} } \right)}}} \right) = n_{r}$, Eq. 3 becomes $a = {{Cr^{2} } \mathord{\left/ {\vphantom {{Cr^{2} } 4}} \right. \kern-\nulldelimiterspace} 4} \cdot \exp \left( {{{n_{r} \left( r \right)} \mathord{\left/ {\vphantom {{n_{r} \left( r \right)} {m_{t} }}} \right. \kern-\nulldelimiterspace} {m_{t} }}} \right)$. Here, the location dependence of the intercept $n_{r}$ is compensated by the factor $r^{2}$. This means, that, with the further knowledge of the inherent thermal diffusivity, thermal tortuosity can be determined:

  $$\tau_{\text{therm}} = \sqrt {\frac{4a}{{Cr^{2} }}\exp \left( { - \frac{{n_{r} }}{{m_{t} }}} \right)}.$$

  (6)

The above results can be validated and extended when Eq. 2 is adjusted to allow for porosity and thermal tortuosity:

$${\Delta }T = \frac{{\phi r_{0} }}{{2 \cdot 2{\pi }r_{0} L\lambda_{0} }}\ln \left( {\frac{{4a_{0} t}}{{Cr_{0}^{2} }}} \right) = \frac{{\phi r_{0} }}{{2A_{0} \lambda_{0} }}\ln \left( {\frac{{4a_{0} t}}{{Cr_{0}^{2} }}} \right) \to {\Delta }T = \frac{{\phi \,\tau_{\text{therm}} r_{0} }}{{2\left( {1 - \phi_{A} } \right) \cdot 2{\pi }\,\tau_{\text{therm}} r_{0} L\lambda_{0} }}\ln \left( {\frac{{4a_{0} t}}{{C\tau_{\text{therm}}^{2} r_{0}^{2} }}} \right)$$

yielding

$$\lambda_{0} = \frac{\phi }{{4{\pi }L\left( {1 - \phi_{A} } \right)m_{t} }}\;{\text{and}}\;a_{0} = \frac{{C\tau_{\text{therm}}^{2} r^{2} }}{4}\exp \left( {\frac{{n_{r} }}{{m_{t} }}} \right).$$

(7)

As expected, the working equation for thermal conductivity does not depend on thermal tortuosity but on porosity whereas the working equation for thermal diffusivity does not depend on porosity but on thermal tortuosity. The latter scenario means that thermal tortuosity (of a porous medium) can be determined without the further knowledge of porosity.

All in all, in their standard configuration, that is based on Eq. 3, THW and THB instruments cannot detect any thermal tortuosity from a run on thermal conductivity. In contrast, from a thermal diffusivity measurement, the related instruments are able to detect thermal tortuosity.

3.2 Basic Transport Equations of Porous Media, PSC-model

For a porous medium composed of a solid part and an interconnected void space that is considered to be completely filled by a fluid, the so-called corresponding thermal diffusivity is, in the simplest case, given by the ratio of the volume-weighted arithmetic means of the overall thermal conductivity,

$$\lambda_{0} = \left( {1 - \phi } \right)\lambda_{1} + \phi \lambda_{2}$$

(8)

and the overall vol. specific heat, respectively:

$$a_{0} = \frac{{\lambda_{0} }}{{\left( {\rho c_{p} } \right)_{0} }} = \frac{{\left( {1 - \phi } \right)\lambda_{1} + \phi \lambda_{2} }}{{\left( {1 - \phi } \right)\left( {\rho c_{p} } \right)_{1} + \phi \left( {\rho c_{p} } \right)_{2} }}\;{\text{with}}\;\phi = \phi_{A}.$$

(9)

Here, the solid and the fluid heat paths run in parallel. The above arithmetic mean of the corresponding vol. specific heats, $\left( {\rho c_{p} } \right)_{1}$ and $\left( {\rho c_{p} } \right)_{2}$, is a result of the law of mixtures. This latter principle only in simple cases holds for the thermal transport properties here dealt with.

3.2.1 PSC-Model

In [1, 2], it is demonstrated that the overall thermal conductivities of the LSFs under test are composed of more than just the two basic solid and fluid shares in Eq. 8. Additionally, there is a third parallel heat path that itself is composed of successively alternating solid and liquid sections. According to the applied parallel-serial conduction (PSC-) model, the thermal conductivity is fairly well predicted by a sum of three terms describing individually the parallel heat-pathways of a saturated frit, solid, fluid and mixed:

$$\lambda_{0} = s_{1} \lambda_{1} + s_{2} \lambda_{2} + s_{12} \lambda_{12} \;{\text{with}}\;\lambda_{12} = \frac{{\lambda_{1} \lambda_{2} }}{{d_{1} \lambda_{1} + d_{2} \lambda_{2} }}\;{\text{and}}\;s_{1} + s_{2} + s_{12} = 1\;{\text{and}}\;d_{1} + d_{2} = 1.$$

(10)

In both cases of simple solid or fluid transport, the above result yields in accordance with Eq. 8:

$$\lambda_{0} \left( {\lambda_{1} > 0,\lambda_{2} = 0} \right) = s_{1} \lambda_{1} = \left( {1 - \phi } \right)\lambda_{1} = {{V_{M} } \mathord{\left/ {\vphantom {{V_{M} } {V_{0} \cdot \lambda_{1} }}} \right. \kern-\nulldelimiterspace} {V_{0} \cdot \lambda_{1} }},$$

(11)

$$\lambda_{0} \left( {\lambda_{1} = 0,\lambda_{2} > 0} \right) = s_{2} \lambda_{2} = \phi \lambda_{2} = {{V_{S} } \mathord{\left/ {\vphantom {{V_{S} } {V_{0} \cdot \lambda_{2} }}} \right. \kern-\nulldelimiterspace} {V_{0} \cdot \lambda_{2} }}.$$

(12)

Instead, it was found out [1] that, for reasons to be explained in Sect. 4.1.1, the dimensionless coefficient $s_{1}$ is equal to $\left( {1 - \left( {\phi + 0.37} \right)} \right)$ rather than $\left( {1 - \phi } \right)$. Consequently, a thermal porosity, $\phi_{\text{therm}}$, was introduced to account for the ‘offset in porosity’, $s_{0}$:

$$\phi_{\text{therm}} = \phi + 0.37 = \phi + s_{0} \;{\text{so that}}\;s_{1} = \left( {1 - \phi_{\text{therm}} } \right)\;{\text{and}}\;s_{2} = \phi_{\text{therm}} - s_{12}.$$

(13)

Equations 11 and 12 have to be adapted accordingly:

$$\lambda_{0} \left( {\lambda_{2} = 0} \right) = \left( {1 - \phi_{\text{therm}} } \right)\lambda_{1} = \left( {\frac{{V_{M} - 0.37}}{{V_{0} }}} \right)\lambda_{1} = \frac{{V_{11} }}{{V_{0} }}\lambda_{1}$$

(14)

and

$$\lambda_{0} \left( {\lambda_{1} = 0} \right) = \left( {\phi_{\text{therm}} - s_{12} } \right)\lambda_{2} = \left( {\frac{{V_{S} + 0.37 - s_{12} }}{{V_{0} }}} \right)\lambda_{2}.$$

(15)

The above result, Eq. 14, implies that the matrix volume is reduced by the offset volume, $s_{0} = 0.37$. This means that only the residual partial-volume $V_{11}$ of an evacuated frit is able for ‘through-conduction’ of heat. In the complementary case, Eq. 15, one would expect that $s_{12} = 0.37$. According to Table 4, this is not true. Apart from that for the vol. specific heat of a saturated frit, the law of mixtures still correctly furnishes:

$$\left( {\rho c_{p} } \right)_{0} = \left( {1 - \phi } \right)\left( {\rho c_{p} } \right)_{1} + \phi \left( {\rho c_{p} } \right)_{1} = \frac{{V_{M} }}{{V_{0} }}\left( {\rho c_{p} } \right)_{1} + \frac{{V_{S} }}{{V_{0} }}\left( {\rho c_{p} } \right)_{2}.$$

(16)

Table 4 Fit coefficients to Eq. 10 and related matrix thermal conductivities, $\lambda_{M}$, of frits Pxxx (cf. Fig. 1). The stated porosity is indicated by $\phi$, the complementary porosity by $\left( {1 - \phi } \right)$

If the void space is saturated with any reasonable thermal conductor ($V_{V} = V_{S}$), one gets for the overall conductivity:

$$\lambda_{0} = \frac{{V_{11} }}{{V_{0} }}\lambda_{1} + \left[ {\frac{{V_{S} }}{{V_{0} }} + 0.37 - s_{12} } \right]\lambda_{2} + s_{12} \lambda_{12} = \frac{{V_{11} }}{{V_{0} }}\lambda_{1} + \frac{{V_{S} }}{{V_{0} }}\lambda_{2} + \left( {0.37 - s_{12} } \right)\lambda_{2} + s_{12} \lambda_{12}.$$

(17)

Obviously, in addition to the three terms of the above approach in Eq. 14, a fourth term, $\left( {0.37 - s_{12} } \right)\lambda_{2}$ comes out. From Table 4, it can be seen that this latter difference does not vanish. Conceivably, the PSC-model correctly predicts the overall thermal conductivities but, itself, is uncomplete. The question why the porosity offset, $s_{0} = 0.37 = {\text{const}}{.}$, is valid for all frits under test is still open.

From Eqs. 14, 15, 16 and 17, it follows for the physical scenario that only a part of the matrix volume, $V_{11}$, can through-conduct heat. Nevertheless, the entire matrix volume, $V_{M}$, is able to store heat. The larger share of the matrix volume, $V_{M} - V_{11}$, only takes part in mixed conduction.

So far, it remains questionable whether the fluid-filled void volume, $V_{V} = V_{S}$, also is through-conducting only partly.

Moreover, as a further consequence of the inequality of the above two kinds of porosity, $\phi$ and $\phi_{\text{therm}}$, Eq. 9 becomes invalid here. This fact is justified by the following brief verification: thermal diffusivity is defined by the balance law of internal energy, u, $\rho {{\partial u} \mathord{\left/ {\vphantom {{\partial u} {\partial t = {\text{div}}\left( {\lambda {\text{grad}}T} \right)}}} \right. \kern-\nulldelimiterspace} {\partial t = {\text{div}}\left( {\lambda {\text{grad}}T} \right)}} \Rightarrow {{\partial T} \mathord{\left/ {\vphantom {{\partial T} {\partial t}}} \right. \kern-\nulldelimiterspace} {\partial t}} = a{{\partial^{2} T} \mathord{\left/ {\vphantom {{\partial^{2} T} {\partial r^{2} }}} \right. \kern-\nulldelimiterspace} {\partial r^{2} }}$. Hence, $\left( {1 - \phi } \right)\rho {{\partial u} \mathord{\left/ {\vphantom {{\partial u} {\partial t \ne \left( {1 - \phi_{\text{therm}} } \right)\lambda \;{\text{div}}\left( {{\text{grad}}T} \right)}}} \right. \kern-\nulldelimiterspace} {\partial t \ne \left( {1 - \phi_{\text{therm}} } \right)\lambda \;{\text{div}}\left( {{\text{grad}}T} \right)}}$.

The departures of the thermal conductivities predicted by the PSC-model and the actual numerical values are between − 2 % and + 0.5 % [1].

3.3 Transient PSC-Model

As mentioned, the PSC-model is ‘thermally’ based on Fourier’s first law and on a specific ‘electrical’ analog model (resistor network) that consists of three resistors in parallel, one of them is constituted by two single resistors in series. This model can fairly well predict the overall thermal conductivity of a parallel and/or serial combination of heat conductors (composite wall equations). However, due to its steady-state character, the PSC-model is not qualified to account for a ‘dynamic’ quantity like thermal diffusivity (unit: m²·s⁻¹).

A transient PSC-model has ‘thermally’ to be based on Fourier’s second law, the partial differential equation (PDE) of heat conduction, and on an ‘electrical’ equivalent circuit in which each resistor R has to be replaced by a parallel RC-element (resistor–capacitor circuit). The role of capacitors is to equivalently represent the ability of a medium to store heat.

To the best of our knowledge, so far, there is no simple transient PSC-model. Instead, various numerical techniques like finite elements, Monte-Carlo or fast Fourier transform are applied on a case-by-case basis, i.e., results are only obtained for a special well-defined scenario. Even minor changes and modifications will require a completely new calculation. It would be more attractive to have available equations of composite walls that can deal with both steady-state and transient conditions and at reasonable accuracy.

Therefore, in the following, a simple model is derived to represent the overall thermal diffusivity of the frits under test. It is demonstrated that, for steady-state conditions, the new transient PSC-model (TPSC) falls back to the PSC-model.

3.3.1 Transient Parallel Heat-Conduction

The overall rate of heat flow along three self-contained pathways, here termed “1”, “2” and “12”, and arranged in parallel, is given by the sum of the partial heat flow rates, $\phi_{0} = \phi_{1} + \phi_{2} + \phi_{12}$. The constant flow rate, $\phi_{0}$, is liberated by, e.g., a transient line heat source, generating a spatiotemporal temperature field within an unbounded homogeneous and isotropic medium that is governed by (Eq. 2):

$${\Delta }T\left( {r,t} \right) \approx \frac{{\phi_{0} }}{{4{\pi }L\lambda_{0} }}\ln \left( {\frac{{4a_{0} t}}{{Cr^{2} }}} \right).$$

(18)

Here, $\lambda_{0}$ and $a_{0}$ are the overall thermal transport properties involved. Both quantities may become functions of the geometrical characteristics of the heat pathway(s) and of time.

First, solving for three individual heat flow rates in parallel and substituting ${{Cr^{2} } \mathord{\left/ {\vphantom {{Cr^{2} } {\left( {4t} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {4t} \right)}} = \sigma$ furnishes the relation:

$$\frac{{\lambda_{0}^{*} \left( \sigma \right) \cdot {\Delta }T_{0} }}{{\ln \left( {\frac{{a_{0} }}{\sigma }} \right)}} = \frac{{s_{1} \lambda_{1} \cdot {\Delta }T_{1} }}{{\ln \left( {\frac{{a_{1} }}{\sigma }} \right)}} + \frac{{s_{2} \lambda_{2} \cdot {\Delta }T_{2} }}{{\ln \left( {\frac{{a_{2} }}{\sigma }} \right)}} + \frac{{s_{12} \lambda_{12} \cdot {\Delta }T_{12} }}{{\ln \left( {\frac{{a_{12} }}{\sigma }} \right)}}$$

(19)

where $\lambda_{0}^{*} \left( \sigma \right) = \lambda_{0}^{*} \left( {r,t} \right)$ is considered a function of location and time. For times, long enough to let the three heat-paths-specific temperatures equilibrate, $\Delta T_{0} \left( \sigma \right) = \Delta T_{1} \left( \sigma \right) = \Delta T_{2} \left( \sigma \right) = \Delta T_{{12}} \left( \sigma \right)$, one gets:

$$\mathop {\lim }\limits_{\sigma \to 0} \lambda_{0}^{*} \left( \sigma \right) = \mathop {\lim }\limits_{\sigma \to 0} \left[ {\ln \left( {\frac{{a_{0} }}{\sigma }} \right)\left[ {\frac{{s_{1} \lambda_{1} }}{{\ln \left( {\frac{{a_{1} }}{\sigma }} \right)}} + \frac{{s_{2} \lambda_{2} }}{{\ln \left( {\frac{{a_{2} }}{\sigma }} \right)}} + \frac{{s_{12} \lambda_{12} }}{{\ln \left( {\frac{{a_{12} }}{\sigma }} \right)}}} \right]} \right].$$

(20)

This basic TPSC-model expression, of course, falls back to the above steady-state result of the PSC-model:

$$\mathop {\lim }\limits_{\sigma \to 0} \lambda_{0}^{*} = \lambda_{0} = s_{1} \lambda_{1} + s_{2} \lambda_{2} + s_{12} \lambda_{12}.$$

(21)

Next, Eq. 19 is solved for the overall thermal diffusivity, $a_{0} = a_{0} \left( \sigma \right)$. Again, for times of practically completed temperature equilibration and together with Eq. 10, one gets the relation:

$$a_{0}^{*} = \exp \left[ {\ln \left( {\frac{{a_{1} }}{\sigma }} \right)\ln \left( {\frac{{a_{2} }}{\sigma }} \right)\ln \left( {\frac{{a_{12} }}{\sigma }} \right)\frac{{s_{1} \lambda_{1} + s_{2} \lambda_{2} + s_{12} \lambda_{12} }}{{s_{1} \lambda_{1} \ln \left( {\frac{{a_{2} }}{\sigma }} \right)\ln \left( {\frac{{a_{12} }}{\sigma }} \right) + s_{2} \lambda_{2} \ln \left( {\frac{{a_{1} }}{\sigma }} \right)\ln \left( {\frac{{a_{12} }}{\sigma }} \right) + s_{12} \lambda_{12} \ln \left( {\frac{{a_{1} }}{\sigma }} \right)\ln \left( {\frac{{a_{2} }}{\sigma }} \right)}}} \right]\sigma.$$

(22)

Finally, the parallel TPSC relation follows²:

$$\mathop {\lim }\limits_{\sigma \to 0} a_{0}^{*} \left( \sigma \right) = a_{0} = a_{1}^{{\frac{{s_{1} \lambda_{1} }}{{s_{1} \lambda_{1} + s_{2} \lambda_{2} + s_{12} \lambda_{12} }}}} \cdot a_{2}^{{\frac{{s_{2} \lambda_{2} }}{{s_{1} \lambda_{1} + s_{2} \lambda_{2} + s_{12} \lambda_{12} }}}} \cdot a_{12}^{{\frac{{s_{12} \lambda_{12} }}{{s_{1} \lambda_{1} + s_{2} \lambda_{2} + s_{12} \lambda_{12} }}}}.$$

(23)

The above power law closely resembles a conductivity weighted geometric mean of the thermal diffusivities, $a_{x}$, involved. In the trivial case of $a_{1} = a_{2} = a_{12} = a_{0}$, the result is $a_{0}$. For, e.g., $a_{12} = 0$, the related conductivity $\lambda_{12} = 0$ must also vanish so that $\mathop {\lim }\limits_{{\lambda_{12} \to 0}} a_{12}^{{\frac{{s_{12} \lambda_{12} }}{{s_{1} \lambda_{1} + s_{2} \lambda_{2} + s_{12} \lambda_{12} }}}} = 1$. Equations 23 and 24 can easily be expanded to deal with more than three parallel heat pathways: the overall thermal diffusivity of $i = 1 \ldots n$ parallel heat paths is given by:

$$a_{0} = \prod\limits_{i} {a_{i}^{{\frac{{s_{j} \lambda_{j} }}{{\sum\limits_{j} {s_{j} \lambda_{j} } }}}} } \;\;\left( {j = 1\ldots\,m} \right).$$

(24)

As well, instead of Eq. 10, an alternative prediction model for thermal conductivity may be applied, e.g., Eq. 8 (Sect. 3.3.3).

Regrettably, both individual derivatives of interest here, ${{\partial a_{0} } \mathord{\left/ {\vphantom {{\partial a_{0} } {\partial a_{2} }}} \right. \kern-\nulldelimiterspace} {\partial a_{2} }}$ and ${{\partial a_{0} } \mathord{\left/ {\vphantom {{\partial a_{0} } {\partial \phi }}} \right. \kern-\nulldelimiterspace} {\partial \phi }}$, are particularly complex. Therefore, locations of the potential extremes are not determined analytically.

3.3.2 Transient Serial Heat-Conduction

The above approach to derive a working equation for the overall thermal diffusivity of parallel composite-transport of heat cannot likewise be applied to a serial combination of heat conductors/reservoirs. The reason behind is a consequence of one of the basic assumptions to solve Fourier’s relevant PDE: an unbounded uniform medium surrounds the line heat source. Here, instead, there are at least two distinct uniform media, or, more general, each succeeding layer bounds the preceding one. The outmost layer still remains unbounded.

It is worth noting here, that, in contrast to the steady-state scenario, the second and/or further following layers might only partly or even not at all be “seen” by a measuring instrument if the time of a run is too short for the ‘probing heat’ to traceable penetrate all layers of interest.

Especially, in the framework of the laser-flash measurement technique, there are various distinct heat transfer models for two or multi-layer specimens to determine the thermal contact resistance and/or the thermal diffusivity of a particular layer [20,21,22]. These working equations generally are based on Green’s functions or similar solution methods and, therefore, are extraordinarily complex and specific in their applications.

For the evaluation of the serial thermal diffusivity, $a_{12}$, here again, a simple approach proved particularly useful. The unconventional approach is based on a time-of-flight-model of a single heat pulse. With this in mind, the line heat-source considered above is examined once more. Now, instead of a stepwise heat pulse, a heat pulse of vanishing width is studied when released to the surrounding medium. The basic working equation from any relevant textbook (cf., e.g., [18, 19]) reads:

$${\Delta }T\left( {r,t} \right) = \frac{H}{{4{\pi }at\rho c_{p} }}\exp \left( {\frac{{-r^{2} }}{4at}} \right).$$

(25)

Here, the enthalpy liberated by the pulsed source is denoted H. At some location, r, from the source, the maximum of the pulse occurs at time:

$$t_{m} = \frac{{r^{2} }}{4a}.$$

(26)

The first two cylindrical layers around the line source are considered to be of thicknesses $r = r_{1} > 0$ and $r = r_{2} - r_{1} \ge 0$, respectively, as well as of individual thermal diffusivities $a_{1}$ and $a_{2} \ne a_{1}$, respectively. The travel time for the heat pulse to pass through the first layer is $t_{1} = {{r_{1}^{2} } \mathord{\left/ {\vphantom {{r_{1}^{2} } {\left( {4a_{1} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {4a_{1} } \right)}}$ and for the second layer $t_{2} = {{\left( {r_{2}^{2} - r_{1}^{2} } \right)} \mathord{\left/ {\vphantom {{\left( {r_{2}^{2} - r_{1}^{2} } \right)} {\left( {4a_{2} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {4a_{2} } \right)}}$. The total time, it takes the pulse to run successively through both layers, is $t_{0} = {{r_{2}^{2} } \mathord{\left/ {\vphantom {{r_{2}^{2} } {\left( {4a_{0} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {4a_{0} } \right)}}$. Accordingly, the overall thermal diffusivity $a_{0}$ has to be chosen so that

$$\frac{{r_{2}^{2} }}{{4a_{0} }} = \frac{{r_{1}^{2} }}{{4a_{1} }} + \frac{{r_{2}^{2} - r_{1}^{2} }}{{4a_{2} }}.$$

(27)

Solving for $a_{0}$ furnishes

$$a_{0} = a_{0} \left( r \right) = \frac{{a_{1} a_{2} r_{2}^{2} }}{{a_{2} r_{1}^{2} + a_{1} \left( {r_{2}^{2} - r_{1}^{2} } \right)}}\;{\text{with}}\;a_{2} > 0\;\;{\text{and/or}}\;r_{2} \ge r_{1}.$$

(28)

Here, the following limits are valid: $\mathop {\lim }\limits_{{r_{2} \to \infty }} a_{0} = a_{2}$ and $\mathop {\lim }\limits_{{a_{2} \to \infty }} a_{0} = a_{1} \frac{{r_{2}^{2} }}{{r_{1}^{2} }}$. Equation 28 can also be expanded to encompass more than two heat conductors/accumulators in a serial heat pathway: the overall thermal diffusivity of $i = 1 \ldots n$ thermal conductors in series reads:

$$a_{0} = \frac{{r_{n}^{2} }}{{\sum\limits_{i = 1}^{n} {\frac{{r_{i}^{2} - r_{i - 1}^{2} }}{{a_{i} }}} }}\;{\text{with}}\;r_{0} = 0.$$

(29)

In order to numerically illustrate the above result, a ‘liquid-saturated template-frit’ is considered. It is composed of the material properties of the (real) matrix P00 and various fictional fluids as saturants, each one of vol. specific heat $\left( {\rho c_{p} } \right)_{fic} = 1{\text{ MJ}} \cdot {\text{m}}^{ - 3} \cdot {\text{K}}^{ - 1}$ and thermal diffusivity $a_{fic} = {{\lambda_{fic} } \mathord{\left/ {\vphantom {{\lambda_{fic} } {\left( {\rho c_{P} } \right)_{fic} }}} \right. \kern-\nulldelimiterspace} {\left( {\rho c_{P} } \right)_{fic} }}$. Figure 3 presents a diagram of the calculated mixed thermal diffusivity $a_{0} = a_{{12\left( {fic} \right)}}$ of this template-frit P00 vs. (fictional) saturants’ thermal diffusivity. According to the above-mentioned limit of $a_{0}$, the curve converges against $a_{{12\left( {fic} \right)}} = 0.633 \cdot {{d_{2}^{2} } \mathord{\left/ {\vphantom {{d_{2}^{2} } {d_{1}^{2} }}} \right. \kern-\nulldelimiterspace} {d_{1}^{2} }} = 1.218$. (For the individual thicknesses of layers $d_{1}$ and $d_{2}$ of the frit P00, refer to the PSC-model coefficients listed in Table 4.) In advance of the presentation of the experimental results in the second part of this report, Fig. 4 presents the real mixed thermal diffusivities vs. the thermal diffusivities of the (real) liquid and gaseous saturants. This curve converges against 1.15 mm²·s⁻¹.

Fig. 3

TPSC-model: (fictional) mixed thermal diffusivity of the serial heat path of frit P00, $a_{12}$ vs. $\lg \left( {a_{S} } \right)$ for fictional fluid saturants (see text)

Fig. 4

Mixed thermal diffusivity of frit P00 vs. thermal diffusivity of liquid and gas saturants (cf. Fig. 3). [The log-plot has been applied for reason of clarity only; nonlinear fit according to TPSC-model, Eq. 22 (${\text{COD: }}R^{2} = 0.99$)]

It is worth noting here that the above time-of-flight approach probably cannot be applied to solve the problem of identifying an overall thermal diffusivity of parallel heat conductors/accumulators (Sect. 3.2.1). We cannot see any promising approach to incorporate the necessary ‘synchronization’ of the individual heat-path temperatures involved.

3.3.3 Transient Parallel-Serial Heat-Conduction/Check-Mark-Function

Finally, by combining Eqs. 23, 24, 28 and 29, one gets the complete TPSC-model for the overall thermal diffusivity of the specific 2 + 1-paths-scenario of the frits under test:

$$a_{0} \left( {\lambda_{1} ,\lambda_{2} ,\lambda_{12} ,a_{1} ,a_{2} ,a_{12} ,r_{1} ,r_{2} ,} \right) = a_{1}^{{\frac{{s_{1} \lambda_{1} }}{{s_{1} \lambda_{1} + s_{2} \lambda_{2} + s_{12} \lambda_{12} }}}} \cdot a_{2}^{{\frac{{s_{2} \lambda_{2} }}{{s_{1} \lambda_{1} + s_{2} \lambda_{2} + s_{12} \lambda_{12} }}}} \cdot \left( {\frac{{a_{1} a_{2} r_{2}^{2} }}{{a_{2} r_{1}^{2} + a_{1} \left( {r_{2}^{2} - r_{1}^{2} } \right)}}} \right)^{{\frac{{s_{12} \lambda_{12} }}{{s_{1} \lambda_{1} + s_{2} \lambda_{2} + s_{12} \lambda_{12} }}}} .$$

(30)

Based on the same fictional material properties as considered for Fig. 3, Fig. 5 shows the overall thermal diffusivity of the fluids-saturated matrix P00 vs. the thermal diffusivity of the fictional saturants. This ‘check-mark-function’, obviously, has a minimal turning point at $\left( {0.1,0.465} \right)$. By comparing the fictional and the real (experimental) data sets (Figs. 5 and 6), one finds the real minimum, in x-direction only slightly shifted from the fictional one, at $\left( {0.09,0.23} \right)$. It will be demonstrated that the deviations between the actual and the predicted data of Fig. 5 are well within the above-mentioned measurement uncertainty of the THB-instrument.

Fig. 5

TPSC-model: thermal diffusivity of the borosilicate 3.3 frit P00 saturated with fictional fluid media of $a_{fic} = {{\lambda_{fic} } \mathord{\left/ {\vphantom {{\lambda_{fic} } {\left( {\rho c_{P} } \right)_{fic} {\text{ with }}\left( {\rho c_{p} } \right)_{fic} = 1{\text{ MJ}} \cdot {\text{m}}^{ - 3} \cdot {\text{K}}^{ - 1} }}} \right. \kern-\nulldelimiterspace} {\left( {\rho c_{P} } \right)_{fic} {\text{ with }}\left( {\rho c_{p} } \right)_{fic} = 1{\text{ MJ}} \cdot {\text{m}}^{ - 3} \cdot {\text{K}}^{ - 1} }}$(see text)

Fig. 6

Thermal diffusivity of liquid saturated frits vs. thermal diffusivity of saturant liquids

As has already been notified, the TPSC-model likewise performs with other reasonable thermal conductivity functions. For example, substituting the commonly used relation $\lambda_{0} = \left( {1 - \phi } \right)\lambda_{1} + \phi \lambda_{2}$ furnishes the diagram, Fig. 7, when once more, fictional saturant properties are assumed. Comparing this latter diagram with the one of Fig. 5, a considerable influence of the third (parallel-serial) heat path on the overall thermal diffusivity can clearly be detected.

Fig. 7

TP(S)C-model: same parameters as of Fig. 5, but now just two parallel heat paths

However, again, from Eq. 30, the above minimum cannot be determined analytically for formal reasons.

4 Experimental Results

An overview of the complete outcome of the THB runs on the thermal diffusivity of fluid saturated frits is presented in Fig. 1 as function of the thermal diffusivities of liquid and gaseous saturants. As has already been mentioned, the independent variable is log-scaled only for reasons of clarity and comprehensibility because this latter variable ranges over more than three orders of magnitude. The entire interval has two obvious gaps. The one on the left-hand side extends between the family of curves called “liquids” and the glass point from 0.143 mm²·s⁻¹ to 0.63 mm²·s⁻¹. The right-hand one ranges from 0.63 mm²·s⁻¹ to 20.63 mm²·s⁻¹ between the glass point and the family of curves named “gases”. Both ‘data holes’ are mainly due to the lack of suitable liquids and gases as saturants. Alternatively, the first gap can easily be closed numerically by means of the predictions of the TPSC-model (see Figs. 3, 5 and 6). The second hole is a “pseudo gap”. This means that, for reasons to be discussed in the second part of this report, the extrapolations of the curves of the GSFs to the origin do not pass through the glass point. Nevertheless, this gap can also be closed numerically in the framework of the new transient model.

The above different behavior of both families of curves (Fig. 1) has already been observed for both corresponding families of the thermal conductivity curves (cf. Figure 2). Here, again, all extrapolations of the LSF curves pass through the glass point whereas the GSF curves do not.

The interval of thermal diffusivity data of saturants between $0.09{\text{ mm}}^{{2}} \cdot {\text{s}}^{ - 1} \le a_{S} \le 172.5{\text{ mm}}^{{2}} \cdot {\text{s}}^{ - 1}$ is depicted in more detail and plotted against the physically correct x-axis-scaling in Fig. 6. This chart includes the almost linear TPSC-interpolation lines (Fig. 5) that bridge the gap. From Fig. 7, it becomes clear that the simple arithmetic mean approach for the so-called corresponding thermal diffusivity, as given by Eq. 8, is not able to correctly represent the actual data sets.

The thermal diffusivities of the GSFs including their matrices (“vacuum”) vs. porosity are presented in Fig. 8. Again, these results are compared with the corresponding thermal-conductivity data sets (Fig. 9). Both matrix data sets almost linearly decline with porosity though the GSF curve shows a piecewise ‘bended’ interval, caused by the four frits P0, P1, P2 and P23. Interestingly, the bend is not realized when the frits are filled with a liquid. The probably morphological reason(s) for this abnormality are not known so far.

Fig. 8

Thermal diffusivity of borosilicate glass 3.3 as well as of evacuated (“vacuum”) and liquid saturated first vs. porosity. (“XXa-YYw” means XX % alcohol and YY % water)

Fig. 9

Thermal conductivity of glass as well as of evacuated (“vacuum”) and liquid saturated frits vs. porosity

The shapes of the thermal conductivity and thermal diffusivity curves of the LSFs both look fairly linear though they are not: the lines are almost horizontal for thermal conductivity and declining for thermal diffusivity.

4.1 Thermal Diffusivity of Evacuated Frits Vs. Thermal Porosity

Figure 10 shows the thermal diffusivity of all nine matrices, P000 to P5 vs. complementary thermal porosity, $\left( {1 - \phi_{\text{therm}} } \right) = \left( {1 - \left( {\phi + 0.37} \right)} \right)$. According to Eqs. 7 and 30, the thermal diffusivities of all matrices under test should be identically equal to the thermal diffusivity of borosilicate glass 3.3, irrespective of their individual complementary porosities. As can be seen in the diagram and in Table 5, here, this is not the case. While the thermal diffusivity of the frit P000 of $\left( {1 - \phi_{\text{therm}} } \right) = 0.43$ achieves 97 % of the supposed numerical value, P5 of $\left( {1 - \phi_{\text{therm}} } \right) = 0.15$ only reaches 27 %.

Fig. 10

Thermal diffusivity of all evacuated frits Pxxx under test and of borosilicate glass 3.3 vs. complementary porosity. The calculated values are determined from the experimental thermal conductivity and the related volumetric specific heats

Table 5 Actual thermal diffusivities of borosilicate glass 3.3 and all matrices under test along with their complementary porosities and matrix volume shares ${{V_{12} } \mathord{\left/ {\vphantom {{V_{12} } {V_{M} }}} \right. \kern-\nulldelimiterspace} {V_{M} }}$

4.1.1 Discussion

As has already been mentioned, the widely applied equation Eq. 9 is formally not applicable for the matrices under test because of the fact that in this particular case the term $\left( {1 - \phi_{\text{therm}} } \right)\lambda_{BG}$, where $\lambda_{BG}$ denotes the thermal conductivity of borosilicate glass, differs from $\left( {1 - \phi } \right)\lambda_{BG}$.

The relevant physical scenario behind thermal porosity, $\phi_{\text{therm}}$, has already been presented in our recent report on the thermal conductivity of the matrices [1]. Here, only a brief summary will be given.

The thermal conductivity of an evacuated porous medium generally depends on complementary porosity, $\lambda_{M} = \lambda_{M} \left( {1 - \phi } \right)$. For the matrices P000 to P5, remarkably, this is not the case. From the relevant measurements, it turned out that not the entire matrix volume, $V_{M} = V_{11} + V_{12}$, allows for through-conduction of heat but only the smaller volume fraction, $V_{11}$ (Table 5). $V_{12}$ is expected only to store heat. While almost half of the matrix volume of P00 through-conducts heat, it is less than one third in case of P5. The reason for this behavior is supposed to be simple: the larger fraction of each matrix volume is composed of the dead-end zones of so-called dead-end grains. These latter glass fragments can be understood as the (solid) complement of (fluid-filled) dead-end pores [23, 24]. During, e.g., transient heat conduction, each dead-end continuously absorbs heat, but, without any active local connection to another grain, can only store it. As a result, the thermal conductivity of the matrix is considerably smaller than expected due to its complementary porosity. This effect can be described by introducing a thermal porosity, $\phi_{\text{therm}} \ne \phi$, in place of (volumetric) porosity. The effect itself is (numerically) predicted by the PSC-model. Since this model is included in the TPSC-model, the related coefficients, $s_{1}$, $s_{2}$ and $s_{12}$ carry on this vital information. (Sect. 3.1.1).

In contrast to the above effect, the observed anomalous porosity-dependent thermal diffusivity of the frits, $a_{0} < a_{BG}$, is, so far, not implemented in the TPSC-model: Eq. 30, furnishes a formally correct result, $a_{0} = a_{BG}^{{\frac{{s_{1} \lambda_{1} }}{{s_{1} \lambda_{1} }}}} = a_{BG}^{1}$ that, consequently, does not contain porosity, $s_{1} \equiv \left( {1 - \phi_{\text{therm}} } \right)$. When instead applying Eqs. 28, 29 along with the condition $r_{2} = r_{1}$, again, one accurately but incompletely gets $a_{0} = a_{BG}$. Therefore, it is supposed that porosity, if at all, does not directly affect the observed irregular variations in thermal diffusivity. When looking for a phenomenon that can explain the experimental findings, the most probable candidate is thermal tortuosity. As already mentioned, this non-dimensional quantity describes the ratio, $\tau_{\text{therm}}$, of the lengths of a winding and a direct (linear) heat path.

In order to incorporate thermal tortuosity into the TPSC-model, the approach to Eqs. 28, 29, 26 was taken to formulate a transient working equation for this non-dimensional quantity. Equation 26 describes the period of time, $t_{1} = {{r_{1}^{2} } \mathord{\left/ {\vphantom {{r_{1}^{2} } {\left( {4a_{1} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {4a_{1} } \right)}}$, it takes a heat pulse to travel through a layer of (linear) thickness, $r_{1}$. Solving for diffusivity furnishes $a_{1} = {{r_{1}^{2} } \mathord{\left/ {\vphantom {{r_{1}^{2} } {\left( {4t_{1} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {4t_{1} } \right)}}$. For a curved heat-path, the actual length, R, is greater than $r_{1}$. By comparing both situations, the latter relation directly yields:

$$\frac{{a_{0} }}{{a_{1} }} = \frac{{r_{1}^{2} }}{{R_{1}^{2} }} \equiv \frac{1}{{\tau_{\text{therm}}^{2} }}.$$

(31)

From this result, it becomes obvious that when $\tau_{\text{therm}}$ of an evacuated porous medium is to be determined, just the thermal diffusivity, $a_{1}$, of the matrix material has to be known further. The experimental values of thermal tortuosity of the evacuated frits are listed in Table 6. The actual heat path of, e.g., P5 stretches almost twice the length of the related linear path making it the longest one of all frits under test (Table 6).

Table 6 Thermal tortuosities of the matrices under test

Figure 11 presents the thermal tortuosity of the matrices vs. complementary porosity in a log–log-plot. This latter scaling was chosen because nearly all of the relevant $\tau \left( \phi \right)$- functions are empirical power laws. Disappointingly, in the relevant literature, there is no such relation for solid transport of heat by a porous system. For the tortuosity of liquid mass-transport pathways, there are various mathematical relations expressing tortuosity as a function of porosity. The best known and proven one is the Bruggeman equation, $\tau \left( \phi \right) = \phi^{ - 0.5}$[25,26,27]. The above log–log-plot with $m = - 0.57$ shows that, if at all valid here, Bruggeman’s law only ‘frit-wise’ applies for five of nine frits.

Fig. 11

Log–log-plot of thermal tortuosity vs. complementary thermal porosity. The slope m of the quasi-linear regression (dashed line) is shown in the legend. “Lin. best fit” means that the data of P0, P1, P2 and P23 were excluded from the regression

Reasonably, the thermal tortuosity of a matrix should depend on morphological aspects like, e.g., the shape of the glass fragments and their interconnectivity. Unfortunately, no such microscopic data about the frits under test are available. Therefore, further investigations on the morphology of the frits are necessary before further dealing with this problem. Even so, a closer look back to Fig. 8 reveals that if the frits are liquid saturated rather than evacuated the characteristic “bend” disappears.

As has already been outlined in Sect. 3, the thermal tortuosity of the matrices under test could not be detected in the framework of the thermal conductivity measurements on the evacuated frits. Furthermore, it is worth noting that any thermal tortuosity concerned with the void space cannot be detected here.

4.2 Thermal Diffusivity of Liquid Saturated Frits (LSFs)

4.2.1 Frit Thermal Diffusivity Vs. Porosity

The thermal diffusivities of the LSFs as functions of porosity are presented in Fig. 8. For comparison reason, Fig. 9 shows the related thermal conductivities measured simultaneously at each run. While the latter data are almost independent of porosity, the thermal diffusivity data imply a possibly linear behavior while decreasing with porosity. Both these scenarios make the respective data sets particularly attractive for PSC-/TPSC-extrapolations beyond their narrow limits at both ends of the interval. However, as has been demonstrated, the underlying relation, Eq. 10, cannot explicitly be solved for the variable $\phi$. This is due to the fact that the mixed-conduction coefficient $s_{12}$ is an extraordinarily complex function of porosity that, so far, cannot be represented in closed form. To get at least a rough idea of the curve shape of $a_{0} \left( \phi \right)$, mixed conduction is disregarded, i.e., Eq. 10 is replaced by Eq. 8. This approximation allows for the much simpler TPSC-model:

$$a_{0} \left( \phi \right) = a_{1}^{{\frac{{\left( {1 - \phi } \right)\lambda_{1} }}{{\left( {1 - \phi } \right)\lambda_{1} + \phi \lambda_{2} }}}} \cdot a_{2}^{{\frac{{\phi \lambda_{2} }}{{\left( {1 - \phi } \right)\lambda_{1} + \phi \lambda_{2} }}}} .$$

(32)

Figure 12 presents the porosity dependent thermal diffusivities calculated for five borosilicate frits that are considered to be saturated with the six liquids under test here. Evidently, at the lower physical limit of the family of curves at $\phi = 0$, the intercept is equal to the thermal diffusivity of borosilicate glass. At the upper physical limit, $\phi = 1$, each intercept of a curve indicates the thermal diffusivity of the relevant saturant. It can numerically be demonstrated that for the given material parameters of the matrix, the degree of linearity achieves its local maximum ($R^{2} \approx 1$) for $\lambda_{L} = 0.75{\text{ Wm}}^{ - 1} \cdot {\text{s}}^{ - 1}$ which here, is closest to the conductivity of water.

Fig. 12

Theoretical characteristics of the thermal diffusivity of fluid-saturated borosilicate frits vs. porosity as predicted by the TP(S)C-model. It is supposed that the frits only provide two parallel heat pathways. The highlighted intercepts on the right-hand y-axis indicate the individual thermal diffusivities of the saturants listed in the legend

Figure 13 again presents the data of toluene as saturant from Fig. 12, but now, in advance of the second part of this paper, together with those of the saturants nitrogen ($\lambda = 0.026{\text{ W}} \cdot {\text{m}}^{ - 1} \cdot {\text{K}}^{ - 1}$ and $a = 21.5{\text{ mm}}^{2} \cdot {\text{s}}^{ - 1}$). It becomes immediately clear that the material with the lower thermal diffusivity ‘slows down’ the rate at which the heat pulse travels whereas the material with the higher thermal diffusivity ‘accelerates’ the rate. Physically, this is a direct consequence of the time-dependent equilibration of local temperatures $\left( {\mathop {\lim }\limits_{\sigma \to 0} a_{0}^{*} \left( \sigma \right)} \right)$.

Fig. 13

Same scenario as of Fig. 12, but now for toluene and nitrogen saturated frits. The log-scale is only for reason of clarity

The experimental thermal diffusivities for the porosity interval covered are individually given by Figs. 14, 15 and 16. The actual numerical values are smaller than those calculated for Fig. 12. So far, it is an open question whether the difference in the calculated and the actual numerical values is due to the above two-parallel paths approximation and/or to potential thermal tortuosities of matrix and/or liquid filled void space.

Fig. 14

Thermal diffusivity of toluene and alcohol saturated frits vs. porosity. Two horizontal lines indicate the individual thermal diffusivities

Fig. 15

Thermal diffusivity of alcohol-water-mixtures saturated frits vs. porosity. The horizontal lines indicate the individual thermal diffusivities

Fig. 16

Thermal diffusivity of water saturated frits vs. porosity. Two horizontal lines indicate the individual thermal diffusivities

4.3 Frit Thermal Diffusivity Vs. Saturants Thermal Diffusivity

Figure 6 shows the overall thermal diffusivity of LSFs against the thermal diffusivity of saturants. For a single view on the fundamental curve shape, Fig. 17 separately exemplifies the actual data points of the frit P00. Figures 18 and 19 show the complete outcome of $a_{0} = a_{0} \left( {a_{L} } \right)$ in two groups of four frits. All above experimental data sets are plotted together with the related predictions of the TPSC-model, Eq. 30. The input data to the latter model are the thermal diffusivities of borosilicate glass, $a_{1} = a_{BG}$, and of the related liquid saturants, $a_{2} = a_{L}$, as well as the fitting parameters of the PSC-model, $s_{1} , \, s_{2} {\text{ and }}s_{12}$, $d_{1} = r_{1} {\text{ and }}d_{2} = r_{2}$ (Table 4). The deviations between the measured and the predicted values are well within the expanded ISO uncertainty of the THB-meter.

Fig. 17

Thermal diffusivity of liquid saturated frit P00 vs. thermal diffusivity of saturants (cf. Figure 5)

Fig. 18

Thermal diffusivity of liquid saturated frits P00 to P2 vs. thermal diffusivity of saturants

Fig. 19

Thermal diffusivity of liquid saturated frits P23 to P5 vs. thermal diffusivity of saturants

Figure 20 presents the numerical values of the eight frit-specific mixed thermal diffusivities, $a_{12} = a_{12} \left( {a_{L} } \right)$, as calculated from Eqs. 28, 29 (cf. Figures 3 and 4).

Fig. 20

Mixed thermal diffusivity, $a_{12}$, against thermal diffusivity of liquid saturated frits (cf. Figures 3 and 4). The fitted lines are the predictions of the TPSC-model

5 Conclusion

The experimental and theoretical findings presented here are twofold and mutually supportive in their effect: first, two novel equations were derived to calculate the overall thermal diffusivity of fluid saturated porous media (TPSC-model). Secondly, the thermal diffusivities of liquid saturated borosilicate glass frits were measured as functions of porosity $\left( {20\;\% \le \phi \le 48\;\% } \right)$ and of the thermal diffusivity of the liquid saturants, $0.091 \le {{a_{L} } \mathord{\left/ {\vphantom {{a_{L} } {\left( {{\text{mm}}^{2} \cdot {\text{s}}^{ - 1} } \right) \le 0.143}}} \right. \kern-\nulldelimiterspace} {\left( {{\text{mm}}^{2} \cdot {\text{s}}^{ - 1} } \right) \le 0.143}}$. The experimental results facilitated the careful testing and successful verification of the TPSC-model. The existing data gaps can be filled with the predictions of this model. ‘Playing’ with it effectively helped interpreting the experimental results obtained. The deviations between the model and the experimental data are well within the expanded ISO-uncertainty limits of the THB-measuring instrument.

The experimental and numerical findings can be widely interpreted based on the already published insights [1, 2] into the mechanisms, the glass frits apply to transfer heat by conduction.

However, so far, it is not clear why all frits share the same offset partial-volume. irrespective of their different porosities. All collected data on thermal conductivity and thermal diffusivity are mutually consistent. Beyond the results reported in the two previous papers, for the evacuated frits, thermal tortuosity could be detected from thermal diffusivity measurements. This phenomenon cannot be disclosed by thermal conductivity runs using transient hot-wire (THW) or THB techniques.

It seems that the thermal diffusivity of a porous medium and generally, the conduction transport properties of its matrix, nowadays, attract progressively more attention, especially in the related basic research. Therefore, it is hoped that our results on liquid saturated glass sieves, that turned out to be a well-suited model substance of porous media, can extend the knowledge about this interesting and challenging class of materials. Especially, for improvements of porous Li-Ion electrodes or of building envelopes, the thermal diffusivity of the matrix is of great interest.

For composite heat-transfer problems like, e.g., modeling of transport phenomena in porous media, it is good practice, to “transform” the current arrangement of thermal resistances into an electrical equivalent circuit of resistors, i.e., an R-network. In order to expand this steady-state scenario to transient processes, the TPSC-relations now allow to deal with networks being composed of RC-elements in parallel as well as in series.

The second part of this paper dealing with the thermal diffusivity of gas-saturated frits is under way.