1 Introduction

Fiber-reinforced polymers (FRP) are used in many industries like aerospace, automotive, energy, or sports equipment due to their excellent mechanical properties and low weight. Defects within FRP such as delaminations, impact damage or moisture can rapidly degrade those material properties. Especially for safety-relevant applications, the availability of suitable non-destructive testing techniques (NDT) is desirable. Pulsed thermography (PT) has proven to be a valuable tool to identify and quantify delaminations in opaque materials as discussed in literature [1,2,3,4,5,6]. Many FRPs like glass-FRP (GFRP) are semitransparent to optical excitation sources in PT experiments, such as lasers or flash lamps. They can also be semitransparent to the wavelength range of the infrared (IR) camera. For the PT experiment, usually the samples are coated to absorb the radiation of the excitation source at the surface of the material. In this case, the absorption within the material does not have to be taken into account. This leads to simpler boundary conditions for modeling the experiments [4, 5]. However, coatings are often undesired because they are very difficult to be removed completely afterwards.

To the authors knowledge, the quantification of delaminations in semitransparent materials without coating has not been performed yet. Common methods for data evaluation like pulsed phase thermography (PPT) and thermographic signal reconstruction (TSR) [7] are not suitable for semitransparent materials with delamination since both methods are based on opaque materials theory. A more suited method could be least square fitting (LSF) [8]. Using this method enables the reconstruction of the experimental data using a mathematical model which describes the heat diffusion within the material. Müller et al. [4] investigated a coated GFRP sample with a real delamination by data reconstruction to achieve a fast computation time. They used an analytical 1D-model to describe the temperature development for an opaque material with a delamination. The reconstruction enables the determination of the depth of the delamination.

In this paper, we extend the approach of Müller et al. to quantify delaminations within semitransparent materials without coating. The semitransparency to the excitation source as well as for the IR camera must therefore be taken into account for the description of the heat diffusion within the material. For homogeneous semitransparent materials without defects, this approach has been discussed in literature [9,10,11,12,13,14]. We investigated a semitransparent GFRP specimen with a real delamination using PT in reflection configuration and a mathematical 1D-model (1-layer and 2-layer models) to quantify the depth of the delamination.

Our mathematical 1D-models consider semitransparency of the specimen (related to the excitation source as well as to the IR camera), thermal losses to the environment at the front and rear side, multilayer systems with thermal contact resistance between the layers, and support the use of an arbitrary temporal shape of the heating pulse to properly describe the measurement conditions. The influence of the thermal contact resistance within a semitransparent material on the temperature development in PT experiments is discussed. We fitted our mathematical 1-layer model to the PT experimental data recorded in reflection configuration at various positions to determine the sample thickness. If the results of the 1-layer model differ strongly from the experimental data, it is assumed that a delamination is present at this position. In these cases, the numerical 2-layer model is used to determine the depth of delamination and the thermal contact resistance. In addition, to gain further insight into the radiation absorption and emission as well as heat diffusion processes and the experimental results, the PT experiment was modeled with a 2D numerical model, yielding synthetic PT data. These data are analyzed with the 1D models as well and are compared with the results from the experiment. This comparison shows that the depth of delamination can be determined quite accurately by the 2-layer model. Finally, we show how the heat loss parameters of the models and the thermal contact resistance value behave in the case of lateral heat flow in the material.

2 Materials and Methods

In this chapter, we describe the investigated specimen, the experimental setup, the mathematical models and the influence of different parameters on the temperature evolution for a semitransparent material with a thermal resistance between the layers. The last two sections focus on data pre-processing and the data evaluation procedure.

2.1 Specimen

The investigated specimen was fabricated and analyzed as part of a project of the European Association of National Metrology Institutes [15], called VITCEA. The sample has the dimensions 240 mm × 50 mm × (5 ± 0.1) mm and consists of 16 unidirectional layers of glass fibers, which were stacked in a quasi-isotropic layout (45°, 0°, − 45°, 90°) in a thermoplastic polyamide PA 12 CF 60 matrix. A notch with 50 mm width was milled centrally into the sample, having a remaining wall thickness of \(L1 = 3.3 {\text{ mm}}\). A conventional tensile load test of 100 kN [16] created a delamination in the depth of the notch.

Figure 1 shows a photograph of the rear side and of the edge of the specimen. The thickness \(L\) of the specimen was measured at many locations far away from the delamination, resulting in \(L = \left( {5 \pm 0.1} \right) {\text{mm}} .\)

Fig. 1
figure 1

Photograph of the specimen from the rear side (a) and from the edge (b). A sketch of the sample with more details is given in Fig. 2

Full size image

The sketch of the specimen (top view and front view) is shown in Fig. 2. The hatched areas describe the delamination area.

Fig. 2
figure 2

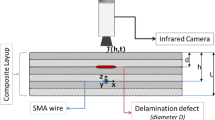
Sketch of the specimen. The dot-dashed line shows the illumination area of the laser and the dashed line the area of data evaluation. The temperature evaluations for position A (x = 68 mm | y = 26 mm) and position B (x = 90 mm | y = 26 mm) are shown in Fig. 10. A photograph of the specimen is shown in Fig. 1

Full size image

The thermal and optical material parameters are shown in Table 1. The optical properties are measured and discussed in Ref. [17] for a \(L = 5\,{\text{mm}}\) thick sample which was produced in the same way. The effective absorption coefficient \(\alpha\) for the wavelength of \(\lambda = 1000\,{\text{nm}}\) (close to the wavelength of our laser of 935 nm) was calculated with a transmission coefficient of \(\tau = 0.034\) and a reflection coefficient \(r = 0.31\) using the approximation formula \(\tau \left( \lambda \right) \approx \left( {1 - r\left( \lambda \right)} \right)e^{ - \alpha L}\) neglecting multiple reflections within the sample. The calculation of the effective absorption coefficient \(\beta\) within the wavelength spectrum of our IR camera was not possible as the transmission coefficient in this wavelength range was zero (investigated specimen thickness \(L = 5\,{\text{mm}}\)) [17]. For a proper determination of the transmission coefficient thinner samples would have been needed. Instead, the effective absorption coefficient \(\alpha\) and \(\beta\) were determined by fitting an analytical model to PT data as described in Ref. [14, 18]. In this study, we also determined the thermal diffusivity perpendicular of the surface of \(D = \left( {2.25 \pm 0.1} \right) \cdot 10^{ - 7} {\text{m}}^{2} \cdot {\text{s}}^{ - 1}\) which is almost equal to the value determined in the VITCEA-project (\(D_{VITCEA} = \left( {2.17 \pm 0.15} \right) \cdot 10^{ - 7} {\text{m}}^{2} \cdot {\text{s}}^{ - 1}\)). We define all optical parameters as effective parameters because the scattering effects within the material are neglected.

Table 1 Thermal and optical material properties for the specimen, determined within the VITCEA-project
Full size table

2.2 Experimental Setup

Pulsed thermography was performed in reflection configuration. An illustration of the experimental setup is shown in Fig. 3. A 300 W laser (diode laser system LDM 500-20 by Laserline GmbH) emitting at 935 nm, widened to a top hat spatial profile of \(68 {\text { mm}} \times 68 {\text{ mm}}\) at a focal distance of 300 mm, was used to heat the sample. We used a laser instead of, e.g., a flash lamp to achieve simple boundary conditions for the mathematical models (spatial homogeneity, monochromaticity, rectangular temporal shape) [19]. The power density at the surface of the test specimen was \(79.8\;{\text{kW}} \cdot {\text{m}}^{ - 2}\). The temporal shape of the laser pulse can be considered as rectangular with a pulse duration \(\tau\), which was set to \(\tau = 375\;{\text{ms}}\). The laser was orientated in such a way that the end of the delamination was in the middle of the illuminated area; see also Fig. 3. The IR camera used is sensitive in the mid-wavelength infrared range (3 µm to 5 µm, InfraTec ImageIR 9300, NETD: \(30\;{\text{mK}}\)). The IR camera was operated at a frame rate of 20 Hz in windowing mode (resolution decreased from \(1280\,{\text{px}} \times 1024\,{\text{px}}\) to \(640\,{\text{px}} \times 512\,{\text{px}}\)) using an integration time of 640 µs (temperature calibration range of \(0\,^\circ {\text{C}}\) to \(60\,^\circ {\text{C}}\)) recording for a duration of 182 s during and after laser heating. The archieved geometrical resolution was \(7.5\;{\text{px mm}}^{ - 1}\).

Fig. 3
figure 3

Illustration of the experimental setup in reflection configuration

Full size image

2.3 Mathematical Models

This chapter briefly describes the 1-layer and 2-layer 1D-models which are fitted to the PT data, as well as the numerical 2D model for generating synthetic PT data. Furthermore, the influence of delaminations in semitransparent materials on the temperature development by PT is discussed.

2.3.1 1D-Models

In this paper, for data analysis, we concentrate on 1D-models to achieve the short computing time needed for the fitting routine for geometry reconstruction. We used a 1-layer model for the sound area and a 2-layer model to describe the delamination in the defect area. Figure 4a shows a sketch of the 1-layer and 2-layer models. We treat the delamination within a semitransparent material mathematically as a thermal contact resistance \(R\), similar as in the opaque case [9]. The thermal contact resistance is defined as

$$R = w/K_{air} ,$$
(1)

where \(K_{air}\) is the thermal conductivity of air and \(w\) is the thickness of the delamination. However, additional influences in a natural delamination such as surface roughness, lateral inhomogeneity of the gap width and heat transfer by air convection influence the value of R. Thus, we do not analyze the value of R in terms of gap width within this publication.

Fig. 4
figure 4

(a) The 1-layer and 2-layer models with thermal losses h at the surfaces. (b) Semitransparency to the incident light beam (dashed line): the light beam is absorbed within the material. Semitransparency to IR radiation: the IR radiation originates not only from the sample surface, but also from inside the sample. Semitransparency is considered for the 1-layer and 2-layer models. The thickness of the arrows depicts the radiation intensity

Full size image

Semitransparency is taken into account using the Beer–Lambert law. Note that the following mathematical models do not consider scattering effects or internal reflections. Thus, the optical parameters are considered as effective parameters only.

The 1D heat diffusion equation for semitransparent materials can be solved using the Laplace transformation as described in the literature [9, 14, 18]. Our 1D-models describe a material that is semitransparent to the wavelength of the excitation source and within the wavelength range of our IR camera as shown in Fig. 4b. In addition, we take into account thermal losses on the surfaces in linear approximation (Fig. 4a) and support the use of any temporal form of the heating pulse to correctly describe the measurement conditions. The model is only exact in the Laplace domain. We performed a numerical inverse Laplace transformation to calculate the temperature in the time domain. For this task, we used the Euler method; see Abate et al. [20].

We extended the analytical 1-layer model to a numerical 2-layer model with a thermal resistance between the layers, using a numerical FEM 1D-model with the commercial software COMSOL Multiphysics 5.3. The change from numerical transformation of an analytical solution in the Laplace domain to a numerical calculation in the time domain was necessary due to instabilities in the numerical transformation in case of the 2-layer system. This model has exactly the same boundary conditions as our analytical model. We used the heat transfer toolbox and coupled it with a partial differential equation (PDE) interface to describe the decrease of the laser intensity within the material (internal heat source due to the semitransparency of the material within the spectral bandwidth of the excitation source according to the Beer–Lambert law). The influence of the semitransparency of the sample in the spectral range of the IR camera is considered by using the measured temperature \(T_{IR}\), given by [21]

$$T_{IR} \left( t \right) = \mathop \smallint \limits_{0}^{L} \beta T_{sim} \left( {z,t} \right)e^{ - \beta z} dz,$$
(2)

where \(L\) is the sample thickness, \(\beta\) is the effective IR absorption coefficient in the spectral range of the IR camera, \(t\) the time and \(T_{sim} \left( {z,t} \right)\) the simulated temperature of the material.

The model was discretized with 51 elements. We used the time-dependent solver with the implicit Backward Differentiation Formula (BDF) method, due to its good stability. The computing time was approx. 3 s (128 GB RAM, 2 × (2.67 GHz, 6-core X5650 CPU)) for a single simulation of the 1D-model. The toolbox LiveLink to MATLAB was used to analyze the simulation data in MATLAB.

In this work, we use the analytical Laplace solution + numerical inverse Laplace transformation for the 1-layer model instead of a 1D 1-layer FEM model, since the computing time is much shorter.

2.3.2 Synthetic PT Data

In addition, we performed two numerical 2D-simulations of our PT experiment, see chapter 3.2.

The advantage of synthetic data is that we know all parameters exactly, especially R and h which are unknown in the experiment. Furthermore, the boundary conditions can be changed very easily, e.g., to investigate the influence of different illumination areas, since the size of the illumination area can change the lateral heat flow within the material.

The specimen geometry is simplified by neglecting the notch and is modeled by a 2D-model (x–z direction) as illustrated in Fig. 2. With one exception, we considered the same boundary conditions as described for the numerical 1D-model. The two 2D-simulations differed only in the boundary condition concerning the size of the illuminated area. In the first 2D-simulation, only a part of the sample is illuminated (from \(x = 68 {\text{ mm}}\) to \(x = 116 {\text{ mm}}\)), similar as in the experiment. In the second 2D-simulation, the whole sample was illuminated for decreasing effects of lateral heat flow. This allows us to compare the influence of the lateral heat diffusion due to the smaller illumination area. The used parameters for the 2D-simulations are shown in Table 2. We define the results of the synthetic PT data with small illumination area as synthPTs (s for small) and with big illumination area as synthPTb (b for big).

Table 2 Parameters of the numerical 2D-model used to obtain the synthetic data
Full size table

2.3.3 Influence of Different Parameters on the Temperature Evolution for a Semitransparent Material with and Without a Thermal Resistance

In order to get a better understanding of the influence of the different parameters on the temperature evolution for a semitransparent material with and without a thermal contact resistance \(R\) within the material, in the following we discuss the temperature development during PT experiment. The influences of the parameters, \(L, D, \alpha , \beta , k,\) and the temporal shape of heating pulse on the temperature development in time domain due to pulsed thermography are discussed in Refs. [13, 14, 22].

Temperature developments were calculated using the 1D-models described above (Sect. 2.3.1). The depth of the delamination \(L1\) as well as the thermal contact resistance \(R\) is varied. The optical and thermal properties are shown in Table 2.

Figure 5a shows a comparison between an opaque and a semitransparent material (1-layer model) with and without thermal losses in a double logarithm scale. The semitransparency within the wavelength range of the excitation source leads to a decrease of the temperature rise at early times, while the effect of finite heat loss is observable at late times. It can be clearly seen that both the heat losses and the semitransparency have a very large influence on the temperature curves and therefore must be considered for a quantitative evaluation of material defects, if material parameters similar to those used in this study are present. The chosen thermal losses of \(12\;{\text{m}}^{2} \cdot {\text{W}}^{ - 1}\) are reasonable, for laboratory conditions see [18, 23].

Fig. 5
figure 5

(a) Temperature development as a function of time at the surface of the sample of pulsed thermography for an opaque (grey lines) and semitransparent (black lines) material with and without thermal losses (1-layer model). (b) Temperature development as a function of time at the surface of a \(5\;{\text{mm}}\) sample for a 2-layer semitransparent material with thermal resistance between the layers in different depths \(L1\). Thermal losses \(h\) in \(\left[ {{\text{W}} \cdot {\text{m}}^{ - 2} \cdot {\text{K}}^{ - 1} } \right]\), \(L\) and \(L1\) in \(\left[ {\text{mm}} \right]\)

Full size image

Figure 5b shows the temperature developments for a 5 mm thick semitransparent material without a delamination (black line) and with a thermal resistance of \(R = 0.01\;{\text{K}} \cdot {\text{m}}^{2} \cdot {\text{W}}^{ - 1}\) in different depths of 1 mm to 4 mm. The thermal contact resistance within the material slows down the heat flow within the material, which leads to heat accumulation and a slower drop in temperature. Thus, the temperature curve is pushed upwards by the thermal contact resistance. The amount of the upwards bend is a function of the thermal contact resistance, as illustrated in Fig. 6a. Here the black lines describe the temperature evolution for a 5 mm thick semitransparent material with different \(R\) values at the depth of 3 mm. The upwards bending is larger for lager R values. In addition, the temperature development for a 3 mm thick sample without \(R\) (grey line) is shown.

Fig. 6
figure 6

(a) Temperature increase for a 2-layer semitransparent material for different thermal resistances R between the 2 layers. (b) Same as Fig. 5b but with thermal losses. Thermal losses \(h\) in \(\left[ {{\text{W}} \cdot {\text{m}}^{ - 2} \cdot {\text{K}}^{ - 1} } \right]\), thermal resistance \(R\) in \(\left[ {{\text{K}} \cdot {\text{m}}^{2} \cdot {\text{W}}^{ - 1} } \right]\), and L and L1 in \(\left[ {\text{mm}} \right]\)

Full size image

Figure 6b shows the results of the temperature development for the 2-layer model with different depths of the delamination like in Fig. 5b, but now with thermal losses. It becomes obvious that the combination of thermal contact resistance, thermal losses and finite component thickness leads to a complex temperature distribution, which is not easily interpretable.

In order to investigate the ability of the PT method to retrieve L1 and R, we analyzed the sensitivity of the normalized temperature \(T_{IR,n} = T_{IR} /{ \hbox{max} }\left( {T_{IR} } \right)\) to these two parameters. According to [11, 14], the sensitivity of normalized \(T_{IR}\) to a given quantity x is defined as

$$S_{x} = \frac{x}{{T_{IR,n} }}\frac{{\partial T_{IR,n} }}{\partial x}, {\text{with }}x = L1\;{\text{or}}\;R.$$
(3)

Figure 7a shows the sensitivity of \(S_{L1}\) and \(S_{R}\) over time for an opaque material (\(\alpha = \infty ,\beta = \infty\)) and Fig. 7b for a semitransparent material with the boundary condition described in Table 2 (\(L1 = 3.3\) mm and \({\text{R}} = 0.01\;{\text{K}} \cdot {\text{m}}^{2} \cdot {\text{W}}^{ - 1}\) for a 1D-2-layer model).

Fig. 7
figure 7

(a) Sensitivity and normalized temperature evolution over time for an opaque material. (b) Sensitivity and normalized temperature evolution over time for a semitransparent material. Used parameters are shown in Table 2 (1D-2-layer model)

Full size image

Additionally, the normalized \(T_{IR}\) are shown in both figures. The extremum of \(S_{L1}\) appears earlier than the extremum of \(S_{R}\). Therefore, \(R\) and \(L1\) are not strongly correlated for the used parameter set. The thermal losses affect the temperature signal especially at late times (see Fig. 7). It is worth mentioning that the absolute sensitivity to \(R\) increases when \(R\) increases.

The extrema of \(S_{x}\) shift with changing \(L1.\) Figure 8 shows the time when the extrema of \(S_{x}\) occurs (\(t\left( {max\left( {S_{x} } \right)} \right).\) The curves do not cross, which means there is no parameter set where \(R\) and \(L1\) are strongly correlated. If the delamination is very deep, the sensitivities to \(R\) and \(L1\) decrease due to the thermal losses (not shown here).

Fig. 8
figure 8

Time when the extrema of \(S_{x}\) occurres as a function of L1. (a) Opaque and (b) semitransparent material. Used parameters are shown in Table 2 (1D-2-layer model)

Full size image

The sensitivity study indicates that \(L1\) and \(R\) can be retrieved from PT data with the same data set. However, due to the existing but limited temporal overlap of the sensitivities to these two parameters, the model has to describe the experimental situation quite well.

2.4 Data Preprocessing

To reduce the complexity and the calculation time, instead of a 2D-reconstruction of the delamination geometry, a pointwise 1D-evaluation approach was chosen. The effect of lateral heat flow could partially be compensated (phenomenologically) by using the linear heat loss parameter \(h\) as free fit parameter. Considerable derivations of the parameter due to lateral heat flow from realistic values between \(8\;{\text{W}} \cdot {\text{m}}^{ - 2} \cdot {\text{K}}^{ - 1}\) and \(14\;{\text{W}} \cdot {\text{m}}^{ - 2} \cdot {\text{K}}^{ - 1}\) can therefore be observed (see below). Altenburg et al. [24] showed that the use of \(h\) to describe lateral heat losses as a free fit parameter leads to improved results in thickness determination of concrete coatings, since lateral heat flows due to inhomogeneous excitation can be better compensated.

The area of data evaluation is shown in Fig. 2 (dashed square). To further speed up the evaluation of the experimental data, we reduced the recorded film from 3640 to 233 thermograms, resulting in 100 thermograms per time decade and an equidistant time step on the logarithmic time scale. The noise of the thermographic signal was further reduced by spatial averaging: The area of data evaluation was divided in to 27 × 24 regions of interest (ROIs), where one ROI contains the mean temperature of \(15 {\text{ px }} \times 15 {\text{ px}}\) (\(2 {\text{ mm }} \times 2 {\text{ mm}}\)).

2.5 Data Evaluation Procedure

The algorithm for fitting the mathematical models to the experimental data is based on Lagarias et al. [25] and is minimizing the mean of the squared differences between the logarithms of the temperature values \(T_{exp} \left( {t_{i} } \right)\) and \(T_{sim} \left( {t_{i} } \right)\), using a linear time-dependent weight (equidistant time step in logarithmic scale) of the data points resulting in a double logarithmic fit.

To evaluate if the experimental data can by described sufficiently well by the fitted model, we quantify the goodness of fit using

$$\begin{array}{*{20}c} {\upzeta^{2} = \left( {\mathop \sum \limits_{i = 1}^{N} \left( {T_{exp} \left( {t_{i} } \right) - T_{sim} \left( {t_{i} } \right)} \right)^{2} /\sigma_{i}^{2} } \right)\frac{1}{N},} \\ \end{array}$$
(4)

where \(\sigma_{i}\) denotes the standard deviation of the experimental temperature in the ROI, calculated for each frame separately. \(N\) is the number of frames in the evaluated part of the sequence and depends on the start time of fitting. Lower values of \(\upzeta^{2}\) correspond to a closer approximation of the experimental data by the model.

The following diagram (Fig. 9) illustrates the data evaluation procedure for each ROI of the experimental data. First, the 1-layer model is fitted to the experimental data and \(\upzeta^{2}\) is calculated to determine whether there is delamination at the position of the ROI or not. If the 1-layer model results differ too strongly from the experimental data, e.g., \(\upzeta^{2} > 0.3\) (see also Sect. 3.1), a delamination within the material is very likely. In this case, the data will be analyzed with the 2-layer model to determine the depth of the delamination.

Fig. 9
figure 9

Diagram of the data evaluation procedure

Full size image

The synthetic data are analyzed with the 2-layer model. On the one hand, the result of the fit parameter can be verified. On the other hand, it could be evaluated how strong the lateral heat flow within the material influences the determination of the depth of delamination, due to the limited illumination area.

3 Experimental Results and Discussion

3.1 Results of the Experimental Data

First, the experimental data (27 × 24 ROIs) were analyzed with the 1-layer model. The fixed and varied parameters are summarized in Table 3. Optical and thermal parameters are fixed, the thickness \(L\), the energy density \(Q\) and the heat loss parameter \(h\) are fit parameters. As mentioned in Sect. 2.4, the parameter \(h\) is considered as a combination of thermal losses to the surroundings and lateral heat losses, although this description is strictly phenomenological.

Table 3 Parameters for the 1D-models
Full size table

In the fit routine only data points with \(t > 5 {\text{ s}}\) were considered, as the temperature development depends only on the material parameters and not on the thickness of the sample for shorter times, see chapter 2.3.

Figure 10 shows the experimental data (grey dots) for the sound area ROI position A (a), and for the delamination area ROI position B (b), respectively (see Fig. 2). The dashed line shows the best fit with the 1-layer model. It can be seen that the model fits the experimental data very well for position A (\(\upzeta^{2} = 0.08\)) and does not fit well for the area B with delamination (\(\upzeta^{2} = 2.71\)).

Fig. 10
figure 10

Experimental data and results of the fitted 1-layer model for sound area ROI position A (a) and defect area ROI position B (b). Only data points for \(t > 5 \;{\text{s}}\) were considered in the fit routine

Full size image

Figure 11a shows the results of the goodness of fit \(\upzeta^{2}\). The 1-layer model describes the experimental data up to \(x = 82\;{\text{mm}}\) very well. This area has no delamination within the material. The boundary between the regions of low and high value of \(\upzeta^{2}\) is between 0.24 and 0.33, thus we chose \(0.3\) as threshold value. The absolute deviation \(\Delta_{L} = |L_{fit} - L_{exact} |\) of the determined thickness \(L_{fit}\) and from the reference thickness \(L_{exact}\) measured with 5 mm (see chapter 2) are shown for all ROIs with \(\upzeta^{2} < 0.3\) in Fig. 11b. The deviations are below \(0.5 {\text{ mm}}\).

Fig. 11
figure 11

(a) Fit results using the 1-layer model of the goodness of fit \(\upzeta^{2}\), (b) the absolute difference of the determined thickness \(L_{fit}\) and of the reference thickness \(L_{exact}\) measured with 5 mm (see chapter 2) for all ROIs with \(\upzeta^{2} < 0.3\) and (c) the thermal loss parameter \(h\) for all ROIs with \(\upzeta^{2} < 0.3\)

Full size image

Figure 11c displays the fit results for \(h\) for all RIOs with \(\upzeta^{2} < 0.3\). The value of \(h\) increases significantly to the edges of the illuminated area, which is consistent with an increased influence of lateral heat flow in the area.

According to the data evaluation procedure, the area for \(x > 82\;{\text{mm}}\) has to be investigated with the 2-layer model.

The experimental data for position B and the results of the 2-layer model are shown in Fig. 12. Compared to the 1-layer model (see Fig. 10b), the 2-layer model describes the experimental data much better with \(\upzeta^{2} = 0.07\). The depth of the delamination \(L1\) is fitted to 3.3 mm.

Fig. 12
figure 12

Analysis of experimental data with the 2-layer model. Experimental data and the result of the fitted 2-layer model for ROI B

Full size image

In the 2-layer model, the total thickness of the specimen (\(L = 5\;{\text{mm}}\)) is defined as fixed parameter. Fit parameters are the depth of delamination \(L1\), the thermal contact resistance \(R\), the absorbed energy density \(Q\), and the thermal loss parameter \(h\) (see Table 3). All data points for \(t > 5 {\text{s}}\) are considered for the fit routine.

Figure 13 shows the results for the depth of the delamination \(L1\), the thermal contact resistance \(R\), thermal losses \(h\) and goodness of fit for the ROIs line for \(x > 82\,{\text{ mm}}\) along section C–C of Fig. 2. The thermal contact resistance (grey line) in Fig. 13a rises from \(x = 82\,{\text{ mm}}\) to \(x = 102 {\text{ mm }}\) from zero to approx. \(0.01 {\text{ K}} \cdot {\text{m}}^{2} \cdot {\text{W}}^{ - 1}\). The yielded depth of the delamination is close to the reference depth of \(3.3\;{\text{mm}}\) in this range (dashed-dot line). From \(x = 102\;{\text{mm}}\) the R value and \(L1\) decreases continuously, whereas \(h\) increases rapidly (see Fig. 13b).

Fig. 13
figure 13

(a) Results of the depth of the delamination L1 and the thermal contact resistance R, (b) the thermal losses \(h\), and (c) goodness of fit values for the 1-layer and 2-layer models

Full size image

Figure 13c shows the goodness of fit for the 2-layer model and as a comparison for the 1-layer model. The 2-layer model can be fitted to the whole ROI line \((\upzeta^{2}\) < 0.3). The 1-layer model is only suitable where no delamination exists.

3.2 Results of the Synthetic Data

The synthetic data synthPTs and synthPTb (see Sect. 2.3.2) were analyzed with the 2-layer model. We used the same fit and fixed parameter as in the previous section. The results of the fitted depth of delamination \(L1\), thermal contact resistance \(R\) and the thermal losses \(h\) are shown in Fig. 14.

Fig. 14
figure 14

Analysis of synthetic data. (a) Results of the depth of delamination L1, the thermal resistance \(R\) and (b) the thermal losses \(h\)

Full size image

If the whole front surface is illuminated (synthPTb, dashed lines), the depth \(L1\) (for \(x > 85\;{\text{mm}}\)), \(R\) (for \(x > 95\;{\text{mm}})\), and \(h\) are close to the modeled values. The parameters deviate only in the transition zone at the end of the delamination area. The results for \(L1\) and \(R\) of the evaluation of the synthPTs data (partial illumination, bold lines) show very similar values up to \(x = 106\;{\text{mm}}\). Especially the results for \(L1\) are close to the modeled values. The thermal loss parameter increases continuously for \(x > 90\;{\text{mm}}\), showing the heat losses due to lateral heat flow.

The comparison of synthPTs and synthPTb show that for \(x > 106\;{\text{mm}}\) the lateral heat flows within the material is the reason for the deviations of \(L1\) and \(R\), caused by the smaller illumination area.

3.3 Comparison of the Synthetic and Real PT Experimental Data

The comparison between the analysis of the experimental data (Fig. 13) and the synthetic data synthPTs (Fig. 14) with small illumination area shows that the curves of \(R\), \(L1\) and \(h\) are very similar. The depth of the delamination shows a plateau up to \(x = 104\;{\text{mm}}\) in both cases. The difference to the exact depth of the delamination is less than 5 %. The synthetic data showed clearly that the lateral heat flow influences the results for the thermal contact resistance, the depth of delamination and the thermal losses. Especially the results for \(R\) and \(h\) are strongly influenced by lateral heat flow. These two parameters can be used in the 1D-model to compensate weak lateral heat flow within the material. However, the values are not realistic in a real 1D case, but the depth of the delamination can be determined very well. Consequently, although good fits can be produced, strong lateral heat flows can cause false values of the fit parameter. However, a large illumination area can reduce the lateral heat flow.

4 Conclusion

In conclusion, we present a method to quantify real delaminations within a semitransparent material (GRFP) using one-dimensional 1-layer and 2-layer models to analyze PT experimental and synthetic thermographic data. The 1D-models are fitted to the PT data to quantify the delamination within the material. The material was not coated, therefore the 1D models consider the semitransparency to the excitation source and to the IR camera.

We determine the thickness of the sample and the area of delamination using the 1-layer model. The area where a delamination exists was identified by a bad agreement of experimental data and the best fit of the model data (goodness of fit). Data from the delamination region was then further investigated with a 2-layer model to quantify the delamination. The results for the depth of the delamination are very close to the real values (difference < 5 %). If a strong lateral heat flow is present within the material, especially at the edges of the illuminated area, the delamination depth deviates from the real value since the 1D-models cannot take the lateral heat flow into account. However, weak lateral heat flow can be very well compensated in the 1D model by the thermal loss and the thermal contact resistance parameters. This was shown by the analysis of synthetic PT data.