1 Introduction

Thermoelectric inhomogeneity is the spatial variation of the Seebeck coefficient δS along a thermoelement. It is an inherent material property, which directly affects the measured Seebeck voltage (emf). Therefore, changes of the measured emfs by moving a thermocouple in a temperature gradient, while the measuring and reference temperatures remain constant, are an indication of variations of the Seebeck coefficient. Furthermore, measured variations of the emf during homogeneity testing are not only a function of the spatial variation of the Seebeck coefficient but also a function of the particular temperature profile.

Thermoelectric inhomogeneity is usually the dominant uncertainty component of the calibration uncertainty of thermocouples and therefore the subject of extensive investigations for its reliable quantitative determination. An overview of the methods and of the design and performance assessment of thermocouple inhomogeneity scanners for the determination of thermoelectric inhomogeneities was published by Webster and White [1]. Further detailed investigations using a linear gradient furnace and a high-resolution homogeneity scanner applied on different thermocouple types can be found in [2, 3]. According to [2], the average Seebeck coefficient \(\bar{S}\left( {x_{0} } \right)\) in the middle of the temperature step ΔT = T2 − T1 between the measuring temperature T2 and the ambient temperature T1 is:

$$\bar{S}\left( {x_{0} } \right) = \frac{{E\left( {x_{0} } \right)}}{{\left( {T_{2} - T_{1} } \right)}}$$
(1)

with E(x0) as the measured emf. If we consider an inhomogeneous thermoelement, the real Seebeck coefficient is the sum of the undisturbed Seebeck coefficient (reference function) and of the spatial variation ΔS(x0), and the measured emf is the sum of the undisturbed emf E(x0) and a part ΔE(x0), caused by the spatial variation of the Seebeck coefficient, respectively.

$$\bar{S}\left( {x_{0} } \right) + \Delta S\left( {x_{0} } \right) = \frac{{E\left( {x_{0} } \right)}}{{\left( {T_{2} - T_{1} } \right)}} + \frac{{\Delta E\left( {x_{0} } \right)}}{{\left( {T_{2} - T_{1} } \right)}}$$
(2)

A transformation of (2) leads to the relationship between the measured emf and the Seebeck coefficient in inhomogeneous thermocouples (6).

$$\left[ {\bar{S}\left( {x_{0} } \right) + \Delta S\left( {x_{0} } \right)} \right] \cdot \left( {T_{2} - T_{1} } \right) = E\left( {x_{0} } \right) + \Delta E\left( {x_{0} } \right)$$
(3)
$$\left[ {\bar{S}\left( {x_{0} } \right) + \Delta S\left( {x_{0} } \right)} \right] \cdot \frac{{\left( {T_{2} - T_{1} } \right)}}{{\Delta E\left( {x_{0} } \right)}} = \frac{{E\left( {x_{0} } \right)}}{{\Delta E\left( {x_{0} } \right)}} + 1$$
(4)
$$\left[ {\bar{S}\left( {x_{0} } \right) + \Delta S\left( {x_{0} } \right)} \right] \cdot \frac{1}{{\Delta S\left( {x_{0} } \right)}} = \frac{{E\left( {x_{0} } \right)}}{{\Delta E\left( {x_{0} } \right)}} + 1$$
(5)
$$\frac{{\bar{S}\left( {x_{0} } \right)}}{{\Delta S\left( {x_{0} } \right)}} = \frac{{E\left( {x_{0} } \right)}}{{\Delta E\left( {x_{0} } \right)}}$$
(6)

The problem in practice is the scaling of inhomogeneities measured at one temperature by using a defined temperature gradient to other temperatures. Jahan and Ballico [4] were the first to show that, under certain conditions, a linear relationship of the thermoelectric inhomogeneity of type S and R thermocouples to the measured emf exists and the inhomogeneity ΔE may be expressed as a percentage of the total thermo-voltage E measured.

Recent investigations of inhomogeneities of both type B thermocouples and Land–Jewell noble metal thermocouples in the temperature range between 600 °C and 900 °C [5] revealed a linear relation of emf changes with temperature caused only by irreversible inhomogeneities. Further investigation showed that this conclusion was also true of other Pt/Rh-alloyed thermocouples [6, 7]. Problems arise when reversible, temperature-dependent inhomogeneities have to be considered. For instance, reversible changes of the thermoelectric homogeneity occur in thermocouples containing Pt/Rh alloys due to the selective oxidation of alloy components especially in the temperature range of approximately 550 °C to 900 °C [8]. Linear extrapolations of homogeneity scanning results of or into temperature ranges where reversible inhomogeneities occur are inevitably erroneous.

This paper describes the results of low-temperature investigations of the thermoelectric inhomogeneity of conventional standardized noble metal thermocouples (types S and R, Au/Pt and Pt/Pd thermocouples) and of non-standardized Pt/Rh-alloyed thermocouples to provide practical evidence of the linear relationship between inhomogeneity and the measured emf also at low temperatures. Immersion profile measurements were carried out in a salt bath at temperatures of 200 °C, 300 °C, 400 °C, and 500 °C. These temperatures are below the critical temperature range of the selective Rh oxidation of Pt/Rh-alloyed thermocouples. The additional investigation of a multi-wire thermocouple consisting of non-standardized Pt/Rh alloys (Pt5%Rh, Pt17%Rh, and Pt20%Rh) and of a pure platinum thermoelement allowed redundant measurements and therefore conclusions about the reasons of changed inhomogeneity signatures of PtRh-alloyed thermocouples at temperatures above 400 °C.

2 Experimental Procedure

One type S, one type R, one Au/Pt, and one Pt/Pd thermocouple were used for the homogeneity tests. In addition, a multi-wire thermocouple with Pt, Pt5%Rh, Pt17%Rh, and Pt20%Rh thermoelements was included in the investigations. All thermocouples were previously in use at different temperatures, i.e., have different homogeneity signatures. Before starting the investigations, all thermocouples were annealed for 24 h at 400 °C in order to have the point defect concentration at a uniform level and to minimize structural changes caused by the scanning temperature, at least below 400 °C.

The immersion profiles of the thermocouples were measured in a salt bath by manually withdrawing them stepwise from a metal protection tube immersed in the liquid salt solution. The emfs were measured by using a Keithley 2182 nanovoltmeter. The temperature of the reference junctions at all measurements was 0 °C, realized by an ice water mixture. The temporal temperature stability of the salt bath during the measurements at 200 °C and 300 °C was ± 2 mK. It increased to ± 10 mK at 400 °C and 500 °C. The spatial temperature homogeneity between maximum immersion (40 cm) and about 15 cm was within ± 5 mK. At immersion depths less than about 15 cm, environmental effects (parasitic heat flux along the thermocouples) resulted in decreasing temperatures. Therefore, only measurement values obtained from the range between 18 cm and 40 cm ensuring a constant measuring junction temperature were considered for the measurement evaluation. Figure 1 shows the temperature profiles of the salt bath at different temperatures, which were determined by using a standard platinum resistance thermometer (SPRT). The associated differentiated least-square fitted temperature gradients are shown in Fig. 2 to identify the kernels [2].

Fig. 1
figure 1

Temperature profiles of the salt bath

Full size image
Fig. 2
figure 2

Differentiated temperature profiles

Full size image

3 Results and Discussion

The scanning data of the investigated thermocouples are presented in the following figures either as emf differences, i.e., as ΔE, between the emf measured during the removal of the thermocouple from the bath and the emf at maximum immersion (40 cm) and/or as relative inhomogeneities, i.e., as ΔE/E, versus the immersion depth. Figures 3 and 4 show the scanning data of the Pt/Pd thermocouple No.06/00. This thermocouple exhibits large inhomogeneities, which increase absolutely with temperature. However, the relative inhomogeneities ΔE/E are almost temperature independent (Fig. 4).

Fig. 3
figure 3

Absolute inhomogeneity of Pt/Pd 06/00 at different temperatures

Full size image
Fig. 4
figure 4

Relative inhomogeneity of Pt/Pd 06/00 at different temperatures

Full size image

The homogeneity scans of the Au/Pt thermocouple 13-03 at 200 °C, 300 °C, 400 °C, and 500 °C in Fig. 5 show only slight absolute inhomogeneities within about ± 0.15 µV when changing the immersion depth. This value corresponds to the uncertainty of the temperature stability of the salt bath of a few mK. Therefore, no reliable statement can be made about the temperature dependence of the inhomogeneities of the Au/Pt 13-03 thermocouple, which are in the order of 5 × 10−5.

Fig. 5
figure 5

Absolute inhomogeneities of Au/Pt 13-03

Full size image

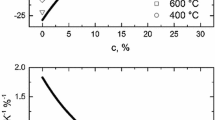
The relative inhomogeneities ΔE/E of the type S and R thermocouples in Figs. 6 and 7 at 200 °C, 300 °C, and 400 °C were also independent of temperature as found for the Pt/Pd and Au/Pt thermocouples in the whole temperature range. At 500 °C, however, the relative inhomogeneities have clearly decreased by about − 4 × 10−4. It appears that structural changes occurred at 500 °C. These changes have an influence on the Seebeck coefficient and therefore on the inhomogeneity. Similar inhomogeneity signatures were found for the non-standardized combinations of Pt5%Rh, Pt17%Rh, and Pt20%Rh against a pure platinum thermoelement, as presented in Fig. 8. A summary of the relative inhomogeneity values ΔE/E of the various Pt/Rh thermocouple combinations at immersion depths between 20 cm and 30 cm can be found in Table 1. Column 5 contains the mean values of ΔE/E calculated from the measurements at 200 °C, 300 °C, and 400 °C. In the last column, the differences ΔDiff between these mean ΔE/E values (200 °C–400 °C) and the relative inhomogeneities at 500 °C are listed.

Fig. 6
figure 6

Relative inhomogeneity of the type S thermocouple 18/01

Full size image
Fig. 7
figure 7

Relative inhomogeneity of the type R thermocouple 13-02

Full size image
Fig. 8
figure 8

Relative inhomogeneities of non-standardized Pt/Rh alloys against pure platinum

Full size image
Table 1 Values of relative inhomogeneities ΔE/E of different Pt/Rh-alloyed thermoelement combinations at temperatures of 200 °C, 300 °C, 400 °C, and 500 °C
Full size table

The independence of the relative inhomogeneities ΔE/E of the emf in the temperature range between 200 °C and 400 °C of the Pt/Rh-alloyed thermocouples confirms that the emf changes ΔE caused only by irreversible inhomogeneities scale approximately linearly with the emf [5]. This is valid also for the pure noble metal thermocouples even up to at least 500 °C. However, the inhomogeneity signatures of the Pt/Rh thermocouples changed when reaching 500 °C. For all five different alloys investigated, a significant decrease of the relative inhomogeneity values was observed at 500 °C (see last column of Table 1).

Repeated measurements of the immersion profiles at 300 °C and 500 °C were performed using the multi-wire thermocouple consisting of the non-standardized Pt/Rh alloys Pt5%Rh, Pt17%Rh, and Pt20%Rh and of a pure platinum thermoelement. Besides the emf measurements of the three Pt/Rh alloys against pure platinum, also two further combinations were measured: Pt17%Rh/Pt5%Rh and Pt20%Rh/Pt5%Rh. The combination of Pt20%Rh/Pt17%Rh generates only very low emfs so that these values could not be used for the analysis of the emf data. The measurement of redundant emf values allowed some cross-checks of the measured immersion profiles to be made along with assessing the uncertainty of the measurements. Before starting these additional measurements, the multi-wire thermocouple was annealed at 400 °C for 24 h, in order to obtain the same initial conditions of the thermoelements as when performing the previous measurements.

As an example, Table 2 shows the data of these additional immersion profile measurements. The columns A, B, and C contain the emf differences ΔE between the emfs measured of the respective combinations during the removal of the thermocouple from the bath and the emf at maximum immersion (40 cm) at 500 °C. The column D is a verification of the accuracy of the measurement. It contains the calculated ΔE values of the combination of Pt17%Rh/Pt, which must be the sum of the ΔE values of the combinations of Pt5%Rh/Pt (A) and Pt17%Rh/Pt5%Rh (C) according to the law of linear superposition of the emfs in a circuit. Comparing the calculated ΔE values of column D with the measured ΔE values in column B between immersion depths (12–40) cm, a very good agreement within a maximal deviation of 0.13 µV was found. Similar agreements were found when assessing the combinations of Pt5%Rh/Pt, Pt20%Rh/Pt, and Pt20%Rh/Pt5%Rh at 300 °C and 500 °C. Derived from this, a value of approx. 0.2 µV can be used as an estimate for the measurement uncertainty of the measurement of the individual immersion profiles.

Table 2 Measured ΔE values of the thermoelement combinations of Pt5%Rh/Pt, Pt17%Rh/Pt, and Pt17%Rh/Pt5%Rh at 500 °C
Full size table

The measured immersion profiles of the three PtRh-alloyed thermoelements against pure platinum at 300 °C and 500 °C were very similar to the previous measurements at these temperatures. Figure 9 shows the differences of the measured immersion profiles of the five suitable thermoelement combinations between 500 °C and 300 °C. The thermoelements combined with the pure Pt wire showed a clear decrease of the homogeneity values and the emf by about (0.5–1.0) µV as found before, but both combinations of Pt20%Rh/Pt5%Rh and Pt17%Rh/Pt5%Rh exhibited only very slightly changed emf signatures along their lengths. A selective Rh oxidation as a cause for the changed inhomogeneity signature and for the lower emfs can be excluded. A possibly formed Rh oxide layer as the result of the previous measurements at 500 °C, which would result in a reduction of the thermoelectric emf because the thermoelectric active Rh content in the alloyed thermoelements would become reduced, would still be present in the subsequent measurements performed, since the dissociation temperature of rhodium oxide is above 900 °C [8], but the annealing temperature here was only 400 °C.

Fig. 9
figure 9

Differences of the inhomogeneities ΔE measured at 500 °C and 300 °C

Full size image

Therefore, the changed inhomogeneity signatures and the reduced emf at 500 °C must be due to reversible ordering processes only in the PtRh-alloyed thermoelements. During the 24-h aging at 400 °C, an equilibrium concentration of one-dimensional lattice defects is established which corresponds to the minimum free energy of the point defects at this temperature. In theory, the temperature dependence of the vacancy concentration in a crystal lattice is described by Eq. 7 [9]:

$${\raise0.7ex\hbox{$n$} \!\mathord{\left/ {\vphantom {n N}}\right.\kern-0pt} \!\lower0.7ex\hbox{$N$}} = e^{{{\raise0.7ex\hbox{${ - E_{s} }$} \!\mathord{\left/ {\vphantom {{ - E_{s} } {kT}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${kT}$}}}} .$$
(7)

N is the number of atoms and n is the number of vacancies in a crystal, Es is the energy of the formation of a vacancy, k is the Boltzmann constant and T is the absolute temperature. Figure 10 shows a fictitious experimentally determined curve of the equilibrium concentration of vacancies (starting with melting temperature Tm). The concentration decreases with lower temperatures, initially following the exponential course (dotted line). At a certain temperature (in our case near the annealing temperature of 400 °C) the exponential curve (straight line) bends to a constant value. At the lower temperatures of 200 °C and 300 °C, the atoms can no longer perform the diffusion and place change processes required to adjust the equilibrium concentration. As a result, the higher concentration of defects of 400 °C remains “frozen”, instead of reaching the concentration of defects which would correspond to the thermal equilibrium at the lower temperatures at 200 °C and 300 °C (dotted line, Fig. 10). At higher temperatures (500 °C) than the annealing temperature of 400 °C, however, the equilibrium concentration of one-dimensional lattice defects corresponding to the new temperature is established relatively quickly due to faster place change processes. These structural changes influence the Seebeck coefficient with the result of a changed inhomogeneity signature and a reduced emf. Such re-ordering processes do not arise in the pure platinum wire at temperatures between 400 °C and 500 °C, as the measurements with the Pt/Pd and Au/Pt thermocouple showed. The almost unchanged inhomogeneity signatures of the combinations of Pt20%Rh/Pt5%Rh and Pt17%Rh/Pt5%Rh at 300 °C and 500 °C are due to compensating effects of the re-ordering processes in both PtRh-alloyed thermoelements of each of the both combinations.

Fig. 10
figure 10

Temperature dependence of the vacancy concentration in a crystal

Full size image

Additional measurements with the PtRh-alloyed thermocouples (including the type S and the type R thermocouple) were performed at 450 °C to find out whether the equilibrium concentration of the vacancies at the annealing temperature of 400 °C corresponds to the concentration to be expected at this temperature according to Eq. 7. Before this additional measurement the thermocouples were annealed at 400 °C for 24 h again. Figure 11 shows the temperature and alloy-dependent relative inhomogeneities of the investigated Pt/Rh-alloyed thermocouples. The results show a deviation from the linear scaling model already at 450 °C. Since the changes in the relative inhomogeneities at temperatures of 450 °C and 500 °C are linear over 1/T starting from 400 °C, it can be assumed that in the temperature range between 400 °C and 500 °C the equilibrium concentration of the vacancies follows the theoretical course. This means, on the other hand, that the deviation from the theoretical course is at temperatures T ≤ 400 °C. Below approx. 400 °C, the vacancy concentration changes only very slowly, so that the linear scaling model can be used for thermoelectric inhomogeneities in PtRh-alloyed thermocouples.

Fig. 11
figure 11

Temperature and alloy-dependent relative inhomogeneities of Pt/Rh-alloyed thermocouples

Full size image

4 Conclusion

The independence of the relative thermoelectric inhomogeneities ΔE/E from the temperature in the range between 200 °C and 500 °C was investigated. The results obtained by using the pure metal thermocouples Au/Pt and Pt/Pd confirmed the assumption that the linear extrapolation of the measured inhomogeneity ΔE may be expressed as a percentage of the total thermo-voltage E measured. For all the Pt/Rh-alloyed thermocouples, this relationship was found to be applicable only to a temperature of about 400 °C. Above this temperature, reversible re-ordering processes occur which have an influence on the inhomogeneity signature and which interfere with the linear ΔE/E correlation. Therefore, as long as only irreversible inhomogeneities exist, for instance caused by contaminations, a linear relationship of inhomogeneity related emf changes with temperature can be applied also at low temperatures, similar to the relationship found for higher temperatures [5, 10].

Thermoelectric drift and inhomogeneity in Pt/Rh-alloyed thermocouples are often caused by relative changes of the alloying thermoelements [5, 11, 12], and not of the pure platinum wire. The comparison of the immersion profiles of the single thermoelements at 300 °C and at 500 °C along with the additional measurement at 450 °C showed that homogeneity-affecting effects already arise at temperatures above 400 °C. These effects are due to changes in the equilibrium concentration of point defects in the PtRh-alloyed thermoelements. A change of the homogeneity of the pure Pt wire is rather implausible, because of the results obtained by using the pure metal thermocouples Au/Pt and Pt/Pd.