The Effect of Pressure and Temperature on the Second-Order Derivatives of the Free Energy Functions for Lower Alkanediols

Abstract

The second-order derivatives of the free energy functions, i.e., isochoric molar heat capacities, isentropic and isothermal molar compressibility, and isobaric and isentropic molar thermal expansion, were calculated in the temperature range from (293.15 to 318.15) K and at pressures up to 100 MPa for 1,2- and 1,3-propanediol; 1,2-, 1,3, and 1,4-butanediol; and 2-methyl-2,4-pentanediol. The data for calculations were obtained by means of the acoustic method. The pressure and temperature dependencies for the above mentioned properties are analyzed and discussed together with the literature data on isobaric molar heat capacities. The observed marked difference between isobaric and isentropic thermal expansion is analyzed as well. The differences in behavior of linear 1,2-diols and $\upalpha ,\upomega$-diols as well as a diol with a branched carbon chain are emphasized. The isentropic and isothermal molar compressibilities are used to evaluate the dimensionality and relative rigidity of H-associates.

1 Introduction

Experimental data of thermodynamic properties at elevated pressures, which are of particular importance in the study of the liquid state, are still rather scarce. This refers, in particular, to hydrogen-bonded liquids that are key substances in the chemical industry and are of utmost importance in biology. Therefore, such liquids are very interesting from both practical and theoretical points of view. Unfortunately, in spite of efforts, their structure and thermodynamics are still not properly understood. Especially interesting are lower alkanediols used on a large scale as chemical intermediates, solvents, and antifreeze; as additives in food, cosmetics, tobacco, and pharmaceutics; as lubricants in the food industry; and as components of operating liquids in refrigerating and thermostatting systems [1]. This group of compounds is also widely used in cryobiology [2] and can be used as protein-stabilizing agents [3, 4]. Moreover, lower alkanediols can be treated as specific model substances (which exhibit two donor and two acceptor functions) for much more complicated molecules and macromolecules of biological materials. Due to the presence of two hydroxyl groups in the alkanediol molecule, intermolecular hydrogen bonding leads to a chainlike or ringlike strong molecular association and spatial structure ordering in the liquid phase. As a consequence, the properties of such substances depend significantly not only on the characteristics of the individual bonds but also on the structure of H-associates. At the same time, alkanediols (first of all $\upalpha , \upomega$-diols) have the ability to form intramolecular hydrogen bonding within the molecule (5-, 6-, or 7-atom, H-bonded rings). The propane- and butanediols, in particular, are interesting because their structures result in different isomers with a possibility of change in the relative positions of hydroxyl groups along the alkyl chain.

The present work complements previous reports about the effect of pressure and temperature on acoustic and thermodynamic properties of selected alkanediols by means of the acoustic method [5–8]. The present study is aimed at the effects of pressure $p$ and temperature $T$ on the second-order derivatives of the free energy functions in order to provide data for a better knowledge about the behavior of hydrogen-bonded liquids under elevated pressures. In particular, the differences in behavior of linear 1,2-diols and $\upalpha , \upomega$-diols as well as a diol with a branched carbon chain will be emphasized. The second-order derivatives of the free-energy functions calculated in this work are: the isochoric molar heat capacity $C_{V}$, isentropic and isothermal molar compressibility, $K_{S}$ and $K_{T}$, and isobaric and isentropic molar thermal expansion, $E_{p}$ and $E_{S}$. The calculations have been made in the temperature range from (293.15 to 318.15) K and at pressures up to 100 MPa for 1,2- and 1,3-propanediol; 1,2-, 1,3, and 1,4-butanediol; and 2-methyl-2,4-pentanediol. All data for calculations are taken from our previous reports [5–8]. It should be noted that the $C_{V}(p,T), K_{S}(p,T), K_{T}(p,T)$, $E_{p}(p,T)$, and $E_{S}(p,T)$ data together with the $C_{p}(p,T)$ data reported previously [5–8] form a compact set of molar thermodynamic properties obtained via speed-of-sound measurements as a function of $p$ and $T$. The advantages of this method (relative simplicity, rapidity, and accuracy) make it a very attractive and reliable alternative to the direct experimental measurements under elevated pressures, for both “classical” organic liquids [9] and room-temperature ionic liquids [10, 11]. It is also worthy of note that according to the concept of Gibbsian and non-Gibbsian properties [12], $C_{p}, E_{p}$, and $K_{T}$ are Gibbsian properties, whereas $C_{V}, E_{S}$, and $K_{S}$ are non-Gibbsian properties. Nevertheless, the latter can be expressed in terms of Gibbsian properties [12].

To the best of the present writer’s knowledge, the properties reported in this work have not been studied yet in such temperature and pressure conditions.

2 Calculations of the Second-Order Derivatives of the Free-Energy Functions at Elevated Pressures by Means of the Acoustic Method

Because at elevated pressures the direct experimental determination of thermodynamic properties is rather difficult, an indirect acoustic method [5–10, 13–16] is very useful. In the assumed absence of dispersion phenomena (dissipative processes can be neglected), the speed of sound $u$ may be regarded as a thermodynamic equilibrium quantity (Newton-Laplace relation) which is closely related to the material constants such as density $\rho$ and the isentropic compressibility coefficient $\kappa _{S}$,

$$\begin{aligned} u=\left( \rho \kappa _{S} \right) ^{-1/2}. \end{aligned}$$

(1)

Generally, the acoustic method is based on the speeds of sound measured as functions of $T$ and $p$ as well as on the density and heat capacity measured as functions of $T$ at atmospheric pressure. For obtaining the related (to the speed of sound) thermodynamic properties, the speed-of-sound data must be firstly approximated and then integrated in the experimental ($p,T$) range. In the calculations, a modified numerical procedure (which is based on the earlier suggestions of Davies and Gordon [14] in this field) according to Sun et al. [13] has been applied. As reference densities and isobaric heat capacities, the smoothing functions of temperature at the reference pressure $p_{0}$ (here atmospheric) were used. Finally, the appropriate integration procedure of the following relation:

$$\begin{aligned} \rho (p,T)=\rho (p_0 ,T)+\int \limits _{p_0}^p u^{-2}\hbox {d}p +TM\int {\alpha _p^2 C_p^{-1} \hbox {d}p} \end{aligned}$$

(2)

gives the isobars of density and isobaric heat capacity covering the pressure and temperature ranges for the speed-of-sound measurements. The first integral on the right-hand side can be obtained directly, whereas for the second integral, an appropriate integration procedure must be used. Note also that the first integral is significantly larger than the second one. Generally, however, the values of the heat capacities obtained in this way are less reliable than the values of densities [5–8, 13, 15] The respective uncertainties estimated by means of the perturbation method [13, 15] (the speed of sound is taken into account as a main source of the uncertainty) are expected to be better than $\pm$0.3 % and $\pm$0.02 % for the isobaric heat capacity and density, respectively [5–8]. However, as reported previously [7, 17], the total uncertainties (including a comparison of most results obtained in our laboratory with those obtained in other laboratories by different methods) can be estimated roughly to be better than $\pm$1 % and $\pm$0.05 % for the heat capacity and density, respectively. In my opinion, however, this is a rather pessimistic estimation, and as stated very recently [18], the uncertainties should be better.

From the basic set of $u(p,T), \rho (p,T)$, and $C_{p}(p,T)$ data reported earlier [5–8], the related properties covering the $(p,T)$ range of the speed-of-sound measurements can be calculated. The $E_{p}(p,T), K_{S}(p,T)$, and $K_{T}(p,T)$ values are calculated directly from previously reported [5–8] coefficients of isobaric thermal expansion $\alpha _{p}(p,T)$, isentropic compressibility coefficient $\kappa _{S}(p,T)$, and isothermal compressibility coefficient $\kappa _{T}(p,T)$, respectively, using formulas:

$$\begin{aligned} E_p&= \alpha _{p} M\rho ^{-1},\end{aligned}$$

(3)

$$\begin{aligned} K_S&= \kappa _{S} M\rho ^{-1},\end{aligned}$$

(4)

$$\begin{aligned} K_T&= \kappa _{T} M\rho ^{-1}, \end{aligned}$$

(5)

where $M$ denotes the molar mass. The values of the calculated $E_{p}(p,T), K_{S}(p,T)$, and $K_{T}(p,T)$ are reported in Electronic Supplementary Material. Simultaneously, the $C_{V} (p,T)$ values were calculated from the relation:

$$\begin{aligned} C_V =C_p -E_p^2 T{ K}_T^{-1}, \end{aligned}$$

(6)

while for calculation of the lesser known $E_{S}(p,T)$ values, the following relation was used:

$$\begin{aligned} E_S =-C_p { K}_S T^{-1}E_p^{-1}. \end{aligned}$$

(7)

3 Experimental

All experimental procedures and techniques for the speed-of-sound measurements as a function of $p$ and $T$, density measurements as a function of $T$ at atmospheric pressure, and isobaric heat capacity measurements as a function of $T$ at atmospheric pressure were reported previously [5–8, 19]. In Table 1, the basic information about the studied samples is summarized together with the literature sources of the original primary data on $u(p,T), \rho (p,T)$, and $C_{p}(p,T)$.

Table 1 Provenance, purity, and references for data on speed of sound $u(p,T)$, density $\rho (p,T)$, and isobaric heat capacity ${C}_{p} (p,T)$ for the alkanediols studied

It should be noted that from all alkanediols studied, 1,4BD shows the highest freezing temperature ($T$ = 292.80 K) at atmospheric pressure [20]. Thus, in the case of 1,4BD, the pressure range at temperatures (293.15, 298.15, and 303.15) K is limited due to freezing. According to [21], the freezing pressure near 50 MPa at $T = 298.15\,\hbox {K}$ corresponds with that at $T$ = 299.11 K, 40 MPa to 70 MPa, estimated from the high-pressure expansivity measurement [22]. And so, the freezing point at atmospheric pressure and data at $T = 298.15\,\hbox {K}$ give a sufficient indication of the range of pressure that might safely be applied in acoustic experiments (46 and 91) MPa at (298.15 and 303.15) K [8] without running into the freezing curve.

All molar masses used in this work are based on the 2007 IUPAC relative atomic masses [23].

4 Results and Discussion

For all the alkanediols discussed in this work, the thermodynamic properties at the temperature 298.15 K and atmospheric pressure are listed in Table 2. Initial inspection of Table 2 reveals essential differences between the $E_{p}$ and $E_{S}$ values, both in sign and magnitude (discussed in Sect. 4.3). Moreover, an approximately linear relation between $E_{p}$ and $K_{T}$ can be observed, i.e., a lower isobaric thermal expansion is associated with a lower compressibility. Some deviations from this linearity are, however, observed for 2MPD2,4 and in particular 1,5PD, i.e., for a diol with a branched carbon chain and a diol where rather older literature data were used.

Table 2 Molar thermodynamic properties of alkanediols at 298.15 K and atmospheric pressure: molar isobaric and isochoric heat capacities, $C_{p}$ and $C_{V}$, molar isentropic and isothermal compressibilities, $K_{S}$ and $K_{T}$, as well as molar isobaric and isentropic expansion, $E_{p}$ and $E_{S}$

4.1 Heat Capacity

Both $C_{p}$ and $C_{V}$ (the second-order temperature derivatives of the Gibbs- and Helmholtz-free energy, respectively) belong to the most important thermophysical properties of matter. They are extensive measurable state functions linked to the temperature dependence of such fundamental thermodynamic quantities as enthalpy, internal energy, and entropy. It should be noted that an extensive review on the importance of heat capacities of non-electrolytes was given recently by Wilhelm [28]. Generally, $C_{p}$ is the quantity of interest from a practical point of view, while $C_{V}$ is the thermophysical property needed in more theoretically oriented work. In other words, in spite of the importance of the isobaric molar heat capacity, a knowledge of the complementary isochoric molar heat capacity is indispensable for a better understanding on the molecular level. Direct calorimetric measurements of $C_{V}$ are rather rare and mostly near the critical point, where the isochoric thermal pressure coefficient is much smaller than at temperatures far below the critical temperature [28]. In this last case, the direct calorimetric determination is very difficult and the molar isochoric heat capacity is determined mostly indirectly by means of the acoustic method; for example, from Eq. 6 or an equivalent [18]. The calculated values of $C_{V}$ are summarized in Table 3.

Table 3 Molar isochoric heat capacities ($C_{V}$) calculated by the use of the acoustic method for 1,2- and 1,3-propanediol, 1,2-, 1,3-, and 1,4-butanediol as well as 2-methyl-2,4-pentanediol at various temperatures ($T$) and pressures $(p)$

As stated in previous work [5–8], the isobaric heat capacities increase with increasing temperature (at constant pressure) and decrease with increasing pressure (at constant temperature). In the investigated ($p,T$) range, however, the effect of pressure is smaller than that of temperature. In other words, the effect of pressure reduces the magnitude of $C_{p}(T)$ by a small amount, without significantly changing its temperature dependence. Figure 1 shows the effect of pressure on $C_{p}$ and $C_{V}$ (for clarity only at $T = 298.15\,\hbox {K}$) for all alkanediols studied, whereas Fig. 2 shows the effect of temperature on $C_{p}$ and $C_{V}$ at $p = 100\,\hbox {MPa}$. As seen, $C_{p}$ decreases with increasing pressure very similarly for the 1,2-, and 1,3-, isomers. In the case of 1,4BD, the dependence is a little weaker and the $C_{p}$ values for butanediols are in the order: 1,2BD $>$ 1,3BD $>$ 1,4BD over the whole investigated range. In the case of propanediols, the $C_{p}$ values are in the order: 1,2PrD $>$ 1,3PrD. Generally, the $C_{p}$ values are in the order: 2MPD2,4 $>$ 1,2BD $>$ 1,3BD $>$ 1,4BD $>$ 1,2PrD $>$ 1,3PrD. In the case of $C_{V}$, the temperature–pressure effects show similar trends as in the case of $C_{p}$, however, the effect of pressure on $C_{V}$ is very weak, much weaker than in the case of $C_{p}$. In practice, $C_{V}$ is almost pressure independent here (especially at lower temperatures). However, it should be noted here that in the case of 2MPD2,4, this very weak pressure dependence of $C_{V}$ shows a positive trend (opposite behavior to that of the linear diols). It is worth noting that in the present study, no minima on the isotherms of heat capacities for investigated alkanediols are observed (probably on account of the limited ($p,T$) range); however, the minima on the isotherms of heat capacities are an inherent property of dense simple liquids [29]. At the same time for highly associated liquids, it is suggested that the minima on the heat capacity isotherms appear only at high temperatures (considerably higher than in the present study) and are shifted to lower pressures with an increase in temperature [29]. From this point of view, the ${C}_{V}$ behavior in the case of 2MPD2,4 is rather unusual, more similar to those for simple liquids than those for highly associated liquids. The magnitude of the $C_{V}$ values (Fig. 1b) is, however, on the same order as in the case of the $C_{p}$ values (Fig. 1a).

Fig. 1

Molar heat capacities, isobaric $C_{p}$ (a) and isochoric $C_{V}$ (b), plotted against pressure $p$ at $T = 298.15\,\hbox {K}$ for: ($\Delta$), 1,2-propanediol; ($\blacktriangle$), 1,3-propanediol; ($\diamondsuit$) 1,2-butanediol; ($\circ$), 1,3-Lbutanediol; ($\bullet$), 1,4-butanediol; and ($\blacksquare$), 2-methyl-2,4-pentanediol. Lines to guide the eye. $C_{p}$ values are taken from [5–8]

Fig. 2

Molar heat capacities, isobaric $C_{p}$ (a) and isochoric $C_{V}$ (b), plotted against temperature $T$ at $p = 100\,\hbox {MPa}$ for: ($\Delta$), 1,2-propanediol; ($\blacktriangle$), 1,3-propanediol; ($\diamondsuit )$ 1,2-butanediol; ($\circ$), 1,3-butanediol; ($\bullet$), 1,4-butanediol; and ($\blacksquare$), 2-methyl-2,4-pentanediol. Lines to guide the eye. $C_{p}$ values are taken from [5–8]

The decrease of $C_{p}$ with increasing pressure (decreasing volume) can be explained by an increasing molecular order. According to Forsman et al. [30], three factors are responsible for the variation of heat capacity with pressure: the free volume for molecular vibrations, intramolecular vibrations, and rotational degrees of freedom. On the one hand, isothermal compression reduces the free volume and the amplitude of molecular vibrations independently of the shape molecules. On the other hand, changes in rotations depend significantly on the symmetry of the molecules and rotations along the longer axis are less hindered by pressure in the case of 1,3PrD and 1,4BD, whereas in the case of 2MPD2,4, hindering is the highest. Thus, the pressure dependence of the heat capacity is weaker for substances consisting of symmetrical molecules than for unsymmetrical ones. Examination of the effect of $T$ and $p$ on heat capacities of branched alkanols leads Cerdeiriña et al. [31] to the conclusion that the association contribution to ($\partial C_{p}/ \partial p)_{T}$ is significantly less important than the non-specific one, whereas ($\partial C_{p}/ \partial T)_{p}$ is dominated by the association contribution. More difficult is the interpretation of ${C}_{V}$, since this quantity depends on the various external and internal degrees of freedom of the molecules.

The pressure behavior of the difference in molar heat capacities,

$$\begin{aligned} C_{p} - C_{V}=TE_p^2 K_T^{-1} \end{aligned}$$

(8)

is shown in Fig. 3 (for clarity only at $T = 298.15\,\hbox {K}$) as the ratio ($C_{p} - C_{V})/R$ where $R$ is the universal gas constant ($R = 8.314\,\hbox {J}\cdot \hbox {mol}^{-1}\cdot \hbox {K}^{-1})$. Note that values for 1,2ED are calculated from the data reported very recently by Atilhan and Aparicio ($\alpha _{p}$ and $\kappa _{T}$ are derived from density measurements under elevated pressures by means of a vibrating-tube densimeter) [32]. Interestingly, $\upalpha , \upomega$-diols show the smallest values of $C_{p} - C_{V}$. Both for propanediols and butanediols, with an increase in the distance between hydroxyl groups, the difference $C_{p} - C_{V}$ decreases. At the same time, the highest values and strongest pressure dependence show 2MPD2,4, i.e., the diol with a branched carbon chain. The magnitude of $C_{p} - C_{V}$ changes in the order: 1,2ED $<$ 1,3PrD $<$ 1,4BD $<$ 1,2PrD $<$ 1,3BD $<$ 1,2BD $<$ 2MPD2,4. Generally, it appears that in all the cases studied, the isotherms of $C_{p} - C_{V}$ do not cross over the pressure and temperature ranges investigated in this study. As has been reported by Randzio et al. [33], also in the case of 1-hexanol, the isotherms do not cross in the pressure and temperature ranges from the saturation line to 400 MPa and (303 to 503) K, respectively. Such behavior is different from that observed for $n-$hexane because the respective isotherms for $n-$hexane exhibit a unique crossing point at 20 MPa for $C_{p} - C_{V} = 5R$ [34]. Thus, the behavior of non-associating liquids differs from the behavior of associating liquids.

Fig. 3

Ratio of the heat capacity difference to gas constant, ($C_{p}-C_{V})/R$, plotted against pressure $p$ at $T = 298.15\,\hbox {K}$ for: ($\Delta$), 1,2-propanediol; ($\blacktriangle$), 1,3-propanediol; ($\diamondsuit$) 1,2-butanediol; ($\circ$), 1,3-butanediol; ($\blacksquare$), 1,4-butanediol; ($\bullet$), 2-methyl-2,4-pentanediol; and ($\star$), 1,2-ethanediol. Lines to guide the eye. In the case of 1,2-ethanediol, data for calculation are taken from [32]

It is also noteworthy that the ratio of heat capacities $C_{p}/C_{V}$ changes along the isobars very slightly. For linear diols, this ratio increases very slowly with increasing temperature, whereas for 2MPD2,4, a slight decrease is observed. However, the ratio $C_{p}/C_{V}$ decreases more evidently with increasing pressure along isotherms.

4.2 Compressibility

As is known, the compressibilities may be considered to be the sum of the instantaneous compressibilities due to the compression of the molecules and intermolecular distance, and the structural compressibility due to the breakdown of the intermolecular H-bonds and the reorganization of the clusters (associates). According to Grineva [35], the values of the molar isentropic compressibility $K_{S} (K_{S} = -(\partial V/ \partial p)_{S})$ and plots of $K_{S}(T)_{p}$ make it possible to draw conclusions about the dimensionality and relative rigidity of H-associates in liquids. Figure 4 shows the values of $K_{S}(T)_{p}$ for alkanediols studied together with the values for 1,2-ethanediol (1,2ED) taken from [24] and [36]. As seen, the dependency of $K_{S}$ on temperature is almost linear. The linearity of the isobars increases with increasing pressure and, at the same time, the higher the pressure the smaller is the temperature dependence. Moreover, the sequence of magnitude of $K_{S}(T)_{p}$ is: 1,2-ED $<$ 1,3PrD $<$ 1,2PrD $<$ 1,4BD $<$ 1,3BD $<$ 1,2BD $<$ 2MPD2,4. The differences in magnitude are very clear at atmospheric pressure (Fig. 4a); however, at elevated pressure $p = 100\,\hbox {MPa}$ (highest pressure in this study), the differences are distinctly smaller (Fig. 4b). Thus, the difference in $K_{S}$ values decreases appreciably with pressure. It is especially visible for isomeric propane- and butanediols. At $p = 100\,\hbox {MPa},$ the values for 1,2- and 1,3-propanediol are very close. A similar behavior is observed for 1,2-, 1,3-, and 1,4- butanediol. This is very interesting. Clustering of $K_{S}$ values for isomeric alkanediols can be related with increasing similarity of local structures with increasing pressures (decreasing volume), or in other words, with a decreasing role of hydrogen bonding with increasing pressures. In the case of butanediols, the highest compressibility of 1,2BD can be explained as a result of lower dimensionality and relatively low rigidity of H-associates in comparison with 1,3BD, and especially 1,4BD [8]. As stated earlier [8], also the effect of density cannot be neglected because, as a general rule, liquids with lower densities (here 1,2BD and 1,3BD) tend to be more compressible. Moreover, as already reported in [8], the above explanation is in agreement with the sequence of the boiling temperatures for isomeric butanediols, i.e., the boiling temperature increases from 1,2BD via 1,3BD to 1,4BD. Finally, we also note that the magnitude of the dielectric permittivity changes in the same sequence, i.e., increases from 1,2BD to 1,4BD [37]. A similar behavior is shown by propanediols. Here, isomer 1,2- also shows a higher compressibility than isomer 1,3- and the density of 1,2PrD is smaller than that of 1,3PrD [6]. The same agreement is observed for normal boiling temperatures (1,2PrD (462.15 K) $<$ 1,3PrD (486.65 K) [20]) and polarities [38]. Very high compressibility, the highest of all the diols under consideration, is seen in 2MPD2,4 due to its branching carbon chain. Thus, the existence of the side methyl group strongly affects the compressibility in comparison with the linear alkanediols.

Fig. 4

Molar isentropic compressibility $K_{S}$ plotted against temperature $T$ at pressure $p = 0.1\,\hbox {MPa}$ (a) and at $p = 100\,\hbox {MPa}$ (b) for: ($\Delta$), 1,2-propanediol; ($\blacktriangle$), 1,3-propanediol; ($\diamondsuit$) 1,2-butanediol; ($\circ$), 1,3-butanediol; ($\bullet$), 1,4-butanediol; ($\blacksquare$), 2-methyl-2,4-pentanediol; and ($*$), 1,2-ethanediol [24, 36]. Lines to guide the eye

Taking into account the data about crystal structures of diols, Grineva [35] postulated that the structure of 1,4BD is characteristic for all subsequent even $\upalpha , \upomega$-diols, while the structure of 1,3PrD is an exception, because a framework of H-associates is formed in the crystals of the higher odd $\upalpha , \upomega$-diols. Generally, it can be assumed that lengthening of the molecule, which is connected with an increased number of possible conformers, leads to higher compressibility. In other words, the magnitude of the $K_{S}$ values for alkanediols studied is sensitive to the carbon chain lengths of the diol molecules, i.e., as the length of the carbon chain is increased, $K_{S}$ increases. Interesting is the relation between the $K_{S}$ values and carbon chain length for a series of $\upalpha , \upomega$-, and 1,2-diols. As shown in Fig. 5a, at $p_{0} = 0.1\,\hbox {MPa}$ and $T = 298.15\,\hbox {K},$ the dependencies between $K_{S}$ and the number of carbon atoms $n$ in the diol molecule are linear; however, the effect of elongation of the carbon chain length in $\upalpha , \upomega$-, and 1,2-diols is different. In the case of 1,2-diols, $K_{S}$ increases more rapidly than in the case of $\upalpha , \upomega$-diols. Fitting the present and literature data [24, 27] ($p_{0} = 0.1\,\hbox {MPa}, T = 298.15\,\hbox {K}$) jointly, with all the points weighted equally, yielded the relations,

$$\begin{aligned}&\hbox { K}_S (1,2\hbox {-diols})=-5.895+12.265n\end{aligned}$$

(9)

$$\begin{aligned}&\hbox { K}_S (\alpha ,\omega \hbox {-diols})=2.776+7.819n \end{aligned}$$

(10)

with a standard deviation from the regression line of ($\pm$0.58 and $\pm 0.16)\,\hbox {m}^{3}\cdot \hbox {PPa}^{-1}\cdot \hbox {mol}^{-1}$, respectively.

Thus, the results show that the $-\hbox {CH}_{2}$ group contribution to $K_{S}$ is clearly higher for isomers with two adjacent hydroxyl group (1,2-), whereas the increase of carbon chain length with a simultaneous increase in the distance between the hydroxyl groups ($\upalpha , \upomega$-) leads to the smaller $-\hbox {CH}_{2}$ group contribution. Similar linear relations are also observed in the case of $K_{T}$ (Fig. 5b). Here, the following dependencies ($T = 298.15\,\hbox {K}, p_{0} = 0.1\,\hbox {MPa}$) are valid:

$$\begin{aligned}&\hbox { K}_T (1,2\hbox {-diols})=-6.80+13.95n\end{aligned}$$

(11)

$$\begin{aligned}&\hbox { K}_T (\alpha ,\omega \hbox {-diols)}=1.19+9.48n \end{aligned}$$

(12)

with a standard deviation from the regression line of ($\pm$0.51 and $\pm$0.81) $\hbox {m}^{3}\cdot \hbox {PPa}^{-1}\cdot \hbox {mol}^{-1}$, respectively. Here, in the fitting procedure, apart from our own data, the $K_{T}$ values calculated from literature data were used [27, 32, 39].

Fig. 5

Molar isentropic $K_{S}$ (a) and isothermal $K_{T}$ (b) compressibility plotted against number of carbon atoms $n$ at $p =$ 0.1 MPa and $T = 298.15\,\hbox {K}$ for: ($\blacktriangle$), 1,2-alkanediols; and ($\circ$), $\upalpha , \upomega$-alkanediols. Straight lines - obtained by fitting of $K_{S}$ (Eqs. 8, 10) and $K_{T}$ (Eqs. 11, 12) values. Data for 1,2-ethanediol taken from [24]. Data for 1,5-pentanediol calculated from [37]. In the case of $K_{T}$, additional data for ($\Delta$), 1-2-alkanediols taken from [32]

As can be expected on the grounds of similarity of the pressure–temperature dependencies of the isentropic and isothermal compressibilities, i.e., intensive volume-specific properties [5–8], also the isobars and isotherms of the molar isothermal compressibility are similar to those observed for the molar isentropic compressibility. In fact, the pressure–temperature dependence of the molar isothermal compressibility $K_{T}$ ($K_{T} = -(\partial V/ \partial p)_{T})$ and plots of $K_{T}(T)_{p}$ are very similar to those for the molar isentropic compressibility. The magnitude of $K_{T}$ (Fig. 6) is of the same order (2MPD2,4 $>$ 1,2BD $>$ 1,3BD $>$ 1,4BD $>$ 1,2PrD $>$ 1,3PrD $>$ 1,2ED) as in the case of $K_{S}$ (Fig. 4). Thus, in the case of both propanediols and butanediolsm, $\upalpha ,\upomega$-diols show also the smallest isothermal compressibility. It can be also concluded that plots of $K_{T}(T)_{p}$ can be used to evaluate the dimensionality and relative rigidity of H-associates in a similar manner as plots of $K_{S}(T)_{p}$, but this application is rather restricted to atmospheric pressure.

Fig. 6

Molar isothermal compressibility $K_{T}$ plotted against temperature $T$ at pressure $p = 0.1\,\hbox {MPa}$ (a) and at $p = 100\,\hbox {MPa}$ (b) for: ($\Delta$), 1,2-propanediol; ($\blacktriangle$), 1,3-propanediol; ($\diamondsuit$) 1,2-butanediol; ($\circ$), 1,3-butanediol; ($\bullet$), 1,4-butanediol; ($\blacksquare$), 2-methyl-2,4-pentanediol; and ($*$), 1,2-ethanediol [24, 36]. Lines to guide the eye

Contrary to linear in practice dependencies on temperature, the dependencies of $K_{S}$ and $K_{T}$ on pressure evidently have a nonlinear character (Fig. 7), and the non-linearity of the $K_{S}$ and $K_{T}$ isotherms increases with increasing temperature (not shown). Simultaneously, both $K_{S}$ and $K_{T}$ depend significantly on pressure for pressures close to atmospheric, while the pressure effect on the compressibility is gradually decreasing with increasing pressure. Thus, all the liquids studied become less compressible as the pressure increases and, at high enough pressure, the liquid approaches a value corresponding to a close-packed structure. In this study, however, this point cannot be assessed directly because the pressure range was not high enough.

Fig. 7

Molar compressibilities, (a) isentropic $K_{S}$ and (b) isothermal $K_{T}$, plotted against pressure $p$ at $T = 298.15\,\hbox {K}$ for: ($\Delta$), 1,2-propanediol; ($\blacktriangle$), 1,3-propanediol; ($\diamondsuit$) 1,2-butanediol; ($\circ$), 1,3-butanediol; ($\bullet$), 1,4-butanediol; ($\blacksquare$), 2-methyl-2,4-pentanediol; and ($*)$, 1,2-ethanediol. Lines to guide the eye. In the case of 1,2-ethanediol, data taken from [32]

The differences between $K_{T}$ and $K_{S}$ are related by the equation,

$$\begin{aligned} K_T -K_S =TE_p^2 C_p^{-1} \end{aligned}$$

(13)

which is expressed in terms of Gibbsian properties only. Figure 8 shows the effect of pressure on this difference in the form of relative changes 100($K_{T }-K_{S})/K_{T}$. As seen, the relative changes fall as the pressure increases. The effect of the pressure is the greatest in the case of 2MPD2,4; however, the relative changes do not exceed 2 % over the whole pressure range. Generally, the relative differences are the smallest for $\upalpha , \upomega$-diols and the greatest for 1,2-diols. In the case of temperature, the effect is weaker, i.e., the relative changes increase very slowly with increasing temperature.

Fig. 8

Relative difference ($K_{T}-K_{S})/K_{T}$ plotted against pressure $p$ at $T = 298.15\,\hbox {K}$ for: ($\Delta$), 1,2-propanediol; ($\blacktriangle )$, 1,3-propanediol; ($\diamondsuit$) 1,2-butanediol; ($\circ$), 1,3-butanediol; ($\bullet$), 1,4-butanediol; and ($\blacksquare$), 2-methyl-2,4-pentanediol. Lines to guide the eye

Note that the relative standard uncertainties of the compressibility values (at elevated pressures) reported in this work are estimated to be $\pm$0.25 % and $\pm$0.5 % for isentropic and isothermal compressibilities, respectively. It should be noted that the agreement of the $K_{T}$ values reported in this work (obtained by the acoustic method) and those calculated from data of Atilhan and Aparicio [32] (derived from $\rho (p,T)$ measurements by means of a vibrating-tube densimeter) is excellent (see Eqs. 11, 12; Fig. 5b). Note also that the results of the pressure study reported by McDuffie et al. [40] (the variable volume cell with bellows) are consciously omitted in this work on account of large deviations between mentioned data (obtained by differentiation procedure of the $\rho (p,T)$ dependencies [40]) and those presented in this work. For example, at atmospheric pressure and room temperature $T = 293\,\hbox {K}$, the deviations of the $\kappa _{T}$ values are approximately $-10$ % and $-11$ % for 1,3BD and 2MPD2,4, respectively. At higher pressures, however, the observed consistency is better, and for example, at 100 MPa the deviations are approximately 1.6 % and 3.2 %. Moreover, summing up this section, all findings stated above confirm a rather known fact that both compressibilities give generally similar information.

4.3 Expansion

As is known, the molar isobaric expansion $E_{p}$ is the second mixed derivative of the Gibbs free energy with respect to pressure and temperature, and can be rather easily obtained directly from volumetric measurements at isobaric conditions. A lesser-known thermodynamic property is the molar isentropic expansion $E_{S}$ (the second mixed derivative of the Helmholtz free energy with respect to pressure and temperature) that is thermodynamically related to the speed of sound and is thus indirectly accessible by the acoustic method. Direct experimental determination in the case of $E_{S}$ is not realizable because of the isentropic conditions. It should be noted that sometimes this property has been qualified as being of little interest [41]. On the other hand, Reis et al. [42] stated that it is a very interesting and useful thermodynamic property, especially in the case of liquid mixtures. An interesting discussion about equations which link isobaric and isentropic expansion is given in [43]. However, as stated in this reference, “complications are encountered in understanding isentropic expansions without the redeeming feature of practical accessibility via an analoque of the Newton-Laplace equation” [43]. $E_{p}$ and $E_{S}$ are defined by partial differentials, i.e., $E_{p} = (\partial V/ \partial T)_{p}$ and $E_{S} = (\partial V/ \partial T)_{S}$, respectively. Thus, $E_{p}$ and $E_{S}$ describe the change in molar volume upon an increase in temperature in isobaric and isentropic conditions, respectively. The values of $E_{p}$ and $E_{S}$ are calculated from Eqs. 3 and 7, and the roughly estimated relative standard uncertainties of the $E_{p}$ and $E_{S}$ values are not larger than $\pm$1.5 % and $\pm$3 %, respectively. So, the obtained $E_{S}$ values are reported in Table 4. As in the case of heat capacities and compressibilities (Eqs. 7, 9), the difference $E_{p}-E_{S}$ can be calculated from Gibbsian properties using the relation

Table 4 Molar isentropic expansion ($E_{S}$) calculated by the use of the acoustic method for 1,2- and 1,3-propanediol, 1,2-, 1,3-, and 1,4-butanediol as well as 2-methyl-2,4-pentanediol at various temperatures ($T$) and pressures $(p)$

$$\begin{aligned} E_p -E_S =K_T C_p E_p^{-1} T^{-1}. \end{aligned}$$

(14)

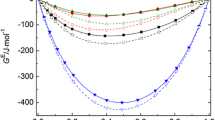
Figure 9 shows the pressure dependence for $E_{p}-E_{S}$ at $T = 298.15\,\hbox {K}$. Generally, $E_{p}-E_{S}$ decreases monotonically with increasing pressure. Note that $E_{p}-E_{S}$ values are approximately ten times greater than $E_{p}$ as a consequence of the magnitude and negative sign of $E_{S}$ (see Fig. 10). Thus, in the first case, the volume increases with increasing temperature at isobaric conditions, whereas volume decreases with the increasing temperature at isentropic conditions in the second case. The changes in volume are however small in isobaric conditions and relatively large in isentropic conditions. For comparison, Fig. 11 shows the $E_{S}$ isotherms for all studied liquids. It can be observed that the curves are not parallel in the investigated ($p,T$) range and the occurrence of a crossing point can be supposed. Unfortunately, the limited ($p,T$) range and the experimental uncertainties cannot give a clear answer and the question is unsolved. It should also be noted that in the case of the $E_{p}(p)$ isotherms indications for such a crossing are not observed in the ($p,T$) range studied.

Fig. 9

Difference $E_{p}-E_{S}$ plotted against pressure $p$ at $T = 298.15\,\hbox {K}$ for: ($\Delta$), 1,2-propanediol; ($\blacktriangle$), 1,3-propanediol; ($\diamondsuit$) 1,2-butanediol; ($\circ$), 1,3-butanediol; ($\bullet$), 1,4-butanediol; and ($\blacksquare$), 2-methyl-2,4-pentanediol. Lines to guide the eye

Fig. 10

Molar expansion (a) isobaric $E_{p}$. and (b) isentropic $E_{S}$ plotted against pressure $p$ at $T = 298.15\,\hbox {K}$ for: ($\Delta$), 1,2-propanediol; ($\blacktriangle$), 1,3-propanediol; ($\diamondsuit$) 1,2-butanediol; ($\Delta$), 1,3-butanediol; ($\bullet$), 1,4-butanediol; and ($\blacksquare$), 2-methyl-2,4-pentanediol. Lines to guide the eye

Fig. 11

Molar isentropic expansion $E_{S}$ plotted against pressure $p$ for (a) 1,2-propanediol, (b) 1,3-propanediol, (c) 1,2-butanediol, (d) 1,3-butanediol, (e) 1,4-butanediol, and (f) 2-methyl-2,4-pentanediol at temperatures: ($\circ$), 293.15 K; ($\square$), 298.15 K; ($\diamondsuit$), 303.15 K; ($\Delta$), 308.15 K; ($\bullet$), 313.15 K; and ($\blacktriangle$), 318.15 K

5 Concluding Remarks

A general inspection of the results shows that a lower compressibility might reasonably be associated with a lower isobaric thermal expansion (Table 2; Fig. 12), and the latter is known to be associated with a low vapor pressure. Interesting is also a strictly linear dependence of $K_{T }$ on $E_{p}$ (Fig. 12) for various pressures along each isotherm for all diols studied (with very close slopes). As seen, the effect of pressure is the highest for 2MPD2,4 and the smallest for 1,2ED.

Fig. 12

Molar isothermal compressibility $K_{T}$ plotted against molar isobaric expansion $E_{p}$ at temperature $T = 298.15\,\hbox {K}$ for: ($\Delta$), 1,2-propanediol; ($\blacktriangle$), 1,3-propanediol; ($\diamondsuit$) 1,2-butanediol; ($\circ$), 1,3-butanediol; ($\bullet$), 1,4-butanediol; ($\blacksquare$), 2-methyl-2,4-pentanediol; and (+), 1,2-ethanediol. In the case of 1,2-ethanediol, data taken from [32]

The analysis of the results for values of $C_{p} - C_{V}, K_{T }-K_{S}$, and $E_{p}-E_{S}$ shows significant differences between $C_{p} - C_{V}$ and $K_{T}-K_{S}$ on the one hand, and $E_{p}-E_{S}$ on the other hand. The values of $C_{p}$ and $C_{V}$, as well as the values of $K_{T}$ and $K_{S}$, have the same sign and differ by less than 15 % and 14 %, respectively, whereas the values of $E_{p}$ and $E_{S}$ have opposite signs and differ very significantly in magnitude. Taking into account that the ratio $C_{p}/C_{V}$ equals $C_{T}/C_{S}$, the similarities in the case of heat capacities and compressibilities are not surprising. Moreover, the constraints for defining heat capacities are in both cases mechanical ($V$ and $p$), while for defining compressibilities are in both cases thermal ($S$ and $T$). On the contrary, the constraints for defining expansions are different, one is thermal ($S$) and the other mechanical ($p$). According to Reis et al. [42], this can be the essential reason for differences in the behavior of isentropic and isobaric expansions. Furthermore, they stated that the analysis of liquid mixtures based on the behavior of $E_{p.}$ cannot be used to deduce the behavior in the case of $E_{S}$. Their findings are accordant with the results of this study, i.e., with observed significant differences in the pressure–temperature behavior of $E_{p}$ and $E_{S}$.

Generally, the most striking is the difference in the properties of 2MPD2,4 and all the rest of the alkanediols studied. In point of fact, this difference is visible for all properties studied. First and foremost, it is due to the difference in the molecular structure: 2MPD2,4 has a branched carbon chain and is a relatively unsymmetrical molecule with terminal non-polar parts (three $\hbox {CH}_{3}$ groups), whereas all the rest of the alkanediols have a linear carbon chain. Also, differences in the behavior between the members of the series of 1,2-diols and $\upalpha ,\upomega$-diols are observed. Among others, for both series, linear relations between $K_{X} (X = S$ or $T$) and the alkyl chain length are observed. This finding is accordant with the reported linear dependencies on a vaporization enthalpy [44–46]. As suggested by Czechowski and Jadżyn [47] on the basis of viscous properties, hydrogen bondings in 1,2-diols tend to create rather cyclic, micelle-like structures, whereas hydrogen bondings in $\upalpha ,\upomega$-diols tend to create rather elongated, layer-like structures. The location of the hydroxyl groups seems to be a determining factor because on the one hand, two adjacent hydroxyl groups at the end of the hydrocarbon chain lead to separation of the polar and nonpolar parts of 1,2-diol molecules and micelle-like structures, and on the other hand, two terminal hydroxyl groups (separated by the $\hbox {CH}_{2}-$ groups) lead to the mentioned-above association in elongated layer-like structures. As reported very recently [48], the location of the hydroxyl groups in positions 1,2- or $\upalpha , \upomega$- leads also to a different miscibility with ionic liquids, i.e., better miscibility of the 1,2-diols compared to $\upalpha , \upomega$-diols with ionic liquids is observed. This finding is not surprising taking into account the strength of the intermolecular hydrogen bonds and is in excellent accordance with the conclusions about the dimensionality and relative rigidity of H-associates obtained from analysis of the plots of $K_{S}(T)_{p}$ (Fig. 4)

Assuming that in liquid alkanediols a local molecular structure, similar to that in liquid water, does exist [49], they can be thought of as a network of hydrogen bonds spread over some specific regions (clusters). The increase in molecular interactions (association) might be explained by an increase in the size of those clusters. This interpretation is concordant with the cluster model of McDuffie and Litovitz [50]. According to this model, an increase in the cluster size, i.e., in the extent of molecular association, should be reflected in an increase in the width of the spectrum of relaxation times, both viscoelastic and dielectric ones. Unfortunately, the results of viscoelastic relaxation studies do not comply fully with the analysis of $K_{S}(T)_{p}$ and $K_{T}(T)_{p}$ because the width of the viscoelastic relaxation time spectrum can be set in the following order: 1,5PD $<$ 2MPD2,4 $<$ 1,3BD [51].

Lastly, it is important to comment on the intramolecular hydrogen bonding ability in diol molecules and its effect on the thermodynamic properties studied. As noted in the introduction, the ability to form intramolecular hydrogen bonding is shown first of all by $\upalpha ,\upomega$-diols. Recently, Haufa and Czarnecki [52] reported the difference in this matter between 1,2- and $\upalpha , \upomega$- isomers of propanediol (1,2PrD and 1,3PrD). Generally, the reports about the role and importance of intramolecular hydrogen bonding in diols in both the liquid and gas phases are numerous. Unfortunately, in spite of many efforts, the question is unsolved. On the one hand, both the experimental and theoretical work suggest the presence of weak intramolecular hydrogen bonding stabilizing the lowest energy conformers [45, 53, 54, 56]. Moreover, the ability to form intramolecular hydrogen bonds increases from the five-membered ring of the 1,2-isomer, via the six-membered ring of the 1,3-isomer, to the seven-membered ring of the 1,4-isomer [55, 56] which is energetically favored. On the other hand, the presence of intramolecular hydrogen bonding in many vicinal diols is questioned [57, 58]. According to [59], the role of intramolecular hydrogen bonding in vicinal diols has a minimal effect on the vapor pressures and vaporization enthalpies. Intramolecular hydrogen bonding in the liquid phase of the lower $\upalpha ,\upomega$-diols does not appear generally to be very important thermodynamically. Generally, intramolecular hydrogen bonding should weaken the ability for intermolecular bonding in the liquid phase, but reported results suggest that diols studied prefer intermolecular hydrogen bonding and the minor importance of intramolecular hydrogen bonding can be stated.

Although, in the present writer’s opinion, the present study extends the knowledge on the pressure–temperature behavior of lower alkanediols, the pressure–temperature ranges are not sufficient to yield more detailed final conclusions. In further investigations, both pressure and temperature increases should be helpful.

6 Summary

By means of the acoustic method, non-accessible directly, the $E_{S}(p,T)$ values for six lower alkanediols are calculated along (five or six) isotherms between (293.15 and 318.15) K at pressures up to 100 MPa. In the same manner also other second-order derivatives of the free energy functions, i.e., ($C_{V}(p,T)$, $K_{S}(p,T), K_{T}(p,T)$, and $E_{p}(p,T))$ are calculated. For all of the above properties, which are not reported previously in the literature, the pressure–temperature effects are emphasized. Generally, apart from two exceptions, the properties studied decrease with increasing pressure. In most cases, for pressures close to atmospheric, the respective values depend significantly on pressure, while with increasing pressure, its effect is gradually decreasing. On the other hand, for all diols studied, an increase of $E_{S}$ with increasing pressure is observed. Moreover, in the case of 2MPD2,4, $C_{V}$ also shows a weak increasing trend with increasing pressure.

For all of the alkanediols studied, a similarity between the pressure–temperature behavior of $C_{p}$ and $C_{V}$ as well as $K_{S}$ and $K_{T}$ was found. At the same time, significant differences in the pressure–temperature behavior of $E_{p}$ and $E_{S}$ were found.

Moreover, clear differences in the behavior of lower linear 1,2-diols and $\upalpha ,\upomega$-diols were found. Also, the effect of a branched carbon chain on the properties studied is evident.