Introduction

“Why do we have to learn this content? This is not relevant to us.” “Dealing with this content would exhaust me.” “I won’t put effort into dealing with this irrelevant content.” These statements from learners facing mathematics are common, particularly from prospective secondary mathematics teachers who show less interest in university mathematics at the beginning of their university studies than mathematics students (Ufer et al., 2017). In these statements, prospective secondary mathematics teachers complain about mathematics courses and do not value the content (reflected in the first statement), relate the content to high costs (reflected in the second statement), and will not put effort into dealing with the content of such courses (reflected in the third statement).

Task values (i.e. students’ perceptions of how important and joyful dealing with a task will be), costs (i.e. the perceived negative consequences when performing the task), and effort (i.e. how much energy or time students would put into dealing with a task) are assumed to be important for students’ educational choices and achievements. In the school context, many empirical studies applying (situated) expectancy-value-cost models (a further development of expectancy-value models from Eccles & Wigfield, 2020) have supported the importance of these constructs for students’ learning processes (Gaspard et al., 2020; Guo et al., 2015; Song & Chung, 2020). First interventions were conducted to increase students’ task values and decrease costs (Hulleman et al., 2017; Parrisius et al., 2020). In the university context, we only know a little about how students’ task values, costs, and effort can be affected by interventions that are, for example, based on specific task designs (e.g. Eichler & Isaev, 2023).

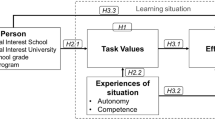
The first aim of the present study is to analyze the effects of a specific task design on task values, costs, and effort. This specific task design is reflected by profession-related tasks that uncover the connection between mathematical learning contents—university mathematics—and the further professional life of students—particularly school mathematics. These profession-related tasks are similar to regular mathematical tasks regarding mathematical demands. The second aim is to analyze whether students with a specific personal trait (i.e. interest in school mathematics) react differently on profession-related tasks. Overall, we contribute to expectancy-value-cost theory by using it in a university context to gain a better understanding of the interplay of task design and personal traits. More specifically, we have analyzed whether offering profession-related tasks to university students affect learners’ task values, costs, and effort, and whether students with a high interest in school mathematics will benefit more from offering these tasks concerning their motivational and behavioral states than those students with a low interest.

Theoretical Background

Conceptualization of Task Values, Costs, and Effort

In (situational) expectancy-value models, expectancies and values are assumed to play a substantial role in educational choices and achievements (Eccles & Wigfield, 2020). Expectancies are the learners’ perceptions of how successful they would be when dealing with learning tasks. Values are the learners’ perceptions of how important and joyful dealing with a task will be. In the current paper, we focus on the role of task values in mathematical learning processes. (Subjective) task values are divided into three different components: intrinsic value (how joyful a task is), attainment value (how personally important it is to engage in a task and be successful when dealing with the task), and utility value (how important the task is for present and future goals; Eccles & Wigfield, 2020; Gaspard et al., 2015). All components of task values are assumed to be important predictors of learning outcomes and correlate empirically strongly with each other (Robinson et al., 2019; Seetee et al., 2021).

We model costs an additional construct besides expectancies and values that can explain learners’ educational choices and achievements (Barron & Hulleman, 2015; Jiang et al., 2018). The construct costs “describes the perceived negative consequences of engaging in a task” (Gaspard et al., 2015, p. 664) and is often divided into different components, such as opportunity costs (“drawbacks associated with lost opportunities due to engaging in a task/domain,” Muenks et al., 2023, p. 4), effort costs (“drawbacks associated with the time and effort that a task/domain requires,” Muenks et al., 2023, p. 4), and emotional costs (“drawbacks due to the stress and anxiety of engaging in a task/domain,” Muenks et al., 2023, p. 4). Costs correlate to the components of task values to a (negligible) small degree (Dietrich et al., 2017; Robinson et al., 2019). Separating costs from values highlights the difference between these two constructs and contributes to clarifying a unique role of expectancies, values, and costs in learning processes.

Another important construct that we focus on is effort. Effort describes how much energy or time learners would put into dealing with a task (Song & Chung, 2020). Rieger et al., (2022, p. 1) define “academic effort” as “an evaluation of the persistence and endurance of one’s behavior in academic situations.” The construct effort can be seen as an outcome variable like achievement and career aspirations and is similar to the behavioral aspect of engagement (Patall et al., 2016). Thus, the construct is closely related to effort management as a learning resource, which is discussed in studies concerning learning strategies (Schiefele et al., 2003). Effort, which we conceptualize as a facet of learners’ behavior in learning processes and thus which we use as an outcome variable (Rieger et al., 2022), should not be mixed with effort costs, which is a facet of costs and addresses students’ perceptions how much energy is required to perform the task (Gaspard et al., 2015). Whereas effort indicates how strong learners will engage in solving the task, effort costs refer to possible exhaustion while solving the task. Empirical studies show only a small relation between effort and task values or costs (Dietrich et al., 2017; Guo et al., 2016).

Effects of Task Design on Task Values, Costs, and Effort

Interventions to Enhance Task Values, Costs, and Effort

Some types of interventions, mainly in the school context, aim to improve learners’ motivation. These interventions are situated at the teacher level by implementing teacher trainings (Gaspard et al., 2021), at the course level by offering specific courses or parts of courses (Wasserman, 2018; Weber et al., 2020), or at the task level by implementing specific tasks or activities (Eichler & Isaev, 2023; Hulleman et al., 2017; Liebendörfer & Schukajlow, 2020). Many of these interventions focus on connecting learning contents to real life (Hulleman et al., 2017; Liebendörfer & Schukajlow, 2020) or to learners’ professional lives, particularly in teacher education programs (Eichler & Isaev, 2023; Wasserman, 2018). Thus, these interventions mainly target improving learners’ utility value (Rosenzweig et al., 2022). Because value components are related to each other, utility value interventions can also affect other value components, for example, intrinsic value (Parrisius et al., 2020) or costs (Hulleman et al., 2017); however, it is not obviously clear in which way and how interventions, which focus on enhancing utility value, also affect other value components or costs.

Teacher Education Programs in Mathematics: the Role of School and University Mathematics

Previous studies have shown that teacher education students for upper secondary schools with a major in mathematics differed from students in a mathematics program regarding their personal characteristics; in particular, these students reported less interest in university mathematics than mathematics students which is one reason why we focus on this specific group of students. To explain teacher education students’ low interest in university mathematics, many researchers have stated that school and university mathematics differ substantially from each other (Engelbrecht, 2010; Gueudet, 2008). Because these students will primarily deal in their further professional life with school mathematics and often do not recognize the connection between school and university mathematics, they do not see the value in dealing with the contents presented in their university mathematics courses. In the following, we briefly describe the contents of such courses and their relation to university and school mathematics.

School mathematics is taught under the label “general education aims” in Germany. Hence, students often solve mathematical tasks that are embedded in real-life contexts (Rach & Heinze, 2017). In contrast, university mathematics is taught as a formal, deductive discipline based on formal-defined, abstract concepts and statements that are proved in a deductive way (Gueudet, 2008). As many researchers have argued that these two forms of mathematics—school mathematics and university mathematics—differ substantially from each other (Di Martino et al., 2023; Engelbrecht, 2010; Liebendörfer & Hochmuth, 2013; Ufer et al., 2017), there is no smooth passage from school to university; rather, there is a (first) discontinuity, which is why many students struggle a lot in the first year of study because of this unknown form of mathematics in their mathematics courses (Di Martino & Gregorio, 2019; Engelbrecht, 2010). Thus, students are stressed and do not connect the two forms of mathematics with each other, which leads teacher education students to place less value on university mathematics and, thus, the content of many university courses (Wasserman, 2018; Weber et al., 2020). After the academic study program, a second discontinuity occurs when students go back to school to work as teachers and do not or cannot use their knowledge about university mathematics to develop substantial learning opportunities.

Interventions in Teacher Education Programs in Mathematics: Theoretical Mechanism and Empirical Evidence

Three important types of interventions for increasing students’ motivation in teacher education programs are teacher trainings (for lecturers or tutors), offering specific courses for students, and changing the task design within the existing courses. These interventions differ in terms of the required resources. Changing the task design in regular courses is less time- and cost-consuming than implementing additional teacher training or offering specific courses for students. In the past, studies have analyzed the effects of so-called profession-related tasks (named “teacher-oriented tasks” in the mentioned study of Eichler & Isaev, 2023). Such profession-related tasks are oriented on specific situations that the teachers are confronted with in their professional practice, for example, evaluating students’ responses or mathematical explanations in textbooks and uncovering the connection between school and university mathematics. In the study conducted by Eichler and Isaev (2023), 72 teacher education students for secondary schools in two first-semester courses participated. The researchers exchanged 25% of the regular mathematical tasks with profession-related tasks in the intervention group. Compared with the control group, where profession-related tasks were not included in the tutorials, beliefs about the relevance of university mathematics for the professional lives of students in the intervention group were maintained throughout the semester. Thus, Eichler and Isaev (2023) have provided the first indications that profession-related tasks and their implementation in university courses can affect students’ beliefs about relevance. In their study, they have analyzed long-term effects of their intervention on students’ beliefs (post-test after one semester). However, to the best of our knowledge, there are no studies that have analyzed the effects of profession-related tasks on task values, costs, and effort, thus focusing on short-term effects (effects in one learning situation). In our study, we contribute to the latter issue.

In which way personal traits moderate the effects of such interventions has been rarely explored. Rosenzweig and Wigfield (2016) suggested examining interventions regarding the effects for students with different prerequisites. In the contexts of school and undergraduate courses, Hulleman and Harackiewicz (2021) reported that utility value interventions worked well, specifically for students with low performance or low self-concept. In the current study, we are interested in clarifying whether profession-related tasks work different for students with different learning prerequisites. Because these tasks uncover the connection between the learning content and school mathematics, it is likely that students with a higher interest in school mathematics will ascribe higher task values and effort and lower costs to profession-related tasks than their fellow students. We conceptualize individual interest as a personal trait which describes a specific relation between a person—that is, a student in the present study—and an object of interest—that is, school mathematics in the current study (Krapp, 2002). Interest comprises an emotion-related and a value-related component and is based on engaging and re-engaging with the object over time (Hidi & Renninger, 2006). Individual interest as a relatively enduring student characteristic has been demonstrated to have a high level of importance for learning outcomes (Köller et al., 2001).

Research Questions and Expectations

In the present study, we focused on the components of task values, costs, and effort in the context of a teacher education study program with a major in mathematics. We analyzed the effects of profession-related tasks on components of task values, costs, and effort and investigated whether a personal trait (i.e. interest in school mathematics) moderates the effect of profession-related tasks. A visual overview of the research questions can be found in Fig. 1.

Fig. 1
figure 1

Graphical illustration of the research questions

Full size image

Effects of Profession-Related Tasks on Components of Task Values, Costs, and Effort

  1. 1.

    Do profession-related tasks stimulate students’ …

    • a) ... intrinsic value, attainment value, utility value for professional life, and utility value for a study program?

    • b) ... costs?

    • c) ... effort?

    Because profession-related tasks uncover the connection between the learning content and students’ professional lives, we expect that students’ utility value for professional life will be stimulated by these tasks. Whether profession-related tasks also affect intrinsic value, attainment value, and utility value for the study program is an exploratory question. We expect that students will report lower costs concerning profession-related tasks. In addition, we assume that students will report that they will invest more effort in dealing with profession-related tasks than with regular tasks.

Interest in School Mathematics as a Moderator of the Influence of Profession-Related Tasks on the Components of Task Values, Costs, and Effort

  1. 2.

    Are students with a high interest in school mathematics stimulated differently by profession-related tasks regarding their …

    • a) ... intrinsic value, attainment value, utility value for professional life, and utility value for study program?

    • b) ... costs?

    • c) ... effort?

    Because profession-related tasks explicitly connect school mathematics with university mathematics, we expect that students with a higher interest in school mathematics will benefit more from offering these tasks concerning their motivational and behavioral states than students with a lower interest in school mathematics.

Methods

Sample

The sample consisted of 133 students (51% female, 47% male, 2% no information) who were enrolled in a mathematics teacher education study program in one of two universities. Here, 38 students were enrolled in a teacher education program for lower track secondary schools at one university, 92 students were in a program for upper track secondary schools at one university or at the second university, and three students did not mention their study program. Most of the students (92%) were in their first year of study. The students voluntarily participated and gave their informed consent.

Design

The study took place at one university as a paper–pencil survey and in a second university as an online survey, here because of COVID-19. The students received incentives for their participation in the form of sweets (university one) or in the form of 10 € by bank transfer (the second university).

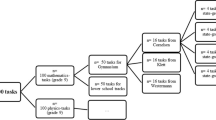
After filling out a questionnaire concerning demographic variables and interest in school mathematics, seven mathematical tasks were presented to the participants (see Fig. 2). They received one task from each task pair randomly. After reading this task, the students rated it according to their task values, costs, and effort. In sum, the students were not asked to solve the tasks but to rate seven mathematical tasks that were each either profession-related or regular.

Fig. 2
figure 2

Design of the study. TV: task values; CO: costs; EF: effort

Full size image

Instruments

Profession-Related Tasks

Because mathematical tasks are an important learning material in mathematical learning processes (e.g. Jordan et al., 2008; Stein & Lane, 1996), we focused on the design of mathematical tasks. Profession-related tasks uncover the connection between the learning content of mathematical university courses—embedded in university mathematics—and the form of mathematics with which teacher education students primarily deal in their professional lives—school mathematics. The tasks only marginally contain the specific situations of teachers’ professional practice but place a greater emphasis on uncovering the connection between university and school mathematics. Precisely, we first uncovered this connection by using the words “school,” “mathematics lessons,” and so forth in the formulation of these profession-related tasks. Second, we explained in which way the content of university mathematics is connected to the content of school mathematics—an example of such an explanation is that it is necessary to show that a given operation of two fractions is incorrect because learners in school often use this incorrect operation. Thus, these profession-related tasks uncover the connection to the latter professional field of teacher education students. Each of these profession-related tasks received a counterpart—a (regular) task dealing with the same mathematical content and requiring the same cognitive demands as the profession-related task but not uncovering the connection between the learning content and the professional field (see Fig. 3).

Fig. 3
figure 3

A sample pair of tasks which was used in this study

Full size image

We developed these tasks in different stages. We chose number theory as the mathematical field to which our tasks belonged. After developing and screening the developed pairs of tasks (regular and profession-related ones) on our own, we involved experts from different fields to judge our tasks. Mathematicians rated the regular tasks as whether they would use them in a lesson for teacher education students. Those experts from mathematics education judged the profession-related tasks; in particular, they checked if the connection between school and university mathematics holds. In addition, 22 students judged if all tasks were understandable (see Rach, 2022). After this development process, we selected seven pairs of tasks, with each pair containing a profession-related task and a regular task. The topics of these tasks were the addition of rational numbers, a binomial theorem, the sum of two even numbers, and so forth. In sum, we developed 14 mathematical tasks that existed in pairs, and the students randomly received one task to rate from every pair.

Questionnaires

To measure the trait variable, we adapted the questionnaire from Ufer et al., (2017). For measuring the motivational and behavioral state variables, we used the scales of Gaspard et al., (2015) and Dietrich et al., (2017) (see the overview in Table 1, see also Seetee et al., 2021).

Table 1 Measurement instruments for components of task values, costs, effort, and personal trait, including sample items, sources, and internal consistency (α) or interrelations (r)
Full size table

Because of time restriction and to avoid fatigue effects, we applied only few items for every construct, e.g., we included only one item for effort and two items to measure two facets of costs, emotional and effort costs. Concerning costs, the students had to estimate the costs which occur when they would solve the tasks. Measuring task values, we concentrated on four components: intrinsic value refers to the enjoyment when dealing with the task, whereas attainment value expresses a personal importance of solving successfully the task. Transferring the idea of Gaspard et al., (2015) to our context, we differentiate utility value into two different facets: utility value for study program, which focus on the usefulness for near goals, and utility value for professional life, which focus on the usefulness for future goals. All statements were rated on a 4-point Likert scale ranging from disagree (1) to agree (4).

Analysis Strategy

We used a cross-classified multilevel design because the ascribed components of task values, costs, and effort depended on three factors: (1) the person (1 to 133), (2) the pair of tasks (1 to 7), and (3) the task version (profession-related or regular task). Because every student received at least one regular and one profession-related task, the design was a within-subject design. Linear mixed models with random and fixed effects provide opportunities to analyze the data while also having the advantage of handling cases with missing values (Hilbert et al., 2019). Modeling with a random effect takes into account that motivational and behavioral state variables can vary across persons and tasks. All analyzed models contained random effects for the person and pair of tasks. Because the variability of components of task values, costs, and effort between persons and tasks was not the focus of our research question, we concentrated on the fixed effects: “Fixed factors are those where all levels of interest are actually included in the experiment” (Magezi, 2015, p. 2). The analyzed model for research question 1 contained a fixed effect for the variable task version (profession-related vs. regular task), and for research question 2, we added in the model interest in school mathematics and the interaction of task version and interest in school mathematics as fixed effects.

The marginal R2 considers only the variance of the fixed effects, while the conditional R2 considers both fixed and random effects (the possibilities to calculate these two types of R2 are shown in Nakagawa & Schielzeth, 2013). Because our research questions addressed fixed effects, we have reported the marginal R2. We standardized all variables beforehand, computed all analyses in R (version 4.3.0), using the package lme4 for the linear mixed models (Bates et al., 2015) and the package effect size for calculating η2 as effect size (Ben-Shachar et al., 2023). Following Cohen (1988), we assume η2 = 0.16 as a large effect, η2 = 0.06 as a medium effect, and η2 = 0.01 as a small effect. Because some dependent variables, for example, effort, were ordinal, we also conducted the analyses concerning these variables with the package ordinal (Haubo, 2019) and obtained results similar to those obtained from analyses with the package lme4.

Results

Preliminary Results

Before answering the research questions, we provide insights into the descriptive statistics of the variables (see Table 2). We have aggregated all variables per person, pair of tasks, and task version.

Table 2 Descriptive statistics of the personal variables
Full size table

The correlations between the components of task values and correlations between the components of task values and costs ranged from medium to large. The correlations between the components of task values or costs and effort were rather small. The correlations between the components of task values, costs, or effort and interest in school mathematics were small to negligible.

Descriptive statistics for the personal variable grouping concerning gender, study program, and year of study can be found in the supplementary material. Remarkable is that students in programs for lower secondary school tracks show unfavorable characteristics than students in programs for upper secondary school tracks. The results do not indicate differences in the personal variables concerning gender and year of study.

Effects of Profession-Related Tasks on Components of Task Values, Costs, and Effort

Research question 1 explored the influence of profession-related tasks on the components of task values, costs, and effort. Table 3 shows the descriptive statistics of the components of task values, costs, and effort, here as aggregated over persons and pairs of tasks, depending on the task version.

Table 3 Descriptive statistics of components of task values, costs, and effort, here depending on the task version
Full size table

We assumed that the students ascribed a higher utility value for professional life, lower costs, and higher effort to profession-related tasks than to regular tasks. The results of the linear mixed models, as shown in Tables 4, 5, and 6 in the supplementary material, partly support our hypotheses: profession-related tasks lead to a higher utility value for professional life (model 4.1, Table 5) with a small to medium effect size and to less costs (model 5.1, Table 6) with a small effect size, whereas we did not find a significant effect on effort (model 6.1, Table 6). In addition, profession-related tasks led to more intrinsic value (model 1.1, Table 4) and possibly higher attainment value (model 2.1, Table 4). All results are also visualized in Fig. 4.

Fig. 4
figure 4

Graphical illustration of the results

Full size image

Interest in School Mathematics as a Moderator of the Effects of Profession-Related Tasks

Research question 2 deals with the issue of whether learners with a high level of interest in school mathematics would benefit more from offering profession-related tasks concerning their motivational and behavioral states. We expected that in particular learners with a high level of interest in school mathematics would value profession-related tasks concerning professional life in contrast to regular tasks higher than other learners and put more effort into dealing with these tasks; in addition, we hypothesized that costs concerning profession-related tasks would be lower than for learners with a low interest in school mathematics. To analyze the impact of interest in school mathematics on the effects of task design on the outcomes, we integrate the interaction effect “Profession-related task × Interest school” in the model.

Our expectations were confirmed for effort (model 6.2, Table 6) with a small effect size but not for utility value for professional life (model 4.2, Table 5) and costs (model 5.2, Table 6): the difference between effort for profession-related tasks and effort for regular tasks is bigger for students who report a higher interest in school mathematics than for other students. The exploratory analyses indicate that offering profession-related tasks stimulates learners with a high level of interest in school mathematics more regarding attainment value (model 2.2, Table 4).

Discussion

Many teacher education students report little motivation to engage with university mathematics. To overcome this lack of motivation, the presented tasks uncovering the connection between the current learning content—that is, university mathematics in the current study—and the form of mathematics with which students will work in their future professional lives—that is, school mathematics in the present study—can be a solution. Such profession-related tasks have been used in practice (Bauer & Kuennen, 2016; Hoffmann, 2021), and initial results have shown that these tasks have (long-term) effects on beliefs (Eichler & Isaev, 2023). However, it is yet not clear which effects these tasks have on students’ task values, costs, and effort. Hence, we analyzed the effects that profession-related tasks have on components of students’ task values, costs, and effort in contrast to regular tasks.

Empirical Findings

Our results have shown that offering profession-related tasks affected students’ utility value for professional life, whereas profession-related tasks had only a minor impact on costs and did not affect students’ effort. The significant effect of task design on utility value for professional life is noteworthy because profession-related tasks are very similar to their regular counterparts regarding the mathematical demands. The advantages of profession-related tasks, in contrast to their regular counterparts, may not be obvious to experts, who have a deep knowledge of the structure of mathematics and are familiar with the school curriculum. Because of their deep knowledge, experts might uncover the connection between the university learning content and the professional field on their own and overlook the importance of profession-related tasks for students. However, uncovering the connection between university learning content and one’s professional field is not easy for novices, such as prospective secondary mathematics teachers, especially at the beginning of their studies.

To explain the unexpected result that there is no indication that profession-related tasks affect effort, we put two explanations forward: (a) task values and effort do not relate to each other and (b) there are only small differences in components of task values between the two task versions in the present study. (a) We assumed that an important reason why students put energy and time into dealing with a task is the value that they ascribe to the task. Thus, if task values increase, then effort will also increase. However, our results cannot support this assumption regarding a positive substantial relation between values and effort—correlative analyses (see Table 2) also indicate only a medium correlation between attainment value and effort and negligible correlations between the other components of task values and effort; this result is in line with the findings of Dietrich et al., (2017). It is possible that other motivational state variables, such as expectancies, play a more substantial role than values when students decide how much effort they will invest when dealing with a task. (b) The profession-related tasks addressed only one component of task values—utility value for professional life—and affected overall task value as a collection of all components of task values only marginally so that the effect of task values on effort may not be visible in the present study. Exploratory results from the present study supported this explanation: intrinsic value, attainment value, and utility value for the study program differed only a little or did not differ at all between profession-related tasks and regular tasks. This unexpected result and the plausible explanations bring forward new ideas for further research. In particular, the role of expectancies or the interaction between expectancies and values may play a prominent role to enlighten students’ learning aspirations also in undergraduate courses (see Song & Chung, 2020, for a study with ninth-graders). The different effects of value interventions on different value facets can contribute to detect interrelations between the value facets which have been analyzed in particular in correlative studies so far.

Our study produced the first results that interest in school mathematics can moderate the effects of profession-related tasks on task values, costs, and effort. However, this was not the case for all components of value: there were moderating effects for attainment value but not for utility or intrinsic value. Consequently, moderating effects depend strongly on the object of interest (i.e. interest in school mathematics) and on the outcomes in students’ learning processes (i.e. components of task values). One explanation for this result is that the intervention targeted the utility component of values. The results may be different if the focus was more strongly placed on increasing all value components. Moreover, we found that interest in school mathematics moderated the effect of profession-related tasks on effort: our results have indicated that attainment value and effort of students with a higher interest in school mathematics will increase more when offering profession-related tasks than for students with a lower interest in school mathematics. Drawing on the results, we do not yet know if the absolute value of interest in school mathematics has an impact on the influence of profession-related tasks or if the relative value of interest in school mathematics compared to interest in university mathematics is more powerful to predict which student group does value profession-related tasks to a higher degree. Our empirical findings add to a wide body of research on task values (e.g. Parrisius et al., 2020), costs (e.g. Robinson et al., 2019), and effort (e.g. Rieger et al., 2022) in mathematics or STEM education.

Theoretical and Practical Implications

We have contributed to a validation of the assumptions of expectancy-value-cost models. Prior research has indicated that expectancy-value-cost models can explain students’ choices on the macro-level, for example, which courses students choose according to their value beliefs (e.g. Aeschlimann et al., 2016; Watt et al., 2012). In the present study, we followed a call for analyzing situational factors (e.g. Schukajlow et al., 2023) and analyzed the expectancy-value-cost models on the micro level, in particular when dealing with mathematical tasks. One significant theoretical contribution of the present study is validating the link between current and future goals and values, as proposed in expectancy-value-cost theory. Highlighting the connection of the tasks to the future profession—like the teaching of mathematics at school in our study—is in line with the students’ current and future goals, thus affecting utility value and costs. However, contrary to the expectations of expectancy-value-cost models, we did not find a link between placing emphasis on the current and future goals in the tasks and attainment and intrinsic value. As we discussed above, one reason for this result might be that we primarily targeted utility value; in addition, because of the moderate relation of utility value to other value components, the effects were not transmitted to attainment and intrinsic value. In terms of the theoretical implications, our study has suggested a need for deep reflection on the role of different goals in expectancy-value-cost models. One important future research question that can contribute to the development of expectancy-value-costs models is as follows: What types of current and future goals are related to what value components? For example, attainment value relates strongly to learners’ own identity (Eccles & Wigfield, 2020). Having a high attainment value means that current and future goals fit with learners’ identity. Thus, in this context, if a short instruction in profession-related tasks targets students’ identity as mathematics teachers, this instruction might help analyze the relationships between different types of goals and value components. Related to this, utility value for professional life does not seem to have a substantial influence on students’ choices in learning processes, in particular on the choice of how much effort students use when dealing with tasks. Reviewing the literature and our results, we cannot identify the reasons why students would use more or less effort in learning situations. Further research could put more emphasis on analyzing in which way the interplay of personal characteristics in a situation, for example, a combination of expectancies and values, and situational characteristics, for example, task design, predicts students’ effort.

Interaction effects are an important part of the expectancy-value-cost models, which have been rarely empirically or theoretically addressed compared with direct effects in the past. In the current study, we assumed that students’ interest, which was found to be important for various learning outcomes (Renninger & Hidi, 2016), might moderate the effects of offering profession-related task on values, costs, and effort. Our findings have supported theoretical considerations about the importance of interest for one of the value components: attainment value. However, because this result was found in an exploratory analysis, future studies are essential to confirm this effect. The question which students will benefit more from offering profession-related tasks concerning their motivational and behavioral states is—apart from our findings concerning interest in school mathematics—still open. Based on the results of Hulleman and Harackiwicz (2021), who reported that utility value interventions work well for students with low self-concept, one can assume that offering profession-related tasks works especially well for students with low self-concept. Because students with low self-concept worry about failures when dealing with mathematical tasks, they may devalue mathematical tasks to protect their identity as prospective secondary mathematics teachers (Gildehaus & Liebendörfer, 2021). Offering profession-related tasks, these students may recognize that these special mathematical tasks are important for their professional development to become a mathematics teacher, and this perception can prevent students from devaluating profession-related tasks. Examining the role of students’ mathematical self-concepts when dealing with profession-related tasks is a worthwhile next step in research on profession-related tasks. Another next step could be to analyze the impact of such tasks on students of different study programs (for upper or lower secondary schools) or year of study because students of different study programs probably differ in their motivation to enroll in the study program and students of different years of study have different experiences with university mathematics. Study motivation and experiences with university mathematics may influence the impact of profession-related tasks on students’ motivational and behavioral states.

In our study, we analyzed how offering profession-related tasks can influence the components of task values, costs, and effort. A further, next step could be to take into account students’ perceptions after dealing with the tasks or the quality of students’ handling of profession-related tasks. The studies of Liebendörfer and Schukajlow (2020) and Hulleman et al., (2017) showed that the quality of handling profession-related materials and conducting profession-related activities is relevant for supporting students’ interest, too.

An important practical implication of our findings is the tasks used. Keeping in mind that profession-related tasks differ from regular tasks only on the surface by uncovering the connection between the university learning content and the professional field, it is noteworthy that students ascribed more utility value for their future professional life to profession-related tasks than to regular tasks. Although the effects of profession-related tasks on task values are only small to medium, it is nevertheless practically relevant because of the following reason: uncovering the connection between school and university mathematics is possible for many mathematical tasks in the first study year and is relatively easy to implement in practice. Thus, to enhance students’ utility value, we have presented a time- and expense-reduced approach which can be described as a wise intervention—an intervention which is based on a social-psychological theory and require little expense (see Gaspard et al., 2021; Hulleman & Harackiewicz, 2021).

As in our approach, the mathematical demands of the tasks did not change, our approach may be better integrated in mathematical courses for teacher education students and may be more popular for instructors than other approaches, such as extra-curricular tasks (Bauer & Kuennen, 2016). To improve all components of task values in practice, it is nevertheless necessary to implement interventions that consist of a set of practices supporting the different components of task values (Rosenzweig et al., 2022). For utility value for professional life, the presented profession-related tasks can serve as one of these practices.

Limitations

When interpreting the results, some limitations must be considered. First, the data consisted of students’ ratings. Following the designs applied in prior studies (e.g. Krawitz & Schukajlow, 2018), the students reported their task values, costs, and effort before solving the problem. It is questionable, however, if the students can give valid statements about their task values, costs, and effort without solving the task. The rationale behind this approach is the assumption that students’ task values, costs, and effort before solving the problem affected the students’ problem-solving process and, consequently, also the students’ learning process (Efklides, 2006; Schukajlow, 2017). Task values, costs, and effort might vary during the problem-solving process and can be considerably different after finishing the solution process. Applying experience-sampling methodology and assessing students’ perceptions at random points during the problem-solving process can help capture the variability of motivational states in future studies. Second, due to COVID-19 we used different methods to collect data—in university one a paper–pencil-questionnaire, in university two an online-questionnaire. Third, we applied short scales to measure the components of task values, costs, and effort to minimize the testing time. Because the students were asked to rate seven tasks, we reduced the statements that referred to each task to a minimum to avoid fatigue effects and to consider ecological validity (see Tanaka & Murayama, 2014). Fourth, in the current study, we used mathematical tasks embedded in number theory. Because number theory is rather close to school mathematics compared with other mathematical fields, for example, group theory, the effects of profession-related tasks may be underestimated. It seems worthwhile to analyze the effects of profession-related tasks in other mathematical fields. Fifth, to analyze the effects of profession-related tasks, we concentrated on task values, costs, and effort which were self-reported by students. In addition to self-reports, measuring motivational states by using students’ arousal or facial expressions can enrich the picture and contribute to future research. In further studies, effects on emotional states, time-on-task, and learning achievement should also be considered.

Conclusion

The current study analyzed the role of profession-related tasks for stimulating students’ values, costs, and effort. Uncovering the connection between university mathematical learning content and school mathematics was found to improve students’ utility value for professional life. Importantly, students with a high level of interest in school mathematics reported putting more effort in solving profession-related tasks in contrast to regular tasks than students with a low level of interest. This study can contribute to different fields: in particular, our findings have theoretical implications for expectancy-value-cost models (e.g. about the relation between current/future goals and value components) and practical implications (e.g. for the design of tasks in university courses).