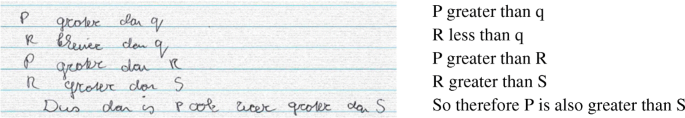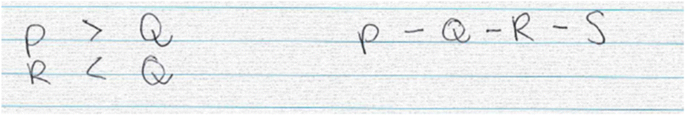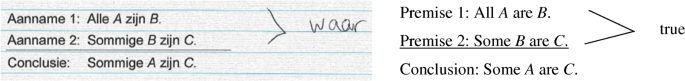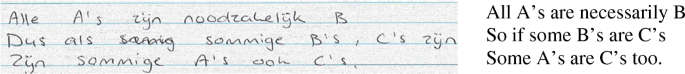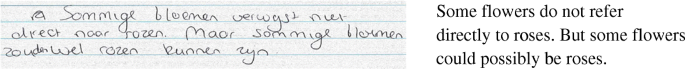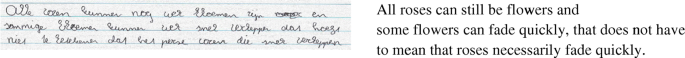Logical Reasoning in Formal and Everyday Reasoning Tasks

Abstract

Logical reasoning is of great societal importance and, as stressed by the twenty-first century skills framework, also seen as a key aspect for the development of critical thinking. This study aims at exploring secondary school students’ logical reasoning strategies in formal reasoning and everyday reasoning tasks. With task-based interviews among 4 16- and 17-year-old pre-university students, we explored their reasoning strategies and the reasoning difficulties they encounter. In this article, we present results from linear ordering tasks, tasks with invalid syllogisms and a task with implicit reasoning in a newspaper article. The linear ordering tasks and the tasks with invalid syllogisms are presented formally (with symbols) and non-formally in ordinary language (without symbols). In tasks that were familiar to our students, they used rule-based reasoning strategies and provided correct answers although their initial interpretation differed. In tasks that were unfamiliar to our students, they almost always used informal interpretations and their answers were influenced by their own knowledge. When working on the newspaper article task, the students did not use strong formal schemes, which could have provided a clear overview. At the end of the article, we present a scheme showing which reasoning strategies are used by students in different types of tasks. This scheme might increase teachers’ awareness of the variety in reasoning strategies and can guide classroom discourse during courses on logical reasoning. We suggest that using suitable formalisations and visualisations might structure and improve students’ reasoning as well.

Introduction

P21's Framework for twenty-first Century Learning describes critical thinking as an important skill to be successful in professional and everyday life situations in an increasingly complex world (P21, 2015). Of great value for critical thinking is ‘reason effectively’, which is explained in the twenty-first century skills framework as “[using] various types of reasoning (inductive, deductive, etc.) as appropriate to the situation” (P21, 2015, p. 4). Liu, Ludu, and Holton (2015) support this view and consider valid logical reasoning as a key element for sound critical thinking. Other authors suggest that improving logical reasoning skills as part of higher order thinking skills is an important objective of education (Zohar & Dori, 2003).

To support the development of critical thinking, it seems essential that teachers devote attention to students’ strategies to reason logically. So far, not much is known about the reasoning processes of secondary school students in different logical reasoning tasks. Therefore, this article addresses this issue by exploring how 16- and 17-year-old students reason within formal reasoning and everyday reasoning tasks. The information provided by this study seems important to increase teachers’ awareness of reasoning strategies used by students and reasoning difficulties they encounter, as well as to be able to develop instruction materials to support and improve students’ logical reasoning skills.

Theoretical Background

Halpern (2014) describes critical thinking as “purposeful, reasoned, and goal-directed” (p. 8) and contends that many definitions of critical thinking in literature use the term “reasoning/logic” (p. 8), so being able to apply the rules of logic can be seen as a requirement for critical thinking. Many studies report difficulties with logical reasoning for different age groups (e.g. Daniel & Klaczynski, 2006; Galotti, 1989; O’Brien, Shapiro, & Reali, 1971; Stanovich, West, & Toplak, 2016). Because of those difficulties, it is by no means certain that secondary school students are able to reason logically and thus develop their critical thinking abilities autonomously.

Formal Reasoning.

The area of logic can be divided into formal logic and informal logic. Aristotle already differentiated between formal logic with syllogisms described in Analytica Priora and ‘dialectics’ in his combined work Topica exploring arguments and opinions (Aristotle, 2015 version). Almost 2000 years later, Gottlob Frege (1848 – 1925) studied and developed formal systems to analyse thoughts, reasoning, and inferences. Also, he developed the so-called ‘predicate logic’, inspired by Leibniz (1646 – 1716), which is more advanced than the ‘propositional logic’ (Look, 2013; Zalta, 2016). Nowadays, those types of systems are often called ‘symbolic logic’ with strict validity as a key aspect (De Pater & Vergauwen, 2005) in which formal deductive reasoning is applied.

In general, formal systems contain a set of rules and symbols and the reasoning within these systems will provide valid results as long as one follows the defined rules (Schoenfeld, 1991). The corresponding reasoning is often called formal reasoning and “characterized by rules of logic and mathematics, with fixed and unchanging premises” (Teig & Scherer, 2016, p. 1). The same use of formal procedures can be found in definitions of logical reasoning as well. For instance “Logical reasoning involves determining what would follow from stated premises if they were true” (Franks et al., 2013, p. 146), and “When we reason logically, we are following a set of rules that specify how we ‘ought to’ derive conclusions” (Halpern, 2014, p. 176).

However, there is no consensus on the term reasoning and it is not exclusively used for formal deductive reasoning or mathematical situations only. Although reasoning in mathematics differs immensely from everyday reasoning (Yackel & Hanna, 2003), even reasoning in mathematical proof is not only a formal procedure, but involves discussion, discovery, and exploration (Lakatos, 1976) and shows us a need for more informal methods when approaching formal reasoning problems.

Informal Reasoning.

In the previous section, we indicated that, dependent on the situation, reasoning demands more than applying rules of logic. For instance, the importance of transforming information as stated by Galotti (1989): “[Reasoning is a] mental activity that consists of transforming given information … in order to reach conclusions” (p. 333) and the role of samenesses as stated by Grossen (1991): “Analogical and logical reasoning are strategies for finding and using samenesses. … logical reasoning applies these derived samenesses in order to understand and control our experience” (p. 343).

The notion of broadening formal methods with more informal methods is not new. Toulmin already discusses the limitations of formal logic for all sorts of arguments in his famous book The Uses of Argument (1958). He distinguishes different logical types to emphasise how logic is used in different fields, such as law, science, and daily-life situations. In his layout of an argument, he schematises the grounds for a claim balanced with reasons that rebut a claim. He also uses qualifiers to indicate the probability of a claim.

Philosophers and educators were also dissatisfied with the dominance of formal logic, that they considered as inappropriate for evaluating real-life arguments, and started in the 1970s an informal logic movement for another approach of analysing arguments stated in ordinary, daily-life language (Van Eemeren et al., 2014). One of the major textbooks still in print today is Logical Self-Defense (Johnson & Blair, 2006), which covers an introduction in “logical thinking, reasoning, or critical thinking … that focuses on the interpretation and assessment of ‘real life’ arguments” (p. xix). In literature, this is often indicated as informal or everyday reasoning, but this term has various meanings, from reasoning originating from formal systems to all reasoning related to everyday life events (Blair & Johnson, 2000; Voss, Perkins, & Segal, 1991). Different from formal reasoning, the reasoning and the conclusions depend on the context and can be questioned on their validity as already shown by Toulmin. Therefore, the topics are open for debate and invite to ponder on justifications and objections. The argument, as the result of the reasoning, often concerns open-ended, ill-structured real world problems without one conclusive, correct response (Cerbin, 1988; Kuhn, 1991). For this, Johnson and Blair (2006) use “acceptable premises that are relevant to the conclusion and supply sufficient evidence to justify accepting it” (p. xiii). The use of acceptable premises can arise from practical reasons to reach a certain goal and often includes presumptions or presuppositions. Walton (1996) uses the term ‘presumptive reasoning’ for this kind of arguments, which he sees as dialogues.

Although presumptive reasoning is not always conclusive or accepted by everyone, it is, in particular if full knowledge is unavailable or unobtainable, according to Walton, the best supplement to describe and discuss everyday life reasoning, for which he uses argumentation schemes. Even though Blair (1999) acknowledges the importance of presumptive reasoning for describing human reasoning and the strength of conclusions derived from the premises, he questions if all arguments are dialogues and discusses the completeness of the schemes.

To sum up, we define informal reasoning as reasoning in ordinary language to construct an argument which requires a critical review of the given premises and transforming of information, as well as finding additional or similar information provided by the problem solver or by external sources.

Towards a Definition for Logical Reasoning in This Study.

Now, we have seen that for well-founded reasoning, formal and informal methods are useful, we need to formulate a definition of logical reasoning for this study, which captures both aspects. A definition of logical reasoning should contain both the context and the way of reasoning, which can consist of formal and informal strategies. In other words, a definition of logical reasoning should not be synonymous with formal deductive reasoning. Important key words taken from the previous sections are ‘derive conclusions’ from Halpern and ‘transforming information’ from Galotti. That can be done with rules derived from formal systems, but that is not a necessity, so informal reasoning will also be part of our definition and thus seen as a valid reasoning process. Therefore, we conclude that logical reasoning involves several steps and define logical reasoning for this study as selecting and interpreting information from a given context, making connections and verifying and drawing conclusions based on provided and interpreted information and the associated rules and processes.

Formal and Everyday Reasoning Tasks.

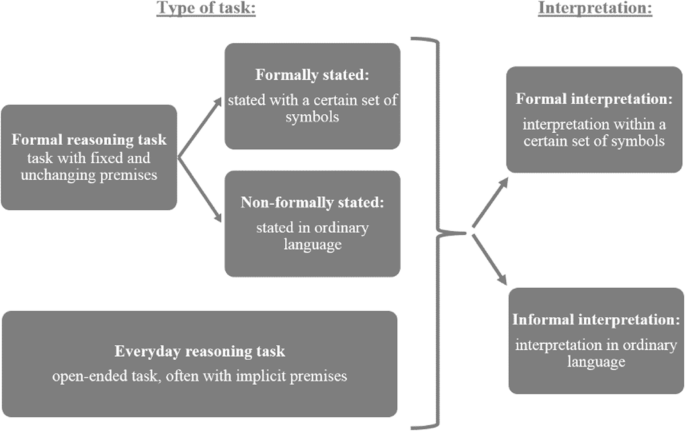
Until now, we focused on the ways of reasoning and stressed the importance of the context. If we want to study how students reason in a variety of contexts, we have to differentiate between closed tasks with one correct answer and more open tasks. For this, we will use Galotti’s (1989, p. 335) division: ‘formal reasoning tasks’ and ‘everyday reasoning tasks’. Formal reasoning tasks are self-contained, in which all premises are provided. For those tasks, established procedures are often available which lead to one conclusive answer. In everyday reasoning tasks, premises might be implicit or not provided at all. For those tasks, established procedures are often not available and it depends on the situation when an answer is good enough. In daily-life situations, everyday reasoning problems “are [often] not self-contained” and “the content of the problem typically has potential personal relevance” (Galotti, 1989, p. 335). For both types of tasks, but for everyday reasoning tasks in particular, selecting and encoding relevant information is of great importance. We will call that the interpretation of the task.

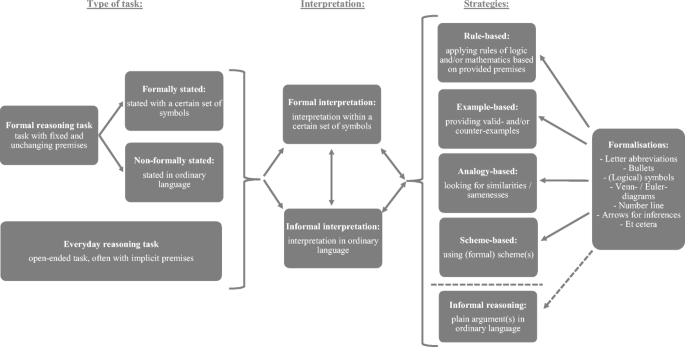
Formal reasoning tasks may be provided in different forms: with symbols and completely in ordinary language without symbols. As shown in Fig. 1, we differentiate formal reasoning tasks in formally stated and in non-formally stated tasks. Formally stated tasks are stated with a certain set of symbols, for example a task with the premises ‘(1) All A are B. (2) All B are C.’ Non-formally stated tasks are tasks stated in ordinary language, for example a task with the premises ‘(1) All mandarins are oranges. (2) All oranges are fruits.’ For each task, students’ reasoning starts with an interpretation of the given information. That might be either a formal interpretation, in other words, an interpretation within a certain set of symbols (e.g. A ⊆ B ⊆ C ⇒ “All A are C”), or an informal interpretation in ordinary language.

Fig. 1

Types of tasks and interpretation

Everyday reasoning tasks are not translatable to formal reasoning tasks and often contain implicit premises as, for instance, in everyday life stories. Like in formal reasoning tasks, students will need to interpret the information in everyday reasoning tasks as well. That can be done completely informally, but a formal representation, such as a schematic overview, might help students to get an overview of the given situation. In this study, we focus both on students’ interpretation and the reasoning strategies that follow from there.

Formalisations.

From prior research among university students (e.g. Lehman, Lempert, & Nisbett, 1988; Stenning, 1996), we conjecture that reasoning in all kinds of situations will benefit from the use of formal representations or formalisations. We will use the term formalisation in its broadest sense, including all sorts of symbols, schematisations, visualisations, formal notations and (formal) reasoning schemes. Stenning (1996) gives support for the role of (elementary) formal notations and rules by mentioning that “learning elementary logic can [emphasis added] improve reasoning skills” (p. 227) and can help to understand formal thoughts and arguments. Also, Lehman et al. (1988) found support for the notion that reasoning in general can improve as a result of teaching formal rules within a particular field. Nonetheless, this does not imply that every formalisation is helpful: The chosen representation should support the thinking process for the specific context, rather than that it should capture all aspects (McKendree, Small, Stenning, & Conlon, 2002). In this study, we will investigate which formalisations are used by the participants and if those formalisations are beneficial.

Research Questions

Since little is known about the reasoning processes of 16- and 17-year-old students in logical reasoning tasks, our aim is to explore their reasoning strategies. Because of its exploratory nature, we selected, according to the division provided in Fig. 1, three elementary types of reasoning tasks: two formal reasoning tasks, to be presented with (formally stated) and without (non-formally stated) symbols, and an everyday reasoning task. Our exploratory study was guided by the following research questions: (1) How do students reason towards a conclusion in formal reasoning and everyday reasoning tasks, whether or not by using formalisations? And (2) what kind of reasoning difficulties do they encounter when proceeding to a conclusion?

Methods

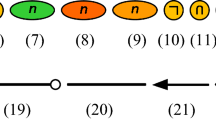
For this exploratory study, we selected closed tasks (formal reasoning tasks) concerning linear ordering and syllogisms and an open-ended newspaper comprehension task (everyday reasoning task). The formal reasoning tasks were presented formally and non-formally, of which the non-formally stated task is a counter-item of the formally stated one. A non-formally stated counter-item is a translation of the corresponding formally stated task in ordinary language and vice versa. Both tasks have similar conclusions as final answer, so that the reasoning processes can be compared. Figures 2 and 3 show these formal reasoning tasks, both formally stated and non-formally stated.

Fig. 2

Formal reasoning tasks about linear ordering, formally and non-formally stated

Fig. 3

Formal reasoning tasks about invalid syllogisms, formally and non-formally stated

Figure 4 shows the everyday reasoning task and this task does not have a counter-item. This newspaper task is an open-ended task with implicit premises and hidden assumptions. In this task, students have to reconstruct the line of the argument. An expert in logic validated all items by checking wording and comprehensibility of the tasks.

Fig. 4

Everyday reasoning task, reasoning in a newspaper article

This selection of tasks captures each category shown in Fig. 1 in which we expect different reasoning strategies and contains familiar and unfamiliar tasks to our students. For each task, we provide example interpretations and solutions below. These solutions are used as reference solutions to check the correctness of students’ answers, but, of course, the reasoning towards a conclusion can differ. In the everyday reasoning task in particular, different formulations are possible.

The linear ordering tasks (see Fig. 2), which are formal reasoning tasks, have ‘P > S’ and ‘Peter is older than Sally’ as correct answers respectively. If taken a formal interpretation, the reasoning can be P > Q > R > S for the order of the letters. If taken an informal interpretation, you can take example ages for the four persons. For example, if Peter is 50 years old, then Quint can be 20 years old, because Peter is older than Quint. Rosie is younger than Quint, so Rosie can be 10 years old. Rosie is older than Sally, so Sally can be 5 years old. In conclusion, if Peter is 50 years old and Sally 5 years old, then Peter must be older than Sally.

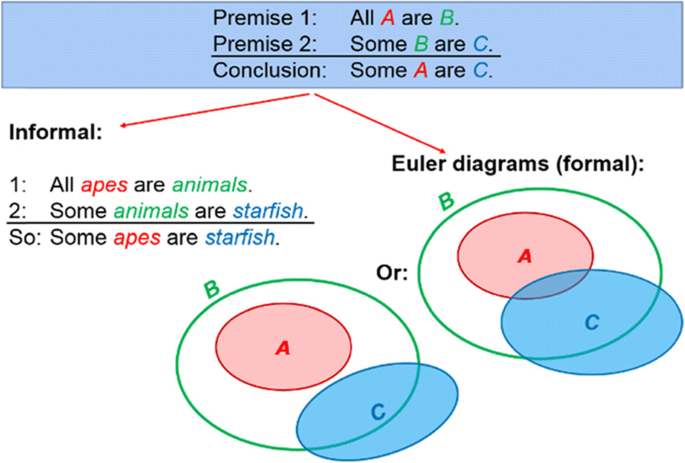
The syllogism tasks (see Fig. 3), which are formal reasoning tasks too, should have ‘does not follow necessarily from the given premises’ as correct answer as the only valid conclusive option. For the formally stated version of the syllogism task, possible formal and informal interpretations are visualised in Fig. 5. At the left, the given syllogism is translated into ordinary language completely and thus called an informal interpretation. In this case, it is example-based with a counterexample in ordinary language, which is, of course, a sufficient explanation why the conclusion does not necessarily follow from these premises. However, it is important to recognise that an example does not always lead to a general conclusion, in particular for valid syllogisms, so in that case, there must be a translation back to the formal setting.

Fig. 5

Formal and informal interpretations of the formally stated syllogism task

The formal interpretation with Euler diagrams at the right of Fig. 5 shows that C does not necessarily overlap with A. In this interpretation, the original given set of letter symbols is used. Similar diagrams can be drawn for the non-formally stated version of the task.

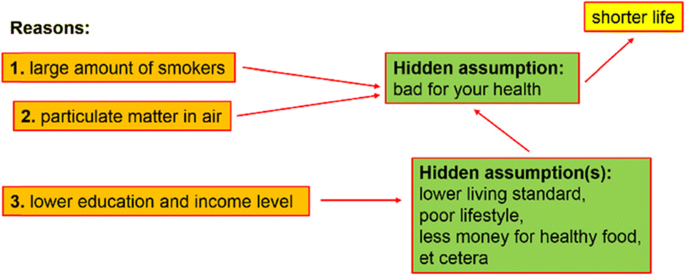
The everyday reasoning task (Fig. 4) requires students to (1) identify the premises (reasons) leading to the author’s conclusion, and (2) to hypothesise how these premises might be connected to the conclusion by using general knowledge or evidence that might support the author’s conclusion. Our example solution (see Fig. 6) is scheme-based with phrases in ordinary language. We analyse such a scheme as a formal interpretation in which the three reasons (the identified premises) are linked directly or indirectly to the author’s conclusion. For the third reason, one needs an additional reasoning step by mentioning another hidden assumption to make the argument complete. We assume that there is sufficient general knowledge on this subject among the participants. The arrows represent if-then statements and are not only part of the formal scheme, but also formalisations in themselves.

Fig. 6

Formal scheme for the everyday reasoning task

Nevertheless, the if-then statements in the scheme can be explained in full sentences too. For the first two reasons, that will look like ‘If people smoke or inhale particulate matter, then it will affect their health and thus shorten their life.’ Such considerations based on common knowledge still show the connection, but it is not yet formalised, neither with a scheme, nor with any symbols and thus considered as a completely informal interpretation (see Fig. 1). As soon as one introduces logical symbols, we will call those symbols formalisations. In combination with the if-then rule, the sentence can be represented as ‘(smoking ∨ inhaling particulate matter) ⇒ unhealthy ⇒ shorter life’.

Participants

Our participants are Dutch secondary school students in their penultimate year of pre-university secondary education (11th graders) and volunteered to participate in think-aloud sessions. The first author of this article was their teacher and they all signed an informed consent. These students did not take advanced mathematics or science, but followed a mathematics course in which logical reasoning has recently become a compulsory domain (College voor Toetsen en Examens, 2016). This study was conducted before the participants received teaching in logical reasoning. In this article, work is discussed from two male (Edgar, James) and two female students (Anne, Susan).

Procedure

We conducted task-based interviews in which students solved logical reasoning tasks aloud (Goldin, 2000; Van Someren, Barnard, & Sandberg, 1994). The interviews were conducted in Dutch and recorded with a smartpen so that verbal and written information could be connected. The students were asked to say aloud everything they were thinking of. The interviewer, who is the first author of this article, refrained from commenting as much as possible, so that ‘free problem-solving’ was a key aspect of the sessions. If a student did not understand the task or thought it was done, the interviewer would ask additional (clarification) questions, but did never provide feedback on the given answers.

Analysis

The transcripts of the interviews were analysed in Dutch and selected parts were translated to English for this article. Students’ task solving was analysed qualitatively in an interpretive way and data-driven (Cohen, Manion, & Morrison, 2007). To get a clear picture of the reasoning process, the data sources, interview transcripts and students’ written notes, were analysed according to our definition of logical reasoning. Our analysis included the following steps: (1) students’ understanding of the task, (2) students’ interpretation of the task, (3) students’ reasoning process and strategies used, (4) students’ use of formalisations and (5) the correctness of students’ final answers. If students switch between interpretations, we will call the predominant interpretation, their main interpretation.

Students’ reasoning in counter-items is intended as an exploration of possible variation in reasoning. Because students worked on only one of each two counter-items, we cannot analyse the differences between individual students’ strategies on alternative versions of similar closed tasks.

To judge the correctness of their final answers, students’ written notes, as well as the interview transcripts, are used and compared. Possible differences are marked and combined with their interpretations and reasoning. We have to note that the verbal explanations in itself can be seen as informal, because if students are asked to do tasks aloud, they use ordinary language, but if explained with a (given) set of symbols, the interpretation of the task can still be formal. Furthermore, the verbal explanations are linked to written notes, in which possible use of formalisations is clearly visible.

Results

Table 1 provides an overview of the results. Thereafter, for each task students’ reasoning will be illustrated in detail.

Table 1 Overview of students’ interpretations, strategies, formalisations and correctness answers

Reasoning with Linear Ordering

Formal reasoning tasks with linear ordering (see Fig. 2) are familiar to the students because these types of tasks are common in primary and secondary education. We summarise the findings first: All four students used rule-based strategies, but their initial interpretation differed. All answers were correct and well-reasoned. Only one student came up with an additional formalisation other than the given symbols. She used a very suitable tool, a number line representation with formal letters symbols, to get a clear overview of the order. We will present a detailed description of the four students.

Formally Stated, Edgar.

Edgar interprets the task in a formal way by copying the formal notation, see first three lines in Fig. 7. After writing that down, his first statements are switching to example-based reasoning (informal interpretation) that involves filling in some numbers (line [1] in transcript). After that, he quickly weighs his two interpretations (lines [2] and [3]) and switches back to the formal situation, by comparing the given letters P, R and S with the symbol for ‘greater than’ (line [4] and Fig. 7). Although the verbal explanations are in words, inherent to thinking aloud, he solves the task by following mathematical rules by staying in the formal system with the corresponding formal symbols. This way of reasoning provides the correct answer quickly and using the given symbols only gives a clear structure: P > R, R > S, P > S.

Fig. 7

Formally stated linear ordering task at the left, Edgar’s written notes at the right

Edgar: [1] well, yes, you could just fill in numbers of course as an example,

[2] well oh no, let's wait[3] we are not going to do that at first

[4] uhm, P is greater than Q, so P is also greater than R, …

Formally Stated, Anne.

After reading the task, Anne starts immediately with a translation of the formal symbols into expressions in ordinary language by writing down ‘greater than’ and ‘less than’ in full, thus giving an informal transformation of most of the formally stated task (see Fig. 8). Although she still reasons with the given formal letters, she switches to ordinary language for applying the mathematical rules. She provides the correct answer.

Fig. 8

Anne’s written notes at the left, English translation at the right

Non-formally Stated, Susan.

Susan translates the non-formally stated version of this formal reasoning task immediately into a formal situation with letter abbreviations for the names and the symbols > and < for ‘older than’ and ‘younger than’. Besides these formal symbols, she puts the letters in sequential order horizontally, which can be seen as a ‘number line’ representation with formal letter symbols, starting with P-Q-R reasoning that Q must be in the middle, see Fig. 9. We call that another formalisation. After adding S as well, she comes to the right conclusion that Peter must be older than Sally, which is a translation from her formal system to the conclusion asked for in ordinary language.

Fig. 9

Susan’s written notes

Non-formally Stated, James.

James reasons in words within the non-formally stated version of this task leading to a correct conclusion. We call his interpretation informal with a correct application of mathematical rules. After the confirmation that he has to write his reasoning down, his written explanation is completely in ordinary language, using the given names and the phrases ‘older than’ and ‘younger than’ (see Fig. 10). So, James’s interpretation is completely informal without switching.

Fig. 10

James’s written notes at the left, English translation at the right

Reasoning with an Invalid Syllogism

Formal reasoning tasks with syllogisms (see Fig. 3) are unfamiliar tasks to these students because they are not used to reasoning within syllogisms. We summarise the findings first: Three of the four students used an informal interpretation, but only two students provided a correct answer. The formally stated version caused difficulties due to not understanding the task or due to incomplete translations to an informal example. Also, the misinterpretation of ‘are’ and the confusion between ‘all’ and ‘some’ are noteworthy. We also found that a recognisable non-formally stated context can support the reasoning, despite some hindrance of real-life experiences concerning the context as well. We present a detailed description of the four students.

Formally Stated, Susan.

Susan shows that she understands that she has to accept the two premises in this formal reasoning task, regardless of their truths by writing “true” behind it, see Fig. 11. Her next step is formalising the given statements even further by introducing the equality sign, see first lines in her written notes in Fig. 12, so she interprets the task completely formally.

Fig. 11

Susan accepts the given premises, English translation at the right

Fig. 12

Formalisations used by Susan, English translation at the right

Susan tries to reason with the given letters four times (see four sections transcript) before she gives up. Again, her verbal explanations are in ordinary language, of course, inherent to thinking aloud, but she uses the given letters and stays in the formal system, so we call that a formal interpretation. In her first try (lines [1] – [7] in transcript), she states that A and B are equal (line [5]), but she cannot connect this with C. In her second try (lines [8] – [14]), she starts with stating that A and B are equal, but cannot connect C with that although saying that some B are not C (line [10]). In her third try (lines [15] – [17]), she says, once more, that A and B are equal, but she cannot connect that with C, because she does not know which B’s are C. The fourth time she writes down the last two lines shown in Fig. 12, connecting some with a symbol for approximately, but that does not help either (lines [18] – [25]). It is important to notice that she uses the equality sign each time as equal to which conflicts with the original premise containing an inclusion.

After underlining her conclusion ‘A ≈ C’ in the fourth try, she gives up and sighs: “I just do not understand the logic of all this” (line [25]). Susan only reasoned with the given letters and formal symbols and did not switch to an informal situation.

Susan: [1] all A are B, …, so is equal

[2] but some of those are C[3] so some are not, some A are not either, some A are

[4] … mmm …

[5] all A are B, so A and B are equal

[6] some B are C, so some B are only A

[7] and some B are C … mmm …

[start reasoning from the beginning again]

[8] all A are B, A and B are equal

[9] some of those are C and some are not

[10] some B are not C

[11] some A, that is also B

[12] some B … some A are C

[13] … but all A are B, and some B are C, some A are C [rereading given syllogism]

[14] no, I don’t think so

[start reasoning from the beginning again]

[15] I think that, … uhm …, if all A are B, A and B are equal

[16] but some B are C, so some of those B’s, that has to be the case, do not necessarily have to be A, because you do not know which B’s are C, because those are equal to C, and A and B are equal, some A are C

[17] ow, I really think this is difficult

…

[start reasoning from the beginning once more]

[18] okay, all A are B [writes down A=B]

[19] some B are C, so approximately [writes down B≈C]

[20] and some A are C, but A and B are equal[21] some of those B are C [writes down behind A=B: ➔ B≈C]

[22] and some A are C [writes down A≈C]

[23] so, my conclusion, … mmm … [underlines A≈C]

[24] I really don’t know

[25] I just do not understand the logic of all this

Formally Stated, James.

James recognises that he does not know how to solve this task in a formal way by expressing “I don’t know”, so he switches to an informal interpretation of the formally stated task: starting with searching for an example in ordinary language. This can be seen as analogy- and example-based reasoning. His explanation is closely related to our example in Fig. 5, but James only looks for one valid example instead of a counterexample. He chooses an example in which ‘some’ represents all apes (line [3] in transcript), because the set of apes not being mammals is empty. We assume that he did not recognise that because of his incorrect conclusion. He tries to use a logical structure ‘if-then’ (lines [2] – [4]) as well, but that does not solve the problem. After the valid conclusion of his example in ordinary language, he tries to explain the validity of his conclusion in a more formal way with the given letters (lines [5] – [7]) and writes that down as well (see Fig. 13). For this, James also states that A and B are equal (line [5]) in the same way as Susan did, and is not able to provide a more precise explanation after clarification questions by the interviewer.

Fig. 13

James’s written notes at the left, English translation at the right

James: [1] okay, well, I am going to have a look with a similar example I think

[2] if, uhm, all humans are apes

[3] some apes are mammals

[4] then some humans are … also mammals

[5] so, I think it is correct, because A and B are equal,

[6] because that is necessarily true,

[7] so if that’s the case for some B, it is also the case for A

Non-formally Stated, Edgar.

Edgar’s interpretation of the non-formally stated version of this formal reasoning task is informal. He draws the correct conclusion quite easily (line [2] in transcript). He also explains, although this is not necessarily true, the possibility that some flowers might refer to roses as well as to other flowers (line [6]), which shows a notion of the rules of logic. In his written notes (see Fig. 14) he also shows that the word flower could contain more than one type of flowers. This reflection is quite strong and shows insight in the generality of a syllogism.

Fig. 14

Edgar’s written notes at the left, English translation at the right

Edgar: [1] uhm… well… let’s see…

[2] yes, you would say that this does not follow logically, because some flowers does not necessarily refer to all roses

[3] let’s see

[4] some, yes,

[5] uhm…

[6] it does not have to mean that roses fade quickly since some flowers might also be daisies or, well, something, or other flowers consequently

Non-formally Stated, Anne.

Anne also draws the right conclusion in the non-formally stated version of this task. She uses an informal interpretation and comes up with a correct answer quickly (line [1] in transcript) and provides a more complete explanation in her next sentence (line [2]), which is similar to her written answer (see Fig. 15). However, Anne is not completely sure about her answer. Asked for an explanation, she says that her uncertainty comes from her knowledge about fading flowers (line [8] and [9]), although she recognises that one cannot conclude that from these premises, which shows that she understands the rules of logic.

Fig. 15

Anne’s written notes at the left, English translation at the right

Anne:  [1] You do not know if it’s the roses that fade, so you also don’t know if some roses fade quickly.

[2] All roses can still be flowers, and some flowers can still fade quickly, but that does not have to mean that roses [sighs] fade quickly.

[3] Yes, I think so.

[4] I am less certain about this one.

…

[5] because roses can still be flowers, but, ow wait, and

[6] … that does not have to mean that, per se, the roses fade quickly,

…

Intvwr: [7] And why are you less sure than in the previous task?

Anne:  [8] uhm… yes, because, some flowers fade quickly, yes, I don’t know, I know, I think it’s difficult to explain, but I am just more in doubt here, because …

[9] I was thinking because I know, of course, that there are many other species of flowers than only roses, only from these premises you cannot see that of course

Reasoning in a Newspaper Article

An everyday reasoning task about the analysis of a newspaper article (see Fig. 4) is considered unfamiliar to these students. We summarise the findings first: Both students used informal interpretations and only some basic formalisations to sum up reasons or make connections even though one of the students (Susan) provided to some extent a schematic overview. Although not essential, they did not build a (strong) formal scheme as, for example, shown in Fig. 6. We present a detailed description of the two students.

Susan.

Susan starts this task with identifying the three premises (step 1) in a structured way by writing down the three reasons mentioned in the article behind bullets (see first three lines Fig. 16). Thereafter, she takes her time to reconsider these reasons, the wording of the task and the phrase ‘hidden assumption’. She writes down “the hidden assumption is that people from Rotterdam live less healthy”, which hypothesises how the premises are linked to the conclusion (step 2). She explains that “it has to do with people’s health” because of the first two reasons, smoking and worse environment, but Susan struggles with an explanation for the third reason: lower education and income level (see line [1] in transcript). This reason demands more evidence. Susan implies that poorer families are the missing connection for the lower income (line [4]). For that, she uses another formalisation, which structures her written notes: an arrow to make the connection. Verbally, she provides a further explanation for the assumption ‘poorer families’ (line [5]), but she did not write that down.

Fig. 16

Susan’s written notes at the left, English translation at the right

Overall, in her verbal explanation, she has connected all the mentioned reasons with a hidden assumption leading to her main assumption ‘poorer health’, which she underlines as well. In her written notes, she uses formalisations at three moments: at the beginning (bullets) for the first step involving identifying the premises, and arrows at two times for connections, either with hypothesised evidence based on her own knowledge (step 2), or to emphasise the main hidden assumption. Her notes provide more or less a schematic overview, but Susan did not compile a complete formal scheme.

Susan: [1] ... mmm, so ... the lower education and income level what does that have to do with ... lower level of education, ... mmm ..., yes, the amount of smokers has to do with health and the high concentration of particulate matter in the air, so it means that the health of people from Rotterdam is worse than the health of other people in the Netherlands

[2] uh, to link, explain how the reasons mentioned are linked to the shorter life, by describing the hidden assumption, uhm ...

[3] The shorter life is caused by ... the ... poorer health in Rotterdam compared to other Dutch people.

[4] Then, the hidden assumption is that poorer health and ... maybe, uh ... lower education and income level, so perhaps poorer families [draws an arrow to connect this with lower education and income level]

[5] ... and they may not buy very expensive and organic food and everything, so they would live less healthy or something, I think the hidden assumption is that they eat less healthy, or live less healthy lives especially, yes that’s what I think

[6] This is what I think, the poorer health [underlines poorer health], that’s the hidden assumption. [adds arrow]

Anne.

Anne underlines the three main reasons in the text: smokers, particulate matter, lower education and income level, which shows that she identified the premises (step 1). After that, she lists the three reasons behind bullets (see Fig. 17). That is the only formalisation she uses. The rest of the reasoning, verbal and written, is done in ordinary language. For the second and third reason, she provides a hidden assumption: “particulate matter is bad for someone and thus shortens one’s life, and the lower education level and the lower income level leads to poorer living conditions and thus shortens one’s life”. She uses her own knowledge to state that particulate matter is bad for someone’s health and to hypothesise that a lower income level leads to poorer living conditions (step 2). However, she forgets to provide a connection for the first reason, so the interviewer asked for further explanations before she added “bad for you and thus” (see top line Fig. 17) for the connection between smoking and shortening one’s life.

Fig. 17

Anne’s written notes at the left, English translation at the right

Overal, Anne identified the premises quite quickly and provided support for the reasons easily. Probably, she assumed that the connection between smoking and a shorter life was generally known, so that she only provided additional evidence after a clarification question by the interviewer.

Conclusions and Discussion

The purpose of this study was to gain insights into the reasoning processes of 16- and 17-year-old pre-university secondary school students on logical reasoning tasks, aimed at fostering their critical thinking skills as an important objective in the twenty-first century skills framework (P21, 2015). In this exploratory study, we investigated (1) the way of reasoning students used in formal reasoning and everyday reasoning tasks and their use of formalisations, and (2) the difficulties they encounter in their reasoning.

In the linear ordering tasks and in the syllogism tasks, students used rule-, analogy- and example-based reasoning strategies. In the newspaper article task, students reasoned partly scheme-based, but mainly in ordinary language only. Except for the formally stated syllogism task, students used appropriate strategies to find correct answers. Although the linear ordering tasks are familiar to the students, both formats (formally and non-formally stated) led to formal and informal interpretations.

Students do not always feel certain about their method and answer, in particular in the syllogism tasks and in the everyday reasoning task. The incomplete written answers in the everyday reasoning task show that our students probably have doubts if their answers are good enough, because they have the feeling that more answers are possible. Even though the newspaper task is taken from an everyday life context and—we expect—recognisable and meaningful, students still fulfil a task for which they expect that there should be one correct answer, as is common in mathematics tasks (e.g. Jäder, Sidenvall, & Sumpter, 2017). The doubt students express is in line with Galotti’s (1989) description for everyday reasoning tasks, because she states that “it is often unclear whether the current ‘best’ solution is good enough” (p. 335) in contrast to formal reasoning tasks where “it is typically unambiguous when the problem is solved” (p. 335).

In our formally stated syllogism task, the students misinterpreted the phrases ‘all…are…’ and ‘some…are…’. Consequently, they did not see that their representations, such as the use of the equality sign as a formal symbol, were not suitable. Susan was completely stuck in the formally stated version and could not find a way out. The misuse of the equality sign (=) for ‘all… are…’ is a common mistake (e.g. Galotti, 1989, p. 336). Stenning and Van Lambalgen (2008) also describe difficulties with understanding and interpreting syllogisms.

An overview of our findings is visualised in a scheme (Fig. 18) as an extension of Fig. 1. We showed that students’ initial interpretations, their first thoughts, do not always match with their later choices, so students seem to switch between formal and informal interpretations. This is visualised by the arrow in the scheme. The strategies included in this scheme are derived from our exploratory study among 16- and 17-year-old students and might not provide a complete overview. Consequently, the overview can be supplemented with argumentation schemes based on presumptive reasoning (Walton, 1996; Walton, Reed, & Macagno, 2008) in further research. Our everyday reasoning task gives only a limited view of students’ possible reasoning strategies, because students were only asked to identify the premises and to use their own knowledge to find connections with the conclusion. They were not asked to find rebuttals or further backing of the claims. The connections provided by the students should be sufficient for justifiable reasoning. This correspondents to the earlier mentioned description from Johnson and Blair (2006) about acceptable premises.

Fig. 18

Types of tasks combined with students’ interpretations and reasoning strategies

Each of the strategies shown in Fig. 18 can be supported by the use of formalisations. For example, in the non-formally stated linear ordering task, Susan used letter abbreviations, mathematical symbols and a number line representation. For cases in which students reason in ordinary language without clearly showing causality, comparison or examples, we added the category ‘informal reasoning’. This category is based on our definition of informal reasoning in the corresponding section in the Theoretical Background. We believe it is important to present ‘informal reasoning’ as separate category in the scheme, because students still managed to construct an argument in ordinary language, but without clearly showing a visible reasoning strategy, such as rule-based, example-based, scheme-based, et cetera.. Therefore, we used a dotted line in Fig. 18. Consequently, in that case, formalisations can only be used to a certain extent as, for example, shown by Anne in her analysis of the newspaper article where she separated her three informal arguments by bullets.

In this article, we hypothesised that suitable formalisations can support the reasoning process and summarised those tools at the right-hand side of Fig. 18. We believe that our hypothesis is strengthened by the findings in this exploratory study. Symbols (like ‘greater than’ and ‘less than’, or the equality sign) and letter abbreviations are suitable tools to shorten notations, while other tools (like a number line representation) are strong tools to visualise information. Although not used by our students, Venn and Euler diagrams are also strong tools to visualise data. However, it is our conviction that the use of formalisations, including visualisations such as Venn and Euler diagrams, is teachable and can be linked to the strategies used by the students, also in everyday reasoning tasks.

A limitation of the study is related to our choice of tasks. In our selection of tasks, we used formally stated tasks and non-formally stated tasks as counter-items for similar reasoning problems. In our design, different students worked on one of the counter-items and therefore, we could not compare the performance of an individual student on both tasks. The non-formally stated tasks were more easily to interpret by the students and led to other strategies, because their prior knowledge was helpful. Hintikka (2001) explains that “in real-life reasoning, even when it is purely deductive, familiarity with the subject matter can be strategically helpful” (p. 46). On the other hand, sometimes our students may doubt their answers, because premises in the task (e.g. Anne in the non-formally stated syllogism task) might conflict with their prior knowledge. In general, this means that our counter-items (formally versus non-formally stated tasks) cannot be considered as equivalent.

Despite the fact that our study has a limitation in the number of participants (small and selective sample) and a limited number of tasks, the information in Fig. 18 shows a variety of reasoning strategies, which is important for teachers to understand the diversity of students’ reasoning and possible difficulties in the interpretations of tasks, in particular for tasks that are not familiar to students or lead to incorrect answers.

Future Research and Recommendations

This study not only shows the complex matter of reasoning and everyday life reasoning in particular, it also confirms that more research is needed as already mentioned by Galotti (1989, 2017). Our exploratory study is a first step to get insights in the reasoning process of 16- and 17-year-old pre-university students and shows a gap between their verbal and written explanations. We will continue our research for an in-depth understanding. Unfamiliar tasks, such as all sorts of non-formally stated syllogisms (formal reasoning tasks) and everyday reasoning tasks seem to be useful contexts to investigate how students solve reasoning tasks and which formalisations, including visualisations, they use. Our definition of logical reasoning, mentioned in the Theoretical Background, fits this future research.

Our results show that students do not structure everyday life contexts automatically, so it is plausible that similar difficulties occur in authentic everyday life reasoning too. In future research, we intend to show that students may be supported by learning more structured reasoning strategies and the use of formalisations and visualisations.

One of the key aspects for lessons in logical reasoning must be classroom discourse when solving reasoning tasks. Lakatos (1976) already stressed the importance of dialogue in the construction of mathematical and logical reasoning. Our research might increase teachers’ awareness of that importance and, more practically, for which Fig. 18 serves as a guideline for discussion. Different interpretations and possible strategies used by students are made explicit and can be used as input for classroom discussions. We suggest that formalisations and visualisations are part of those discussions and might establish a deeper understanding. Above all, logical reasoning tasks where several ways of reasoning are possible, are highly connected to the twenty-first century skills (P21, 2015), and thus with the development of critical thinking skills.