Non-routine problem solving is important in elementary school mathematics (Kolovou, 2011). An example is when students have to create a paper model of a 12-sided dice. Students cannot simply apply a strategy, but have to recall, use, and combine facts, skills, procedures, and ideas in a new and meaningful way to solve the problem. This requires creative and flexible thinking (Schoevers et al., 2019; Warner, Alcock, Coppolo, & Davis, 2003), which is also considered important in other disciplines in elementary education, such as visual arts (Sawyer, 2014). However, in educational practice, most teachers do not provide many opportunities for students to act creatively in mathematics (Gravemeijer, 2007; Kolovou, 2011) and visual arts (Bresler, 1999; Elfland, 1976). This might be largely due to the highly structured curriculum and mathematical textbooks that leave little room for these opportunities and may constrain creative practices that the teachers feel able and willing to engage in (Dobbins, 2009; Kolovou, 2011). The Mathematics, Arts, Creativity in Education (MACE) program was designed to change educational practice in this respect. The program aimed to teach domain-specific and overlapping learning goals of visual arts and geometry and to promote students’ creative skills in both disciplines, by creating opportunities for students to act creatively in an integrated visual arts and geometry context. To reach the goals of the program, a lesson series for students was designed along with a professional development (PD). This study evaluated the intended effects of the MACE program.

Integrating Mathematics and Arts Education

The mathematical domain of geometry in education has the aim to teach students to understand and explain geometric phenomena from reality and to order and organize spatial situations (Jones, 2002; Van den Heuvel-Panhuizen & Buys, 2005), such as to draw a map or to reason about the effect of the height of the sun on the length of the shadow. This also requires students to obtain geometrical vocabulary to explain these phenomena (Buijs, Klep, & Noteboom, 2008). Furthermore, the ability to solve geometrical problems is considered important, since it is central to mathematics (Kolovou, 2011) and can be a way to construct new mathematical knowledge (Levav-Waynberg & Leikin, 2012). Problem solving requires creative thinking: students need to be able to combine known concepts, skills, procedures, and ideas from mathematics and other domains in a new way to solve the problem (Schoevers et al. 2019), which can contribute to the construction of new knowledge and deeper understanding of geometrical concepts (Levav-Waynberg & Leikin, 2012; Warner et al., 2003). Based on these core aspects of geometry education, we defined geometrical ability in this study as students’ ability to understand and explain geometric phenomena, to describe these phenomena by using geometrical vocabulary, and to creatively solve geometrical problems.

Visual arts education has the aim to teach students to develop their visual-imaginative abilities by using their experiences of reality and visualizing these experiences (Braakhuis, Von Piekartz, Vogel, & De Graaf, 2012). The main aspects of visual arts education are visual art production, perception (observing, interpreting, and analyzing) and reflection (thinking and speaking about a visual art product during or after its production; Haanstra, 2014). The (cyclic) creative process is central in teaching the visual arts curriculum (Sawyer, 2014; Stichting Leerplanontwikkeling, 2015).

Thus, in both visual arts and geometry, creative processes play a central role. One of the key cognitive processes of creativity is to overcome fixation on ideas and to break away from established mindsets. Currently, visual arts and mathematics are usually taught in separate disciplines, and students, as a consequence, rely on the highly familiar knowledge and routines specific for these domains. We hypothesize that by integrating mathematics and visual arts education, students will be stimulated to integrate different conceptual systems from both disciplines, which could activate students to create something new and meaningful (Haylock, 1987; Plucker & Zabelina, 2009).

The MACE Pedagogy

The MACE pedagogy comprises the following key features: visual arts perception, open activities, reflection, communication with peers, and a specific role of the teacher. In this section, we elaborate on these features and describe how these can enhance students’ ability in both geometry and visual arts. The more formal features of the program (e.g. duration and number of lessons) are discussed in the “Methods” section.

Visual arts perception plays a role right at the start of the MACE lesson series. Artworks are discussed in a whole-class setting by using an interactive whiteboard in relation to the interdisciplinary lesson theme (e.g. in a lesson about perspective: Can you tell me how the photo would have looked like if the photographer had used another point of view?) and with the use of visual thinking strategies (e.g. “What’s happening in this picture?,” “What do you see that makes you say that?,” “What more can we find?”; Housen, 2002). Students thus learn to observe and analyze the visual aspects of a piece of art, to consider the view of others, and to reflect on and discuss about possible interpretations (Hailey, Miller, & Yenawine, 2015). Educating visual arts perception also enables students to extract shapes and objects from a visual scene which, in turn, can influence their recognition and representation of visual information (Kozbelt, 2001; Tishman, MacGillivray, & Palmer, 1999). Since artworks are discussed in an interdisciplinary context, students may learn to recognize and represent the visual aspects in artworks such as “space,” “shapes,” and “composition” (Stichting Leerplanontwikkeling, 2018). Furthermore, visual arts perception could improve students’ geometrical reasoning when they are asked to imagine how an artwork would look like if particular changes were made (Tishman et al., 1999; Walker, Winner, Hetland, Simmons, & Goldsmith, 2011).

Furthermore, within the MACE program, open activities are used in which students have to produce a visual artwork related to a theme at the boundaries of visual arts and geometry (e.g. perspective or symmetry). The activities contain problems for which students do not know predetermined or obvious solutions (Kolovou, 2011). Activities are “open” if they invite different solutions and if problem solving methods are open for interpretation (Silver, 1995). For example, in one of the open tasks of the MACE program, students have to make a three-dimensional representation of a two-dimensional painting by using free materials like egg boxes or paper rolls. These type of activities can stimulate students to visualize their experiences, by exploring materials, meaning, and several visual aspects (Stichting Leerplanontwikkeling, 2018). In addition, students may learn to order and organize spatial situations that require geometrical reasoning (e.g. how certain objects need to be structured to construct the three-dimensional representation of the painting). Furthermore, investigation and manipulation of the materials and thus exploration of the physical environment can help students to form visuospatial and sensorimotor representations of geometrical structures that are embedded in the environment. This may advance their thinking during geometrical problem solving (Carbonneau, Marley, & Selig, 2013; Núñez, Edwards, & Matos, 1999).

Reflection at the end of each lesson is considered very important within this integrated pedagogy. The knowledge and skills acquired during visual arts reception and production may still be rather implicit. It is important that students learn to reflect on their (creative) process of producing an artwork, and to communicate about the thinking processes with classmates and their teacher. By clarifying what was going on and what they have learned, the implicit knowledge and skills acquired can be made explicit; reflection can extend and modify existing knowledge (Chi, De Leeuw, Chiu, & Lavancher, 1994).

Communication with peers is highly promoted in the MACE lessons. Students are stimulated to collaborate in the learning activities, and situations are created in which they are asked to communicate, discuss, and exchange their ideas. In this way, students can compare their ideas and view ideas from different standpoints, which can enhance creative thinking (Beghetto & Kaufman, 2010; Taggar, 2002). It can also increase students’ learning in geometry, because they have to explain their thinking and they get feedback and encounter other points of view (Jarvis, 2001). This may enable students to reach a higher level of understanding (Van den Heuvel-Panhuizen & Drijvers, 2014) and encourage (geometrical) language development (Van Lier, 1996).

Also, a specific role of the teacher is required in the MACE lessons. Teachers are advised to act as a facilitator: asking questions to extend students’ thinking and reasoning, instead of merely transferring knowledge (Bostic, 2011). In addition, they are stimulated to use academic geometrical vocabulary, for example in reformulating students’ thinking, to improve the geometrical vocabulary of their students (Henrichs & Leseman, 2014). To stimulate creativity, teachers are advised to create an open atmosphere in which students’ ideas are central, to ask open and activating questions that invite students to generate multiple answers, and to be open to these ideas (Davies et al., 2014; Schoevers et al., 2019). Although this specific role of the teacher is explained in the MACE teaching manual, also, a PD program for teacher was designed to assist teachers in implementing the MACE lesson series in educational practice.

Aim of the Study

The aim of the current study was to investigate the effects of the MACE program on students’ geometrical ability and perception of visual arts in a quasi-experimental design. The comparison condition consisted of students that received regular (textbook-based) geometry and visual arts education. Compared with students who received the regular geometry lessons, students who received the MACE lessons could engage in open, hands-on, and interdisciplinary activities; had more opportunities to express, discuss, and exchange ideas with classmates and teachers; and had more time to reflect on the lesson. The presence of these aspects in the MACE lessons, relative to the absence or reduced presence of these aspects in the regular textbook-based geometry lessons, were the reasons to hypothesize that students in the MACE program would improve more in geometrical ability than students in the comparison condition. More specifically, students were expected to better explain and understand geometric phenomena than students in the comparison group, to use more geometrical words to explain these phenomena, and to think more creatively in solving geometrical problems. Furthermore, we hypothesized that students who received the MACE program would observe and describe more geometrical aspects in visual artworks, compared with students in the comparison condition, because in regular visual arts education, visual artworks are seldom discussed, and especially not with a specific focus on the geometrical aspects (Kruiter, Hoogeveen, Beekhoven, Kieft, & Bomhof, 2016).

Methods

Participants

In this study, 2909 students in grades 3, 4, 5, and 6 situated in 121 classes and 57 schools participated. Students varied in socioeconomic background and mathematical ability. 4th, 5th, and 6th grade teachers were recruited for the MACE program by sending flyers to 428 regular elementary schools in all regions of the Netherlands. 11.68% of the schools were willing to participate. To evaluate the effect of the MACE lesson series and the MACE PD program, the participating schools were assigned to one of three conditions. Although we planned to randomly assign schools to the three conditions, this was not completely possible. For logistic reasons, schools had to be within a reasonable traveling distance of the PD training locations. Furthermore, some teachers were not available for the MACE PD program. In the first condition, the teachers followed the MACE PD program and taught the MACE lesson series to their students; in the second condition, the teachers taught the lesson series, but without following the PD program; teachers in the third condition taught regular geometry lesson from existing mathematical textbooks (but were offered to follow the MACE program after the study). Since geometry lessons are taught irregularly, spread over the school year, a lesson series was established for this study in which geometry lessons from various Dutch mathematical textbooks were combined to have the same time and intensity of geometry instruction as in the MACE program. In this way, students in the comparison group received the same geometrical content as students in the MACE program, but in a regular way. Geometry lessons from mathematical textbooks were used that were similar in geometrical content, but different from MACE lessons in pedagogy and enrichment with visual arts aspects. In the study, 10 classes and 197 students dropped out, because teachers experienced a too high workload (6.8% of the total number of students). In Table 1, the three groups are described.

Table 1 School and class characteristics
Full size table

The MACE Program

The MACE program consisted of a lesson series for fourth, fifth, and sixth grade students in which geometry and visual arts education were integrated along with a PD program for teachers (Keijzer, Oprins, De Moor & Schoevers, 2018). In a pilot study with 15 teachers, an initial version of the program was formatively evaluated and adjusted afterwards.

Description of the MACE Lessons.

The series of MACE lessons consisted of nine lessons which took each 60 – 90 minutes; five lessons related to the theme space and four to the theme patterns. Each lesson started with a whole-class introduction (15 – 25 minutes), in which students observed and discussed visual artworks in relation to the topic of the lesson. The introduction was followed by an open activity in which students created an artwork (25 – 30 minutes). During the activities, students worked mostly in (small) groups. A lesson ended with whole-class reflection (10 minutes), in which students’ creative process and products were discussed as well as what students had learned.

Below we describe the MACE lesson “playing with perspective” in more detail. In Appendix 1, a short description of each MACE lesson is given. In the lesson “Playing with perspective,” the teacher starts with an introduction in which six artworks are discussed in which the artists have explored perspective and viewpoints, such as the artwork “Another World” by M.C. Escher and photo’s in which photographers manipulated perspective. Questions that a teacher could ask during this introduction are stated in the manual, such as “How did the artist created this effect?,” “Can you tell something about the viewpoint of the artist and what could be the reason for this?,” and “How would the photo look like when they would have used another point of view?.” After the introduction, students make photos in which they create visual illusions by playing with perspective and point of view in groups of 3 – 4 students in- or outside the school building. After 15 – 20 minutes, students select their two best photos. At the end of the lesson, the teacher discusses the selected photos of the students and the process of making the photos in a whole-class setting. Questions that the teacher could ask are stated in the manual, such as “What effect did you want to create?,” “What did you do to create this effect?,” “What perspective did you use?,” and “Where would you stand if we would draw a map?”. Furthermore, the teacher has to ask students to reflect on what they have learned.

Description of the PD Program.

The PD program for teachers consisted of five sessions (2.5 hours each), guided by experts in the field of mathematics and visual arts education. After each PD session, teachers taught one or two MACE lessons in their own schools (see also Fig. 1). The aim of the PD program was to train teachers how to stimulate students’ creative thinking in this integrated visual arts and mathematics program. A further aim was to create a positive attitude of the teachers towards geometry, visual arts, and the integration of both. A third aim was to increase teachers’ geometrical knowledge and their pedagogical content knowledge of geometry and visual arts education.

Fig. 1
figure 1

An overview of the MACE program

Full size image

Within the PD program, active learning was considered important. Therefore, interactive methods were used in the sessions. Teachers, for example, had to experience the MACE lessons themselves, watched film fragments of other teachers, and had to design a hypothetical learning trajectory. Afterwards, teachers always had to discuss and reflect on these activities. The content of the PD program was related to the classroom practice. Furthermore, reflection on the MACE lessons was important; it could support on-going learning and encourage change.

Regular Geometry Lesson Series

A lesson series was established for the comparison group in which geometry lessons from several widely used Dutch mathematical textbooks were combined and adjusted to have the same time and intensity of geometry instruction as in the MACE lesson series. We considered mathematical textbook lessons as regular geometry lessons, because most teachers, especially in the Netherlands, use mathematical textbooks to teach the geometry curriculum (Hop, 2012). Most used Dutch mathematics textbooks mainly offer closed-ended routine problems (Van Zanten & Van den Heuvel-Panhuizen, 2018). The (type of) problems, duration, and lesson structure of these textbook-based geometry lessons were applied and used in the regular geometry lesson series for the comparison condition. The regular geometry lessons series consisted of 7 lessons, of which four related to two and three dimensionality, block constructions, floor maps, and perspective. The other three lessons were related to patterns, symmetry, and rotation. The regular geometry lessons took between 30 and 40 minutes. Each lesson started with a short whole-class introduction (5 – 10 minutes) in which the subject of the lesson was introduced. Afterwards, students independently worked on geometry problems in a workbook (15 – 20 minutes). These were mainly multiple choice problems. The lesson was completed by a short (5 minute) whole-class reflection on the lesson.

Instruments

Geometric Ability Test.

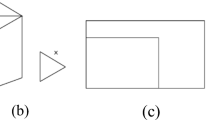
The GAT measured whether students understood and could explain geometrical phenomena. The GAT was developed for this study. The test took between 20 and 30 minutes and was stopped after 30 minutes. The test consisted of 11 geometry problems. The test started with four closed-ended routine problems that called upon spatial sense and spatial visualization (see the left sample question in Fig. 2) and ended with seven art-geometry problems in which students mainly had to reason geometrically in relation to a painting (see the right sample question in Fig. 2). As the test was specifically developed for this study, no information on item difficulty and other item characteristics was available. Therefore, within problem type, the order of the problems was randomized and the same for all students to prevent unknown order effects. Two equivalent versions (i.e. A and B) of the GAT were respectively used as pre- and posttests.

Fig. 2
figure 2

Sample questions of the GAT

Full size image

Scoring.

The spatial visualization problems were relatively straightforward with clearly one correct answer. Therefore, one point was given for a correct answer and zero points for an incorrect answer. The geometry problems related to visual arts were more complex and could also yield partially correct solutions. Therefore, two points were given for an answer in which students showed to be able to reason correctly about geometric phenomena (e.g. when students explained why things in front of the painting are bigger than in the back of the painting and, for example, would use the term perspective). One point was given for an answer in which the reasoning was not complete (e.g. “by painting a line down in a curve”). Zero points were given for answers in which the question was repeated or there was no reasoning about the question involved (e.g. “because when you paint you can make everything”). The last art-geometry question of the test was considered too difficult for grades 4 and 5; only 9% of the students scored one or two points (Hopkins & Antes, 1978). Therefore, this question was not used in this study. Furthermore, 27.1% of the students were able to finish the GAT in the maximum time of 30 minutes. Therefore, we calculated an average score based on the number of questions the students were able to complete. The maximum score that could be obtained was 1.6. Since items were not in an ascending order of difficulty, this was the most valid way to calculate a total score.

Reliability and Validity of the GAT.

Test-retest reliability of version A is acceptable (r = 0.66) and good for version B (r = 0.77). Alternative forms reliability of the GAT is sufficient (r = 0.80). Furthermore, forms A and B are similar regarding difficulty of the items. Criterium validity of the GAT, as measured by the correlation between the GAT and general math ability score, was moderate (r = 0.40 – 0.42), but sufficient since the mathematical domain geometry covers only a small part of the general mathematical ability test. Tests at the pre- and posttests were scored by four raters. Interrater reliability (IRR) was sufficient to excellent for all items on both the pre- and posttests (κ = 0.81 – 1.00, ICC = 0.67 – 1.00). In line with our expectations, the internal consistency of the GAT was not very high for both versions (version A, α = 0.62; version B, α = 0.58), because the GAT represents a heterogeneous set of skills.

Geometrical Vocabulary.

Active geometrical vocabulary was scored if students correctly used geometrical words in the open questions of the GAT. A list of geometrical words was composed by using the learning goals of elementary school geometry education (Van den Heuvel-Panhuizen & Buys, 2005) and elementary school teacher education (Van Zanten, Barth, Faarts, Van Gool, & Keijzer, 2009). We distinguished between tier 1 and tier 2 words (Henrichs & Leseman, 2014). Domain-general academic tier 3 words were not included in this study, because they were not of interest. Tier 1 words are geometrical words used in a daily language environment (e.g. “turned” or “flat”). Tier 2 words are domain-specific academic geometrical words used in mathematics education (e.g. “vertical,” “horizontal,” “square,” and “triangle”). The complete list of words can be found in Appendix B.

Scoring.

The total number of words, of tier 1 and of tier 2 words appearing in the writings, was counted for each question in the GAT. Regarding tier 2 words, a token (i.e. total number of tier 2 words used) and type score (i.e. the number of different tier 2 words used) were calculated. Since, these measures were highly correlated (r > 0.90), we only used the token score. Next, a ratio of the number of tier 2 geometrical words to the total number of words used was calculated for each question of the GAT. This ratio was calculated to adjust for differences in students’ wordiness. A total score for the GAT was calculated by averaging the ratio scores of the different questions. Geometrical vocabulary was scored by four raters. IRR was good in this study with regard to the total word written (ICC > 0.99), the number of tier 1 words (ICC > 0.88), and the total number of tier 2 words (ICC > 0.86) for both the pre- and posttests.

Geometrical Creativity Test.

The domain-specific Geometrical Creativity Test (GCT) was used to measure geometrical creative thinking (see also Fig. 3). It was developed for this study and based on the Mathematical Creativity Test used in the study of Schoevers, Kroesbergen and Kattou (2018). The GCT took between 20 and 30 minutes and was stopped after 30 minutes. It consisted of four geometry questions and one problem-posing question, which were open-ended and could have multiple correct answers. Multiple solution and problem posing tasks are commonly used to measure creativity in mathematics (Leikin, Koichu, & Berman, 2009; Leikin, 2009). Students were instructed to provide multiple, but distinct solutions, which moreover had to be original. In the problem-posing questions, students were asked to pose mathematical questions based on a photo. Version A was used for the pretest, and version B was used for the posttest.

Fig. 3
figure 3

A sample question of the GCT version A

Full size image

Scoring.

For the scoring of the GCT, we used the scoring scheme of Leikin for creativity in the individual solution space (Leikin, 2009; Levav-Waynberg & Leikin, 2012). Within this scheme, a distinction between fluency, flexibility, and originality is made. The scheme was further elaborated in Leikin (2009); Levav-Waynberg and Leikin (2012); and Leikin et al. (2009). Fluency was calculated by adding the number of correct answers for each question. Based on the scheme, each solution was scored on flexibility and originality. Next, a final score per solution was calculated as the product of Flexibilityi × Originalityi. Afterwards, a creativity score per question was computed as: Fluencyj × (∑ (Flexibilityi × Originalityi)). The sum of these creativity scores was used as total score.

Reliability and Validity of the GCT.

With regard to the test-retest and alternative forms of reliability, we used the fluency score (as described by Kattou, Kontoyianni, Pitta-Pantazi, & Christou, 2013) as indicator of creativity. Test-retest reliability of versions A (r = 0.84) and B (r = 0.89) are good. Alternative forms reliability of the GAT is sufficient (r = 0.68). Furthermore, the difficulty of both versions was similar. In this study, the GCT was scored by seven raters. IRR was sufficient to excellent for all scores per solution on both pre- and posttests (ICC = 0.72 – 0.99). In line with our expectations, the internal consistency of the GCT was not very high in this study for both versions (version A, α = 0.68; version B, α = 0.55), because geometry comprises a heterogenous set of knowledge and skills.

Visual Arts Assignment.

In the Visual Arts Assignment (VAA), students have to write down as much as they can about a painting (see Fig. 4) in answering the following questions: “What is going on in this painting?,” “What do you see that makes you say that?,” and “What more can you find?”(Housen, 2002). The same task was used as a pre- and posttests.

Fig. 4
figure 4

Emmanuel De Witte—Interior with a woman at the virginal (Museum Boijmans van Beuningen, Rotterdam, the Netherlands)

Full size image

Scoring.

A scoring scheme for the VAA was created for this study based on literature about visual arts perception in education (see Table 2; KPC-Groep, 2000; Stichting Leerplanontwikkeling, 2015; Van Onna & Jacobse, 2008). The VVA was scored on four aspects that were related to geometry, namely “space,” “space suggestion,” “shape,” and “composition.” We scored how often each aspect occurred in the written text of the student. Furthermore, the number of words written was counted. Next, each score on each aspect was divided by the number of words written and multiplied by 100, to take the talkativeness of students into account. The pre- and posttests were scored by five raters. Interrater reliability of most aspects was good to excellent (ICC = 0.76 – 99).

Table 2 Scoring aspects of the VVA
Full size table

Procedure

Data were collected in the fall of 2017 by the first author and twelve research assistants with a bachelor or master’s degree in (special) education. Before the start of the MACE program, in one session, the pretests were administered to the whole class by a research assistant who read aloud the test instructions. Posttests were administered after the MACE program in the same way as the pretests. Furthermore, teachers had to provide information about students’ age, gender, mathematical ability (based on the national mathematical ability tests), and the educational level of both students’ parents, based on information from school records. Pre- and posttests were coded afterwards by the same research assistants. Research assistants received extensive training and had to reach sufficient interrater reliability with the master coder before they were allowed to administer the pre- and posttests in the classroom, to conduct observations in the classroom, and to code part of the tests. Passive informed consent of the parents was obtained before the start of the study. 0.8% of the students did not have consent for this study.

Analyses

To take the nested structure of the data into account, multilevel analyses with three levels were conducted in HLM6 (Hox, Moerbeek, & Van de Schoot, 2018). The first level represented the repeated measurements (pre- and posttest), as nested within individuals. The second level represented the students, and the third level the classes. It was not necessary to include the school level as a fourth level, since there was only little variance in the different pretests located at this level (1 – 5% of the variance). For each outcome variable, first a base model was created with time as a predictor. In a second model, student-level covariates were added to control for spuriousness: grade, gender (Frost, Hyde, & Fennema, 1994), SES (Crane, 1996), and general mathematical ability. It was expected that students’ general mathematical ability would not have an effect on students’ performance on the VAA and student’s use of geometrical vocabulary, and therefore, this variable was not used as a covariate in the multilevel models related to these measures. Furthermore, it was expected that students with a low SES would score lower on the GAT, GCT, and VAA (Crane, 1996). Therefore, we controlled for low SES by using two dummy variables: students with a low SES and students with a very low SES. Students had a very low SES if elementary school was the highest completed education of at least one of the parents. Since only a small percentage of students had a very low SES, we also included students with a low SES: vocational education was the highest completed education of both parents. In a third model, third-level predictors were added as dummy variables: lesson series condition and PD program condition. Furthermore, two class-level covariates were added that were expected to influence the results of the effects of the MACE program: the number of MACE lessons given by the teacher and the number of MACE PD sessions followed by the teacher. In the fourth model, the random slope of time was added to investigate whether students’ growth on an outcome variable differed per class. In the fifth model, dummy variables of condition (whether or not students had received MACE lessons and whether or not the teachers had participated in the MACE PD program) were added as predictors of the slope of time to investigate whether differences between classes could be explained by conditions.

Before the multilevel analyses were conducted, data were screened and prepared and a missing value analysis was conducted. On the pretest, between 6.6 and 9.2% of the data were missing. On the posttest, between 9.7 and 10.6% of the data were missing. Data were missing because some students were ill or for other reasons not present in the class during the test administration. Furthermore, assumptions for multilevel analysis were checked (Hox et al., 2018). The sample size was sufficient, as calculated with SPA-ML (Moerbeek, 2015), based on a desired power of 0.80 and an assumed effect size of 0.30 in a three-level model. Furthermore, the assumption of linearity was met for all variables; however, for one variable, an outlier was detected and deleted (tier 2 academic words in the GAT on student level). In addition, the assumption of normally distributed residuals was mildly violated for the residuals at the first and second level of the GCT. However, this was not considered a problem since the maximum likelihood estimator is robust against this violation with a large sample size (Hox et al., 2018). Normality of residuals was more seriously violated for the geometry words used in the GAT, and for the aspects on the VAA. Therefore, robust standard errors were used and reported (Hox et al., 2018).

Results

In Tables 3, 4, 5, and 6, the means and standard deviations of students’ pre- and posttest scores on the GAT, geometrical vocabulary, GCT, and VAA are described. In Table 7, Spearman correlations between all measures on the pretest are presented. The correlations, for example, indicated that the measures of geometrical ability—GAT, GCT, and daily geometrical words—are significantly positively related. However, students’ use of academic geometrical words was negatively related to the GAT, GCT, and daily geometrical words.

Table 3 Descriptive statistics of students’ scores on the GAT
Full size table
Table 4 Descriptive statistics of ratio scores of geometrical vocabulary
Full size table
Table 5 Descriptive statistics of the GCT
Full size table
Table 6 Descriptive statistics of the VAA
Full size table
Table 7 Spearman correlations between the measures on the pretest
Full size table

Multilevel analyses showed that there was a linear relation between time and students’ scores on the GAT, t(3831) = 18.71, p < 0.001. On average, students’ scores on the GAT increased between the pre- and posttests. Furthermore, the relation between time and the GAT differed per class, χ2(88) = 343.50, p < 0.001. These differences, however, could not be explained by the MACE lessons series (t(90) = 1.61, p = 0.11), nor by the MACE PD program (t(90) = − 0.29, p = 0.77). In Table 8, only the results of the final model are presented. The results of all other models are included in Appendix 3.

Table 8 Multilevel results (final models) regarding geometrical ability
Full size table

With regard to geometrical vocabulary, a significant linear relationship was found between time and students’ use of daily (tier 1 t(4083) = 4.74, p < 0.001) and academic geometrical words (tier 2 t(4083) = − 4.11, p < 0.001) in the GAT. The proportion of daily geometrical words increased between the GAT pre- and posttests, but decreased for academic geometrical words. The rate of improvement differed between classes (tier 1 χ2(92) = 263.58, p < 0.001; tier 2 χ2(92) = 134.52, p < 0.01); students in some classes improved more regarding their use of daily and academic geometrical words in the GAT than students in other classes. With regard to the daily geometrical words (tier1), the difference could be explained by the participation in the MACE program (t(94) = 2.60, p < 0.05), but not by participation in the MACE PD program (t(94) = − 1.42, p = 0.16). When a class had received the MACE lesson series, the positive relation between time and daily geometrical words (tier 1) used in the GAT became stronger. With regard to academic geometrical words (tier 2), the difference between classes could not be explained by the MACE lesson series (t(94) = 0.36, p = 0.72), nor by participation of the teacher in the MACE PD program (t(94) = 0.99, p = 0.33). See Table 8 for the final models of the geometrical words used in the GAT.

Furthermore, multilevel analyses showed a linear relationship between time and geometrical creativity (t(3977) = 3.04, p < 0.01). On average, students’ scores on the GCT increased between the pre- and posttests. Furthermore, we found that the rate of improvement on the GCT varied between classes, χ2(90) = 238.94, p < 0.001. This variation, however, could not be explained neither by the MACE lesson series (t(91) = 0.74, p = 0.46) nor by the MACE PD program (t(91) = − 1.28, p = 0.20; see final model in Table 8).

Regarding visual arts perception, a linear relationship was found between time and the aspects “space” as used in the VAA (t(4206) = 7.80, p < 0.001), “space suggestion”(t(4206) = 2.37, p < 0.05), and “composition” (t(4206) = 6.19, p < 0.001). Students, on average, described more of these aspects in the VAA posttest compared with the VAA pretest. The rate of improvement on the aspects “space”(χ2(94) = 260.57, p < 0.001), “space suggestion” (χ2(94) = 232.81, p < 0.001), and “composition” (χ2(94) = 300.95, p < 0.001) differed between classes; students in some classes improved more in their use of these aspects in describing visual artworks than students in other classes. These differences between classes could be explained by the MACE lesson series (space, t(94) = 3.66, p < 0.01; space suggestion, t(94) = 2.14, p < 0.05; composition, t(94) = 4.88, p < 0.001). However, the MACE PD program did not show such an effect (space, t(94) = − 1.02, p = 0.31; space suggestion, t(94) = 1.13, p = 0.26; composition, t(94) = − 0.30, p = 0.76).

Regarding the aspect of shape used in the VAA, no linear relationship with time was found (t(4206) = 0.39, p = 0.70), indicating that students, on average, did not describe this aspect more frequently in the VAA posttest compared with the VAA pretest. This relation was the same for all classes (χ2(94) = 94.96, p = 0.45), indicating no effect of condition. The final multilevel models regarding the aspects used in the VAA are presented in Table 9. The results of the other models can be found in Appendix 3.

Table 9 Multilevel results (final models) regarding the aspect used in the VAA
Full size table

Discussion

The MACE program aimed to teach the (overlapping) curriculum goals of visual arts and the mathematical domain of geometry, and to promote students’ creative skills in both disciplines, by creating opportunities for students to act creatively in an integrated visual arts and geometry context. The program was evaluated in a quasi-experimental study in which students were assigned to three conditions: (1) students who received the MACE lesson series from their teachers who received a PD program, (2) students who received the MACE lesson series, and (3) students who received regular geometry lessons. Students’ growth between pre- and post-measurements of geometrical ability and visual arts perception were examined to test the effect of the conditions.

Students’ ability to understand and explain geometrical phenomena improved in all conditions. However, contrary to our expectations, no differences between conditions were found. A possible explanation is that the lessons of the comparison condition were actually also an intervention that improved regular geometry education. Teachers indicated that the lessons they taught were similar to regular geometry lessons, but that they enabled more interaction between students than they were used to. As a consequence, students in the comparison condition had more than in regular lesson opportunities to explain their thinking, to receive feedback, and to encounter other points of view (Jarvis, 2001), which could have enhanced their geometrical thinking (Beghetto & Kaufman, 2010; Taggar, 2002). Furthermore, more interaction between students could also evoke reflection, which might have enabled students to reach the same level of understanding as students who participated in the MACE program (Van den Heuvel-Panhuizen & Drijvers, 2014). Furthermore, in the comparison condition, the lessons were offered in a sequence, while usually the 4 to 6 geometry lessons are spread over the school year. Interestingly, our analyses showed that students in some classes significantly improved more on their ability to understand and explain geometrical phenomena than students in other classes. Differences between classes could not be explained by the type of lessons they received. This result seems to imply that for students’ ability to understand and explain geometrical phenomena, the content and structure of the lesson material are of less importance than other factors. Plausible factors could be the implementation of the lesson and the quality of the teacher. For example, despite the teaching materials and its related teaching approach, some teachers may stimulate more communication between students than other teachers, or may be better able to ask open questions that can extend students thinking, reasoning, and understanding than other teachers (Bostic, 2011). Future research should investigate these possible factors.

Students’ geometrical creative thinking also improved in all conditions, but—contrary to our expectations—did not differ between the conditions. We expected that implicitly and explicitly stimulating students to act creatively and think divergently (Sawyer, 2014), especially in integrated visual arts and geometry lessons, would lead to more improvement in students’ geometrical creativity compared with students who did not receive such stimulation. Although we found in a qualitative case study that students expressed more mathematically creative ideas and solutions in classroom dialogues during the MACE lessons than they did during a regular mathematics lesson (Schoevers et al., 2019), one MACE lesson per week may not be enough to bring large improvement of students’ geometrical creativity.

Regarding students’ use of geometrical vocabulary to explain geometric phenomena, we found a partial effect of the MACE program. Students who participated in the MACE program increased in their use of daily geometrical words proportional to the total number of words in their written explanations in the geometrical ability test more than the students who received regular geometrical lessons. However, the increase of students’ daily geometrical words was not a goal of the MACE program. Instead, increase of the use of academic geometrical words was a goal, which however was not influenced by the MACE program. In fact, students in all conditions used less academic geometrical words, controlled for the number of words in the written explanations at the posttest. Furthermore, contrary to our expectations, no effect was found for the MACE PD program. Since the importance and stimulation of geometrical words was emphasized both in the manual of the lesson series and in the PD program, we expected the students’ use of academic geometrical words to increase. One explanation for these results is that students used more words at the posttest to explain their answers compared with that at the pretest, but did not use more academic geometrical words. As a result, the proportion of academic geometrical words used decreased.

In contrast to the previous results, we did find that students’ perception regarding geometrical aspects in visual arts changed. As expected, students who received the MACE lesson series showed more improvement in describing geometrical aspects addressed in the lesson series (i.e. space, space suggestion, and composition, but not regarding the aspect of shape) in a visual artwork compared with students in the comparison group. Since students had to observe and analyze visual artworks mainly with regard to the aspects of space and patterns in every MACE lesson, they apparently changed their recognition of visual information in visual artworks in this respect (Kozbelt, 2001; Tishman et al., 1999). The aspect of shapes played a smaller role in the lesson series, explaining why no effects were found with regard to this aspect. Participation of the teacher in the MACE PD program did not affect students’ perception of the spatial aspects of visual art, probably because—as teachers indicated—the teaching manual of the MACE lesson series was elaborate and clear. For example, many sample questions related to the spatial aspects of visual art were stated in the manual. Since the teaching manual was well elaborated, the PD program probably had not much added value and did not affect students’ perception of spatial aspects of visual art.

Limitations and Future Research

It is important to take the limitations of the present study into account. A first limitation is that we were not able to randomly assign the teachers and students to the different conditions. A second limitation is the used measure of geometrical creativity. Although this measure, a multiple solution task, is commonly used in the field (Leikin, 2009), it may not have been sensitive enough to do full justice to the multidimensional construct of geometrical creativity. The measure does provide information on the cognitive aspect of geometrical creativity, but other measures could be used in future research to measure other dimensions of creativity as well, such as how creativity was verbally or non-verbally expressed by students in the classroom. A third limitation is that no classroom observations were conducted in the comparison group. If these would have been conducted, classroom factors could have been investigated that could possibly explain the differences between classes in students’ growth in understanding and explaining of geometric phenomena. Furthermore, another comparison group could have been used. Our current comparison group also received a lesson series with regular geometry lessons. The lessons differed in several aspects from the MACE lessons. However, we were not able to investigate differences with regard to real educational practice, in which geometry lessons are usually taught spread over the whole school year.

Conclusion

The MACE program had the aim to teach the (overlapping) curriculum goals of visual arts and the mathematical domain of geometry, and to promote students’ creative skills in both disciplines by creating opportunities for students to act creatively in an integrated visual arts and geometry context. Where in regular education, geometrical concepts are directly and time-efficiently taught, students that received the MACE lesson series reached the same level of geometrical understanding with open lessons in which they were able to express themselves creatively. Although students who received the MACE lesson series did not improve more on geometrical creativity and academic geometrical vocabulary than students who followed regular education, students did improve more in their ability to perceive geometrical aspects in visual arts and their use of daily geometrical words to describe geometric phenomena.

For educational practice, the results of this study imply that teachers could use the integrated MACE lesson series instead of regular geometry lessons, in order to teach the geometry curriculum and visual arts perception. Teaching in this integrated way may save time for teachers who experience a lot of time pressure to teach the curricula. If the integrated MACE approach and pedagogy are also applied to other mathematics lessons during the week, the integrated MACE approach may also be more effective for students’ creative skills. However, more research is necessary. This study is to our knowledge the first that evaluated the effectivity of integrated visual arts and geometry education with a clear theoretical framework and research design. The study and the theoretical framework can be a valuable contribution to research on interdisciplinary arts and mathematics education.