Abstract
Gap waveguide technology is particularly attractive for the design of passive elements in mm-wave systems. Recently, the so-called zero-gap implementation has proved to be very robust to manufacturing tolerances, while at the same time keeping the low loss associated to the contactless standard gap waveguide. In this paper, a Chebyshev filter working at 145 GHz based on this idea and intended to be used in a wireless communication system is designed and optimized. A conventional milling technique has been used in its fabrication, and good measured results have been obtained in a single-pass process.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Since the introduction of gap waveguide technology ten years ago [1], its use has been progressively extending to the design of components at increasingly higher frequencies. The main advantage of this technology for enabling manufacturing in millimeter range frequencies is the contactless characteristic. In any of the different proposed versions of the technology [2], components are manufactured in two pieces that do not require to ensure good electrical contact when they are assembled together.
Among the different versions of this technology, the groove version [3, 4] is the most suitable for the upper band of the millimeter range as it is the one with lower losses [2] and also because the conventional transitions for standard waveguides can be directly used to characterize the prototypes. In addition, the gap that was originally included in the first version of this technology can be suppressed as demonstrated in [5], consequently making the technology more robust to manufacturing tolerances. The designs made with this version are quite similar to designs made with conventional rectangular waveguides.
Along these years, band-pass filters in groove gap waveguide technology have been proposed. Some initial designs were made in the microwave frequency range [6], and later on, designs in the Ka band [7] and the popular 60-GHz band [8] have been also presented. Some more examples of filters designed with this version of the technology can be found in [9], [10], and [11].
The manufacturing of the required bed of nails (BoN) to implement this technology is typically made by milling. This technique has limited the designs at frequencies above V-band, as the pillars became too fragile. Some examples of manufacturing this technology with micromachine process were presented in [12]. However, nowadays, the manufacturing of pins or pillars with tiny dimensions and good accuracy is possible and in this work we propose for the first time the design and manufacturing of a band-pass filter at D-band.
In this paper, a zero-gap groove gap waveguide band-pass filter, designed and optimized to operate at 145 GHz, is presented. The details about the chosen topology and the design procedure are explained in Section 2. A demonstrator was successfully manufactured and measured. Some experimental results are discussed in Section 3, and finally, some conclusions about the potential of this technology are drawn.
2 Filter Design
A five-pole Chebyshev design was chosen for a center frequency of 145 GHz and a return loss level of 20 dB within a 6.5-GHz bandwidth. That corresponds to a ripple of only 0.044 dB in that passband. The filter coefficients are shown in Table 1.
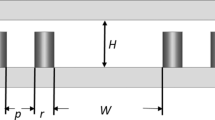
The impedance inverter model described in [13] was used to implement an iris-coupled waveguide filter. In this case, a groove waveguide was employed, keeping solid walls only for the cavities separations in which the irises are opened. Regarding the BoN, square pillars with a nominal side dimension a = 0.25 mm and a period p = 0.5 mm for both x and y directions were chosen. A pin arrangement in rows was selected to speed up the milling process by virtue of the minimization of the number of sweeps during the manufacturing process.
A pillar height h = 0.648 mm was selected. This value, in a zero-gap implementation, coincides with the rectangular waveguide height of the WR5.3 standard that will be used at the I/O ports as explained later.
Some simulations of the dispersion diagrams of the unit cell were carried out for the aforementioned parameters. Under lossless conditions, the dispersion diagram for the zero-gap implementation exhibits a forbidden frequency band up to 230 GHz. If a constant air gap of 0.025 mm, related to a possible manufacturing inaccuracy, is assumed, the forbidden band still extends from 66 to 212 GHz. That means that even if the lid is not in electrical contact with all the pillars, the BoN structure would continue blocking sideways propagation in our band of interest.
A separation of 1.651 mm was set between the centers of the pillars that define the groove cavities. This value is the nominal WR6 waveguide width and enables the operation of the filter well over the cutoff frequency of the fundamental mode. Three rows of pillars proved to provide sufficient blockage to assimilate the rectangular groove waveguide to a conventional one. Finally, lateral walls were added to fully enclose the filter into its package. Figure 1 shows all the described elements for one of the filter sections.
Using the commercial full-wave simulator CST Microwave Studio Ⓒ, the S-parameters for 20 different iris sizes were calculated with the aim of characterizing the coupling through the iris in terms of two parameters: the normalized coupling coefficients Kij and the phase correction for each T section, ϕ. Figure 2 displays the results for the simulated cases together with the interpolated curves that were used in the next step of the design.
Then, the filter coupling coefficients were calculated from the gi in Table 1 as described in [13], namely k01 = k56 = 0.415, k12 = k45 = 0.145 and k23 = k34 = 0.106.
These values were then applied to the curves in Fig. 2 to obtain the iris widths and cavity lengths of Table 2. Note that a correction in the fractional bandwidth \({\Delta }=\frac {\lambda _{1}-\lambda _{2}}{\lambda _{0}} \) was introduced due to the lack of a clear definition of the effective gap-groove waveguide width, that directly affects the propagation constant β and hence λ. Besides, the rows of pins have been positioned equispaced in each cavity of length li, that is, between the pair of irises that define each cavity. Despite the small differences in the positions of the pillars with respect to the regular cartesian grid with period p, there is not going to be important changes in the BoN behavior.
Given that the filter was going to be measured with WR5.3 waveguides to cover D-band and beyond, two transitions were needed from that geometry to the WR6 width used in the design. This represented an additional challenge in the design and realization since the filter passband is very close to the WR5.3 lower cut-off frequency. To this end, the distance between the pillars that conform to the groove has been linearly tapered between wg1 = 1.401 mm and wg2 = 1.2954 mm in seven rows between the filter ports and the first irises as shown in Fig. 3. The lateral distance between the three pillars (outwards) has been kept equal to the period p.
Finally, the inner corners of the cavity defined by the metal enclosure were rounded to model the actual result when using rotary cutters in the milling process. A radius R = 0.125 mm was chosen for this purpose. Figure 4 shows the filter layout and all the relevant geometrical parameters. The total size of the inner cavity is 14.934 × 4.401 mm.
3 Filter Realization and Characterization
The filter has been manufactured by a commercial supplier using traditional milling machining techniques. The achieved milling accuracy is estimated to be around 2 μ m. A schematic view from the simulations and the realized structure can be depicted in Fig. 5 and consists of the lower structure containing the pillars and the other half being the waveguide cover. One of the advantages of the gap structure is that the waveguide cover does not need to touch all pillars as mentioned. The filter finish has been realized using 1-μ m gold plating.
The characterization has been performed using Keysight N5222B PNA Microwave Network Analyzer using VDI extenders for the D-band. A waveguide calibration kit from VDI for the WR5.1 waveguide has been employed in the calibration procedure using TRL calibration kit and 16× sweep averaging with 401 frequency points.
The filter passband is shown in Fig. 6 comparing simulated and measured characteristics for the reflection and transmission coefficients. The filter exhibits an insertion loss of IL > − 2.2 dB over a passband bandwidth of 6 GHz (141–147 GHz). The 20-dB stopband rejection is at 150 GHz, and a rejection of better than − 50 dB is achieved above 160 GHz. The filter characteristics across the D-band is illustrated in Fig. 7. One can clearly depict a second passband around 210 GHz. The transmission and reflection characteristics across the band are very smooth without any additional resonances.
The overall characteristic is shifted in frequency by around 1 GHz, which is due to the Au plating of the pillars and the waveguide structure with a thickness of 1 μ m. This can be easily corrected for in future realizations by defining the according milling files. It should be emphasized that the results obtained are based on first-pass design without dedicated corrections for the milling process.
The filter shall be incorporated in a wireless communication system, which demands a low dispersion and flat group delay. Figure 8 provides measured and simulated results for the group delay versus frequency. Apart from the discussed frequency shift and a slightly higher absolute value for the group delay as compared to the predicted value, the group delay is in excellent agreement with simulations and is very smooth in the passband.
4 Conclusion
The designed filter has proved to have a good response in terms of matching, insertion loss, and group delay, being all of them very close to the expected values and it is suitable as a building block in wireless communication systems.
From a broader point of view, the flexibility and robustness of the zero-gap implementation make it a good candidate for the design of passive circuits in mm-wave frequency bands.
Change history
22 September 2022
A Correction to this paper has been published: https://doi.org/10.1007/s10762-021-00782-x
References
P. Kildal, E. Alfonso, A. Valero-Nogueira, and E. Rajo-Iglesias, Local Metamaterial-Based Waveguides in Gaps Between Parallel Metal Plates, IEEE Antennas and Wireless Propagation Letters 8 (2009), 84.
E. Rajo-Iglesias, M. Ferrando-Rocher, and A.U. Zaman, Gap Waveguide Technology for Millimeter-Wave Antenna Systems, IEEE Communications Magazine 56 (2018), no. 7, 14.
A. Berenguer, V. Fusco, D.E. Zelenchuk, D. Sánchez-Escuderos, M. Baquero-Escudero, and V.E. Boria-Esbert, Propagation Characteristics of Groove Gap Waveguide Below and Above Cutoff, IEEE Transactions on Microwave Theory and Techniques 64 (2016), no. 1, 27.
E. Rajo-Iglesias and P. Kildal, Groove gap waveguide: A rectangular waveguide between contactless metal plates enabled by parallel-plate cut-off, 2010.
A. Vosoogh, A. Uz Zaman, V. Vassilev, and J. Yang, Zero-Gap Waveguide: A Parallel Plate Waveguide With Flexible Mechanical Assembly for mm-Wave Antenna Applications, IEEE Transactions on Components, Packaging and Manufacturing Technology 8 (2018), no. 12, 2052.
A.U. Zaman, P. Kildal, and A.A. Kishk, Narrow-Band Microwave Filter Using High-Q Groove Gap Waveguide Resonators With Manufacturing Flexibility and No Sidewalls, IEEE Transactions on Components, Packaging and Manufacturing Technology 2 (2012), no. 11, 1882.
E.A. Alós, A.U. Zaman, and P. Kildal, Ka-Band Gap Waveguide Coupled-Resonator Filter for Radio Link Diplexer Application, IEEE Transactions on Components, Packaging and Manufacturing Technology 3 (2013), no. 5, 870, DOI https://doi.org/10.1109/TCPMT.2012.2231140.
A. del Olmo-Olmeda, M. Baquero-Escudero, V.E. Boria-Esbert, A. Valero-Nogueira, and A.J. Berenguer-Verdú, A novel band-pass filter topology for millimeter-wave applications based on the groove gap waveguide, 2013. https://doi.org/10.1109/MWSYM.2013.6697780.
A.K. Horestani and M. Shahabadi, Balanced Filter With Wideband Common-Mode Suppression in Groove Gap Waveguide Technology, IEEE Microwave and Wireless Components Letters 28 (2018), no. 2, 132.
M. Rezaee and A.U. Zaman, Realisation of carved and iris groove gap waveguide filter and E-plane diplexer for V-band radio link application, IET Microwaves, Antennas Propagation 11 (2017), no. 15, 2109.
B. Ahmadi and A. Banai, Direct Coupled Resonator Filters Realized by Gap Waveguide Technology, IEEE Transactions on Microwave Theory and Techniques 63 (2015), no. 10, 3445.
S. Rahiminejad, H. Raza, A.U. Zaman, S. Haasl, P. Enoksson, and P. Kildal, Micromachined gap waveguides for 100 GHz applications, 2013.
R.J. Cameron, C. Kudsia, and R. Mansour, Microwave Filters for Communication Systems: Fundamentals, Design and Applications, Wiley, New York, 2007.
Acknowledgments
The authors would like to thank the staff of TU Darmstadt in Germany for providing access to the measurement equipment.
Funding
This work has been partly funded by EU Commission within the H2020 Ultrawave project, Spanish Government under project TEC-2016-79700-C2-2-R, and by Chairs of Excellence project appointment at the Universidad Carlos III de Madrid, Madrid, Spain.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interests
The authors declare that they have no conflict of interest.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Vazquez-Roy, J.L., Rajo-Iglesias, E., Ulisse, G. et al. Design and Realization of a Band Pass Filter at D-band Using Gap Waveguide Technology. J Infrared Milli Terahz Waves 41, 1469–1477 (2020). https://doi.org/10.1007/s10762-020-00729-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10762-020-00729-8