1 Introduction

Diabetes is a growing problem that currently affects more than the 9% of the world population [1]. With prevalence rates increasing, the World Health Organization projects that diabetes will be the seventh leading cause of death by 2030 [2]. Managing the disease requires close monitoring of the glucose levels in the human blood, even multiple times per day for the genetically predisposed type I diabetes patients [3]. Glucose monitoring is currently performed by the painful, unhygienic and indiscreet procedure of drawing blood from the fingertips using a lancet and an electrochemical strip that is subsequently inserted into a glucose monitor device. There is currently no commercially widespread system that allows the monitoring of glucose levels using a painless and non-invasive method [4].

A variety of research methodologies targeting non-invasive estimation of blood glucose levels which do not rely on drawing blood or interstitial fluids have been investigated in the past. Many radio frequency (RF) methods have focused on using lower microwave frequencies (up to 20 GHz), and have employed different setups to measure relatively high glucose concentrations in controlled samples by extracting the sample’s permittivity. For example, dielectric spectroscopy was used in [5] to measure blood plasma in the range 0.5–20 GHz, and resonant cavity setups have been employed in [6, 7] operating between 2 and 3 GHz. Frequency ranges between 1.0–2.5 GHz [8] and 5.0–8.5 GHz [9] have also been used in configurations with antenna sensors. Higher microwave frequencies have been proposed in [10,11,12], but in a different context than in the present work. Only a limited number of experiments have been performed in the millimeter wave regime [11,12,13,14,15]. Specifically, the work presented in [13,14,15] showed a glucose study performed in a rat, where its glucose levels were changed intravenously by injecting glucose and insulin. Finally, the work in [16] used THz waves to detect water content changes in tissue, which can often indicate diabetic foot syndrome (albeit not directly measuring glucose level changes).

In our earlier work, a strong correlation between RF signal transmission and glucose concentration was demonstrated for saline laboratory samples loaded with glucose [17,18,19,20,21]. The system comprised two opposing patch antennas operating around 60 GHz, connected to a Network Analyzer (VNA). A tissue sample (typically a few mm thick) was sandwiched between the antennas while RF signal transmission through the sample was monitored. This work showed that transmission is preferred (as opposed to reflection only) because it has significantly higher sensitivity to glucose changes, particularly in the range between 58 and 62 GHz [17]. This occurs because the electromagnetic (EM) wave interrogates a much larger volume of glucose sample (or blood) through transmission, penetrating several millimeters inside the tissue. The work on this paper is an improved version of the system in [17], which has been developed to sense relative glucose changes in thin live tissues.

Another version of the system was tested in a proof-of-concept in vivo investigation in humans, showing promising initial results [21], but no consistent clean detection of glucose level changes. This is because several uncertainties were introduced when testing with live humans, such as uncontrolled skin and ambient temperatures and unwanted motion of the tissue being sampled due to the reactions of the subjects. Therefore, we could not categorically demonstrate that only blood glucose level changes were being detected. As a result, it was essential to perform a study in a more controlled environment using anesthetized animals. In contrast to the work in [19], the experimentally measured signal changes in the work presented here also match well analytical predictions, providing solid evidence for true glucose spike detection.

The system was used to perform an animal study on an anesthetized pig at Northwick Park Institute for Medical Research, London, UK. To the best of our knowledge, this study demonstrates for the first time a clear correlation of transmitted mm-wave signals with glucose levels changes in large animals.

Pigs are ideally suitable for this type of experiments because they are a good model for human obesity and diabetes since they have a similar cardiovascular anatomy, metabolism, and lipoprotein profile [22]. Additionally, it has been found that pigs are ideal for measuring a broad range of blood glucose concentrations within short time cycles [23].

In particular, our preliminary report [24] on this animal study has shown that, after an intravenous injection of 50 g of glucose, the blood glucose levels in pigs increased quickly and returned to the fasting concentration within 18–45 min after the injection. Moreover, a pig’s blood glucose level can drop to as low as 0.3–0.6 mmol/l, which would be considered hypoglycemic in humans and thus would be considered a dangerous level to measure in human participants. The ability to safely induce this range of hypo to hyper and back to hypoglycemic blood concentration in a short period is ideal for testing a novel glucometer through several cycles in a single experimental session. In addition, since the animals are anesthetized, there is little uncertainty introduced in the measured signals due to the subject’s motion.

The rest of the paper is organized as follows. Section 2 presents a summary of the glucose sensing system design and specifications, which have been presented and analyzed in more detail in our previous papers. Section 3 presents laboratory transmission measurements through water-based glucose samples at varying controlled concentrations, which are used to optimize the system and test its sensitivity ahead of the animal study. Section 4 reports the animal study measurement procedure,. The results of this study can be found in Section 5. A discussion on the validity of the study and suggestions for future work are presented in Section 6. Finally, Section 7 presents the conclusions of this study.

2 System Design

2.1 Description of the Glucose Sensing System

A more detailed description of the system can be found in [21]. Here, we summarize the key system aspects that are important to this animal study.

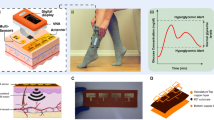
The main component of the glucose sensing system consists of a pair of opposing patch antennas (approximately 15 × 15 mm) operating in the V-band between 58 and 62 GHz with 3 GHz 10-dB bandwidth. Additional characterization of the antenna and simulations can be found in our previous work [20]. The antennas are enclosed in a custom-designed 3D-printed plastic holder and placed on a positioner capable of adjusting the antenna-sample distance to obtain optimal transmission results. A sample is placed between two acrylic windows and the two antennas, as shown in Fig. 1. The reflected and transmitted signals are measured using a VNA.

Fig. 1
figure 1

a Schematic version of the glucose sensing system. The sample is placed between two acrylic windows and 2 mm wave antennas that are connected to the VNA. b Photograph of the system with an acrylic tank filled with a controlled glucose solution as a sample. c Photograph of a similar system as b but the acrylic tank has been replaced by a pig’s ear in the animal study

Full size image

The 58–62 GHz band was chosen for two reasons: first, the wavelength (5 mm in free space) is short enough to allow the use of few millimeter-sized antennas and thus appropriate for implementing compact sensing systems; second, the skin depth at these frequencies is relatively large (0.5 mm approximately), thereby allowing good penetration through living tissues, beyond just sampling the skin surface.

2.2 Impact of the System’s Operating Frequency

For the system to monitor glucose changes (Δg) through mm-wave transmission data, the difference in the amplitude of the transmitted signal (ΔS21) must be higher than the uncertainty (ΔE) of the measurement instrument for the lowest desired glucose change in humans, which is estimated as Δg = 0.86 mmol/l (0.015 wt%) [25, 26]. The changes in Δg and ΔS21 are dependent on the frequency and the signal to noise ratio (SNR) of the setup; the changes in ΔE are dependent only on the SNR of the VNA used in our measurement system. Fig. 2 presents the analytically calculated optimal frequency for the lowest desired glucose changes against sample thickness for different noise floor values. This optimal frequency for our system was specifically calculated for Keysight’s E8361A PNA, using the highest noise floor (− 110 dB) specified in the instrument’s calibration specifications and assuming 0 dBm input power.

Fig. 2
figure 2

Optimal frequency of operation for different sample thicknesses and noise values. The graph was produced assuming an input power of 0 dBm. The red solid line shows to the optimal frequencies obtained when the noise corresponds to the noise floor specified on the calibration specifications of the E8361 A PNA (− 110 dBm). The green dotted line corresponds to the optimal frequency obtained when the noise is − 137 dBm. The blue dashed line corresponds to the optimal frequency obtained when the noise considered for the calculations (− 164 dBm) is the thermal noise obtained at room temperature (26.9°C) and for a bandwidth of 10 Hz

Full size image

For a given sample thickness, a higher frequency leads to larger ΔS21, which is preferable. However, the absolute value of S21 is decreased due to the increased attenuation (the sample becomes electrically thicker), and will at some point surpass the uncertainty ΔΕ of the PNA. The optimal frequency against sample thickness shown in Fig. 2 (solid line) is the maximum frequency for which the increasing uncertainty remains below the desired ΔS21 change corresponding to Δg = 0.86 mmol/l.

In the frequency range of 58–62 GHz where the system’s antennas were designed to operate in this study, Fig. 2 suggests that our instrument (E8361A PNA) can measure with enough accuracy the lowest desired glucose change in a sample within the typical thickness of a pig’s ear (2.5–3 mm). This figure also shows that for larger SNRs corresponding to lower noise values, higher frequencies would be more suitable to detect given changes in glucose. At the same time, thicker samples would be better sampled with lower frequencies.

3 Preliminary Study with Controlled Water-Based Glucose Samples Mimicking the Pig’s Ear

In our previous work [17], a linear relationship was obtained between the transmission coefficient S21, and the amount of glucose in the sample using open waveguides as transmitting and receiving sensors. To confirm the same correlation using patch antennas and samples that can mimic transmission through the pig’s ear, a preliminary experimental study with controlled water-based glucose solutions was performed, assisted by analytical calculations to determine the expected transmission levels.

The controlled glucose solutions were placed in an acrylic (ε = 2.53, tanδ = 0.0119 at 60-GHz [27]) tank. The transversal dimensions of the tank were determined using a simplified analytical calculation such that they exhibit similar transmission levels as the transmission through a 3 mm thick animal tissue (3 mm is the typical pig ear thickness). For this calculation, we approximated the ear with a three-layer stack model: two 1mm skin (ε = 7.98, tanδ = 1.366 at 60 GHz [28]) layers sandwiching a 1mm layer of blood (ε = 10.1, tanδ = 1.09 at 60 GHz [29]). The transmission coefficient was calculated using the standard transmission and reflection equations for a plane wave incident on a transversely infinite layer [30]. The same method was used to calculate the transmission through the acrylic tank containing water.

Free space losses, connector losses, and antenna gains were added to the losses calculated by the three-layer analytical model, in order to obtain more accurate transmission values. For our specific system, connector losses are 0.3 dB per connector (one for each antenna); each antenna’s gain is 10.4 dB and the path loss is 20 dB. The expected transmission coefficients are shown in the third column of Table 1, along with the value that was experimentally measured in the fourth column for comparison. The transmission levels calculated for the skin-blood-skin model appeared to be similar to the transmission levels obtained for a “3-2-3” tank, acrylic (3 mm)-water (2 mm)-acrylic (3 mm). These analytically calculated transmission coefficients are shown in the second column of Table 1.

Table 1 Analytical transmission coefficients for a skin-blood-skin slab at 60.25 GHz and acrylic-water-acrylic slab at 58.60 GHz. The second column shows the ideal transmission coefficient values. The third column shows the transmission coefficients when the system losses are added to the ideal values. The fourth column shows the agreement with the experimentally measured transmission coefficient
Full size table

This simplified analysis indicated that a tank with 2 mm thick water sample would yield similar transmission results as the expected transmission through a pig’s ear. Such a “3-2-3” acrylic tank, with surface area 60 mm by 40 mm, was then constructed for the water-based transmission measurements. The experimental setup used was as shown in Fig. 1a, replacing the sample with the 3-2-3 tank. For these measurements, the antennas were separated by 13.1 mm. Note that the 3 mm thick walls of the tank were chosen for mechanical stability reasons and that the acrylic material does not affect the transmission levels as significantly as the water-based solution placed in between.

After determining the most suitable tank configuration to match the skin-blood-skin model transmission levels, we performed transmission measurements by filling the tank with different glucose solutions of varying concentrations, ranging from 267 to 1.4 mmol/l. Between each solution, distilled water was inserted in the tank to avoid contamination between samples, following the same procedure as in our previous work [17].

Figure 3 presents the transmission coefficient against glucose concentration for the measurements and the analytical calculation. For both cases, there is a linear relationship between the transmission coefficient and the amount of glucose, with a 0.005 dB/(mmol/l) slope for the measurement and a 0.011 dB/(mmol/l) slope for the analytical calculation. In the measurement, the error bars represent the standard deviation of the six measurements that were performed. This standard deviation varies between 0.12 and 0.18 dB depending on the glucose solution. In this case, the standard deviation depends on the measured transmission level, lower transmission levels exhibit higher standard deviations due to the lower SNR.

Fig. 3
figure 3

Transmission against glucose concentration at 58.60 GHz. The solid line corresponds to the measured transmission coefficient using the setup from Fig. 1a. The error bars were obtained after six rounds of measurements. The dashed line corresponds to the analytical calculations, the error bars in this case are due to inaccuracies in the measurement of the dielectric constant of the glucose solutions

Full size image

The discrepancy in slope values between the analytical calculation and the measurements can be attributed to two different factors: discrepancy in the material properties and difference in the excitation of the transmitted signal. The analytical calculation uses fitted first order Debye models to the measured data to model the glucose samples. These measurements are subject to experimental errors and temperature drifts. Therefore, the measured properties of the samples used for the analytical calculations might be slightly different than the properties of the samples used in the experiments. Further discussion of this source of error can be found in our previous work [17]. The differences in excitation source in the analytical calculations and the measurements can also be a source of discrepancy, noting that all the analytical calculations assume plane waves while the measurements where performed using patch antennas.

4 Measurement Procedure

The glucose sensing system was attached to a pig’s ear over a 6 h period, while controlled glucose-loaded solutions were intravenously injected at regular intervals, causing spikes in the animal’s blood glucose concentration. The glucose concentration changes were monitored using the transmission of the RF signal, as well as a spectrophotometric clinical blood chemistry analyzer (iLab 650 by Diamond Diagnostics) and a commercially available glucometer (Contour Next EZ by Bayer).

In total, five glucose cycles were induced to the animal, as shown in Fig. 4. Each cycle started by injecting a sterile sample made of glucose diluted in a saline solution (0.9% NaCl) intravenously. When the sample was injected, the glucose levels spiked within a few seconds. After about 1 h, the glucose in the bloodstream gradually returned to the pre-injection level and then the next cycle was induced. The glucose injected was 8 g for the first and second cycles, 10 g for the third cycle, and 12 g for the fourth and fifth cycles. These samples were prepared in-house using sterile equipment and following the same procedure as the one followed in the previous work [17].

Fig. 4
figure 4

Glucose levels against time. This plot shows the five glucose cycles. The gray vertical lines correspond to the glucose injection times and the numbers next to them show the amount of glucose injected on each cycle

Full size image

The specific amount of glucose injected was estimated to produce a sufficiently high glucose peak within safety limits. In typical intravenous glucose tolerance tests (IVGTT), a value of 250 mg of glucose per kilogram of body mass is loaded [31]. In our study, 500 mg/kg of mass glucose loading was used to test the system over wider concentration ranges. Blood samples were extracted every 30 s while the glucose spike lasted (typically for the first 11 min after the glucose injection), and then less frequently every 1, 2, and 5 min while the glucose levels were returning to normal values.

Before the study started, the glucose sensing system was calibrated without the antennas in place using a Keysight Electronic Calibration Module (N4694). Subsequently, the antennas were attached, and the system was placed in the first position in the ear. Transmission and reflection measurements were continuously recorded over the 6 h period that the animal was subjected to the blood glucose test. The duration of each RF measurement was 12 s. These results were then correlated in time to the invasive blood measurements in post-processing.

In each cycle, different antenna positions on the ear and different distances between antennas were tested, in order to observe detuning effects and how the transmission was affected. During the two first cycles, the antennas were placed on top of a vein and separated by 18 mm. For the third cycle, the antennas were placed on top of the same vein but, in this case, separated by 10.9 mm. For the fourth and the fifth cycles, the antennas were located at the edge of the ear (where no vein was running through) and separated by 14.9 mm. The reflection results for each of these cases are shown in the previous work from the authors [24]. This exercise concluded that higher glucose sensitivity and best results were achieved when the antennas were placed on top of a vein and were separated by 10.9 mm. The differences in the antenna distances and glucose concentrations for each of the five measured cycles did not allow us to measure under the same conditions more than once, in order to check the repeatability and stability of the in vivo data; this objective will be pursued in a subsequent animal study.

5 Results

First, we estimate the transmission coefficient difference that is expected to be observed when injecting 10 g of glucose into the animal, in order to assess whether the expected system sensitivity in (2) is in acceptable agreement with our measured in vivo data. Since glucose (C6H12O6) has a molar mass of 180 g/mol, a total of 55 mmol of substance are injected into the animal’s bloodstream. Since pigs typically have a blood volume of 65 ml/kg [32], the 22 kg subject of the study would carry approximately 1.43 l of blood. Hence, the expected additional concentration of blood glucose in the animal soon after injection is approximately Δg = 55/1.43 l = 38.5 mmol/l. For a d = 3 mm thick tissue sample such as the ear, the sensitivity value was calculated in [21] as S = 5.4 × 10−3 dB/((mmol/l)/mm), which yields an expected transmission coefficient change equal to ΔS21 = S*Δg*d = 0.62 dB.

We note that an analytical time-dependent estimation of the change in glucose levels is not possible at this stage, as there are too many processes involved in affecting the glucose level concentration, such as the injection of insulin by the pancreas and the circulation of blood and glucose around the vessels of the body.

Figure 5 shows the blood glucose levels from the iLab650 and the Contour Next EZ and the transmission results from our sensor against time for the third glucose cycle. The iLab650 and the glucometer results show that after the glucose is injected in the bloodstream, there is an immediate and expected spike on the glucose content in blood. During this spike, the glucose levels reached a maximum of 50 mmol/l (50 mmol/l is the maximum reading that the iLab650 and the glucometer offer and therefore the glucose spike could be higher). After the glucose spike, the additional amount of glucose present in the bloodstream is naturally regulated by the animal’s pancreas, and the glucose level slowly returns to a pre-injection value, 11.5 mmol/l. A similar behavior is observed for the transmitted signal through our system in Fig. 5. Transmission levels reach a spike of − 55.6 dB and then regularly drop to − 56.2 dB. This difference is 0.6 dB, which is in line with the expected value of 0.62 dB provided by the analytical calculation.

Fig. 5
figure 5

Transmission coefficient at 60.25 GHz and glucose level against time. The iLab650, red dashed line, and the glucometer, green dotted line, results correspond to the left y-axis and the transmission coefficient, blue solid line, corresponds to the right y-axis. The time has been offset to have t = 0 min for the injection time. The transmission data shown in the figure has been subjected to a moving average post-processing method to minimize the noise in the signal

Full size image

Figure 5 also shows that there is a 13 min delay between the venous blood glucose spike and the sensor glucose speak. The invasive method used during the experiments extracts the glucose values directly from arterial blood. However, in this study, the non-invasive method was placed along the ear. This area can cause a delay in blood glucose spike for two reasons. First, it is located further away from where the glucose solution was injected. Second, although the area is convenient for the sensor placement, it is not particularly rich in blood and contains significant amounts of interstitial fluid. It is well known that glucose spikes in interstitial fluid can have typical spike delays between 5 and 20 min, depending on the area under test [33]. As a result, the measured 13 min delay is inevitable for the particular setup examined here. Future tests will be performed in other areas rich in blood and closer to the injection point, in order to minimize this delay.

6 Results Discussion

In this section, we wish to comment on the validity of the above animal study results, to compare directly with other work in mm-waves for glucose sensing and to outline possible options for improving the system sensitivity.

The work presented has shown that the system in its current form could detect spikes in glucose levels using transmission of mm-waves. While only a single proof of concept-measured result is presented (Fig. 5), the collected data are consistent with the expected signal when considering the physiology of the animal’s body and the physics of the signal changes during transmission through lossy tissue. The measured spike in S21 levels (0.60 dB) agrees well independently with both analytical calculations (0.62 dB, section 5) and the laboratory measurements of the simplified model, acrylic tank with the glucose-loaded water, (0.40 dB, section 3). This supporting evidence relies on accurate measurements for the dielectric relaxation models of glucose in liquids. The time delay in the S21 signal peaking is also understood based on the locations that were sampled (jugular vein for the invasive measurement and the ear for the non-invasive one).

This work complements earlier results in the field with in vivo tests done in rats and humans using mm-wave transmission. In [14], a proof of concept was presented for detecting glucose changes in rats. The glucose changes were closer to the human physiological levels than what presented in this work, and the authors experimented with introducing insulin to the animal to better control the glucose levels. In rats, however, the sample area (ear) was very thin accentuating the sensitivity of the measurements to sensor placement and blood drawn. In the human work published by the authors of this paper [20], the results were not supported by simulations and were more prone to errors due to the uncertainties introduced by sampling hands (mainly skin temperature changes and hand motion causing changes in the received signals). The work presented here does not suffer from these uncertainties and thus increases the body of evidence that mm-wave transmission is a viable technique for detecting glucose changes.

While the system presented here is capable of detecting glucose spikes, it is natural to wish to improve its sensitivity so that it can detect more physiologically relevant glucose level changes (4–10 mmol/l) and thus become diagnostically useful. Considering that the expected sensitivity of the system is 5.4 × 10−3 dB/((mmol/l)/mm) [20], for a 0.86 mmol/l change to be accurately detected over a 3 mm tissue, a change in S21 of 0.01 dB should be reliably detected. This can be achieved by (i) improving the SNR at the receiving end of the system and (ii) ensuring that external factors such as skin temperature and motion are carefully monitored and their effects subtracted from the raw transmission signal. To decrease the uncertainty of the measurements by increasing the SNR, we plan to integrate a thin metamaterial matching layer [34] in combination with a linear amplifier. Moreover, the next generation system will incorporate multiple sensors to monitor environmental factors that can affect the signal, such as temperature and motion.

7 Conclusions

This paper presents a laboratory prototype system to measure glucose changes in the bloodstream. The system consists of two patch antennas operating around 60 GHz placed on opposing sides of a sample. Transmission measurements through a pig’s ear were collected during a glucose blood test. A known amount of glucose was injected to the pig’s bloodstream inducing hyperglycemia to the animal. During the test, transmission measurements were recorded every 12 s. Moreover, blood samples were simultaneously taken and analyzed for their glucose concentration using an iLab650 equipment and a commercial glucometer. Transmission measurements correlated with direct blood glucose measurements, both featuring spikes followed by a slow decay in the signal. The transmission measurements presented a 13-min time delay when compared to the actual blood glucose measurements. This delay is expected based on the location chosen for the transmission measurements, which is not rich in blood but rather interstitial tissue.

These preliminary results suggest that the proposed system has the potential to detect glucose changes in the bloodstream. Future work will test the repeatability of these measurements and the accuracy of estimating glucose changes directly from changes in the signals transmitted by our experimental system.