Abstract
The ‘THz Torch’ concept was recently introduced by the authors for providing secure wireless communications over short distances within the thermal infrared (10-100 THz). Unlike conventional systems, thermal infrared can exploit front-end thermodynamics with engineered blackbody radiation. For the first time, a detailed power link budget analysis is given for this new form of wireless link. The mathematical modeling of a short end-to-end link is provided, which integrates thermodynamics into conventional signal and noise power analysis. As expected from the Friis formula for noise, it is found that the noise contribution from the pyroelectric detector dominates intrinsic noise. From output signal and noise voltage measurements, experimental values for signal-to-noise ratio (SNR) are obtained and compared with calculated predictions. As with conventional communications systems, it is shown for the first time that the measured SNR and measured bit error rate found with this thermodynamics-based system resembles classical empirical models. Our system analysis can serve as an invaluable tool for the development of thermal infrared systems, accurately characterizing each individual channel and, thus, enables the performance of multi-channel ‘THz Torch’ systems to be optimized.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Until very recently, there has been little in the way of enabling technologies within thermal infrared (ca. 10-100 THz) part of the frequency spectrum to support wireless communications. However, the authors previously demonstrated that the thermal infrared (IR) offers opportunities for developing secure communications within this largely unregulated part of the electromagnetic spectrum. The ‘THz Torch’ concept, recently introduced by the authors, fundamentally exploits engineered blackbody radiation, by partitioning thermally-generated spectral power into pre-defined frequency channels; the energy in each channel is then independently pulsed modulated to create a robust form of short-range secure communications in the far/mid infrared [1–7]. For example, an octave bandwidth (25-50 THz) single-channel link with a data rate of 760 bps was reported [3, 4]. Multi-channel ‘THz Torch’ systems were introduced with multiplexing schemes to increase the level of security, at the physical layer; first with frequency division multiplexing (FDM) [2, 4] and then very recently with frequency-hopping spread-spectrum (FHSS) [5]. Indeed, the resilience to both interception and jamming with 2,560 bps FDM and 640 bps FHSS systems was demonstrated in [5]. Furthermore, the radiation mechanisms associated with the thermal transducer were analysed in [7].
There have been many short-range wireless communications systems operating at different wavelengths. In the visible (390 < λ [nm] < 760) and near infrared (760 < λ [nm] < 2,500) ranges, light-emitting diodes (LEDs) have been widely used to establish wireless communications links due to the superior illumination efficiency, high modulation speed and low cost [8–11]. Wavelengths from 780 to 950 nm are currently the best choice for infrared indoor wireless systems. In this range, low cost LEDs are readily available and this wavelength matches the peak responsivity of inexpensive silicon photodiodes [11]. The Infrared Data Association (IrDA) has established a complete set of protocols for wireless infrared communications. For the Infrared Physical Layer Specification (IrPHY), LEDs with wavelength of 850 to 900 nm are employed, having data rates starting from 2.4 kbps up to 1 Gbps (GigaIR). The transmission ranges are: 1 m for standard applications, 0.2 m for low-power-to-low-power applications and several meters for GigaIR [12]. The primary drawback of radiation in visible and near infrared (NIR) bands relates to eye safety; it can pass through the human cornea and be focused by the lens onto the retina, where it can potentially induce thermal damage [8]. The cornea is opaque to radiation at wavelengths beyond approximately 1,400 nm, greatly reducing potential ocular hazards. Therefore, from a safety perspective, it is believed that the infrared C-band (1,530-1,565 nm) may be better suited. Unfortunately, the photodiodes available for this range, which are made of Ge or InGaAs, have much higher costs and capacitances per unit area than silicon-based detectors [8]. Furthermore, NIR systems experience atmospheric absorption, scattering losses and scintillation effects [13], although it is not considered to be a hurdle for short-range communications.
By operating in the mid- or long-wavelength infrared (MWIR or LWIR) regions, enhanced link and increased transmission range can be achieved, due to a lower susceptibility to atmospheric affects [14]. Although LEDs operating at MWIR have been demonstrated [15–17], the output power decreases at longer wavelengths, from W power levels in the NIR range to several μW at a wavelength of 4.6 μm [16]. On the other hand, the unit price increases, from tens of cents up to hundreds of dollars. These facts limit the real-world applications of LEDs at such wavelengths. Within MWIR and LWIR ranges, semiconductor lasers or nonlinear optical devices are generally preferred for free-space wireless communications. The MWIR spectral band, defined from 3 to 5 μm, is considered to be eye-safe, with a low loss atmospheric window and have low thermal and solar background emissions [18]. A short-range wireless link using an interband cascade laser has been demonstrated, having a 70 Mbps data rate and 1 m transmission range [19]. A long distance (i.e., >5 km) free-space communications link has also been reported using an optical parametric oscillator device, showing the potential for realistic battlefield scenarios [18].
In the LWIR range, the 8 to 14 μm atmospheric transmission window is often employed for free-space wireless communications, due to its superior penetration of atmospheric obscurants such as fog, smoke and dust [20]. In the past, 10 μm CO2 lasers were deployed, in spite of their limitations of large size, high power consumption and inability to modulate at high speeds [21]. More recently, the emerging quantum cascade laser (QCL) technology has drawn broad attention for MWIR and LWIR applications, due to its compact size, be-spoke emission characteristics and improved power efficiency [22–24]. However, these laser sources are still considered luxury (non-ubiquitous) products on the domestic market, and only high-end users (e.g., scientific or military) can afford and/or physically accommodate.
Compared to wireless communications systems at other wavelengths, our thermodynamics-based system is inherently low cost and can be secure [5]. With the former, thermal sources and detectors are employed to establish the communications link, significantly decreasing the cost for the complete system. Furthermore, the output power level of the transmitter can be controlled simply by changing the bias current. Although 800 nm systems based on LEDs have similar cost and complexity, they are not spectrally tunable and the output power from LEDs has to be limited under a certain threshold, due to safety considerations. Our wireless communications system has its shortest operating wavelength of >3 μm and can be considered to be eye-safe. With the latter, it has been experimentally verified that in order to undermine the inherent immunity to interference and interception, both the jammer and intruding receiver, respectively, must be designed to have: (1) a significant amount of overlapping spectral channel bandwidths; (2) similar modulation frequency; (3) line of sight detection and (4) synchronized hopping pattern (with FHSS) [5]. It should be noted that although such thermal-based sources offer many benefits (e.g., simplicity, ease of tuning and affordability), the main drawback is that there is no signal coherency. Thus, only the intensity of the band-limited output power can be controlled and detected. Moreover, due to the large thermal time constants associated with the sources and detectors, as well as issues associated with spreading loss, this wireless communications link is expected to work at lower data rates and over a shorter range.
To assess the performance of this thermodynamics-based link, accurate signal and noise power link budget analysis is required. In this paper, for the first time, we report on the detailed power link budget analysis for the thermal infrared wireless communications system using engineered blackbody radiation. Here, a generic 4-channel system, with a 640 bps data rate per channel and a transmission range of 1 cm is investigated as a function of channel transmitter bias currents. The calculated output signal and noise voltages from each of the uncorrelated channel receivers are compared with measured values. Furthermore, the signal-to-noise ratios (SNRs) for each channel are measured, showing good agreement with calculated results.
2 System overview
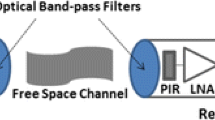
The basic architecture for a single-channel ‘THz Torch’ link is shown in Fig. 1 [1–6]. With our particular setup, the transmitter consists of five miniature incandescent light bulbs connected in series. The emitted output power is then filtered by an optical coating THz band-pass filter (BPF) and the band-limited thermal power is modulated using on-off keying (OOK) with polar non-return-to-zero (NRZ) pulses. One of the key advantages of this technology is that power amplification is not required, which would be technologically difficult and prohibitively expensive to implement at terahertz frequencies. Instead, increasing the level of transmit power can be as easy as increasing the bias current through the bulb array and/or increasing the number or size of the bulbs. The received output power is first filtered (by a THz BPF identical to that at the transmitter) and then detected; the pyroelectric infrared (PIR) sensor creates an electrical signal that is amplified and digitized by the back-end electronics, which contains a baseband (BB) low noise amplifier (LNA), baseband BPF and Schmitt trigger.
Basic architecture for ultra-low cost ON-OFF keying ‘THz Torch’ wireless link (reproduced from [5]).
The overall signal power link budget breaks down into three blocks (transmitter, free space channel and receiver), as shown in Fig. 2. Here, I filament is the radiant intensity of the tungsten filament; T G is the power transmittance of the bulb’s glass envelope; I primary and I secondary are the radiant intensity from primary and secondary radiation mechanism, respectively; \( {T}_{THz\_BPF} \) is the average power transmittance of the optical coating band-pass filter; I TX is the total radiant intensity from the channel transmitter’s source; L FS is the free space channel loss; P RX is the peak-to-peak power incident on the sensor; R V is the voltage responsivity of the PIR sensor; u is the output RMS voltage from the detector; \( {A}_{BB\_LNA} \) is the voltage gain of the baseband LNA; \( {A}_{BB\_BPF} \) is the voltage gain of the baseband BPF; and V out is the output RMS voltage at the channel receiver.
3 Transmitter output radiant intensity
The incandescent light bulb represents a convenient thermal IR blackbody source. Given that it has an absolute temperature of T [K] and can be approximated as a blackbody radiator with emissivity ε(λ,T), its spectral radiance can be calculated using Planck's law
where λ [m] is the wavelength in free space; h [J s] is the Planck constant; c [m/s] is the speed of light in vacuum; and k B [J/K] is the Boltzmann constant.
Similarly, the gas surrounding the filament can also be approximated as a blackbody, emitting at ambient temperature T 0 [K]. Assuming the gas and the filament have the same temperature and wavelength dependent emissivity the net radiance emanating from the filament is given by
Taking the effective radiating area into account and then integrating over the spectral band of interest, the band-limited net output radiant intensity can be expressed as
where A eff [m2] is the total effective radiating area of the radiator; λ 1 and λ 2 are the free space wavelengths associated with the lower and upper frequency of interest, respectively.
In our case, the output radiant intensity can include both primary radiation from the tungsten filaments (in the spectral region dominated by high transmittance through the glass envelope) and secondary radiation from the bulbs’ glass envelopes (in the spectral region dominated by high absorption within the glass envelope), which are heated by their filaments. The radiant intensity from the primary radiation can be expressed as
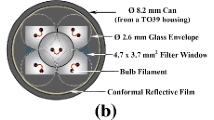
where T filament represents the working temperature for all identical filaments, A eff_filament = A filament /2 [m2] is the estimated total effective radiating area for five filaments, A filament = 12.73 mm2 for the five filaments [4], and T G (λ) is the power transmittance of the glass envelope in thermal equilibrium.
A material’s emissivity is normally defined as a function of both wavelength and temperature. However, to a good approximation for our application, the filament can be assumed to be a ‘grey surface’, thus, removing its wavelength dependency. Measured data for the average emissivity of tungsten, as a function of temperature, has been previously sourced from [25] and empirically fitted by the following [4]
Using measured data for the complex index of refraction [26], the power transmittance, reflectance and absorbance can be calculated using the methodology described in [27]. Fig. 3 shows the calculated values against frequency for typical (soda lime silica) window glass at a room temperature of 293 K. It can be seen that typical window glass can be considered opaque below ~60 THz. For most thermal infrared applications, this would only allow its use in its transparent region between ca. 70 to 100 THz. Fortunately, for our ‘THz Torch’ applications, the high absorbance will provide a secondary source of blackbody radiation within the opaque spectral region of the glass.
The radiant intensity from the secondary radiation can be expressed as
where A eff_glass [m2] is the total effective radiating area for the glass envelopes and ε glass (λ, T glass ) is the emissivity of the glass envelope having an outer surface temperature T glass . Here, we assume that ε glass (λ, T glass ) does not change significantly as temperature increases from the ambient room temperature of 293 K to the highest elevated temperature of 366 K; this is a reasonable assumption, as stated in [25]. Furthermore, according to Kirchhoff's law of thermal radiation, emissivity is equal to the power absorbance when in thermodynamic equilibrium. Therefore, the absorbance shown in Fig. 3 can be used as the frequency-dependent emissivity of the glass envelope to give ε glass (λ).
With our particular 5-bulb array configuration, the radiant intensity from secondary radiation can be further separated out into two parts: the central higher temperature region and its surrounding lower temperature region. Therefore, (7) and (8) can be re-written as
where T high and T low are the average temperatures for the high and low temperature regions, respectively; A eff_glass_high ≈ D 2 (1 − π/4) = 1.45 mm2 is the effective total radiating area of the higher temperature region from within our five-bulb array; \( {A}_{eff\_ glass\_ low}\approx 8\pi {\left(\mathrm{D}/2\right)}^2=42.47 \) mm2 is the effective total radiating area of the lower temperature region; and D is the diameter of the bulb’s glass envelope (2.6 mm in our case) [4].
The calculated filament temperatures [4] and the measured glass envelope temperatures over different regions within the source (using a FLIR E60 thermal imaging camera), are given in Table 1, for different bias currents. Note that the average temperature of the glass envelope is only slightly higher than the low temperature, since \( {A}_{eff\_ glass\_ high}\ll {A}_{eff\_ glass\_ low} \). By splitting the radiant intensity from secondary radiation into two parts, the temperature distribution and output radiant intensity estimation can be described more accurately.
The overall total radiant intensity from the transmitter, with contributions from both radiation mechanisms, can be expressed by
where, \( {A}_{THz\_BPF}=3.7\times 4.7 \) mm2 is the aperture size for the THz BPF, \( {A}_{eff\_ glass}={A}_{eff\_ glass\_ high}+{A}_{eff\_ glass\_ low}\approx 43.92 \) mm2, giving an transmitter aperture efficiency of \( \frac{A_{THz\_BPF}}{A_{eff\_ glass}}\approx 40\%. \)
Four 1 mm thick optical coating filters, sourced from Northumbria Optical Coatings Ltd. [28], are employed to define four non-overlapping frequency bands within the far/mid-infrared spectral range. The measured transmittances for each filter are given in Fig. 4, from 17 to 100 THz, and Table 2 [28]. The calculated net spectral radiance from primary and secondary radiation, at a bias current of 44 mA, is also shown in Fig. 4. It should be noted that when the total effective radiating areas of \( {A}_{eff\_ filament} \) and \( {A}_{eff\_ glass} \) are taken into account for the filament and glass envelope, respectively, the resulting radiant intensities are of the same order of magnitude from the two sources of radiation [7]. Furthermore, it is clearly shown that at a bias current of 44 mA, Channel A, C and D are expected to have higher output radiated power, as the spectral radiance peaks locate within the pass bands of their respective filters at this bias point. On the other hand, Channel B is away from either radiation peaks, giving the lowest output radiated power of the four channels, as will be confirmed experimentally in Section 5.
4 Free space losses
Free space losses include both spreading losses and atmospheric attenuation. With the latter, clear conditions are assumed throughout. If one considers the transmitter to be a point source Lambertian radiator, which radiates uniformly in all directions, the free space loss L FS can be calculated by applying Lambert’s cosine law to give
where T ATMOSPHERIC is the atmospheric power transmittance averaged across the channel bandwidth for a specific propagation distance (1 cm in our case); A S = 3 × 3 mm2 is the area of the detector’s sensing element; R = 13.8 mm is the total transmission distance in free space between the point source and detecting element of the PIR sensor (i.e., 1 cm distance between transmitter and receiver, plus the 2 mm space between the bulbs and the optical coating filter, plus the 1.8 mm distance between the receiver’s optical coating filter and sensing element); θ is the angle between the central line of sight and the offset from the surface normal of the detector (zero in our case).
For short-range communications, T ATMOSPHERIC is expected to be unity. To confirm this, Line-By-Line Radiative Transfer Model (LBLRTM) simulation software is used. This is an accurate, efficient and highly flexible model for calculating spectral transmittance and radiance, representing the best approach for calculating the atmospheric attenuation for each of the four channels.
LBLRTM extracts absorption line parameters from the HITRAN line database [29], as well as additional line parameters from other sources. It incorporates the water vapor continuum absorption model, as well as continuum extinctions for carbon dioxide, oxygen, nitrogen and ozone [30]. Since only generic atmospheric attenuation is being investigated in this section, a horizontally homogeneous atmospheric profile based on the values given at sea-level for the US Standard 1976 Model [31] is assumed, where temperature and atmospheric pressure are 288.15 K and 101.325 kPa, respectively. The 1976 US Standard atmosphere was defined to be representative of annual average conditions experienced at mid-latitudes. Note that the effects of atmospheric ionization from solar radiation is not an issue at the wavelengths considered. Furthermore, at the shorter wavelengths (≳75 THz, i.e., ≲4 μm) considered in this study, the influence of scattering from atmospheric aerosol (dust, smoke, etc.) might be expected to increase and this process is not accounted for in LBLRTM. However, over the shortest paths considered here, this effect should not be significant.
The calculated mean transmittance, as a function of the propagation distance from 1 mm to 1 km, for our 4-channel ‘THz Torch’ system is given in Fig. 5(a). In addition, Fig. 5(b) to 5(d) show the simulated transmittances across the spectrum from 10 to 100 THz, with a resolution of 300 MHz, for various distances. It can be confirmed that in principle, a single-channel ‘THz Torch’ wireless link operating in Channel D (75-89 THz) can operate up to a range of ~1 km; although in order to minimize the significant spreading losses, collimating lenses would be needed at both the transmitter and receiver. In practice, a realistic transmission range of a few meters can be expected. The transmittances for all channels exceed 83%, with Channel A and D greater than 98%, which is acceptable and can be easily compensated for by increasing the source bias current.
Conversely, Channel B (42-57 THz) has the worst atmospheric transmittance performance, due to the very high water absorption, limiting the effective range to approximately 1 m with the use of collimating lenses. Between these extremes, Channel C (60-72 THz) is partially affected by carbon dioxide, as is Channel A (15-34 THz) that also suffers from atmospheric absorption from ozone and water vapor over longer distances. It is interesting to note that banded-average atmospheric transmittance does not follow any simple scaling law with distance. As a result, accurate signal power link budget calculations require the use of atmospheric attenuation modeling software simulations to be performed for a specific bandwidth, time of day, precipitation, site locations (i.e., taking into account transmission path inhomogeneity), etc.. Nevertheless, for a range of only 1 cm, the simulated mean transmittances for each channel are given in Table 3.
5 Receiver output signal voltage
At the receiver, the incident power \( {L}_{FS}\kern0.3em \cdot \kern0.3em {I}_{TX}(T) \) passes through a THz BPF and the resulting received power P RX (T) at each PIR sensor can be estimated using the following
Since mechanical optical choppers are employed, with our prototype hardware implementation, power is transmitted sinusoidally and, therefore, P RX (T) is representative of peak values. The LME-553 PIR sensor from InfraTec GmbH was chosen for its ability to detect incoherent band-limited power, having also an ultra-wide bandwidth, room temperature operation, being ultra-low cost and having a relatively fast response time (~1 ms) [32]. Its output RMS voltage u(T) is proportional to the incident radiation power P RX (T), representing a square-law detector operating in its linear region:
where \( {R}_V\left[\mathrm{V}/\mathrm{W}\right] \) is the voltage responsivity of the PIR detector. In our case, the LME-553 PIR sensor is made from lithium tantalate (LiTaO3), with an additional black absorption layer [32]. Here, without any optical filtering, the maximum RMS voltage responsivity is quoted as 6,500 V/W (centered at a 100 Hz chopping frequency) [32]. For a speed of 320 Hz, the roll-off value of RMS voltage responsivity is approximately 90% of its maximum value, giving an estimated responsivity of 5,850 V/W.
Considering the voltage gains from the back-end electronics, the output RMS voltage can be expressed as
where \( {A}_{BB\_LNA}=99.4 \) and \( {A}_{BB\_BPF}=1.06 \) with our prototype demonstrator.
The calculated and measured output RMS voltages V out (T) for each channel receiver are shown in Fig. 6(a) and 6(b), respectively, as a function of source bias current. When compared to predictions, it can be seen that there is good agreement in both trends and values. Note that only measured RMS voltages up to ~2.83 V were recorded, as the detector saturates when the peak-to-peak voltage reaches ~8 V. As expected, the output signal voltage increases as the transmitter’s source bias current increases. It was seen in Section 4 that there is negligible atmospheric attenuation with any of the channels over this short distance. However, from Fig. 6(a), it can be seen that Channel D exhibits the most significant voltage increase with biasing current. The reason for this is that primary radiation dominates (due to the high power transmittance and low power absorbance of the glass envelope), increasing from 80 to 131 THz, and Channel D is the nearest to the spectral radiance peak, as seen in Fig. 6(c).
Similarly, Channel A benefits from the spectral radiance peak of the secondary radiation source (due to the low power transmittance and high power absorbance of the glass envelope) increasing from 31.7 to 35.6 THz and from 32.3 to 37.9 THz for low and high temperature regions, respectively. Furthermore, Channel B is the least responsive, because it is the furthest away from any spectral radiance peaks and/or associated tails.
There are additional loss mechanisms that have not yet been taken into consideration. For example, the LiTaO3 pyroelectric material with black absorption layer does not have a flat absorptive spectral response across the entire thermal infrared. As a result, the voltage responsivity will be wavelength dependent, with a decreasing value below its cut-off frequency of ~15 THz [33]. Also, in practice, the transmitter aperture efficiency of 40% does not take into account diffraction effects or any significant mechanical misalignments. Finally, specular and molecular reflections have not been included in the atmospheric attenuation calculations. These additional loss mechanisms require detailed numerical CAD modeling, which is beyond the scope of this study. Nevertheless, a good agreement has been achieved between the predicted and measured receiver output signal voltages, for all channels, using our end-to-end signal power link budget analysis.
6 Receiver output noise voltage
To determine the signal-to-noise ratio (SNR) performance of the ‘THz Torch’ communications system, the noise analysis for each channel receiver must also be undertaken. The additive intrinsic noise for each channel can be separated out into two sources: noise from the front-end sensor and noise from the back-end electronics. The block diagram for the complete channel receiver is illustrated in Fig. 7(a). Within each channel receiver, a dual-sensor configuration is employed, where two identical PIR sensors LME-553 are used; one is a dummy sensor that is opaque to the environment, to minimize unwanted microphonic effects caused by mechanical/acoustic vibrations incident to the pyroelectric material. The output from each PIR sensor will pass through the buffering stage and is then amplified and filtered, before it is threshold detected by the Schmitt trigger (ST); the output of which is a polar NRZ signal. Intrinsic noise will be generated at each stage, and combined with noise contributions from all previous stages. The total noise of the channel receiver is evaluated at the output of the baseband BPF, as shown in Fig. 7(b). Note that without a THz BPF the intrinsic noise performance would not be channel specific. Also, noise contribution from the ST is not included here as signal and noise power are measured at the output of the baseband BPFs.
6.1 Pyroelectric infrared sensor noise sources
The pyroelectric sensor transduces not only the useful incident thermal power but also ambient background noise power. Here, the received OOK-modulated thermal pulse is detected by the resulting surface temperature differences, giving rise to surface charges (due to the pyroelectric effect), which in turn generates a short circuit current. This extremely low current, supplied by the high impedance of the pyroelectric material, is then converted to the required output voltage by an integrated transimpedance amplifier (TIA) having a similarly high input impedance.
With our current mode TIA-based PIR sensor (LME-553) there are a number of intrinsic noise sources, which include: temperature noise V NT , due to temperature fluctuation; dielectric noise V ND , due to the dielectric loss associated with the pyroelectric material; noise from the input resistance V NR ; noise from the large feedback resistor V NFB ; current noise from the TIA’s operational amplifier (op-amp) V NI ; and voltage noise from the op-amp V NU . Each of these noise contributions will now be considered in turn, for completeness, as there is no single reference that covers all possible contributions.
6.1.1 Temperature noise V NT
When the sensing element is in thermal equilibrium with its surroundings, there will be no output voltage. However, temperature fluctuation will cause a response from the sensing element, resulting in the following voltage-noise spectral density [34]
where α is the absorbance of the pyroelectric sensing element, which quantifies how much incident thermal power will be absorbed by the material; \( {G}_T=\frac{H_P}{\tau_T}\kern0.3em \left[\mathrm{W}/\mathrm{K}\right] \) is the thermal conductance of the pyroelectric sensing element; \( {H}_P={c}_P^{\prime }{d}_P{A}_S\left[\mathrm{J}/\mathrm{K}\right] \) is the heat capacity; c ′ P [J m− 3 K− 1] is the volume-specific heat capacity; d P [m] is the thickness of the pyroelectric sensing element; A S [m2] is the surface area of the pyroelectric sensing element; and τ T [s] is the thermal time constant of the PIR detector. For our current mode TIA-based PIR sensors, the voltage responsivity R V is given by [34]
where \( {\omega}_m=2\pi {f}_m\left[\mathrm{rad}/\mathrm{s}\right] \) is the angular frequency of the modulation signal; f m is the modulation frequency; p[C m− 2 K− 1] is the pyroelectric coefficient of the sensing element; R FB [Ω] is the feedback resistance of the integrated op-amp; \( {\tau}_E \)= R FB ⋅ C FB [s] is the electrical time constant for the integrated op-amp; and C FB [F] is the feedback capacitance.
6.1.2 Dielectric noise V ND
The pyroelectric sensing element acts as a dielectric, with an associated Johnson-Nyquist voltage-noise spectral density expressed as [35]
where \( {C}_P=\frac{\varepsilon_0{\varepsilon}_r{A}_S}{d_P} \) [F] is the electrical capacitance of the pyroelectric sensing element; \( {\varepsilon}_0\left[\mathrm{F}/\mathrm{m}\right] \) and ε r are the permittivity of free space and dielectric constant of the pyroelectric material, respectively; and tanδ P is the dielectric loss tangent. It can be seen that this noise contribution is modulation frequency dependent, and proportional to the electrical capacitance, as well as the feedback resistance of the integrated op-amp. This noise contribution is more significant at higher modulation frequencies.
6.1.3 Input resistance noise V NR and feedback resistor noise V NFB
Both contributions are Johnson-Nyquist noise, generated by the thermal agitation of the charge carriers within the large integrated op-amp feedback R FB [Ω] and input R input [Ω] resistors at thermal equilibrium. The respective voltage-noise spectral densities are given by [37]
and
6.1.4 Op-amp current noise V NI
The integrated op-amp also generates noise from within the PIR detector. The voltage-noise spectral density introduced by the associated current noise can be expressed as [37]
where \( {i}_{opamp}\left[\mathrm{A}/\sqrt{\mathrm{Hz}}\right] \) is the equivalent input current-noise spectral density.
6.1.5 Op-amp voltage noise V NU
The voltage-noise spectral density associated with V NU is due to the equivalent input noise voltage of the integrated op-amp, which can be expressed as [37]
where u opamp [\( \mathrm{V}/\sqrt{\mathrm{Hz}} \)] is the equivalent input voltage-noise spectral density; R eq = R input || R FB || R P [Ω] is the equivalent resistance of the circuit; \( {R}_P=\frac{1}{\omega_m{C}_p \tan {\delta}_P}\left[\Omega \right] \) is the equivalent resistance of the pyroelectric sensing element; \( {\tau}_E^{\prime }={R}_{eq}\cdot {C}_{eq} \) [s] is the electrical time constant of the equivalent circuit; C eq = (C P + C input + C FB ) [F] is the equivalent capacitance of the circuit; and C input [F] is the input capacitance of the integrated op-amp.
6.1.6 Total voltage-noise spectral density V N-LME-553 for a single LME-553 detector
Fig. 8 shows the calculated voltage-noise spectral densities for each individual noise source for the LME-553 PIR detector. An insert table of all associated parameters is also given. Note that for the parameters not specified in LME-553 datasheets, typical values for similar LiTaO3 type PIR detectors have been given (indicated by *).
From these calculations, it can be seen that V NFB dominates at lower modulation frequencies, due to the large feedback resistor. At modulation frequencies above 200 Hz, V NU dominates, because of the large equivalent input voltage-noise spectral density at the input of the op-amp. It is also shown that V ND surpasses all but V NU above 200 Hz. Noise from temperature fluctuation, input resistance and op-amp current noise, are less significant.
The overall voltage-noise spectral density V N-LME-553 can be calculated from the summation of each individual noise source contribution:
Fig. 9 shows the calculated overall voltage-noise spectral density and the measured results given by the LME-553 datasheet [32]. It can be seen that there is excellent agreement at low frequencies; discrepancy above this frequency is mainly due to not having exact values for all parameters. For example, in order to obtain C P , which will significantly affect the value of C eq and \( {\tau}_E \)′, the thickness of the pyroelectric material d P had to be assumed to be a typical value of 30 μm [38]. This will introduce inaccuracy in calculating V NU and V ND , especially at high frequencies where these noise sources dominate.
Calculated and measured [32] total voltage-noise spectral density for the LME-553 detector.
By integrating over the modulation bandwidth, assuming a 1 Ω reference load resistance, the total noise power for a single LME-553 PIR sensor can be calculated as
where f m1 = 1 Hz and f m2 = 1 kHz are the lower and upper modulation frequency, respectively. The noise power is calculated to be 0.84 μW. Note that there are a number of additional sources of unwanted signals at the PIR sensor (mostly associated with the environment), such as atmospheric noise, fluctuations in ambient temperature, stray electromagnetic interference and microphonics. These extrinsic effects can only be modelled once specific ambient deployment conditions are known and thus are not considered further here.
After identifying the intrinsic noise sources associated with the LME-553, its noise equivalent power (NEP) and specific detectivity D * can be calculated, as shown in Fig. 10(a) and 10(b), respectively. These results are also compared with associated measured data [32]. It can be seen that the predicted and measured results have a good fit over three orders of magnitude in the modulation frequency.
Calculated and measured [32] noise equivalent power and specific directivity for LME-553 detector.
6.2 Back-end electronics noise sources
The back-end electronics is used to further amplify the output signal from the PIR sensor and also filter-out unwanted noise from the PIR sensor. With our particular circuit, two identical PIR sensors were used for noise reduction. The output from each detector passes through a unity gain buffer amplifier. The small-signal output voltage will be amplified by a common low-noise instrumentation amplifier (INA), having a designed voltage gain of 100. The signal from the output of the INA is then filtered by a 4th-order Sallen-Key Butterworth baseband BPF, having a designed center frequency of 320 Hz. Therefore, the noise from the back-end electronics include: voltage and current noise from the external op-amps (OPA227) used in buffer and filter stages; voltage and current noise from the instrumentation amplifier (INA163); and noise from all the resistors. It should be noted that burst and avalanche noise sources associated with op-amps are too small to be considered further [40].
Noise analysis for the back-end electronics can be performed using an analog circuit-based simulation program. Resistors having resistance R are represented by Johnson-Nyquist noise by default (having voltage-noise spectral density \( \sqrt{4{k}_BTR} \)). However, not all macros contain correct noise information for op-amps and INAs. Therefore, the uncorrelated voltage and current noise sources were added to the input of the op-amps and the INA. The current and voltage noise sources have two different noise contributions: Johnson-Nyquist noise, which has a flat spectral density; and flicker noise, which dominates at low frequencies. Fig. 11(a) and 11(b) show the noise models for the OPA227 and the INA163, respectively. In the noise model, a current-controlled voltage source (CCVS) with a transresistance of 1 Ω is applied to convert current-noise spectral density to voltage-noise spectral density. The simulated voltage and current noise spectral densities for OPA227 and INA163 are shown in Fig. 11(c).
Since the noise sources for each component have been modelled, the output voltage-noise spectral density for the back-end electronics can be calculated from
where A INA is the voltage gain of the INA. The output noise power from the complete back-end electronics \( {N}_{BE}={\displaystyle {\int}_{f_{m1}}^{f_{m2}}{V}_{N- BE}^2d{f}_m} \) is predicted to be 3.52 nW, over a modulation bandwidth from 1 Hz to 1 kHz.
If noise from both LME-553 PIR detectors are considered uncorrelated, the overall voltage-noise spectral density for the complete channel receiver is expressed as
where \( {V}_{N-LME-553- output}={V}_{N-LME-553}\cdot {A}_{BB\_LNA}\cdot {A}_{BB\_BPF} \) represents the voltage-noise spectral density contributed by a single LME-553 at the output of the back-end electronics; \( {A}_{BB\_LNA}={A}_{buffer}\cdot {A}_{INA} \) and A buffer = 1 is the voltage gain of the buffer stage. The calculated intrinsic noise power for the complete channel receiver is N receiver = 6.52 mW, over a modulation bandwidth from 1 Hz to 1 kHz.
Fig. 12 shows the simulated voltage-noise spectral density for a single LME-553 PIR detector and back-end noise sources for the channel receiver. As expected, the former predominantly dominates the channel receiver; while the latter can be ignored at all but very low modulation frequency (where flicker noise dominates).
6.3 Channel receiver noise measurements
The noise performance for each channel receiver is measured directly using a PicoScope 2205 MSO digital oscilloscope. A noise floor at 65 μVRMS was first recorded by short-circuiting the high-impedance input of the oscilloscope. The duration of the measurements was 5 minutes for each channel. Since RMS values of noise voltage can be measured directly, the corresponding total noise power can be calculated, as shown in Table 4, where Opaque and Filter denote the PIR detector having either a blocked aperture or filled with its assigned channel THz BPF, respectively. When compared with the calculated value of N LME − 553 = 0.84 μW, the measured values are 2 to 3 times higher. This discrepancy is due to two main practical reasons: first, the calculated values were obtained by integrating over a modulation bandwidth from 1 Hz to 1 kHz, while the noise coupled into the PIR sensor is much wider. Second, in practice, the PIR sensor is exposed to background ambient conditions; extrinsic noise sources in situ are coupled into the detector, but are not included in the simulations. It should be noted that the calculations are based on values from the data sheet, which does not give information on measurement conditions.
When considering the output noise power from the complete channel receiver, there is generally good agreement; for Channels C and D their measured values are smaller than the predicted value of N receiver = 6.52 mW. This is because there is no THz BPF applied in the simulations (i.e. values are not channel dependent). When the channel THz BPFs are included, more of the extrinsic ambient background noise is filtered out as the channel frequency increases, leading to lower measured values when compared to those calculated. Also, the noise sources from the two PIR detectors are considered to be totally uncorrelated in the calculation, which may not be the case in practice.
6.4 Measured output signal-to-noise ratio (SNR)
Since both the signal and noise properties of this wireless communications system have been measured, assuming a 1 Ω reference load resistance, the measured output SNR can be calculated as
To validate the results, measured end-to-end SNRs (which takes all previously recorded values of source bias current into account) are compared against calculated values, resulting in the scatter plot shown in Fig. 13. In Fig. 13, SNR values were obtained by varying the source bias current from 44 to 80 mA and the transmission range from 1 to 3 cm, to obtain different receiver output signal voltages. In general, the measured SNR values agree well with the predicted data. In low SNR conditions, the measured results tend to be higher than predicted. This is because the calculated noise power is higher than measured, for Channels B, C and D – resulting in lower calculated SNRs.
Fig. 14 shows the measured bit error rate (BER) against measured SNR. The measured BER was obtained using the methodology described in [5], where an end-to-end binary data stream having 2×106 bits was used. When no bit errors were observed, actual BER values are considered to be smaller than 10-6 and, therefore, not shown. A simple empirical curve fit is also shown in Fig. 14, given by
It can be seen that (29), with our polar signaling, resembles the classical relationship \( BER=0.5\kern0.5em {e}^{-\left({E}_b/{N}_0\right)} \) obtained for the optimum differential binary phase-shift keying (DBPSK) [41]. When compared to DBPSK, our existing hardware prototype demonstrator requires much higher values of SNR for the same levels of BER. Therefore, Fig. 14 and (29) provide a useful tool for predicting the performance of this system. By applying other techniques, such as forward error correction (FEC) algorithms, the BER and overall performance for the complete system is expected to be improved.
7 Conclusion
In this paper, a detailed end-to-end power link budget analysis for the newly introduced thermal infrared wireless communications link has been investigated for the first time. Here, a number of assumptions have had to be made, in order to limit the scope and depth of this work. Nonetheless, the predicted output RMS voltages from each receiver of our multi-channel ‘THz Torch’ system agree well with independent measurements. It has been shown that, with our thermodynamics-based technology, the range of the wireless link has the potential to reach ~1 km, as dictated by the simulated mean transmittance. In practice, such transmission distance is very challenging, due to the spreading loss of the thermal source. However, with proper beam collimating and focusing, a realistic transmission distance of several meters can be expected. For this transmission range, the mean transmittances for all the defined channels are still >80%. Preliminary measured results using two collimating lenses showed an increased transmission distance from centimeters to tens of centimeters. Moreover, the overall noise performance is dominated by the front-end PIR sensor, as found with conventional electronic/photonic systems.
The results from this detailed power link budget analysis can create a useful insight into the practical operation at both component and systems levels. With further refinement, it will prove to be an invaluable tool for engineering optimal performances with single and multi-channel systems. For example, with the former, channel frequency allocation can be optimized to promote longer ranges. With the latter, signal levels can be adaptively controlled and equalized, simply by changing the source bias currents for each channel, thus, balancing out the performance (e.g., having the same minimum output SNR across the channels) of the complete multi-channel system. With both, spreading loss is an important factor that limits the transmission range; this issue can be improved considerably by employing collimating lenses, as with optical systems. In addition, more channels can be introduced to overcome limited response times for a single PIR sensor, to further increase data rates, while also improving the resilience of the system to interception and jamming at the physical layer.
References
S. Lucyszyn, H. Lu and F. Hu, “Ultra-low cost THz short-range wireless link”, in IEEE International Microwave Workshop Series on Millimeter Wave Integrated Technologies, Sitges, Spain, 49-52 (2011)
F. Hu and S. Lucyszyn, “Ultra-low cost ubiquitous THz security systems”, in Proc. of the 25th Asia-Pacific Microwave Conference (APMC2011), Melbourne, Australia, 60-62 (2011) (Invited)
F. Hu and S. Lucyszyn, “Improved ‘THz Torch’ technology for short-range wireless data transfer”, in IEEE International Wireless Symposium (IWS2013), Beijing, China, 1-4 (2013)
F. Hu and S. Lucyszyn, “Emerging thermal infrared ‘THz Torch’ technology for low-cost security and defence applications”, Chapter 13, in “THz and Security Applications: Detectors, Sources and Associated Electronics for THz Applications”, NATO Science for Peace and Security Series B: Physics and Biophysics, ed. By C. Corsi and F. Sizov (Springer, Netherlands, 2014), 239-275
X. Liang, F. Hu, Y. Yan and S. Lucyszyn, “Secure thermal infrared communications using engineered blackbody radiation”, Scientific Reports, Nature Publishing Group, vol. 4 (2014)
X. Liang, F. Hu, Y. Yan and S. Lucyszyn, “Link budget analysis for secure thermal infrared communications using engineered blackbody radiation”, XXXI General Assembly and Scientific Symposium of the International Union of Radio Science (URSIGASS 2014), Beijing, China, (2014)
F. Hu and S. Lucyszyn, “Modelling miniature incandescent light bulbs for thermal infrared 'THz Torch' applications”, Journal of Infrared, Millimeter, and Terahertz Waves, Springer, doi:10.1007/s10762-014-0130-8 (2015) in press
J. M. Kahn and J. R. Barry, “Wireless infrared communications”, Proceedings of the IEEE, vol. 9219, no. 97, 265-298 (1997)
T. Komine and M. Nakagawa, “Fundamental analysis for visible-light communication system using LED lights”, IEEE Transactions on Consumer Electronics, vol. 50, no. 1, 100-107 (2004)
A. H. Azhar, T.-A. Tran and D. O. Brien, “A Gigabit/s indoor wireless transmission using MIMO-OFDM visible-light communications”, IEEE Photonics Technology Letters, vol. 25, no. 2, 171-174 (2013)
H. Elgala, R. Mesleh and H. Haas, “Indoor optical wireless communication: Potential and state-of-the-art”, IEEE Communications Magazine, vol. 49, no. 9, 56-62 (2011)
J. B. Carruthers, “Wireless infrared communications”, Wiley Encyclopedia of Telecommunications, vol. 2002, no. 1, 1-10 (2002)
J. Ma, L. Moeller and J. F. Federici, “Experimental comparison of terahertz and infrared signaling in controlled atmospheric turbulence”, Journal of Infrared, Millimeter, and Terahertz Waves, doi: 10.1007/s10762-014-0121-9 (2014)
A. Hood, A. Evans and M. Razeghi, “Type-II Superlattices and Quantum Cascade Lasers for MWIR and LWIR Free-Space Communications”, in Proc. SPIE 6900, Quantum Sensing and Nanophotonic Devices V, doi:10.1117/12.776376 (2008)
E. J. Koerperick, D. T. Norton, J. T. Olesberg, B. V. Olson, J. P. Prineas and T. F. Boggess, “Wireless infrared communications”, IEEE Journal of Quantum Electronics,, vol. 47, no. 1, 50-54 (2011)
Microsensor Technology, “LED specifications”, 2013. [Online]. Available: http://ir.microsensortech.com/leds.htm
Boston Electronics Corporation, “Optically immersed 7.0 μm LED”, 2009. [Online]. Available: http://www.boselec.com/products/documents/IRSourcesWEBLED11-12-10.pdf
N. S. Prasad, “Optical Communications in the mid-wave IR spectral band”, in “Free-Space Laser Communications: Principles and Advances”, Optical and Fiber Communications Reports, ed. By A. K. Majumdar and J. C. Ricklin (Springer, New York, 2008), 347-391
A. Soibel, M. W. Wright, W. H. Farr, S. A. Keo, C. J. Hill, R. Q. Yang and H. C. Liu, “Midinfrared interband cascade laser for free space optical communication”, IEEE Photonics Technology Letters, vol. 22, no. 2, 121-123 (2010)
E. Leitgeb, T. Plank, M. S. Awan, P. Brandl, W. Popoola, Zabih Ghassemlooy, F. Ozek and M. Wittig, “Analysis and evaluation of optimum wavelengths for free-space optical transceivers”, in IEEE 12th International Conference on Transparent Optical Networks (ICTON), 1-7 (2010)
M. Achour, “Free-space optics wavelength selection: 10 μm versus shorter wavelengths”, Journal of Optical Networking, vol. 2, no. 6, 127-143 (2003)
Y. Yao, A. J. Hoffman and C. F. Gmachl, “Mid-infrared quantum cascade lasers”, Nature Photonics, vol. 6, 432-439 (2012)
S. Blaser, D. Hofstetter, M. Beck and J. Faist, “Free-space optical data link using Peltier-cooled quantum cascade laser”, Electronics Letters, vol. 37, no. 12, 778-780 (2001)
A. Pavelchek, R. G. Trissel, J. Plante and S. Umbrasas, “Long-wave infrared (10-micron) free-space optical communication system”, in Proc. SPIE 5160, Free-Space Laser Communication and Active Laser Illumination III, doi: 10.1117/12.5049406 (2004)
D. R. Lide (Ed.), CRC Handbook of Chemistry and Physics, CRC Press, 77th edn (1996)
M. Rubin, “Optical properties of soda lime silica glasses”, Solar Energy Materials, vol. 12, no. 4, 275-288 (1985)
S. Lucyszyn and Y. Zhou, “Characterising room temperature THz metal shielding using the engineering approach”, PIER J., vol. 103, 17-31 (2010)
Northumbria Optical Coatings Ltd., “Online catalogue”, 2006. [Online]. Available: http://www.noc-ltd.com/catalogue
S. A. Clough, M. W. Shephard, E. J. Mlawer, J. S. Delamere, M. J. Iacono, K. Cady-Pereira, S. Boukabara, and P. D. Brown, “Atmospheric radiative transfer modeling: a summary of the AER codes”, Journal of Quantitative Spectroscopy & Radiative Transfer, vol. 91, no. 2, 233-244 (2005)
M. W. Shephard, S. A. Clough, V. H. Payne, W. L. Smith, and S. Kireev, “Performance of the line-by-line radiative transfer model (LBLRTM) for temperature and species retrievals: IASI case studies from JAIVEx”, Atmospheric Chemistry and Physics, vol. 9, no. 19, 7397-7417 (2009)
U.S. Committee on Extension to the Standard Atmosphere (COESA), “The U.S. Standard Atmosphere 1976”, 1976. [Online]. Available: http://www.astrohandbook.com/ch09/standard_atmos_1976.pdf
InfraTec, “LME-553 datasheet”, 2012. [Online]. Available: http://www.infratec-infrared.com/Data/LME-553.pdf
Gentec Electro-Optics (Gentec-EO), “Absorption curves for THz-BL”, 2014. [Online]. Available: http://gentec-eo.com/Content/downloads/absorption-curves/Curves_THz_2014_V1.0.pdf
InfraTec, “Detector basics”, 2011. [Online]. Available: http://www.infratec.de/fileadmin/media/Sensorik/pdf/Appl_Notes/Application_Detector_Basics.pdf
S. T. Liu and D. Long, “Pyroelectric detectors and materials”, Proceedings of IEEE, vol. 66, no. 1, 14-26 (1978)
R. W. Whatmore, “Pyroelectric devices and materials”, Reports on Progress in Physics, vol. 49, no. 12, 1335-1386 (1986)
DIAS Infrared GmbH, “Pyroelectric infrared detectors”, 2006. [Online]. Available: http://www.dias-infrared.de/pdf/basics_eng.pdf
InfraTec, “Advanced features of InfraTec pyroelectric detectors”, 2012. [Online]. Available: http://www.infratec.eu/fileadmin/media/Sensorik/pdf/Appl_Notes/Application_Advanced_Features.pdf
InfraTec, “JFET and operation amplifier characteristics”, 2001. [Online]. Available: http://www.infratec.eu/fileadmin/media/Sensorik/pdf/Appl_Notes/Application_JFET.pdf
Texas Instruments, “Application report SLVA043B: noise analysis in operational amplifier circuits”, 2007. [Online]. Available: http://www.ti.com/lit/an/slva043b/slva043b.pdf
F. Xiong (Ed.), Digital Modulation Techniques, Artech House, Inc., 2nd edn (2006)
Acknowledgements
This work was partially supported by the China Scholarship Council (CSC).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Hu, F., Sun, J., Brindley, H.E. et al. Systems Analysis for Thermal Infrared ‘THz Torch’ Applications. J Infrared Milli Terahz Waves 36, 474–495 (2015). https://doi.org/10.1007/s10762-014-0136-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10762-014-0136-2