Improving the Learning of Mechanics Through Augmented Reality

Abstract

This study investigates to which extent students’ understanding of the physical phenomenon of torque can be improved through the use of visualization technology, in particular of augmented reality (AR). The students in the first-year course Mechanics I at KTH participated in the study by taking two tests on torque. In between those tests, a subgroup of students participated in a user study where they used an AR application to solve problems regarding torque. The results of the pre-test and the post-test indicate that the subgroup who used the app improved their understanding of torque to a greater extent than the ones who did not use the app. However, a larger sample space would be required to obtain a complete statistical characterization of the reported (qualitative and quantitative) improvement.

1 Introduction

Technology has become a very naturally integrated part of our everyday lives. We constantly find ways to solve problems and enhance experiences through the use of technology, and education is not an exception. A recent review study (Vinuesa et al. 2020) shows that using advanced technology may help to increase the education quality. Technology-Enhanced Learning (TEL) can roughly be described as when technology is used in educational settings with the purpose of enhancing the students learning. On the other hand, Augmented Reality (AR) is a technology that is being increasingly used for educational purposes. With its possibility to supplement the real world with computer-generated objects, thus allowing an extension of reality, it enables the user to experience otherwise impossible scenarios (Yuen et al. 2011). This property opens up for many possible areas of use in education, providing teachers with richer tools of explanation. Using technology in education can be a way to implement Active Learning (AL), which is defined as “anything that involves students in doing things and thinking about the things they are doing” (Bonwell and Eison 1991). As discussed below, research shows that students learn better when the educational environment encourages them to be actively involved in their own learning (Prince 2004; Freeman et al. 2014; Kontra et al. 2015).

In order to assess the role that technology can play in learning, in this work we consider the epistemological framework of constructivism. Piaget (1964), one of the pioneers within constructivism, claimed that learning “is provoked, [...], as opposed to spontaneous”, meaning that in order to learn you need to actively experience. According to Piaget, individuals need to construct their own knowledge, and when exposed to new information, this is compared with previously acquired information, either the previous beliefs are adjusted or one gets reassurance that the already constructed knowledge is indeed correct. Note that constructivism promotes a “learning-by-doing” approach which motivates the technology-enhanced active-learning environment of this study. Thus, AL can be viewed as a form of applied constructivism. It is a learning configuration built on the assumption that students construct their own knowledge, rather than on the traditional image of the students being solely recipients. According to the review on AL by Prince (2004) there is a widespread support for more engaging teaching methods, although varying in strength. All the research that he examined confirmed improvement in learning outcomes as a consequence of active engagement, leading to the conclusion that such teaching approach should be encouraged. On the other hand, Freeman et al. (2014) showed that AL is effective in Science, Technology, Engineering and Mathematics (STEM) education and led to increased performance in examination. Comparing traditional lecturing with a more active approach, they concluded that AL is to be promoted and could lower failure rates, thus inspiring more individuals to pursue a STEM degree. Furthermore, by measuring activity in the sensorimotor brain regions, Kontra et al. (2015) found that physical experience in physics education indeed enhances learning. They examined regions in the brain that “add kinetic detail and meaning to students’ thinking”, and they observed that these regions were activated while performing the physical experiments. The students, as a consequence, showed signs of enhanced learning demonstrated by increased quiz scores.

Making teaching and learning more effective has always been of interest throughout history. The possibilities that arouse with modern technology were harvested immediately. Educational films were introduced in the beginning of the twentieth century, slide projectors were a standard aid in the 1950s classrooms (Saettler 2004), and with the arrival of internet the possibilities have become endless. One use of technology in education is to create an active learning environment. And although TEL does not necessarily imply AL, obtaining a more active setting is a common result of including technology in teaching. Rutten et al. (2012) reviewed a decade worth of research regarding the usefulness of computer simulations assisting traditional education forms in science education. This review of the literature showed clear evidence of traditional instruction being enhanced by the use of computer simulations, specifically in laboratory exercises. For instance, Dori and Belcher (2005) used software in a redesigned classroom for teaching first-year Physics at the Massachusetts Institute of Technology. The focus was specifically on electromagnetism, which is a particularly challenging concept for the students, and the researchers believed that their Technology-Enabled Active Learning (TEAL) environment would positively contribute to their understanding. The study analysed the cognitive and effective results of the students, coming to the conclusion that the TEAL setup had significantly improved student performance.

When it comes to the particular technological resource to use, Sung et al. (2016) concluded (after reviewing over 100 studies) that mobile devices have a more positive effect in education than desktop computers. Nevertheless, such a positive effect is only obtained when the instruction style is adapted in such a way that cooperative study and self-directed learning are promoted (Liu et al. 2014; Lan et al. 2015). If steered in this way, the use of mobile devices for teaching is expected to enhance the development of additional high-level skills (Frohberg et al. 2009; Zucker and Light 2009), but the available studies merely focus on the improvement regarding the course content (Sung et al. 2016). Another aspect that should be exploited to a larger extent is the possibility of obtaining instant feedback from the students using the mobile device (Ozcelik and Acarturk 2011), and this is connected to the fact that a specific training for the teachers may be the best away to achieve such improvements (Penuel 2006). It is therefore important, when using technology for teaching, to create the right environment in terms of technology, teaching style and student awareness (Liu et al. 2012; Gao et al. 2016).

1.1 Contributions of This Work

In this work, we developed a technological tool to help students (and possibly the general public) to understand concepts of physics through visualization. This study will therefore investigate whether an AL setting using technology, in particular AR, can be useful for students in their learning of physics phenomena. This work is framed in the context a Mechanics I course from first year at KTH. Based on student performance in exams from previous years, we identified that the concept of torque is particularly challenging for the students, and it is a threshold concept studied early in the course which is required to understand the more advanced topics covered later. Therefore, our AR environment was designed to help the students to learn and apply this concept, as discussed below. We note that similar AR-based methodologies could be developed and applied in the context of other study areas, for instance linear algebra (where the vector product is also very relevant) or aerospace engineering.

This article is organized as follows: in Sect. 2 we provide an overview of the literature on AR in education; the methodology employed for this work is discussed in Sect. 3; the results are presented in Sect. 4, while the discussion can be found in Sect. 5; finally the conclusions of the work, together with an outlook, are provided in Sect. 6.

2 Overview of Augmented Reality in Education

As the name reveals, this technology is based on the augmentation of reality, meaning that the real world is enhanced through the addition of virtual elements. The interactive experience through the AR-enabled immersion allows the users to feel as if they were affecting reality, while they are really just manipulating the computer-generated effects. AR is a kind of technology which could be useful for educational purposes given the constructivist framework in which this study is performed. For instance, nowadays 92 % of the Swedish population have a smartphone (InternetStiftelsen 2019), which makes AR an accessible technology, since most¹ smartphones contain a gyroscope, an accelerometer and a camera, the three parts a phone needs to be able to support AR applications. In an overview of AR in education, Yuen et al. (2011) state that one of the main purposes behind research in the field is that AR has great potential to improve productivity in real-world tasks. In terms of education, AR is believed to have potential to engage and stimulate students, nurture their creativity and imagination, and help to teach them concepts that are difficult, or even impossible to experience in the real world.

One of the first studies to examine the potential of augmented reality in the education of mechanical engineering was Web3D-AR (Liarokapis et al. 2004) in 2004. While the core concepts of AR in engineering education were originally explored in this paper, here we also review the vast advancements in technological platform of the last decade. PhysicsPlayground is a project developed by Kaufmann and Meyer (2008) with the intention to show how education can benefit from using technology. PhysicsPlayground is an AR application that helps to visualize e.g. forces, counterforces, speed and velocity. The hardware necessary for using this application is a Head-Mounted Display (HMD), a wireless pen and a Personal Interaction Panel (PIP). Note that in this case, the hardware requirements may limit the accessibility to a greater audience. Furthermore, this study did not evaluate the effectiveness of their application in improving learning. Vaughan et al. (2017), inspired by the fact that active participation has been proven to enhance learning in STEM courses, included an AR sandbox in an undergraduate introductory course in soil science. The results of a qualitative survey filled out by the participating students showed that they all reported a deeper understanding of the studied phenomena such as water flow, erosion and soil formation. Due to the use of a sandbox, together with the required technology, accessibility is also a limitation in this project. A different implementation of AR was proposed by Dünser et al. (2012), who considered a book augmented through the use of a Hand-Held Device (HHD) to increase the understanding in secondary school Physics. They performed a quantitative test on a group of students, half of which used the book with augmentation, while the other half studied the book without augmentation. Keeping in mind that the test groups were small, the study showed that AR has the potential to support the teaching of spatial concepts that could benefit from being visualized in three dimensions (3D). Although books are accessible, this method still relies on the use of a HHD, a fact that reduces the accessibility of this AR framework.

An interactive AR environment was implemented by Liarokapis and Anderson (2010) in Informatics and Multimedia classes. They concluded that AR can be used as a complementary tool to traditional teaching in a laboratory environment, in order to help students to better understand complex concepts. The participating students could choose between using HMDs or simply a standard display monitor, among which the second increases the accessibility of the educational environment. On the other hand, Liarokapis et al. (2004) developed a web-based AR application for teaching mechanical engineering, as mentioned above. They did not evaluate possible learning outcomes, but the approach was more accessible than the ones discussed above because it only required a personal computer (PC) with internet access. Jamali et al. (2015) developed a mobile AR application for medical students, the main topic of which was the human skeleton. They called the application Human anatomy in Mobile Augmented Reality (HuMAR). Since this application was based on a mobile phone and a tablet, it can be considered as relatively accessible. The results of pre-/post-tests showed improvements in knowledge, behaviour and attitude amongst the students after using the HuMAR application. Finally, the Science Center To Go (SCeTGo) is a European-Union funded project developed by Davidsson et al. (2012), where they tested different ways in which AR and mobile devices could support science classes in secondary school. The goal was to use “off-the-shelf” technology, making it as accessible as possible. The students being part of activities using AR, such as obtaining geometrical data samples outdoors, were all very positive towards the different way of taking the class, and the new setting did result in enhanced discussion and collaboration among the students. Teachers were also mostly positive but stressed the fact that in order to become ubiquitous in a school environment, the technology needs to be low-cost and run smoothly. A recent study by Fidan and Tuncel (2019) employs an AR setting based tablets, with moderately high accessibility, aimed at teaching concepts of physics in secondary school. They conducted a thorough assessment of the impact of the AR framework on student development, and they observed improved learning measured both qualitatively and quantitatively. A wide range of topics were covered in this study, including forces, mass, friction, energy, pressure and work.

In the present study, our main motivation is to develop an AR environment which is as accessible as possible. Furthermore, and following Kirkwood and Price (2014), quantitative evaluation will be performed in order to assess whether there is any actual contribution of the technology to the understanding of the studied subject. Moreover, qualitative data will be gathered and analysed for a more complete understanding of the impact of the prototype on the students’ learning. In Table 1 we summarize the features of the AR studies discussed above, as well as the ones of this study. It is interesting to note that, from the studies under consideration, only in the present work and the one by Fidan and Tuncel (2019) both qualitative and quantitative evaluation of the learning outcome was conducted. In this work a slightly higher accessibility is possible due to the use of smartphones instead of tablets.

Table 1 Summary of related work, color coded from low to mid and to high accessibility

3 Methodology

In this section we will discuss the techniques employed in the present work. First, in Sect. 3.1 we describe the AR prototype, and we introduce the physical concept of torque. Second, in Sect. 3.2 we discuss a think-aloud session aimed at identifying problems with visualization and usability. Finally, in Sect. 3.3 we explain the approach adopted to measure the learning enhancement through the use of the AR app. In particular, we describe the test design and we discuss the statistical analysis and the scoring system used to assess the performance improvement.

3.1 Prototype

A prototype in the form of an AR application was developed and evaluated to see whether the learning process of the concept torque could be enhanced by means of visualization. The prototype was developed using the cross-platform game engine Unity² together with Vuforia³, a software-development kit that enables the use of AR in mobile applications. The development of the software was done through an iterative process where the application was continuously evaluated by the three authors. When an alpha version was ready, a think-aloud user study focusing on usability and visualization was performed (see more details in $\S$??). The gathered data was taken into consideration when finishing the beta version of the app. In the application, torque is visualized through two examples (see Fig. 1): a wrench tightening a bolt to visualize torque applied at a point and a door opening and closing, to visualize torque applied with respect to an axis. Let us recall that the torque $\overrightarrow{M}_\mathrm{O}$ of a force $\overrightarrow{F}$ applied at point A, with respect to another point O, is calculated as:

$$\begin{aligned} \overrightarrow{M}_\mathrm{O}=\overrightarrow{r}_{\mathrm{OA}} \times \overrightarrow{F}, \end{aligned}$$

(1)

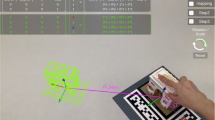
where $\overrightarrow{r}_{\mathrm{OA}}$ is the position vector (which defines the location of A with respect to O), $\times$ denotes vector product and $\overrightarrow{(\cdot )}$ indicates vector quantities. The user can control the magnitude of the position vector $\overrightarrow{r}_{\mathrm{OA}}$, as well as the magnitude and the orientation of the force vector $\overrightarrow{F}$. When the force is applied by the user pressing the “play” button, the torque vector and its projected component on the directions normal to the plane (wrench example) and parallel to the axis of rotation (door example), are shown on the screen. The corresponding object moves according to the applied torque, and the calculation of the corresponding vector product can be observed in the upper part of the screen. In Fig. 2 we can see an example of the application being used, and a video of its usage can be found in the Supplementary Material 1.

Fig. 1

Two screen captures from the mobile phone with the application exemplifying the augmented-reality (AR) learning platform for mechanics. The left screenshot shows the concept of torque as it is applied to a point exemplified by a wrench tightening a bolt. The right screenshot shows the concept of torque applied to an axis using a door opening by its handle. Both examples visualize the vectors over the 3D models of the objects in the scene. Furthermore, they write and update the equations on top. As the user moves the wrench or the door handle, the vectors and the equations change dynamically. The user inputs the magnitude of the position (red) and force (green) vectors with the red and green sliders at the bottom of the application. Also, the user can modify the angles of the force vector with the circles labelled alpha and beta at the bottom of the screen. Finally, the user can play, pause and rewind the application of forces in the system and watch an animation of the results while reading the updated equations. This direct mapping between what is visible and what is computed is a major affordance of AR for learning mechanics

Fig. 2

Example of the application in use, where both the real world and the augmented reality on the screen can be seen. In this scenario, the user holds the phone with the camera pointed at the image on the assignment. The system uses this image to register the coordinate space of the world to render the augmented-reality scene from the perspective of the phone camera. The user can move and rotate the camera to appreciate and understand the scene from different perspectives. The user can read the equations of the system at the top of the application. Furthermore, the user can change the setup, i.e. change forces, distances, and angles, using the interface at the bottom with sliders and knobs. When changing these parameters, the user can gain both visual insight from the vectors on the screen and mathematical intuition from the equations on top. This direct manipulation, together with the immersive visualization and the real-time equation updating are major affordances of AR in learning mechanics

The two different examples were made using basic 3D models provided in Unity, mixed with imported, pre-made models such as the wrench and bolt, and a self-made model for the arrow. The arrow was modelled using the 3D modelling program Blender. After creating the scenes they were placed on image targets, which are necessary for the AR app to know where to render the modelled scene. When the Vuforia-powered app recognises the target through the phones camera, the app renders the model placed on that specific target. In order to get the model to move, Unity’s built-in functionality of applying e.g. force and torque was used. Unity allows to classify objects as rigid bodies, thus opening up the possibility to apply real-life physics to the objects. Through scripting, the forces applied to the objects were regulated by controls, visualized by the arrows and the torque was activated when pressing the play button.

3.2 Visualization and Usability

To evaluate the usability of the AR application (also denoted as app in this study), a user study in the form of a think-aloud session was performed with a group of three graduate students who studied both visualization and interaction design. The participants’ continuous loud thinking allows for usability mishaps to be detected during the process of completing a particular task. These students were considered to be able to provide relevant feedback since they all have a background in both interaction design and visualization studies. In individual sessions, the participants were first instructed to apply a torque to the displayed figure. Since this is the main function of the application, it was considered relevant to investigate how intuitively could this task be carried out. After completing the first task, the users were asked whether they could find additional information regarding the concept of torque in the app. Finally, the participants were encouraged to provide feedback on possible improvements of the usability and visualization of the app. No questions were answered, nor any help was given by the interviewer during the session. The user study was performed on an iPhone X running with iOS 13.1.3. All participants had previous basic knowledge of torque, although it was acquired many years ago. This session resulted in qualitative data that was taken into account when finishing the development of the prototype.

3.3 Measuring Learning Enhancement

Despite the assumption that individuals learn by doing, the potential learning enhancement needs to be proved and therefore measured. Kirkwood and Price (2014) stated that many studies discuss enhancement without defining exactly in which sense, and thus in many cases the approach adopted to measure any improvement is not appropriate. They emphasize the importance of clearly stating how one defines enhancement, not assuming that technology enhances learning, and carefully choosing relevant methods of measuring. In this work, we consider what Kirkwood and Price (2014) denoted as supplementing existing teaching. The most common (and perhaps most objective) way of measuring learning outcomes when adopting this approach is to assess quantitative improvements, and this is what we will consider as enhancement in this work. The improvement can be measured using pre-test/post-test results, i.e. having the participants take a test before the experiment, then retake a similar test after the experiment and compare the results. The outcome will also be compared with the results of a group that takes the same tests but does not use the AR application in between. Note that, although the quantitative improvement is an objective measurement, it lacks the possibility of portraying the quality in learning enhancement (Kirkwood and Price 2014). Thus, we complement the testing with a qualitative form investigating the experienced improvement or stagnation in understanding of the studied phenomenon. The evaluation method in this study therefore followed a convergent parallel design (Creswell and Clark 2017), gathering both quantitative and qualitative data simultaneously.

The most important aspect to evaluate was whether the developed application could enhance the learning of torque among mechanical engineering students. To this end, after an initial lecture on the subject, a pre-test consisting of one question regarding torque was carried out. The students then got to volunteer for the second user study: a lab session using the AR application to answer questions regarding torque. The session ended with the students filling out a qualitative form. Finally, a post-test consisting of multiple questions was held, where two of them examined the concept of torque (note that one of them was similar to the one in the pre-test). The results of the pre- and post-test constitute the quantitative data of this study, complemented with qualitative data from the previously mentioned form. The evaluation approach is described in more detail in Sect. 3.3.1.

3.3.1 Test Design

The students in the Mechanics I course participated in a lecture on torque. A couple of weeks after the lecture, the students were given the opportunity to solve a problem on torque, without any particular preparation, and this problem was graded. This task is labelled as pre-test in the Supplementary Material 2. After around one week, the students were invited to participate in a workshop to practice the interpretation and calculation of the torque by means of the AR app. The activities in this workshop are labelled as AR Session in the Supplementary Material 2. Around four weeks after this, the students took a partial exam in the Mechanics I course, where two problems were related to torque calculation. These two tasks are labelled as post-test in the Supplementary Material 2. Note that not all the students who took the post-test were part of the pre-test or the AR session, and a schematic representation of this is provided in Fig. 6. A total of 26 students volunteered to participate in the workshop, which was designed as a user study with the developed AR prototype. It is important to note that when experimenting with early prototypes of technological interventions in a learning context, it is beneficial to run pilot studies of modest sample sizes to focus first on the usability of the technology before delving deeper into the impact the tools may have on the learning outcomes. These studies are typically short, from a few hours to a few weeks, and involve few participants, from 5 to 30. Studies aimed at learning outcomes will typically recruit at least tens of participants and last at least several weeks if not months or even years. The present study is a pilot to determine the usability of the technological intervention and a pre-investigation to forecast possible impacts. The course instructor acquired consent from the program director to run this study and announced in class to the students: “My collaborators and I would like to recruit your participation in a research study. The aim of the study is to test the learning potential of an augmented-reality smartphone application aimed at understanding mechanical torque. Your participation will be anonymous and voluntary. You may cease to participate even after you volunteer without any penalty to you. Your performance in the study will not be a measure of your ability to learn but of the application to support learning. Your performance in the study will not negatively impact your performance in this course in any way. On the other hand, while we will not reward or compensate your participation with academic credit or financially, your participation may improve your learning of the core material of this course and this improvement would materialize as a higher final grade. Participation in this study does not pose any physical or personal risk higher than that present in normal office and classroom conditions. You will not interact with hazardous materials or in hazardous conditions. All the material gathered about your participation will be kept anonymous. Please, contact me by email if you wish to participate. Thank you for considering to participate. Do you have any questions?”. By contacting the researcher through email, participants stated their consent to participate under the conditions stated above. From the 26 volunteers, 12 actually attended the session. The students could work individually but they were encouraged to work together since it has been shown that cooperation (i.e., in the context of peer instruction) increases engagement (Crouch and Mazur 2001). Since having the goal of performing a specific task has been proven effective for closing the gap between what is expected to learn and what is actually learned (Hattie and Timperley 2007), the lab session included a task sheet where the example illustration of the tasks were the image targets needed for the AR application (see the AR Session section of the Supplementary Material 2). The tasks were exploratory, focused on trying to get the students to understand the concept of torque rather than performing specific calculations. The session ended with the students being asked to fill out a form, which was meant to provide complementary qualitative data regarding experienced improvement in understanding. The form was also intended to lead to a self-evaluation on their general motivation in the course, the latter in order to know the ambition level of the students who participated. As stated above, few weeks later a post-test consisting of multiple questions was carried out in the Mechanics I course. Two of the questions were about torque, and one was very similar to the question in the pre-test. The results could then be compared with those of the pre-test, and further compared with the results of the group who did not use the application. These results constitute the quantitative assessment of the improvement in understanding of torque. Note that the pre- and the post-tests, together with the tasks and the questionnaire in the AR session, can be found in the Supplementary Material 2.

3.3.2 Statistical Analysis and Scoring System

We estimated that the study would need to include about 500 people to statistically determine the smallest difference of proportion observed with a power of 80% and significance level of 95% (see Sect. 4.3 for the calculations), while the amount of available students was only 39. It is important to note that this study does not aim at reproducibility of the learning outcomes. It lacks the statistical power for that. Rather, it is a demonstration of the feasibility of the technology. It focuses on usability and utility. We address the questions: “Can engineering students use it?”, and “Do they get and perceive value by using it?”. In order to answer the question “Can people learn more by using the tool?” we would need more people and a longer study for that. As a starting point of such a quantitative study, statistical analyses were performed to properly evaluate any performance improvements. The first analysis was a statistical hypothesis testing of proportions within the same population during different stages, a test which aims to examine whether possible differences between proportions are statistically significant. The procedure starts with declaring a null hypothesis ($H_{0}$), which states that there is no difference between the two proportions being compared ($p_{1}$ and $p_{2}$). Secondly, an alternative hypothesis ($H_{A}$) is defined, stating that there is a difference between the proportions. That difference is defined according to whether the test is one- or two-sided. If the test is two-sided, the $H_{A}$ will be the opposite of $H_{0}$, i.e. the proportions are not equal. On the other hand, if the test is one-sided the test will be more effective, but only one of the options $p_{1} > p_{2}$ or $p_{1} < p_{2}$ can be investigated. This is formulated as follows:

$$\begin{aligned} H_{0}: p_{1} = p_{2}; \quad H_{A}: p_{1} \ne p_{2} \text {,} \quad p_{1} > p_{2} \quad \text {or} \quad p_{1} < p_{2}. \end{aligned}$$

(2)

The considered proportions were the students who passed the pre-test ($p_{1}$) and the proportion of students who passed the tasks on torque in the post-test ($p_{2}$) in each of the groups, i.e. the one that used the app and the one that did not. Due to the small sample size in this study, a one-sided approach was chosen and only the scenario that $p_{1} < p_{2}$ was analysed to maximize the possibility of seeing any possible improvements. This was a relevant approach since the raw data showed positive tendencies of change rather than negative, i.e. the students had better results on the post-test compared to the pre-test. Furthermore, this decision was motivated due to the results seen in the form, where a large majority answered that the app contributed to their understanding of torque. Hence, there was no reason to believe that the app would have caused negative effects on the students’ test results. The statistical analysis was performed using the software environment for statistical computing R⁴, through the graphical user interface (GUI) R Commander. We ran the test prop.test⁵ with a confidence level of 95 %.

When comparing the results between the groups, a grading system was developed in order to be able to analyze the average results of both groups in a reasonable way due to the limitations caused by a small sample size and the grading of only pass or fail. Note that this grading system differs from the one adopted in the actual exam, because the present system aims at assessing the improvement with respect to the pre-test. The system was designed to favor improvement in the test results and especially regarding task 2 in the post-test since it was the most similar to the task in the pre-test. It is important to note that the tasks are labelled in the Supplementary Material 2, and the notation task 2 and task 3 refers to the order of the tasks in the exam, which included problems on other topics. The scores for task 2 therefore depend on the result from the pre-test while task 3 is scored individually. Hence, a student who did not pass the pre-test but passed both tasks on the post-test would receive the highest score while a student who passed the pre-test and failed both tasks on the post-test would receive the lowest score. The points were assigned as shown in Fig. 3. The average score from each group was calculated and Welch’s t-test was performed to compare those averages. Welch’s t-test evaluates the hypothesis that two averages generated from groups of different sizes are equal. Thus, the hypotheses are formulated as follows:

$$\begin{aligned} H_{0}: \mu _{1} = \mu _{2}; \quad H_{A}: \mu _{1} \ne \mu _{2}, \end{aligned}$$

(3)

where $\mu _{1}$ and $\mu _{2}$ are the averages in each group. This analysis was also performed using R, through t.test⁶ with a confidence level of $95\%$. The sample populations of the engineering students at a major upper education technical university like KTH are not a representative sample from general populations. They have self-selected into the upper 25th percentile of their graduating cohorts from high school. Their grade performance is skewed toward the top of the scales. Once the scales are re-normalized for higher-level education, the curve typically remains skewed towards the upper levels of achievement in grading criteria. Yet and according to Borg et al. (1989), in terms of learning outcomes and skills acquired, the underlying distribution remains normal, thus justifying the use of Welch’s t-test in the present context.

Fig. 3

Summary of the grading system for the pre-test and the post-test. The system was designed to highlight improvements between the pre- and post-test in Task 2 given that it was the most similar task to the pre-test. Task 3 is scored individually. Thus, a student that failed the pre-test and succeeded at both post-test tasks would get the highest score (30). A student that passed the pre-test and failed both post-test tasks would get the lowest possible score (−15). The boxes are color-coded green for passed and red for failed

4 Results

Here we will discuss the main results of the study, divided into different categories. We first describe the visualization and usability results based on the feedback from the students in Sect. 4.1. Second, we describe the degree to which enhanced learning was achieved in Sect. 4.2, focusing on qualitative (from the forms filled in by the participants) and quantitative results (based on the performance on the pre- and post-tests). Finally, additional statistical analyses on the quantitative data are presented in Sect. 4.3.

4.1 Visualization and Usability

The three participants in the think-aloud user study were first instructed to apply torque to the AR figures. They all expressed that they found the controls of the vectors very intuitive, since the changes in the displayed objects appeared immediately on the screen. However, they all also expressed confusion regarding the labels of the controls and did not understand what the controls did just by reading the label. The label that produced most questions from the participants was the one regarding changing the magnitude of the position vector (see Fig. 1). This is perhaps not surprising, but given the fact that the students of the Mechanics I course are very familiar with this concept, this label was finally not changed. Secondly, the participants were asked to find the instructions on how to use the app. One participant completely missed the upper part of the application because the lower part, consisting of the control panel seen in Fig. 1, was very colorful and drew all his attention, while the other two found the information button in the upper right corner without problems. No action was taken on this point either, since the confused participant also found the information button quickly after realizing the existence of the upper part of the screen. We expect that the users will be able to solve this after enough practice time. In addition to the two explicit instructions, the participants were asked to generally review the usability of the app and express possible concerns. One general suggestion of improvement was that the explanation of torque, which can be found under information, could benefit from containing an example figure and not only text. Another suggestion was that the vectors could be changed dynamically on the screen, so the applied torque would increase or decrease while the figure was moving. Both suggestions were considered to be good ideas for future development, but not necessary for the next stage of the project.

4.2 Enhanced Learning

4.2.1 Qualitative Results: User Study

The form consisted of two main questions:

• How hard do you find the Mechanics course so far?

• Did the app contribute to your understanding of torque?

The answers to the questions by the 12 participants in the user study are represented in Fig. 4. Both questions were followed by a mandatory request to motivate their answers. As can be seen in Fig. 4 (top), 8 out of the 12 participants found the course to be on the hard side of the difficulty spectrum. None of the participants in the user study considered the course to be very easy. Regarding the second question, Fig. 4 (bottom) shows that 11 out of the 12 students answered that they believed the app had contributed to their understanding of the studied concept. These results are consistent with the notion that new technology, particularly when an interactive physical representation of the phenomenon is enabled, is well received by the students. In particular, we created what is called a direct manipulation interface Hutchins et al. (1985). While a textbook provides figures and equations and interactive desktop applications may provide a window into the effects of the change in vector magnitude and direction to the factors in the equation, it is only through AR that the learner is able to have an interface to directly manipulate the equation, with a real-world first-person perspective of the direction and magnitude of the mechanical setup. Learners can see it from their eyes, in real time, and through their hands on manipulation.

Fig. 4

Answers to the questions (top) “How hard do you find the mechanics course so far?”, and (bottom) “Did the app contribute to your understanding of torque?”. The panels show how many students chose each option

Fig. 5

Comparison of the two main questions labelled by user and the chosen preferred example in the app. Note that 8 of 12 participants preferred the Door over the Wrench example and that 8 of 12 participants rated the app “contributing” (3) or “very contributing” to understanding (4)

In Fig. 5 we see a comparison of the results from the two main questions, labelled by which of the two presented examples the participant preferred. Note that three out of the four students who found the course the easiest, preferred the example with the wrench. Only one other student preferred the same example, and that student can be found on the other side of the spectrum regarding the perceived difficulty of the course. The same group, i.e. students rating the course as relatively easy, also spans the whole scale of experienced contribution from the app to their understanding of torque, from 1: Nothing to 4: Very much. The five participants who found the course to be hard, but not very hard, all preferred the door example, and also found the app to have contributed relatively much to their understanding of torque. The three remaining students all found the course to be very hard and believed that the app helped them in their understanding, albeit reporting a milder perceived contribution than the previous group. Out of the four students who found the app the least helpful (answering 1 and 2), two found the course easy rather than hard, and preferred the wrench example. The other two found the course very hard and preferred the door example. When asked to motivate their response on the app contribution, the answers from this group were diverse. One student (who found the course easy) said that they understood the theory and rather needed help with calculations, which they found that the app did not help with. Another student (who found the course hard) however, answered that they did not find the app helpful since they did not have enough knowledge about the theory and hence could not get any help from the app. Recurrent comments made from the participants that reported increase in understanding thanks to the app were that they found the visualization very helpful. Examples of those comments are: “While realistic examples are great, it’s nice to be able to apply vectors and I would say it’s easier to visualise the vectors and their impact, it helps with the logic”; “It was easier when you could see it in 3D and try out the different forces on positions”.

4.2.2 Quantitative Results: Pre- and Post-test

The pre-test consisted of one question regarding torque. The post-test consisted of eight questions whereof two regarded torque. One of the two post-test questions, task 2, was very similar to the pre-test question while the other post-test question on torque, task 3, differed slightly. This can be observed in the Supplementary Material 2. The distribution of the students in the Mechanics I course, throughout the process of this study, is mapped out in Fig. 6. Regarding how the students performed on the tests, Fig. 7 (top) shows the number of participants who passed and failed the different tasks. The results are shown for all the students, i.e. the ones who used the app and the ones who did not. The same is represented in Fig. 7 (bottom), with the difference that this one only includes the students who participated in both tests, and answered all three questions about torque. The graphs show that the proportions of students who passed are higher in the post-test task 2, task 3, and both, compared to the pre-test in all groups except in one case (no app, post-test task 2 and 3), where the proportion was unchanged. Another interesting trend shown in Fig. 7 is that the proportion of students who passed is higher in all the cases (pre-test, post-test per task, and both tasks on post-test) in the group who used the app compared to the group who did not, and also compared with the total of both groups. Perhaps the most pertinent result in this study is that of possible improvements in learning amongst the participating students, which is shown in Fig. 8. In this figure it can be observed the students’ improvement, deterioration or stagnation of test results in the post-test’s tasks on torque, compared to their pre-test results. In task 2, the group who did not use the app shows a larger improvement than the group who did. However, they also show a larger deterioration than the group who had used the app. In task 3, the group of students who used the app stands for both the larger improvement and deterioration in proportion to the group who did not.

Fig. 6

Student distribution mapped out over the different stages of the study. Note that 6 of the students that took the pre-test did not take the post test and that all the students that did not take the pre-test (8) in fact took the post-test

Fig. 7

Number of students who passed (darker color) versus the ones who failed (lighter color) each of the tests. Note that for direct visual comparison the columns show percentages and not absolute values, so they are all of equal height. The top panel shows all the students, while the bottom one only shows the students who participated in the pre- and post-tests. Note that in this bottom figure there are 25 students all together and that the sum of no-app and app add up to the total of 25 as well. The clearest difference here is the right-most case of post-test task 2 and 3, where 4 out of 13 (30.77%) passed without the app and 5 out of 8 (62.5%) passed with the app

Fig. 8

Improvement (green), stagnation (white) and deterioration (red) of the test results in the post-test tasks on torque compared to their pre-test results. In task 2, the group who did not use the app shows a larger improvement than the group who did. However, they also show a larger deterioration than the group who had used the app. In task 3, the group of students who used the app stands for both the larger improvement and deterioration in proportion to the group who did not

4.3 Statistical Analysis: Calculations

The results presented until this point are based on observations from the raw data. In the following, we discuss whether the observed trends are statistically significant. In order to analyze the possible improvement of the students who participated in both the pre-test and the post-test, the question asked for each group (the app users and the no-app users) was: “Is the proportion of students who passed the post-test larger than the the proportion who passed the pre-test?” A statistical hypothesis test was performed to answer that question for each of the following pairs of proportions:

• Passed pre-test vs Passed post-test task 2

• Passed pre-test vs Passed post-test task 3

• Passed pre-test vs Passed post-test, both tasks 2 and 3

• Passed pre-test vs Passed post-test, any of task 2 or 3

The group who participated in the app session and took both tests consisted of 8 people, while the students who did not use the app but also took both tests summed up to 17 (see Fig. 6 for an overview of the distribution of students). The resulting P values (using a significance level of 95%) after comparing the above mentioned proportions within each group respectively, can be seen in Fig. 9. The only improvements that are statistically significant at a confidence level of $95\%$, i.e. having a P value lower than 0.05, are the pre-test vs post-test task 2 and the pre-test vs post-test any of task 2 or 3 in the group who did not use the app. None of the observed improvements in pass/fail ratios within the group who used the app can be considered statitically significant, as expected from the small sample size.

Fig. 9

Comparing proportions of students who passed the various assignments. (Left) Group who did not use the app and (right) group who used the app. Resulting P values are shown for comparison

To calculate the approximate sample size that would have been necessary to get statistical significance when comparing proportions in our study, we used the method proposed by Whitley and Ball (2002). Firstly we calculate the standardized difference, sd:

$$\begin{aligned} sd = \frac{(p_{1} - p_{2})}{\sqrt{\overline{p}(1-\overline{p})}}; \quad \overline{p} = \frac{(p_{1}+p_{2})}{2}, \end{aligned}$$

(4)

where $p_{1}$ and $p_{2}$ are the two proportions and $\overline{p}$ is the mean of those proportions. When making this estimation of sample size we considered the comparison of proportions in the study with the smallest difference, which was $p_{1} = 0.625$ and $p_{2} = 0.5$. This leads to:

$$\begin{aligned} \overline{p} = \frac{(0.625+0.5)}{2} = 0.5625; \quad sd = \frac{(0.625-0.5)}{\sqrt{0.5625(1-0.5625)}} = 0.25. \end{aligned}$$

(5)

Secondly, following Fig. 1 in Whitley and Ball (2002) with a statistical power of 80%, a confidence level of $95\%$ and having a standardized difference of 0.25, we find that the required sample size would be approximately 500 people in total. Using this method, we are assuming equally sized sample groups. Since we compared proportions from within the same group (app users’ pre-test result with app users’ post-test result and the same for no-app users), the condition of equal sized sample groups is met. Each group would therefore need to contain $500/2 = 250$ people. Thus, ideally one would need 500 participants, i.e. a group of 250 students that used the app and performed both tests, as well as a group of 250 students who did not use the app but performed both tests.

On the other hand, after grading the participants in the two groups, i.e. app users and non-app users, the average scores from each group were 13.1 and 11.5, respectively. In other words, according to the scoring system proposed in this study, the group who used the app exhibits a better ratio of improvement than the group who did not. Moreover, by applying Welch’s t-test, the significance in the difference between the averages was examined using a significance threshold of 0.05. The test result of $\textit{P} = 0.8104 \gg 0.05$ concludes that we cannot discard the null hypothesis that the averages are equal and the difference between them can therefore not be regarded as statistically significant.

5 Discussion

The results of this study indicate that the AR application helped most of the students to improve their understanding of torque. However, the collected data was not from a large enough sample to be able to find statistical significance in the results. Interestingly, the group of students who received most from the application were those who had some grasp of the theory. Moreover, the answers on the form from the app session helped to substantiate the tendencies observed in the pre-/post-test comparison. These tendencies did not reflect signs of improvement within each group. There were also indications that the app users did improve on their test results to a greater extent than the group who did not use the app. The fact that 11 out of 12 participants in the app session answered that the app had helped their understanding of torque supports the shown trend. Furthermore, time has to be considered as a possible influencing factor when seeing improvements among the students. The fact that they had more time and therefore more opportunity to study before the post-test, may be one of the factors explaining the observed improvement from both groups. The group who used the app showed tendencies of greater improvement than the group who did not, which speaks in favor of the app having had an additional impact, besides time, on the improvement. This observation is supported by other similar AR studies (Fidan and Tuncel 2019), in which both qualitatively and quantitatively improvement is reported.

Nevertheless, the proportion of students who passed the pre-test in the app-using group was bigger than the proportion in total, i.e. including all students regardless of the fact that they had used the app or not. This could indicate that the participants in the app session already had a better understanding of torque and therefore they were more likely to perform better in the post-test as well. Future studies should consider randomly distributing students into the app and the no-app groups in order to discard this possibility, whilst keeping in mind the ethical aspect of not offering to a random set of students a teaching method that will probably help them perform better.

Another question that requires reflection is whether the best approach for this study was AR, or whether a simpler 3D visualisation could have had an equivalent effect. The reason for choosing AR was mainly for the accessibility it provides, since it is available in a majority of smartphones. Other technologies such as Virtual Reality were discussed but discarded due to the lack of accessibility, an aspect that was prioritized due to the constraints in an educational environment. Additionally, the possibility of immersion, a core feature of AR, was crucial in deciding among the various alternative technologies. Unlike a standard 3D simulation, AR generates the feeling of actually affecting the reality rather than something that obviously only exists on a screen. It is possible that a 3D visualisation would yield comparable results, but this would require further investigation.

6 Conclusions and Outlook

In order to investigate the opportunities and challenges to enhance learning of torque through visualization with AR, a prototype in the form of an AR smartphone app was developed. The effect of the prototype on students learning was tested by holding a pre-test and a post-test in a basic Mechanics course. A subgroup from the class participated in a user study where they used the AR application to solve problems regarding torque. The results showed indications that visualization through AR of a physical phenomenon which was considered a threshold concept did help students to better understand it. The students who participated in the study using the developed AR application improved their test results to a greater extent than the students who did not use the application. It was however not possible to obtain statistically significant results, since a much larger sample size would be needed to do so. Note that other similar studies (Fidan and Tuncel 2019) have documented quantitative improvement using AR, a fact that supports the positive trends obtained here.

The indication that the AR application improved the students’ understanding of torque motivates further research within the area. To statistically confirm the observed trends, the estimation of sample size done in this work indicates that a group of approximately 500 students would be necessary. The study could also be performed using students in other courses, or at other universities, with larger classes to shorten the time it would take to reach 500 participants. In order to reach a large amount of users in a short time, another alternative could be to integrate the app into a Massive Open Online Course (MOOC). That would enable the app to be used by many during one course round since MOOCs often allow for unlimited amounts of students to participate (Martínez et al. 2020). Deploying the app on platforms such as the App Store or Google Play Store could also be an option, opening up for the possibility of users all over the world to use it. Furthermore, if instead of just pass and fail grades, a higher granularity in the grades was considered, smaller variances could be detected and perhaps it would be sufficient with a smaller sample size to observe statistical significance.