Abstract
The selection of individuals with similar characteristics from a given population have always been a matter of interest in several scientific areas: data privacy, genetics, art, among others. This work is focused on the maximum intersection of k-subsets problem (kMIS). This problem tries to find a subset of k individuals with the maximum number of features in common from a given population and a set of relevant features. The research presents a Greedy Randomized Adaptive Search Procedure (GRASP) where the local improvement is replaced by a complete Tabu Search metaheuristic with the aim of further improving the quality of the obtained solutions. Additionally, a novel representation of the solution is considered to reduce the computational effort. The experimental comparison carefully analyzes the contribution of each part of the algorithm to the final results as well as performs a thorough comparison with the state-of-the-art method. Results, supported by non-parametric statistical tests, confirms the superiority of the proposal.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
A well-known issue in the selection of individuals from a certain population consists of maximizing the features that the selected individuals have in common. This issue has resulted in a wide variety of optimization problems, where the objective usually consists of maximizing the relations between two different sets of elements, without considering the relations among elements in the same subset.
One of the most studied problems of this family is the Maximum Edge Biclique (MEB) problem (Peeters 2003), where the objective is to find a biclique in a given graph with the maximum number of edges. This problem has been widely studied from different perspectives using both, exact and heuristic approaches (Pandey et al. 2020; Wang et al. 2018). Furthermore, several variants for this problem have been also presented, considering new constraints such as the balance between subsets (Li et al. 2020), or weights in the elements to be selected representing their relevance (Pandey et al. 2020).
This research is focused on studying a problem of the family of the MEB, which tries to include constraints from real-world applications, denoted as the maximum intersection of k-subsets problem (kMIS). It is formally defined as follows: let \(E = \{e_1, e_2, \ldots , e_n\}\) be a set of elements, where each e has a set of features \(F_e \subseteq F\), being F the set of available features. It is worth mentioning that the number of features of each elements ranges from 1 to |F|. Then, given an integer number k, the objective of kMIS is to select a subset of k elements from E that shares the maximum number of features in common from F. Then, an instance for this optimization problem is defined by the 3-tuple \(I = (E, F, k)\).
A feasible solution for the kMIS is defined as a set of exactly k elements extracted from E. Then, given a solution \(S \subset E\), with \(|S| = k\), the objective function value \(k\text {MIS}(S)\) is evaluated as:
The goal of kMIS is then to find a solution \(S^\star \) with the maximum value of \(k\text {MIS}(S^\star )\). More formally,
being \({\mathbb {S}}\) the set of all feasible solutions of kMIS.
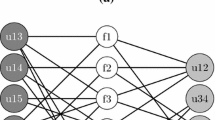
Figure 1a depicts an instance for the kMIS with 4 elements, \(E = \{e_1, e_2, e_3, e_4\}\), and 5 available features, \(F = \{f_1, f_2, f_3, f_4, f_5\}\), to be related to. Features present in each element are represented with a line between the element and the feature. For the sake of clarity, each line is highlighted with the same color as the element. For example, features associated to \(e_1\) are \(F_{e_1} = \{f_1, f_2, f_3\}\), to \(e_2\) are \(F_{e_2} = \{f_1, f_2, f_3, f_5\}\), and so on.
Assuming that \(k = 3\), any feasible solution consists of selecting three elements from E. We depict in Fig. 1b and c two different solutions, denoted as \(S_1\) and \(S_2\). On the one hand, \(S_1\) is conformed with the elements \(S_1=\{e_1, e_3, e_4\}\). On the other hand, \(S_2\) contains the elements \(S_2=\{e_1, e_2, e_3\}\). Regarding \(S_1\), the value of the objective function is computed as \(k\text {MIS}(S_1) = |F_{e_1} \cap F_{e_3} \cap F_{e_4}| = 1\). If we perform the same evaluation over \(S_2\), we obtain \(k\text {MIS}(S_2) = |F_{e_1} \cap F_{e_2} \cap F_{e_3}| = 3 \). Therefore, solution \(S_2\) is better than \(S_1\) in the context of kMIS.
This problem presents several real-life applications in a wide variety of areas. Authors in Vinterbo (2002) show that the kMIS is applicable for controlling the data privacy. In particular, elements represent people for which the privacy must be preserved, while features represent specific attributes that each person can have. Then, the objective is to publish the maximum amount of attributes of people for performing data analytics without violating the privacy of the people involved. Thus, a company can publish a set of attributes if and only if, at least, k people have the same attributes in common. Another relevant application emerges in the context of genetics, where it is required to identify k genes with the maximum number of features in common to conform DNA Microarray (see (Nussbaum et al. 2010) for further details). Finally, in Bogue et al. (2014) a novel application related with recommender systems is presented. Specifically, each element identifies a musical artist and features represents people interested in music. An artist is related to a person if he/she is fan of that musical artist. Then, the objective here is to find a set of k musical artists maximizing the number of fans to conform a musical event, playlist, etc. Notice that kMIS can be easily extended to different areas such as selecting the most popular courses to be served in a restaurant, for instance.
The kMIS was originally defined in Vinterbo (2002), and it was proven to be \({\mathcal {N}}{\mathcal {P}}\)-hard in Xavier (2012), being also hard to approximate. However, for two special types of instances the kMIS can be optimally solved in polynomial time. Specifically, a polynomial delay algorithm is proposed in Ganter and Reuter (1991), which enumerates all closed sets of feasible solutions by representing the instance as a bipartite graph and enumerating all maximal cliques of this graph if the value of k is bounded by a constant. Additionally, authors in Nussbaum et al. (2010) showed that, for some special types of instances which are the convex bipartite graphs, the kMIS can be solved in polynomial time.
In Bogue et al. (2014) an exact method based on an integer programming formulation for the kMIS is presented, which leverages a fast preprocessing method to start the search from. However, as an exact procedure, it requires long computing times for optimally solving small and medium size instances. Additionally, they proposed three linear integer programming models as well as a constructive heuristic for the kMIS, where two of the presented formulations were adapted from Acuña et al. (2014), while the last one is a completely original proposal, being the most efficient exact method for the kMIS.
In spite of the difficulty of finding optimal solutions for the kMIS, it has been mainly ignored from a heuristic point of view. As far as we know, there is only a previous work that tackles the kMIS from a heuristic perspective (Dias et al. 2020), which proposes the combination of several heuristic and metaheuristic algorithms for providing high quality solutions in small computing times. The main proposal is based on the Variable Neighborhood Search (VNS) framework, proposed by Mladenović and Hansen (1997), with the aim of leveraging the systematic changes of neighborhood for improving the solutions found during the search. In particular, they extends the constructive procedure proposed in Bogue et al. (2014) for dealing with several solutions simultaneously combining them with Path Relinking. Additionally, they propose a Reactive VNS method which modifies the shaking phase of VNS by including a greedy randomized selection of the solutions to be selected. Finally, the method is able to escape from local optima by moving to a large neighborhood in case of stagnation.
The remaining of the paper is structured as follows: Section 2 introduces a novel solution representation used in this research, Sect. 3 presents the algorithmic proposal based on GRASP, Sect. 4 describes Tabu Search as an alternative for the GRASP improvement phase, Sect. 5 describes the thorough computational experimentation carried out to analyze the performance of the proposed algorithms and, finally, Sect. 6 draws some conclusions derived from this research as well as highlights possible future research for this problem.
2 Solution representation
Given an instance \(I=(E,F,k)\), a direct implementation for the kMIS would consider that a solution is represented by the set of selected elements from E. However, it is important to take into account the performance of the most common operations over this solution representation. If we consider this set solution representation, the evaluation of a given solution is performed by intersecting the features in common among all selected elements, which can be computationally demanding for medium and large instances. With the aim of accelerating this process, we consider the use of bitsets as it was originally proposed in Dias et al. (2020). To achieve further improvements, we propose to cache solution information during the search. This mechanism allows the algorithm to reduce the number of operations performed, resulting in shorter computing times.
A bitset is defined as a binary array where each element can take the values 0 or 1. In order to model the kMIS, each element \(e \in E\) has its own bitset B of size |F|, where a value of 1 at position p indicates that the feature \(f_p\) is present in \(F_{e}\). Therefore, in order to evaluate the features in common between two elements \(e_i\) and \(e_j\), it is only required to perform the AND logical operation between \(B_i\) and \(B_j\), which can be computed in constant time. This behavior allows us to considerably accelerate the search process.
Table 1 shows the bitset representation and evaluation of the objective function when considering solutions \(S_1\) and \(S_2\) presented in Fig. 1. As it was depicted above, element \(e_1\) has features \(f_1\), \(f_2\), and \(f_3\), which is illustrated with a 1 in the table. Symmetrically, features \(f_4\) and \(f_5\) are not present in \(e_1\), therefore, the corresponding positions are set to 0. The feature representation of the remaining elements can be trivially deduced. The rows highlighted in bold indicate the elements selected in each solution (i.e., \(S_1 = \{e_1, e_3, e_4\}\) and \(S_2 = \{e_1, e_3, e_3\}\)).
The last row of the table represents the result of applying the AND logical operator over the bitsets of the selected elements. In particular, for \(S_1\) the only active bit in the result is the one corresponding to \(f_3\), which is the only feature in common for the selected elements (i.e., \(e_1\), \(e_3\), and \(e_4\)). In the case of \(S_2\), the common features are \(f_1\), \(f_2\), and \(f_3\), which are the ones with a 1 in the resulting bitset.
The objective function value is evaluated as the cardinality of the resulting bitset, being 1 in the case of \(S_1\) and 3 for \(S_2\), as expected. It is worth mentioning that this operation can be also performed in constant time.
In terms of computational complexity, all operations are performed in constant time, resulting in a complexity of O(1), which is quite better than the complexity of performing the intersection of the features of the selected elements, which have a complexity of O(|F|). If the number of features is less than or equal to the CPU word size, then the intersection is guaranteed to be performed in constant time. Otherwise, the representation of the CPU word size must be split into parts to achieve high performance (which can be done directly by the programming language). We refer the reader to Komosko et al. (2016); San Segundo et al. (2006) for a more detailed description about this feature. Therefore, we will use this solution representation for the remaining of the paper.
3 Algorithmic proposal
This work proposes an algorithm based on the Greedy Randomized Adaptive Search Procedure (GRASP) methodology. GRASP is a multi-start metaheuristic presented in Feo and Resende (1989), but it was not formally defined until (Feo et al. 1994). It is conformed by two main phases: construction and local improvement. The former is intended to generate a high quality and diverse solution from scratch (Glover and Kochenberger 2006), while the latter is responsible for finding a local optimum with respect to certain neighborhood. The main idea of GRASP relies on the inclusion of randomization during the construction phase in order to increase the diversity of the search. Contrary to a completely greedy construction phase, each GRASP construction results in a different solution, thus guiding the search to different directions to explore a wider portion of the search space. In particular, we perform 1000 complete GRASP iterations (construction and improvement phase), returning the best solution found during the search. See (Duarte et al. 2015; Pérez-Peló et al. 2020; Casas-Martínez et al. 2021) for recent successful applications of the GRASP metaheuristic in a diverse family of combinatorial optimization problems. Algorithm 1 shows the pseudocode of the GRASP scheme.

The method requires three input parameters: I, the instance that is going to be solved; \(\alpha \), which controls the greediness / randomness of the constructive procedure; and \(\Delta \), the number of iterations of GRASP to be performed.
The algorithm iteratively construct and improve a fixed number of \(\Delta \) solutions (steps 2–8). For each iteration, a solution is constructed from scratch (step 3) following one of the constructive procedures presented in Sect. 3.1. Then, either the local search presented in Sect. 3.2 or the Tabu Search described in Sect. 4 is applied with the aim of further improving the initial solution (step 4). Once the solution is improved, it is checked if it is the best solution found or not (step 5). If so, the best solution is updated (step 6). The method ends returning the best solution found during the search (step 9).
3.1 Construction phase
The constructive procedures designed for the kMIS leverages the solution representation described in Sect. 2 with the aim of generating good starting points for the subsequent local improvement in short computing times. In particular, we propose two different constructive procedures that alternates the greedy and random phases of the GRASP methodology.
The first constructive procedure, named Constructive Greedy-Random (CGR), follows the traditional GRASP scheme. Algorithm 2 shows the pseudocode of the proposed constructive procedure.

As it is customary in GRASP, the first element is selected at random to favor diversity (step 1). Then, the selected element is included in the solution (step 2) and the candidate list CL is conformed with all the elements in E but the first selected element (step 3). The method then iteratively adds elements to the solution under construction by following a greedy criterion (steps 4–12).
In each step, the minimum (\(g_{\min }\)) and maximum (\(g_{\max }\)) value of the greedy function considered to guide the construction among all the candidates are evaluated (steps 5–6). It is recommendable to use a greedy function value which requires a small computational effort since, in each iteration, all the candidates must be evaluated. In the context of kMIS, the efficient representation of a solution presented in Sect. 2 allows the constructive procedure to directly use the objective function as greedy function. In particular, the greedy function value for an element c, denoted as g(c) is evaluated as the number of features that the elements already included in the solution have in common with c. In terms of the solution representation, the value of the greedy function is obtained by performing the logical operation AND between the features of the elements in the partial solution and the features of c.
Then, a threshold \(\mu \) is computed to determine which elements are able to enter in the restricted candidate list RCL (steps 7–8). In particular, the threshold depends on an input parameter \(\alpha _{\textit{GR}}\), which is in the range 0-1. Notice that, if \(\alpha _{\textit{GR}}=0\), then \(\mu = g_{\max }\), and only those elements whose greedy function value is equal to \(g_{\max }\) are considered in the RCL, resulting in a totally greedy algorithm. On the contrary, if \(\alpha _{\textit{GR}}=1\), \(\mu \) takes the value of \(g_{\min }\), and all the elements are included in the RCL, becoming a completely random procedure. Therefore, the larger the value of \(\alpha _{\textit{GR}}\), the more greedy the algorithm is. Section 5 discusses the most appropriate value for this parameter.
The next element to be added to the solution under construction is selected at random from the RCL (step 9). Finally, the CL is updated by removing the selected element to avoid repeated elements in the solution. The method ends when k elements have been selected from E, returning the constructed solution (step 13).
Having defined the constructive procedure CGR, it is interesting to perform a computational complexity analysis. In particular, the while loop presents a complexity of O(k) since it performs exactly k iterations. The maximum complexity of the instructions inside the loop is O(n) since it is necessary to traverse all the elements once, storing \(g_{\min }\) and \(g_{\max }\) during the traversal. To reduce the computational effort, the RCL is not explicitly created, so the selection of the next element is performed in O(1). Then, the complete constructive procedure presents a complexity of \(O(k \cdot n)\).
The second constructive procedure, named Constructive Random-Greedy (CRG) is based on the idea of swapping the greedy and random phases inside the traditional GRASP framework. Algorithm 3 presents the pseudocode of CRG.

Analogously to CGR, the first element is selected at random, constructing the candidate list CL (steps 1–3). As in CGR, the method iteratively adds elements to the solution under construction until obtaining a feasible solution, i.e., \(|S| = k\) (steps 4–9). Then, CRG swaps the greedy and random phases. In particular, the restricted candidate list RCL is constructed by randomly selecting \(\alpha _\textit{RG} \cdot |\textit{CL}|\) elements from the CL (step 6). Then, the selection of the next element is performed in a greedy manner by choosing the best element among those included in the RCL.
Notice that, in this case, the parameter \(\alpha _{\textit{RG}}\), which is also in the range 0-1, produces a totally greedy algorithm when it takes the value 1, since all elements are included in the CL. Values close to 0 results in a small size RCL, which is equivalent to an almost completely random selection of candidates. Again, the best value for this parameter is discussed in Sect. 5.
Similarly to CGR, we perform a computational complexity analysis of CRG. In this case, the while loop again performs exactly k iterations, resulting in a complexity of O(k). Inside the loop, the method needs to traverse \(\alpha _{\textit{RG}} \cdot n\) elements, presenting a complexity of \(O(\alpha _{\textit{RG}} \cdot n)\). Then, the complexity of CRG is \(O(k \cdot \alpha _{\textit{RG}} \cdot n)\), which is better than the complexity of CGR since the value of \(\alpha _\textit{RG}\) is bounded in the range [0,1]. Then, the smaller the value, the better the complexity, since it needs to evaluate a smaller number of candidates in each iteration.
3.2 Local improvement
The second stage of the GRASP methodology consists of finding a local optimum with respect to a certain neighborhood starting from the constructed solution. The literature of GRASP have considered both, simple and more complex local search heuristics for this stage. Indeed, some works have included a complete metaheuristic such as Variable Neighborhood Search (Gao et al. 2019), or even Genetic Algorithms (Saad et al. 2018), in the second phase of GRASP with the aim of further exploring the search space.
In this work, a simple but effective local search is proposed with the aim of finding a local optimum in short computing times. The first element that should be identified to define a local search procedure is the move operator that is applied in the search. In particular, since a feasible solution for the kMIS is conformed with exactly k elements, and with the objective of always maintaining the feasibility of the solutions explored in the neighborhood, a swap move is proposed. Given an element \(e_i \in S\) and an element \(e_j \in (E \setminus S)\), this move swaps \(e_i\) with \(e_j\). In mathematical terms,
The definition of a movement allows us to precisely describe the neighborhood that is explored in the proposed local search, named as N(S), as the set of solutions that can be reached from S by performing a single swap move. More formally,
Having defined the move operator and the neighborhood generated by this move operator, the last element required to define a local search is the way in which this neighborhood is traversed. Two traditional strategies are usually considered: best and first improvement. On the one hand, best improvement explores the complete neighborhood of a given solution, performing the swap move that leads to the highest quality solution. On the other hand, first improvement performs the first move that ends in a better solution than the starting one.
Since best improvement requires the exploration of the complete neighborhood in each iteration, it is usually much more computationally demanding than first improvement. In the context of kMIS, we select first improvement with the aim of maintaining short computing times when including the local search procedure. Notice that the order in which the solutions in the neighborhood are explored is relevant when considering a first improvement approach so, to avoid biasing the search, we perform a random traversal in each iteration. Algorithm 4 shows the pseudocode of the proposed local search.

This local search is executed until we cannot improve. The method starts setting the Improve value to False (step 2). Then, it randomly traverses the elements in S (step 3). For each element \(e_i \in S\), a bitset without considering \(e_i\) is saved at \(B'\), with the aim of having cached the bitset of the solution in case of \(e_i\) is removed (step 4). The inner for loop (step 5) randomly traverses each element that is not in S, and stores in \(B''\) the resulting bitset of performing the AND logical operation with element j, which simulates that \(e_j\) is included in the solution (step 6). If an improvement is found (step 7), the exchange is finally performed (step 8) and the improve value is set to True (step 9). Then, in step 10, the exploration of the neighborhood is stopped (since an improvement has been found, and the method performs a new iteration. This procedure ends when no improvement is found (step 14), returning the local optimum with respect to the defined neighborhood (step 15).
Notice that this local search presents a high performance since it is able to perform just the moves that lead to an improved solution by using the solution representation based on bitsets. In particular, storing in \(B'\) the bitset obtained by removing the element \(e_i\) allows the search to perform this evaluation just once for each element, instead of performing the swap move in each iteration of the search. Similarly, to decide if the move is an improvement or not, the algorithm just need to perform a single AND logical operation with the candidate element \(e_j\) to be included in the solution. If the size of the resulting bitset is larger than the objective function value of the best solution found during the search, the move is performed since it lead to a better solution.
4 Tabu Search
Alternatively to the standard local search proposed in Sect. 3.2, we present a Tabu Search (TS) algorithm to further improve the solutions generated using the constructive procedures described in Sect. 3.1. TS was originally presented in Glover et al. (1998) as a method to help local search methods to escape from local optimality (see (Martí et al. 2018) for a successful application of this metaheuristic). One of the key elements within TS is the inclusion of an adaptive memory during the search.
As it was aforementioned in Sect. 3.2, each solution S has an associated neighborhood N(S) which is conformed with all the solutions that can be reached with a single swap move from S. Local search methods scan this neighborhood, only allowing movements that lead to better solutions, stopping when no improvement is found in N(S). On the contrary, TS allows the method to perform swap moves that lead to worse solutions. In this case, the solutions that can be explored are selected from a restricted neighborhood \(N^\star (S)\), which is a modification of the original N(S) but excluding a subset of solutions according to the history of the states that have already been visited during the search. In this paper we only consider the short-term memory (STM) design, which basically consists of storing the last elements that have been included in a solution. Specifically, given a solution S, an element \(e_i \in S\), and an element \(e_j \in (E \setminus S)\), the proposed TS method performs a move \(\textit{Swap}(S, e_i, e_j)\), where the element \(e_j\) is set to tabu-active, including it in memory, denoted with STM.
Therefore, the TS explores a reduced neighborhood \(N^\star (S)\) defined as follows:
This neighborhood contains all the solutions from N(S) except those that are reached by removing an element that is already in the STM. An element is in the STM during a number of predefined iterations, which is defined by a search parameter named \(\tau \), known as tenure in the context of Tabu Search. After performing \(\tau \) iterations, the tabu status of the element is released, allowing the algorithm to consider it in the search again.
The second key element of TS is that the best swap move in the neighborhood is performed, even if it leads to a solution of lower quality, thus diversifying the search, and escaping from local optimum. In other words, in case that no improvement is found during the current iteration, the TS performs the move with the least deterioration in quality with respect to the objective function value. Since the best move is always performed, a new termination criterion must be defined. Specifically, a maximum number of iterations without improvement \(\gamma \) is considered in this proposal (see Sect. 5 for a detailed analysis on the selection of this value).
Algorithm 5 shows the pseudocode of the proposed Tabu Search algorithm. TS requires from four input arguments: I, which is the instance to be solved; S, which is the initial solution; \(\tau \), the tenure; and \(\gamma \), the maximum number of iterations without improvement allowed.

The method starts by creating the empty Short Term Memory STM (step 2). As it was aforementioned, TS iterates until reaching the stopping criterion, which is a maximum number of iterations without improvement (steps 4–29). In each iteration, it is required to store the least deteriorating move in case there is no improvement (step 6). Then, as in the local search, the method randomly traverses the set of selected elements in the incumbent solution S, excluding those marked as tabu active in the STM (steps 7–23). Each element \(e_i\) is considered for its removal, so a bitset \(B'\) is created with the intersection of all the bitsets of the elements in S but \(e_i\), and it is cached to avoid repeating this evaluation. The next phase consists of selecting the element which will replace \(e_i\) in the solution (step 9-22). In order to do so, a bitset \(B''\) is created as the result of performing the AND operator between the cached bitset \(B'\) and the bitset of the candidate element \(e_j\) (step 10). If the number of active bits in \(B''\) is larger than the objective function value of the incumbent solution, an improvement is found (step 11), so the move is actually performed (step 12) and the number of iterations without improvement is reset to 0 (step 14), also updating the best solution found (step 15). Notice that if a move is performed, it is necessary to mark the inserted element as tabu active, including it in the STM (step 16). Since the STM has a limited size defined by \(\tau \), if the number of elements already in STM is equal to \(\tau \), then the oldest element in STM is removed, losing its tabu active category. In this case, the search starts again from the new best solution (step 17). If there is no improvement, but the number of active bits outperforms the best possible move tested in the current iteration (step 24), then the least deteriorating move is updated (step 20). Finally, if no improvement is found during the complete iteration (step 24), the least deteriorating move is performed (step 25), increasing the number of iterations without improvement (step 26). The element included in the solution is also marked as tabu active (step 27). The method ends when no improvement is found after \(\gamma \) consecutive iterations, returning the best solution found during the search.
To sum up, the TS method proposed in this work is based on the efficient local search presented in Sect. 3.2, including a short-term memory to avoid removing from the incumbent solution those elements which have been recently added. TS allows the exploration of a more diverse solution space than the original local search by exploring solutions which are not strictly better than the incumbent one. The effect of increasing the diversification solutions using TS is deeply analyzed in Sect. 5.
5 Experiments and results
This section has two main objectives. On the one hand, the search parameters of the proposed algorithms, as well as the different variants, must be analyzed. On the other hand, it is necessary to evaluate the performance of the algorithm presented with the aim of comparing it with the best method found in the state of the art.
The experiments are divided into two phases with the aim of satisfying the two aforementioned objectives of this section: preliminary and final experiments. The former are devoted to select the best components for the proposed algorithm, while the latter consists of a competitive testing against the best method found in the literature for the kMIS.
The proposed algorithm has been implemented in Java 11, and all the experiments have been performed in an AMD EPYC 7282 (2.8 GHz) and 8 GB RAM. The set of instances considered in the comparison is the one used in (Dias et al. 2020), which is the best method found in the literature. It consists of 238 instances where the number of elements and features ranges from 32 to 300. We refer the reader to (Dias et al. 2020) for a detailed description on the considered testbed.
5.1 Preliminary experiments
The preliminary experiments are designed for selecting the best search parameters and the best components to be included in the final version of the algorithm. With the aim of avoiding overfitting, these experiments only considers a subset of 27 out of 238 representative instances (approximately 10% of the total set of instances), selected at random from the complete set.
All the experiments in this section report the following metrics: Avg., the average objective function value; Time (s), the computing time measured in seconds; Dev (%), the average deviation with respect to the best result of the experiment; and # Best, the number of best solutions found in the experiment. All this metrics are computed across the instances considered in the corresponding experiment. In all the experiments the best results are highlighted in bold font.
The search parameters that must be configured in the final algorithm are: \(\alpha _{\textit{GR}}\) and \(\alpha _{\textit{RG}}\), for the constructive phase of GRASP; \(\tau \), the tenure of the Tabu Search; and \(\gamma \), which is the stopping criterion of Tabu Search (maximum number of iterations without improvement). Additionally, the best constructive procedure must be selected between CGR and CRG, and the effect of each improvement method must be analyzed.
The first experiment is devoted to select the best value for the \(\alpha _{\textit{GR}}\) and \(\alpha _{\textit{RG}}\) parameters, considering the values \(\{0.25, 0.50, 0.75, \textit{RND}\}\) for both of them, where RND indicates that it is selected at random in each iteration. We analyze the global performance of the constructive procedure coupled with the local search (i.e., a complete GRASP variant). Table 2 shows the results for \(\alpha _{\textit{GR}}\), where each row reports the average results for each GRASP variant.
Analyzing these results, \(\alpha _{\textit{GR}} = \textit{RND}\) emerges as the best value for this parameter. The computing time is equivalent for all the variants, but the random selection in each iteration is able to reach a larger number of best solutions. Table 3 shows the same experiment when selecting CRG as constructive procedure to tune the best value of \(\alpha _{\textit{RG}}\).
In this case, the best value for \(\alpha _{\textit{RG}}\) is \(\alpha _{\textit{RG}}=0.50\), presenting the best results in all the metrics except the computing time, emerging as the best value for CRG. This behavior is partially explained by the increase of the diversification when considering smaller values of \(\alpha _{\textit{RG}}\), which allows the local search to explore a more diverse set of solutions, thus leading to obtain better results. Therefore, \(\alpha _{\textit{RG}}=0.50\) is selected for the remaining experiments.
Having selected the best \(\alpha _{\textit{GR}}\) and \(\alpha _{\textit{RG}}\) parameters, the next experiment is devoted to compare the results obtained by the GRASP variant that considers CGR as constructive procedure and the one that uses CRG. Table 4 shows the results obtained in this experiment.
As can be seen in the results, although GRASP\(_{\text {GR}}\) is slightly faster than GRASP\(_{\text {RG}}\), the differences between them in terms of computing time are negligible. However, if we now analyze the quality of the solutions provided, GRASP\(_{\textit{RG}}\) emerges as the best variant, obtaining a smaller average deviation (0.57 vs. 1.91) and a larger number of best solutions found (23 vs. 20). Therefore, we select GRASP\(_{\text {RG}}\) as the best variant for the kMIS.
The next experiment is oriented to evaluate the influence of the efficient local search proposed in Sect. 3.2. In this case, we have replaced the direct implementation of local search in GRASP\(_{\text {RG}}\) with the efficient one. Naturally, the quality obtained with both algorithms is the same. For the sake of brevity, we omit the inclusion of the detailed results. We only highlight that the efficient algorithm is, on average, over 30 times faster than the straightforward implementation, achieving a speedup larger than 50x in the most complex instances. This implies that with the new efficient local search, the algorithm requires, on average, less than one second to finish. Therefore, we include the efficient local search as the local improvement phase of GRASP\(_{\text {RG}}\).
The next preliminary experiment is intended to evaluate the influence of considering Tabu Search instead of the local search method in the improvement stage of the GRASP algorithm. It is worth mentioning that the local search method in which Tabu Search is based is the efficient one.
Tabu Search requires from two input parameters as described in Sect. 4: \(\tau \), the tenure; and \(\gamma \), the number of iterations without improvement used as stopping criterion. Since these two parameters are quite related between them, we have decided to perform a full-factorial experiment considering the values \(\tau = \{0.1, 0.2, 0.3, 0.4, 0.5\}\) and \(\gamma = \{5,10,15,20,25\}\). Notice that we do not include values larger than 0.5 for the tenure since it would include in the tabu list almost all the elements already in the solution. Table 5 shows the results obtained in terms of computing time (on the left) and average deviation (on the right).
The results have been depicted in a heatmap, in such a way that the best values of each table are highlighted in green, while the worst ones are highlighted in red, following a gradient through yellow color for the intermediate values. If we first analyze the computing time, as expected, the larger the value of \(\gamma \), the larger the computing times, while it decreases with the increment in \(\tau \) value, being \(\gamma =5\) and \(\tau =0.5\) the fastest variant. Naturally, allowing more iterations without improvement requires more computing time and, similarly, increasing the size of the tabu list limits the local search exploration, reducing the computational effort. If we now analyze the average deviation obtained by each variant, the best value is achieved when considering \(\tau =0.1\) and \(\gamma =25\). However, it is the most computationally demanding configuration so, in order to find a balance between quality and computing time, we select \(\tau =0.5\) and \(\gamma =5\) as the best search parameters. The rationale behind this is that it is able to reach a deviation really close to the best one (0.68% vs. 0.15%), but being almost six times faster than the best result (2.27 seconds vs. 12.76 seconds).
The final preliminary experiment is intended to evaluate the influence of considering Tabu Search instead of the local search method in the improvement stage of the GRASP algorithm. It is worth mentioning that the local search method in which Tabu Search is based is the efficient one. Table 6 shows the results obtained by both approaches, denoted as GRASP\(_{\text {RG+TS}}\) and GRASP\(_{\text {RG+LS}}\).
As it can be derived from the results, GRASP\(_{\text {RG+TS}}\) is able to outperform GRASP\(_{\text {RG+LS}}\) configured with a classical local search in terms of deviation (0.31 vs. 1.03) and number of best solutions found (26 vs. 22) by requiring slightly larger computing times (2.27 seconds vs. 0.60 seconds). Despite the additional computation required by GRASP\(_{\text {RG+TS}}\), the increment in the computing time remains negligible mainly due to the efficient representation of the solution described in Sect. 2.
Therefore, we identify as our best variant the algorithm GRASP\(_{\text {RG}}\) with CRG(0.50) and Tabu Search as improvement strategy (based on the efficient implementation of the local search method) configured with \(\tau =0.5\) and \(\gamma =5\).
5.2 Competitive testing
The competitive testing is devoted to evaluate the performance of our best approach when comparing it with the best previous method found in the related literature, named Reactive VNS. In particular, Reactive VNS is a Variable Neighborhood Search algorithm where the shaking stage has been improved with a greedy randomized selection of the next solution to be selected. In order to have a fair comparison, we have executed both algorithmsFootnote 1 in the same computer.
For this experiment, the complete set of 238 instances has been used. They are divided into three different sets following the same scheme as in Dias et al. (2020). In particular, the first set contains 78 instances where the number of elements is equal to the number of available features, i.e., \(|E|=|F|\). The second set refers to those instances where there are more elements than features available (\(|E|>|F|\)), and the third set contains the instances where the set of available features is larger than the number of elements (\(|E|<|F|\)). The second and third set is conformed with 80 instances each one.
Table 7 shows the results obtained when performing 10 independent executions of each algorithm for each instance in order to avoid the bias produced by the random parts of each proposal. For each class of instances (denoted as classe), we report the best, worst, and average value of the objective function obtained in the 10 executions. For the sake of brevity, this Section reports a summary table. We refer the reader to Table 8 in the Appendix for the individual results over each instance.
If we first analyze the best solution found by each algorithm, we can clearly see the superiority of GRASP with respect to Reactive VNS, being able to reach the best values in 7 out of 8 classes of instances, while Reactive VNS reaches the best value (or equal to GRASP) in a total of 4 classes. With respect to the worst solution found, both methods perform similarly, being GRASP better or equal than Reactive VNS in 5 classes, while Reactive VNS is better or equal than GRASP in 6 classes. Analyzing the behavior of the algorithms on average, GRASP reaches the best values in 6 classes, while Reactive VNS is only able to reach the best value in 2 classes. Therefore, GRASP emerges as a competitive method for the kMIS in terms of objective function value.
Since Reactive VNS is able to achieve a slightly better result in the instances on classe 7, we have decided to deeply analyze this subset. Having a close look on the individual results shown in the Appendix, it is worth mentioning that, in most of the instances, all the features can be selected, which is not a common scenario in real-life applications.
One of the key aspects of the proposed algorithm is its efficiency, obtaining a remarkable improvement with respect to the previous method in terms of computing time. In particular, GRASP\(_{\text {RG+TS}}\) is, on average, 9 times faster than Reactive VNS, being 13 times faster in the most complex class. If we perform a deeper analysis on the computing time, GRASP\(_{\text {RG+TS}}\) requires 5.35 seconds for the most complex instance, while Reactive VNS requires 160.96 seconds, achieving a maximum speedup of 32x. These results highlights the relevance of leveraging the solution structure to cache information, thus avoiding the repetition of unnecessary evaluations. Furthermore, performing only those moves that leads to an improvement also has a positive impact in the computational effort.
Finally, in order to confirm these results, the well-known non-parametric pairwise Wilcoxon test is applied. The obtained p-value smaller than 0.00001 indicates that there exists statistically significant differences between both algorithms, confirming the superiority of GRASP\(_{\text {RG+TS}}\). Therefore, GRASP\(_{\text {RG+TS}}\) emerges as the most competitive algorithm for dealing with the kMIS problem.
6 Conclusions
In this work, a Greedy Randomized Adaptive Search Procedure (GRASP) is presented for providing high quality solutions for the maximum intersection of k-subsets problem (kMIS). An efficient representation of the solution allows us to design a fast algorithm which is able to generate solutions in approximately one second on average, where the best method in the literature requires about 20 seconds. Two constructive procedures are proposed, where the first one follows the traditional GRASP scheme while the second one swaps the random and greedy stages resulting in better results. The design of the local search reduce the computing time required to find a local optimum by avoiding those moves that would lead to a worse quality solution. Additionally, a Tabu Search method based in this efficient local search is presented, allowing the final algorithm to escape from local optima where the traditional local search get stuck. This behavior is shown in a thorough experimental comparison where the effect of each part of the algorithm is analyzed. The results are supported by non-parametric statistical tests which confirms that there are statistically significant differences between the proposed method and the best algorithm found in the literature.
The future lines of research with respect to kMIS are focused in further improving the obtained results by increasing the diversity of the search without deteriorating the quality of the solutions. In order to do so, reactive strategies will be included in both GRASP and Tabu Search, which may help the algorithm to dynamically adapt to different sets of instances. Finally, strategies such as Iterated Greedy which partially destructs and reconstruct the solution might lead to better results, but requiring more computing time.
Data Availibility Statement
All the data and source code is available in https://grafo.etsii.urjc.es/kmis
Notes
We thank the authors of Dias et al. (2020) for kindly providing us the source code.
References
Acuña, V., Ferreira, C.E., Freire, A.S., Moreno, E.: Solving the maximum edge biclique packing problem on unbalanced bipartite graphs. Discrete Appl. Math. 164, 2–12 (2014)
Bogue, E.T., de Souza, C.C., Xavier, E.C., Freire, A.S.: An integer programming formulation for the maximum k-subset intersection problem. In: Fouilhoux, P., Gouveia, L.E.N., Mahjoub, A.R., Paschos, V.T. (eds.) Combinatorial Optimization, pp. 87–99. Springer International Publishing, Cham (2014)
Casas-Martínez, P., Casado-Ceballos, A., Sánchez-Oro, J., Pardo, E.G.: Multi-objective grasp for maximizing diversity. Electronics 10(11), 1232 (2021)
Dias, F.C., Tavares, W.A., de Freitas Costa, J.R.: Reactive VNS algorithm for the maximum k-subset intersection problem. J. Heuristics 26(6), 913–941 (2020)
Duarte, A., Sánchez-Oro, J., Resende, M., Glover, F., Martí, R.: Greedy randomized adaptive search procedure with exterior path relinking for differential dispersion minimization. Inf. Sci. 296, 46–60 (2015)
Feo, T.A., Resende, M.G.: A probabilistic heuristic for a computationally difficult set covering problem. Oper. Res. Lett. 8(2), 67–71 (1989)
Feo, T.A., Resende, M.G., Smith, S.H.: A greedy randomized adaptive search procedure for maximum independent set. Oper. Res. 42(5), 860–878 (1994)
Ganter, B., Reuter, K.: Finding all closed sets: a general approach. Order 8(3), 283–290 (1991)
Gao, Y., Gao, X., Li, X., Yao, B., Chen, G.: An embedded GRASP-VNS based two-layer framework for tour recommendation. IEEE Trans. Serv. Comput. (2019)
Glover, F., Laguna, M.: Tabu search. In: Handbook of combinatorial optimization, pp. 2093–2229. Springer (1998)
Glover, F.W., Kochenberger, G.A.: Handbook of metaheuristics, vol. 57. Springer Science & Business Media (2006)
Komosko, L., Batsyn, M., San Segundo, P., Pardalos, P.M.: A fast greedy sequential heuristic for the vertex colouring problem based on bitwise operations. J. Comb. Optim. 31(4), 1665–1677 (2016)
Li, M., Hao, J.K., Wu, Q.: General swap-based multiple neighborhood adaptive search for the maximum balanced biclique problem. Comput. Oper. Res. 119, 104922 (2020)
Martí, R., Martínez-Gavara, A., Sánchez-Oro, J., Duarte, A.: Tabu search for the dynamic bipartite drawing problem. Comput. Oper. Res. 91, 1–12 (2018)
Mladenović, N., Hansen, P.: Variable neighborhood search. Comput. Oper. Res. 24(11), 1097–1100 (1997)
Nussbaum, D., Pu, S., Sack, J.R., Uno, T., Zarrabi-Zadeh, H.: Finding maximum edge bicliques in convex bipartite graphs. In: International Computing and Combinatorics Conference, pp. 140–149. Springer (2010)
Pandey, A., Sharma, G., Jain, N.: Maximum weighted edge biclique problem on bipartite graphs. In: Conference on Algorithms and Discrete Applied Mathematics, pp. 116–128. Springer (2020)
Peeters, R.: The maximum edge biclique problem is NP-complete. Discrete Appl. Math. 131(3), 651–654 (2003)
Pérez-Peló, S., Sánchez-Oro, J., Duarte, A.: Finding weaknesses in networks using greedy randomized adaptive search procedure and path relinking. Expert Syst. 37(6), e12540 (2020)
Saad, A., Kafafy, A., Abd-El-Raof, O., El-Hefnawy, N.: A grasp-genetic metaheuristic applied on multi-processor task scheduling systems. In: 2018 13th International Conference on Computer Engineering and Systems (ICCES), pp. 109–115. IEEE (2018)
San Segundo, P., Galán, R., Matía, F., Rodríguez-Losada, D., Jiménez, A.: Efficient search using bitboard models. In: 2006 18th IEEE International Conference on Tools with Artificial Intelligence (ICTAI’06), pp. 132–138. IEEE (2006)
Vinterbo, S.A.: A note on the hardness of the k-ambiguity problem. Tech. Rep. DSG-TR-2002-006, Decision Systems Group/Harvard Medical School, 75 Francis Street, Boston, MA 02115, USA (2002)
Wang, Y., Cai, S., Yin, M.: New heuristic approaches for maximum balanced biclique problem. Inf. Sci. 432, 362–375 (2018)
Xavier, E.C.: A note on a maximum k-subset intersection problem. Inf. Process. Lett. 112(12), 471–472 (2012)
Acknowledgements
This research was funded by “Ministerio de Ciencia, Innovación y Universidades” under grant ref. PGC2018-095322-B-C22, “Comunidad de Madrid” and “Fondos Estructurales” of European Union with grant refs. S2018/TCS-4566, Y2018/EMT-5062.
Funding
Open Access funding provided thanks to the CRUE-CSIC agreement with Springer Nature.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Casado, A., Pérez-Peló, S., Sánchez-Oro, J. et al. A GRASP algorithm with Tabu Search improvement for solving the maximum intersection of k-subsets problem. J Heuristics 28, 121–146 (2022). https://doi.org/10.1007/s10732-022-09490-8
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10732-022-09490-8