Abstract
Realizing the full individual and population-wide benefits of antiretroviral therapy for human immunodeficiency virus (HIV) infection requires an efficient mechanism of HIV-related health service delivery. We developed a system dynamics model of the continuum of HIV care in Vancouver, Canada, which reflects key activities and decisions in the delivery of antiretroviral therapy, including HIV testing, linkage to care, and long-term retention in care and treatment. To measure the influence of operational interventions on population health outcomes, we incorporated an HIV transmission component into the model. We determined optimal resource allocations among targeted and routine testing programs to minimize new HIV infections over five years in Vancouver. Simulation scenarios assumed various constraints informed by the local health policy. The project was conducted in close collaboration with the local health care providers, Vancouver Coastal Health Authority and Providence Health Care.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 Antiretroviral therapy and the HIV epidemic
Human immunodeficiency virus (HIV) infection is a major contributor to disease burden [38, 50, 62] and a leading cause of death [88]. Globally, 35 million people are living with HIV. Treatment has advanced enormously in recent years, although a vaccine or a cure is still likely to be years away. Combinations of drugs known as highly active antiretroviral therapy (HAART)Footnote 1 have the capacity to dramatically alter the course of HIV disease, improving health outcomes and extending life expectancy.
HIV brings on a progressive failure of the immune system. Untreated infection generally proceeds to acquired immunodeficiency syndrome (AIDS) within eight to twelve years. The first stage of disease is the highly infectious acute phase that lasts six to eight weeks, followed by a long asymptomatic latent phase preceding the onset of AIDS. This natural disease progression may be interrupted through treatment with HAART, which restricts viral replication and thereby slows immune system deterioration.
The risk of HIV transmission is influenced by viral load—the amount of virus circulating in the bloodstream. HAART has the potential to reduce HIV transmission by as much as 96 % [18]. Therefore, antiretroviral treatment also functions as a method of prevention [55]. Several studies found a decline in HIV diagnoses after improved access to HAART, providing empirical support for a prevention effect at the population level [19, 54, 56, 79]. These observations form the rationale for the Treatment as Prevention (TasP) public health strategy, which aims to combat the HIV epidemic through improved access to HAART.
1.2 Challenges in treatment access
Access to HAART is inequitable around the world. Marginalized groups with high HIV prevalence often face the greatest barriers to health care access. Only about 30 % of people living with HIV in low and middle income countries receive treatment [38]. HAART coverage is inadequate in resource-rich countries as well. For example, only 25 % of people living with HIV in the USA have suppressed viral load [26]. As of 2011, an estimated 65 % of HIV-positive individuals were potentially infectious due to unsuppressed viral load in British Columbia (BC), Canada [59]. The World Health Organization (WHO), other international bodies, and a growing number of national governments are integrating TasP into guidelines and policies to reduce HIV transmission, as well as HIV-related morbidity and mortality. In 2014, the Joint United Nations Programme on HIV/AIDS (UNAIDS) announced ambitious new testing and treatment coverage targets in order to achieve viral suppression for 73 % of all people living with HIV/AIDS by the year 2020 [39].
Expanding treatment coverage poses significant operational challenges [20, 83]. Treatment transforms HIV infection into a chronic condition; therefore, HIV management demands a shift to a chronic disease service delivery model [24]. HAART must be taken for life to maintain viral load suppression, improved health, and low infectiousness. This requires an effective mechanism for the sustained delivery of a continuum of health care services that range from HIV testing and linkage to care, through to long-term monitoring and retention in treatment. Numerous gaps and inefficiencies in the HIV care continuum have been documented [26, 33, 59]. Implementation studies and ongoing projects worldwide are evaluating the effectiveness of TasP strategies in overcoming these obstacles to treatment delivery [30, 83]. TasP was evaluated in British Columbia during 2010–2013 through the Seek and Treat for the Optimal Prevention of HIV/AIDS (STOP HIV/AIDS) pilot project [36].
1.3 The role of HIV testing
Clearly, diagnosis of HIV infection is a prerequisite for treatment. Until recently, the WHO has recommended routine voluntary HIV testing with counselling in generalized epidemics and targeted testing to individuals presenting with the signs and symptoms of HIV infection in concentrated epidemics [86]. The HIV epidemic in most countries outside of sub-Saharan Africa is concentrated in key populations, including men who have sex with men (MSM), injection drug users (IDU), and female sex workers (FSW). Targeted HIV testing is usually employed in these countries. In sub-Saharan Africa, routine voluntary testing is recommended because HIV prevalence is high in the general population [27].
Recently updated WHO guidelines include provider-initiated testing at health care facilities serving populations most at risk for HIV. These guidelines also go a step further, recommending the implementation of an appropriate mix of routine and targeted testing delivery models based on the local epidemiological context and available resources to ensure equitable access to HIV testing and counselling [87]. A re-examination of the traditional dichotomized approach to HIV testing is now necessary to develop nuanced strategies that better address the need to diagnose HIV as early in the course of the infection as possible [9, 84, 87].
Over the past decade, some jurisdictions with concentrated epidemics have already begun to challenge conventional testing recommendations. Routine testing in non-traditional settings was found acceptable and effective in several studies, including in Argentina [75], Spain [40], and the UK [67, 78]. On the other hand, a study in the USA found only modest gains in new diagnoses—most of these late in the course of infection—through non-targeted HIV screening in an emergency department [34]. Nevertheless, economic modelling studies consistently find routine screening to be cost-effective in terms of increased quality-adjusted-life-years (QALYs) [47, 48, 64, 65, 71, 89], although the impact varies by the state of the epidemic and model assumptions. Routine testing guidelines and policies already exist in a few countries with concentrated epidemics. For example, the U. S. Preventive Services Task Force has recently recommended screening for the general population, reinforcing the routine testing policy launched by the Center for Disease Control already in 2006 [57]. Routine testing is recommended in the United Kingdom for any setting with HIV prevalence above 0.2 % [35].
Targeted testing has been the default policy in Canada. In Vancouver, British Columbia, Vancouver Coastal Health (VCH) and Providence Health Care (PHC)—local organizations that oversee HIV testing—have undertaken a pilot project within the context of the STOP HIV/AIDS initiative to evaluate routine HIV testing in hospitals [32]. In parallel, we conducted a resource allocation analysis of Vancouver’s HIV testing program to identify strategies to achieve optimal TasP outcomes.
1.4 Mathematical models of HIV testing programs
Resource allocation models for HIV health services have been under-utilized in the past [3, 11, 44, 87]. Existing models focus mainly on prevention and treatment rather than testing. Alistar and Brandeau provide an overview of the literature on resource allocation models [2], in which they describe three main methodologies: linear models, deterministic nonlinear epidemic models, and stochastic agent-based models. In contrast to linear models, epidemic models capture non-linear epidemic growth and can account for changes in epidemic outcomes due to interventions. Stochastic agent-based models are more complex and have been used to study mixed interventions.
Modelling analyses have largely approached HIV testing from a health economics perspective to evaluate the cost effectiveness of HIV testing programs [4, 5, 6, 31, 37, 48, 41]. These studies, which we review below, differ from our operational approach, which seeks ways to utilize a previously allocated budget for the best possible effect on population health.
Cost-effectiveness models have been used to determine optimal HIV testing frequencies for high-risk groups [31, 48]. Gray et al. [31] used a stochastic agent-based model to assess the impact on HIV incidence of increasing testing coverage and frequency for gay men in New South Wales, Australia. They found that in the current testing and treatment environment, further increases in the testing rate would only modestly reduce HIV incidence. However, increasing testing coverage and frequency is likely to have a greater impact on incidence in jurisdictions with lower testing levels. Lucas and Armbruster [48] used a simple model without disease dynamics to assess the cost-effectiveness of increasing testing rates in screening high-risk groups in the United States. They found that the testing rates recommended by the Centers for Disease Control are too conservative and that increasing the rate of testing is cost-effective for all risk groups.
Katz et al. [41] used a nonlinear deterministic model to determine potential changes in HIV prevalence associated with promoting home-use testing as an alternative to testing in clinics for MSM in Seattle, USA. They found that HIV prevalence would increase in this scenario even with an overall greater testing rate, because the length of the HIV infection-to-detection window period for home-use testing is 90 days, as opposed to 15 days for clinic-based testing. They also determined the required window-period for home-use testing that would decrease HIV prevalence.
The relative effectiveness of random HIV screening and contact tracing was analyzed by Hyman et al. [37] using two differential equation models: the differential infectivity model and the staged-progression model. In the former, newly infected individuals enter one of several compartments with specific infectivities. This captures risk behaviour variation in the population. The epidemic in this model is driven by “superspreaders” who frequently engage in high-risk behaviours. In the staged-progression model, individuals progress through disease stages with different infectivities, which represent the acute, latent, and AIDS stages of HIV infection. The differential infectivity model captures differences in infectivity between individuals, while the staged-progression model captures variation in infectivity over time for a single individual. The authors find that contact tracing is more effective in controlling the spread of HIV if epidemic dynamics follow the differential infectivity model. However, random screening is more effective if epidemic dynamics follow the staged-progression model.
Armbruster and Brandeau analyzed the cost effectiveness of mixed contact tracing and screening strategies in a series of papers [4–6]. They approach the problem using both compartmental models [4, 6] and a network model [5]. Generally, they find that there is a threshold investment in testing programs required to achieve cost-effective control of an endemic disease. Investment in testing programs beyond this level leads to diminishing returns and is not cost effective. The cost-effectiveness threshold depends on the mix of contact tracing and screening programs and there is an optimal mix of testing programs, which minimizes total testing costs at threshold. The authors consider not only HIV, but also other chronic infectious diseases, such as tuberculosis, hepatitis B, and hepatitis C.
Additionally, operations research has been applied to determine the optimal procedure for identifying all positive blood samples in a routine screening program [82]. Specifically, the authors compared the efficiency of directly testing individual samples to testing sub-groups of samples prior to individual testing. This method to optimize screening for infectious diseases in large populations was first used during World War II for syphilis screening [21, 82]. Optimal algorithms for testing large numbers of samples were also investigated by Abolnikov and Dukhovny using queueing theory; they found that the optimal testing approach depends on HIV prevalence in the population [1].
We are not aware of previous analyses that use operations research to optimize existing testing programs by reallocating resources among testing activities. This paper describes an operational analysis in which we assume an a priori testing budget and seek to optimally allocate resources between targeted and routine testing programs to achieve the best public health outcomes. Our focus on testing resources was motivated by the priorities of the public health stakeholders on the team, who manage Vancouver’s HIV testing program. However, the influence of testing on the HIV epidemic depends strongly on the entire follow-up and treatment framework. Vancouver follows a test and treat policy [29], in which treatment is offered at no cost to patients, immediately after an HIV diagnosis. Therefore, to assess the epidemic impact of testing program interventions, we consider HIV testing in the context of the entire continuum of HIV care. We explore the TasP objective of preventing infections by optimizing resource allocation to minimize new HIV infections over five and ten years.
1.5 Collaboration background
From 2010–2013, Vancouver Coastal Health and Providence Health Care were participants in the STOP HIV/ AIDS Treatment as Prevention implementation pilot project in Vancouver. Aligned with TasP goals, VCH and PHC sought ways to boost case finding and early HIV diagnoses. We assembled a team of operations research and VCH/PHC public health experts to carry out the mathematical modelling analysis to improve the performance of Vancouver’s HIV testing program.
Prior to the collaboration, VCH/PHC partners developed a conceptual framework for categorizing HIV testing activities to facilitate planning and management of the testing program. Similarly, the operations research participants brought to the collaboration their previously developed conceptual framework for modelling the HIV care continuum in Vancouver. The team decided to integrate the VCH/PHC testing framework into a continuum of HIV care model to produce a highly customized modelling tool for answering questions of interest to the local public health stakeholders. The model was developed jointly, with frequent consultations and meetings of the entire team to ensure that the relevance of the model to the practical public health questions was retained. The project concluded with several meetings with the team dedicated to interpretation of the findings and their relevance to programming and policy.
2 System dynamics to model the HIV care continuum
Health services in the continuum of HIV care include testing programs; linkage of the newly diagnosed to care; clinical assessment; monitoring for clinical indicators of treatment initiation, adverse events and drug resistance; long-term retention in treatment; and hospital care. Components of the care continuum are interdependent—a change in one has the potential to trigger changes in others—creating a complex system with outcomes that are often difficult to predict or quantify. Therefore, the full impact of a single intervention is most accurately assessed in the context of the entire system. System dynamics modelling is well suited to capturing complex feedback structures within systems.
The causal loop diagram in Fig. 1 is a high-level depiction of relationships among elements of the HIV care continuum. In the diagram, arrows represent positive and negative causal influences between elements of the system. The small, circular arrows represent two feedback loops. For example, consider an intervention that improves the efficiency of an HIV testing program. As people living with HIV are diagnosed and referred to further care, the proportion of the infected population engaged in care and receiving antiretroviral therapy grows. Those who achieve viral suppression and adhere to HAART have a reduced probability of transmitting HIV. Fewer new infections eventually leads to a drop in new diagnoses. Figure 1 shows how this feedback loop spans the entire continuum of HIV care.
The system dynamics model of the HIV care continuum in Vancouver we describe in this paper is coupled to a non-linear compartmental HIV transmission model. Mathematically, both system dynamics models and compartmental transmission models are systems of coupled ordinary differential equations. Therefore, the combined model is simply a large nonlinear system of ordinary differential equations, which relates testing strategies to HIV incidence, the number of new infections per unit time. This model is used to find optimal allocations of testing resources, which minimize the total number of new infections over five and ten years.
3 Developing a qualitative model
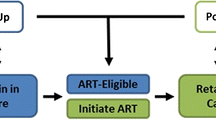
We developed a qualitative model of Vancouver’s continuum of HIV-related health services—incorporating a detailed representation of the testing program—to guide construction of the system dynamics model. Through interviews with system experts, including HIV physicians and public health representatives, we identified key activities and decisions, which were documented using the Unified Modelling Language (UML) [60] activity diagram shown in Fig. 2. UML was originally developed as a visual modelling language for software design. The application of UML in the context of simulation model development is discussed by Sonnessa [76]. UML activity diagrams provide a graphical depiction of system workflow. Their visually intuitive structure facilitated our discussions with system experts, while the precise UML syntax served as a blueprint for constructing the system dynamics model described in Section 4. Below, we explain the diagram in Fig. 2, starting at the black circle at the top left and proceeding through the public health, community care and acute care sectors of the health care system, which are shown as separate swim lanes.
A Unified Modelling Language (UML) diagram of the continuum of HIV care in Vancouver. Activities take place in the public health, community care, and acute care sectors of the health care system, depicted as separate swim lanes. Boxes with rounded corners are events. Purple and pink diamonds represent decision and merge points, respectively. Vertical bars with multiple out arrows are logical or statements for events that may occur simultaneously, whereas multiple in arrows represent logical and statements, which means that all prior events must occur before moving forward. Pink boxes represent epidemic outcomes of the HIV care continuum. Patients may die and leave the system at any stage
In the Public Health swim lane, the event boxes Identify Populations at Risk, Identify Cases and Test for HIV show HIV testing activities in a simplified form. If the test is negative, further tests may follow. A positive test leads to the Diagnose Infection event. Each new diagnosis triggers Partner Notification, which is a public health service to identify and offer HIV testing to partners of HIV cases. The newly diagnosed are either linked or lost to care, as shown by Link to Care from Public Health Sector or Patient Lost to Follow-Up, respectively.
In the Community Care swim lane, health service providers Identify Cases for testing and offer a Test for HIV. A negative test result may lead to further testing, whereas a positive result leads to the event Diagnose Infection. Each diagnosis triggers a Report to Public Health and partner notification. In parallel to partner notification, a newly diagnosed individual may be linked to care by the test provider (Link to Care from Community Care Sector) or through public health. If neither avenue is successful, the patient is lost to follow-up.
In the Acute Care swim lane, HIV testing may be administered to patients presenting with symptoms suggestive of HIV infection, or through routine screening for HIV (Identify Cases via Diagnostics or Screen). As in community care, all newly diagnosed infections are reported to public health officials and are either linked to care by the test provider, linked to care from public health, or lost to follow-up.
Patients diagnosed with HIV while in a hospital may undergo Clinical Assessment in Acute Care. All others linked to care undergo initial Clinical Assessment in community care, including viral load testing. Clinical assessment may have various outcomes. Patients in the acute or latent phase of infection may proceed to monitoring with or without treatment initiation, as indicated by the Acute and Latent events, or Acute on HAART and Latent on HAART events, respectively. Patients with AIDS trigger the event Diagnose AIDS in Acute Care. Finally, patients may become disengaged from the health care system after initial assessment in the Patient Lost to Follow-Up event.
Once in care, it is possible to initiate treatment, achieve viral suppression, experience treatment interruptions, or become non-adherent to treatment regimens, as shown by the vertical arrows between the Latent or AIDS events, Latent on HAART or AIDS on HAART events, and Latent Suppressed or AIDS Suppressed events. The events labelled Suppressed refer to patients who are virally suppressed on HAART. The events labelled on HAART refer to treatment failure, non-adherent cases, and those who have not yet achieved viral suppression. After the onset of AIDS, hospitalization may result for patients who are not virologically suppressed, which is indicated by arrows from AIDS and AIDS on HAART down to Hospitalization – ICU or Hospitalization – General Medical Bed.
Sustained viral suppression reduces morbidity, mortality, and risk of HIV transmission, which is indicated by the arrows from Latent Suppressed and AIDS Suppressed to the outcomes Sustained Suppressed Viral Load, Reduced Morbidity and Mortality and HIV Incidence. Fewer new infections lead to a reduction in HIV Prevalence, which in turn influences the yield of positive diagnoses through testing in the three health care sectors. These population health outcomes reflect the combined effects of interventions and are measures of the efficiency of the HIV care continuum.
We incorporated a detailed representation of Vancouver’s HIV testing program into the qualitative model in Fig. 2 by adapting a conceptual framework developed by VCH for categorizing their HIV testing activities. In Vancouver, HIV diagnoses may occur through targeted testing based on an identified HIV risk; routinely offered voluntary testing in high HIV-prevalence settings, for example detox centres; or routine testing programs in acute care settings, such as hospital departments for internal medicine, renal or cardiac services. Expansion of the routine testing program to family practices, primary care clinics, and other general health care settings was under consideration during our collaboration and has subsequently moved forward. However, the only general health care setting included in our model is acute care in hospitals because data were not available for other general health care settings at the time of the analysis.
The VCH testing framework considers the key populations of men who have sex with men, injection drug users and street-based female sex workers. In addition to reaching key populations, routine testing in general health care settings also reaches the general population. A summary of the VCH testing framework as incorporated into the model is given in Table 1.
4 System dynamics model
The activities and decision points in the UML activity diagram of Fig. 2 were translated into the stocks and flows of a system dynamics model. In the model, we combine the IDU and street-based FSW into one key population, because they are closely linked in Vancouver. A 2006 cohort study of street-based FSW found that 60 % were engaged in injection drug use [74]. Therefore, there is substantial cross-transmission between these groups. Furthermore, VCH confirmed that the two groups have similar risks for acquiring HIV. We denote this combined key population in the model as IDU-FSW.
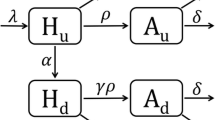
Independent system dynamics models were constructed for each of the subpopulations MSM, IDU-FSW, and the general population. As shown in Fig. 3, each model consists of 17 compartments representing stocks of undiagnosed and diagnosed groups. Susceptible, HIV-negative individuals S may become infected and subsequently progress through the acute E, latent L, and AIDS A phases of infection. Diagnoses can take place during any infection phase, either through targeted testing, routine testing in high prevalence settings or routine testing in acute care. Following testing and diagnosis (flows a, b, and c in Fig. 3), there is a period of waiting to be linked to care, represented by the five compartments denoted by W, with subscripts indicating disease state and method of diagnosis. Due to the short six to eight week duration of the acute phase [14] and the delay in engagement in care after diagnosis, we make the simplifying assumption that patients can only be linked to care in the latent or AIDS phase of infection. Once in care, patients may be: (i) off treatment ( L C and A C ), (ii) receiving treatment yet not have achieved viral suppression ( L T and A T ), or (iii) receiving treatment and virologically suppressed ( L S and A S ). Patients may also leave care after diagnosis and become lost to follow up ( L O and A O ).
System dynamics model of the HIV care continuum in Vancouver. Labels for flows of new diagnoses from each stage of infection are a: targeted testing and routine testing in high prevalence settings; b: routine testing in acute care; c: diagnoses through symptom-based testing. Labels for stocks are S: HIV-negative, susceptible to infection; E: undiagnosed HIV-positive in acute phase; L: undiagnosed HIV-positive in latent phase; A: undiagnosed HIV-positive with AIDS; W: waiting to be linked to care. Subscripts for L and A are O: out of care; C: in care, off treatment; T: treated, not virologically suppressed; S: treated, virologically suppressed. Death from each compartment is not shown but taken into account. The flow “1”, is used to link different portions of the diagram
4.1 Model assumptions
The subpopulations MSM, IDU-FSW, and the general population are treated as independent and non-interacting in the model. These groups are socially, and to some extent, geographically distinct in Vancouver. The size of any bridge groups have not been precisely estimated. A mathematical model developed to study HAART expansion in British Columbia assumed that 5 % of the MSM population and 6.5 % of the IDU population belong to both key populations [46]. The assumption of minimal overlap was supported by surveillance data from the British Columbia Centre for Excellence in HIV/AIDS (BC-CfE) [46] and expert opinion of our public health partners. No equivalent estimates for interactions of key populations with the general population are currently available. While we might expect some interaction between IDU-FSW and the general population through clients of FSW in the general population, it is important to note that the IDU-FSW key population does not include brothel-based sex workers or sex work through escort agencies. Based on the expert optinion of our public health partners, HIV prevalence among these sex workers is quite low, because they receive frequent HIV testing. Clients of street-based sex workers are often engaged in injection drug use and, therefore, are also members of the IDU-FSW key population in the model. We will investigate the potential impact of bridge groups in future analysis using a network model.
British Columbia practices a test and treat policy for HIV management [29]. Local guidelines recommend treatment for everyone living with HIV, except for elite controllers and long-term non-progressors, who are infected but have the biological capacity to maintain low or undetectable viral load without treatment [16]. Antiretroviral therapy is supplied by the province at no cost to patients. This immediate treatment policy in BC differs from international recommendations: WHO guidelines for treatment initiation are based on CD4 cell count, which is an indicator of the health of the immune system. To reflect this culture of willingness to treat and be treated, treatment in our model may be initiated upon linkage to care. Although physicians usually offer immediate treatment, there is a minority of patients who choose to remain in care and begin treatment only when symptoms arise. To simplify the model, we assume that these patients will not be treated until hospitalization due to an AIDS-related illness or the onset of AIDS.
In the model, progression from being on HAART to being on HAART with viral suppression occurs at a rate corresponding to the mean time required to achieve viral suppression. In practice, individuals may move in and out of a virologically suppressed state due to short treatment interruptions or low adherence to the treatment regimen. We address this by using data on the proportion of the population on treatment, but not virologically suppressed, to calibrate an effective suppression level for the L S and A S compartments. We assume that death rate and infectiousness are not affected by treatment status until an individual has achieved viral suppression and those who do achieve viral suppression are assumed to have the same life expectancy [70].
Retention rates in Vancouver are high, with approximately 88 % of people diagnosed with HIV retained in care at the end of 2013 [15]. We assume that patients not retained in care are those who never engaged in care after a possible initial clinical assessment. Although some individuals not retained in care may have become disengaged from the health care system at a later time, there is no data available on when this occurs. For individuals not in care, entry to care may occur after the onset of AIDS, when medical attention becomes necessary.
In practice, AIDS patients who are hospitalized may start treatment either during their stay or upon discharge. To capture this opportunity for initiating treatment, we model hospitalization as a trigger for treatment initiation. Since the average length of stay in the hospital due to an AIDS-related illness is less than 11 days [8], we do not consider in-hospital dynamics. Therefore, to simplify the model, there is no hospital compartment and patients who are hospitalized move to either the treatment compartment A T or to the in care off treatment compartment A C . We assume that hospitalization occurs only due to AIDS-related illnesses and virally suppressed patients are not hospitalized.
We also assume that the HIV epidemic in Vancouver is approximately in equilibrium at the time of model initiation. This assumption simplified calibration and validation of the model. Validity of this approximation does not require the state of the epidemic to be constant in recent years. Rather, if the epidemic is evolving at a rate much slower than the response time of the model, then we can assume adiabatic or moving stationary evolution of the dynamical system over recent years. This assumption is supported by data on the number of new diagnoses, which is a commonly used, albeit not necessarily accurate, proxy for the number of new infections. The estimated number of incident HIV infections in British Columbia has been relatively stable, falling from 418 cases in 2007 to 368 in 2012 [56]. Furthermore, in the VCH jurisdiction the number of new diagnoses has also been relatively stable in recent years, decreasing from 164 in 2009 to 151 in 2013 [15]. The most significant perturbation to the HIV epidemic was the introduction of HAART, which occurred in 1996, well before the time of model initiation.
4.2 Model equations
The time evolution of each subpopulation in the system dynamics model is governed by the system of ordinary differential Eqs. 1–17. Each equation corresponds to a model compartment in Fig. 3. The superscript i denotes the subpopulations, where i is 1 for MSM, 2 for IDU-FSW, and 3 for the general population. Therefore, the total number of equations is 51. A complete list of model parameters is given in Tables 2 and 3.
Equation 1 determines the time evolution of the susceptible compartment S. The rate of flow into compartment S is set equal to the total population death rate in order to maintain a constant population. The natural death rate for subpopulation i is denoted d i. There is an additional HIV-related death rate d a for the AIDS phase of infection. This additional death rate is the same for all subpopulations.
Susceptibles in each subpopulation are infected at a rate given by a bilinear contact term that is proportional to the number of infected individuals times the number of susceptible individuals. The proportionality constant, which is termed the infectivity, is the probability per unit time of disease transmission from a single infected individual to a single susceptible individual. It depends on both behavioural and biological factors, such as the viral load of the infected individual. Behavioural factors which influence infectivity include condom use and needle exchange programs. The prevalence of male circumcision in the population will also influence the infectivity for female to male sexual transmission. The force of infection, defined as the rate at which susceptible individuals acquire HIV, is the infectivity times the number of infected individuals.
The baseline infectivity β i for subpopulation i is defined to be the infectivity when the infected individual is in the latent stage of the disease. When the infected individual is in the acute or AIDS stages, the infectivity is increased through multiplying by δ a or δ b , respectively. Furthermore, β i is decreased through multiplying by δ d or δ h when individuals are diagnosed or treated, respectively. Hospitalized patients have their infectivity further reduced by the factor δ p . The infectivity modifiers δ a , δ b , and δ h are the same for all subpopulations, because they account for the impact of changes in viral load on infectivity. The infectivity modifier δ d arises from changes in the risk behaviour of patients after diagnosis. Although this could be different for the subpopulations, there is no data available to calibrate this difference. Therefore, we made the simplifying assumption that δ d is the same for all subpopulations. The infectivity modifier δ p for hospitalized patients is also assumed to be the same for all subpopulations.
Following infection, individuals progress through the acute phase E, latent phase L, and AIDS phase A of undiagnosed HIV, as described in Eqs. 2–4. The mean duration of the acute phase and latent phase are 1/τ a and 1/τ l , respectively. Undiagnosed individuals in states E and L are typically asymptomatic. Therefore, diagnosis in these compartments occurs at a rate proportional to the undiagnosed prevalence in the population being tested within each subpopulation. The number of tests per unit time in each testing stream for subpopulation i is \({\lambda _{n}^{i}}\), where n is 1 for targeted testing, 2 for routine testing in high prevalence settings, or 3 for routine testing in acute care. Conversely, the AIDS phase of HIV infection is typically symptomatic. Therefore, HIV diagnosis in the AIDS phase occurs at a constant rate ρ u , which represents the average time from the onset of AIDS to the time of seeking health care. A portion of these diagnoses are attributed to routine testing in acute care based on historical numbers and the remaining AIDS diagnoses are equally attributed to targeted testing and routine testing in high prevalence settings.
An important limitation of compartmental models is that they assume perfect mixing of the population. In this context, the probability of a test yielding a positive diagnosis is simply the fraction of the undiagnosed population that is HIV positive. However, this fails to capture the important concept of testing reach, wherein HIV-positive individuals have varying probabilities of being tested. Therefore, modifying factors for each subpopulation and testing program were introduced. For diagnosis in the acute stage of infection and subpopulation i, the modifying factors are denoted by a i. The modifying factors for the latent stage of infection are \({b^{i}_{j}}\), for subpopulation i and testing program j. In the model, the probability of a test being positive is the naive compartmental model probability, given by the HIV prevalence in the undiagnosed segment of the subpopulation, times the modifying factor. Data is not available for these modifying factors and they are treated as calibration parameters in the model.
Equations 5 through 9 correspond to compartments W E a through W c , which represent patients waiting to be linked to care, depending on the method of testing and stage of infection at diagnosis. Compartment W E a represents individuals in the acute phase of infection, who were diagnosed via targeted testing or routine testing in high prevalence settings. Similarly, compartment W L a represents those in the latent phase of infection who were diagnosed via targeted testing or routine testing in high prevalence settings. Compartments W E b and W L b represent individuals diagnosed in the acute phase and latent phase via routine testing in acute care settings, respectively. Compartment W c represents those diagnosed via symptom-based testing during the AIDS phase of infection. We assume that all of these patients are hospitalized after diagnosis to treat an AIDS defining illnesses.
Equations 10–13 describe the population dynamics of individuals in the latent phase of HIV who have been diagnosed. The subpopulation of diagnosed but not retained in care is denoted by L O ; the subpopulation in care but not on treatment is denoted by L C ; the subpopulation on treatment but not suppressed is denoted by L T ; and the subpopulation with suppressed viral load is denoted by L S . Equations 14–17 describe the dynamics of corresponding compartments for individuals in the AIDS phase of infection.
Linkage to care occurs at rate γ. A fraction ℓ of patients are not retained in care and enter compartment L O or A O . The probability of starting treatment after being linked to care from compartments W E a or W L a is h 1. The probability of starting treatment after being linked to care from compartments W E b , W L b or W c is h 2. Patients may also initiate treatment with the onset of AIDS or after an HIV-related hospitalization, which occur with probabilities h 3, and h 4, respectively. Hospitalization occurs at rate ρ ν . Treatment interruptions occur at rate ζ and individuals on treatment achieve viral suppression at rate ν. The mean time from diagnosis in the acute or latent phase of infection to AIDS is 1/τ d .
The system of Eqs. 1–17 was solved numerically in matlab using the function ode45, a 4 th and 5 th order Runge-Kutta method with variable time step [72]. No numerical instability problems were encountered.
4.3 Parameters and data sources
Parameter estimation was based on data from our public health partners (VCH and PHC), the British Columbia Centre for Excellence in HIV/AIDS (BC-CfE), public health reports [14, 15, 77, 80, 81] and published literature [10, 22, 49, 51, 52, 85]. A complete list of model parameters, values, and references is given in Table 2.
The model parameters for the monthly rate of targeted tests and routine tests in high prevalence settings were calibrated from the average testing rate from January 2010 through October 2012. The number λ 3 of routine tests per month in acute care were calibrated from the acute care testing rate during the sustained implementation of the STOP HIV/AIDS acute care strategy, from July 2012 through June 2013.
Data from the provincial Drug Treatment Program was provided by the BC-CfE, which is responsible for dispensing all HIV antiretroviral treatment in the province. Data for the year 2011 were used to estimate model parameters for the proportion of patients starting treatment within one month of diagnosis and the mean time to achieve viral suppression. The mean time for linkage to care, 1/γ, was calibrated from the VCH report [81]. The proportion of diagnosed individuals ℓ who are not retained in care was calibrated from a VCH 2013 public health report [15]. Hospitalization rates in the model are based on British Columbia data from the BC-CfE Drug Treatment Program and the BC Ministry of Health administrative databases [22].
The rate at which patients start treatment in the model was calibrated as follows. Let α i be the probability of starting treatment within one month of diagnosis, where the category of diagnosis i is 0 for all new diagnoses, 1 for acute and latent phase diagnoses outside of acute care, and 2 for AIDS diagnoses and all diagnoses in acute care. Similarly, let h i be the probability of starting treatment after being linked to care, where i denotes the category of diagnosis as above. Compartmental models are continuous or large population approximations to stochastic agent-based models in which the length of time that agents spend in a state is exponentially distributed. Therefore, it follows from standard properties of the exponential distribution that α i is given by
where γ is the rate per month of linkage to care. Furthermore, we have that
where k is the fraction of all patients linked to care after diagnoses in acute care or in the AIDS stage of infection.
The parameter h 2 is estimated from data and the fraction k is determined through model dynamics. Therefore, we solve for h 1 using Eqs. 18 and 19 to obtain
This expression for h 1 is substituted into Eqs. 11 and 12.
The modifying factors for the infectivity in the acute and AIDS phases of infection are not specific to Vancouver and estimates were taken from the literature [10]. Estimates of the average length of the latent and AIDS phase of HIV infection were also also taken from the literature [52]. Vancouver data on the change in infectivity after diagnosis were not available and it was necessary to estimate this modifier from the literature [49]. However, the change in infectivity after diagnosis results from behaviour change and this is likely to depend on the counselling and followup programs in the health care jurisdiction.
4.4 Model calibration and validation
The model has five free parameters each for the MSM and IDU-FSW populations and three free parameters for the general population, for a total of 13 free parameters that are determined through model calibration. These parameters are listed in Table 3. Model calibration was done at equilibrium, because we have assumed in Section 4.1 that the HIV epidemic is close to equilibrium at the time of model initiation.
There are three infectivity parameters, one for each of the subpopulations. These infectivities are difficult to calculate from data because this would require accurate estimates of the frequency of potential transmission acts and various factors which modify the probability of HIV transmission per act, including condom use, prevalence of other sexually transmitted diseases, and male circumcision. Therefore, these infectivities were treated as free parameters and were determined through model calibration.
The modifying factors a i and \({b^{i}_{j}}\) for the probability of a diagnosis in the acute phase and latent phase of infection, respectively, were introduced in Section 4.2 to account for testing reach. There are a total of ten diagnosis modifying factors. MSM and IDU-FSW each have an acute phase modifier and one for each of the testing programs. The general population only has two diagnosis modifiers, because routine testing in high prevalence settings and targeted testing do not apply to the general population. Data were not available for the diagnosis modifying factors and they were treated as free parameters, which were determined through calibration.
Data used for model calibration and validation are listed in Table 4. Data on the number of new diagnoses were available from multiple sources. VCH provided the number of new diagnoses stratified by testing program for the years 2010–2012. The British Columbia Centre for Disease Control (BCCDC) and the Drug Treatment Program of the BC-CfE both provided data on the total number of new diagnoses; however, they were unable to stratify new diagnoses by testing program. The total number of new diagnoses in 2011 reported by the BCCDC [14] is similar to the total number reported by VCH. However, the annual numbers of new diagnoses reported by BCCDC and VCH are historically lower than the annual number from the Drug Treatment Program. Data from the BC-CfE Drug Treatment Program are considered to be more accurate [36]. The average value of the ratio ϕ of the total number of new diagnosis from the Drug Treatment Program to the total number of new diagnosis from VCH is 1.2 for the years 2007–2009, which are the most recent three years of common data. Data from VCH on the number of new diagnoses by testing program were corrected by multiplying by ϕ=1.2.
Vancouver Coastal Health Authority provided surveillance data from the STOP HIV/AIDS project on the proportion of diagnoses during the acute phase of infection, determined through viral load testing; however they were only able to stratify these data by testing program and not by subpopulation. Therefore, we had to assume that within each testing program, the proportion of diagnoses in the acute phase of infection is the same for all subpopulations.
Table 4 lists the 19 data values that were used for model calibration and validation. We used 18 of these data points to calibrate the 13 free parameters, employing a nonlinear least squares fit. Therefore, calibration is over-determined by 5 degrees of freedom, which is sufficient for model validation. An additional data value, the percentage of the diagnosed population on treatment, was used for independent out-of-sample validation. The model for each of the three subpopulations were calibrated independently, because they are treated as noninteracting subpopulations.
4.4.1 Calibration of the MSM and IDU-FSW populations
We fit five model parameters for each of the MSM and IDU-FSW subpopulations. Denoting the MSM subpopulation by superscript i=1 and the IDU-FSW subpopulation by superscript i=2, these parameters are the HIV infectivity β i, the modifier a i for the probability of a positive diagnosis in the acute phase of infection, the modifier \({b^{i}_{1}}\) for the probability of a positive diagnosis in the latent phase of infection for targeted testing, the modifier \({b^{i}_{2}}\) for routine testing in high prevalence settings, and the modifier \({b^{i}_{3}}\) for routine testing in acute care. Data used for optimization were HIV prevalence; the number of new diagnoses from targeted testing, routine testing in high prevalence settings, and routine testing in acute care; and the proportion of diagnoses in the acute phase of infection for each of targeted testing, routine testing in high prevalence settings, and routine testing in acute care. For each subpopulation i, these data points are denoted in corresponding order by \({y^{i}_{j}}\), for \(j=1,2,\dots ,7\). All data values are listed in Table 4.
We calibrated the parameters for the MSM and IDU-FSW subpopulations by weighted nonlinear least squares fit, defined by minimizing the objective functions
where \({\mathbf {x}}^{i} = \left (\beta ^{i} \, , \, a^{i}\, , \, {b^{i}_{1}}\, , \, {b^{i}_{2}}\, , \, {b^{i}_{3}}\right )\) is the parameter vector and the model output corresponding to the data point \({y^{i}_{j}}\) is \(\tilde {y}_{j}^{i}\left ({\mathbf {x^{i}}}\right )\).
Minimizing the objective function in Eq. 21 is a 5-dimensional optimization problem. Each evaluation of the objective function requires finding the equilibrium solution to the system of Eqs. 1 through 17. High-dimensional, computationally expensive optimizations are difficult to solve and often require a parallelized approach [73].
We reduced the dimensionality of the problem in each subpopulation by performing a parallelized direct grid search over the parameters a i. Therefore, each problem is now a 4-dimensional optimization involving a fixed value of a i. These 4-dimensional optimizations were solved using the simulated annealing algorithm implemented in the matlab function simulannealbnd [23, 58]. Initial values for the simulated annealing algorithm were obtained using a visual trial-and-error approach to model calibration. Values of the best-fit parameters are given in Table 3.
4.4.2 Calibration of the general population
We fit HIV infectivity β 3 and the modifiers a 3 and \({b^{3}_{3}}\) for the probability of a positive diagnosis in the acute phase and latent phase of infection, respectively, for routine testing in acute care. Data used for optimization are HIV prevalence \({y^{3}_{1}}\), total new diagnoses per year for the general population \({y^{3}_{2}}\), the proportion of new diagnoses occurring in the acute phase of infection for routine testing in acute care settings \({y^{3}_{3}}\), and the proportion of the infected population undiagnosed \({y^{3}_{4}}\). These are listed in Table 4. Calibration was performed using a weighted nonlinear least-squares fit, defined by minimizing the objective function
where x 3 = \(\left (\beta ^{3}\, , \, a^{3} \, , \, {b^{3}_{3}}\right )\) is the parameter vector and \(\tilde {y}^{3}_{j}\left ({\mathbf {x}}^{3}\right )\) is the model output corresponding to the data point \({y^{3}_{j}}\).
Optimization of the objective function was carried out using the pattern search algorithm implemented in the matlab function patternsearch [7, 45]. Values of the best-fit parameters are given in Table 3.
4.4.3 Calibration and validation results
The model was calibrated to the end of 2013. Calibration and validation results are provided in Table 4. The model gives similar output to data on the percent of diagnosed on treatment, new diagnoses due to routine testing in high prevalence settings, and new diagnoses due to routine testing in acute care. HIV prevalence estimates for the MSM and IDU-FSW subpopulations fall within the estimated range of prevalence given in [51], where the upper and lower estimates from the data were calculated using low estimates for the number infected with high estimates on population size, and high estimates for the number infected with low estimates of population size, respectively. However, the model predicts slightly lower than expected prevalence for the general population. Part of this discrepancy could be attributed to a possible decrease in prevalence among the general population in recent years.
The model predicts a lower than expected number of new diagnoses due to targeted testing among MSM. However, the data used for calibration was an average from 2010 to 2012, which is during the STOP HIV/AIDS pilot project when testing was significantly increased. It is possible that new diagnoses have decreased since then, as we are validating the model to the end of 2013. The model also underestimates the proportion of new diagnoses during the acute phase of infection for routine testing in acute care of the IDU-FSW subpopulation. However, data on the stage of infection at time of diagnosis is difficult to collect and this could simply represent inaccuracy in the data.
The model is most reliable for short-term projections, because it was validated against recent data on the percentage of positive test results. Testing yield may change over time as the epidemic evolves and potentially becomes more concentrated in groups that are hard to reach. For example, the yield of positive tests obtained in acute care settings is unlikely to continue at current levels. Trends in testing yield over time are not yet known because any previous trends were altered by the recent STOP HIV/AIDS pilot project.
5 Resource allocation analysis
5.1 Optimization scenarios
We use the system dynamics model to determine resource allocation strategies among HIV testing programs under various constraints that minimize the cumulative number of new HIV infections in Vancouver over five or ten years. We consider the four simulation scenarios listed in Table 5 for allocating resources among targeted testing, routine testing in high prevalence settings and routine testing in acute care. We evaluated both the reallocation of existing testing resources (Scenario 1) and the distribution of resources following a hypothetical increase to the total testing budget of up to 200 % (Scenarios 2, 3 and 4).
In Scenario 1, we seek the optimal distribution of existing resources between the three testing programs. In Scenario 2, we hold existing resources fixed at the current allocation and determine the optimal allocation of new resources only. In Scenario 3 we remove this constraint and determine the optimal allocation of the entire testing budget. For Scenarios 1 to 3, we assume that resources allocated to a testing program were distributed among each of the relevant subpopulations in proportion to the current distribution of resources. With this constraint, 52 % of resources for targeted testing and 25 % of resources for routine testing in high prevalence settings were dedicated to testing programs for MSM and the remaining resources to IDU-FSW. In Scenario 4, we remove the constraint on subpopulations and determine the optimal allocation of resources over both testing programs and subpopulations. Accordingly, resource allocation in Scenario 4 is optimized for the following five programs: targeted testing for MSM, targeted testing for IDU-FSW, routine testing in high prevalence settings for MSM, routine testing in high prevalence settings for IDU-FSW, and routine testing in acute care for all populations.
Targeted testing is typically associated with a high yield of positive diagnoses, has a higher cost per test and reaches a comparatively small portion of the population (low population reach). Routine testing is generally associated with a lower yield of positive HIV diagnoses, is relatively inexpensive, and potentially has a greater population reach. Therefore the optimization scenarios seek to balance the cost and diagnostic yield of each type of test to minimize HIV incidence.
All scenarios were evaluated over a five-year time horizon and we also evaluated Scenario 1 over a ten-year time horizon. The model was calibrated to year 2013 and evaluated over the time periods 2014–2018 or 2014–2023, for the ten-year horizon.
Optimization was performed for Scenarios 1 to 3 using the patternsearch algorithm [7, 45] in matlab to find the optimal strategy when allocating resources in two dimensions. For Scenario 4, allocating resources over five dimensions was computationally challenging. The fixed budget constraint reduced this to a four dimensional problem, which we optimized using a parallelized layered approach over increasingly smaller domains. We began with the simulated annealing algorithm simulannealbnd [23, 58] in matlab. The result was then refined using a parrarelized direct grid search in two dimensions and a pattern search algorithm in the remaining two dimensions. To further refine the results, we applied matlab’s fmincon function for interior point optimization [17].
5.2 HIV test costs and determining the testing budget
Precise estimates for the cost of each type of HIV test were not available for this analysis. Furthermore, the cost of tests within the three main categories of testing that we considered is likely to vary according to the testing venue and the operational specifics of the testing program. However, targeted tests are always more expensive because they require a greater investment in dedicated human resources and infrastructure. A routine testing program makes use of existing health care infrastructure and any additional investment required is likely to be minimal.
For our analyses, we assumed that laboratory costs for all three types of tests are identical. We further assumed that the cost for a single routine test is the same regardless in which setting it is administered. Without information on testing costs and the total testing budget, we chose to consider a range of relative costs for targeted and routine tests from 1:1 through 9:1. This range was based on a combination of expert feedback from the public health partners and a United Kingdom Health Protection Agency report on pilot studies that determined the relative costs of routine and targeted tests [35].
The assumed cost ratio combined with data on the number of HIV tests administered in each setting was used to determine the total pool of testing resources. Therefore, the total resource pool is defined in terms of the number of routine tests the program can administer, rather than a dollar amount. A consequence of calculating available resources in this manner is that the total testing budget varies depending on the assumed cost ratio. For example, for the same distribution of resources among testing programs, the total dollar value of the budget is greater for the 9:1 than for the 5:1 cost ratio assumption.
5.3 Scenario 1: optimal allocation of existing resources
In Scenario 1, we hold the total testing budget fixed and seek to reallocate existing resources among testing programs. Figure 4 compares the current distribution of resources in Vancouver with the optimal distribution of existing resources for the testing programs listed in Table 1, over 5 and 10 years. If the cost of a targeted and a routine test are equal, then, as expected, all of the resources should be allocated to targeted testing. When the cost ratio of a targeted test to a routine test increases above a threshold, which is approximately 1.68 for five-year incidence and 1.66 for ten-year incidence, then the optimal allocation of testing resources changes abruptly to all resources allocated to routine testing.
Second thresholds are reached at cost ratios of approximately 5.13 and 3.09 for the five-year and ten-year time horizons, respectively. Above these values, the optimal resource allocation consists of a mix of routine testing in high prevalence settings and routine testing in acute care. For the 9:1 cost ratio, the optimal allocation of resources to routine testing in acute care reaches 12 % and 23 % for the five-year and ten-year time horizons, respectively.
These results show that benefits derived from the high diagnostic yield for targeted testing quickly diminish due to its relatively high cost. Achieving the optimal mix of testing programs would require moving resources away from targeted testing and into routine testing in high prevalence settings. For lower cost ratios, corresponding to smaller total budgets, the optimal strategy additionally requires shifting resources from routine testing in acute care to routine testing in high prevalence settings.
Cumulative incidence after resource optimization for the five and ten-year time horizons are plotted in Fig. 5. With no optimization, the model predicts 896 and 1792 new infections over the next five and ten years, respectively. At the point where the optimal allocation of resources switches from all targeted testing to all routine testing, the two modes of testing have equal impact on incidence. Therefore, optimization will not reduce incidence, which is apparent in the graphs in Fig. 5. Optimally reallocating resources would avert between 18 to 114 cases over five years for cost ratios in the range of 1:1 to 9:1. This equates to a 2 % to 13 % reduction in incidence. Over ten years, between 52 and 298 new infections would be averted, which is a 3 % to a 17 % reduction in incidence.
The qualitative results for five and ten years are similar. However, more resources should be allocated to routine testing in acute care if a longer time frame is considered. We also examined the impact of five-year versus ten-year testing program optimization by assuming a 7:1 cost ratio and computing ten-year cumulative incidence for three optimizations: 5-year optimization in which the testing program is optimized for the first five years, but allowed to run for ten years; 5+5-year optimization in which the testing program is optimized for the first five years and then re-optimized again after five years has passed; and 10-year optimization in which the testing program is initially optimized for the entire ten years. Cumulative incidence at the end of ten years is 1543 cases with 5-year optimization, 1542 cases with 5+5-year optimization, and 1541 cases with 10-year optimization. As expected, the lowest number of cases is with 10-year optimization and the highest is with 5-year optimization. However, the differences of only one case are negligible, especially given potential uncertainties in projecting model parameters forward for ten years. Virtually all of the outcome gains are achieved with testing program optimization over a five-year time horizon. Therefore, for the remainder of the paper we consider only five-year optimizations.
Sensitivity analysis with respect to model parameters is performed in the Appendix for the 5:1 cost ratio. The optimal distribution of testing resources is qualitatively robust under variation in the model parameters. The strongest sensitivity is to the infectivity multipliers δ d and δ v for diagnosis and viral suppression, respectively. An increase in either δ d or δ v leads to a decrease in the threshold above which the optimal distribution of resources is a mix of routine testing in high prevalence settings and routine testing in acute care.
5.4 Scenario 2: optimal allocation of new resources
We increase the total testing budget and optimize the allocation of new resources among the three testing programs, while keeping the allocation of existing resources unchanged. Only reallocation of new resources is considered, because existing programs may be rooted in commitments and public health responsibilities of the health authorities. For this scenario, we only consider cumulative incidence over five years.
Figure 6 shows surface plots of the optimal distribution of resources as a function of both cost ratio and budget increase. Cross-sections of the surface plots for five cost ratios are shown in Fig. 7. As with Scenario 1, all testing resources should be allocated to targeted testing, for the 1:1 cost ratio. The switching point at which all resources should be allocated to routine testing in high prevalence settings varies slightly with the size of the budget increase. The switching point decreases from approximately 1.82 for a 50 % budget increase to 1.65 for a 200 % budget increase.
The optimal allocation of testing resources is a mix of routine testing in high prevalence settings and routine testing in acute care for sufficiently large budget increases or sufficiently high cost ratios. This reflects the fact that it becomes increasingly optimal to allocate some resources to routine testing in acute care as both initial and additional testing resources become larger.
Cumulative five-year incidence is plotted as a function of increased testing resources in Fig. 8, with the new resources either prorated according to the current distribution or optimally allocated among the three testing programs. If testing resources are increased by 200 %, then optimally allocating the additional resources averts 29, 54, and 73 new infections, if the cost ratio is 3:1, 5:1, and 7:1, respectively, corresponding to a 4 % to 9 % reduction in incidence.
5.5 Scenario 3: optimal allocation of all resources with budget increase
We extend Scenario 2 by optimizing both new and existing testing resources. The objective function minimized is again cumulative incidence over five years. Figure 9 shows the optimal allocation of the entire testing budget for cost ratios up to 9:1 and budget increases up to 200 %. Constant cost ratio cross sections are plotted in Fig. 10. Similarly to the previous scenarios, all resources should be allocated to routine testing when the cost of a targeted test is below a switching point, which lies at 1.82 with no budget increase and 1.65 with a 200 % budget increase.
The optimal allocation of the entire testing budget is qualitatively similar to the optimal allocation of new resources only in Scenario 2. However in Scenario 3, routine testing should be split between high prevalence settings and acute care at smaller cost ratios and budget increases. In the limit of no budget increase, Scenario 3 corresponds to Scenario 1 and allocating resources to routine testing in acute care becomes optimal when the cost ratio exceeds approximately 5.5:1. The amount of resources that should be allocated to routine testing in acute care increases with both the cost ratio and the size of the budget increase. For a cost ratio of 9:1 and a budget increase of 200 %, approximately 39 % of testing resources should be allocated to routine testing in acute care and the balance to routine testing in high prevalence settings. A 200 % budget increase followed by the optimal allocation of the entire testing budget leads to a 14 % to 23 % decrease in incidence, for cost ratios ranging from 1:1 to 9:1, respectively.
5.6 Scenario 4: optimal allocation of new resources oversubpopulations
We relax all constraints on the reallocation of resources for this scenario. Cumulative five-year incidence is minimized for cost ratios up to 9:1 and budget increases up to 200 %. In contrast to the previous scenarios, new testing resources may now be allocated to targeted testing for MSM, targeted testing for IDU-FSW, routine testing in high prevalence settings for MSM, routine testing in high prevalence settings for IDU-FSW, or routine testing in acute care. Therefore, optimization is over a four-dimensional domain, because total resources are fixed.
Figures 11 and 12 show the optimal allocation of the entire testing budget for cost ratios up to 9:1 and budget increases of up to 200 %. Allocating resources to targeted testing for MSM is not optimal for any of the cost ratios or budget increases studied.
At a 1:1 cost ratio all resources should be split between routine testing of the MSM population in high prevalence settings and targeted testing of IDU-FSW. For no budget increase, all resources should be allocated to routine testing of MSM in high prevalence settings. The percentage of resources that should be allocated to targeted testing of IDU-FSW increases to approximately 25 %, with a budget increase of 200 %. These results reflect the fact that routine testing in high prevalence settings for MSM has a higher yield of positive HIV diagnoses than targeted testing, whereas the opposite is true for IDU-FSW.
If the cost ratio is greater than a switching point between 1.5 and 2.0 (depending on the budget increase), then allocating resources to targeted testing for IDU-FSW is no longer optimal. The optimal allocation of resources becomes a mix of routine testing in high prevalence settings for MSM and IDU-FSW. However, minimal incidence is achieved if most of the resources for routine testing in high prevalence settings are dedicated to the MSM subpopulation.
As in the other scenarios, for a large enough cost ratio or budget increase, allocating some resources to routine testing in acute care becomes optimal. For example, with a 9:1 cost ratio and a 200 % increase in budget, five-year cumulative incidence is minimized at 44 % of resources allocated to routine testing in high prevalence settings for MSM, 22 % of resources allocated to routine testing in high prevalence settings for IDU-FSW, and the balance of resources allocated to routine testing in acute care. This scenario would avert 227 new infections, which is a 25 % reduction in incidence.
5.7 Prevention of HIV infections
We consider the above scenarios from the perspective of the potential number of HIV infections that are averted, compared to the expected number of new infections with no intervention. Infections are averted in Scenarios 2–4 both because the testing budget is increased and the allocation of testing resources is optimized. The expected number of new infections over five years with neither a budget increase nor resource allocation is 896.
Table 6 shows the number of infections that our model predicts would be averted by an increase in the testing budget: without resource reallocation; with optimal allocation of new resources by testing program (Scenario 2); with optimal reallocation of all resources by testing program (Scenario 3), and with optimal reallocation of all resources by both testing program and subpopulation (Scenario 4). The column with no budget increase for Scenario 3 corresponds to Scenario 1. For the case where the budget is increased without optimization, new resources are added in proportion to their assumed current distribution between testing programs and subpopulations. Without optimization, the number of new tests added to each testing program is independent of the cost ratio, although the distribution of resources does depend on the cost ratio.
The additional gain from optimizing the entire budget, as opposed to optimizing new resources alone, is strongest for small increases to the testing budget. As the budget increases, the new resources account for a larger proportion of the entire budget.
The benefits of optimal resource allocation are apparent from Table 6. For cost ratios greater than 5:1, the least constrained of the optimization strategies (Scenario 4) averts approximately as many infections with a 50 % budget increase as the most constrained optimization strategy (Scenario 2) does with a four times greater budget increase. Furthermore, even with no budget increase the least constrained optimization strategy averts 15 % more infections than a 200 % budget increase without optimization, at a 5:1 cost ratio.
6 Discussion
6.1 HIV Treatment as Prevention
The ambitious HIV Treatment as Prevention targets for expanding antiretroviral coverage announced by UNAIDS in 2014 are intended to end the HIV epidemic in the foreseeable future. Achieving this goal will require a vast investment of resources. In the current climate of fiscal constraints, smart investments that deliver the best results for the least cost are going to be more important than ever. Our analysis demonstrates at the level of one municipal jurisdiction how utilizing operations research modelling to optimize resource allocation within an HIV testing program could prevent a substantial number of new infections. We showed that optimal allocation of new testing resources can prevent infections. However, even without increasing the budget, HIV infections could be reduced by as much as 17 % over five years just through optimal allocation of existing resources.
The operations research methods we employed may be applied at the level of a single health facility or at the scale of an entire country. They may also be extended to optimizing not just testing programs, but other components of the care continuum. This implies numerous potential applications for optimizing resource allocation to improve both the efficiency and the effectiveness of the HIV care continuum. However, it is important that there be a much greater awareness of these methods and their wider application in planning for the optimal allocation of limited HIV testing and treatment resources [3, 11, 44, 87].
6.2 Optimizing the HIV continuum of care
The term “cascade of care”, often used in the literature [42], evokes an image of the HIV care continuum as a failing system, with a steady outflow of patients lost to care at every step from HIV testing to long-term retention in care. However, the HIV care continuum is strongly interlinked and its components interact in complex ways. We optimized HIV testing in the context of the entire care continuum, with our analysis limited to changing the testing program only. HIV treatment programs responded to the increased inflow of diagnosed patients, but were not otherwise optimized or expanded. The prevented infections we predicted originate from improved diagnosis boosting the demand for treatment downstream in the system and not specifically from improved treatment delivery. Improving multiple components of the care continuum at the same time would act synergistically to avert more infections [26]. The optimization we performed for HIV testing could be applied to the collection of HIV treatment and care services involved in linking and retaining patients on HAART.
Optimally functioning testing and treatment programs both influence epidemic dynamics through feedback loops. Thus, optimizing separately managed and funded programs in parallel is likely to influence the optimal resource allocation within each program. For this reason, coordination between components of the HIV care continuum is another area where HIV service delivery could be substantially improved. An important question to investigate in future research is the extent to which coordinated optimization of the HIV care continuum could improve population health outcomes.
System-wide optimization would likely be even more potent than single program optimization in enhancing the overall performance of the health care system and improving the effectiveness of TasP. This would certainly require a radical change in how the health care budget is allocated, although long-term benefits could be substantial. We have seen in Scenario 4 that relaxing all constraints on the flow of investment to testing activities prevents the greatest number of infections. Similarly, optimizing the entire health care budget across the HIV care continuum is likely to be the most efficient way to achieve the best public health outcomes for the least cost. Clearly, there are many practical constraints on system optimization that would be difficult and perhaps inadvisable to change. However, initiating planning from a system optimization stance, and accommodating constraints as needed, may be the best way to improve overall system performance.
6.3 The role of routine HIV testing
Routine testing in high prevalence settings prevented the most new HIV infections in Vancouver in our model. This is readily explained by the combination of lower routine testing costs and high HIV prevalence in the target population. At the start of our analysis, only about 20 % or less (depending on the cost ratio assumed) of the total VCH testing budget was dedicated to routine testing in high prevalence settings. In sharp contrast, our analysis predicts that investing at least 80 % or more of the budget in routine testing in high prevalence settings is optimal. Thus scaling up routine testing in these settings may be an important area for program improvement.
A less obvious finding was that routine testing in hospitals, where HIV prevalence is lower, still prevents more infections than targeted testing. In all simulation scenarios, routine testing in hospitals contributed an increasing proportion to the optimal testing mix as resources become more abundant, either through a sizeable budget increase or because lower relative per test costs permit more testing to be carried out. The influence of testing on epidemic dynamics can explain this observation. Intense routine testing of key populations in high prevalence settings is likely to eventually contain the spread of HIV and further investment would produce diminishing returns. Once this occurs, it becomes more advantageous to introduce or expand routine testing in hospitals. Routine testing becomes even more important when the testing program is optimized over ten years. These findings show that the optimal testing strategy changes over time as the epidemic evolves in response to the intervention. Therefore, continued monitoring, evaluation, reassessment and adjustment of the HIV testing program is likely to be key to maintaining optimal program performance over time.
Our results provide strong evidence that routine testing would prevent HIV infections and could make a positive contribution to controlling Vancouver’s concentrated epidemic. Targeted testing was not part of the optimal testing mix in most scenarios, because of its high associated cost. However, there are important practical reasons for retaining targeted testing within a comprehensive testing program. For example, contact tracing is a targeted testing activity which involves notifying partners of newly diagnosed cases that may have been exposed to HIV. Contact tracing, although expensive, is the mainstay of public health practice and there is an ethical responsibility to counsel and offer testing to individuals who may have been exposed to HIV infection. Also, marginalized people, especially the homeless or those injecting drugs in parks or on the streets, may not seek health care and, thus, have limited access to HIV tests through routine testing offered at health care venues. Resource-intensive targeted outreach programs may be the only HIV testing opportunity for this group of people. For these reasons, targeted testing remains indispensable. One way to ensure that testing resources are used effectively may be to review and streamline targeted testing activities, retain essential programs, and replace inefficient or redundant targeted programs with routine testing.
6.4 HIV testing in key affected populations
In the mid-1990’s, Vancouver experienced North America’s worst HIV epidemic, caused by wide-spread injection drug use in the Downtown Eastside neighbourhood. HIV prevalence among IDU climbed to 40 %. A comprehensive public health response that included harm reduction measures such as the introduction of needle exchange programs, the opening of North America’s first supervised injection site, and frequent HIV testing, succeeded over the following decade in containing the epidemic [63]. New infections have dropped significantly and now about 70 % of new infections affect MSM [15]. Testing activities shifted, but have not caught up with the extent of the change in the epidemic. The apportionment of testing activities among the three main affected populations in Vancouver is currently suboptimal.
We found that by optimizing testing resource allocation between subpopulations, the greatest impact on reducing HIV transmission in Vancouver would be achieved by spending 50 % or more of the entire testing budget on routine testing at health care venues with an MSM clientele, about 30 % on the IDU-FSW subpopulation and the remainder on routine testing in hospitals. Even in combination with essential targeted testing, such as contact tracing and outreach testing in bathhouses, prioritizing routine testing for MSM is likely to achieve significant positive public health outcomes.
6.5 Strengths and limitations
An important strength of our analysis is that our model draws on multiple data sources and provides a detailed representation of the local HIV epidemic and health care system in Vancouver. This facilitated the analysis of locally relevant public health questions. However, the model can also be modified and transferred to other jurisdictions in British Columbia by calibrating to similar epidemics. With more extensive changes, our approach can also be applied to other HIV epidemics in Canada or internationally.
UML activity diagrams are beginning to find applications as communication tools in developing system dynamics models. The UML diagram we developed greatly facilitated the organization and model implementation of qualitative information provided by system experts.
Our analysis also has some limitations, in addition to the model assumptions described in Section 4.1. We used an ordinary differential equation model, which assumes that subpopulations are homogeneous. Additionally, we assumed that these subpopulations were non-interacting. The latter assumption was necessary due to lack of data on group interactions. Agent-based or network models could be used to address this issue.
Sensitivity analysis performed in the Appendix shows that the model results are sensitive to the extent that infectivity is reduced after diagnosis, because of behaviour change by the diagnosed individual. Vancouver-specific data is not currently available for this change in risk behaviour and it was necessary to use data from a meta-analysis for high risk sexual behaviour [49]. However, the reduction in risk behaviour after diagnosis is likely to depend on both post-diagnosis counselling and the key population. Further data on this would improve model accuracy, as well as provide insight into the importance of post-diagnosis counselling and followup in the HIV care continuum.
Data on the diagnostic rate for routine testing in acute care settings were contributed by three Vancouver hospitals that participated in the routine testing pilot study. One of these was Saint Paul’s Hospital, which serves Vancouver’s Downtown Eastside where injection drug use and HIV are most prevalent in the city. For this reason, Saint Paul’s Hospital is likely to have a higher rate of HIV diagnoses than other hospitals and health care facilities serving the general population. As the routine testing programs expands and new testing data become available, it will be possible to estimate diagnostic yield from a larger sample of general health care providers.
In this paper, we focused on optimizing resource allocation to prevent new HIV infections. However, preventing HIV-related morbidity and mortality are also high priority public health goals. We explore this topic in another study. Furthermore, we considered only optimal outcomes to restrict the scope of the analysis. In public health practice, near-optimal solutions often have substantial practical relevance. We will present a detailed analysis of near-optimal results separately.
As mentioned earlier, our optimization of HIV testing assumed an otherwise unchanging health care system, despite simultaneous HIV treatment expansion that has been taking place through the STOP HIV/AIDS pilot project in Vancouver. More accurate predictions of the optimal mix of testing programs could be generated in the context of the other system changes. We leave this for future research.
6.6 Implications for policy and public health practice
The contribution that routine HIV testing could make to reducing HIV transmission in Vancouver is a key policy-relevant finding in this study. Routine testing guidelines in the USA have been in place since 2006 [12]. Currently, the US Centre for Disease Control’s High Impact Prevention campaign emphasizes routine HIV testing for populations with high HIV prevalence [53]. France [25] and the UK [35] also have routine HIV testing programs in place. There are no national guidelines in place for routine HIV testing in Canada. British Columbia was the first province in Canada to evaluate the potential of routine testing in acute care settings and to update provincial HIV testing guidelines to explicitly recommend routine HIV testing [61]. Our analysis was part of the evidence considered in developing the guidelines, as will be discussed in an upcoming evidence review, which will be made publicly available online by Vancouver Coastal Health.
The results of our analysis have also been included in discussions and initiatives to improve HIV testing practices both in Vancouver and in the province of British Columbia. This project introduced public health partners to the value of optimizing the allocation of testing resources. It also provided stakeholders with multiple options for changing programming and policy, along with generating estimates of the potential benefit that taking a specific course of action may bring. For example, we showed that optimizing the allocation of all available testing resources after a budget increase could avert 3 % to 66 % more new infections (depending on budget size and relative costs of HIV tests) than optimizing the allocation of new resources only. We further showed that relaxing all constraints on resource allocation and investing additional resources from a budget increase in testing programs for men who have sex with men could result in 11 % to 144 % more new infections averted than optimally allocating only new resources among only the three testing programs. Furthermore, cost ratios for targeted and routine tests vary across facilities in Vancouver and may be modified to some extent through operational or programmatic changes. Therefore, our results showing outcomes for various cost ratios can help stakeholders fine-tune testing programs at the facility level.
6.7 The modelling collaboration
Proven approaches for applying modelling results to decision-making and collaboration case studies are of keen interest in health care operations research. There are often formidable barriers to integrating operations research findings into the decision-making process. The way decisions are made is therefore an important area of inquiry in the operations research literature [2, 43]. Lasry et al. [44] addressed this by developing the spreadsheet model System for HIV/AIDS Resource Allocation (S4HARA), which combines principles of efficient resource allocation with non-quantifiable political, social, and ethical factors influencing decision-making process.
Our analysis has successfully contributed to stakeholder discussions about programming and policy. Even without formal analysis of the collaboration, we can identify some factors that helped the project succeed. First of all, the project was jointly subsidized by all partners through academic grants and stakeholder funding. This created an atmosphere of equal participation and helped our group engage in defining shared goals for the analysis. The public health partners and mathematical modellers in the group held frequent face-to-face meetings, working sessions, and presentations. This was essential in developing avenues for effective communication, including building a common vocabulary and shared set of working concepts that helped frame discussions about the research problems and solutions. Finally, a crucial factor in the success of the project was the merging of two conceptual frameworks, each contributed by the two groups of partners in the collaboration. The operations research team contributed a conceptual framework for a system dynamics model of the continuum of HIV care, and the public health participants contributed a conceptual framework for organizing testing activities in Vancouver. Integrating the testing framework into the continuum of care model guaranteed that model results were meaningful and had direct and specific relevance to public health partners in the terms that they were accustomed to thinking about their testing program.
6.8 Conclusions
With the availability of highly effective treatment to prevent HIV-related morbidity, mortality, and transmission, the need for efficient testing strategies to promote early diagnosis has become paramount in recent years [13]. We used system dynamics modelling and optimization of resource allocation to find strategies for improving the performance of Vancouver’s HIV testing program by minimizing cumulative HIV incidence over five or ten years.
The optimal resource allocation strategy favours routine testing in high prevalence settings, even with a modest cost advantage over targeted testing. If the cost advantage is greater, or if the available testing budget is larger, then a mix of routine testing in high prevalence settings and routine testing in hospitals is most effective in averting new HIV infections. For the HIV epidemic in Vancouver, the greatest impact on incidence would be achieved by allocating approximately half of the testing resources to routine testing in high prevalence settings for MSM, with the remainder divided between routine testing in high prevalence settings for IDU-FSW and routine testing in hospitals. Expensive targeted testing programs, such as contact tracing and outreach programs, remain essential but should be specialized, streamlined, and reserved for situations when they are most needed to ensure the best use of Vancouver’s HIV testing resources.
The optimal mix of testing programs will change over time as testing, treatment, and other interventions to combat the HIV epidemic are implemented and take effect. Therefore, constant monitoring and evaluation of testing and other interventions should be integrated into public health programming to allow intervention strategies to be tailored to changing conditions in a timely manner. This will maintain high performance and the most efficient use of testing resources over the long term. Operations research can play a crucial role in supporting this process. However, to fully realize the potential of operations research, active engagement of stakeholders in a collaborative process is essential, and addressing barriers to the use of operations research results for informing policy must remain a top priority.
Notes
Highly active antiretroviral therapy (HAART) and antiretroviral therapy (ART) are used interchangeably in the literature.
References
Abolnikov L, Dukhovny A (2003) Optimization in HIV screening programs. J Appl Math Stoch Anal 16(4):361–374
Alistar SS, Brandeau ML (2012) Decision making for HIV prevention and treatment scale up: bridging the gap between theory and practice. Med Decis Making 32(1):105–117
Alistar SS, Long EF, Brandeau ML, Beck EJ (2014) HIV epidemic control – a model for optimal allocation of prevention and treatment resources. Health Care Manag Sci 17(2):162– 181
Armbruster B, Brandeau ML (2007) Optimal mix of screening and contact tracing for endemic diseases. Math Biosci 209(2):386–402
Armbruster B, Brandeau ML (2007) Contact tracing to control infectious disease: when enough is enough. Health Care Manag Sci 10(4):341–55
Armbruster B, Brandeau ML (2010) Cost-effective control of chronic viral diseases: finding the optimal level of screening and contact tracing. Math Biosci 224(1):35–42
Audet C, Dennis JE (2003) Analysis of generalized pattern searches. SIAM J Optim 13(3):889–903
Berry SA, Fleishman JA, Moore RD, Gebo KA (2012) Trends in reasons for hospitalization in a multisite United States cohort of persons living with HIV, 2001-2008. J Acquir Immune Defic Syndr 59(4):368–375
Beyrer C, Baral SD, Weir BW, Curran JW, Chaisson RE, Sullivan PS (2014) A call to action for concentrated HIV epidemics. Curr Opin HIV AIDS 9(2):95–100
Boily MC, Baggaley RF, Wang L, Masse B, White RG, Hayes RJ, Alary M (2009) Heterosexual risk of HIV-1 infection per sexual act: systematic review and meta-analysis of observational studies. Lancet Infect Dis 9(2):118–129
Brandeau M (2013) OR in public health: A little help can go a long way. In: Zaric GS (ed) Operations research and health care policy, international series in operations research & management science, vol 190. Springer, New York, pp 17–36
Branson BM, Handsfield HH, Lampe MA, Janssen RS, Taylor AW, Lyss SB, Clark JE, Centers for Disease Control and Prevention (CDC) (2006) Revised recommendations for HIV testing of adults, adolescents, and pregnant women in health-care settings. Morbid Mortal Wkly Rep Recomm Rep 55(R-14):1–17
Branson BM, Viall A, Marum E (2013) Expanding HIV testing: back to the future. JAIDS 63 Suppl 2:S117–21
British Columbia Centre for Disease Control (2011) HIV annual report 2011. http://www.bccdc.ca/NR/rdonlyres/54BFF7F2-E283-4E72-BF2A-73EC2813F0D1/0/HIV_Annual_Report_2011_20111011.pdf
British Columbia Centre for Excellence in HIV/AIDS (2013) HIV monitoring quarterly report for Vancouver Coastal Health – fourth quarter 2013. http://stophivaids.ca/STOP/wp-content/uploads/monitoring_reports/2013/VCHA-Monitoring-Report-13Q4-FINAL-Feb14.pdf
British Columbia Centre for Excellence in HIV/AIDS (2013) Therapeutic guidelines: Antiretroviral (ARV) treatment of adult HIV infection. http://www.cfenet.ubc.ca/therapeutic-guidelines/adult
Byrd RH, Gilbert JC, Nocedal J (2000) A trust region method based on interior point techniques for nonlinear programming. Math Prog 89(1):149–185
Cohen MS, Chen YQ, McCauley M, Gamble T, Hosseinipour MC, Kumarasamy N, Hakim JG, Kumwenda J, Grinsztejn B, Pilotto JH, Godbole SV, Mehendale S, Chariyalertsak S, Santos BR, Mayer KH, Hoffman IF, Eshleman SH, Piwowar-Manning E, Wang L, Makhema J, Mills LA, de Bruyn G, Sanne I, Eron J, Gallant J, Havlir D, Swindells S, Ribaudo H, Elharrar V, Burns D, Taha TE, Nielsen-Saines K, Celentano D, Essex M, Fleming TR, HPTN 052 Study Team (2011) Prevention of HIV-1 infection with early antiretroviral therapy. N Engl J Med 365(6):493–505
Das M, Chu PL, Santos GM, Scheer S, Vittinghoff E, McFarland W, Colfax GN (2010) Decreases in community viral load are accompanied by reductions in new HIV infections in San Fransisco. PLoS ONE 5(6):e11,068
Deeks SG, Lewin SR, Havlir DV (2013) The end of AIDS: HIV infection as a chronic disease. Lancet 6736(13):1–9
Dorfman R (1943) The detection of defective members of large populations. Ann Math Stats 14(4):436–440
Druyts EF, Yip B, Lima VD, Burke TA, Lesovski D, Fernandes KA, McInnes CW, Rustad CA, Montaner JS, Hogg RS (2009) Health care services utilization stratified by virological and immunological markers of HIV: evidence from a universal health care setting. HIV Med 10(2):88–93
Eglese RW (1990) Simulated annealing: a tool for operations research. Eur J Oper Res 46(3):271–281
Farmer PE (2013) Shattuck lecture. Chronic infectious disease and the future of health care delivery. New Engl J Med 369(25):2424–2436
Fernandez-Gerlinger MP, Bernard E, Saint-Lary O (2013) What do patients think about HIV mass screening in France? A qualitative study. BMC Public Health 13(1):526
Gardner EM, McLees MP, Steiner JF, del Rio C, Burman WJ (2011) The spectrum of engagement in HIV care and its relevance to test-and-treat strategies for prevention of HIV infection. Clin Infect Dis 52(6):793–800
Gómez-Olivé FX, Angotti N, Houle B, Klipstein-Grobusch K, Kabudula C, Menken J, Williams J, Tollman S, Clark SJ (2013) Prevalence of HIV among those 15 and older in rural South Africa. AIDS Care 25(9):1122–1128
Gonzalez-Serna A, Chan K, Yip B, Chau W, McGovern R, Samji H, Lima VD, Hogg RS, Harrigan R (2014) Temporal trends in the discontinuation of first-line antiretroviral therapy. J Antimicrob Chemother 69(8):2202–2209
Granich R, Gilks C, Dye C, Decock K, Williams B (2009) Universal voluntary HIV testing with immediate antiretroviral therapy as a strategy for elimination of HIV transmission: a mathematical model. Lancet 373(9657):48–57
Granich R, Gupta S, Suthar AB, Smyth C, Hoos D, Vitoria M, Simao M, Hankins C, Schwartlander B, Ridzon R, Bazin B, Williams B, Lo Y R, McClure C, Montaner J, Hirnschall G (2011) Antiretroviral therapy in prevention of HIV and TB: update on current research efforts. Curr HIV Res 9(6):446–469
Gray RT, Prestage GP, Down I, Ghaus MH, Hoare A, Bradley J, Wilson DP (2013) Increased HIV testing will modestly reduce HIV incidence among gay men in NSW and would be acceptable if HIV testing becomes convenient. PLoS ONE 8(2):e55449
Gustafson R, Montaner J, Sibbald BJ (2012) Seek and treat to optimize HIV and AIDS prevention. CMAJ 184(18):1971
Hall HI, Frazier EL, Rhodes P, Holtgrave DR, Furlow-Parmley C, Tang T, Gray KM, Cohen SM, Mermin J, Skarbinski J (2013) Differences in human immunodeficiency virus care and treatment among subpopulations in the United States. JAMA Intern Med 173(14):1337–1344
Haukoos JS, Hopkins E, Conroy AA, Silverman M, Byyny RL, Eisert S, Thrun MW, Wilson ML, Hutchinson AB, Forsyth J, Johnson SC, Heffelfinger JD (2010) Routine opt-out rapid HIV screening and detection of HIV infection in emergency department patients. JAMA 304(3):284–292
Health Protection Agency (2011) Time to test for HIV: expanding HIV testing in healthcare and community services in England. Final report 2011. http://www.bhiva.org/documents/Publications/Time_to_test_final_report__Sept_2011.pdf
Heath K, Samji H, Nosyk B, Colley G, Gilbert M, Hogg RS, Montaner JS (2014) Cohort profile: seek and treat for the optimal prevention of HIV/AIDS in British Columbia (STOP HIV/AIDS BC). Int J Epidemiol 43(4):1–9
Hyman JM, Li J, Stanley EA (2003) Modeling the impact of random screening and contact tracing in reducing the spread of HIV. Math Biosci 181(1):17–54
Joint United Nations Programme on HIV/AIDS (UNAIDS) (2013) UNAIDS report on the global AIDS epidemic 2013. http://www.unaids.org/en/media/unaids/contentassets/documents/epidemiology/2013/gr2013/UNAIDS_Global_Report_2013_en.pdf
Joint United Nations Programme on HIV/AIDS (UNAIDS) (2014) 90-90-90: An ambitious treatment target to help end the AIDS epidemic. http://www.unaids.org/sites/default/files/media_asset/90-90-90_en_0.pdf
Jover-Diaz F, Cuadrado JM, Matarranz M, Calabuig E (2012) Greater acceptance of routine HIV testing (opt-out) by patients attending an infectious disease unit in Spain. J Int Ass Phys AIDS Care 11(6):341–4
Katz DA, Cassels SL, Stekler JD (2014) Replacing clinic-based tests with home-use tests may increase HIV prevalence among Seattle men who have sex with men: evidence from a mathematical model. Sex Transm Dis 41(1):2–9
Kilnarx PH, Mutasa-Apollo T (2013) Patching a leaky pipe: the cascade of HIV care. Curr Opin HIV AIDS 8:59–64
Lasry A, Carter MW, Zaric GS (2008) S4HARA: System for HIV/AIDS resource allocation. Cost Eff Resour Alloc 6:7
Lasry A, Richter A, Lutscher F (2009) Recommendations for increasing the use of HIV/AIDS resource allocation models. BMC Public Health 9 Suppl 1:S8
Lewis RM, Shepherd A, Torczon V (2007) Implementing generating set search methods for linearly constrained minimization. SIAM J Sci Comput 29(6):2507–2530
Lima VD, Johnston K, Hogg RS, Levy AR, Harrigan PR, Anema A, Montaner JSG (2008) Expanded access to highly active antiretroviral therapy: a potentially powerful strategy to curb the growth of the HIV epidemic. J Infect Dis 198(1):59–67
Long EF, Brandeau ML, Owens DK (2010) The cost-effectiveness and population outcomes of expanded HIV screening and antiretroviral treatment in the United States. Ann Intern Med 153(12):778–89
Lucas A, Armbruster B (2013) The cost-effectiveness of expanded HIV screening in the United States. AIDS 27(5):795–801
Marks G, Crepaz N, Senterfitt JW, Janssen RS (2005) Meta-analysis of high-risk sexual behavior in persons aware and unaware they are infected with HIV in the United States. J Acquir Immune Defic Syndr 39(4):446–453
Mathers CD, Loncar D (2006) Projections of global mortality and burden of disease from 2002 to 2030. PLoS Med 3(11):e442
McInnes CW, Druyts E, Harvard SS, Gilbert M, Tyndall MW, Lima VD, Wood E, Montaner JSG, Hogg RS (2009) HIV/AIDS in Vancouver, British Columbia: a growing epidemic. Harm Reduct J 6:5
Mellors JW, Rinaldo CRJ, Gupta P, White RM, Todd JA, Kingsley LA (1996) Prognosis in HIV-1 infection predicted by the quantity of virus in plasma. Science 272(5265):1167–1170
Mermin J (2014) The future of HIV prevention. JAMA 308(4):347–348
Montaner JS (2011) Treatment as prevention – a double hat-trick. Lancet 378(9787):208–209
Montaner JS, Hogg R, Wood E, Kerr T, Tyndall M, Levy AR, Harrigan PR (2006) The case for expanding access to highly active antiretroviral therapy to curb the growth of the HIV epidemic. Lancet 368(9534):531–536
Montaner JSG, Lima VD, Harrigan PR, Lourenco L, Yip B, Nosyk B, Wood E, Kerr T, Shannon K, Moore D, Hogg RS, Barrios R, Gilbert M, Krajden M, Gustafson R, Daly P, Kendall P (2014) Expansion of HAART coverage is associated with sustained decreases in HIV/AIDS morbidity, mortality and HIV transmission: the “HIV Treatment as Prevention” experience in a Canadian setting. PLoS ONE 9(2):e87,872
Moyer VA, on behalf of the US preventive services task force (2013) Screening for HIV: U.S. preventive services task force recommendation statement. Ann Intern Med 159(1):51–60
Nikolaev AG, Jacobson SH (2012) Simulated annealing. In: Gendreau M, Potvin J (eds) Handbook of metaheuristics. 2nd edn. Springer, New York
Nosyk B, Montaner JSG, Colley G, Lima VD, Chan K, Heath K, Yip B, Samji H, Gilbert M, Barrios R, Gustafson R, Hogg RS (2013) The cascade of HIV care in British Columbia, Canada, 1996–2011: a population-based retrospective cohort study. Lancet Infect Dis 3099(13):1–10
Object Management Group (CopyrightⒸ1997-2013) Unified Modeling Language (UML). http://www.uml.org
Office of the Provincial Health Officer of British Columbia (2014) HIV testing guidelines for the province of British Columbia. http://hivguide.ca
Ortblad KF, Lozano R, Murray CJL (2013) The burden of HIV: insights from the Global burden of disease study 2010. AIDS 27(13):2003–2017
O’Shaughnessy MV, Hogg RS, Strathdee SA, Montaner JS (2012) Deadly public policy: what the future could hold for the HIV epidemic among injection drug users in Vancouver. Curr HIV/AIDS Rep 9(4):394–400
Paltiel AD, Weinstein MC, Kimmel AD, Seage GR, Losina E, Zhang H, Freedberg KA, Walensky RP (2005) Expanded screening for HIV in the United States – an analysis of cost-effectiveness. N Engl J Med 352(6):586–595
Paltiel AD, Walensky RP, Schackman BR, Seage GR, Mercincavage LM, Weinstein MC, Freedberg KA (2006) Expanded HIV screening in the United States: effect on clinical outcomes, HIV transmission, and costs. Ann Intern Med 145(11):797–806
Public Health Agency of Canada (PHAC) (2011) Summary: Estimates of HIV prevalence and incidence in Canada, 2011. http://www.phac-aspc.gc.ca/aids-sida/publication/survreport/estimat2011-eng.php
Rayment M, Thornton A, Mandalia S, Elam G, Atkins M, Jones R, Nardone A, Roberts P, Tenant-Flowers M, Anderson J, Sullivan AK (2012) HIV testing in non-traditional settings–the HINTS study: a multi-centre observational study of feasibility and acceptability. PLoS ONE 7(6):e39530
Saltelli A (2002) Making best use of model valuations to compute sensitivity indices. Comput Phys Commun 145(2):280–297
Saltelli A, Ratto M, Andres T, Campolongo F, Cariboni J, Gatelli D, Saisana M, Tarantola S (2008) Global sensitivity analysis. The primer. Wiley. Chichester
Samji H, Cescon A, Hogg RS, Modur SP, Althoff KN et al (2013) Closing the gap: increases in life expectancy among treated HIV-Positive individuals in the United States and Canada. PLoS ONE 8(12):e81355
Sanders GD, Bayoumi AM, Sundaram V, Bilir SP, Neukermans CP, Rydzak CE, Douglass LR, Lazzeroni LC, Holodniy M, Owens DK (2005) Cost-effectiveness of screening for HIV in the era of highly active antiretroviral therapy. N Engl J Med 352(6):570– 585
Shampine LF, Reichelt MW (1997) The MATLAB ODE suite. SIAM J Sci Comput 18(1):1–22
Shan S, Wang GG (2010) Survey of modelling and optimization strategies to solve high-dimensional design problems with computationally-expensive black-box functions. Struct Multidisc Optim 41:219–241
Shannon K, Rusch M, Shoveller J, Alexson D, Gibson K, Tyndall MW (2008) Mapping violence and policing as an environmental-structural barrier to health service and syringe availability among substance-using women in street-level sex work. Int J Drug Policy 19(2):140–147
Socías ME, Hermida L, Singman M, Kulgis G, Díaz Armas A, Cando O, Sued O, Pérez H, Hermes R, Presas JL, Cahn P (2013) Routine HIV testing among hospitalized patients in Argentina. is it time for a policy change? PLoS ONE 8(7): e69517
Sonnessa M (2004) Modelling and simulation of complex systems. PhD thesis, Dipartimento di Informatica, Università di Torino. http://eco83.econ.unito.it/dottorato/michele_sonnessa/sonnessa_thesis.pdf
Canada Statistics (2012) Health profile, Vancouver HSDA, June 2012. http://www12.statcan.gc.ca/health-sante/82-228/index.cfm?Lang=E
Sullivan AK, Raben D, Reekie J, Rayment M, Mocroft A, Esser S, Leon A, Begovac J, Brinkman K, Zangerle R, Grzeszczuk A, Vassilenko A, Hadziosmanovic V, Krasnov M, Sönnerborg A, Clumeck N, Gatell J, Gazzard B, d’Arminio Monforte A, Rockstroh J, Lundgren JD (2013) Feasibility and effectiveness of indicator condition-guided testing for HIV: results from HIDES I (HIV indicator diseases across Europe study). PLoS ONE 8(1):e52845
Tanser F, Bärnighausen T, Grapsa E, Zaidi J, Newell ML (2013) High coverage of ART associated with decline in risk of HIV acquisition in rural KwaZulu-Natal, South Africa. Science 339(6122):966–971
Urban Health Research Initiative of the British Columbia Centre for Excellence in HIV/AIDS (2009) Drug situation in Vancouver. http://www.cfenet.ubc.ca/sites/default/files/uploads/publications/dsiv2009.pdf
Vancouver Coastal Health and Providence Health Care (2012) STOP HIV/AIDS quarterly monitoring report. Quarter 3, 2012. http://www.vch.ca/media/STOP_HIV_AIDS_Quarterly_Monitoring_Report.pdf
Wein LM, Zenios SA (1996) Pooled testing for HIV screening: capturing the dilution effect. Oper Res 44(4):543–569
Williams B, Wood R, Dukay V, Delva W, Ginsburg D, Hargrove J, Stander M, Sheneberger R, Montaner J, Welte A (2011) Treatment as prevention: preparing the way. J Int AIDS Soc 14(Suppl 1):S6
Wilson D, Hoare A, Regan D, Wand H, Law M (2008) Mathematical models to investigate recent trends in HIV notifications among men who have sex with men in Australia. http://kirby.unsw.edu.au/sites/default/files/hiv/attachment/Final+NCHECR+Modelling+Report.pdf
Wood E, Schechter MT, Tyndall MW, Montaner JSG, O’Shaughnessy MV, Hogg RS (2000) Antiretroviral medication use among injection drug users: two potential futures. AIDS 14(9):1229–1235
World Health Organization (WHO) (2007) Guidance on provider-initiated HIV testing and counselling in health facilities. http://www.unicef.org/aids/files/PITCGuidance2007_Eng.pdf
World Health Organization (WHO) (2013) Consolidated guidelines on the use of antiretroviral drugs for treating and preventing HIV infection: recommendations for a public health approach. http://www.who.int/hiv/pub/guidelines/arv2013/download/en
World Health Organization (WHO) (2013) The top 10 causes of death. Fact sheet no 310. http://www.who.int/mediacentre/factsheets/fs310/en/index.html
Yazdanpanah Y, Sloan CE, Charlois-Ou C, Le Vu S, Semaille C, Costagliola D, Pillonel J, Poullié AI, Scemama, O, Deuffic-Burban S, Losina E, Walensky RP, Freedberg KA, Paltiel AD (2010) Routine HIV screening in France: clinical impact and cost-effectiveness. PLoS ONE 5(10):e13132
Acknowledgments
To recognize the significant intellectual contributions of a number of public health partners in this project, the Vancouver HIV Testing Program Modelling Group is included as a coauthor on this paper. Members of this group, in addition to the listed authors, are Tim Chu, Ellen Demlow, Silvia Guillemi, Kendra McPherson, Meaghan Thumath, Lynn Tran, and Benita Yip. We also gratefully acknowledge support and contributions by Lukas Ahrenberg, Chris Buchner, Patty Daly, Guillaume Colley, Mark Gilbert, Scott Harrison, Julie Kille, Allison Macbeth, Val Munroe, Afshan Nathoo, Bojan Ramadanovic, Jat Sandhu and Susan Shurgold. We thank Dr. Cynthia Chan of the VCH Department of Family and Community Practice for helpful discussions and support. This study was funded through a grant to KV from the Canadian Institutes for Health Research (grant #: 126782). Funding was also provided by the British Columbia Centre for Excellence in HIV/AIDS, Vancouver Coastal Health Authority, and Providence Health Care. SK was supported in part by a MITACS Accelerate Internship in partnership with Merck, Canada. Computational resources were provided by the IRMACS Centre, WestGrid, and Compute Canada / Calcul Canada. We are grateful for the detailed and insightful comments of the anonymous reviewers on the first version of this manuscript, which lead to major revisions of the analysis and text. The project was conducted in collaboration with the STOP HIV/AIDS team at Vancouver Coastal Health and Providence Health Care, the BC Centre for Excellence in HIV/AIDS, and the BC Centre for Disease Control.
Author information
Authors and Affiliations
Consortia
Corresponding author
Appendix: Sensitivity analysis
Appendix: Sensitivity analysis
Some model parameters are not well known or are hard to quantify. This is particular true of parameters which involve behavioural factors, such as reduction in risk behaviour after diagnosis, adherence to treatment, transmission mode, and the interaction of individuals with the health care system. These parameters are the infectivity multiplier δ d after diagnosis, the infectivity multiplier δ v when virally suppressed, the mean time 1/ρ u to diagnosis after onset of AIDS, the mean time 1/τ d to AIDS after diagnosis, the proportion h 2 of patients initiating treatment after diagnosis in acute care or in AIDS phase, the proportion h 3 of patients initiating treatment immediately after the onset of AIDS, and the proportion h 4 of patients initiating treatment after discharge from hospital. Additionally, some parameters are strongly associated with assumptions made to simplify the model. These are the proportion ℓ of individuals not retained in care and the proportion α 0 of patents initiating treatment within one month of diagnosis.
Multivariate variance-based methods of sensitivity analysis were used to study the sensitivity of model output to changes in parameter values. The total effect sensitivity index of a model parameter is a measure of its contribution to model output variation, as well as all higher order effects due to its interactions with other parameters [69]. The inclusion of higher order effects in the sensitivity index accounts for nonlinear response of the model to variation in model parameters. Model output is defined as a random variable Y, which is a function \(Y=f(X_{1},X_{2},\dots ,X_{n})\) of the model parameter random variables X i . The total effect index for parameter X i is defined to be
where E denotes expectation, V denotes variance with respect to all parameters, and \(V\left [Y \mid X_{{\sim }i}\right ]\) is the conditional variance with all parameters held fixed, except X i . For large numbers of parameters, calculating S i may be computationally expensive. However, we utilize an efficient Monte-Carlo-based algorithm described in [68] and [69, Section 4.6] for computing total effect indices.
Model output was taken to be equilibrium prevalence for the purpose of computing the total effect sensitivity indices. The results for the above-mentioned parameters are given in Table 7. We find that the infectivity multipliers after diagnosis δ d and after viral suppression δ v account for 81 % of all variance caused by the set of parameters considered. Therefore, we focus on these two parameters to determine the sensitivity of our results to variation in model parameters.
The optimal allocation of testing resources to minimize five-year incidence for the 5:1 cost ration is shown as a function of δ d and δ v in Fig. 13. At the base values of the parameters, 100 % of resource should be allocated to routine testing in high prevalence settings. If the multiplier δ v is increased from its base value of 0.04 to 0.30 and δ d is increased from its base value of 0.32 to 1.00, then approximately 80 % of resources should be allocated to routine testing in high prevalence settings and the remaining resources to routine testing in acute care. This demonstrates relatively little change in our conclusions, even if the infectivities after diagnosis and being virally suppressed in treatment are increased to the largest reasonable values. The main impact of the infectivity being greater than estimated after diagnosis or treatment is that implementing routine testing in acute care settings becomes optimal at a lower cost ratio.
The number of five-year averted infections at the optimal resource allocation for each value of δ d , δ v is calculated and plotted in Fig. 13. All other parameters remain set to the calibration values in Table 3. As expected, higher values for the infectivity multipliers lead to few averted infections. For δ d between 0 and 1 and δ v between 0 and 0.30, the number of averted infections varies between 49 and 79 cases. Therefore, the number of averted infections is sensitive to the value of the infectivity; although, the optimal resource allocation strategy is not strongly sensitive to reasonable variations in the infectivity.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Kok, S., Rutherford, A.R., Gustafson, R. et al. Optimizing an HIV testing program using a system dynamics model of the continuum of care. Health Care Manag Sci 18, 334–362 (2015). https://doi.org/10.1007/s10729-014-9312-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10729-014-9312-0