Abstract
To gain a competitive edge, companies must continually invest in new product development (NPD), and must decide how to strategically allocate limited resources. The most critical NPD activity is the accurate assessment of the attractiveness of new products, simultaneously considering favorable factors (project value and strategic fit) and unfavorable factors (project risks), especially in robust companies in developing countries. In the NPD development process, the attractiveness of products is often evaluated using information that is imprecise or ambiguous. Fuzzy logic is well-suited to inform NPD decision-making. Thus, a comprehensive method considering both favorable and unfavorable factors, and using a fuzzy weighted average to devise a fuzzy possible-attractiveness rating (FPAR) of an NPD project for portfolio selection, is proposed in this paper. FPAR is a measurement of information, which is able to retain the multiplicity of that information. The proposed evaluation technique was demonstrated using a Taiwanese company as an example. The results indicated that this method provided an accurate assessment of overall product attractiveness, necessary for obtaining organizational buy-in, and can effectively aid managers to conduct sensitive analyses, balance the impact of changes in strategy, and receive quick feedback on the results of such changes.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Technological innovations and new business practices, as well as mounting market competition worldwide, have forced many firms, such as Google, Apple, Alexion Pharmaceuticals, and Tesla Motors, to accelerate new product development (NPD) to maintain long-term growth and sustainability (Hammond et al. 2006; Oke et al. 2007). New product portfolio selection is crucial and vital for successful innovation. However, portfolio decisions are difficult because of the combinatorial complexity involved in allocating limited resources to develop a multiplicity of new products; moreover, necessary information is often incomplete or ambiguous, and selection criteria are interdependent and often conflict (Loch and Kavadiaa 2002; Zapata et al. 2008). To assist managers in new product portfolio selection, numerous decision-enhancing tools, such as mathematical programming, economic models, option pricing theory, scoring models, and analytical hierarchy approaches, have been developed. However, most of these techniques have both practical and theoretical limitations (Griffin 1997; Henriksen and Traynor 1999; Hans et al. 2007); these approaches are unable to take holistic views, provide limited information on financial results, and offer dubious probabilities of completion (Kornfeld and Kara 2011; Griffin 1997; Kornfeld and Kara 2011). Furthermore, mathematical portfolio approaches have tended to provide inadequate understandings of risk and information, and are unable to handle multiple interrelated criteria (Lin and Chen 2004). They generally fail to recognize interrelationships with respect to the payoffs of combined utilization of resources (Griffin 1997; Lin and Chen 2004; Ghasemzadeh and Archer 2000), and address only some of the aforementioned issues (Zapata et al. 2008). Finally, managers typically perceive such techniques to be too difficult to use and understand (Griffin 1997; Kornfeld and Kara 2011).
Portfolio management is a complex, dynamic process involving substantial decision-making. Managers must allocate a limited set of resources to projects in a manner that balances risk and reward, and aligns with their strategies, which may not be easily expressed in numerical values. Conventional “crisp” evaluation approaches are inadequate to suitably or effectively inform such decisions. People are capable of understanding and analyzing obscure and imprecise events, but this level of comprehension is difficult to incorporate into existing analytical methods. Therefore, NPD decisions are executed primarily on the basis of expert opinions expressed not in numbers, but in linguistic terms, which are inherently vague. One way to objectively capture the meaning of linguistic terms is to use the fuzzy logic approach to associate each term with a possibility distribution (Dubois and Prade 1988). By using the concepts of multicriteria decision-making (MCDM), and a fuzzy-weighted average technique, a fuzzy possible-attractiveness rating (FPAR) was devised to conduct for new product portfolio selection. The proposed fuzzy logic new product portfolio selection model (FLNPPSM), integrating strategic fit and both product value and risk into a flexible formulation, can effectively aid managers dealing with ambiguity and complexity in the portfolio selection process. The development of FPAR and FLNPPSM is the main contribution of this paper.
2 Literature Review
Portfolio management is critical, yet complex, and a wide variety of project selection models have been devised. These can be grouped into three general categories: strategic management approaches, benefit measurement methods, and mathematical programming approaches (Cooper et al. 1998).
Strategic management approaches emphasize the connection between innovative projects and strategy, and illuminate issues of risk and strategic balance in portfolios (Cooper et al. 1998). In portfolio selection, the decision to allocate resources to various new core and new generation products, or to product families, derivatives, or enhancements, is driven by business strategy. Strategic considerations dominate the decision to pursue certain R&D projects or new product development. In the literature, a number of tools, such as the bubble diagram (Roussel et al. 1991), the portfolio map (Groenveld 1997), and the “strategic bucket” method, have been developed to evaluate the fitness of NPD projects with a company’s strategy. The strategic bucket method illustrates the links between projects and a company’s strategy; however, it does not address portfolio balance or the maximization of returns.
Benefit measurement methods maximize portfolio value by financial or nonfinancial measures. In the literature, a number of approaches, such as the merit-cost value index (Henriksen and Traynor 1999), the Q-sort (Souder and Mandakovic 1986), the analytical hierarchy process (Brenner 1994), data envelopment analysis (Linton et al. 2007), financial models (Chun 1994), probabilistic financial models (Bard et al. 1988), and option pricing theory (Perlitz et al. 1999), have been developed to estimate the potential benefits of NPD projects. In these methods, projects are selected sequentially by score. Often criticized for their over-reliance on financial data, these methods are unable to optimize the mix of projects, and cannot account for uncertainty. Consequently, certain studies have used the criterion of conditional stochastic dominance (Ringuest et al. 2000) or the mean-Gini analysis (Ringuest et al. 2004) to assist risk-adverse decision-makers in conducting projects with numerous uncertain variables.
Mathematical programming models optimize the commercial value of a portfolio within predetermined resource constraints, by using linear, nonlinear, integer, dynamic, goal, and stochastic mathematical models. These models maximize value, but pay scant attention to balance, or to the alignment of a portfolio with a company’s strategy. Such models rely on financial projections of the commercial value of each project (Dickinson et al. 2001), and principally rely on a single criterion; consequently, they may suffer from a high degree of uncertainty and reduced credibility (Cooper et al. 1988). However, in recent years, mathematical programming and project selection models have become more practical and realistic. Beaujon et al. (2001), for example, developed a mixed integer programming model to determine an optimal project portfolio, considering project concepts and the estimated project value within the selected portfolio. Dickinson et al. (2001) proposed the concept of a dependency matrix, representing complex interdependencies between projects, and also developed an optimal portfolio model to be used over multiple time periods.
NPD is characterized by a high degree of complexity, ambiguity, and vagueness, in addition to the difficulties involved in accurate quantitative evaluation. Fuzzy logic is a powerful tool to inform decisions involving imprecise, ambiguous, and vague phenomena that can only be expressed in linguistic, rather than numerical, terms. Fuzzy logic therefore enables effective and efficient quantification of imprecise information in the reasoning process, and decision-making based on vague and incomplete data (Machacha and Bhattacharya 2000). In recent decades, to reduce complexity, ambiguity, and uncertainty, numerous fuzzy analysis and decision tools have been developed to assist managers in making more satisfactory NPD screening decisions (Coffin and Taylor 1996; Machacha and Bhattacharya 2000; Kuchta 2001; Lin and Chen 2004; Lin and Hsieh 2004; Chen et al. 2006; Carlsson and Fuller 2007; Wang and Hwang 2007). For example, Coffin and Taylor (1996) and Machacha and Bhattacharya (2000) applied fuzzy logic to both software products and R&D project selection. Kuchta (2001) used fuzzy numbers to present the current net value and resource utilization of individual projects. Other researchers first used the fuzzy analytic hierarchy process to prioritize the relative importance of various evaluation criteria (Chen et al. 2007). Moreover, both a general weighted average (Chen et al. 2006) and a fuzzy weighted average (Chen et al. 2007) have been applied to consolidate fuzzy ratings and weightings of evaluation criteria to obtain the fuzzy performance value of each project. Because the fuzzy weighted average approach produces a more informative result, Lin and Chen (2004) used this technique to devise a fuzzy possible-success rating for a new product. Lin and Hsieh (2004) used a system based on fuzzy logic and fuzzy integer linear programming to develop a strategic portfolio selection model. To balance risk and revenue, align projects with strategy, and estimate the value of R&D project options, Carlsson and Fuller (2007) incorporated future cash flow estimates into their portfolio selection model. Wang and Hwang (2007) considered each stage of a new product project similar to purchasing an option on a future investment, and developed a fuzzy real-options valuation model, combined with fuzzy integer linear programming, to conduct portfolio selection.
Ayag and Ozdemir (2009) developed a fuzzy analytical network process-based approach to evaluate a set of conceptual design alternatives developed in an NPD environment to determine the option that satisfied both the needs and expectations of customers, and the engineering specifications of the company. Lin et al. (2010) combined the analytical hierarchy approach and the fuzzy integral method with MCDM techniques to construct a value-created model to evaluate new mobile communication package offerings. Combining fuzzy set theory and multicriteria group decision-making, Wei and Chang (2011) used the criteria of project performance, project delivery, and project risk, to propose a new approach to select NPD project portfolios. In the same vein, Ho et al. (2013) also developed a multicategory and multistandard approach using fuzzy value-based time limits to conduct NPD project portfolio selection.
To sustain long-term consistent corporate growth in the current, turbulent, increasingly challenging environment, robust companies, especially in developing countries in Asia, must allocate a limited set of resources to projects in a manner that balances risk and reward, and aligns with their strategies. Previous studies have generally concentrated on only a few dimensions for evaluating projects, such as benefits (Carlsson and Fuller 2007; Wang and Hwang 2007), corporate strategies (Lin and Hsieh 2004; Lin et al. 2010), and benefits and risks (Lin and Chen 2004; Wei and Chang 2011), and have tended to neglect potential risks, such as organizational factors or technical uncertainties (Chen et al. 2006, 2007). Furthermore, models based on complex methodologies that are not generally understood are unconvincing and cannot obtain organizational buy-in (Griffin 1997). Hence, a comprehensive, flexible project selection method that offers an overall possible-attractiveness rating is required to meet the practical needs of many companies.
3 Fuzzy Logic
For the purpose of application, the basic properties of fuzzy logic needed in this study are introduced, and an additional discussion can be found in a book by Klir and Yuan (1995).
3.1 Linguistic Variables
Linguistic variables can be used to analyze situations too vague or ill-defined to be reasonably described quantitatively. A linguistic variable is a variable whose values are words or sentences in natural or artificial language. For example, linguistic rather than numerical variables to denote temperature would be not hot, hot, very hot and quite hot, rather than 20, 25, 32, or 35 \(^{\circ }\)C. Furthermore, by the approximate reasoning of fuzzy set theory, linguistic values can be represented by fuzzy numbers. For example, for the linguistic values {Worst, Very Poor, Poor, Fair, Good, Very Good, Excellent}, the fuzzy numbers approximating these linguistic rating values are listed in Table 1. Although many forms of fuzzy numbers can be used to represent linguistic values, triangular fuzzy numbers were used in this paper because they can be easily specified by experts. Furthermore, under certain weak assumptions, such use immediately complies with the relevant optimization criteria (Pedrycz 1994). A linguistic value can also be represented by a membership function graph. For example, the linguistic value of “Good” in Table 1 is represented by the following membership function:
3.2 Fuzzy Weighted Average
The fuzzy weighted average is an integrated measure of information that consolidates the fuzzy ratings and weightings of all factors to be measured; thus, it represents the overall attractiveness of a new product. Several methods have been devised for calculating fuzzy weighted averages (Kao and Liu 2001; Lee and Park 1997).The fractional programming approach developed by Kao and Liu (2001) was adopted to compute fuzzy weighted averages.
The fuzzy ratings and the fuzzy importance weights of the criteria were denoted by \(R_{1}, R_{2} , \ldots , R_{n}\) and \(W_{1}, W_{2} , \ldots , W_{n}\), respectively. With n criteria, the fuzzy weighted average of \(R_{i}\) and \(W_{i}\) was defined as
According to the fractional programming approach, \(t = 1/\sum _{i=1}^{n} W_{i}\) and \(v_{i} = tw_{i}\). Thus, the lower and upper bounds of the specific \(\upalpha \)-cut of \(Y\) were calculated by
By enumerating different \(\upalpha \) values, the membership function \(Y\) was constructed.
3.3 Fuzzy Ranking Method
Because fuzzy numbers, unlike real numbers, do not always yield a totally ordered set, selecting the optimal projects for development from a set is difficult. To resolve this problem, numerous fuzzy ranking methods to compare fuzzy numbers have been developed (Chen and Hwang 1992). The ranking of fuzzy numbers used in this study was based on Chen and Hwang’s left and right fuzzy ranking method (Chen and Hwang 1992). The crisp score of a fuzzy number \(M\) was obtained as follows:
Let x \(\in \) R and given a maximizing set and a minimizing set, respectively, as
The right score of \(M\) was obtained as:
The left score of \(M\) was obtained as:
The total scores of \(M\) are then computed as:
4 Method and Algorithm
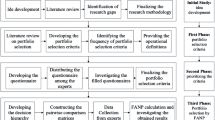
The FLNPPSM, as shown in Fig. 1, contains three main stages. The first stage is the new product prescreening, in which senior managers determine a set of critical characteristics which a new product must meet, informed by their business and new product strategies. The second stage is individual new product scoring: on the basis of changes in the business environment, managerial goals, and company competency, managers develop a set of criteria which a new product should meet, to rate its attractiveness. In the third stage, projects are prioritized and resources allocated. The stepwise procedure is as follows:
-
(1)
Collect and study project-related data.
-
(2)
Select criteria for scoring strategic fit, product value, and project risk.
-
(3)
Define linguistic terms as well as associated membership functions for measurement.
-
(4)
Assess criteria by using linguistic terms and translating them into fuzzy numbers.
-
(5)
Aggregate fuzzy numbers to obtain fuzzy the strategy fit, fuzzy value, and fuzzy risk ratings of various new product development projects.
-
(6)
Align portfolio strategy weights, and consolidate strategy fit, fuzzy value, and fuzzy risk ratings, to obtain fuzzy possible-attractiveness rating.
-
(7)
Rank fuzzy possible-attractiveness ratings.
-
(8)
Reconfirm attractiveness and allocate resources to select projects.
5 Case Study
The proposed evaluation procedure was implemented in new product portfolio selection in an international information technology (IT) product company in Taiwan, to evaluate its effectiveness.
5.1 Subject
BIT Company is a robust growing company, and according to Business Week, was one of the top 100 IT companies in the world in 2002. BIT has executed successful development programs for the past 40 years, and offers networked digital lifestyle products, categorized them into four groups: (1) network displays, (2) digital media, (3) imaging networks, and (4) networking and communications. In 2010, BIT had revenues of $10.5 billion. Every year, BIT invests 3–4 % of its revenue in R&D and NPD. Employing more than 2,000 researchers at four R&D centers worldwide, BIT strengthens internal integration vertically, through the value chain, and horizontally, across product platform lines.
5.2 New Product Portfolio Selection: Concept Model
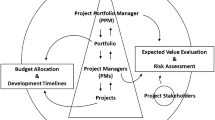
NPD is a complex process and a business risk. NPD requires substantial monetary and nonmonetary commitments, but the costs of the consequences of failure are even greater. The CEO of BIT has mandated that all new product proposals must be thoroughly analyzed and evaluated before undergoing full-scale development. BIT seeks to develop an attractive and integrated portfolio containing high-value projects, with an appropriate balance in the type and number of projects. As suggested by previous studies (Dickinson et al. 2001; Lin and Hsieh 2004; Carlsson and Fuller 2007; Killen et al. 2012; Ho et al. 2013), BIT established a framework for new product portfolio selection, revised most recently in 2013, as shown in Fig. 2. The framework provides a holistic, systematic procedure to understand the relationship between uncertainty in dynamic environments, and the organizational mechanisms used to minimize uncertainty and capture new product opportunities.
To select a new product portfolio, the BIT steering committee determined the rate of NPD investment distributed to each characteristic. Then, projects were evaluated based on technological opportunities, changes in customers’ requirements, the competition, the commercial potential in the market, the goals and competitive strategies of the company, the core technology owned by the company and human resources, equipment capability and capacity, and company business planning. Afterward, through the evaluation process, a completely new core product, a platform product, an addition to the product family, plus add-ons and enhancements to projects, were evaluated and determined by the steering committee. To accurately assess the attractiveness of new products, the assessment process determined (1) to what degree the new products met the business and marketing strategy of the company, (2) to what degree the new products contributed to the corporation and influence future growth prospects, i.e., industry attractiveness, competitive advantage, technological suitability and potential for gaining product advantage, and (3) whether there was risk involved (organizational risk, technological uncertainty, and market competitiveness). These three processes were proposed for various projects using the same axis and plane. Through this evaluation, the NPD projects proposed within a company were comprehensively assessed from the perspectives of strategy, level of contribution, and practicality. The ultimate purpose of this framework was to provide useful decision architecture for senior managers or enterprise directors to determine the allocation of the NPD portfolio investment.
5.3 Application of FLNPPSM
To create a portable storage device with a built-in wireless display, enabling users to both play and record digital information, BIT decided to invest $300–400 million in three to five (depending on cost) new-platform product development projects in 2011–2012. After prescreening, nine new digital network platform products proposed by the company’s four business groups passed the first evaluation, thereby becoming new platform product candidates in November 2010. To determine the most appropriate products and characteristics to be developed, BIT established a new product portfolio selection committee composed of 13 experts and senior managers from the business planning and global strategy, marketing, engineering/technology, new business project office, and finance departments, organized and led by the vice president of business planning and marketing.
The purpose of this research was explained to the selection committee. To collect data accurately reflecting BIT’s strategy and selection process, the manager of business planning held a briefing session to introduce the company’s new product portfolio selection concept model (see Fig. 2). Meanwhile, the pros and cons of various approaches to portfolio selection (as mentioned in literature review) were explained. The new product selection framework was used to conduct new product portfolio selection was undertaken as follows:
-
(1)
Collect and study project-related data. Before proceeding with the assessment, the evaluators studied data and information related to the new product projects. Nine new-platform product managers held a briefing session to address product-concept development, market and technical data, and a cursory financial forecast; key data in the debriefing included the United States census and market studies.
-
(2)
Product concept development: a description of how the product planner began with secondary data such as demographic, gender equality, economic environment, employment and wages, education, infrastructure, expenditure trends, competitive analysis, etc., and in-depth interviews with a small group of customers, were collected. Perceptual mapping was used to understand market conditions, conjoint analysis was used to develop the general idea into a detailed new product concept, and the features and price of the product were specified, as well as customer communication. The feedback of a focus group was incorporated.
-
(3)
Preliminary market data: marketplace was assessed by examining the existence, probable size, and acceptance of the market using archival research and keyword searches of various trade magazines, commercial databases, and reports, as well as in-house and personnel sources.
-
(4)
Preliminary technical data: a technical appraisal, including a solution and probable architecture, as well as costs, time, and risks, was undertaken by searching the technical literature, utilizing in-house technical expertise, conducting brainstorming and creative problem-solving sessions, and reviewing competitors’ product solutions.
-
(5)
Preliminary business data: sales, costs, and requisite investments were generally assessed, and a preliminary risk forecast was executed.
Based on previous projects, the evaluators recognized that despite the availability of both technical and market data, the “first cut” analysis was still marked by ambiguity and uncertainty. The data the analysis was based on may have been obtained in a specific context, such as a developed country, limiting its applicability to markets in developing countries, such as China, India, and countries in the Association of Southeast Asian Nations. Data is often unavailable in developing countries, and the reliability of data that is available is suspect. Because the attributes of new products may not be exactly ideal, different criteria were balanced and integrated. The CEO desired a method able to account for the uncertainty of each factor, as well as multiplicity, to provide an overall indication of the attractiveness of each new product; such a method would enable evaluators to measure ambiguous criteria by differentiating between high, medium, and low values, rather than numerical values. Furthermore, because linguistic values are able to account for ambiguity and a multiplicity of meanings, and the information obtained can be expressed as a range in a fuzzy set rather than as single values, fuzzy logic was applied to the decision-making process. The concept of fuzzy logic, linguistic values and their associated membership functions, fuzzy weighted average, and the application of fuzzy logic to business decisions were explained to the managers participating in this study. For facilitating managers understand and convince them, a simple example using only three actors was used to demonstrate the efficacy of the FLNPPSM system. This step can help managers understand and create confidence in a new selection approach.
The next step in the product selection process was to determine the criteria to evaluate the proposed products. New products are selected not only because of the value they offer, but also based on their fit to the business strategy, and the risk involved in developing them. Thus, different departmental managers provided typical planning cases as references. Finally, on the basis of their own selection architecture and criteria, and referring to assessment factors in previous studies (Coldricka et al. 2005; Jolly 2003; Stewart and Mohamed 2002), the committee updated the architecture and criteria as shown in Table 2.
Subsequently, linguistic terms as well as associated membership functions for measuring the strategic fit, product value, and project risk were defined. The ad hoc usage of linguistic terms and corresponding membership functions is characteristic of fuzzy logic. Many popular linguistic terms and corresponding membership functions have been proposed for linguistic assessment (Chen and Hwang 1992). For the sake of convenience, instead of eliciting linguistic terms and corresponding membership functions from the experts, some were obtained directly from past data, and others were modified to account for BIT’s situation. The rating scale R= {Worst [W], Very Poor [VP], Poor [P], Fair [F], Good [G], Very Good [VG], Excellent [E]} was used to rate various projects based on strategic fit and product value criteria. The possible scale \(\hbox {R}'\) = {Extremely High [EH], Very High [VH], High [H], Fairly High [FH], Medium [M], Fairly Low [FL], Low [L]} was used to estimate the possibility of project development risk. The weighting scale W = {Very Low [VL], Low [L], Fairly Low [FL], Fairly High [FH], High [H], Very High [VH]} was used to evaluate the relative importance of the various criteria. All the scales and their associated membership functions are listed in Table 1.
The criteria were assessed by translating linguistic terms into fuzzy numbers. To assess the criteria, the committee discussed the nature of the marketplace, competitive circumstances, technological opportunities, customer requirements, the complexity of products/processes, as well as the strategy, capabilities and resources of the company. As shown in Table 2, the experts subsequently used the linguistic terms to directly assess the rating/risk characterizing the degree of the effect/impact of various factors on the attractiveness of the NPD project. Concurrently, the team of experts evaluated the relative importance of each criterion on the basis of their own experience and knowledge. Delphi iterative procedures were used to facilitate a consensus on the assessment of different criteria and their relative importance to the company. The results of the linguistic assessment of new product \(\hbox {P}_{1}\) by the team of experts are shown in Table 3. On the basis of the corresponding relation between linguistic terms and fuzzy numbers as listed in Table 1, the linguistic terms of rating and weight in Table 3 were approximated by fuzzy numbers, the results of which are shown in Table 4. Applying the same processes, the team of experts also evaluated the other eight new product projects.
The fuzzy numbers were aggregated to obtain the fuzzy strategic fit rating (FSFR), the fuzzy value rating (FVR), and the fuzzy risk rating (FRR) of the NPD project. According to the fuzzy weighted average definition, the FSFR, FVR, and FRR were obtained by aggregating the rating and weight fuzzy numbers of the criteria and subcriteria. Using the expressions (2a) and (2b), the FSFR, FVR, and FRR were obtained. The fuzzy business strategic fit \((\hbox {FA}_{1})\) and the FSFR of project \(\hbox {P}_{1}\) were computed by:
By applying the same fuzzy operation, the FVR and the FRR of the NPD project \(\hbox {P}_{1}\) were obtained. Table 5 lists the assessment results of new product project \(\hbox {P}_{1}\), as assessed by the team of experts. Subsequently, the FVRs, FRRs, and FSFRs of the other eight new product projects were obtained.
The portfolio strategy-weights were aligned with consolidated strategic fit, value, and risk ratings to obtain fuzzy possible-attractiveness ratings. To balance the strategic fit, product value, and development risks of the project, strategy-weighting obtained on the basis of strategic fit, value, and risk of the project were assessed as “Very High,” “High,” and “High,” respectively. Because development risk is an unfavorable factor, the fuzzy weighted average integrated favorable and unfavorable factors, and the FPAR of a project was defined as
where \(W_{i},i= A, B, C\), are the weights of the strategic fit, product value, and project development risk, respectively, and \(\hbox {FRR}'\) = (1, 1, 1) \(\ominus \) FRR.
By applying this definition, the FPAR of new product project \(\hbox {P}_{1}\) was obtained using the FSFR, FVR, and the FRR listed in Table 5, and the strategy-weighting set determined by the corporate steering committee, and computed as
The other eight FPARs of new product projects were obtained using this process, as listed in Table 6.
To select a new product portfolio, the nine FPARs of new product projects were ranked using the ranking method presented in Eqs. (3)–(7), and the scoring values for the FPARs of the nine new product projects were obtained. The ranking values are shown in Table 7.
5.4 Comparative Study
A survey by Cooper et al. (2001) on portfolio management models concluded that using more than one selection method yielded superior results, because no single method offers superior performance in all areas. To ascertain the efficiency of this method, a comparative study of the fuzzy logic approach and the factor-weighting (direct assessment) approach was executed by the evaluation committee.
The factor-weighting approach neglects ambiguity and multiplicity in linguistic assessments. In the evaluation process, evaluators usually use a crisp scale to represent the value of a criterion. For a triangular fuzzy number parameterized by the triplet \(A\) = (a, b, c), parameter “b” yields the maximal grade of \(f_{A}(\hbox {x})\), i.e., \(f_{A}(\hbox {b})=1\), which is the most probable value of the evaluation data. Thus, in the comparison study, a crisp scale, by which the most probable value of the fuzzy number was chosen to represent the linguistic values of the merit rating and the importance weighting, was used. For example, the linguistic term “Fairly” was represented by the fuzzy number (0.3, 0.5, 0.7) using the linguistic approach, and by 0.5 using the crisp approach.
The attractiveness ratings generated were compared with those derived from the fuzzy logic approach, the results of which are listed in Table 8. Both approaches exhibited similar results. However, the attractiveness ratings generated by the fuzzy logic approach were expressed in terms of value ranges, and provide an overall indication of pertinent attractiveness, allowing managers a high degree of flexibility in decision-making. As an example, the attractiveness rating of project \(\hbox {P}_{1}\) had the fuzzy value (0.378, 0.622, 0.823). Qualitatively, this suggested that \(\hbox {P}_{1}\) is probably attractive. However, the crisp rating of 0.621, generated by the factor-weighting approach, may suggest a different inference or provide less rich information.
5.5 Sensitive Analytical Study
New product selection is profoundly linked to the project’s strategic fit, product value, and project risk, and the divergent strategies of various firms can be reflected in the differential weighting given to various attributes. To study the impact of various weightings yielded by FPAR-generated portfolio strategies, the evaluation committee conducted a sensitive analysis.
Four scenarios were studied: (1) “High” versus “Fairly High” on project-risk weighting (Scenarios 1 and 2), (2) “High” versus “Very High” on project-value weighting (Scenarios 2 and 3), (3) “Very High” versus “High” on strategic fit weighting (Scenarios 3 and 4), and (4) “High” strategic fit and “Fairly High” project-risk weighting versus, “Very High” strategic fit and “Fairly Low” project-risk weighting (Scenarios 4 and 5). The FPARs of the nine new product projects were compared with those derived using a different portfolio strategy, as listed in Table 7.
Regarding the FPAR, one can observe that (1) the higher the project-risk weighting of a new product project, the lower the degree of the FPAR for the project; (2) the higher the product-value weighting of a new product project, the higher the degree of the FPAR; and (3) the higher the project strategic fit weighting of a new product project, the higher the degree of the FPAR. These trends can also be used to explain why a “Very High” weighting on strategic fit, a “Very High” on product value, and a “Fairly Low” on project risk in Scenario 5 generated a higher degree of FPAR than the other four scenarios. Furthermore, ratings derived using a different portfolio strategy weighting exhibited little difference in value. However, the sequence generated by the different portfolio strategy setting seemingly leads to a very similar conclusion. The five most attractive new product projects were consistently \(\hbox {P}_{6}\), \(\hbox {P}_{3}\), \(\hbox {P}_{1}\), \(\hbox {P}_{5}\), and \(\hbox {P}_{9}\).
5.6 Reconfirm Attractiveness of New Product Projects
Once the five most attractive new product projects were ascertained, the evaluation committee determined a linguistic label whose meaning was the same as (or closest to) the meaning of the FPARs from the natural-language expression set to represent the attractiveness level (AL), to reconfirm the level of project attractiveness, obtain organizational buy-in, and guide managers in their final decision. In general, three methods for translating the membership function back into a linguistic function have been proposed (Schmucker 1985): (1) Euclidean distance, (2) successive approximation, and (3) piecewise decomposition. The Euclidean distance method is the simplest to implement and the most intuitive representation of the degree of proximity (Guesgen and Albrecht 2000).
In the Euclidean method, the Euclidean distance is calculated from the given fuzzy number to each number representing the natural-language expression set. In the natural language expression set AL, the distance between the FPAR (known) and each fuzzy \(\hbox {AL}_\mathrm{i}\) (unknown) \(\in \) AL was calculated by
where \(p = \{x_{0}, x_{1}, \cdots , x_{m}\} \subset \) [0, 1] so that 0 \(= x_{0} < x_{1} < {\ldots }< x_{m}=1\). Let \(p\) = {0, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5, 0.55, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9, 0.95, 1}. Then, the distance from the FPAR to each of the members in the AL set was calculated, and the closest natural expression with the minimum distance was identified.
In this case, the natural language expression of attractiveness level set, AL = {Extremely Attractive [EA], Very Attractive [VA], Highly Attractive [HA], Attractive [A], Slightly Attractive [SA], Non-Attractive [NA]}, were used to label the linguistics and corresponding membership functions, which are shown in Fig. 3. Using Eq. (8), the Euclidean distance D from the FPAR of \(\hbox {P}_{9}\) to each member in set AL was calculated as
Thus, by matching a linguistic label with the minimum D, the attractiveness of the \(\hbox {P}_{9}\) development was determined to be “Highly Attractive,” as shown in Fig. 3. By again applying Eq. (8), the attractiveness level of \(\hbox {P}_{6}\) was obtained, and was similarly determined to be “Highly Attractive,” as shown in Fig. 3.
Linguistic levels to match fuzzy-possible-attractiveness-ratings {Non-Attractive [NA] (0, 0.15, 0.3); Slightly Attractive [SA] (0.15, 0.3, 0.45); Attractive [A] (0.3, 0.45, 0.6); Highly Attractive [HA] (0.4, 0.55, 0.7); Very Attractive [VA] (0.55, 0.7, 0.85); Extremely Attractive [EA] (0.7, 0.85, 1.0)}
5.7 Resource Allocation and Project Selection
The BIT sensitive analytical study indicated that the FPARs of the five most attractive new product projects were high, and even the least attractive projects had an FPAR of 0.317–0.834, and consequently, were far from unattractive. Because the total investment was set at $300–400 million, and the total cost estimation of the four most attractive projects (\(\hbox {P}_{6}\), \(\hbox {P}_{3}\), \(\hbox {P}_{1}\), and \(\hbox {P}_{5})\) was $381 million, after a reconfirming discussion and approval of the final evaluation result, the committee recommended that projects \(\hbox {P}_{6}\), \(\hbox {P}_{3}\), \(\hbox {P}_{1}\), and \(\hbox {P}_{5}\) be selected as the new product development slate for 2011–2012. Although they were rated as highly attractive projects, the four most attractive projects may confront obstacles that could block successful implementation. To enhance the possibility for success of the four new products selected for development, the corporate steering committee mandated that the evaluation committee investigate and identify which factors within each project required the most urgent improvement, to develop an action plan be implemented to ameliorate such adverse factors and facilitate success.
6 Discussion and Conclusion
In an increasingly competitive, globalized marketplace, NPD is crucial for the survival of high-technology firms. Companies must evaluate their NPD from the perspective of new projects in their portfolios. This research highlighted the importance of new product portfolio selection. Because of the complexity, ambiguity, and incomplete information involved in new product portfolio selection, a comprehensive fuzzy-logic-based portfolio selection model applying linguistic approximation and fuzzy sets was developed. The proposed method considers both favorable and unfavorable factors and uses a fuzzy weighted average to build an FPAR for an NPD project that maintains the multiplicity of linguistic meaning and the ambiguity of factormeasurements.
This model was developed using the concept of MCDM and adapted for an IT product provider, which served as a case study to validate the model and approach. The company and managers involved in this case study were generally comfortable and pleased with the design and use of the approach. The perceptions of the managers employing this approach, compared with traditional approaches such as factor-weighting, were that the fuzzy attractive rating does aggregate and purify the subjective judgments and clarify the overall indication of the relevant possibility, covered by imprecision and ambiguity, and also ensures that the decisions made in the selection process are not biased. Furthermore, this approach allows managers a high degree of flexibility in decision-making. In the case study, the FPAR of \(\hbox {P}_{1}\) and \(\hbox {P}_{3}\) were (0.378, 0.622, 0.823) and (0.369, 0.624, 0.834), respectively. Qualitatively, these ratings suggest that the proposed product \(\hbox {P}_{3}\) was more attractive than \(\hbox {P}_{1}\), whereas the proposed product \(\hbox {P}_{1}\) was a more certain success than \(\hbox {P}_{3}\). Thus, the main contribution of this research is the development of an algorithm which clarifies and purifies the ambiguity, imprecision, and uncertainty of evaluation factors, appropriately modifies the fuzzy weighted average technique to incorporate both favorable and unfavorable factors, and enables software to be developed to support MCDM, especially when considering all the factors in new product portfolio selection. This study provides potential value to companies by offering a rational structure to reflect on imprecise or ambiguous phenomena commonly present in many business environments, and accounting for the uncertainty of each factor to assure a reasonably realistic and sharp evaluation. This study is potentially valuable to researchers in its demonstration of still another application of fuzzy logic. Furthermore, compared with existing studies (Lin and Hsieh 2004; Chen et al. 2006, 2007; Carlsson and Fuller 2007; Wang and Hwang 2007; Lin et al. 2010; Wei and Chang 2011), the proposed approach offers the following distinct features:
-
(1)
This approach comprehensively incorporates favorable (strategic fit and product value) and unfavorable (project development risk) evaluation factors, and each dimension is consolidated separately to maintain an individual rating. This approach provides flexibility in sensitive analysis, and balances the impact of strategic changes on the solution. Moreover, the approach allows for quick feedback on the results of such changes, as exemplified by the case study presented in this report.
-
(2)
This approach appropriately modified the fuzzy weighted average technique to consolidate the fuzzy ratings and weightings of all factors, including the unfavorable ones, and maintained multiplicity to provide a holistic image and richer picture of a project’s attractiveness (as shown in Fig. 3). This project attractiveness rating is realistic, informative, reliable, and convincing, and is able to facilitate organizational buy-in.
-
(3)
This approach allows multidisciplinary teams to be involved in the evaluation of major criteria, elements criteria, and subcriteria, the linguistic terms, the membership functions and the consolidation method to enable a broad view of the problem. Furthermore, this approach allows momentum to be created, and evaluation outputs to be translated into comprehensive implementation.
Although the case study demonstrated the usefulness of the model for new product portfolio selection, there is room for future validation and improvement. Therefore, it is hoped that more managers will be encouraged to adopt this method. A single case study or a number of case studies do not necessarily demonstrate the relative performance and success of this model. Further research is required to fine-tune the proposed model and to compare the efficiency of different models for new product portfolio selections.
Evaluation levels and personnel involved inevitably vary between firms, and situations and requirements vary according to both products and companies. Firms in high-tech industries, focused on gaining the competitive advantage through innovation, may employ criteria and strategies different from those employed in firms in mature industries, seeking to compete as low-cost providers of proven technologies.
Finally, the fuzzy logic approach has certain limitations. Competitive situations and requirements vary from one company to another; hence, each company must establish a unique membership function appropriate to its specific environment and considerations. Furthermore, the computation of a fuzzy weighted average is complicated and not easily appreciated by managers. However, the necessary assessment calculations can be executed using a computer, to increase accuracy while reducing both the calculation time and error.
References
Ayag Z, Ozdemir RG (2009) A hybrid approach to concept selection through fuzzy analytic network process. Comput Ind Eng 56:368–379
Bard JF, Balachandra R, Kaufmann PE (1988) An interactive approach to R&D project selection and termination. IEEE Trans Eng Manag 35:139–146
Beaujon GJ, Marin SP, McDonald GC (2001) Balancing and optimizing a portfolio of R&D projects. Nav Res Logist 48:18–40
Brenner MS (1994) Practical R&D project prioritization. Res Technol Manag 37:38–42
Carlsson C, Fuller R (2007) A fuzzy approach to R&D project portfolio selection. Int J Approx Reason 44:93–105
Chen HH, Lee AHI, Tong Y (2006) Analysis of new product mix selection at TFT-LCD technological conglomerate network under uncertainty. Technovation 26:1210–1231
Chen HH, Lee AHI, Tong Y (2007) Prioritization and operations NPD mix in a network with strategic partners under uncertainty. Expert Syst Appl 33:337–346
Chen SJ, Hwang CL (1992) Fuzzy multiple attribute decision making methods and application. Springer, Berlin
Chun YH (1994) Sequential decisions under uncertainty in the R&D project selection problem. IEEE Trans Eng Manag 40:404–413
Coffin MA, Taylor BW (1996) Multiple criteria R&D project selection and scheduling using fuzzy logic. Comput Oper Res 23:207–220
Coldricka S, Longhurstb P, Iveya P, Hannis J (2005) An R&D options selection model for investment decisions. Technovation 25:185–193
Cooper RG, Edgett SJ, Kleinschmidi EJ (1998) Portfolio management for new product. Perseus, Reading, MA
Cooper RG, Edgent SJ, Kleinschmidt EJ (1988) Best practices for managing R&D portfolios. Res Technol Manag 41:20–33
Cooper RG, Edgent SJ, Kleinschmidt EJ (2001) Portfolio management for new product development: results of an industry practices study. R&D Manag 31:361–380
Dickinson MW, Thornton AC, Graves S (2001) Technology portfolio management: optimizing interdependent projects over multiple time periods. IEEE Trans Eng Manag 48:518–527
Dubois D, Prade H (1988) Possibility theory—an approach to computerized processing of uncertainty. Plenum, New York
Ghasemzadeh F, Archer NP (2000) Project portfolio selection through decision support. Decis Support Syst 29:73–88
Griffin A (1997) PDMA research on new product development practices: updating trends and benchmarking best practices. J Prod Innov Manag 14:429–458
Groenveld P (1997) Roadmapping integrates business and technology. Res Technol Manag 50:48–55
Guesgen HW, Albrecht J (2000) Imprecise reasoning in geographic information systems. Fuzzy Sets Syst 113:121–131
Hammond JS, Keeney RL, Raiffa H (2006) The hidden traps in decision making. Harv Bus Rev 84:118–126
Hans EW, Herroelen W, Leus R, Wullink G (2007) A hierarchical approach to multi-project planning under uncertainty. Omega 35:563–577
Henriksen AD, Traynor AJ (1999) A practical R&D project-selection scoring tool. IEEE Trans Eng Manag 46:158–169
Ho YC, Hsu WC, Chang CC (2013) Multi-category and multi-standard project selection with fuzzy value-based time limit. Int J Innov Comput Inf Control 9(3):971–989
Jolly D (2003) The issue of weightings in technology portfolio management. Technovation 23:383–391
Kao C, Liu ST (2001) Fractional programming approach to fuzzy weighted average. Fuzzy Sets Syst 120:435–444
Killen CP, Jugdev K, Drouin N, Petit Y (2012) Advancing project and portfolio management research: applying strategic management theories. Int J Proj Manag 30:525–538
Klir GJ, Yuan B (1995) Fuzzy sets and fuzzy logic: theory and applications. Prentice-Hall, New Jersey
Kornfeld BJ, Kara S (2011) Project portfolio selection in continuous improvement. Int J Oper Prod Manag 31:1071–1088
Kuchta D (2001) A fuzzy mode for R&D project selection with benefit, outcome and resource. Eng Econ 46:164–180
Lee DH, Park D (1997) An efficient algorithm for fuzzy weighted average. Fuzzy Sets Syst 87:39–45
Lin CL, Chen CW, Tzeng GH (2010) Planning the development strategy for the mobile communication package based on consumers’ choice preferences. Expert Syst Appl 37:4749–4760
Lin CT, Chen CT (2004) A fuzzy-logic-based approach for new product Go/NoGo decision at the front end. IEEE Trans Syst Man Cybern A Syst Hum 34:132–142
Lin C, Hsieh PJ (2004) A fuzzy decision support system for strategic portfolio management. Decis Support Syst 38:383–398
Linton JD, Morabito J, Yeomans JS (2007) An extension to a DEA support system used for assessing R&D projects. R & D Manag 37:29–36
Loch CH, Kavadiaa S (2002) Dynamic portfolio selection of NPD programs using marginal returns. Manag Sci 48:1227–1241
Machacha LL, Bhattacharya P (2000) A fuzzy logic-based approach to project selection. IEEE Trans Eng Manag 47:65–73
Oke A, Burke G, Myers A (2007) Innovation types and performance in growing UK SMEs. Int J Oper Prod Manag 27:735–753
Pedrycz W (1994) Why triangular membership functions? Fuzzy Sets Syst 64:21–30
Perlitz M, Peske T, Schrank R (1999) Real options valuation: the new frontier in R&D project evaluation? R & D Manag 29:255–269
Ringuest JL, Graves SB, Case RH (2000) Conditional stochastic dominance in R&D portfolio selection. IEEE Trans Eng Manag 47:478–484
Ringuest JL, Graves SB, Case RH (2004) Mean-Gini analysis in R&D portfolio selection. Eur J Oper Res 154:157–169
Roussel RA, Saad KN, Erickson JJ (1991) Third generation R&D: managing the link to corporate strategy. Harvard Business Press, Boston
Schmucker KJ (1985) Fuzzy sets, natural language computations and risk analysis. Computer Science Press, USA
Souder WE, Mandakovic T (1986) R&D project selection models. Res Manag 29:36–42
Stewart R, Mohamed S (2002) IT/IS projects selection using multi-criteria utility theory. Logist Inf Manag 15:254–270
Wang J, Hwang WL (2007) A fuzzy set approach for R&D portfolio selection using a real options valuation model. OMEGA 35:247–257
Wei CC, Chang HW (2011) A new approach for selecting portfolio of new product development projects. Expert Syst Appl 38:429–434
Zapata JC, Varma VA, Reklaitis GV (2008) Impact of tactical and operational policies in the selection of a new product portfolio. Comput Chem Eng 32:307–319
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Lin, CT., Yang, YS. A Linguistic Approach to Measuring the Attractiveness of New Products in Portfolio Selection. Group Decis Negot 24, 145–169 (2015). https://doi.org/10.1007/s10726-014-9384-8
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10726-014-9384-8