1 Introduction

Negotiation Support Systems (NSS) support human negotiators in their bargaining processes. In doing so, they have to fulfill two functions: communication support and decision support (Lim and Benbasat 1992; Braun et al. 2005; Kersten and Lai 2007). The communication component enables users, who in the case of web-based systems might be geographically distributed, to exchange arguments or offers, or engage in even richer forms of communication. The importance of communication support is well understood in the literature. Most systems offer a text-based communication platform, which is sometimes enhanced by features like a classification of message types (Schoop et al. 2003), or chat-like facilities to enable the instant exchange of messages (Kim et al. 2006).

In contrast to the communication component, the functionalities which an NSS should offer in terms of decision support are less well understood. Most existing NSS, including academic research systems like Negotiation Advisor (Rangaswamy and Shell 1997), Inspire (Kersten and Noronha 1999), Invite (Strecker et al. 2005) or NegoIsst (Schoop et al. 2003), as well as commercial systems like SmartSettle (Thiessen et al. 1998; Thiessen and Soberg 2003), contain features to elicit users’ preferences in the form of a utility function and tools to evaluate offers the user is going to send or has received from the opponent in terms of those utilities. However, they do not support the user by actively suggesting offers which could be sent to the opponent.

This rather low level of involvement of NSS in critical decisions within the actual bargaining process was already recognized in the early literature on NSS. Vetschera (1990) classified the level of support an NSS could offer to users into (i) facilitation, which focuses on supporting only the communication process, (ii) interactive guidance, which directs the decision processes of users and thus guarantees that desirable properties like efficiency are achieved, and (iii) normative guidance, which actually proposes solutions fulfilling certain properties like efficiency or fairness criteria. In a later classification, Kersten and Lai (2007) distinguished three somewhat different levels of systems. The first two levels of their classification consist of passive systems offering process and calculation support to the users and active facilitation-mediation systems, which support users in the generation of offers. Systems at the third level, which they call proactive intervention-mediation systems, consult and advise the user by e.g. making suggestions about possible offers without an explicit request for such advice by the user. Similarly, Braun et al. (2005) consider the task “[t]o suggest offers and agreements” ((Braun et al. 2005, p. 6)) as essential for NSS, which, according to their opinion, can best be provided by artificial intelligence methods.

While many authors have thus called for a more active role of NSS for quite some time, actual systems implementing such concepts are still rare. One exception is eAgora developed by Chen et al. (2005). This system contains software agents which not only analyze and criticize offers a user is considering, but also actively suggest alternative offers that might be attractive for the user to send. However, eAgora only considers the current step of the bargaining process and generates offers which provide a utility value close to a concession level specified by the user.

In the present paper, we introduce more elaborate models for suggesting offers that one negotiator could send to his or her counterpart. Our approach is characterized by two features:

  • It is based on a perspective of the entire bargaining process rather than on a single bargaining step of a negotiator. Thus it takes into account desirable features of the process and its outcomes, like Pareto efficiency of the final (although not necessary intermediate) outcomes, or reciprocity of concessions. The perspective we follow in this process model is therefore more that of a facilitator or a mediator, rather than an expert advising only one side of the negotiation.

  • These desirable properties of the bargaining process can best be described in terms of utility values, while negotiators communicate via offers which are formulated in terms of negotiation issues. We therefore have to take the mapping between utility values and offers (and vice versa) into account.

By considering desirable attributes of the bargaining process, our models introduce a normative component into negotiation support. The balance between normatively desirable properties of outcomes and autonomy of negotiators has always been an important topic in NSS research. As Rangaswamy and Starke (2000) put it, the task of an NSS is “...to prompt the parties toward jointly optimal agreements ...although the parties always remain in control of the outcome” ((Rangaswamy and Starke 2000, p. 49)). The simultaneous quest for normatively desirable properties of the process and its outcomes on one hand and autonomy of users on the other is not necessarily a contradiction. Consider for example another important field of decision support, decision making under risk. Prescriptive theories like expected utility theory (Schoemaker 1982) are based on a set of axioms defining how rational decisions under risk should be made. On the other hand, different shapes of utility functions can still represent a wide variety of individual preferences toward risk. In a similar way, we parameterize the bargaining process to allow users to choose from a range of possible negotiation tactics, while still ensuring that the entire process fulfills the requirements we formulate.

Desirable process properties like reciprocity of concessions or efficiency of outcomes require preference information in form of utility values of both parties—based on MAUT (Keeney and Raiffa 1976), VIP (Climaco and Dias 2006), TOPSIS (Wachowicz 2010) or other multi-attribute preference models. We therefore consider an NSS to play the role of a trusted third party, to whom both sides reveal their true preferences without strategic misrepresentation. The models we develop in this paper could also be used to unilaterally support one party. In that case, the supported party would need to provide some estimate about the other party’s preferences, similarly to the system developed by Lim (1999), possibly in the form of incomplete information (Sarabando et al. 2012).

The second contribution of our work is the mapping that is provided between utility values and bargaining issues. As has already been argued in the early literature on NSS (e.g. Kersten 1988), bargaining takes place in three different spaces: the decision space of decision variables controlled by the parties, the outcome space of objectively determined consequences of the decisions taken, and the utility space, which is formed by the parties’ subjective evaluations of outcomes. In the present paper, we do not consider a situation involving hidden agendas (Kersten and Szapiro 1987), and thus assume that the decision and outcome spaces are identical. Offers are made in terms of outcome variables (e.g. the price in a buyer-seller negotiation), and we do not consider a separate decision space. While the utility functions of the parties provide a mapping from the outcome space to the utility space, the inverse mapping has rarely been considered in the NSS literature.

The conceptual framework which forms the basis of our research is illustrated in Fig. 1. We develop a model of a bargaining process, which is, on one hand, based on certain requirements we impose on the process, and, on the other, leaves room for control by the user. This model of the bargaining process is formulated in the utility space, and the bargaining process in terms of utilities is then mapped to offers in the issue space. Since the dimensionality of the issue space in multi-attribute negotiations is likely to be higher than that of the utility space (which is two-dimensional in case of bilateral bargaining), the mapping from utility space to outcome space is not always unique. Thus it leaves room for additional control by the user.

Fig. 1
figure 1

Conceptual framework

Full size image

The remainder of our paper is structured as follows: In Sect. 2, we review related models from literature, in particular models of the bargaining process originating in different fields of research. In Sect. 3, we introduce the requirements we impose on the bargaining process. The actual models are developed in Sect. 4 and illustrated by a numerical example in Sect. 5. Section 6 concludes the paper by summarizing its main results and providing an outlook onto future research.

2 Related Literature

Three distinct streams of literature are relevant and informative for the research topic of this paper: (i) The axiomatic bargaining approach, which determines negotiation outcomes normatively, (ii) the strategic bargaining approach, which derives solutions from dynamic interaction models, and (iii) the multi-criteria decision making (MCDM) approach, which provides models to support improvement-based and concession-based negotiation processes. The brief review of these approaches that provide useful input for our project also highlights some drawbacks concerning their applicability for decision support in negotiations, which also motivates this study and the approach proposed here.

The axiomatic approach was the first one to deal with the mechanisms of bargaining from a game theoretical perspective. It was introduced, together with a formal definition of the bargaining problem, in the seminal contribution of Nash (1950). Following the axiomatic approach, one first has to determine desirable properties for the negotiation outcome, which are formulated as axioms. For the Nash bargaining solution (Nash 1950) these axioms are (i) invariance to linear utility transformations, (ii) Pareto-optimality, (iii) symmetry, and (iv) independence of irrelevant alternatives. Another well known axiomatic solution is the Raiffa solution, which was first proposed by Raiffa (1953). An axiomatic formulation of that solution was later developed by Kalai and Smorodinsky (1975). Therefore, it is also known as Kalai-Smorodinsky solution. These two solutions share the first three axioms, The fourth axiom of Nash, independence of irrelevant alternatives, was often criticized and is replaced by monotonicity in the Raiffa solution.

Based on these axioms, solution concepts are derived that determine an (usually unique) outcome of the negotiation. The Nash solution is the alternative that maximizes the product of the differences between the negotiators’ utilities and their conflict payoffs (Nash 1950). The conflict payoff is the exogenously determined payoff in case no settlement is reached in the negotiation. The Raiffa or Kalai-Smorodinsky is the point on the Pareto-frontier where both negotiators receive equal proportions of their utility differences between the conflict point and the utopia point. The conflict point is defined as in the Nash solution, the utopia point is the (usually infeasible) combination of the maximal utility values for both negotiators. Later research on the axiomatic approach accepted and combined these two solution concepts, but criticized the reference points to be unrealistic. Rational negotiators should not consider them as relevant as conflict will never occur if there is at least one alternative superior to the conflict as stated in Nash’s formulation of the bargaining problem (Felsenthal and Diskin 1982). Alternative reference points proposed were the midpoint of the negotiation (in the issue space) and the minimax point—also called minimal utility point, which is the combination of the negotiators’ minimal achievable utility when the opponent achieves his optimal solution. Roth (1977) and Thomson (1981) used the Nash solution concept with the minimax point, Rosenthal (1976) and Gupta (1989) the Raiffa solution concept with the minimax and the midpoint, respectively.

The axiomatic approach, although creating a basis for later research on negotiation, faces two major drawbacks related to negotiation support. The first one results from its theoretical basis in cooperative game theory. As in any cooperative game model, the way by which the solution is reached—i.e. the specific actions, interactions and strategies of the parties—is not discussed. These approaches only present a formula to calculate the solution, but do not discuss how the solution is reached and implemented. If one aims at supporting negotiations as an interactive process of information and offer exchange, this is not sufficient. Second, negotiation problems are formulated in terms of utility values, however, there might be several offers with different issue configurations that lead to the same vector of utilities (Osborne and Rubinstein 1990). Even if the utility vectors proposed by axiomatic approaches are helpful, they still could leave room concerning which alternative in the issue space to settle for.

Later initiatives tried to develop dynamic game models that demonstrate the interactions that lead to axiomatic solutions. A number of dynamic bargaining models were found to result in the Nash solution like Nash’s demand game (Nash 1953), Zeuthen’s conflict-risk game (Harsanyi 1956) or Rubinstein’s alternating offers game (Rubinstein 1982). Later, Mumpower (1991) analyzed the effect of generic negotiation strategies like log-rolling or splitting the difference on the outcome in various negotiation problems. Though these strategic bargaining approaches unraveled the dynamic processes that might result in normative solutions, their focus is to justify these solutions rather than to describe or support actual negotiation processes. Furthermore, they also operate in the utility space or consider only one single issue.

Rubinstein’s alternating offers game with fixed time costs or discounts (Rubinstein 1982) formed the basis to overcome this restriction. Rather than looking at only one issue or aggregating several issues into one utility value, game theorists more recently started to analyze multiple (usually two) issue negotiations on an issue-by-issue basis (Lang and Rosenthal 2001). Game theorists for example analyzed issue-by-issue bargaining under fixed agenda (Fershtman 1990), agenda setting for issue-by-issue bargaining (Busch and Horstmann 1999a), compare issue-by-issue and bundle offer protocols (Lang and Rosenthal 2001; Inderst 2000) and analyze the signaling of private information through agenda setting (Bac and Raff 1996; Busch and Horstmann 1999b). Though formulated in (a stylized) issue space, these models usually suggest that agreements are found in the very first round of the negotiation to avoid negative aspects of time costs or discounts. Their usability for the support of actual negotiation processes is therefore limited.

While game theoretic models usually consider only one or two outcome dimensions per party, MCDM approaches consider multiple issues separately. Starting from a long tradition of MCDM methods for individual decision makers, these methods have been extended to situations involving multiple decision makers. Process models have been proposed for groups of decision makers with homogeneous interests (e.g. Climaco and Dias 2006) and also for negotiations between parties with conflicting interests. In the latter field, one can distinguish improvement-based and concession-based MCDM approaches to negotiation (Teich et al. 1994).

The improvement-based MCDM approach to bargaining was inspired by the “single negotiation text” procedure applied in the Camp David negotiations between Egypt and Israel (Fisher 1978; Fisher and Ury 1981). Parties start from a common ground (their minimal consensus or the status quo of their conflict) and seek Pareto-improvements to their tentative agreement to eventually end up with an (nearly) efficient outcome. This process is often supported by a mediator. Recently, quantitative trade-off methods for logrolling procedures were proposed (Tajima and Fraser 2001) to reach integrative agreements in multiple-issue negotiations via a series of Pareto-improvement steps. The procedure is comparable to the post-settlement settlement approach suggested by Raiffa (1985) to improve tentative agreements reached in negotiations. A similar approach is implemented as a post-settlement phase in several NSS like Negotiation Advisor (Rangaswamy and Shell 1997), Inspire (Kersten and Noronha 1999), or Invite (Strecker et al. 2005). Other improvement-based MCDM approaches do not require complete information about the parties’ preferences, but determine offers in an interactive process between the parties and the mediator (which also could be a software system) (Teich et al. 1994). Models that follow the improvement-based negotiation process using the “method of improving direction” (Ehtamo and Hämäläinen 2001) were first proposed for two party settings (Teich et al. 1996; Ehtamo et al. 1999) and later generalized to many party many issue negotiations (Ehtamo et al. 2001). Experimental NSS, e.g. the web-based Joint Gains (Kettunen and Hämäläinen 1999), have been developed to implement this approach. The improvement-based negotiation process is quite promising from a behavioral perspective. It might be easier for negotiators to accept an additional gain during a negotiation than to have to give in. However, even proponents of this approach (e.g. Teich et al. 1994) find it to have only minor influence in research and practice and state that the concession-based approach is more widely used.

In a concession-based process, both parties start with inconsistent and often extreme opening offers and then continuously make concession toward a joint agreement. First attempts to model decision making in negotiations as a series of concessions date back to Rao and Shakun (1974), who consider the sequential and alternating decision problem of making a fixed concession in a single issue negotiation. The authors state that the model can be generalized to multiple issues if exact tradeoffs between issues are known. However, this is rarely the case and furthermore an increasing number of issues renders the approach computationally complex. Recent approaches in automated negotiations extend the concept of single issue concession tactics, which can be based on time or reciprocity, to generate multiple issue offers (Faratin et al. 1998; Lee and Chang 2008). The formulation of such decision making functions for autonomous software agents is one of the major tasks of automated negotiation research (Jennings et al. 2001). In most approaches, multi-issue offers are formed as a combination of concessions generated by specific tactics for each issue (Faratin et al. 1998). This, however, can cause inefficiencies as the potential for logrolling and integrative outcomes is ignored. Other strategies use single issue tactics to determine the utility value of the next offer to propose—and therefore also the extent of the next concession (Lee and Chang 2008). However, these approaches leave the actual offer in the issue space to be determined.

Other approaches base their support on the generation of some form of group preferences from individual preferences. Decision makers then are assumed to make concessions to settle for an alternative preferred by the group. For example, Jaramillo et al. (2005) developed the decision support system Multi-Decision-Makers Equalizer which elicits the preferences of the decision makers and then proposes a balanced solution in the negotiation area which is determined by the decision makers’ favored alternatives. If the decision makers do not agree on this balanced solution, the system asks them to relax their demands following a logrolling procedure—i.e. giving in in issues of lower importance to gain in issues of higher importance—which builds the basis for the generation of the next balanced solution. Similarly the decision support system NegocIAD (Espinasse et al. 1997) determines individual preorders of alternatives following the PROMETHEE approach as a basis for a collective preorder. If no alternative is found that is mutually acceptable, the decision makers are informed about how the weights and evaluations of their individual preferences could be changed to make an alternative acceptable for all parties. These approaches differ from the one proposed in this paper in that they focus on determining the final outcome but do not provide much information on the process to achieve it—i.e. the offers exchanged during the negotiation.

In contrast, the approach proposed by Lai and Sycara (2009) explicitly focuses on offer generation and also takes into account the possibility of incomplete information. In a first step, the size of the concession is determined by a time-based strategy. The method used to calculate an actual offer in issue space which implements this concession depends on the information available. If only information about the focal party’s preferences is available, an offer is generated that implements the determined utility level and minimizes the Euclidean distance between the offer and the last offer of the opponent. If no information about preferences is available, a mediator collects some information about both parties’ preferences and uses this information to improve the proposed baseline offer to a similar offer on the Pareto-frontier. While this approach, like the approach proposed in this paper, focuses on generating offers with desirable properties, we focus on properties of each concession step rather than solely the final outcomes.

3 Requirements for a Concession Process Model

Though we want to leave freedom of choice with the supported negotiator, support for the negotiation process needs some guiding rules, which we introduce in this section. Based on the negotiation literature discussed below, we formulate three requirements: (i) real concession-making, (ii) reciprocity and (iii) value creation. We consider these properties to be important for each negotiation step, i.e. each offer proposed by either party. As long as each step fulfills these three requirements, the whole process clearly features these properties, too.

In supporting real negotiations, one needs to consider the typical negotiation process, which is often observed in empirical studies. Usually, negotiators start from inconsistent extreme positions in their favor. In an interactive sequence of offers, they make concessions and relax their demands to eventually reach an agreement. Concessions are therefore an essential ingredient of any (realistic) negotiation process. However, there is no consensus in the negotiation literature about the concept of concessions. Concessions can be seen as changes in the issue space, in utility space, or some combination of both. Different interpretations also result from referring to just the focal negotiator, or also including the opponent’s perspective.

In the classification of bargaining steps for multi-issue negotiations introduced by Filzmoser and Vetschera (2008), changes in issue values are analyzed from the perspective of a focal negotiator. According to this classification, a concession is a bargaining step that does not change any issue to a more preferred option, and moves to a less preferred option in at least one issue. The previous offer is thus strictly preferred to the current offer proposed by the focal negotiator. This approach is useful if one has only information about the preferences of one party, as it might often be the case. However, if available, information about the opponent’s preferences should be taken into account for a more detailed analysis of negotiation steps.

Our approach therefore starts by looking at the bargaining process in the utility space and considers offers in the issue space later on (see Fig. 1). Therefore, we adopt the classification of Bosse and Jonker (2005), which takes into account the effect of a step for both parties in terms of utilities. In this classification, an offer can lead to a negotiation step that affords for each of the parties either a higher or a lower utility. The possibility of equal utility after a step for either or both sides is neglected for simplicity. An offer sequence resulting in higher utility for both sides—i.e. a Pareto improvement—is called a fortunate step. The opposite move that results in lower utility for both sides an unfortunate step. Making an offer that leads to higher utility for the focal negotiator and lower utility for the opponent is called a selfish step. Finally an offer that affords higher utility to the opponent and lower utility to the negotiator making the offer is called a concession step. This change in utilities for both parties by two subsequent offers of one side is what we perceive as a real concession in this study. In terms of the classification by Filzmoser and Vetschera (2008), this also includes trade-off steps, in which utility losses in some issues are partially offset by utility gains in other issues.

One could argue that Pareto-improvement steps are more desirable as they lead to a gain for both parties. However, this gain is just a temporal one. As the parties started from inconsistent positions, they have to make concessions to reach an agreement and, therefore, it is likely that such gains have to be given up later in the process. Giving up something that has just been gained might be problematic from a psychological point of view, and could undermine the prospects of an agreement in a negotiation. Moreover, it could also prolong the negotiation process.

The requirement of concession making determines a sector in the utility space in which the next offer to propose should be located, i.e. the area with higher utility for the opponent and lower utility for the negotiator making the offer. However, the size of this concession remains to be determined. Pruitt (1981) studied the effect of different concession patterns and found that too large concessions could lead to exploitation and unfavorable agreements, too small concessions to more beneficial agreements, however, at the cost of reduced prospects of reaching one. This illustrates the typical negotiation dilemma, aspects increasing the prospects of a favorable agreement simultaneously decrease the prospects to reach an agreement at all. Bartos (1977) provides an orientation for a desirable concession magnitude in his “simple model of negotiation”. Fair concession making means that concessions made by a negotiator should reciprocate the concessions received from the opponent. Thus, the own utility the opponent lost with his last offer compared to his penultimate offer should be returned by the negotiator by proposing an offer with a utility level that compared to the last offer of the negotiator offsets the opponent’s utility loss. The approach is comparable to the modified tit-for-tat strategy recently proposed for software agents in automated negotiations (Shakun 2005; Filzmoser 2010). We therefore define the requirement of reciprocity via the comparison of the utility given up by the opponent in his or her last step, in relation to the utility the opponent gains from the current step of the focal negotiator.

In defining the requirement of real concessions, we explicitly excluded the possibility of a Pareto-improving step. However, the eventual goal of a negotiation process is still to reach the Pareto frontier. This can be achieved if each step increases total value in terms of the joint utility of both negotiators. We therefore denote our last requirement as the value creation property. Value creation compares the utility given up by the focal negotiator to the utility gain of the opponent in the same step and requires that the opponent’s gain exceeds the utility loss by the focal negotiator.

4 The Analytical Concession-Advising Technology Model (AC-AT)

Following the framework shown in Fig. 1, we will first present our model of the bargaining process in the utility space, and then describe how points in the utility space can be mapped to specific offers in the issue space.

4.1 Bargaining Process in the Utility Space

Our model represents the entire bargaining process, and takes the interaction between bargaining steps by the focal negotiator and the opponent into account. Nevertheless, its basic building block is one bargaining step by the focal negotiator. We consider important that negotiators have the opportunity to exercise control over the bargaining process at each single step. The model not only takes the previous history into account, but also goes beyond a single step. It thus can be used to extrapolate future bargaining steps. Such an extrapolation, of course, requires assumptions about the opponent’s behavior, as well as assumptions that the user does not change his or her opinion, and thus parameter settings remain constant, throughout the remaining process.

Our model describes a concession-based bargaining process, which consists of individual offers made by the two parties. As long as no compromise is reached, these offers are incompatible with each other. In their own offers, each party demands a higher utility for itself and offers a lower utility to the opponent than in the offers made by the opponent (Vetschera 2009). The preconditions for each bargaining step consist of

  • The previous offer made by the same negotiator, which provides a utility of \(u^0_{own}\) to the focal negotiator and \(u^0_{opp}\) to the opponent.

  • The concession which the opponent has made in his or her previous step. We denote the decrease in utility which the opponent has accepted in his or her last bargaining step by \(\delta \) and assume that \(\delta \) will always be greater than zero. This assumption will automatically be fulfilled if our model is used to symmetrically support both parties, since it generates a concession at each step.

Denote the utility values which are achieved by the new offer \(\mathbf x\) of the focal negotiator by \((u_{own}(\mathbf{x}), u_{opp}(\mathbf{x}))\). The first requirement, that an offer corresponds to a real concession by the focal negotiator, is then described by the condition

$$\begin{aligned} u_{own}(\mathbf{x}) < u^0_{own} \end{aligned}$$
(1)

Furthermore, reciprocity demands that

$$\begin{aligned} u_{opp}(\mathbf{x}) \ge u^0_{opp} + \delta \end{aligned}$$
(2)

Finally, value creation in a bargaining step can be represented by the condition that

$$\begin{aligned} u_{own}(\mathbf{x})+u_{opp}(\mathbf{x}) > u^0_{own}+u^0_{opp} \end{aligned}$$
(3)

Equations (1), (2), and (3) define a region in the utility space in which new offers that fulfill all three requirements must be located. Of course, offers must also be technically feasible, which means that they must fulfill whatever constraints on issue values exist in the negotiation problem. Since these constraints refer to issue values, we denote them in general by \(\mathbf{x} \in X\).

Within this feasible region, the selection of a utility vector (and an actual offer in terms of issue values which leads to this utility vector) is controlled by the negotiator. According to the dual concern model of negotiations (Thomas 1992; Pruitt 1983), the attitudes of a negotiator in a negotiation process can be described by a concern for one’s own outcome, and for the outcome of the opponent. We therefore consider the trade-off rate between the focal negotiator’s own utility and the utility of the opponent as the central parameter through which users can control the negotiation process.

Starting from the previous offer \((u^0_{own},u^0_{opp})\), we therefore consider a concession path, which is defined by the equation

$$\begin{aligned} u_{own}(\mathbf{x}) + \alpha \; u_{opp}(\mathbf{x}) = u^0_{own} + \alpha \; u^0_{opp} \end{aligned}$$
(4)

The parameter \(\alpha \), which is selected by the user, is the user’s trade-off rate between the two parties’ utilities and indicates how much own utility the focal negotiator would give up to increase the utility of the opponent by one unit. A value of \(\alpha \le 0\) would indicate that the focal negotiator only makes Pareto-improving steps, but no real concessions. We therefore require \(\alpha >0\). From (3), it is also obvious that \(\alpha <1\) must hold, otherwise, the step would destroy value.

In fact, within a given negotiation, \(\alpha \) can be restricted even further. Denote the utility vector that is obtained from the opponent’s last offer by \((u^p_{own}, u^p_{opp})\). Note that the indices \(own\) and \(opp\) still refer to the focal negotiator and the opponent, respectively. Since it is not necessary to concede more than what would be required to reach this point, \(\alpha \) can be limited to

$$\begin{aligned} \alpha \le \frac{u^0_{own}-u^p_{own}}{u^p_{opp}-u^0_{opp}} \end{aligned}$$
(5)

The bound (5) can be further tightened if \((u^p_{own}, u^p_{opp})\) is dominated. Let \(u^*_{opp}\) be the optimal objective value of the problem

$$\begin{aligned} \begin{array}{l} u_{opp}(\mathbf{x}) + \rho \; u_{own}(\mathbf{x})\rightarrow \max \\ \mathrm{s.t.} \\ u_{own}(\mathbf{x}) \ge u^p_{own} \\ \mathbf{x} \in X \end{array} \end{aligned}$$
(6)

i.e. the maximum utility the opponent can achieve without decreasing the utility of the focal player beyond what was already conceded to him. In model (6), \(\rho \) is a small parameter which serves to avoid weakly dominated solutions if the problem maximizing \(u_{opp}(\mathbf{x})\) has multiple optima. Since \(u^*_{opp} \ge u^p_{opp}\), (5) can be tightened to

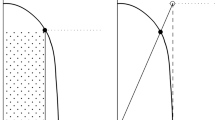
$$\begin{aligned} \alpha \le \min \left( 1, \frac{u^0_{own}-u^p_{own}}{u^*_{opp}-u^0_{opp}} \right) \end{aligned}$$
(7)

However, in many negotiations, not all issues are continuous, so that for some issues only discrete values are allowed. In that case, the feasible set shown in Fig. 2 is no longer convex, but consists only of some discrete points in the utility space. In that case, it is possible that no solutions exist which exactly fulfill Eq. (4). We therefore extend the concession path (4) to a concession cone, which contains all potential new offers of a negotiator close to the concession path. The concession cone can be described through the two constraints

$$\begin{aligned} \begin{array}{l} u_{own} + (\alpha - \tau ) u_{opp} \le u^0_{own} + (\alpha - \tau ) u^0_{opp} \\ u_{own} + (\alpha + \tau ) u_{opp} \ge u^0_{own} + (\alpha + \tau ) u^0_{opp} \\ \end{array} \end{aligned}$$
(8)

where \(\tau \) is a system parameter indicating how far one can deviate from the concession path. Figure 2 illustrates the concepts introduced so far.

Fig. 2
figure 2

Concession cone

Full size image

The choice of parameter \(\alpha \) has a strong effect on the negotiation process. Figure 3 shows different types of negotiation paths that can be obtained. In these graphs, we assume that both parties select similar values for \(\alpha \). This is not necessarily the case, this assumption only serves to better illustrate the effects of different values of \(\alpha \). The leftmost part shows a path that would be obtained if \(\alpha \) were set to a negative value (which, as we argue, should not be allowed). The negotiators first make Pareto-improving offers. However, they reach the efficient frontier very quickly, and at points which are still far apart. To reach a compromise, they then have to move along the Pareto frontier, which means they have to give up a comparatively large amount of their own utility for each unit gained by their opponent. Furthermore, they have to give up all the utility which they gained from the initial move to the Pareto frontier. Since it is probably particularly hard to give up benefits which one has just obtained, we require parties to make real concessions throughout the bargaining process and thus avoid this situation.

In the middle part of Fig. 3, both parties have chosen a positive, but low value of \(\alpha \). They still reach the Pareto frontier at separate points, but are not as far from each other as in the first scenario. In the last scenario, both parties chose a comparatively large value of \(\alpha \). Their negotiation paths intersect at an inefficient point, from which they then can look for mutual improvements using a single negotiation text (Fisher 1978) or post settlement settlement (Raiffa 1985) approach.

Fig. 3
figure 3

Different paths realized by different values of parameter \(\alpha \)

Full size image

4.2 Issue Values

The constraints we have defined so far refer only to utility values. However, the negotiation problem itself will have constraints which define the feasible outcomes of the negotiation. These constraints are typically defined in terms of issue values, not in terms of utility values. We therefore have to establish a connection between issue values and utility values to incorporate these constraints into our model.

Several NSS provide analytical support by means of utility elicitation and calculating utility values for offers. This kind of support is for example offered in Inspire (Kersten and Noronha 1999), Invite (Strecker et al. 2005), NegoIsst (Schoop et al. 2003), or SmartSettle (Thiessen et al. 1998; Thiessen and Soberg 2003). All these systems assume an additive utility function of the form

$$\begin{aligned} u(\mathbf{x}) = \sum _k w_k v_k(x_k) \end{aligned}$$
(9)

where \(\mathbf{x} = (x_1, \ldots , x_K)\) is the \(K\)-dimensional vector of issue values describing an offer \(\mathbf{x},\,w_k\) is the weight assigned to issue \(k\), and \(v_k(\cdot )\) is the partial utility function for issue \(k\).

Without loss of generality, we assume that all issue values are scaled to \(0 \le x_k \le 1\) and that for the focal negotiator zero indicates the least preferred and one the most preferred value in each issue. The most simple case is a linear partial utility function of the form \(v(x_k) = x_k\). In that case, equation (9) can be simplified to

$$\begin{aligned} u(\mathbf{x}) = \sum _k w_k x_k \end{aligned}$$
(10)

and Eq. (10) can directly be used as a constraint linking utility and issue values in an optimization model. If preferences of the opponent are in the opposite direction to that of the focal negotiator for some attributes, (e.g. the buyer’s and the seller’s preferences for the price of a good), this can be represented in model (10) by replacing \(x_k\) with \(1-x_k\).

However, such simple linear models often do not adequately represent the preferences of negotiators. Thus NSS offer more elaborate preference models. Many preference models used in NSS are based on conjoint analysis. They consider only discrete values in each attribute, and allow the user to assign utility values to each issue value independently, and not necessarily as a linear function of the issue value. As a generalization of this concept, we also consider the case of piecewise linear partial utility functions (Jacquet-Lagreze and Siskos 1982). Such a piecewise linear function can be represented in an optimization model using the convex combination method introduced by Dantzig (1963).

To simplify the notation, we assume that partial utility functions \(v_k(x_k)\) are scaled to \(0 \le v_k(x_k) \le w_k\). Thus it is no longer necessary to consider the weights explicitly. Denote a set of \(n+1\) discrete values in attribute \(k\) by \(\{ x_{k,0}, x_{k,1}, \ldots , x_{k,n} \}\). The piecewise linear utility function assigns utility \(v_{k,i}\) to issue value \(x_{k,i}\) and is linear between these points. Let \(x_k\) denote the issue value for which we want to compute the utility value, which is denoted by \(v_k\).

We write \(x_k\) as a linear combination of two neighboring values \(x_{k,i-1}\) and \(x_{k,i}\). Without loss of generality, \(x_k\) can be expressed as

$$\begin{aligned} x_k = \sum ^n_{i=0} s_{k,i} x_{k,i} \end{aligned}$$
(11)

where

$$\begin{aligned} \sum _i s_{k,i} =1 \end{aligned}$$
(12)

and only two neighboring factors \(s_{k,i-1}\) and \(s_{k,i}\) are greater than zero. To represent this constraint on the \(s_{k,i}\), we define a set of binary variables \(y_{k,i}\). Variable \(y_{k,i}\) is set to one if \(x_{k,i-1} \le x_k \le x_{k,i}\), and to zero, otherwise. If \(y_{k,i}=1\), only factors \(s_{k,i-1}\) and \(s_{k,i}\) can take on non-zero values. This is represented through the constraints

$$\begin{aligned} \begin{array}{l} s_{k,0} \le y_{k,1} \\ s_{k,i} \le y_{k,i} + y_{k,i+1} \; \; i=1,\ldots ,n-1 \\ s_{k,n} \le y_{k,n} \\ \end{array} \end{aligned}$$
(13)

Since the utility function is assumed to be linear between the supporting points, the same weights are used for \(x_{k,i}\) and \(v_{k,i}\) and, therefore, \(v_k\) can be expressed as

$$\begin{aligned} v_k = \sum ^n_{i=0} s_{k,i} v_{k,i} \end{aligned}$$
(14)

If only discrete values are allowed in attribute \(k\), the model can be simplified to

$$\begin{aligned} \begin{array}{l} \displaystyle x_k = \sum ^n_{i=0} s_{k,i} x_{k,i} \\ \displaystyle v_k = \sum ^n_{j=0} s_{k,i} v_{k,i} \\ \displaystyle \sum ^n_{i=0} s_{k,i} = 1 \\ \displaystyle s_{k,i} \in \{0,1 \} \end{array} \end{aligned}$$
(15)

Finally, the entire utility function can be represented by the constraint

$$\begin{aligned} u = \sum _k v_k \end{aligned}$$
(16)

In the following models, we will simply use the notation \(u(\mathbf{x})\) to indicate that the models contain the constraints necessary to represent the appropriate type of utility function for each issue.

4.3 Optimization Models

The constraints we have formulated so far define a region in the utility space and associated issue values, which fulfill our requirements for a bargaining process. To simplify the notation in this section, we denote the region in utility space which is bounded by constraints (1), (2), (3), and (8) by \(C\). The feasible set in terms of issue values is denoted by \(X\). The intersection of \(C\) and the image of \(X\) in the utility space corresponds to the “concession cone” shown in Fig. 2.

In this subsection, we formulate several optimization problems on that set of constraints, which can be used to support the negotiator. In particular, we consider two types of problems:

  • Prediction of likely negotiation outcomes given a certain strategy. These models can be used to help the negotiator to select a value for parameter \(\alpha \) by pointing out possible consequences of that parameter choice.

  • Offer generation models can be used by the system to actively generate possible offers.

4.3.1 Prediction Models

Prediction models construct a negotiation path similar to the patterns shown in Fig. 3 by following the concession path of the focal negotiator until it reaches the efficient frontier. Depending on the type of issues, two cases can be distinguished as illustrated in Fig. 4.

Fig. 4
figure 4

Prediction models

Full size image

If all issues involve continuous values, it is possible to follow exactly the concession path (4). The point at which this path reaches the Pareto frontier (point A in Fig. 4) can then be found by solving the following optimization problem:

$$\begin{aligned} \begin{array}{l} t \rightarrow \max \\ \mathrm{s.t.} \\ u_{own}(\mathbf{x}) = u^0_{own} - t \cdot \alpha \\ u_{opp}(\mathbf{x})= u^0_{opp} +t \\ \mathbf{x} \in X \end{array} \end{aligned}$$
(17)

If some issues involve discrete values, the entire concession cone has to be used. An objective function which is orthogonal to the concession path is given by \( u_{opp}(\mathbf{x})- \alpha u_{own}(\mathbf{x})\). However, this function could generate dominated solutions. We therefore propose to maximize \(u_{opp}(\mathbf{x})\), correcting again for the possibility of weakly dominated solutions by adding the focal negotiator’s own utility with a small weighting factor \(\rho \). We, therefore, obtain the model

$$\begin{aligned} \begin{array}{l} u_{opp}(\mathbf{x})+ \rho u_{own}(\mathbf{x}) \rightarrow \max \\ \mathrm{s.t.} \\ (u_{own}(\mathbf{x}), u_{opp}(\mathbf{x})) \in C \\ \mathbf{x} \in X \end{array} \end{aligned}$$
(18)

which would lead to point B in Fig. 4.

Models (17) and (18) only extrapolate the focal negotiator’s own offers, but do not take into account the behavior of the opponent. Although the system has information about the value of \(\alpha \) used by the opponent, we argue that using this value in such a prediction model would reveal too much information about one party’s strategy to the other party and thus should be avoided. Still, it might be useful for one negotiator to analyze the likely outcome of a negotiation process under the assumption that the opponent uses e.g. the same strategy (i.e. the same value of \(\alpha \)) as oneself, or is particularly tough \((\alpha =0)\) or very conceding \((\alpha =1)\). We denote the value of the opponent’s concession parameter to be used in such an analysis by \(\beta \).

In the case of continuous issue values, the intersection point between the two concession paths can be directly computed. The conditions for intersection are

$$\begin{aligned} \begin{array}{c} u^0_{own} -\alpha t = u^p_{own} +s \\ u^0_{opp} + t = u^p_{opp} - \beta s \end{array} \end{aligned}$$
(19)

Solving (19) for \(s\) and \(t\) gives the intersection point

$$\begin{aligned} \begin{array}{l} \displaystyle u_{own}=\frac{u^p_{opp}-\alpha \beta u^0_{opp} +\beta (u^p_{own}-u^0_{own})}{1-\alpha \beta } \\ \displaystyle u_{opp}=\frac{u^0_{own} - \alpha \beta u^p_{own}+ \alpha (u^0_{opp} - u^p_{opp})}{1 - \alpha \beta } \end{array} \end{aligned}$$
(20)

If this point is feasible, the situation corresponds to the rightmost part in Fig. 3 and the system can proceed to determine a point on the efficient frontier which dominates it. If the point defined by (20) lies outside the feasible region, the two points where the concession paths reach the Pareto frontier can be obtained by model (17) with the necessary modifications to apply it for the other party.

In the case of discrete issue values, an intersection point between both concession paths does not necessarily exist. It is, however, possible to identify two points in the two concession cones which are closest to each other. This problem formulation also allows to consider both the cases of a feasible intersection and the case of no intersection simultaneously.

Denote by \((u_{own}(\mathbf{x}_{own}), u_{opp}(\mathbf{x}_{own}))\) and \((u_{own}(\mathbf{x}_{opp}), u_{opp}(\mathbf{x}_{opp}))\) the two points selected from the focal negotiator’s and the opponent’s concession cone, respectively. The two concession cones are denoted by \(C_{own}\) and \(C_{opp}\). In order to be able to calculate the distance between these two points in a linear programming framework, we use the \(\ell _1\) norm to measure the distance. In general terms, the model to find points in both concession cones which are closest to each other is

$$\begin{aligned} \begin{array}{l} |u_{own}(\mathbf{x}_{own})- u_{own}(\mathbf{x}_{opp})| + |u_{opp}(\mathbf{x}_{own})- u_{opp}(\mathbf{x}_{opp})| \rightarrow \min \\ \mathrm{s.t. } \\ (u_{own}(\mathbf{x}_{own}), u_{opp}(\mathbf{x}_{own})) \in C_{own} \\ (u_{own}(\mathbf{x}_{opp}), u_{opp}(\mathbf{x}_{opp})) \in C_{opp} \\ \mathbf{x}_{own}, \mathbf{x}_{opp} \in X \end{array} \end{aligned}$$
(21)

This can be transformed into a linear programming model:

$$\begin{aligned} \begin{array}{l} z_1 + z_2 \rightarrow \min \\ \mathrm{s.t.} \\ u_{own}(\mathbf{x}_{own})- u_{own}(\mathbf{x}_{opp}) \le z_1 \\ u_{own}(\mathbf{x}_{opp})- u_{own}(\mathbf{x}_{own}) \le z_1 \\ u_{opp}(\mathbf{x}_{own})- u_{opp}(\mathbf{x}_{opp}) \le z_2 \\ u_{opp}(\mathbf{x}_{opp})- u_{opp}(\mathbf{x}_{own}) \le z_2 \\ (u_{own}(\mathbf{x}_{own}), u_{opp}(\mathbf{x}_{own})) \in C_{own} \\ (u_{own}(\mathbf{x}_{opp}), u_{opp}(\mathbf{x}_{opp})) \in C_{opp} \\ \mathbf{x} \in X \end{array} \end{aligned}$$
(22)

If the optimal objective value of model (22) is zero, we have found an intersection point between both concession cones, and a point on the Pareto frontier dominating it can be identified. If the optimal objective value of (22) is strictly positive, \((u_{own}(\mathbf{x}_{own}), u_{opp}(\mathbf{x}_{own}))\) and \((u_{own}(\mathbf{x}_{opp}), u_{opp}(\mathbf{x}_{opp}))\) are two points on the Pareto frontier, which can be communicated to the negotiator to illustrate the possible range in which an efficient compromise could be reached by concessions along the Pareto frontier.

4.3.2 Offer Generation

The main issue in offer generation is to find a point in \(C\) which can be implemented by “nice” issue values. Issue values are nice if they are not too dissimilar to the focal negotiator’s previous offer, or the offer from the opponent, or some combination of the two offers. We therefore use the distance to some reference vector in issue space as the main objective in these models. If the focal negotiator’s own offer is used as a reference vector, this will also lead to comparatively small concessions. It is quite likely that points in the concession cone which can be generated by offers similar to the focal negotiator’s last offer also have utility values similar to that offer and are, therefore, located on or close to the left boundary of the concession cone.

Denote by \(\mathbf{x}^0 = (x^0_1, \ldots , x^0_K)\) the reference vector of issue values for which we want to generate a similar offer \(\mathbf{x} = (x_1, \ldots , x_K)\). To measure similarity, we consider two possibilities: The \(\ell _1\) norm

$$\begin{aligned} \sum _k |x^0_k - x_k | \end{aligned}$$
(23)

and the augmented Tchebycheff norm

$$\begin{aligned} \max _k |x^0_k - x_k| + \rho \sum _k |x^0_k - x_k| \end{aligned}$$
(24)

The \(\ell _1\) norm minimizes the total deviation, but allows for compensation and thus could generate offers which are very different from the previous offer in one issue, and similar or even equal to the previous offer in all other issues. The augmented Tchebycheff norm focuses on the largest change across all issues and thus will generate a more even change in all issues. The correction term in (24) serves to avoid dominated solutions, i.e. offers which deviate more than necessary in issues other than the one with the largest deviation.

For the \(\ell _1\) norm, we can formulate the following (mixed integer) linear programming model:

$$\begin{aligned} \begin{array}{l} \displaystyle \sum _k z_k \rightarrow \min \\ \mathrm{s.t.} \\ \displaystyle x^0_k - x_k \le z_k \; \forall k \\ \displaystyle x_k - x^0_k \le z_k \; \forall k \\ \displaystyle (u_{own}(\mathbf{x}), u_{opp}(\mathbf{x})) \in C \\ \mathbf{x} \in X \end{array} \end{aligned}$$
(25)

The augmented Tchebycheff norm can be implemented through the following model:

$$\begin{aligned} \begin{array}{l} z + \rho \sum _k z_k \rightarrow \min \\ \mathrm{s.t.} \\ z_k \le z \; \forall k \\ x^0_k - x_k \le z_k \; \forall k \\ x_k - x^0_k \le z_k \; \forall k \\ (u_{own}(\mathbf{x}), u_{opp}(\mathbf{x})) \in C \\ \mathbf{x} \in X \end{array} \end{aligned}$$
(26)

Both models (25) and (26) will simultaneously generate a utility vector and an offer in the issue space to implement it. They could be augmented by additional constraints on both vectors, e.g. upper or lower bounds on the concessions a negotiator is willing to make. Such constraints would allow the negotiator to control not only the direction of the concession path (via the parameter \(\alpha \)), but also the step size of movements along that path. In some cases, a small step size (as it is implicitly obtained by minimizing the difference to the focal negotiator’s previous offer) will be advantageous because it avoids large concessions and leaves flexibility to adjust the search direction more often during the process.

While there are clear advantages of small concessions, a lower bound on concessions might be necessary if our model is seen in a dynamic context. By definition of the concession mechanism and parameter \(\alpha \), the utility loss for the party making an offer is smaller than the utility gain for the opponent. The condition of reciprocity, however, is based on the previous loss of utility by the opponent. Therefore, in the next step, a negotiator will only make an offer which increases the opponent’s utility by less than the previous utility increase the party making the offer has received. This would lead to a sequence of gradually decreasing concession steps.

It should be noted that this phenomenon will only occur if both parties exactly make the suggested offers in several steps. We view our approach as decision support rather than as a strict prescription, so we do not expect this to become a serious problem in actual negotiations. However, if our approach is used to simulate negotiations (as in the following numerical example), such a gradual reduction of steps could be observed.

From a technical point of view, this problem could easily be overcome by defining reciprocity in terms of the utility value a party has gained, and require that each party makes a concession that increases the opponent’s utility by the same amount as the party making the offer has gained from the opponent’s previous step. Although one could also claim that this is a reasonable condition for reciprocity, this approach has the major disadvantage of involving a direct comparison of utilities between the parties, which is visible to the party making the offer. Noting how much utility the opponent is gaining from a particular step could allow a party to obtain additional information about the opponent’s preferences, which the opponent might not want to reveal. The way we have defined reciprocity only compares utility values of the opponent, which can be hidden from the party making the offer throughout the process. We therefore suggest to base the definition of reciprocity on a comparison of the opponent’s utility loss and gain, as defined above, and, if necessary, introduce a minimal concession level to avoid the problem of diminishing concession steps.

Other extensions and modifications of the model are also possible. The distance-based approach is not limited to the distance to just one reference point, or to using only one norm. It would also be possible to simultaneously minimize the aggregate distance to several reference points. In the case of the \(\ell _1\) norm, aggregation could be performed by forming the sum of distances to all reference points, an aggregation of the \(\ell _\infty \) norm could consider the maximum difference in any issue to any reference point. It is also possible to present the results of minimizing both norms to the negotiator, who then can choose between several potential offers which are structurally different, but still imply the same effects in terms of utility values. However, when providing such options, one has to be careful to avoid cognitive overload of negotiators.

5 Numerical Example

As an illustration of the approaches presented in last section, we chose the Nelson-Amstore case introduced by Raiffa et al. (2002, Ch.14). Nelson, a construction firm, negotiates with Amstore, a retail chain, to build a new store for them. The three issues to agree upon are price, design and time of completion. In the original version of the case, only discrete values for the three attributes are considered. There are five levels for price, two levels for design and 7 levels for completion time, resulting in a total of \(5 \times 7 \times 2 = 70\) possible alternatives. The marginal utility values for the three attributes are given in Raiffa et al. (2002, p. 250) and the resulting utility values of all 70 alternatives for both parties in Raiffa et al. (2002, pp. 251–252).

To illustrate the application of our models to problems involving continuous issues, we modified the example and considered both price and completion time to be continuous issues. We assume that the marginal value functions for both attributes are piecewise linear and interpolate between the discrete points given in Raiffa et al. (2002, p. 250). The resulting functions are shown in Fig. 5. Design is still considered a discrete issue, for which we also used the original values of Raiffa et al. (2002, p. 250), i.e. Nelson assigns a marginal utility of 20 to the basic design, and Amstore a marginal utility of 10 to the enhanced design, and both assign zero to the respective other deign.

Fig. 5
figure 5

Marginal utility functions for attributes Price and Completion time for both parties in the example

Full size image

For Nelson, price and time are maximizing issues and design is a minimizing one, while Amstore has the opposite preferences. Therefore, the most preferred alternative for Amstore is (10M$, improved, 20d), whereas the most preferred alternative for Nelson is (12M$, basic, 26d). We further assume that the system has complete information about both negotiators’ preferences. See Raiffa et al. (2002) for full information on issue weights and partial utility functions of the two parties in the Nelson-Amstore case.

5.1 Preconditions

There are different preconditions for the two models described above. The prediction model requires concession sizes and is symmetric. Therefore, two offers from each party have to be available. The offer generation model, however, is asymmetric focusing on only one party, from this party only one offer has to be known while two offers of the opponent are required.

We assume that Nelson made the initial offer (12M$, basic, 22d), which yields an utility of \(u^{Nelson}_0=92\) and for the opponent \(u^{Amstore}_0=18\). The counteroffer by Amstore is assumed to be (10M$, basic, 20d) with utilities \(u^{Nelson}=20\) and \(u^{Amstore}=90\). For illustration, we consider two scenarios for both optimization models. First, we assume that the negotiating parties follow a rather aggressive approach choosing \(\alpha \)-values of 0.2, both. In the second example, we assume that both negotiators are more conceding and therefore choose \(\alpha \)-values of 0.6.

5.2 Prediction

We assume the two offers stated above, (12M$, basic, 22d) and (10M$, basic, 20d) respectively are concessions from the optimal alternatives of the two parties, (12M$, basic, 26d) and (10M$, improved, 20d) for Nelson and Amstore, respectively. Figure 6 shows the concession paths for the parameters \(\alpha ^{Amstore}=\alpha ^{Nelson}=0.2\) and \(\tau =0.1\). Table  1 shows the offers and corresponding utility values for this setting. As we can see in Fig. 6, the two negotiators reach the efficient frontier rather quickly at \(x_3^{Amstore}\) and \(x_3^{Nelson}\), respectively. They must increase their \(\alpha \)-values thereafter to generate offers and reach an agreement.

Fig. 6
figure 6

Prediction with \(\alpha ^{Amstore}=\alpha ^{Nelson}=0.2\)

Full size image
Table 1 Issue and utility values for \(\alpha ^{Amstore}=\alpha ^{Nelson}=0.2\)
Full size table

Figure 7 shows the effect of changing the \(\alpha \)-values to \(\alpha ^{Amstore}\) = \(\alpha ^{Nelson}\) = 0.6 (leaving \(\tau \) unchanged at 0.1). The concession paths of the two negotiators now intersect at \(u^{Nelson}_0\) = 60.5 and \(u^{Amstore}_0\) = 64.9. In Table  2 we again see the offers and corresponding utility values under these conditions.

Fig. 7
figure 7

Prediction with \(\alpha ^{Amstore}=\alpha ^{Nelson}=0.6\)

Full size image
Table 2 Issue and utility values for \(\alpha ^{Amstore}=\alpha ^{Nelson}=0.6\)
Full size table

5.3 Offer Generation

As stated above, for the offer generation model it is necessary that the opponent already made a concession. Therefore we consider a similar scenario as above with (12M$, basic, 22d) followed by (10M$, basic, 20d) and Nelson making a concession by proposing (11.5M$, basic, 21d), with corresponding utility values of \(u^{Amstore}=44\) and \(u^{Nelson}=83\). We again present two scenarios using \(\alpha \)-values of 0.2 and 0.6 for both parties, and \(\tau =0.1\) in both scenarios. For the example, we set the minimum concession size in terms of the opponent’s utility to two percent.

Figure 8 shows that negotiators have to make offers along the efficient frontier if they chose a rather aggressive approach. The grey line with black border shows their path to and along the efficient frontier, the dots being the intersection points of their concession paths with the frontier. Table 3 depicts the corresponding issue values and utilities.

Fig. 8
figure 8

Offer generation with \(\alpha ^{Amstore}=\alpha ^{Nelson}=0.2\)

Full size image
Table 3 Issue and utility values for \(\alpha ^{Amstore}=\alpha ^{Nelson}=0.2\)
Full size table

With \(\alpha \)-values of 0.6, negotiators converge but their concession paths do not intersect. Therefore Amstore will accept as soon as Nelson has proposed a more attractive offer than Amstore’s last one. The scenario illustrated in Fig. 9 and Table 4 provides the corresponding issue values and utilities.

Fig. 9
figure 9

Offer generation with \(\alpha ^{Amstore}=\alpha ^{Nelson}=0.6\)

Full size image
Table 4 Issue and utility values for \(\alpha ^{Amstore}=\alpha ^{Nelson}=0.6\)
Full size table

6 Conclusions and Future Research

In this paper, we proposed analytical models that should help negotiators to determine the size of concessions and the actual offers to make. Compared to axiomatic and strategic bargaining models from game theory, which focus on the questions of what points in utility space should be chosen by the negotiators and how this choice can be explained by their dynamic interaction, our approach considers an exchange of offers specified in issue space. Moreover, compared to the MCDM approaches discussed in the literature review, our approach utilizes the more intuitive—and commonly used—concession-based rather than improvement-based negotiation process. Concession sizes in the offer exchange depend on the suggested desirable properties of negotiation processes, i.e. concession-making, reciprocity and value creation. Based on these restrictions in the utility space, the configuration of actual offers is determined in a way that minimize the distance to a reference offer in terms of issue values.

The numerical example in the previous section not only demonstrated the functioning and possible implementation of our model, but also that within one and the same negotiation problem, different combinations of \(\alpha \)-values and opening offers can lead to rather different negotiation processes. This illustrates the flexibility of the proposed approach and the amount of possible control by the negotiator. We plan extensive computational experiments with different parameterizations of the model in a simulation study for sensitivity analysis. This is necessary to gain insights about the precise relationships between model parameters, negotiation processes, and outcomes. For this purpose we will systematically change the combinations of \(\alpha \)- and \(\tau \)-values and opening offers, but also the negotiators’ preferences and thereby the underlying negotiation problem.

A major next step beyond such computational experiments is the actual application of the approach in negotiations involving human negotiators. We envision two possible uses of our approach: It can provide a tool for individual negotiators, e.g. as a component of NSS that would be used by negotiators who need more active advice concerning concession making for (efficient) agreements. Furthermore, the approach can be used as a tool in negotiation research, in particular to implement a negotiation agent that acts as an uniform opponent to reduce variance in negotiation experiments.

As a first step towards the actual use of our approach in (experimental) negotiations, an implementation of the model as part of the NSS NegoIsst (Schoop et al. 2003) is being developed. This implementation will allow us to test the approach in the context of experimental negotiations, to evaluate different design variants (like the use of different norms or reference solutions in the generation of offer proposals), and most importantly, to observe the general attitude of users toward this type of approach. One particular concern in this context is that the system acts as a kind of omniscient observer, who knows the preferences of both sides. Users might either reject advice that is based on information not available to themselves, or they might try to play with the system to extract at least some information about the opponent’s preferences from it. The extent to which such behavior will actually occur can only be determined in experiments with real participants.

Another potential use of our approach is to develop a “uniform opponent” to be used in negotiation experiments. The analysis of experimental results only at the individual level is misleading. As negotiation is a social or joint decision making problem, no party can force an agreement but only the break-off of negotiations. Therefore, when analyzing the results of negotiation experiments, one must consider matching effects, i.e. the influences of the combination of different types of negotiators with different strategies and attitudes towards negotiation. This undesirably adds to the variance of experimental results and to the complexity of the analysis of negotiation experiments. Consider the differences in outcomes when matching e.g. two patient, one patient and one impatient, or two impatient negotiators, this aspect has to be elicited and controlled for in experiments. An even greater challenge is posed by individual and quite fundamental demographic factors like gender, which were found to have influence on negotiation outcomes, but cannot be controlled by e.g. priming of subjects.

Here the concession making model can be used to reduce the variance as one party can be modeled to always follow the same behavior (strategy) by using constant values of \(\alpha \) and \(\tau \) in a programmed response. However, the resulting concession path does not ignore the opponent’s behavior—i.e. it is not a strict sequence of moves to follow—but reflects it through the variable \(\delta \), which will not only vary at different points in time in one negotiation but also between negotiations. If a software agent that follows the model responds to the offers from the actual participant and starts with an extreme opening offer, all data for calculating further offers is available. Therefore, no additional parameterization is necessary. This approach also allows to study the effects of different strategies in a more realistic setting, as it takes into account and adapts to the behavior of the opponent. Furthermore, it makes control of one party easier and less prone to errors than just telling one party to behave according to predefined rules.

Although we therefore see considerable potential for applying the proposed models, they also have some limitations. The optimization models formulated in this paper are all based on the assumption of additive preference functions. However, the assumption of additivity is only required to obtain a linear (or mixed integer linear) optimization model. The approach can thus easily be extended to other types of preference functions by employing nonlinear programming models. The basic requirement that a preference model needs to fulfill for our approach is that the evaluation of each offer can be described by one value. This allows to formulate the requirements on the concession path in similar terms as the utility space we have been using in the present paper. This requirement is fulfilled by all forms of (linear or nonlinear) multi-attribute value functions, and similar approaches. Even some outranking methods used in multicriteria decision aid can generate such scalar evaluations. For example, in the PROMEHTEE method (Brans and Vincke 1985), offers can be evaluated in terms of their net flows, although this evaluation would require information about all possible offers. An interesting approach to use outranking methods in NSS was recently proposed by Wachowicz (2010), who used the ELECTRE Tri sorting method, and represented the evaluation of offers by the index of the class into which they are sorted. Although this evaluation can no longer be represented analytically as a constraint in a standard mathematical programming problem, it probably can be incorporated into our framework by using other optimization techniques. The application of our approach to such different preference models could therefore provide a promising area for future research.

Another direction in which our approach can be extended is the specification of negotiation tactics. Presently, negotiation tactics are represented in the model by one parameter \((\alpha )\). This representation is quite coarse, and future refinements could use a more differentiated approach to represent negotiation tactics. In this way, it should be possible to construct tools that can be fine-tuned by negotiators to support them in the task of generating offers.