Abstract
I conjecture non-zero bare masses for nearly standard-model photons or gluons, derived from quantum-mechanical localization at a cosmological scale. That entails the existence of photon or gluon Bose–Einstein (BE) condensates in a comoving Friedmann–Lemaitre–Robertson–Walker geometry. I derive tantalizing results that set the inter-particle distance in these BE condensates almost at the nucleon scale and a corresponding critical temperature of condensation almost at the end of the quark epoch or the beginning of quark–gluon confinement. My estimates for particle mass and number density in these BE condensates suggest remarkable relations among fundamental constants, \(h, c, G, \Lambda \), at the most microscopic and cosmological scales of quantum and relativity theories.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The theory of quantum mechanics (QM) and quantum fields (QFT) on the one hand, and the theory of general relativity (GR) on the other hand, form the two greatest pillars of modern physical science. Each theory accounts for phenomena on a vast range of scales, where each theory has been confirmed with astonishing precision by experiments and observations conducted with instrumentation of unprecedented sophistication or size. Yet ranges of primary success of each theory do not quite overlap. A unified theory that may encompass ‘all’ scales of the observable universe remains to be conclusively established. That poses more and more formidable challenges, but scientific progress advances relentlessly.
In this paper I examine a relation, based on the uncertainty principle, between the smallest of scales for particle masses and the largest of scales for the size of the observable universe. That leads to the hypothesis that ‘dark energy’ associated with the cosmological constant, \(\Lambda \), may consist of Bose–Einstein (BE) condensates of massive photons or gluons at rest in the freely falling comoving frame of the Friedmann–Lemaitre–Robertson–Walker (FLRW) geometry. I formulate my ideas at an elementary level, although either proving or disproving any aspect of them is far from elementary. Thus I will also provide some introductory context to my formulation.
2 FLRW geometrodynamics
The cosmological principle and observation that our universe is homogeneous and isotropic on a very large scale leads to a relatively simple Robertson–Walker (RW) metric: see, for instance, Ref. [1, p. 362] or Ref. [2, p. 343]. Solutions of correspondingly symmetric Einstein field equations lead to two Friedmann–Lemaitre (FL) equations for the dynamical evolution of the ‘scale factor’ R(t) of the RW metric, as a function of ‘cosmic time’ t: see, for instance, Ref. [1, p. 379] or Ref. [2, p. 355]. I refer to that metric evolution as FLRW geometry or geometrodynamics.
The FL equation for \([{dR}/{dt}]^2\) contains an effective repulsive or ‘anti-gravitational’ potential, \(-c^2 \Lambda R^2 /3\). Einstein’s positive cosmological constant, \(\Lambda \), can be further re-interpreted as resulting from a relativistic ‘perfect fluid’ with a negative pressure or tension, \( p_{\Lambda }\), opposite to the energy density, \(\rho _{\Lambda }\). The ‘dark energy’ density of our accelerating observable universe is currently estimated to be [1, 2]
where \(m_p c^2 \simeq 938\, {{\mathrm {MeV}}}\) represents the proton rest-energy mass. I assume that \(\rho _{\Lambda }\) has remained constant since the end of ‘inflation’ at about \(t \sim 10^{-32} \,{\mathrm{s}}\), although \(\rho _{\Lambda }\) hardly affected the decelerating expansion of R(t) till much later, when it turned into an accelerating expansion around \( 7 \times 10^{9}\) years.
There is no classical analogue of hydrodynamic equations for perfect fluids having \( - p_{\Lambda } = \rho _{\Lambda }\): see, for instance, Ref. [3, p. 298]. However, there is no contradiction with that either, since forces on fluid elements actually derive from pressure gradients. In fact, ‘freely falling outward’ associated with negative pressure in a GR perfect fluid can be understood intuitively and formally in a number of ways, beside direct inspection of the FL equation for \({d^2R}/{dt^2}\): Ref. [2, see pp. 104, 355, 371], for example.
Eventually, the effective repulsive potential \(-c^2 \Lambda R^2 /3\) will dominate the time evolution in the FL equation for \([{dR}/{dt}]^2\). That will approach an exponentially accelerating de Sitter universe, reducing to an event horizon \(\sqrt{3/ \Lambda }\) for all future times [4].
In the FLRW geometry, the average energy density of either baryonic matter, \(\rho _{bm}\), or ‘dark matter,’ \(\rho _{dm}\), scale as \(R^{-3}\), as generally expected for energy-matter densities. However, the ‘dark energy’ density, \(\rho _{\Lambda }\), is a fundamental constant, independent of R. That is why ‘dark energy’ eventually prevails and accelerates the cosmic expansion of R(t).
3 What may contribute to ‘dark energy’
In order to build a bridge between FLRW geometrodynamics and QFT, I conjecture that
Here, \(\lambda _g\) refers to the Compton wavelength of either photons or gluons as described in the standard model (SM) of elementary particles, except for having acquired a certain minimal but still finite mass \(m_g\).
While a Compton wavelength for electrons, \(\lambda _e \simeq 2425 fm\), was originally introduced to characterize their scattering of massless photons, \(\lambda _m = \frac{h}{m c}\) maintains a more general and profound meaning in QFT. Indeed, \(\lambda _m\) enters the uncertainty principle as a localization that entails the creation of a rest mass with energy \(m c^2\), according to special relativity (SR). Correspondingly, \(\lambda _m\) enters explicitly or implicitly most fundamental QM and QFT equations for massive particles and fields.
In Eq. (2), the ‘comparable’ \(\sim \) sign indicates that numerical coefficients, most likely different for photons and gluons, should enter into precise relations if or when quantitative theories are developed. At this stage, connecting through the \(m_g\) mass most fundamental constants of quantum mechanics and relativity, such as h, c and \(\Lambda \), across most microscopic and cosmological scales, provides just a tantalizing clue, somewhat complementary to that of Planck scale, but in the opposite infra-red limit. However, G does not enter directly into Eq. (2), nor does any other coupling constant of electro-weak or strong interactions. Thus, Eq. (2) reflects exclusively a ‘minimal cosmological quantum-localization principle’ for particles physically confined within our observable universe, namely particles that could otherwise be theoretically massless in an infinite Minkowski space-time without scale.
Assuming Eq. (2), the conceivably minimal cosmological rest-energy mass of nearly gauge bosons is of the order of
Upper bounds to the photon rest-energy mass, \(m_{\gamma } c^2\), have been determined by a variety of experiments, observations or inferences, [5,6,7,8,9,10] ranging from \(m_{\gamma } c^2 < 10^{-18} \,{ { \mathrm {eV}}} \) to perhaps even lower limits of galactic origin, yielding \(m_{\gamma } c^2 < 3 \times 10^{-27}\,{{\mathrm {eV}}} \). Whatever the case, any such upper bound remains several orders of magnitude greater than the conceivable minimum of Eq. (3).
A heuristic consideration of Eq. (3) derives from the fact that mass is a continuous variable with physical dimensions and without any apparent quantization. Masses are neither large nor small in the absolute. Mass scaling poses formidable conceptual and technical challenges to renormalization in QFT. A ‘zero mass’ sets no scale and it is not even a mass: it is a ‘zero,’ as in the ideals of mathematics. Any mass is equally and infinitely large compared to ‘zero.’ An ‘infinitesimally small’ or a ‘vanishing’ mass is an entirely different concept. In GR, ‘test particles’ with vanishing mass all follow the same time-like geodesics. Null geodesics are altogether different, although needed to represent a limiting condition. There is however no definitive requirement in GR that exactly massless particles should exist in reality. In fact, Einstein disliked even the concept of ‘particle’ and he finally succeeded with others in proving that geodesic equations ultimately derive from GR field equations [4]. So, in either QFT or GR it would be more consistent to assume that all ‘particles’ have some finite mass, or none would, I suppose.
A powerful principle of local gauge invariance in QFT initially assumes that particles are massless. However, through ingenious mechanisms of symmetry breaking, massive particles are generated, except for photons and gluons, which are maintained as massless gauge bosons in the SM of elementary particles [5, 6]. The SM is a theory developed by many masters over several decades, making remarkable predictions and receiving extraordinary experimental confirmations, including the most recent discovery of a likely Higgs boson, which is indeed responsible for a spontaneous symmetry breaking mechanism of mass generation.
Still, the SM assumes from beginning to end that space and time are perfectly flat and infinite, as in Minkowski space-time. However, the space-time structure of GR is much more complicated, as in FLRW geometrodynamics. In particular, the observable universe appears to have had a beginning and develop finite horizons, while expanding with an acceleration consistent with a GR cosmological term or a ‘dark energy,’ according to the standard model of cosmology or \(\Lambda \)-CDM [1, 2]. Thus, spontaneous symmetry breaking and other theorems in QFT that maintain the existence of massless gauge bosons in the SM cannot definitively rule out a relation such as Eq. (3).
It is often said that electric charge conservation requires massless photons. That is not necessarily so. For instance, Proca-Lagrangian electromagnetic theory for massive vector bosons allows charge conservation upon Lorenz-gauge fixing [7]. However, spontaneous symmetry-breaking of the Higgs model that derives from the original Goldstone theorem maintains exact global-phase gauge invariance and a massless photon in order to provide exact conservation of electric charge [6]. Charge conservation is one of the few remaining symmetries believed to be exact. For example, electron decay has never been observed [11, 12]. Still, minuscule violations of charge or color conservation laws may not be definitively ruled out on a cosmological scale.
Exactly massless photons or gluons are also required to make local gauge QFT’s renormalizable. On the other hand, renormalization theories have already been developed to such a degree of sophistication that it is hard to say whether or not some could be further generalized to accommodate minuscule mass terms violating local gauge invariance on a cosmological scale. In fact, such terms may even help to cut off some infra-red divergencies [5, 6].
It may also be possible to frame Eq. (2) as resulting from some kind of symmetry breaking, [13, 14] with the exact symmetry and a corresponding ‘non-observable’ recovered when \(\Lambda \rightarrow \) 0.
In Einstein’s formulation of SR, constancy of the ‘speed of light’ or ‘celerity,’ c, is a central postulate assumed to yield and hold for all Lorentz transformations of the infinite Minkowski space-time. In particular, constancy of the ‘speed of light’ is needed in SR to synchronize all clocks at rest in any given Lorentzian frame. Yet, SR cannot account for gravity and cannot be globally exact, unless there is no matter nor energy up to infinity. When any of that is introduced anywhere, constancy of the speed of light is valid only as a first-order approximation locally in a freely falling Lorentzian frame. Therein, cosmological corrections to \(c = {{\mathrm {const}}}\) for massive photons would only be of the order of \(\frac{1}{2} {\Lambda \lambda ^2} \simeq 10^{-65}\) for wavelengths \(\lambda \) of visible light, say. Thus, GR also may not definitively rule out a relation such as Eq. (3).
4 BE condensates of photons and gluons
According to Eqs. (1) and (3), there may thus be a BE condensate in the FLRW geometry with a number density
where \(l_P = \sqrt{ \frac{h G}{c^{3}} } \simeq 4 \times 10^{-35}\,{{\mathrm{m}}}\) denotes Planck length.
According to that estimate, the average distance between massive bosons in a BE condensate phase is of the order of
Since the size of nucleons is of the order of 1fm, we expect that quark–gluon confinement begins at that scale, while asymptotic freedom may begin at the scale of 0.1fm. Given cancellations in the tens of orders of magnitude in performing my estimates, it is not so disappointing to find that \(d_g\) is only about 16 times greater than one fermi.
One still has to demonstrate, however, that in BE condensates massive photons or gluons, randomly distributed at rest on the FLRW geometry, slightly attract isotropically one another, thus contributing to the negative pressure \(p_\Lambda = - \rho _{\Lambda }\) associated with ‘dark energy.’ That requires consideration of total symmetrization of a ‘universe wavefunction,’ entirely correlated throughout it. Total wavefunction symmetrization is generally expected to result in effective attractive potentials [15]. However, the global structure of FLRW geometry makes it very difficult to account for extreme long-range correlations while deriving local equations of state in GR.
Presumably, massive gluons are nearly non-interacting in the limit of asymptotic freedom. Yet, gluons carry color charges, except for color singlets. Gluons in color-singlet states are generally excluded, as they would mediate long-range strong interactions among hadrons, which are not observed [5, 6]. Possibly gluon complexes condense in a BE ground state as to minimally attract one another, thus providing the minimal negative pressure required in Eq. (1). However, strong relativistic gluon-gluon or gluon–quark nonlinear interactions generally require consideration of effective masses acquired through dynamical chiral symmetry breaking mechanisms [16]. By contrast, photons carry no electric charge and do not interact with each other. Thus minimal tension in Eq. (1) may more readily derive from effective attraction in the total wavefunction symmetrization for the BE ground state of photons in FLRW geometry.
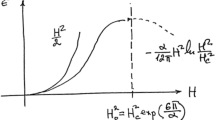
Whatever the case, let us proceed to estimate the critical temperature, \(T_c\), of BE condensation of massive bosons. Assuming for their ordinary phase a nearly relativistic energy-momentum free-particle relation, \(\epsilon \simeq c p\), the density for just about all their excited states at \(z=1\) fugacity is [15]
Here \(g_s = 3\) is the \(S =1\) spin degeneracy for massive bosons and \(\zeta (3) \simeq 1.202\). Equating \(n_{ex}\) to \(n_g\) of Eq. (4) determines the threshold at which bosons begin to condense ‘en masse’ into the ground state. That yields
and a critical temperature
This estimate of massive boson BE condensation reaches to the end of the quark epoch, at about \(10^{-6}\) s and \(10^{12}\) K, when quarks and gluons began to confine and form hadrons. Once again, that provides a tantalizing clue. This massive gluon BE condensate would then behave like that of a near-ideal Bose gas, which differs from its antecedent, a quark–gluon plasma, which is thought to behave like a near-ideal Fermi liquid. Amazingly, both energy regions are already accessible to current accelerators, such as the Large Hadron Collider.
5 Components of ‘dark matter’
All relations and estimates that I derived are based on considerations of ‘dark energy.’ However, they may also have consequences for some components of ‘dark matter.’ Elementary kinematic calculations with my estimates demonstrate that elastic scattering of nearly free photons or gluons in their BE condensates by non-relativistic leptons or quarks may transfer only minimal energies of the order of \(m_g c^2\) to those bosons, because of the enormous mass differential. Some components of dark matter may thus derive from ‘clumping’ in BE condensates of massive photons or gluons around ordinary matter. Alternatively, ‘cold’ non-relativistic bosons could be pulled out of those BE condensates by baryonic matter. Then massive bosons at low energies in their ordinary phase could contribute to some components of dark matter, since ‘dark energy’ could in principle provide virtually unlimited reservoirs for their ordinary phase production. Thus slow-moving photons or gluons could gravitate and orbit along bound time-like geodesics around compact objects, galaxies or clusters of galaxies, contributing to ‘dark matter’ clouds or halos around that ordinary matter.
Other kinds of ultralight bosons further beyond the SM are considered as candidates for dark matter [17]. Perhaps methods of gravitational wave searches devised for their detection around black holes [18] can also be extended to even lighter SM bosons that I propose. Given the precise parameters provided in Eqs. (3) and (4), any number of GR simulations could be run to investigate whether such SM bosons could account for any contribution to ‘dark matter’ structure in the formation of galaxies or clusters of galaxies. However, extensive studies and reviews of ultralight scalars makes them more likely candidates of dark matter components [13].
6 What about gravitons?
Gravitational waves have been extensively demonstrated and recently also directly detected. Gravitational waves propagate virtually at speed c and \(S = 2\) gravitons are presumed to be their carrying quanta. May gravitons also have a mass \(m_g\) of the order required by the ‘minimal cosmological quantum-localization principle’ expressed in Eq. (2)? If they did, gravitons could be ideally ‘cold’ constituents of both ‘dark matter’ and ‘dark energy.’ On the other hand, gravity still appears to be profoundly different from the electro-weak and strong interactions considered in QFT. Whether gravitational waves may or may not propagate exactly at the ‘speed of light’ is a matter for further speculation or inquiry [8, 19].
7 Prospects
Literature regarding scalar field dark matter (SFDM) or fuzzy DM is of particular interest [13, 20,21,22,23]. That may involve a relativistic scalar field theory with gravity, satisfying an Einstein Klein-Gordon equation derived from a corresponding action integral. Particle quanta of the scalar field \(\phi \) are estimated to have a mass of the order of \(m_{\phi } c^2 \sim 10^{-22} \,{{{\mathrm {eV}}}} \), in order to address problems arising from numerical simulations and studies based on standard \(\Lambda \)-CDM models, which predict cusped central halo densities and too many sub-halos and satellite galaxies, contrary to observations. Elaborate theories of BE condensates of SFDM have been developed. Ultra-light scalars, which exists as BE condensates, can behave as a cosmological constant when the mass of the scalar field is small compared to the Hubble parameter, while acting as dark matter when that mass becomes comparable to the Hubble parameter, all in natural units. Still, axions in the most appropriate mass range primarily contribute to dark matter, rather than dark energy [13]. Nevertheless, it may be possible to extend advanced mathematical formulations of SFDM or fuzzy DM theories to a massive vector boson field \(\phi ^{\mu }\) such as I consider to contribute primarily to dark energy: see, for instance, Refs. [97–101] as quoted in Ref. [22]. Such more advanced mathematical formulations are beyond the scope of this paper, but not that of current expertise [13, 20,21,22,23].
8 Conclusions
In conclusion, I have proposed a conjecture of non-zero standard-model photon or gluon bare masses based on quantum-mechanical localization at a cosmological scale. That entails the formation of massive boson Bose–Einstein condensates at rest in a freely-falling comoving Friedmann–Lemaitre–Robertson–Walker geometry. I have derived tantalizing results that set the inter-particle distance in these condensates almost at the nucleon scale and a corresponding critical temperature of condensation almost at the end of the quark epoch or the beginning of quark–gluon confinement. Gluon complexes may have to be considered for their Bose–Einstein ground state, whereas a condensate of single massive free photons may more readily form. More advanced mathematical formulations developed to study scalar field or fuzzy dark matter in particular [13, 20,21,22,23] may be further applied to massive vector boson fields such as I consider to contribute primarily to dark energy.
References
Hobson, M.P., Efstathiou, G.P., Lasenby, A.N.: General Relativity: An Introduction for Physicists. Cambridge University Press, Cambridge (2006)
Schutz, B.F.: A First Course in General Relativity, 2nd edn. Cambridge University Press, Cambridge (2009)
Fetter, A.L., Walecka, J.D.: Theoretical Mechanics of Particles and Continua. McGraw Hill, London (1980)
Rindler, W., Essential Relativity: Special, General, and Cosmological, Revised 2nd Ed., Springer-Verlag, Berlin (1979)
Quigg, C.: Gauge Theories of the Strong, Weak, and Electromagnetic Interactions, 2nd edn. Princeton University Press, Princeton (2013)
Mandl, F., Shaw, G.: Quantum Field Theory, 2nd edn. Wiley, New York (2010)
Jackson, J.D.: Classical Electrodynamics, 3rd edn. Wiley, New York (1999)
Goldhaber, A.S., Nieto, M.M.: Photon and graviton mass limits. Rev. Mod. Phys. 82(1), 939–979 (2010). https://doi.org/10.1103/RevModPhys.82.939. arXiv:0809.1003
Pani, P., et al.: Black-Hole bombs and photon-mass bounds. Phys. Rev. Lett. 109, 131102 (2012). https://doi.org/10.1103/PhysRevLett.109.131102
Dolgov, A.D., Zeldovich, Y.B.: Cosmology and elementary particles. Rev. Mod. Phys. 53(1), 1–39 (1981). https://doi.org/10.1103/RevModPhys.53.1
Nakamura, K., et al.: (Particle Data Group), Review of particle physics. J. Phys. G: Nucl. Part. Phys. 37(7A), 075021 (2010)
Agostini, M., et al.: (Borexino Collaboration) Test of electric charge conservation with Borexino. Phys. Rev. Lett. 115(23), 231802 (2015). arXiv:1509.01223 10.1103
Hui, L., Ostriker, J.P., Tremaine, S., Witten, E.: Ultralight scalars as cosmological dark matter. Phys. Rev. D 95, 043541 (2017). https://doi.org/10.1103/PhysRevD.95.043541. arXiv:1610.08297v2 [astro-ph.CO]
Lee, T.D.: Particle Physics and Introduction to Field Theory (Contemporary Concepts in Physics, Vol. 1), 1st Ed., Harwood Academic Publishers, NY; Particle Physics: Symmetry, Chapter 9, pp. 177–188 (1981)
Pathria, R.K., Beale, P.D.: Statistical Mechanics, 3rd edn. Academic Press, Elsevier (2011)
Aguilar, A.C., et al., Pion and Kaon structure at the Electron-Ion Collider, arXiv:1907.08218v2 [nucl-ex]
Brito, R., et al.: Gravitational wave searches for ultralight bosons with LIGO and LISA. Phys. Rev. D. 96, 064050 (2017). https://doi.org/10.1103/PhysRevD.96.064050. arXiv:1706.06311v2 [gr-qc]
Isi, M., et al.: Directed searches for gravitational waves from ultralight bosons. Phys. Rev. D. 99, 084042 (2019). https://doi.org/10.1103/PhysRevD.99.084042. arXiv:1810.03812v3 [gr-qc]
Arkani-Hamed, N., Georgi, H., Schwartz, M.D.: Effective field theory for massive gravitons and gravity in theory space. Ann. Phys. 305, 96–118 (2003). https://doi.org/10.1016/S0003-4916(03)00068-X. arxiv: hep-th/0210184
Hu, W., Barkana, R., Gruzinov, A.: Fuzzy cold dark matter: the wave properties of ultralight particles. Phys. Rev. Lett. 85, 1158 (2000). https://doi.org/10.1103/PhysRevLett.85.1158. arXiv:astro-ph/0003365
Li, B., Rindler-Daller, T., Shapiro, P.R.: Cosmological constraints on Bose–Einstein-condensed scalar field dark matter. Phys. Rev. D 89, 083536 (2014). https://doi.org/10.1103/PhysRevD.89.083536. arxiv:1310.6061v2
Lee, J.W.: Brief history of ultra-light scalar dark matter models. EPJ Web of Conf. 168, 06005 (2018). https://doi.org/10.1051/epjconf/201816806005;. arXiv:1704.05057v2 [astro-ph.CO]
Lee, J.W.: Characteristic size and mass of galaxies in the Bose–Einstein condensate dark matter model. Phys. Lett. B 756, 166–169 (2016). https://doi.org/10.1016/j.physletb.2016.03.016;. arXiv:1511.06611v2 [astro-ph.GA]
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Resca, L.G. Minimal cosmological masses for nearly standard-model photons or gluons. Gen Relativ Gravit 52, 14 (2020). https://doi.org/10.1007/s10714-020-2663-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10714-020-2663-6