Abstract
Recently Pikovski et al. (Nat Phys 11:668, 2015) have proposed in an intriguing universal decoherence mechanism, suggesting that gravitation may play a conceptually important role in the quantum-to-classical transition, albeit vanishingly small in everyday situations. Here we analyze information transfer induced by this mechanism. We show that generically on short time-scales, gravitational decoherence leads to a redundant information encoding, which results in a form of objectivization of the center-of-mass position in the gravitational field. We derive the relevant time-scales of this process, given in terms of energy dispersion and quantum Fisher information. As an example we study thermal coherent states and show certain robustness of the effect with the temperature. Finally, we draw an analogy between our objectivization mechanism and the fundamental problem of point individuation in General Relativity as emphasized by the Einstein’s Hole argument.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Emergence of the classical world from quantum has been a long standing problem. Theory of decoherence [1, 2] is one of the attempts to resolve it. In the recent paper [3], Pikovski et al. proposed a universal decoherence mechanism due to the gravitational time dilation [4]. Unlike some of the earlier proposals, e.g. due to Diósi [5] or Penrose [6], the mechanism of Pikovski et al. does not require an immediate departure from unitarity. It has generated a lively debate as to weather the effect is real [7,8,9,10] or is it really gravity-related [9, 11]. In this work we will not enter this discussion but rather assume the mechanism of [3] to be true and examine the gravity-mediated information transfer it entails.
Let us recall the idea behind the mechanism of Pikovski et al. [3]. In gravitational field time flows differently depending on the position in the field, which leads to a position-dependent gravitational redshift of frequencies. This effect has been one of the classical tests of general relativity, starting with the experiment of Pound and Rebka [12], and has been recently confirmed over an astonishingly small height difference of 33 cm in the Earth gravitational field [13]. Thus, systems which have some natural frequencies associated with their dynamics, like harmonic oscillators, will effectively couple to the position in the gravitational field. If we now promote this reasoning to the quantum domain, then the position-frequency correlation will in general lead to a position decoherence if (some of) the oscillatory degrees of freedom are left unobserved. This, in turn, will lead to a loss of visibility, if one performs an interferometric experiment, and this loss can be directly related to the proper time difference at different heights. Since the gravitational coupling is weak, the effect requires a macroscopic amount of oscillators \(N\sim 10^{23}\) to obtain reasonable decoherence rates (milliseconds for micrometric height differences) [3]. A surprising aspect of the mechanism of Pikovski et al. is that there is no position information storage in the local oscillator degrees of freedom (which we will simply call the environment) if the latter are initially in a thermal equilibrium. Thus, decoherence happens without a localized which-path information in the sense that a reduced state of any portion of the environment is unchanged by the evolution, and for short times is driven by the internal energy dispersion [3, 14].
However, as pointed out by Zurek [15], decoherence alone is generally not enough for the emergence of such an important aspect of the classical world as its objective character. Briefly speaking, one has to show that during the decoherence process there is a redundant transfer of information into the environment and this information is accessible to multiple observers. Here, we perform such studies in the universal gravitational decoherence model and show that many identical copies of the position information can be deposited in the environment if the latter is in a non-stationary state. Our main tool are the so called Spectrum Broadcast Structures (SBS) [16, 17]—an approach evolved from the quantum Darwinism idea [15, 18] and based on direct studies of, what we call, an extended state. This is a quantum state of the system plus a part of its environment and its analysis goes beyond the standard methods of the decoherence theory (e.g. the Master equation techniques), which deal with the reduced state of the system only. Using the simplified model of [3], we solve for the extended state and show that on short time-scales there are general regimes where it approaches the SBS form. This in turn, implies that the universal gravitational decoherence leads to a redundant position information storage in the environment and hence its objectification [15, 17]. The efficiency of this storage is governed by the Quantum Fisher Information (QFI) (see e.g. [19]), analogously to decoherence being dependent on the energy dispersion [3]. Going beyond the general short-time analysis (cf. [14, 20]), we study in detail an example of the internal degrees of freedom prepared in thermal coherent states and the information transfer efficiency as a function of the temperature. We study the formation of the SBS and as a by-product derive a form of an information gain – disturbance uncertainty relation.
An information storage in the internal degrees of freedom for interference experiments in gravitational field has been already studied, e.g. in [21]. However, the internal degrees of freedom were treated there in a standard for open quantum systems way—were traced out and their effect on the visibility studied. This approach cannot show how exactly information about the system is proliferated in the environment, e.g. if there are many records of the same information being formed and information becomes objective. Here we present a more refined analysis, dividing the internal degrees of freedom into observed and unobserved parts, which allows to study such questions.
Let us also mention that there exist some general results within the quantum Darwinism [22] and SBS [23] approaches concerning, so called, pure decoherence Hamiltonians considered also here, and suggesting that the whole class leads to the emergence of objectivity. However, in the first work, based on quantum Chernoff information, the result is strictly speaking derived only for two-dimensional central systems and is in part based on somewhat heuristic typicality arguments, concerning quantum Chernoff information. Moreover [22] provides no timescales of the objectification process. The second mentioned result [23] is in turn based solely on statistical arguments, the derived time-scales are very general in nature, and is again bounded to finite dimensions only. Thus, to convincingly prove the appearance of objectivity during the universal gravitational decoherence, one has to study the model in more detail from the quantum-information perspective. This is what we do here. We end our work with an intriguing and rather speculative analogy between the gravity-induced information transfer and the, so called, point individuation in General Relativity (see e.g. [24] for a modern review).
2 Extended state dynamics under the universal gravitational decoherence
Let us begin with our main tool—Spectrum Broadcast Structures (SBS). We briefly introduce them below, referring the reader to e.g. [16, 17] for more information. SBS is defined as a multipartite quantum state of the system plus a portion of its environment of the following form:
with
Here \({|i\rangle _{}}\) are the so called pointer states into which the system (the center of mass here) has decohered, \(p_i\) are the initial pointer probabilities, and \(\varrho ^{(k)}_i\) are states of the fragments of the internal degrees of freedom. The condition (2), meaning that the states \(\varrho ^{(k)}_i\) have orthogonal supports for different pointer index i, ensures that they are one shot perfectly distinguishable. This, together with (1), implies that the same state of the decohered CM, labeled by the index i, can be read off from many portions of the environment without any disturbance (on average) to the extended state. This, in turn leads, to a form of an emergent objectivity [15, 17] of the state of the system: all the observers will see the same state of the system without disturbing neither the state nor each other. Conversely, as proved under certain assumptions in [17], it can be shown that demanding objectivity, in the sense of information redundancy and non-disturbance in its extraction, leads to SBS. In this sense SBS are responsible for some form of classicality—the emergent objectivity.
Our main goal is to show that during the universal gravitational decoherence there are regimes such that the extended state of the center-of-mass (CM) of a decohering particle plus a fraction of its internal degrees of freedom (serving as an environment) approaches the SBS form (1)–(2). Following [3], we consider a compound system with a large number of internal degrees of freedom, effectively described by uncoupled harmonic oscillators (e.g. a large molecule), placed in a gravitational filed. We separate the motion into the center-of-mass motion and the internal oscillations. With such a division, the CM is treated as a (virtual) central system and the internal oscillators as its environment. In this work, contrary to the previous studies [3, 9, 14], we will assume that only a part of the internal oscillators can be traced out, while the other is left for an observation. This in fact represents a very common situation of an indirect observation [15] and forces us to study the extended state of the central system plus the observed part of its environment [16, 17]. Assuming applicability of the energy-mass relation to the Klein–Gordon equation in a weak gravitational field and non-relativistic velocities, the corresponding approximate Hamiltonian was derived in [3, 25]:
where \(H_{cm}\) is a center-of-mass Hamiltonian depending on the canonical variables X, P, \(H_0\) is the internal (oscillatory) degrees of freedom Hamiltonian, and \(\Phi (X)\) is the Newtonian gravitational potential. The crucial step is now an assumption that this is a valid Hamiltonian in the 1st quantization too, symbolically \(H_{tot}\rightarrow \hat{H}_{tot}\). Some further simplifications can be made [3]: (i) neglecting \(H_{cm}\) as compared to the rest; (ii) neglecting the special-relativistic kinematical term \(P^2/2M^2c^2\); (iii) assuming a homogeneous gravitational field (e.g. from the Earth) \(\Phi (X)=gX\), where g is the gravitational acceleration. This finally leads to the Hamiltonian:
Let us stress again that although motivated by the field-theoretical arguments [3] this is a quantum mechanical Hamiltonian and we work in the 1st quatization. As we already mentioned, \(H_0\) describes just a collection of N independent oscillators (one can think of degrees of freedom of a large molecule [3]) so that (we neglect the zero-point energy):
This evolution can be easily solved, recalling that \(\Phi (\hat{X})=g\hat{X}\) and writing with the full formality:
where we used the expansions \(\mathbf{1}=\int dX {|X\rangle _{}}{}_{}\langle X|\), \(\hat{X} = \int dX X {|X\rangle _{}}{}_{}\langle X|\). Calculation of the exponential series of the above Hamiltonian is easy due to the orthogonality of the position eigenstates. This finally gives the full system evolution:
where
are the red-shifted frequencies. We apply (7) to an initial state, assumed to be \(\varrho _{tot}(0)=\varrho _0\otimes \bigotimes _i\varrho _{0i}\), and divide the oscillators into two fractions: the observed one of a size \(N_o\) and the unobserved, containing \(N_\perp \) oscillators, \(N_o+N_\perp =N\). The exact sizes are not important for our considerations, apart from \(N_o,N_\perp \) scaling with the total number N (this defines what we call a macrofraction), as we will be tacitly assuming a thermodynamic-type of a limit \(N\rightarrow \infty \) [16]. Tracing the unobserved part of the environment, gives what we call the extended state and what will be our main object of the study:
where \(\varrho _0(X,X')\equiv {}_{}\langle X'|\varrho _0{|X\rangle _{}}\),
and
is what can be called a partial decoherence factor [15]. Unlike in standard approaches to open quantum systems, which is also the case of [3], here it arises due to tracing out only a fraction of oscillators (their number denoted \(N_\perp \)) and not the whole environment. It controls a trace-norm decay of off-diagonal, in the position basis of the CM, operator terms in \(\varrho _{ext}(t)\) [16, 26]. We note that it depends only on the height separation \(\Delta X\equiv X'-X\).
3 General short-time approximation: the role of Quantum Fisher Information and energy dispersion
Let us first perform a short-time analysis [3, 14] for times such that all the phase differences in (11) are small:
or equivalently for times much smaller than the time-dilation induced change of the oscillation periods. This is the basic approximation we will use in the following two Sections. Decoherence factor in this approximation has been found in [3, 14] and reads:
where \(\Delta H_{0i}^2\equiv \hbox {tr}(\varrho _{0i}\hat{H}_{0i}^2) - [\hbox {tr}(\varrho _{0i}\hat{H}_{0i})]^2\) is the variance of the ith oscillator energy, calculated in the initial state \(\varrho _{0i}\). Let us assume that the amount of the unobserved oscillators is very large so that we may use the Law of Large Numbers to write the sum above in a more compact form as an ensemble average over the unobserved oscillators. This is somewhat similar e.g. to the usual introduction of a spectral density to describe the environment [1, 2]. Let the unobserved frequencies \(\omega \) be distributed with some probability \(p_\perp (\omega )\) such that the average \(\langle \langle \Delta H_{0}^2\rangle \rangle \equiv \int d\omega p_\perp (\omega ) \Delta H_{0\omega }^2\) exists (note that in general the initial states are also \(\omega \)-dependent). Then:
giving the decoherence time in a form resembling the energy-time uncertainty relation:
This decoherence time will be within the validity of the used approximation (12) if for all the relevant frequencies \(\omega \) the cumulative energy variance is big enough:
Let us now study the distinguishability conditions (2). The post-interaction states of the internal oscillators (we recall that some of them are left for observation and thus cannot be traced out) read:
We are interested in the information they carry about the position X, as measured by their distinguishability Since \(U^{(i)}_t(X)\) is generated by the red-shifted local Hamiltonian \(\hat{H}_{0i}(X)\), it is obvious that any initial state \(\varrho _{0i}\) preserved by \(\hat{H}_{0i}(X)\), \([\varrho _{0i},\hat{H}_{0i}(X)]=0\), will encode no information at all and this is the situation of [3]. However, here we assume a generic, mixed \(\varrho _{0i}\). As a measure of state distinguishability we choose the state fidelity (also called generalized overlap or Bhattacharyya coefficient) \(B(\varrho ,\sigma )\equiv \hbox {tr}\sqrt{\sqrt{\varrho }\sigma \sqrt{\varrho }}\) [16, 27]. There are of course other measures, for example quantum Chernoff information, providing a tighter than the fidelity upper bound on the probability of discrimination error (see e.g. [28]). However, as we are ultimately interested in a perfect distinguishability (cf. (2)), the weaker character of the bound is not so important as \(B\rightarrow 0\) implies that both quantum Chernoff information and the probability of error vanish (in fact B provides also a lower bound for the probability of error [27]). As B is easier to calculate (no optimization involved, cf. [28]), we choose to work with it. Let us consider the fidelity:
which is a function of the separation \(\Delta X\) only, since the states \(\varrho _t^{(i)}(X)\) differ by an unitary rotation depending on \(\Delta \phi _i\) (12):
For short times (12), we develop B in a series in \(\Delta X\), using first the definition of the Bures distance \(d_B\) [29] \(B(\Delta X)=1-1/2[d_B(\Delta X)]^2\) and then the fact that an infinitesimal Bures distance is given by 1/4 of the quantum Fisher information (QFI) \(F(\varrho _{0i};\hat{H}_{0i})\) [30]. We get the following short-time approximation:
By the famous quantum Cramer–Rao bound, \(F(\varrho _{0i};\hat{H}_{0i})\) sets the lower bound on the precision of the experimental estimation of \(gt\Delta X/(\hbar c^2)\). It thus has a very clear operational meaning and a fundamental importance e.g. for the recently popular field of quantum metrology [31]. \(F(\varrho _{0i};\hat{H}_{0i})\) can be given in terms of the eigenvalues and eigenvectors of the initial state \(\varrho _{0i}=\sum _n \lambda _n {|\lambda _n\rangle _{}}{}_{}\langle \lambda _n|\) as [19]:
We see that if the initial state of the environment \(\varrho _{0i}\) is diagonal in the basis of \(\hat{H}_{0i}\), then obviously \(F(\varrho _{0i};\hat{H}_{0i})=0\) and this degree of freedom is unable to encode position information about the central system as mentioned earlier. This is an example of a general phenomenon—If the environment is prepared in a state stationary w.r.t. the system-environment coupling, the observers will not be able to decode any information about the system using local measurements and thus such state will not get objective in the sense discussed here.
Let us now consider more general, and in many cases more realistic, situation where we allow for a grouping of the states (17) in order to concentrate information they carry. This can be viewed as a sort of a coarse-graining of the internal degrees of freedom [16] and represent a general situation where each observer has access to a subsystem of the environment rather than a single degree of freedom. We thus divide the observed part of the internal oscillators, which we stress is a different part of the environment from the one giving rise to decoherence (11), into a number of smaller fractions, called macrofractions, and denoted \(mac_1, \dots , mac_{\mathcal M}\). For simplicity we will assume them to be all of an equal size \(N_{mac}\), scaling with the total number of the observed degrees of freedom \(N_{mac}\equiv \mu N_{o}\), \(0<\mu <1\). More importantly, we assume \(N_{mac}\) to be large enough to effectively use the Law of Large Numbers (LLN) again [32]. Those fractions may also be thought of as representing macroscopic portions of the environment accessible to multiple observers and can be viewed as reflecting some sort of detection thresholds, e.g. the equipment sensitivity [16, 17]. Macrofraction states are given by the products:
taken over all degrees of freedom in a given macrofraction. Since, crucially, fidelity separates w.r.t. the tensor product, \(B(\bigotimes _i\varrho _i,\bigotimes _i\sigma _i)=\prod _i B(\varrho _i,\sigma _i)\), one easily obtains:
Crucially, the product here is taken over different degrees of freedom than those entering the decoherence factor (11). Here this is a fraction of the observed degrees of freedom, while in (11) those were the unobserved ones. This implies that the behavior of distinguishability \(B^{mac}_t(\Delta X)\) and the partial decoherence factor \(\Gamma _t(\Delta X)\) is in general not correlated (as it would be if both quantities were calculated for the same degrees of freedom when \(|\Gamma ^{mac}_t(\Delta X)|\le B^{mac}_t(\Delta X)\)), since each degree of freedom can have a different dynamics (here—a different frequency \(\omega _i\)) and couple differently to the central system (CM here). Thus, both functions (11) and (23) must be calculated independently [16]. In the short-time regime, we immediately obtain from (20):
Just like before, to make the expression more compact, let us introduce a probability \(p_{mac}(\omega )\) such that the average QFI \(\langle \langle F_{0}\rangle \rangle \equiv \int d\omega p_{mac}(\omega ) F[\varrho _0(\omega );\hat{H}_{0\omega }] \) exists. We note that now this probability is concentrated over the frequencies corresponding to a given macrofraction, which are in general different from the ones that define the decoherence factor. We obtain a formula similar to (14) but with the average variance substituted for the average quantum Fisher information:
The exponential decay of this approximation with \(N_{mac}\) can be viewed as a simple justification for the introduced coarse-graining: while it may happen that the SBS (1)–(2) is not formed on a “microscopic” level of single internal degrees of freedom, it may still be approached at the coarse-grained level of macrofractions. Expression (25) defines the distinguishability time-scale in analogy to the decoherence time-scale (15):
Condition (12) is fulfilled when the cumulative QFI is large compared to the relevant energies:
We note that since \(F(\varrho _{0i};\hat{H}_{0i})\le 4\Delta H_{0i}^2\) [19], \(\tau _{dst}\ge \tau _{dec}\) if we consider \(N_\perp =N_{mac}\). Thus, it is faster to decohere than to concentrate information in the environment (cf. [23]). A brief comment is in order: The formulas (14, 25) are valid for arbitrary initial states of the internal degrees of freedom. In the case of pure initial states, the state fidelity reduces to the state overlap so both expressions become identical functionally, although they depend on different degrees of freedom. Thus, pure initial states, although fully captured by our analysis, are less interesting than mixed ones.
4 Spectrum Broadcast Structure formation for short times
We now study the consequences of the above results for the extended state (9). Our main question is if the state (9) is close to the SBS form (1). We first note that the decoherence and distingushability times strongly depend on the height separation \(|\Delta X|\). One can view (14, 25) from another perspective: For a fixed time t satisfying (12), there are characteristic coherence and indistinguishability lengths:
We want to use this and approximate the double integral in (9) by discrete sums. We fix t, and change the integration variables in (9) to \(\bar{X}\equiv (X+X')/2\) and \(\Delta X=X'-X\) so that \(X=\bar{X}-\Delta X/2\), \(X'=\bar{X}+\Delta X/2\), and:
Then, since \(\Gamma _t(\Delta X)\approx 0\) for \(|\Delta X |>\Delta X_c\), we can limit the \(\Delta X\) integration range and obtain:
We now Taylor-expand the integrand in \(\Delta X\), treating it as a small quantity. This can be done for the functions \(\varrho _0\left( \bar{X}-\Delta X/2,\bar{X} +\Delta X/2\right) \), \(\Gamma _t(\Delta X)\) and the operator \(\hat{U}^{(i)}_t(\bar{X}-\Delta X/2)\) as they are all analytic functions of their arguments, but not with the vectors \({|\bar{X}-\Delta X/2\rangle _{}}\). Thus, in the leading order the integral (33) reads:
(we note that the contribution from the integration range \(\bar{X} \sim \Delta X\) is of the order of \(\Delta X_c^2\) and is thus included in the last term). We now make use of the condition (31). We break the first integral into intervals of equal lengths \(\Delta X_d\), centered at some points \(\bar{X}_k\):
where \(\Delta \bar{X}\) is the integration variable inside each interval. Assuming \(\Delta X_d\) to be small, we may repeat the above approximation, expanding everything that is smooth in \(\bar{\Delta } X\) and keeping the lowest term. We obtain:
where \(p_0(X)\equiv \varrho _0(X,X)={}_{}\langle X| \varrho _0{|X\rangle _{}}\) and we used (17). Changing once again the integration variables to sum and difference of \(\Delta X, \Delta \bar{X}\), \(\Delta _\pm \equiv (\Delta X \pm \Delta \bar{X})/2\):
we obtain:
where \(\bar{\Delta }\equiv (\Delta X_c+\Delta X_d)/2\). Note that the integrals in \(\Delta _\pm \) are separated now which allows us to introduce the smeared position states:
Using them and the partition of \(N_o\) into the macrofractions, we can finally rewrite (38) as:
The macrofraction states \(\varrho _t^{mac}(\bar{X}_k)\) are by the above construction almost perfectly distinguishable for different \(\bar{X}_k\), since their separation is \(\sim \Delta X_d\). Thus, the CM position is decohered to within \(\bar{\Delta }\) and is stored in the internal degrees of freedom in many identical copies. The structure (40) is a version of the Spectrum Broadcast Structure for continuous variables. Please note its coarse-grained character in the variable X. Our analysis here is somewhat heuristic. Mathematically rigorous proof would consist in showing how fast the actual extended state approaches some ideal SBS depending on the decoherence and the fidelities. We will postpone this non-trivial mathematical question to a more specialized publication, pointing that for finite dimensional systems this question was solved in [26]. It is shown there that indeed the trace distance of the actual extended state to some ideal SBS is bounded by the decoherence factor and the macroscopic fidelities.
5 An example of information encoding: displaced thermal environments
As an illustration of the above general reasoning, we consider the the internal degrees of freedom to be prepared in thermal coherent states:
where \(\hat{D}(\alpha )\) is the displacement operator (assumed here the same for all the oscillators) and \(\varrho ^{(i)}_{th}\equiv \text {e}^{-\beta \hat{H}_{0i}}/Z_i\), \(Z_i\equiv \hbox {tr}(\text {e}^{-\beta \hat{H}_{0i}})\), \(\beta \equiv 1/(kT)\). Those states no longer commute with \(\hat{H}_{0i}\) and we have:
where \(\langle \hat{A}\rangle _{th}\equiv \hbox {tr}(\varrho _{th}\hat{A})\) and \(\mathrm {cth(\cdot )}, \mathrm {th(\cdot )}\) stand for the hyperbolic cotangent and the hyperbolic tangent respectively. As a digression, we note that the reciprocal dependence on the temperature of the non-thermal parts above, leads to a formal relation:
In light of the short-time expressions (13) and (20), it may be interpreted as a type of an information gain-versus-disturbance relation (cf. e.g. [33]). Here, the disturbance to the central system (in a form of a non-thermal contribution to the decoherence) is characterized by \(\Delta H_{0i}^2-(\Delta H_{0i}^2)_{th}\), while the environment information gain by \(F(\varrho _{0i};\hat{H}_{0i})\). The meaning of (44) here is that the hotter the environment is, the stronger is its decohering power but the lesser is its information capacity [34]. One should stress that (44) applies only for a specific case of displaced thermal states. Its validity and form for more general states and relation to known results of a similar kind [21] will be studied elsewhere.
One can go beyond the above short-time analysis and give a compact and exact expressions for \(|\Gamma _t(\Delta X)|\) and \(B_t(\Delta X)\) for arbitrary times. A direct calculation for a single band \(\omega _i\) leads to:
where \(|\Gamma ^{th}_t(\Delta X)|\equiv [1+2\bar{n}_i(\bar{n}_i+1)(1-\cos \Delta \phi _i)]^{-1/2}\), \(\bar{n}_i\equiv \langle \hat{n}_i\rangle _{th}\). Calculation of \(B^i_t(\Delta X)\) is more involved, we perform them in “Appendix A”, where we find:
The above single-band functions are periodic in time (hidden in \(\Delta \phi _i\) (12)) and obviously there is no SBS formation at the level of single environments. However, for macrofractions, described by a collection of randomly distributed \(\omega _i\) [34], the corresponding decoherence and fidelity factors become quasi-periodic functions of time:
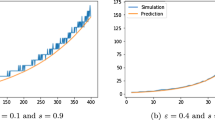
and the random phases \(\Delta \phi _i\) may lead to their effective damping. This, however, depends on the temperature (apart from the other factors kept fixed) as e.g. for a high temperature \(\frac{k_BT}{\hbar \omega _i}\rightarrow \infty \), \(|\Gamma _t^i(\Delta X)|=O\left( \frac{\hbar \omega _i}{k_BT}\right) \) while \( B_t^i(\Delta X)=1-O\left( \frac{\hbar \omega _i}{k_BT}\right) \). For a low temperature in turn, the initial states (41) become pure and \(B_t^i(\Delta X)=|\Gamma _t^i(\Delta X)|\), which follows from \(B({|\psi \rangle _{}}{}_{}\langle \psi |, {|\phi \rangle _{}}{}_{}\langle \phi |)=|\langle \psi |\phi \rangle |\). An example of the intermediate regime \(k_BT\approx \hbar \omega _i\) is shown in Fig. 1 . We see that for big enough macrofraction sizes (cf. [20]), both decoherence factor and fidelity decay, indicating the SBS formation. We note a very long, compared to usual decoherence times, time-scale of this process, caused by the weak nature of the gravitational coupling. The times become much shorter for macroscopic (\(N\sim 10^{23}\)), rather than mesoscopic fraction sizes.
(Color online) Time dependencies of \(|\Gamma _t(\Delta X)|\) (green dotted line) and \(B_t(\Delta X)\) (solid magenta) for intermediate temperatures \(T=10\)K (\(k_BT\approx 3\hbar \omega _{max}\)). Plot a shows a single-oscillator case, where the observed and the unobserved fractions consist of a single oscillator each. The unobserved (traced out) oscillator has a frequency of \(\omega _\perp =3.6\times 10^{11}\hbox {s}^{-1}\), while the observed one \(\omega _o=4.9\times 10^{11}\hbox {s}^{-1}\), which clearly demonstrate that they couple differently to the center of mass and it is possible that \(|\Gamma _t(\Delta X)|\approx 1\), but \(B_t(\Delta X)<1\). Plot b shows \(N_\perp =N_{mac}=10^3\) random oscillators, drawn independently for the observed and the unobserved fractions from an uniform distribution over \([1\dots 5]\times 10^{11}\hbox {s}^{-1}\). The other parameters are \(\Delta X=10^{-6}\)m, \(|\alpha |=1\), common to both plots. Note the extremely long decay times in (b) due to the small macrofraction sizes as compared to the gravitational interaction strength
6 Conclusions
We have analyzed information transfer to the internal degrees of freedom during the universal gravitational decoherence of [3], using the recently developed methods of Spectrum Broadcast Structures [16, 17]. We have shown that generically, on short time scales there is an SBS formation, implying a redundant encoding of the center-of-mass position in the internal degrees of freedom during the decoherence. Importantly, we have derived the relevant time-scales of the process, given by the energy dispersion and the Quantum Fisher Information. The role of the latter in the SBS formation have not been recognized before. The resulting SBS has a natural coarse-grained structure, appropriate for the continuous variable case, reflecting finite coherence and distinguishability lengths.
Going beyond the short-time analysis, we have analyzed the case when the internal degrees of freedom are prepared in a displaced thermal states. This breaks the symmetry with respect to the free internal evolution and allows for the information encoding in the environment, unlike in the purely thermal case of [3]. We have shown that for big enough macrofraction sizes, there are temperature regimes where the SBS is being formed. As a by-product of this analysis we have derived a form of an information gain-versus-disturbance relation (44).
We finish with some speculations on the analogy between the above information transfer process and the, so called, point individuation in General Relativity. As emphasized by the famous Einstein’s Hole argument, active diffeomorphism invariance of General Relativity forbids assigning a physical meaning not only to coordinate charts but to very (mathematical) manifold points as well. This has led to a still active debate over the ontology of space-time and physical objectivity of space-time points [24, 35]. A way out of the situation is to define space-time points using coincidences of matter, e.g. as intersection points of particles’ world-lines. This process is called space-time point individuation (or objectivization), and the degrees of freedom used are called individuating fields. The peculiarity of the theory is that individuation can be in principle achieved in a fully dynamical way by the metric field itself, provided it satisfies the Einstein equations [36, 37].
On the other hand, the SBS structure (40) encodes a certain form of point objectivity as well: Indirect observation of the position through any of the environmental macrofractions will always give the same result \(\bar{X}_k\), leaving the CM located around \(\bar{X}_k\) and without any disturbance, on average, to the global state. This observer-invariance and non-disturbance (which may be viewed as a type of a time-invariance) can be taken as a basis of an operational definition of objectivity [15], in this case of the (approximate) position. Moreover, it can be shown that under some general assumptions the only state structure compatible with so defined objectivity is precisely the SBS [17] and that it is generic for macroscopic quantum measurements [23]. An intriguing question thus arises if the gravitational decoherence mechanism may also lead, through the SBS, the the point individuation? This would be an example of a quantum individuation.
There are of course some obvious differences. First of all, described here gravity-generated SBS provides objectivization of points of space only, not of space-time events (see however [6]). But we have used just a first correction to the non-relativistic Schrödinger equation [25] rather than e.g. Tomonaga–Schwinger evolution law, which could be a future direction. Second, by the very construction there is a finite precision (28) and resolution (29) with which a point can be localized. Both of these parameters parameters improve with the macrofraction size, which suggests that objective points may be macroscopic phenomena and the objectivity breaks down at some microscopic scales (cf. macro-objectivity idea [38]). Answers to these questions may shed some light on what happens with the space-time at microscopic scales.
References
Joos, E., Zeh, H.D., Kiefer, C., Giulini, D.J.W., Kupsch, J., Stamatescu, I.-O.: Decoherence and the Appearance of a Classical World in Quantum Theory. Springer, Berlin (2003)
Schlosshauer, M.: Decoherence and the Quantum-to-Classical Transition. Springer, Berlin (2007)
Pikovski, I., Zych, M., Costa, F., Brukner, Č.: Universal decoherence due to gravitational time dilation. Nat. Phys. 11, 668 (2015)
Misner, C.W., Thorne, K.S., Wheeler, J.A.: Gravitation. W. H. Freeman, San Francisco (1973)
Diósi, L.: A universal master equation for the gravitational violation of quantum mechanics. Phys. Lett. A 120, 377 (1987)
Penrose, R.: On gravity’s role in quantum state reduction. Gen. Relativ. Gravit. 28, 581 (1996)
Bonder, Y., Okon, E., Sudarsky, D.: Questioning universal decoherence due to gravitational time dilation. Nat. Phys. 12, 2 (2016)
Bonder, Y., Okon, E., Sudarsky, D.: Can gravity account for the emergence of classicality? Phys. Rev. D 92, 124050 (2015)
Diósi, L.: Centre of mass decoherence due to time dilation: paradoxical frame-dependence (2015) arXiv:1507.05828
Pikovski, I., Zych, M., Costa, F., Brukner, Č.: Time dilation in quantum systems and decoherence: questions and answers (2015) arXiv:1508.03296
Pang, B.H., Chen, Y., Khalili, F.Y.A.: Universal decoherence under gravity: a perspective through the equivalence principle. Phys. Rev. Lett. 117, 090401 (2016)
Pound, R.V., Rebka Jr., G.A.: Apparent weight of photons. Phys. Rev. Lett. 4, 337 (1960)
Chou, C.W., Hume, D.B., Rosenband, T., Wineland, D.J.: Optical clocks and relativity. Science 329, 1630 (2010)
Adler, S.L., Bassi, A.: Gravitational decoherence for mesoscopic systems. Phys. Lett. A 380, 390 (2016)
Zurek, W.H.: Quantum Darwinism. Nature 5, 181 (2009)
Korbicz, J.K., Horodecki, P., Horodecki, R.: Objectivity in a noisy photonic environment through quantum state information broadcasting. Phys. Rev. Lett. 112, 120402 (2014)
Horodecki, R., Korbicz, J.K., Horodecki, P.: Quantum origins of objectivity. Phys. Rev. A 91, 032122 (2015)
Brandao, F.G.S.L., Piani, M., Horodecki, P.: Generic emergence of classical features in quantum Darwinism. Nat. Commun. 6, 7908F (2015)
Tóth, G., Apellaniz, I.: Quantum metrology from a quantum information science perspective. J. Phys. A Math. Theor. 47, 424006 (2014)
Zych, M., Pikovski, I., Costa, F., Brukner, Č.: General relativistic effects in quantum interference of “clocks”. J. Phys. Conf. Ser. 723, 012044 (2016)
Zych, M., Costa, F., Pikovski, I., Brukner, : Quantum interferometric visibility as a witness of general relativistic proper time. Nat. Commun. 2, 505 (2011)
Zwolak, M., Riedel, C.J., Zurek, W.H.: Amplification, redundancy, and quantum Chernoff information. Phys. Rev. Lett. 112, 140406 (2014)
Korbicz, J.K., Aguilar, E.A., Ćwikliński, P., Horodecki, P.: Generic appearance of objective results in quantum measurements. Phys. Rev. A 96, 032124 (2017)
Stachel, J.: The hole argument and some physical and philosophical implications. Living Rev. Relativ. 17, 1 (2014)
Lämmerzahl, C.: A Hamilton operator for quantum optics in gravitational fields. Phys. Lett. A 203, 12 (1996)
Mironowicz, P., Korbicz, J.K., Horodecki, P.: Monitoring of the process of system information broadcasting in time. Phys. Rev. Lett. 118, 150501 (2017)
Fuchs, C.A., van de Graaf, J.: Cryptographic distinguishability measures for quantum-mechanical states. IEEE Trans. Inf. Theory 45, 1216 (1999)
Calsamiglia, J., Muñoz-Tapia, R., Ll, Masanes, Acin, A., Bagan, E.: Quantum Chernoff bound as a measure of distinguishability between density matrices: application to qubit and Gaussian states. Phys. Rev. A 77, 032311 (2008)
Bengtsson, I., Życzkowski, K.: Geometry of Quantum States: An Introduction to Quantum Entanglement. Cambridge University Press, Cambridge (2016)
Braunstein, S.L., Caves, C.M.: Statistical distance and the geometry of quantum states. Phys. Rev. Lett. 72, 3439 (1994)
Giovannetti, V., Lloyd, S., Maccone, L.: Advances in quantum metrology. Nat. Photon 5, 222 (2011)
This coarse graining, introduced in the present context in [16], is analogous to e.g. description of liquids: Each point of a liquid (a macro-fraction here) is in reality composed of a suitable large number of microparticles (individual oscillators). Same technique is also used in a mathematical approach to von Neumann measurements using, so called, macroscopic observables; see e.g. Sewell G 2015 On the mathematical structure of quantum measurement theory. Rep. Math. Phys. 56, 271 and the references therein
Buscemi, F., Hayashi, M., Horodecki, M.: Global information balance in quantum measurements. Phys. Rev. Lett. 100, 210504 (2008)
Tuziemski, J., Korbicz, J.K.: Dynamical objectivity in quantum Brownian motion. EPL (Europhys. Lett.) 112, 40008 (2015)
Callender, C., Huggett, N. (eds.): Physics Meets Philosophy at the Planck Scale: Contemporary Theories in Quantum Gravity. Cambridge University Press, Cambridge (2001)
Stachel, J., in Earman, J., Janis, I., Massey, G.J., Rescher, N. (eds.): Philosophical Problems of the Internal and External Worlds, Essays on the Philosophy of Adolf Grünbaum, University of Pittsburgh Press, Pittsburgh (1993)
Lusanna, L., Pauri, M.: Explaining Leibniz-equivalence away: dis-solution of the hole argument and physical individuation of point. Stud. Hist. Philos. Mod. Phys. 37, 692 (2006)
Tuziemski, J., Korbicz, J.K.: Objectivisation in simplified quantum Brownian motion models. Photonics 2(1), 228 (2015)
Acknowledgements
We would like to thank K. Rzążewski, R. Horodecki and P. Horodecki for discussions. We acknowledge the financial support of the John Templeton Foundation through the Grant ID #56033.
Author information
Authors and Affiliations
Corresponding author
Appendix A. Fidelity for displaced thermal states
Appendix A. Fidelity for displaced thermal states
Here we calculate \(B[\varrho _t^{(i)}(X),\varrho _t^{(i)}(X')]\), where
\(\varrho _{0i}=\hat{D}(\alpha )\varrho ^{(i)}_{th}\hat{D}(\alpha )^\dagger \) is the displaced thermal state and \(U^{(i)}_t(X)=\text {exp}[-i\omega _i(X)t\hat{n}_i]\). We start by rewriting the state as
To arrive at the above expression we inserted in (A.1) the resolution of identity \(I= U_t^{(i)}(X)^\dagger U_t^{(i)}(X)\) between the left displacement operator and the state and its conjugate version between the state and right, conjugated, displacement operator. Then we used the fact that: (i) the unitary commutes with the thermal state (ii) \( U_t^{(i)}(X) \hat{D}(\alpha ) U_t^{(i)}(X)^\dagger = \hat{D}(\alpha e^{-i\omega _i(X)t} )\). Dropping dependence on i and using (A.1) we obtain:
where
and we have pulled the extreme left and right displacement operators out of both the square roots and used the cyclic property of the trace to cancel them out. The phase factors resulting from composition of remaining displacement operators cancel out as both unitary operators under the square root are Hermitian conjugates of each other. Next, we use the corresponding P-representation for the middle \(\varrho _{th}\) under the square root in (A.3):
where \(\bar{n}=1/(e^{\beta \omega }-1)\), \(\beta \equiv \hbar /(k_B T)\). Indicating the Hermitian operator under the square root in (A.3) by \(\tilde{B}_t\), we obtain:
The next step is to calculate explicitly the square root in the equation above. For this aim we expand \(\rho _0\) in the Fock basis:
Replacing it in Eq. (A.6) we have:
with:
Using the Fock basis \({|j\rangle _{}}\) representation of coherent states one may explicit the scalar product \(\langle j|\gamma +\eta _t\rangle \). Accordingly Eq. (A.8) gets:
We now show that this equation is formally equivalent to that of a thermal state introduced in Eq. (A.5). For this aim, we underline that we are interested in the square root of the operator \(\tilde{B}_t\), rather than in itself. Therefore, there is a freedom of rotating \(\tilde{B}_t\) by a unitary operator, and in particular a displacement one:
In particular we find:
where we have omitted the irrelevant phase factor arising from the action of the displacement. We replace Eq. (A.12) into Eq. (A.10). Dropping displacement operators due to Eq. (A.11) and introducing the variable:
one obtains:
In order to calculate explicitly the square root we recall the Fock expansion in Eq. (A.7). Finally, we get:
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Korbicz, J.K., Tuziemski, J. Information transfer during the universal gravitational decoherence. Gen Relativ Gravit 49, 152 (2017). https://doi.org/10.1007/s10714-017-2319-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10714-017-2319-3