Abstract
As the Earth system is exposed to large anthropogenic interferences, it becomes ever more important to assess the resilience of natural systems, i.e., their ability to recover from natural and human-induced perturbations. Several, often related, measures of resilience have been proposed and applied to modeled and observed data, often by different scientific communities. Focusing on terrestrial ecosystems as a key component of the Earth system, we review methods that can detect large perturbations (temporary excursions from a reference state as well as abrupt shifts to a new reference state) in spatio-temporal datasets, estimate the recovery rate after such perturbations, or assess resilience changes indirectly from stationary time series via indicators of critical slowing down. We present here a sequence of ideal methodological steps in the field of resilience science, and argue how to obtain a consistent and multi-faceted view on ecosystem or climate resilience from Earth observation (EO) data. While EO data offers unique potential to study ecosystem resilience globally at high spatial and temporal scale, we emphasize some important limitations, which are associated with the theoretical assumptions behind diagnostic methods and with the measurement process and pre-processing steps of EO data. The latter class of limitations include gaps in time series, the disparity of scales, and issues arising from aggregating time series from multiple sensors. Based on this assessment, we formulate specific recommendations to the EO community in order to improve the observational basis for ecosystem resilience research.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Article Highlights
-
Substantial differences exist in defining vegetation “resilience” and its estimators, creating sometimes unnecessary uncertainty
-
Progress has been made in constructing indicators of resilience, but there are underappreciated caveats associated with the measurement process of Earth observations
-
Novel developments and increasing diversity in datasets from Earth observations, in combination with theoretical insights, can help to improve resilience monitoring from space
1 Introduction
Concerns have been raised that different terrestrial ecosystems might respond to ongoing anthropogenic climate and land-use change with abrupt and potentially catastrophic regime shifts. Indeed, several vegetation ecosystems, such as the Amazon and other tropical rainforests, but also drylands or boreal forests, have been suggested to be potential Earth system tipping elements (Lenton et al. 2008; Armstrong McKay 2022; Boers et al. 2022). To reliably project the future fate of terrestrial ecosystems and to assess the risk of local- to regional-scale regime transitions it is crucial to be able to measure their resilience based on empirical spatiotemporal data.
The resilience of an ecosystem is often qualitatively defined as the ability of the system to cope with disturbances, where a disturbance is “any relatively discrete event in time that disrupts ecosystem, community, or population structure and changes resource pools, substrate availability, or the physical environment” (White and Pickett, 1985). Disturbances are usually induced by anthropogenic or natural discrete events which act to perturb a system away from its dynamic equilibrium, after which the system gradually recovers. In principle, disturbances do not necessarily have to be extreme or rare, though practically they need to be large and rare enough to be distinguished from the normal variability of the system.
We note that, in this review, “equilibrium” refers to any state of the system that does not show significant changes in its properties over time, except when external forces impose a change. A special case of an equilibrium is a fixed point x* where the evolution operator f of an autonomous dynamical system dx/dt = f(x) becomes 0, i.e., f(x*) = 0 (for example, see Kuznetsov 2004). Under more complicated conditions with time varying forcing, one can define a “pullback attractor” to which the system converges when the initial condition is applied at a time point shifted infinitely into the past (Chekroun et al. 2011). This perspective of equilibrium is purely mathematical and differs from the concept of thermodynamic equilibrium in physical systems, which refers to a state of maximum entropy for a given set of constraints.
From a dynamical systems perspective, a local and a global notion of resilience can be distinguished (Holling 1973; Krakovská et al 2023). The local perspective applies close to an equilibrium state and defines resilience as the recovery rate after a perturbation (e.g., Smith et al. 2022). Such a perturbation could be a single disturbance event. If the perturbation is small, and the reference state is a stable equilibrium in the sense of dynamical systems theory, this definition of resilience is the fixed point’s stability, expressed by the eigenvalue of the slowest mode of recovery (Holling 1973). This equilibrium-based notion of resilience has been coined as “engineering resilience” (Pimm 1984).
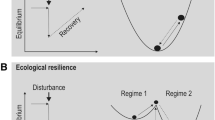
In contrast, the global perspective defines resilience by how large a perturbation must be for the system to not recover from it at all. In dynamical systems terms, this non-equilibrium based definition refers to the width of a basin of attraction, or “ecological resilience” (Holling 1973) and is sometimes also called “latitude” (Walker et al. 2004). Figure 1 illustrates these two perspectives of resilience with a widely used analogy, where the system’s state is represented by a ball in a potential landscape.
These two views of resilience are not unrelated. A system can only display engineering resilience if it also has ecological resilience regarding a disturbance (Fig. 2, case 1). Environmental change (captured as a slowly changing parameter in models) can reduce the width of the basin and at the same time make it less steep around the equilibrium. As a consequence, the system is more vulnerable to disturbances, first in the sense that it shows a smaller recovery rate, and second in the sense that these disturbances can tip the system to an alternative state (Fig. 2, case 2). In the extreme case, the whole basin and with it the stable equilibrium disappears at a so-called bifurcation point (Fig. 2, case 3). At this point, both ecological resilience (basin width) and “engineering” resilience (recovery rate) would decrease to zero. Consequently, indicators measuring “engineering resilience”, which are closely related to the concept of critical slowing down (CSD), are often referred to as “early warning signals” of abrupt shifts associated with a loss of ecological resilience (Scheffer et al. 2009). It is, however, a common misconception to believe that resilience monitoring (in the sense of measuring changes in engineering resilience) would only be informative if alternative equilibria existed; even when alternative equilibria do not exist, the engineering resilience measures the recovery capacities of the system. This also means that CSD indicators alone do not provide any informative value on the existence of alternative equilibria (Kéfi et al. 2013).
Idealized cases of abrupt events and how they are related to different kinds of resilience, and resilience indicators. case I (blue): A large external state perturbation happens, and thereafter the system recovers gradually. The recovery time measures “engineering resilience”. case II (yellow): A similar event occurs but this time the external shock is larger (or the resistance of the system smaller), so that the system does not show “ecological resilience”, i.e.,, it does not return to the previous state. case III (red): A gradual parameter change drives rapid change in the system because it crosses a bifurcation point where the old equilibrium disappears
Another quantifier of resilience which to some degree integrates the above two views can be defined based on mean first exit times from a given basin of attraction to the basin of attraction of an alternative equilibrium (Ciemer et al. 2019; Arani et al. 2021). A given state is naturally more resilient in this sense if the expected first passage time to the alternative basin is longer. To first approximation, the resilience in terms of mean first exit times depends on the width and depth of the basin of attraction, as well as on the strength of the noise. This quantifier of resilience can be called global in distinction to the local concept of engineering resilience. For an excellent in-depth review of different concepts of ecosystem resilience we refer to Dakos and Kéfi (2022).
In this review, we focus on terrestrial ecosystems and how to measure changes in their resilience to disturbances under increasing anthropogenic pressures, as an important field of application for Earth observation (EO) systems. The motivation for this article is to work out major conceptual as well as practical caveats that need to be addressed before the value of novel and better resolved EO data can be manifested in monitoring resilience (and changes thereof) in the Earth system. While recent studies have argued for enhanced and improved resilience monitoring, highlighting specific examples (Lenton et al. 2022; Lenton et al. 2024), we here discuss in more detail regarding the conceptual, practical and computational challenges of data analysis, in light of the most recent literature.
Some of the discussed caveats are not exclusive to EO data, but all of them are important to consider in EO-based resilience monitoring. Our intention is (i) to make “data users” (e.g., Earth system modelers and dynamical systems experts) aware of these challenges and of arising opportunities, and (ii) to make “data producers” (e.g., remote sensing experts) more aware of the specific requirements that resilience monitoring implies for the data. We believe that both would contribute to more meaningful resilience assessments by future studies. The majority of work discussed in this article focuses on engineering resilience and the closely related concept of CSD; first, because there are arguably more observed examples of disturbance and recovery than examples of crashes without recovery, and second because it is less clear how to accurately define/measure ecological resilience mathematically and in practice.
We will first (Sect. 2) discuss the conceptual challenges associated with resilience quantification. After that, we focus on the practical problems related to estimating ecosystem resilience from EO data. To this end, we review how engineering resilience has been measured in practice using two different approaches.
The first approach (Sect. 3) is by computing properties of the recovery process after single large perturbations. This includes methods that detect disturbances in time series (Sect. 3.1) and methods that quantify recovery rates after such disturbances (Sect. 3.2). This can be considered the direct way to estimate the recovery rate and thus engineering resilience.
The second approach (Sect. 4) is to infer engineering resilience indirectly, from the normal variability of the system as it is permanently adjusting to many small perturbations. The fact that the recovery rate can be inferred from natural variability is suggested by theoretical insights, such as those from the theory of stochastic dynamical systems (Kuehn 2011) and the fluctuation–dissipation theorem (Kubo 1966). These theoretical relationships have only recently been empirically validated in vegetation ecosystems (Smith et al. 2022; Smith and Boers 2023a, 2023b). The major advantage of this second approach is that it allows to measure resilience everywhere and not only where large perturbations have occurred, and continuously in time. We discuss metrics to measure resilience indicators from permanent fluctuations (Sect. 4.1), and ways to cope with long-term trends and seasonality (Sect. 4.2) and spatially and mechanistically complex ecosystems (Sect. 4.3).
In Sect. 5, we discuss future opportunities and challenges for resilience monitoring using EO data. As more and more data with higher and higher resolutions from different sensors is becoming readily available, the vision to monitor vegetation resilience from EO data can be seen as a Big Data challenge. However, this requires both meaningful measures of resilience in high-dimensional systems and a way to automate their computation as well as the detection of significant changes, and there might be limitations associated with EO data. Finally, Sect. 6 provides a brief summary and our most important conclusions.
2 Challenges in Defining Resilience
2.1 Diversity of Resilience Metrics
The concept of resilience has been a central topic in the field of ecology for approximately 50 years (Yi and Jackson 2021). Defining resilience is challenging, not only because of differences in definitions and semantics, but also because of the difficulties in finding appropriate metrics to quantify resilience. While ecological and engineering resilience as outlined in Sect. 1 are the most common categories, other definitions of resilience exist, and many variants are used when quantifying resilience (Ingrisch and Bahn 2018; Yi and Jackson 2021).
The term ‘resilience’ is also used differently in different scientific disciplines and contexts, and even where the qualitative definitions appear to be the same, the mathematically defined metrics can differ. In principle, there are two kinds of challenges in trying to define resilience. The first is a conceptual challenge of how to precisely define resilience and distinguish it from other related properties. Often, different studies focus on different properties of disturbances and recovery processes, but nonetheless use the same terminology (Ingrisch and Bahn 2018; van Meerbeek et al. 2021), which can create unnecessary confusion, adding to the actual epistemic uncertainties. The second kind of challenge arises when such concepts are applied to observations of geoscientific or ecological systems, where practical estimation problems occur (e.g., arising from uncertainties and gaps in the measurement process or biases induced by other effects). We will deal with conceptual challenges in this section, while later sections focus on more practical problems associated with applying the definitions to EO data.
Regarding conceptual challenges, an important factor is that the recovery rate generally varies over time in systems with more than one dimension (e.g., an ecological model describing several coexisting species), even if the linearisation around the fixed point is valid. In the following, we assume that the one-dimensional simplification is justified. A more complete formal definition and comparison of resilience properties in higher dimensions is given in Arnoldi et al. (2016).
Even in a one-dimensional setting, a great deal of ambiguity arises from the fact that there are several properties that characterize and influence the recovery process (as shown in Fig. 2, case 1), and that one can measure: the magnitude of the disturbance, the ratio between this magnitude and the size of the external perturbation (resistance or robustness, also called Lloret’s resilience, see Lloret et al. 2011), the total duration of the recovery process, the ratio between disturbance magnitude and duration (abruptness), the initial pulse rate, the rate of recovery (engineering resilience), the area under the pulse curve (see Jentzsch and White 2019, and Fig. 1 therein), the magnitude of the perturbation needed to change an ecosystem to a different set of processes and structures (Angeler and Allen 2016), as well as combinations of multiple properties (Mitra, Kurths and Donner, 2015). In systems more complex than the simple dynamical systems shown above, it can also happen that the system does recover to some extent, but not fully (i.e.,, an intermediate type between the blue and yellow trajectory in Fig. 2), which is referred to as the degree of recovery (e.g., see Tao et al. 2022). For a comprehensive review of resilience metrics, see Yi and Jackson (2021) and Dakos and Kefi (2022).
Among the mentioned properties of disturbance and recovery phenomena, resistance is arguably among the most popular quantifiers (Pimm 1984; Ingrisch and Bahn 2018). Resistance has been defined as the ability of individuals or ecosystems to persist or stay essentially unchanged under a disturbance (Grimm and Calabrese 2011; Nimmo et al. 2015). The higher the resistance, the smaller is the impact of a given disturbance on ecosystem state variables. Therefore, resistance is typically defined based on the concurrent impact of a disturbance, quantified either by the (relative) difference or ratio of the state variable before and following a disturbance (Yi and Jackson 2021), and is closely related to disturbance severity used as characteristics of disturbance regimes in ecology (Turner 2010).
Resistance has also been included as one component of engineering resilience, next to recovery rate (Holling 1996). However, resistance is a property that is different from the recovery rate from a perturbation (Ingrisch and Bahn 2018) (though in a simple one-dimensional dynamical system setting, both should be proportional), and it can be insightful to consider both when assessing resilience. Particular care has to be taken when controlling for one of them to estimate the other. Even when the same qualitative definition of resilience is used (e.g., recovery rate), it matters how the quantified resilience is normalized in order to obtain unitless quantities. For example, the same absolute recovery time will lead to different recovery rates depending on whether one normalizes the time series by the baseline (reference state) value, or by the impact (amplitude) of the perturbation (Ingrisch and Bahn 2018), which is determined by the system’s resistance.
In the following, if not specified further, we refer to resilience as the engineering resilience in the sense of a recovery rate that is not normalized with the resistance. We will discuss some of the associated conceptual challenges in Sect. 2.2 and the practical problems of its estimation from Earth observations in Sect. 3 and 4.
2.2 Conceptual Challenges
Real ecosystems are much more complex than the idealized dynamical systems shown in Figs. 1 and 2. Hence, a number of additional caveats have to be kept in mind when assessing their resilience.
-
(i)
Equilibrium assumption.
The notions of equilibrium (a stable fixed point in terms of dynamical systems) and out-of-equilibrium is questionable in complex ecosystems that might be better described with chaotic dynamics even under constant environmental conditions (Hastings and Wysham 2010). Another caveat is how to define a system’s equilibrium in practice. Examples for a predefined state can be the empirically observed long-term average (Ingrisch and Bahn 2018), but typically covering only a few years given observational constraints, or it can be defined in absolute terms such as the FAO (Food and Agriculture Organization of the United Nations) definition of forests (> 40% tree cover, 5 m height), yet how different definitions impact the outcome of resilience assessments remains largely not well quantified.
-
(ii)
High dimensionality.
Even in case one-dimensional concepts apply mathematically (as mentioned above), there is typically a variety of variables to work with. Yi and Jackson (2021) consequently argue that it is challenging to calculate ecosystem resilience by a single universally applicable measure or method. For example, multiple state variables have been used to estimate resilience, some related with a system’s functioning (e.g., tree growth, assessed by basal area increment or tree ring width), others related with a system’s state (e.g., leaf area or vegetation indices related to photosynthetic activity, assessed by optical remote sensing) or a system’s composition (e.g., species richness). These reflect different facets of ecological systems that do not necessarily correspond to the same measures of “resilience”. As an example, when observing a deviation of the normalized Difference Vegetation Index (NDVI), the post-recovery NDVI, even if similar to pre-disturbance NDVI, may represent a different species composition or even another vegetation state (e.g., shrubs, grasslands instead of trees; Buma 2012). It is hence important to be aware of and clearly state the variables and mechanisms one aims to resolve, which also affects the sampling time (see below). For example, the generation time of a tree species may reflect the time scale of recovery for a forest after a severe dieback event, but may not matter for the recovery of leaves or biomass after less extreme events. Furthermore, measurable variables typically correspond to proxies of state variables, rather than the state variables themselves (e.g., spectral vegetation indices as proxies for photosynthetic activity/productivity). Given this complexity, it is generally of advantage to have knowledge on the drivers and main ecosystem processes involved, in order to make meaningful choices on relevant variables to assess the resilience of the system. This also applies to the right time period and sampling intervals, as we will discuss below.
-
(iii)
Interactions between disturbance and recovery time-scales.
Ecosystems with low resilience will only slowly regain their pre-disturbance state, or may not ever recover completely. The essential metric used to assess resilience is thus ‘recovery time’ or ‘recovery interval’, which needs to be interpreted in light of the disturbance interval. As an example, a system taking 100 years to recover is likely to fully recover if disturbances only occur every say 500 years, but if same system is disturbed every 50 years, it will never reach its pre-disturbance state (see Senf and Seidl 2021a, b), and its response to later perturbations might change due to nonlinear or even irreversible legacy effects (Hansen et al. 2022; Anderegg et al. 2020).
This is an important point to consider, as changing disturbance frequencies (i.e.,, due to climate change) might change the resilience of a system even though recovery times stay similar. To judge whether a system is actually at risk of experiencing a permanent state change, we hence need to consider both changing recovery times but also changing disturbance intervals. An example of this is increasing fire frequency observed in some regions, where ecosystems will be stuck in successional stages because they reburn before late-successional stages can be reached (a so-called fire-trap; see Freeman et al. 2017 and Hoffmann et al., 2020). In contrast, changes in ecosystem composition in response to changes in fire frequency can also promote resilience, depending on the ecosystem property under consideration, e.g., increased carbon storage (Mack et al., 2021).
Additionally, the recovery to a given state depends on changes in the forcing, e.g., drought recovery might be faster if coinciding with increased water availability. An alternative way to assess recovery is to evaluate how ecosystem function is changed following a disturbance. This can be quantified by evaluating departures of the sensitivity of the target variable(s) to forcing drivers relative to a long-term sensitivity (functioning) baseline (Yu et al., 2022; Wu et al. 2022).
-
(iv)
Memory effects and system boundaries.
As explained in point (iii), the time scale separation of an abrupt disturbance and the consequential slow recovery is an idealization. Many ecological systems exhibit memory (Ogle et al. 2015; Cranko Page et al. 2022) and specifically stress memory (Walter et al., 2013; Ruehr et al. 2019). Ecological memory might lead to altered responses to perturbations, either by conferring increased or reduced resistance (Gessler et al. 2020; Wu et al. 2022). Increased resistance might result from positive legacy effects of responses to disturbance. For example, investment in root growth during drought (McDowell et al. 2008) might attenuate impacts of a subsequent drought, or reduced competition due to mortality might increase resources available for surviving individuals (Gessler et al. 2020). Reduced resilience following disturbance might result from functional impairment (e.g., damage to the plants’ hydraulic system; see e.g., McDowell et al., 2016; Ruehr et al. 2019; Wagner et al. 2023). Further, some disturbance resistance strategies might increase vulnerability to subsequent disturbances. For example, drought avoidance strategies like stomatal closure or defoliation might increase the risk of carbon starvation and long-term metabolic decline (Poyatos et al. 2013; McDowell et al., 2016), increasing tree vulnerability to biotic attacks. In addition, these effects likely depend on the magnitude of the disturbance impact (Ruehr et al. 2019).
Hence, one needs to keep in mind that concurrent impacts might not only reflect the direct disturbance effect, but also the legacy effects from similar or other types of past disturbances due to stress memory (Gessler et al. 2020; Bastos et al. 2021; Anderegg et al. 2020). It has therefore been proposed to quantify resistance by the concurrent sensitivity to a given disturbance driver (ΔV/ΔF, with state variable V and forcing F, Fu et al., (2020); Xiao et al. (2023)), which better allows to estimate “the persistence of relationships within a system” (Holling 1973), and allows to compare shorter periods of time (Fu et al. 2020). It should be noted, however, that these are also likely to be time-scale dependent (Linscheid et al. 2021).
Besides these challenges related to time scales, resistance and resilience can also be hard to disentangle practically because of the presence of climate-ecosystem and ecosystem-biogeochemical feedbacks. For example, the precipitation-evaporation feedback (Eltahir and Bras 1996) leads to the fact that precipitation at a certain location is not an external driver, but already affected by the response of the ecosystem to other drivers, or the same drivers at other locations. Another example is that increased carbon storage under more frequent fires reported by Mack et al. (2021) was linked to higher nutrient availability, hence, the direct effect of fires in isolation (as might be possible to be studied in models) is not well separable in observations. It is hence not always possible to observe the internal ecosystem dynamics and external stressors separately from each other.
-
(v)
Value judgements and other subjective choices.
In highly complex (socio-)ecological systems, it also matters whether the restored ecosystems fulfill the same functions (or provide similar ecosystem services) as prior to the perturbation, i.e., if they can adapt to change in a way that is judged as beneficial (Helfgott 2015). In this sense, “resilience” has more facets than just the recovery to a previous state, or the persistence in remaining in a certain regime. It has been argued that it is a feature of resilience for systems to be self-organized (rather than just changing when being forced); and to permanently change in order to adapt to the environment by learning. For instance, species and hence ecosystems permanently change due to evolution. It is then particularly relevant to decide which function or property of the system shall be the focus (“resilience of what to what?”; Carpenter et al. 2001; Cutter 2016), and, in case of socio-ecological systems, “resilience for whom?” (Cutter 2016). If the structure and/or composition changes, but from a human perspective the ecosystem provides the same function, we might still call it resilient. In this sense, there is also a subjectivity that depends on the selected functions (or ecosystem services) and how we value them (e.g., timber production rate, species diversity, habitat for particular species). As different functions can have distinctive resilience, it matters which ones we focus on, which is necessarily a strongly human-based perspective. In this article, we however ignore these value-related issues and focus on the conceptual and practical challenges when defining and measuring resilience for a given ecosystem property or function.
3 Recovery from Individual Perturbations
As outlined above, when referring to resilience as the return rate to equilibrium after disturbances, one can hope to measure resilience by identifying large state perturbations and then estimating the recovery time empirically (van Nes and Scheffer 2007). In principle, this involves two steps: (i) detecting sufficiently large and sufficiently abrupt shifts in order to identify a clear starting time for the recovery process, and (ii) measure the time the system needs to recover. Both aspects need a conceptual choice and quantification of a reference state before the perturbation and after recovery. Closely related to measuring the recovery time, one can also on the same basis measure the recovery rate directly by fitting an exponential function to the part of the time series between the perturbation and the time when the system has fully recovered (Smith et al. 2022). As explained in Arnoldi et al. (2016), this method assumes that the recovery rate does not change during the recovery process, i.e., that the initial and asymptotic recovery are identical. This is only guaranteed in one-dimensional systems, or in case the perturbation happens in the direction of the eigenvector with the largest negative eigenvalue.
3.1 Methods for Detecting Abrupt Shifts
Sudden and large perturbations of a state variable can result from (i) disturbances from which the system can recover (Fig. 2 case 1, blue trajectory), (ii) large disturbances that push the system into an alternative state (Fig. 2 case 2, yellow trajectory) or (iii) “tipping points” originating from the internal nonlinear dynamics of the system, which can be triggered by only small and gradual changes in external conditions (Fig. 2 case 3, red trajectory), and can be practically irreversible. The first kind is useful to probe the linear stability (engineering resilience) of the system, whereas the second and third are associated with ecological resilience and result in a transition to an alternative state. In observed complex systems, it is often not clear into which of these (idealized) classes an abrupt shift falls, in particular shortly after the shift has occurred. However, all three are important events to be monitored before they can be assessed further.
Interestingly, methods to detect irreversible shifts and methods to detect large anomalies (temporary disturbances) are closely related (Flach et al. 2017; Bathiany et al. 2020). For instance, integrating a time series (i.e., computing the cumulative sum) will convert an extreme event into an abrupt persistent shift. Vice versa, differentiating (computing the difference between subsequent data points) turns an abrupt transition back into an extreme event. Consequently, a very fundamental and successful detection approach (depending on the length of the time series) works via computing the cumulative sum of a time series and then detecting extreme values (Basseville and Nikiforov 1993).
It is important to be able to detect extreme or abrupt shifts fully automatically, i.e., without the need for visual inspection to identify candidates of events. First, automatic detection allows more objective and reproducible results, and second, EO datasets are increasing in number, length, and resolution, thus increasing the amount of data that needs to be monitored and processed, which would be hardly possible by eye. A similar development is occurring for climate models of climate and parts of the Earth system.
Several detection strategies with an increasingly large number of algorithms have been developed and applied in the Earth sciences to detect abrupt shifts automatically (see, e.g., Aminikhanghahi and Cook 2017). Historically, an important application of such methods was to remove artificial offsets in observational time series, introduced by changes in the measurement process (e.g., when replacing one instrument by another). To this end, so-called change-point detection methods were introduced which detect the points in time where a sudden change in the statistical properties (usually the mean) of a time series occurs. These change-point detection frameworks involve fitting specific parametric models to time series (e.g., using ramp regression as a piecewise linear model; see Mudelsee 2000), and testing for the likelihood that different models are needed to explain the data in each segment before and after a suspected change-point (Reeves et al. 2007; Bai and Perron 2003; Zeileis et al. 2003). Such a task can also be framed as a model selection problem and information criteria can be applied (Jamali et al. 2014; Reeves et al. 2007).
Originally, several assumptions had to be made when applying these methods, which are too restrictive in the case of time series from climate or ecological systems. Consequently, change-point detection methods have been extended to be able to cope with large autocorrelation (Mudelsee 2000; Rodionov 2004, 2006; Wang 2008; Ducré-Robitaille et al. 2003), trends and non-stationary/non-iid residuals (Matyasovszky 2011; Gallagher et al. 2013), seasonality (Verbesselt et al. 2010a), non-Gaussian distributions (Lazante 1996; Chu 2002), as well as measurement and dating uncertainties (Goswami et al., 2018).
Despite these improvements, almost all methods still are restricted to univariate time series. EO data (like simulated data), in contrast, provides spatio-temporal information, allowing for detection methods that focus on a certain spatial scale of interest, and take spatial connections into account in order to improve statistical significance and to classify abrupt shifts in terms of their spatio-temporal structure (Bathiany et al. 2020). Table 1 summarizes some typical examples of applications in the climate sciences, which share the particular target of detecting real abrupt climate shifts (as opposed to artificial shifts in the measurement process).
Inspired by ecological disturbances, many techniques for detecting abrupt changes in annual time series of optical medium resolution remote sensing data have been developed. Such techniques assume that a sudden shift in the vegetation community, e.g., by fire, will result in a measurable change in the annual spectral reflectance properties. Detecting changes is mostly done by classical change-point detection algorithms, but those methods are increasingly combined with supervised classification models to filter out falsely detected breaks. Examples of such products are available for Canada (White et al. 2017) and Europe (Senf and Seidl 2021a, b).
3.2 Quantifying Recovery After Perturbations
After having identified a perturbation of the system, for instance with the methods discussed in Sect. 3.1, and under the assumption that the system is ecologically resilient (can recover to its old state), quantitative properties of the recovery can be measured in order to quantify the system’s “engineering resilience”. As explained in Sect. 1, in this framework, more resilient vegetation or ecosystems will return to their previous state (or a predefined state) more quickly. In practice, the disturbance can be thought of as a drought, fire, storm, or any other event that leads to an abrupt change in structure and frees resources for the development of new vegetation. In principle, it is the recovery rate which quantifies what we introduced as “engineering resilience” above, i.e., the linear stability of the system’s state in terms of dynamical systems theory. However, we will discuss in this section that it matters how this property is defined precisely (in particular, if and how the time series are normalized), and how it is measured.
The simplest way to measure recovery time is to define a reference state, and measure how long it takes for a given ecosystem to return to that reference after disturbance (Senf and Seidl 2021a, b; Wu et al. 2022; Bastos et al. 2011). This provides a time scale for recovery, which can be interpreted as a recovery rate. The main practical difficulties here are defining the reference state, and estimating the recovery time in the presence of other perturbations, which can make it difficult to estimate when the recovery process has ended. This stands in contrast to the detection methods introduced in Sect. 3.1, which typically do not require defining any baseline state a priori. Another practical difficulty in EO applications is that time series might not be long enough to robustly define a long-term reference state. Circumventing this caveat is the motivation of space-for-time approaches, discussed in Sects. 4.3 and 5.8.
To quantify the reference state the system recovers to (baseline value), one typically uses either the pre-disturbance state, or a baseline value from an undisturbed control treatment (if available). As mentioned in Sect. 2, it is a subjective choice whether the recovery is formulated in terms of absolute values, or normalized with regard to the baseline or the disturbance impact (Ingrisch and Bahn 2018). In any case, it matters whether the reference state can be well quantified using the data sources available. For instance, the recovery in NDVI or similar spectral indices will reach pre-disturbance values quite quickly after disturbances, even though this will be driven by understory plants and early vegetation (for example, see Bastos et al. 2011). Using reference states with more clearly defined ecological metrics (e.g., common definitions of forest based on tree cover and height) might overcome such problems, but require more advanced data. Here, novel developments in remote sensing might help close this gap (e.g., using LiDAR data to look specifically at structural recovery; see Stritih et al. 2023), but these are still experimental and not widely applicable to assess resilience.
In practice, a pre-defined time period after the disturbance is often selected, and the regrowth capacity is evaluated. A wide variety of measures have been applied that compare the conditions after the disturbance to a reference condition and potentially also the condition at the end of the disturbance (e.g., Frazier et al. 2018; Tao et al. 2022; Lloret et al. 2011; Van Meerbeek et al. 2021). These measures express the regrowth relative to the disturbance impact (e.g., the recovery magnitude relative to the disturbance magnitude) or to the reference state itself. Essentially, measuring regrowth in this way corresponds to measuring recovery, but with different definitions of what the reference state is.
The choice of reference pre-disturbance values varies widely across studies, some considering only the single year before disturbance (Thurm et al. 2016; Sohn et al. 2016) as reference, but most using the mean values of the 2–3 years prior to disturbance (Yi and Jackson (2021). In such short periods, it is likely that the state variable is influenced by the natural interannual variability of many ecological systems (Zhu et al. 2017; Li et al. 2022), risking to lose representativeness. Therefore, in more recent studies, longer-term reference periods have been used to quantify impacts (Flach et al. 2018; van Schaik et al. 2018; Bastos et al. 2021), yet long time series prior to disturbance might not always be available.
Another problem with using recovery time as an indicator of resilience is that it assumes that recovery will be complete after some fixed time. However, systems might take decades to centuries to reach pre-disturbance values, especially for systems composed of long-living organisms such as forests. The observation length of many data series is hence shorter than the recovery interval. This makes it especially difficult to assess changes in recovery over time, which would be of interest to detect changes in resilience caused by, e.g., climate change. Early indicators of recovery might already serve as a proxy for the long-term developmental trajectory, which yet remains to be empirically validated (Seidl and Turner 2022).
Instead of measuring the time span until a “recovery” criterion is met, it might be advantageous to directly quantify the recovery rate by fitting an exponential function to the section of a time series after a disturbance (Fig. 3) (Smith et al. 2022; Bastos et al. 2011). Based on an assumed linear dynamical systems framework, the recovery of a system after a perturbation should be exponential. Hence, the exponent of an exponential function fitted to the time series of restoration directly quantifies the recovery rate of an ecosystem.
Observed perturbations and recovery in vegetation optical depth (65.625°N, 155.875°W) as measured by passive microwave data (Moesinger et al. 2020). Top: full time series from 1992–2016, raw time series in black, with deseasonalized and detrended time-series residual in blue. bottom: period from 1999–2012; Large disturbances as those in 1999 and 2008 are an opportunity to estimate the recovery rate using an exponential fit
4 Recovery from Continuous Perturbations
The problem with estimating resilience via direct estimation of the recovery rate is that one needs time series that exhibit large perturbations and that it will practically be close to impossible to measure resilience changes over time in this way. In this Section, we will discuss time series that show no large disturbances but permanent variability. Though the resilience indicators obtained from such permanent small perturbations are arguably more indirect than the recovery from single large perturbations, theory predicts a relationship between them and the advantage is that we do not need to rely on the presence and detection of large perturbations as discussed in Sect. 3.
4.1 Statistical Resilience Indicators
In the absence of large externally-induced perturbations, the internal variability of the system can also be used to gain insight in the resilience of a system to external influences. That is because the internal ‘fluctuations’ of a system typically contain information about the system’s response to external influences, as stated by the fluctuation–dissipation theorem (Kubo 1966) in statistical mechanics. It is worth noting that this link has also been observed in climate models (Cionni et al. 2004; Gritsun and Branstator 2007; Leith 1975). Hence, interpreting a system’s variance and autocorrelation (in short, AC1, using a time lag of one resolved time step) as indicators of linear stability has become a widely adopted and straightforward approach across various fields.
Such an empirical approach is particularly relevant when monitoring systems that might be losing resilience, or even approaching a bifurcation point. When moving toward such a point, the dynamics of the system will typically exhibit critical slowing down (CSD). The initial discovery of this phenomenon can be traced back to statistical physics (Gaspard et al. 1995; Solé et al. 1996; van Kampen 1981). Subsequently, it has been investigated in the field of ecology (Wissel 1984; Oborny et al. 2005) and climate research (Kleinen et al. 2003; Held and Kleinen 2004). Critical slowing down refers to the situation where a system takes longer to return to its equilibrium state following a perturbation, indicating a decrease in its recovery rate. In this regard, indicators of CSD aim to detect a loss in “engineering resilience” (decreasing linear stability) as a proxy of closeness to a bifurcation point. It is the crossing of such a point that finally causes a catastrophic transition to an alternative state (loss of Ecological resilience), and therefore typically is seen as an impact-relevant property.
When a system approaches a bifurcation-induced tipping point, its dynamics tend to resemble a red noise process, wherein each state becomes more similar to its past state, leading to an increase in autocorrelation (Wiesenfeld 1985). Simultaneously, the slowness of the system causes a rise in variance as subsequent random fluctuations accumulate due to the slower and slower decay of these fluctuations (Wiesenfeld and McNamara 1986). Consequently, both variance and autocorrelation progressively increase until the system reaches a bifurcation point. This theory has prompted the use of rising variance and autocorrelation as “early warning signals” for impending bifurcations (Scheffer et al. 2009). Additionally, other related indicators have been proposed, such as higher statistical moments (Guttal and Jayaprakash 2008a) and spatial correlations in spatially extended systems (Dakos et al. 2010; Donangelo et al. 2010; Guttal and Jayaprakash 2008b).
There are several practical and conceptual limitations associated with these statistical resilience indicators (Bathiany et al. 2016a). First, practical limits exist because these methods require long time series with sufficiently slow and gradual change in the external forcing (i.e.,, a time-scale separation between external forcing and internal system dynamics). Second, on a conceptual level, these indicators might lack predictive power, because they might detect false positives due to, e.g., multiplicative noise (Bathiany et al. 2013), negative feedbacks in most of the measured regime, or inertial effects (Wagner and Eisenman 2015; Boulton and Lenton 2015; Bathiany et al. 2016b), the confounding effect of colored or non-stationary noise (Dakos et al. 2012), and the large spatial complexity of real-world systems (Bathiany et al. 2013; Held and Kleinen 2004). As an example, if a given climatic driver shows changes in its AC1, then the ecological metric will too (assuming sensitivity remains), which would be reflected in resilience change, while functioning was actually maintained.
There have been some recent advances however to mediate some of these problems. In particular, Boers (2021) introduced a new restoring rate parameter λ as a resilience indicator that is not prone to false alarms based on changes in the properties of the driving noise when using a more general regression method than autocorrelation (see also Boettner and Boers 2022), while Clarke et al. (2023) analyze the ratio of spectra (ROSA) of the system state variable relative to a forcing variable. Moreover, spatial information from EO records can be increasingly beneficial by allowing (i) to generate more data about systems than we would have in case of univariate time series (often by making a “space-for-time” assumption), and (ii) to assess spatial resilience indicators that can complement univariate indicators like autocorrelation, variance or feedback parameter λ (Dakos et al. 2010; Boulton et al. 2022).
Recent work has further linked the statistical measures of resilience to the recovery rate discussed in Sect. 3, over a globally distributed set of ecosystem recoveries. Smith et al. (2022) found that the theoretically expected relationship between AC1/Variance and recovery rate broadly held in empirical vegetation EO data, indicating that AC1 and variance can indeed be related to the recovery rate after a disturbance. This implies that AC1 and variance can be used to estimate how fast a system will recover after a shock, and provide another potential avenue to estimate recovery times and, hence, changes in resilience.
4.2 Pre-processing Time Series to Derive Resilience Indicators
Estimating the resilience of a system using Critical Slowing Down indicators (e.g., the restoring rate λ, lag1-autocorrelation (AC1) or variance) generally requires that the time series describing the system is stationary—that is, without seasonality or trends. Stationarity helps to avoid conflating normal seasonal variations with changes in short-term oscillations, which are signals of changes in system resilience, and avoids biases in the resilience indicators induced by trends in the time series. Therefore, data has to be pre-processed before statistical resilience indicators can be computed from it. It has been shown that the methodology to detect so-called anomalies is typically very important for the detection of extremes (Flach et al. 2017) as well as the estimation of resilience indicators and their trends (Smith and Boers 2023b). We note that these procedures to remove e.g., seasonality and trends are not necessary for estimating recovery times after large and rare perturbations as those discussed in Sect. 3, which focuses on the actual recovery after a perturbation (Verbesselt et al. 2010a).
A wide variety of approaches exists to remove seasonal and long-term trends from data (Smith and Boers 2023b; Verbesselt et al. 2016); the most suitable method is driven by the data set in question. For example, highly seasonal data such as NDVI or other vegetation time series can be decomposed into a trend and seasonal component with harmonic models treating seasonality as a combination of sine waves (e.g., BFAST, Verbesselt et al. 2010a; Verbesselt et al. 2010b, Masiliunas, 2021). There is no one optimal deseasoning method; the efficacy of different procedures depends strongly on the underlying signal that is to be isolated. In addition to the deseasoning method itself, additional parameters such as the length of any seasonal or annual smoother, the choice of a stable reference period with which to construct anomalies, and the number of overlapping sine functions used to represent annual seasonality can have a strong influence on the resultant deseasoned residual.
The type of long-term trend removed is also important to consider—removing a linear trend from non-linear data can leave undesirable traces in the time series that will influence estimates of changing resilience (Smith and Boers 2023b; Verbesselt et al. 2010a; Verbesselt et al. 2016). If, after detrending, the time series still contains a trend, estimating AC1 and variance (or other resilience metrics) based on a rolling window will artificially inflate local autocorrelation, as compared to a locally flat time series. Thus, a trend that fluctuates through time can induce changes in AC1 which might be confused with AC1 changes driven by high-frequency fluctuations or changes in the system dynamics. The impacts of these combined deseasoning and detrending methods can be seen in Fig. 4; not all methods perform equally well at reconstructing a stationary residual, and each leave distinct traces in the inferred changes in AC1 through time. It is important to carefully consider both the means of removing seasonality and trend, and how that procedure can influence resulting estimates of system resilience.
Impacts of deseasoning/detrending procedures on a simple toy model (from Smith and Boers 2023b, Fig. 1) for a system moving Toward a bifurcation induced transition. Left column: seasonality modeled using a regular sine curve, right column: seasonality varies in amplitude and timing between years. A, B Time series with (black) and without (blue) noise. C, D Perfect deseasoning via removing the a-priori known seasonality curve. E, F Deseasoned time series via a harmonic fit and rolling mean (red), via long-term daily means and a linear detrender (black) and via STL (purple). Gray shading covers periods where rolling mean and STL detrending is uncertain due to incomplete time windows. G, H AC1 computed over a five-year rolling window for each method of removing seasonality and trend. While all models show an increase in AC1 as a transition approaches, not all methods preserve the monotonic increase in AC1 from (A, B). Dashed lines indicate less reliable AC1 values due to incomplete moving time windows, shaded areas cover one STD from the mean. Figure license: https://creativecommons.org/licenses/by/4.0/
There also exist methods which remove both trend and seasonality in tandem, such as Seasonal Trend Decomposition by Loess (STL) (Cleveland et al. 1990). STL has the benefit of removing more complex seasonal signals (i.e.,, not sine waves) and dynamic trends (i.e.,, changing trends through time). However, overfitting, e.g., by fitting high-order splines, can remove portions of the dynamics of the system that are actually part of changing system dynamics—and hence potentially resilience, and not of the seasonality or trend (Fig. 4).
It should be emphasized that no method of deseasoning and detrending is perfect—each will have limitations that need to be considered (Smith et al. 2023; Verbesselt et al. 2016). The non-stationarity of the resilience indicators that one desires to measure can often not be separated from other non-stationary features because they occur on similar time scales. For example, if seasonality strongly increases through time, a single harmonic model fit to the whole time series will leave traces in the residual, as it is focused on removing the average signal through time. This effect could be removed by locally fitting harmonic models (e.g., every three years), with the potential downside of leaving step-changes in the residual year-on-year. In short, the potential limitations of deseasoning methods—and their knock-on effects on resilience estimates—need to be carefully considered. Therefore, careful attention is needed when fitting time series in order to explore the residuals.
4.3 Multivariate Approaches and Spatial Resilience Indicators
In the previous sections, we focused on the analysis of time series of a single state variable, so-called univariate time series. However, in practice, often more data is available, be it time series of multiple state variables or time series of spatial evolution.
Multivariate data is useful because natural systems are complex systems that have many processes acting on, and interacting across, different time scales and affecting different state variables and/or locations differently. For instance, the growth rate varies from one plant type to the other, and soil water dynamics play out on shorter time scales compared to plant dynamics. Multivariate data therefore ‘samples’ the full variety of processes in a system better compared to univariate data, which can lead to better resilience estimates. Mathematically, this means that multivariate data enables the estimation of multiple modes (“eigenvalues and eigenvectors”) compared to univariate methods that are typically limited to one mode only.
To use multivariate data, often the univariate methods from the previous sections are extended to a multivariate setting using mode decomposition methods to derive eigenvalue–eigenvector pairs from a time series. One of the most widely-used techniques for this is a principal component analysis, for which a singular value decomposition (SVD) of the multivariate (i.e.,vector-valued) time series \(X\) forms the basis. The downside of the use of such methods is that the time ordering of the original time series is completely disregarded when constructing the eigenvectors. It is, however, possible to explicitly account for this time ordering, for example, using dynamic mode decomposition (DMD) (Kutz et al. 2016). A detailed and practically focused methodology can be found in e.g., Weinans et al. (2019).
Once such a mode decomposition has been obtained, the system’s resilience can be derived from it. A naive implementation would be to look at the least stable eigenvalue–eigenvector pair (i.e., the eigenvalue with the highest real part) as this mode corresponds to the slowest recovering dynamics. However, this mode might not always correspond to the relevant dynamics. For example, when the eigenvalue has imaginary parts it could correspond to oscillatory dynamics, such as seasonality (see also Sect. 4.2). If this is not the case, it could also happen that the system has very slow dynamics that are always present but do not contain information on the system’s resilience. For instance, in semi-arid areas, vegetation patterns migrate slowly over a landscape (DeBlauwe 2012; Bastiaansen et al. 2020) but that dynamics has little to do with the restorative dynamics of the vegetation. Hence, looking at all modes might be necessary to obtain the proper resilience signal.
Proper analysis of these time series using multivariate methods can lead to more accurate resilience estimates and/or reduce the required time span of the data at hand (Weinans et al. 2019; Weinans et al. 2021; see also e.g., Bastiaansen et al. 2021 for exposition of this in the context of global climate models). A number of methods have recently also been further developed and assessed that allow for the automatic detection of abrupt shifts (Bathiany et al. 2020), extreme events (Flach et al. 2017) and changing resilience indicators (Weinans et al. 2021) in multidimensional systems. There is particularly high potential to look at multivariate recovery indicators from remote sensing, with some recent evidence in the literature that multivariate indicators could indeed improve the assessment of post-disturbance recovery (Morresi et al. 2019). When monitoring forests, data on vegetation coverage, tree density, tree height, above-ground biomass, soil moisture and many more might be present (Lechner et al. 2020), and satellite data nowadays typically has high enough resolution to capture spatial patterns, such as those appearing in semi-arid regions (Bastiaansen et al. 2018; DeBlauwe et al. 2008; Veldhuis et al. 2022) or in peatlands (Eppinga et al. 2008). Also, Viana-Soto et al. (2022a) derive fractions of trees, non-treed vegetation and bare ground from remote sensing data, which allows one to study recovery trajectories in a 3D space spanned by those three land covers. A particularly promising approach in this direction is to apply machine learning methods in order to identify optimal indicators (Bury et al., 2021).
When spatial data is available, it is also possible to use the form of the eigenvector instead of the eigenvalue (or in combination with) to estimate the system’s resilience. Here, the idea is that the destabilizing eigenvector of spatially extended systems has some striking characteristics that can be used as a metric (Held and Kleinen 2004; Dakos et al. 2010; Guttal and Jayaprakash 2008b). That is, when a system approaches a bifurcation-induced tipping point, it might do so in a very specific way, thus displaying specific spatial characteristics. Precisely which characteristics to look for varies from system to system. For example, in spatially homogeneous systems the spatial correlation tends to increase when a tipping point is approached (Dakos et al. 2010). In a similar vein, it is also possible to look at the spatial variation or decorrelation length. However, for spatially patterned systems, typically the spatial correlation does not precede critical shifts, and one should look for different signs (Bastiaansen et al 2020; Kéfi et al 2014). For instance, the patchiness of some dryland ecosystems, known for exhibiting spatially patterned states, seems to increase as they approach a critical shift (Kéfi et al 2014).
The strength of these spatial early warning signs is that they do not require lengthy time series to be available. However, they do require a dataset with enough spatial detail. Therefore, in particular for systems where constant monitoring is hard, or for systems that have strong seasonality, infrequent analysis of the spatial structure of a snapshot of the system might be a good alternative.
5 Challenges and Opportunities of EO-Based Resilience Monitoring
5.1 Technological Advances in Observing Terrestrial Vegetation
The challenges of resilience monitoring discussed above in principle apply to all Earth observation records. Before we highlight how these challenges manifest themselves in current datasets and applications, we here provide a very brief summary of recent developments in the retrieval of terrestrial vegetation datasets from Earth observations.
In principle, satellites measure radiative fluxes which by a retrieval algorithm are translated into products that are meant to represent a property on the ground, like vegetation coverage or biomass. The measurement can be passive or active. Passive remote sensing measures the properties of solar radiance reflected by the Earth surface, or radiance emitted by the Earth itself. Active remote sensing systems send artificially generated radiation Toward the Earth and measure its reflection properties, such as intensity and polarization. The latter category includes observation systems such as radar and lidar.
A common and largely available passive EO technology is multispectral imaging, where satellites collect data over multiple wavelength regions, such as the visible, near-infrared, and shortwave infrared part of the electromagnetic spectrum. Multispectral data form the basis of widely used vegetation indices like the Normalized Difference Vegetation Index (NDVI) or the Enhanced Vegetation Index (EVI). They are closely (though not linearly) related to photosynthesis and thus plant vigor and productivity. Yet, NDVI as well as EVI saturate in regions with high biomass (Sellers 1985; Liu et al. 2011), and the short wavelengths render them tainted by atmospheric conditions such as clouds and aerosols (Samanta et al. 2012). In addition, seasonal changes in sun-sensor geometry can lead to serious artifacts (Morton et al. 2014).
Radiometry, and its passive-microwave products such as Vegetation Optical Depth (VOD), overcome these obstacles, as biomass density drives the natural emission of radiance from the vegetation itself and the attenuation of natural emissions from the soil (Liu et al. 2011; Konings et al. 2019; Li et al. 2021; Schmidt et al. 2023). Also, improved plant surface temperature measurements from ECOSTRESS (Fisher et al., 2020) allow insights into physiological mechanisms like stomatal control and hence into the water and carbon cycle and land–atmosphere coupling. Radiometry’s drawback is its low spatial resolution. In contrast, the measurement of backscatter from actively sent microwave signals, as done by synthetic aperture radar (SAR) technology allows for resolutions at meter-scale (Konings et al. 2019). SAR provides insights into terrain structure, vegetation canopy structure, and soil moisture. Besides classical multispectral and SAR-based indices, novel indices such as solar-induced chlorophyll fluorescence (SIF) can even better reveal photosynthetic activity and phenology (Zhang et al. 2022).
Finally, recent spaceborne LiDAR missions, such as GEDI and ICESat-2, provide near-global and global sampling of 3D forest information. Initial exploration of those data focused on combining GEDI samples of forest heights (relative height observations) with Landsat and Sentinel-2 images to derive global, wall-to-wall 30 m and 10 m canopy height maps, respectively (Potapov et al., 2021). These global products will enable a global analysis of canopy height time series in the future, and in turn engineering resilience studies on forest regrowth. Nevertheless, the canopy heights should be used critically as potential systematic effects in satellite LiDAR height observations may lead to an underestimation of forest regrowth (Milenkovic et al. 2022). ICESat-2, on the other hand, already provides time series of forest heights as this mission, in contrast to GEDI, samples along the same tracks and seasonally since 2018. Besides forest height, both GEDI and ICESat-2 provide information on vertical vegetation profile metrics such as leaf area index and canopy gaps (Dubayah et al. 2021), but the exploration of those variables in resilience studies is yet to come (see Stritih et al. 2023 for an example).
On the one hand, these novel developments provide us with a richer and much better resolved database on which resilience monitoring can rely. We provide a timely review of recent developments in the next section, with focus on forest monitoring. On the other hand, a number of conceptual and practical caveats need to be resolved in order to harvest the full potential of these developments. To raise awareness of the gap between current practices in the generation of EO data and the requirements of resilience monitoring, we discuss the most apparent and urgent limitations in Sect. 5.4–5.9.
5.2 Monitoring Resilience in Aquatic and Marine Ecosystems
Although examples in the rest of this review focus on terrestrial ecosystems, the notion of ecosystem resilience in general, the potential to monitor it with remote sensing, and the above conceptual and practical challenges all apply to aquatic and marine ecosystems in a similar way. For example, shallow lakes have been a prototypical example for the potential existence of alternative stable states (Scheffer and Jeppesen 2007), which differ in the turbidity of the water. In principle, earth observation by satellite-borne sensors can be useful for probing the resilience of such aquatic systems (Oezkundakci and Lehmann, 2019). A large body of research also focuses on the resilience of coastal wetlands, e.g., by observing the recovery after droughts, hurricanes and other storms, heavy precipitation and fluvial flooding. Such studies make use of a large number of remote sensing sources such as MODIS and Landsat (Tahsin et al. 2018), vegetation-based indices (Balogun et al. 2020) and sometimes use the classical statistical resilience indicators as outlined in Sect. 4.1 (Zhao and Li 2022). Moreover, similar detection methods to automatically detect abrupt shifts as outlined in Sect. 3 are being developed and applied in the marine sciences (Yang et al. 2022). Other ecosystems under investigation are giant kelp forests (Cavanaugh et al. 2019), coral reefs (Knudby et al. 2014) and seagrass ecosystems (Clemente et al., 2023), with particular concern of tipping in these systems (van de Leemput et al. 2016; van der Heide et al., 2011). While returning to terrestrial applications in the remaining sections, we point out that some of the same challenges as discussed throughout this review also apply to aquatic and marine ecosystems as well.
5.3 Developments in Earth Observations with Regard to Terrestrial Ecosystem Resilience Monitoring
In recent years, Earth observation has become a major tool in assessing resilience (Nikinmaa et al. 2020; De Keersmaecker 2022; Senf 2022), often involving the technological advances outlined in the previous section. Special focus has been put on forest ecosystems, because forests globally are changing in response to climate change and increasing land use pressures (McDowell et al. 2020). For instance, recovery from disturbance such as windthrow, bark beetle outbreaks or fire have been estimated from optical remote sensing time series in order to assess the forest’s capacity to return to similar spectral conditions than before disturbance (White et al. 2019; White et al. 2022; Chirici et al. 2020). Most of those studies made use of free image archives such as Landsat (Wulder et al. 2019), which provides long enough time series to estimate recovery signals in forests. The use of Landsat also allows for the quantification of historic disturbance events (Senf and Seidl 2021a, b; Hansen et al. 2013), which in turn can be used to estimate recovery by space-for-time substitution. More specifically, combining the historic information on disturbances with recent data on forest structure, such as derived from airborne or spaceborne Light Detection and Ranging (LiDAR) data, allows to create chronosequences of structural attributes (e.g., canopy cover, height) over variable years post-disturbance (Viana-Soto et al. 2022b; Stritih et al. 2023; Senf et al. 2019). From those chronosequences, it can be estimated how quickly forests return to certain structural states or recover certain functions, which substantially increases the applicability of the result in ecosystem management (but see also discussion in Sect. 5.4). Similar results can be achieved also without the pitfalls of space-for-time substitution (Johnson and Miyanishi 2008) by recent developments in Earth observation, including machine learning regression (Senf and Seidl 2021a, b), synthetic spectral unmixing analysis (Senf et al., 2020) or artificial intelligence (Liu et al., 2023). Those novel approaches convert the spectral signals into interpretable units, such as canopy cover or biomass, allowing for example for the assessment of community change after fire disturbances (White et al. 2023; Viana-Soto et al. 2022a). Novel sensor systems, including spaceborne hyperspectral data or Radar, will likely add important information to ecosystem resilience, but their full potential hasn’t been explored yet.
5.4 Signal Versus Functional Recovery
Many remote sensing based recovery studies use signal recovery as a measure of resilience. Signal recovery is derived from a time series of a single remote sensing observable, being it a spectral index, e.g., NDVI or RVI (the radar vegetation index, Saatchi 2019a, b), or a biogeophysical variable derived from the radiance measurements, e.g., the fraction of absorbed photosynthetic radiation (fAPAR) derived from solar-reflective measurements, or vegetation optical depth (VOD) from microwave observations. Yet, by focusing on a single ecosystem property, signal recovery does not always reveal to what extent the same level of processes or structure are retained in the system. For instance, while after a disturbance the NDVI signal of a tropical forest may recover to its pre-disturbed state, the secondary forests are known to be structurally and functionally different (Caughlin et al., 2021). In addition, signal recovery does not provide information on the process behind the recovery. For instance, monocultures can be more sensitive to diseases but recover relatively fast when they are replanted. Yet, the fast signal recovery capacity of these monocultures does not necessarily reflect their resilience to disturbances. Consequently, it is important to find a proxy variable measurable by remote sensing which represents the in-situ property under investigation. If this is not directly possible, multivariate approaches based on several, independent remote sensing observables, and additional knowledge on the relationships of time scales may help constrain the recovery process quantitatively.
5.5 Spatial and Temporal Resolution
The scale of EO measurements rarely matches up with the system under study, neither in space nor in time. For example, Landsat has a theoretical revisit time of ~ 16 days (or much longer in areas with frequent cloud cover), which is too low to capture some of the dynamics of many ecosystems. To track phenological changes, or the response to extreme events like droughts or storms, daily resolution would be required. Conversely, MODIS with a daily repeat time lacks the spatial resolution to resolve small-scale features on the spatial scale of individual trees that can be picked out with Landsat data (30 m resolution). The trade-off between time and space becomes even more of an issue when very-high-resolution optical and Synthetic-aperture radar (SAR) are used, which, depending on the satellite constellation and priority of the ground target in the acquisition plan, may provide only a few acquisitions per year. It is not always clear what the optimal spatial or temporal resolution to study a given system is, and to what extent EO data captures the dynamics well enough to estimate changes in resilience through time. Multi-scale approaches, i.e., tackling a problem using various spatial and temporal resolutions, might make resilience assessments from EO data more robust. Also, it is strongly recommended to first define the scales necessary to understand a system and then choose the appropriate EO dataset, and not vice versa (Senf 2022).
5.6 Data Gaps
Gaps are common in EO data, e.g., due to cloud cover, smoke, snow and frozen ground, fog, and in the case of radar and very-high-resolution optical imagery, because of prioritization in the acquisition plan. For optical data, gaps are particularly a problem in the tropics, where cloud cover is frequent and persistent. For microwave data, large seasonal gaps may occur when the soil is frozen, covered with snow, or inundated. Gaps can cause problems both in theoretical resilience metrics (e.g., AC1, variance) and engineering metrics (recovery time). For example, gaps in a time series can bias AC1 and variance if the number of measurements over a given time period fluctuates, or if there are sporadic large jumps through time (Ben-Yami et al. 2023; Smith and Boers 2023b). Engineering resilience metrics can also be biased by missing data by either under- or over-estimating the length of a recovery due to missing data at the start or end of the perturbation or recovery period. More generally, deseasoning and detrending methods do not always take missing data into account, and can yield inconsistent results when data is sparse (Smith and Boers 2023b; Verbesselt et al. 2016). Many statistical methods can handle time series with data gaps without gap filling (e.g., by computing variance or autocorrelation from only the existing values). However, the gap properties (gap size, frequency etc.) should certainly be taken into account carefully when preprocessing time series to derive robust resilience indicators. For example, masking an artificial stationary time series with the same gap structure as in the observed data can give an estimate of gap-induced biases (Ben-Yami et al. 2023).
5.7 Time Series Length
Most resilience methods require long time series, i.e., at least long enough to cover the recovery of a single disturbance event or even a multiple of the decorrelation time scale when using statistical resilience metrics like the recovery rate λ, AC1 or variance. Especially for systems with slow internal dynamics, such as forests with long regeneration times, this might be problematic given the relatively short length of the satellite record in general, let alone individual instruments. Besides, the time series length should also allow for a joint analysis of the recovery and disturbance regime. For example, as outlined in Sect. 2.2, a system that takes 50 years to recover and is subject to a lower disturbance frequency will be able to restore most important properties, while a system with a higher disturbance frequency than the recovery period will likely have a higher chance of shifting into a state change (Senf and Seidl 2021a, b). Finally, a sufficiently long time series is required to separate cyclic changes from long-term change (see also Sect. 4.2).
However, because EO data acquisitions have become widespread and frequent only recently, many available data sets are relatively short. Very few of the early remote sensing instruments are still being used, and most missions have ended or been supplanted by newer satellites. Thus, for long-term time series analysis such as the quantification of resilience changes, data from multiple satellites need to be considered. This requires a thorough homogenization of random and systematic differences between instruments, either at the level of radiometric or spectral properties (radiances, reflectances, backscatter, or brightness temperatures; e.g., Xiong et al. 2020) or starting from biogeophysical variables derived from single sensors (e.g., Moesinger et al. 2020; Preimesberger et al. 2021).
5.8 Space-for-Time Substitution
Even though most EO products still have insufficient length to robustly assess ecosystem resilience, it is now getting easier to obtain high-resolution spatial data. Consequently, it is an appealing idea to use a space-for-time substitution. The idea to infer temporal information from spatial differences is not new; for instance, different succession stages in forest development can be identified by looking at species composition at different sites (Picket, 1989). Besides such qualitative comparisons, it is also suggested to use a similar space-for-time approach for quantitative studies (Blois et al 2013), which might also be suitable for resilience monitoring. Here, one could for instance study spatial data along an environmental gradient to get insight into the temporal evolution in accordance with the changing conditions (e.g., to assess Amazon rainforest regrowth; Milenkovic 2022). The spatial resilience indicators as outlined in Sect. 4.3, which are justified from the theory of stochastic dynamical systems, are one promising approach in this context—at least in case their validity to describe the resilience of complex ecosystems can be confirmed. Another example of a space-for-time approach is the diagnosis of multimodal distribution of tropical tree cover for a similar range of mean annual precipitation (Staver et al. 2011; Hirota et al. 2011). If the tree cover data can be understood as a representation of the same stochastic system (space-for-time replacement applies), this finding implies the existence of multiple stable states under the same annual rainfall conditions, and hence potential tipping points in tropical forests. Caveats related to the retrieval and classification of tree cover from satellites in this context have been largely resolved (Hanan et al., 2014; Staver and Hansen 2015).
However, there are also caveats and doubts regarding the validity of space-for-time replacements (Damgaard 2019). Most prominently, the fundamental assumption behind space-for-time methods is that temporal and spatial evolution are comparable and have the same drivers, and that other environmental factors, that differ spatially, can be neglected. This assumption is likely to not hold under present-day conditions where CO2 fertilization, climate change and nutrient deposition play together, so that systems are not close to equilibrium. Also, even in equilibrium, there are usually more possible explanations for multimodality of the data distribution than the existence of multiple stable states. For example, a bimodality in tree cover states can also be imposed by bimodal environmental effects like human activity (Wuyts et al. 2017), other climate variables than annual mean precipitation (Good et al. 2016) or by nonlinear and transient growth dynamics (Yin et al. 2014). Also, the noise of a system might often have a higher spatial correlation compared to its temporal correlation. As far as we are aware, there are no comprehensive theoretical studies of this assumption in the context of resilience monitoring. Future research in this direction might reveal the merit of such approaches.
5.9 Impact of Data Artifacts on Resilience Metrics
The need to reduce gaps in satellite datasets (see Sect. 5.6) and to generate longer time series than the lifetime of a satellite, has motivated the construction of datasets from multiple instruments. In resilience research however, multi-instrument records pose serious challenges to the methodology used to detect change, e.g., how much of the change can be attributed to environmental shifts, and how much is simply due to the use of more precise instruments, different satellite retrieval schemes, changes in satellite overpass times, or other measurement changes? harmonization efforts (e.g., Moesinger et al. 2020; Preimesberger et al. 2021) usually focus on mean and variance to enable the detection of trends (e.g., changes in leaf area index through time). Unfortunately, harmonization of higher-order statistics such as autocorrelation has received less attention. This implies that satellite datasets may be biased even though they have been evaluated in terms of mean values, and extra care must be taken to ensure that changes in resilience indicators can really be attributed to environmental change (Smith et al. 2023). Further collaboration is needed between environmental scientists and the data curation and creation community to document the potential impacts of changing satellite mixes on resilience indicators, and to better document what statistical measures can be safely evaluated up to what precision.
Artificial data features that can remain after insufficient preprocessing can also be a cause of an erroneous resilience assessment. In principle, these are general issues with remote sensing products, but can be particularly relevant for resilience estimators even if the products might show unbiased mean values. For example, when aggregating overlapping images from neighboring orbits, the spectral properties of the same object may be different just because the images have different looking angles to the object (Dorigo 2012). This may cause artifacts in the time series, e.g., additional noise, and ultimately lead to a false detection of change. Thus, it is important to report what radiometric and geometric corrections were applied to the satellite data to ensure that the data is analysis ready. Sometimes, particularly in high resolution synthetic aperture radar data with strongly oblique view angles, a ground object itself causes artifacts. For example, when a patch of vegetation is completely removed, e.g., after a clear-cut event, pixels along the patch edge in the near-field of the radar satellite remain in the “shadow”, i.e., are occluded by the neighboring forests. Such radar image artifacts cause an abrupt drop of the signal, which facilitates the deforestation detection (Bouvet et al. 2018), but does not recover, because the pixel remains in the radar shadow of the neighboring forest. Including such pixels in the analysis may lead to a false interpretation of forest recovery.
6 Conclusions, Recommendations, and Outlook
We have outlined conceptual and practical challenges of monitoring ecosystem resilience and resilience changes from EO data. We first discussed the long-standing diversity and subtlety in defining resilience conceptually, beyond the general classes of ecological versus “engineering” resilience. Given the large variety of resilience quantifiers, particular care should be taken in future research articles when naming and describing the particular approach taken. In this regard, “resilience” should be considered a topic or a qualitative group of system properties, and distinguished from particular quantifiers, which should be named more precisely and with more care.
We also discussed methods to detect and quantify abrupt shifts (in ecological systems: disturbances), the recovery time and statistical indicators of linear stability (recovery rate, AC1, variance, spatial correlations and others). Besides the need to acknowledge the general limitations of such methods (like the validity of the stochastic system or statistical robustness), we emphasized several additional caveats arising from data uncertainties. Many of these uncertainties arise from combining different sensors (Smith et al. 2023), from gaps in the time series (Ben-Yami et al. 2023), and from detrending and deseasoning the data (Verbesselt et al. 2016; Smith and Boers 2023b).
It has consequently been shown that for some vegetation types resilience measures are not necessarily consistent with each other even given the same data (Smith and Boers 2023b), which points to potential data uncertainties or simply unsuitable EO data for quantifying the relevant aspects of vegetation dynamics, preventing the use of these measures.
Despite the growing availability of EO data, there remain several key limitations to its use in monitoring terrestrial ecosystem resilience and its changes, particularly in near-real-time applications, maintaining a gap between the development of novel remote sensing techniques and their applications for ecosystem resilience monitoring (also see Senf 2022). Many of these limitations are areas of active research, and can be ameliorated through improved models, data processing schemes, and longer time series.
Based on our assessment above, we make the following key recommendations:
-
1.
There is need for more clarity in resilience studies on (i) the definitions of resilience used, (ii) what the ecological metric actually refers to (vegetation cover, biomass, composition, function, or other), and (iii) the careful choice and clear definition of reference states considered.
-
2.
Innovations are needed in ways for dealing with inherent seasonal and phenological variations in EO time series (e.g., indices such as NDVI). Some systems have high inter-annual variability, and awareness and best practices are required to deal with it.
-
3.
Large opportunities arise from the availability of higher spatial resolution imagery such as the Sentinels (1 and 2), and future Very High Spatial resolution satellite missions (e.g., Home—Copernicus Contributing Missions Online). Key here is to see which methods are able to measure resilience by analyzing spatial variability (heterogeneity), establish whether space-for-time assumptions can be justified, and further explore the possibility of estimating resilience via the potential of artificial intelligence, making use of the multitude of geo-spatial data, on different aspects of the ecosystem, that are currently available (Smith et al. 2023).
-
4.
Time series are becoming longer, and are also available in near real time. They should be processed carefully regarding seasonality and the treatment of gaps and other uncertainties, and the limitations should be documented in a way that allows for quantitative uncertainty estimates of statistical indicators.
-
5.
The suitability of remote-sensing datasets for resilience analyzes should be better verified, especially for high-biomass regions like the tropical forests. As biomass might be the most indicative parameter of rainforests, radar and radiometry in the very low frequency range (P- or L-band) should be desirable due to the deeper penetration from below the canopy. Here, upcoming satellite missions such as the European Copernicus Biomass and American NISAR mission are promising. Furthermore, future availability of in-situ measurements, for example based on terrestrial or airborne LiDAR campaigns, are recommended to evaluate the different data sets, especially in these regions.
-
6.
Novel measurements such as land surface temperature (e.g., the future Copernicus Land Surface Temperature Monitoring satellite mission, NASA’s CIRiS CubeSat, and commercial space based alternatives), vegetation structure (e.g., vegetation height via GEDI, ICESAT-2, and future BIOMASS mission) and fluorescence (e.g., via the future ESA FLEX satellite mission) provide direct biophysical variables to monitor terrestrial vegetation dynamics of the ecosystem. Before directly utilizing them in describing ecosystem change and recovery, one should first understand the uncertainties and limitations associated with those novel products as they are often optimized for other applications than resilience monitoring, or the pre-processing is simplified to foster big-data handling and processing.
-
7.
Knowledge transfer and closer collaborations between marine, aquatic and terrestrial ecologists and remote sensing experts may create synergies in monitoring ecosystem resilience in different realms.
Overall, we conclude that it is beneficial that there are more and more applications of different resilience indicators (“early warning signals”) to Earth observations (EO). These observations can provide advantages, e.g., higher spatial coverage and hence spatial indicators, potentially by leveraging space-for-time relationships. However, it is vital to be aware of the caveats associated with data generation.
We also note that the research community designing retrieval algorithms and generating EO datasets on the one hand, and the community interested in diagnosing and interpreting ecosystem resilience (often ecologists, climate scientists and applied mathematicians) on the other, are still not in sufficiently close scientific contact. This brings the risk of generating datasets without a well-defined scope of use, and the risk of (mis)using satellite datasets for resilience monitoring despite technical and statistical biases.
We hence see the need for closer collaborations that help close the gap between what EO data can offer and the requirements of EO users. Specific questions of this dialog should at least comprise: What variables are needed for what purpose? On what resolution? Which statistical properties should be optimized, and how are biases communicated? How should gaps and multi-sensor products be compiled by EO scientists? We specifically recommend better transparency and documentation in this regard. Only then can the value of long and frequent observations from space live up to their great potential, and help us get a clear view on the resilience of the Earth system, and help society navigate into a safe future.
References
Aminikhanghahi S, Cook DJ (2017) A survey of methods for time series change point detection. Knowl Inf Syst 51:339–367
Anderegg WRL et al (2020) Divergent forest sensitivity to repeated extreme droughts. Nat Clim Change. https://doi.org/10.1038/s41558-020-00919-1
Angeler A (2016) Quantifying resilience. J Appl Ecol 53(3):617-624. https://besjournals.onlinelibrary.wiley.com/doi/epdf/10.1111/1365-2664.12649
Arani B et al (2021) Exit time as a measure of ecological resilience. Science. https://doi.org/10.1126/science.aay4895
Armstrong McKay D et al (2022) Exceeding 1.5 °C global warming could trigger multiple climate tipping points. Science. https://doi.org/10.1126/science.abn79
Arnoldi J-F, Loreau M, Haegmann B (2016) Resilience, reactivity and variability: a mathematical comparison of ecological stability measures. J Theor Biol 389:47–59
Bagniewski W, Ghil M, Rousseau DD (2021) Automatic detection of abrupt transitions in paleoclimate records. Chaos Interdiscip J Nonlinear Sci 31:113129. https://doi.org/10.1063/5.0062543
Bai J, Perron P (2003) Computation and analysis of multiple structural change models. J Appl Econom 18:1–22
Balogun A-L et al (2020) Spatio-temporal analysis of oil spill impact and recovery pattern of coastal vegetation and wetland using multispectral satellite landsat 8-OLI imagery and machine learning models. Remote Sens 2020(12):1225
Basseville M, Nikiforov IV (1993) Detection of abrupt changes. Theory and application/Michèle Basseville, Igor V Nikiforov, Englewood Cliffs, N.J.: Prentice Hall; London: Prentice-Hall International (Prentice Hall information and system sciences series). Available online at http://people.irisa.fr/Michele.Basseville/kniga/kniga.pdf.
Bastiaansen R, Jaïbi O, Deblauwe V, Eppinga MB, Siteur K, Siero E, Rietkerk M (2018) Multistability of model and real dryland ecosystems through spatial self-organization. Proc Natl Acad Sci 115(44):11256–11261
Bastiaansen R, Doelman A, Eppinga MB, Rietkerk M (2020) The effect of climate change on the resilience of ecosystems with adaptive spatial pattern formation. Ecol Lett 23(3):414–429. https://doi.org/10.1111/ele.13449
Bastiaansen R, Dijkstra HA, von der Heydt AS (2021) Multivariate estimations of equilibrium climate sensitivity from short transient warming simulations. Geophys Res Lett 48:e2020GL091090. https://doi.org/10.1029/2020GL091090
Bastos A, Gouveia CM, DaCamara CC, Trigo RM (2011) Modeling post-fire vegetation recovery in Portugal. Biogeosciences 8:3593–3607. https://doi.org/10.5194/bg-8-3593-2011
Bastos A, Orth R, Reichstein M, Ciais P, Viovy N, Zaehle S, Anthoni P, Arneth A, Gentine P, Joetzjer E, Lienert S (2021) Vulnerability of European ecosystems to two compound dry and hot summers in 2018 and 2019. Earth Syst Dyn 12:1015–1035. https://doi.org/10.5194/esd-12-1015-2021
Bathiany S, Claussen M, Fraedrich K (2013) Detecting hotspots of atmosphere–vegetation interaction via slowing down—Part 1: a stochastic approach. Earth Syst Dynam 4:63–78. https://doi.org/10.5194/esd-4-63-2013
Bathiany S et al (2016a) Beyond bifurcation: using complex models to understand and predict abrupt climate change. Dyn Stat Clim Syst 2016:1–31. https://doi.org/10.1093/climsys/dzw004
Bathiany S, van der Bolt B, Williamson MS et al (2016b) Statistical indicators of Arctic sea-ice stability—prospects and limitations. Cryosphere 10:1631–1645. https://doi.org/10.5194/tc-10-1631-2016
Bathiany S, Hidding J, Scheffer M (2020) Edge detection reveals abrupt and extreme climate events. J Clim 33(15):6399–6421
Beaulieu C, Chen J (2012) Sarmiento JL (2012): Change-point analysis as a tool to detect abrupt climate variations. Philos Trans Royal Soc a: Math Phys Eng Sci 370(1962):1228–1249. https://doi.org/10.1098/rsta.2011.0383
Ben-Yami M, Skiba V, Bathiany S et al (2023) Uncertainties in critical slowing down indicators of observation-based fingerprints of the Atlantic overturning circulation. Nat Commun 14:8344. https://doi.org/10.1038/s41467-023-44046-9
Blois JL, Williams JW, Fitzpatrick MC, Jackson ST, Ferrier S (2013) Space can substitute for time in predicting climate-change effects on biodiversity. Proc Natl Acad Sci 110(23):9374–9379. https://doi.org/10.1073/pnas.1220228110
Boers N (2021) Observation-based early-warning signals for a collapse of the Atlantic meridional overturning circulation. Nat Clim Chang 11:680–688
Boers N, Ghil M, Stocker T (2022) Theoretical and paleoclimatic evidence for abrupt transitions in the Earth system. Environ Res Lett 17:093006. https://doi.org/10.1088/1748-9326/ac8944
Boettner C, Boers N (2022) Critical slowing down in dynamical systems driven by nonstationary correlated noise. Phys Rev Res 4:013230. https://doi.org/10.1103/PhysRevResearch.4.013230
Boulton CA, Lenton TM (2015) Slowing down of North Pacific climate variability and its implications for abrupt ecosystem change. Proc Natl Acad Sci USA 112:11496–11501. https://doi.org/10.1073/pnas.1501781112
Boulton CA et al (2022) Pronounced loss of Amazon rainforest resilience since the early 2000s. Nat Clim Change 12:271–278. https://doi.org/10.1038/s41558-022-01287-8
Bouvet A et al (2018) Use of the SAR shadowing effect for deforestation detection with Sentinel-1 time series. Remote Sens 10(8):1250
Buma B (2012) Evaluating the utility and seasonality of NDVI values for assessing post-disturbance recovery in a subalpine forest. Environ Monit Assess 184:3849–3860. https://doi.org/10.1007/s10661-011-2228-y
Bury TM et al (2021) Deep learning for early warning signals of tipping points. PNAS 118(39):e2106140118. https://doi.org/10.1073/pnas.2106140118
Canny J (1986) A computational approach to edge detection. IEEE Trans Pattern Anal Mach Intell. https://doi.org/10.1109/TPAMI.1986.4767851
Carpenter S et al (2001) From metaphor to measurement: resilience of What to What? Ecosystems 2001(4):765–781. https://doi.org/10.1007/s10021-001-0045-9
Caughlin TT, Barber Alvarez-Buylla C, Asner GP, Glenn NF, Bohlman SA, Wilson CH (2021) Monitoring tropical forest succession at landscape scales despite uncertainty in Landsat time series. Ecol Appl 31(1):e02208. https://doi.org/10.1002/eap.2208
Cavanaugh KC, Reed DC, Bell TW, Castorani MCN, Beas-Luna R (2019) Spatial Variability in the Resistance and Resilience of Giant Kelp in Southern and Baja California to a Multiyear Heatwave. Front Mar Sci 6:413. https://doi.org/10.3389/fmars.2019.00413
Chekroun MD, Simonnet E, Ghil M (2011) Stochastic climate dynamics: random attractors and time-dependent invariant measures. Physica D 240(21):1685–1700
Chirici G, Giannetti F, Mazza E et al (2020) Monitoring clearcutting and subsequent rapid recovery in Mediterranean coppice forests with Landsat time series. Ann for Sci 77:40. https://doi.org/10.1007/s13595-020-00936-2
Chu PS (2002) Large-scale circulation features associated with decadal variations of tropical cyclone activity over the Central North Pacific. J Clim 15:2678–2689
Ciemer C et al (2019) Higher resilience to climatic disturbances in tropical vegetation exposed to more variable rainfall. Nat Geosci 12:174–179. https://doi.org/10.1038/s41561-019-0312-z
Cionni I, Visconti G, Sassi F (2004) Fluctuation dissipation theorem in a general circulation model. Geophys Res Lett 31:L09206. https://doi.org/10.1029/2004GL019739
Clarke JJ, Huntingford C, Ritchie PD, Cox PM (2023) Seeking more robust early warning signals for climate tipping points: the ratio of spectra method (ROSA). Environ Res Lett 18(3):035006. https://doi.org/10.1088/1748-9326/acbc8d
Clemente KJE, THomsen MS, Zimmermann RC (2023) Thomsen MS and Zimmermann RC (2023) The vulnerability and resilience of seagrass ecosystems to marine heatwaves in New Zealand: a remote sensing analysis of seascape metrics using PlanetScope imagery. Remote Sens Ecol Conserv 9(6):803–819
Cleveland RB et al (1990) STL: a seasonal-trend decomposition procedure based on loess. J off Stat 6(1):3–73
Cranko Page J, De Kauwe MG, Abramowitz G, Cleverly J, Hinko-Najera N, Hovenden MJ, Liu Y, Pitman AJ, Ogle K (2022) Examining the role of environmental memory in the predictability of carbon and water fluxes across Australian ecosystems. Biogeosciences 19:1913–1932. https://doi.org/10.5194/bg-19-1913-2022
Cutter SL (2016) Resilience to What? Resilience for Whom? Geogr J 182(2):110–113. https://doi.org/10.1111/geoj.12174
Dakos V, Kéfi S (2022) Ecological resilience: what to measure and how. Environ Res Lett 17:043003. https://doi.org/10.1088/1748-9326/ac5767
Dakos V, van Nes EH, Donangelo R, Fort H, Scheffer M (2010) Spatial correlation as leading indicator of catastrophic shifts. Thyroid Res 3:163–174. https://doi.org/10.1007/s12080-009-0060-6
Dakos V, van Nes EH, D’Odorico P, Scheffer M (2012) Robustness of variance and autocorrelation as indicators of critical slowing down. Ecology 93:264–271. https://doi.org/10.1890/11-0889.1
Damgaard C (2019) A critique of the space-for-time substitution practice in community ecology. Trends Ecol Evol 34(5):416–421. https://doi.org/10.1016/j.tree.2019.01.013
De Keersmaecker W et al (2022) Evaluating recovery metrics derived from optical time series over tropical forest ecosystems. Remote Sens Environ 274:112991. https://doi.org/10.1016/j.rse.2022.112991
Deblauwe V, Barbier N, Couteron P, Lejeune O, Bogaert J (2008) The global biogeography of semi-arid periodic vegetation patterns. Glob Ecol Biogeogr 17:715–723. https://doi.org/10.1111/j.1466-8238.2008.00413.x
Deblauwe V, Couteron P, Bogaert J, Barbier N (2012) Determinants and dynamics of banded vegetation pattern migration in arid climates. Ecol Monogr 82(1):3–21. https://doi.org/10.1890/11-0362.1
Donangelo R, Fort H, Dakos V, Scheffer M, van Nes EH (2010) Early warnings for catastrophic shifts in ecosystems: comparison between spatial and temporal indicators. Int J Bifurc Chaos 20:315–321. https://doi.org/10.1142/S0218127410025764
Donges J et al (2011) Nonlinear detection of paleoclimate-variability transitions possibly related to human evolution. PNAS 108(51):20422–20427. https://doi.org/10.1073/pnas.1117052108
Dorigo WA (2012) Improving the robustness of cotton status characterization by radiative transfer model inversion of multi-angular CHRIS/PROBA data. IEEE J Sel Top Appl Earth Obs Remote Sens 5(1):18–29. https://doi.org/10.1109/JSTARS.2011.2171181
Drijfhout S (2015) Catalog of abrupt shifts in intergovernmental panel on climate change climate models. Proc Natl Acad Sci USA 112:E5777–E5786. https://doi.org/10.1073/pnas.1511451112
Dubayah R, Tang H, Armston J, Luthcke S, Hofton M, Blair J: GEDI L2B canopy cover and vertical profile metrics data global footprint level V002, Publisher: NASA EOSDIS land processes DAAC, Release Date: 2021-04-16T00:00:00.000Z, https://doi.org/10.5067/GEDI/GEDI02_B.002
Ducré-Robitaille J-F, Vincent LA, Boulet G (2003) Comparison of techniques for detection of discontinuities in temperature series. Int J Climatol 23:1087–1101. https://doi.org/10.1002/joc.924
Eltahir EAB, Bras RL (1996) Precipitation recycling. Rev Geophys 34(3):367–378. https://doi.org/10.1029/96rg01927
Eppinga MB, Rietkerk M, Borren W, Lapshina ED, Bleuten W, Wassen MJ (2008) Regular surface patterning of peatlands: confronting theory with field data. Ecosystems 11:520–536. https://doi.org/10.1007/s10021-008-9138-z
Erhardt T et al (2019) Decadal-scale progression of the onset of Dansgaard-Oeschger warming events. Clim past 15:811–825
Fisher JB et al (2020) ECOSTRESS: NASA’s next generation mission to measure evapotranspiration from the international space station. Water Resour Res. https://doi.org/10.1029/2019WR026058
Flach M et al (2017) Multivariate anomaly detection for Earth observations: a comparison of algorithms and feature extraction techniques. Earth Syst Dynam 8:677–696. https://doi.org/10.5194/esd-8-677-2017
Flach M, Sebastian S, Fabian G, Ana B, Alexander B, Miguel DM (2018) Contrasting biosphere responses to hydrometeorological extremes: revisiting the 2010 western Russian heatwave. Biogeosciences 15:6067–6085. https://bg.copernicus.org/articles/15/6067/2018/bg-15-6067-2018.pdf
Frazier RJ, Coops NC, Wulder MA, Hermosilla T, White JC (2018) Analyzing spatial and temporal variability in short-term rates of post-fire vegetation return from Landsat time series. Remote Sens Environ 205:32–45. https://doi.org/10.1016/j.rse.2017.11.007
Freeman ME et al (2017) Defining the fire trap: extension of the persistence equilibrium model in mesic savannas. Austral Ecol 2017(42):890–899. https://doi.org/10.1111/aec.12516
Fu Z et al (2020) Sensitivity of gross primary productivity to climatic drivers during the summer drought of 2018 in Europe. Philos Trans Royal Soc b: Biol Sci 375(1810):20190747
Gallagher C et al (2013) Changepoint detection in climate time series with long-term trends. J Clim 26(14):4994–5006
Gaspard P, Nicolas G, Provata A (1995) Spectral signature of the pitchfork bifurcation: Liousville equation approach. Phys Rev E 51:74. https://doi.org/10.1103/PhysRevE.51.74
Gessler A et al (2020) The way back: recovery of trees from drought and its implication for acclimation. New Phytol 228(6):1704–1709
Good P et al (2016) Are strong fire–vegetation feedbacks needed to explain the spatial distribution of tropical tree cover? Glob Ecol Biogr 25(1):16–25. https://doi.org/10.1111/geb.12380
Goswami B et al (2018) Abrupt transitions in time series with uncertainties. Nat Commun. https://doi.org/10.1038/s41467-017-02456-6
Grimm V, Calabrese JM (2011) What is resilience? A short introduction. In: Deffuant G, Gilbert N (eds) In: viability and resilience of complex systems understanding complex systems. Springer, Heidelberg
Gritsun A, Branstator G (2007) Climate response using a three-dimensional operator based on the fluctuation–dissipation theorem. J Atmos Sci 64:2558–2575. https://doi.org/10.1175/JAS3943.1
Guttal V, Jayaprakash C (2008a) Changing skewness: an early warning signal of regime shifts in ecosystems. Ecol Lett 11(5):450–460. https://doi.org/10.1111/j.1461-0248.2008.01160.x
Guttal V, Jayaprakash C (2008b) Spatial variance and spatial skewness: leading indicators of regime shifts in spatial ecological systems. Theor Ecol 2:3–12. https://doi.org/10.1007/s12080-008-0033-1
Hanan NP et al (2014) Analysis of stable states in global savannas: is the CART pulling the horse? Glob Ecol Biogeogr 23(3):259–263. https://doi.org/10.1111/geb.12122
Helfgott AER (2015) Operationalizing resilience: conceptual, mathematical and participatory frameworks for understanding, measuring and managing resilience, Ph.D. thesis. Adelaide, SA: The University of Adelaide
Hansen MC et al (2013) High-resolution global maps of 21st-century forest cover change. Science 342(6160):850–853. https://doi.org/10.1126/science.1244693
Hansen WD et al (2022) Global forests are influenced by the legacies of past inter-annual temperature variability. Environ Res Ecol 1:011001. https://doi.org/10.1088/2752-664X/ac6e4a
Hastings A, Wysham DB (2010) (2010) Regime shifts in ecological systems can occur with no warning. Ecol Lett 13:464–472. https://doi.org/10.1111/j.1461-0248.2010.01439.x
Held H, Kleinen T (2004a) Detection of climate system bifurcations by degenerate fingerprinting. Geophys Res Lett 31:L23207. https://doi.org/10.1029/2004GL020972
Hirota M et al (2011) Global resilience of tropical forest and savanna to critical transitions. Science 334(6053):232–235. https://doi.org/10.1126/science.1210657
Hoffmann WA (2020) Better lucky than good: How savanna trees escape the fire trap in a variable world. Ecology 101(1):e02895. https://doi.org/10.1002/ecy.2895
Holling CS (1973) Resilience and stability of ecological systems. Annu Rev Ecol Syst 4:1–23. https://doi.org/10.1146/annurev.es.04.110173.000245
Holling CS (1996) Engineering within ecological constraints. Chapter: engineering resilience versus ecological resilience. National academies of sciences, engineering, and medicine. 1996. Engineering within ecological constraints. Washington, DC: The National Academies Press. https://doi.org/10.17226/4919
Ingrisch J, Bahn M (2018) Toward a comparable quantification of resilience. Trends Ecol Evol 33(4):251–259. https://doi.org/10.1016/j.tree.2018.01.013
Jamali S, Seaquist J, Eklundh L, Ardö J (2014) Automated mapping of vegetation trends with polynomials using NDVI imagery over the Sahel. Remote Sens Environ 141:79. https://doi.org/10.1016/j.rse.2013.10.019
Jentzsch A, White P (2019) A theory of pulse dynamics and disturbance in ecology. Ecology 100(7):e02734
Johnson EA, Miyanishi K (2008) Testing the assumptions of chronosequences in succession. Ecol Lett 11(5):419–431. https://doi.org/10.1111/j.1461-0248.2008.01173.x
Kéfi S, Dakos V, Scheffer M, van Nes E, Rietkerk M (2013) Early warning signals also precede non-catastrophic transitions. Oikos 112(5):641–648
Kéfi S, Guttal V, Brock WA, Carpenter SR, Ellison AM, Livina VN, Dakos V (2014) Early warning signals of ecological transitions: methods for spatial patterns. PLoS ONE 9(3):e92097. https://doi.org/10.1371/journal.pone.0092097
Kleinen T, Held H, Petschel-Held G (2003) The potential role of spectral properties in detecting thresholds in the Earth system: application to the thermohaline circulation. Ocean Dyn 53:53–63. https://doi.org/10.1007/s10236-002-0023-6
Knudby A et al (2014) Remote sensing and modeling of coral reef resilience. In: Finkl CW, Makowski C (eds) Remote sensing and modeling: advances in coastal and marine resources, coastal research library 9. Springer, Switzerland
Konings AG, Rao K, Steele-Dunne SC (2019) Macro to micro: microwave remote sensing of plant water 1085 content for physiology and ecology. New Phytol 223:1166–1172. https://doi.org/10.1111/nph.15808
Krakovská H, Kuehn C, Longo I (2023) Resilience of dynamical systems. Eur J Appl Math. https://doi.org/10.1017/S0956792523000141
Kubo R (1966) The fluctuation-dissipation theorem. Rep Prog Phys 1966(29):255. https://doi.org/10.1088/0034-4885/29/1/306
Kuehn C (2011) A mathematical framework for critical transitions: Bifurcations, fast–slow systems and stochastic dynamics. Physica D 240(12):1020–1035. https://doi.org/10.1016/j.physd.2011.02.012
Kutz JN, Brunton SL, Brunton BW, and Proctor JL (2016) Dynamic mode decomposition: data-driven modeling of complex systems. Society for Industrial and Applied Mathematics
Kuznetsov YA (2004) Introduction to dynamical systems. In: elements of applied bifurcation theory. Applied mathematical sciences, vol 112. Springer, New York, NY. https://doi.org/10.1007/978-1-4757-3978-7_
Lazante JR (1996) Resistant, robust and non-parametric techniques for the analysis of climate data: theory and examples, including applications to historical radiosonde station data. Int J Climatol 16(11):1197–1226. https://doi.org/10.1002/(SICI)1097-0088(199611)16:11%3c1197::AID-JOC89%3e3.0.CO;2-L
Lechner AM, Foody GM, Boyd DS (2020) Applications in remote sensing to forest ecology and management. One Earth 2(5):405–412. https://doi.org/10.1016/j.oneear.2020.05.001
Leith CE (1975) Climate response and fluctuation dissipation. J Atmos Sci 32:2022–2026
Lenton TM et al (2008) Tipping elements in the Earth’s climate system. PNAS 105(6):1786–1793. https://doi.org/10.1073/pnas.0705414105
Lenton TM et al (2022) A resilience sensing system for the biosphere. Phil Trans Roy Soc 377(1857):20210383. https://doi.org/10.1098/rstb.2021.0383
Lenton TM, Abrams JF, Bartsch A et al (2024) Remotely sensing potential climate change tipping points across scales. Nat Commun 15:343. https://doi.org/10.1038/s41467-023-44609-w
Li X, Wigneron JP, Frappart F, Fan L, Ciais P, Fensholt R, Moisy C (2021) Global-scale assessment and inter-comparison of recently developed/reprocessed microwave satellite vegetation optical depth products. Remote Sens Environ 253:112208. https://doi.org/10.1016/j.rse.2020.112208
Li N, Sippel S, Winkler AJ, Mahecha MD, Reichstein M, Bastos A (2022) Interannual global carbon cycle variations linked to atmospheric circulation variability. Earth Syst Dynam 13:1505–1533. https://doi.org/10.5194/esd-13-1505-2022
Linscheid N, Mahecha MD, Rammig A, Carvalhais N, Gans F, Nelson JA et al (2021) Time-scale dependent relations between Earth observation based proxies of vegetation productivity. Geophys Res Lett 48:e2021GL093285. https://doi.org/10.1029/2021GL093285
Liu YY, de Jeu RAM, McCabe MF, Evans JP, van Dijk AIJM (2011) Global long-term passive microwave satellite-based retrievals of vegetation optical depth. Geophys Res Lett. https://doi.org/10.1029/2011GL048684
Liu S et al (2023) The overlooked contribution of trees outside forests to tree cover and woody biomass across Europe. Sci Adv. https://doi.org/10.1126/sciadv.adh4097
Lloret F, Keeling EG, Sala A (2011) Components of tree resilience: effects of successive low-growth episodes in old ponderosa pine forests. Oikos 120(12):1909–1920. https://doi.org/10.1111/j.1600-0706.2011.19372.x
Mack MC et al (2021) Carbon loss from boreal forest wildfires offset by increased dominance of deciduous trees. Science 372:280–283. https://doi.org/10.1126/science.abf3903
Marwan N, Donges JF, Zou Y, Donner RV, Kurths J (2009) Complex network approach for recurrence analysis of time series. Phys Lett A 373:4246–4254. https://doi.org/10.1016/j.physleta.2009.09.042
Masiliunas D, Tsendbazar N-E, Herold M, Verbesselt J (2021) BFAST lite: a lightweight break detection method for time series analysis. Remote Sens 13:3308. https://doi.org/10.3390/rs13163308
Matyasovszky I (2011) Detecting abrupt climate changes on different time scales. Theor Appl Climatol 105:445–454. https://doi.org/10.1007/s00704-011-0401-4
McDowell NG et al (2008) Mechanisms of plant survival and mortality during drought: why do some plants survive while others succumb to drought? New Phytol 178(4):719–739
McDowell NG et al (2016) Multi-scale predictions of massive conifer mortality due to chronic temperature rise. Nat Clim Change 6:295–300
McDowell NG et al (2020) Pervasive shifts in forest dynamics in a changing world. Science 368:eaaz9463. https://doi.org/10.1126/science.aaz9463
Milenković M, Reiche J, Armston J, Neuenschwander A, De Keersmaecker W, Herold M, Verbesselt J (2022) Assessing Amazon rainforest regrowth with GEDI and ICESat-2 data. Sci Remote Sens 5:100051. https://doi.org/10.1016/j.srs.2022.100051
Mitra C, Kurths J, Donner R (2015) An integrative quantifier of multistability in complex systems based on ecological resilience. Sci Rep 5:16196. https://doi.org/10.1038/srep16196
Moesinger L, Dorigo W, de Jeu R, van der Schalie R, Scanlon T, Teubner I, Forkel M (2020) The global long-term microwave vegetation optical depth climate archive (VODCA). Earth Syst Sci Data 12:177–196. https://doi.org/10.5194/essd-12-177-2020
Morresi D, Vitali A, Urbinati C, Garbarino M (2019) Forest spectral recovery and regeneration dynamics in stand-replacing wildfires of central Apennines derived from Landsat time series. Remote Sensing 11(3):308. https://doi.org/10.3390/rs11030308
Morton DC et al (2014) Amazon forests maintain consistent canopy structure and greenness during the dry season. Nature 506:221–224. https://doi.org/10.1038/nature13006
Mudelsee M (2000) Ramp function regression: a tool for quantifying climate transitions. Comput Geosci 26:293–307
Nikinmaa L, Lindner M, Cantarello E et al (2020) Reviewing the use of resilience concepts in forest sciences. Curr for Rep 6:61–80. https://doi.org/10.1007/s40725-020-00110-x
Nimmo DG, Mac Nally R, Cunningham SC, Haslem A, Bennett AF (2015) Vive la résistance: reviving resistance for 21st century conservation. Trends Ecol Evol 30(9):516–523. https://doi.org/10.1016/j.tree.2015.07.008
Oborny B, Meszena G, Szabo G (2005) Dynamics of populations on the verge of extinction. Oikos 109:291–296
Ogle K et al (2015) Quantifying ecological memory in plant and ecosystem processes. Ecol Lett 18(3):221–235
Özkundakci D, Lehmann MK (2019) Lake resilience: concept, observation and management. NZ J Mar Freshwat Res 53(4):481–488. https://doi.org/10.1080/00288330.2019.1647855
Perreault L, Bernier J, Bobée B, Parent E (2000) Bayesian change-point analysis in hydrometeorological time series. Part 1. The normal model revisited. J Hydrol 235:221–241
Pickett ST (1989) Space-for-time substitution as an alternative to long-term studies. Long-term studies in ecology: approaches and alternatives. Springer, Newyork, pp 110–135
Pimm SL (1984) The complexity and stability of ecosystems. Nature 307:321–326. https://doi.org/10.1038/307321a0
Potapov P et al (2021) Mapping global forest canopy height through integration of GEDI and Landsat data. Remote Sens Environ 253:112165. https://doi.org/10.1016/j.rse.2020.112165
Poyatos R et al (2013) Drought-induced defoliation and long periods of near-zero gas exchange play a key role in accentuating metabolic decline of Scots pine. New Phytol 2013(200):388–401. https://doi.org/10.1111/nph.12278
Preimesberger W, Scanlon T, Su C-H, Gruber A, Dorigo W (2021) Homogenization of structural breaks in the global ESA CCI soil moisture multisatellite climate data record. IEEE Trans Geosci Remote Sens 59(4):2845–2862. https://doi.org/10.1109/TGRS.2020.3012896
Reeves J et al (2007) A review and comparison of changepoint detection techniques for climate data. J Appl Met Clim 46:900–915
Riechers K, Boers N (2021) Significance of uncertain phasing between the onsets of stadial–interstadial transitions in different Greenland ice core proxies. Clim past 17(4):1751–1775. https://doi.org/10.5194/cp-17-1751-2021
Rodionov SN (2004) A sequential algorithm for testing climate regime shifts. Geophys Res Lett. https://doi.org/10.1029/2004GL019448
Rodionov SN (2006) Use of prewhitening in climate regime shift detection. Geophys Res Lett. https://doi.org/10.1029/2006GL025904
Rousseau DD et al (2017) (MIS3 & 2) millennial oscillations in Greenland dust and Eurasian aeolian records—a paleosol perspective. Quatern Sci Rev 169:99–113. https://doi.org/10.1016/j.quascirev.2017.05.020
Ruehr NK et al (2019) Beyond the extreme: recovery of carbon and water relations in woody plants following heat and drought stress. Tree Physiol 39:1285–1299. https://doi.org/10.1093/treephys/tpz032
Saatchi S (2019) sar methods for mapping and monitoring forest biomass. Ch. 5, SAR handbook, comprehensive methodologies for forest monitoring and biomass estimation, April
Saatchi S (2019) SAR methods for mapping and monitoring forest biomass. SAR handbook: comprehensive methodologies for forest monitoring and biomass estimation. Eds. Flores A, Herndon K, Thapa R, Cherrington E. NASA. 2019. https://doi.org/10.25966/hbm1-ej07
Samanta A, Ganguly S, Vermote E, Nemani RR, Myneni RB (2012) Why is remote sensing of Amazon forest greenness so challenging? Earth Interact 16:1–14. https://doi.org/10.1175/2012EI440.1
Scheffer M, Jeppesen E (2007) Regime shifts in Shallow Lakes. Ecosystems 10:1–3
Scheffer M, Bascompte J, Brock WA et al (2009) Early-warning signals for critical transitions. Nature 461:53–59. https://doi.org/10.1038/nature08227
Schmidt L et al (2023) Assessing the sensitivity of multi-frequency passive microwave vegetation optical depth to vegetation properties. Biogeosciences 20:1027–1046. https://doi.org/10.5194/bg-20-1027-2023
Schütz N, Holschneider M (2011) Detection of trend changes in time series using Bayesian inference. Phys Rev E 84:021120. https://doi.org/10.1103/PhysRevE.84.021120
Seidl R, Turner MG (2022) Post-disturbance reorganization of forest ecosystems in a changing world. PNAS 119(28):e2202190119. https://doi.org/10.1073/pnas.220219011
Sellers PJ (1985) Canopy reflectance, photosynthesis and transpiration. Int J Remote Sens 6:1335–1372. https://doi.org/10.1080/01431168508948283
Senf C (2022) Seeing the system from above: the use and potential of remote sensing for studying ecosystem dynamics. Ecosystems 25:1719–1737. https://doi.org/10.1007/s10021-022-00777-2
Senf C, Seidl R (2021a) Mapping the forest disturbance regimes of Europe. Nat Sustain 4:63–70. https://doi.org/10.1038/s41893-020-00609-y
Senf C, Seidl R (2021b) Post-disturbance canopy recovery and the resilience of Europe’s forests. Glob Ecol Biogeogr. https://doi.org/10.1111/geb.13406
Senf C, Müller J, Seidl R (2019) Post-disturbance recovery of forest cover and tree height differ with management in Central Europe. Landscape Ecol 34:2837–2850. https://doi.org/10.1007/s10980-019-00921-9
Senf C et al (2020) A generalized regression-based unmixing model for mapping forest cover fractions throughout three decades of Landsat data. Remote Sens Environ 240:111691
Smith T, Boers N (2023a) Global vegetation resilience linked to water availability and variability. Nat Commun 14:498. https://doi.org/10.1038/s41467-023-36207-7
Smith T, Boers N (2023b) Reliability of vegetation resilience estimates depends on biomass density. Nat Ecol Evol. https://doi.org/10.1038/s41559-023-02194-7
Smith T, Traxl D, Boers N (2022) Empirical evidence for recent global shifts in vegetation resilience. Nat Clim Chang 12:477–484. https://doi.org/10.1038/s41558-022-01352-2
Smith T, Zotta R-M, Boulton CA, Lenton TM, Dorigo W, Boers N (2023) Reliability of resilience estimation based on multi-instrument time series. Earth Syst Dynam 14:173–183. https://doi.org/10.5194/esd-14-173-2023
Sohn JA, Saha S, Bauhus J (2016) Potential of forest thinning to mitigate drought stress: a meta-analysis. For Ecol Manage 380:261–273
Solé RV, Manrubia SC, Luque B, Delgado J, Bascompte J (1996) Phase transitions and complex systems. Complexity 1:13–26. https://doi.org/10.1002/cplx.6130010405
Staver AC, Hansen MC (2015) Analysis of stable states in global savannas: is the CART pulling the horse?—a comment. Glob Ecol Biogeogr. https://doi.org/10.1111/geb.12285
Staver AC et al (2011) The global extent and determinants of savanna and forest as alternative biome states. Science 334(6053):230–232. https://doi.org/10.1126/science.1210465
Stritih A, Senf C, Seidl R (2023) Alternative states in the structure of mountain forests across the Alps and the role of disturbance and recovery. Landscape Ecol 38:933–947. https://doi.org/10.1007/s10980-023-01597-y
Tahsin S, Medeiros SC, Singh A (2018) Assessing the resilience of coastal wetlands to extreme hydrologic events using vegetation indices: a review. Remote Sens 10:1390
Tao S, Chave J, Frison PL, Le Toan T, Ciais P, Fang J, Saatchi S (2022) Increasing and widespread vulnerability of intact tropical rainforests to repeated droughts. Proc Natl Acad Sci 119(37):e2116626119
Thurm EA, Uhl E, Pretzsch H (2016) Mixture reduces climate sensitivity of Douglas-fir stem growth. For Ecol Manage 376:205–220. https://doi.org/10.1016/j.foreco.2016.06.020
Turner MG (2010) Disturbance and landscape dynamics in a changing world. Ecology. https://doi.org/10.1890/10-0097.1
van de Leemput I et al (2016) Multiple feedbacks and the prevalence of alternate stable states on coral reefs. Coral Reefs 2016(35):857–865. https://doi.org/10.1007/s00338-016-1439-7
van der Heide T (2011) Positive feedbacks in seagrass ecosystems—evidence from large-scale empirical data. PLoS ONE 6(1):e16504
van Kampen N (1981) Stochastic Processes in Physics and Chemistry. North Holland, New York
van Nes EH, Scheffer M (2007) Slow recovery from perturbations as a generic indicator of a nearby catastrophic shift. Am Nat 169:738–747. https://doi.org/10.1086/516845
van Meerbeek K, Jucker T, Svenning J-C (2021) Unifying the concepts of stability and resilience in ecology. J Ecol 109(9):3114–3132. https://doi.org/10.1111/1365-2745.13651
van Schaik E et al (2018) Changes in surface hydrology, soil moisture and gross primary production in the Amazon during the 2015/2016 El Niño. Phil Trans Roy Soc 373(1760):20180084
Veldhuis MP, Martinez-Garcia R, Deblauwe V, Dakos V (2022) Remotely-sensed slowing down in spatially patterned dryland ecosystems. Ecography 2022:e06139. https://doi.org/10.1111/ecog.06139
Verbesselt J et al (2010a) Detecting trend and seasonal changes in satellite image time series. Remote Sens Environ 114:106–115. https://doi.org/10.1016/j.rse.2009.08.014
Verbesselt J et al (2010b) Phenological change detection while accounting for abrupt and gradual trends in satellite image time series. Remote Sens Environ 114(12):2970–2980. https://doi.org/10.1016/j.rse.2010.08.003
Verbesselt J, Umlauf N, Hirota M, Holmgren M, van Nes EH, Herold M, Scheffer M (2016) Remotely sensed resilience of tropical forests. Nat Clim Change 6(11):1028–1031. https://doi.org/10.1038/nclimate3108
Viana-Soto A, Okujeni A, Pflugmacher D, García M, Aguado I, Hostert P (2022a) Quantifying post-fire shifts in woody-vegetation cover composition in Mediterranean pine forests using Landsat time series and regression-based unmixing. Remote Sens Environ 281:113239. https://doi.org/10.1016/j.rse.2022.113239
Viana-Soto A et al (2022b) Assessing post-fire forest structure recovery by combining LiDAR data and Landsat time series in Mediterranean pine forests. Int J Appl Earth Obs Geoinf 108:102754. https://doi.org/10.1016/j.jag.2022.102754
Wagner TJW, Eisenman I (2015) False alarms: how early warning signals falsely predict abrupt sea ice loss. Geophys Res Lett 42:10333–10341. https://doi.org/10.1002/2015GL066297
Wagner Y et al (2023) Relationships between xylem embolism and tree functioning during drought, recovery, and recurring drought in Aleppo pine. Phys Plant. https://doi.org/10.1111/ppl.13995
Walker B, Holling CS, Carpenter SR, Kinzig A (2004) Resilience, adaptability and transformability in social–ecological systems. Ecol Soc 9:5
Walter J et al (2013) Ecological stress memory and cross stress tolerance in plants in the face of climate extremes. Environ Exp Bot 94:3–8
Wang XL (2008) Accounting for autocorrelation in detecting mean shifts in climate data series using the penalized maximal t or F test. J Appl Meteorol Climatol 47(9):2423–2444. https://doi.org/10.1175/2008JAMC1741.1
Weinans E, Lever JJ, Bathiany S, Quax R, Bascompte J, van Nes EH, van de Leemput IA (2019) Finding the direction of lowest resilience in multivariate complex systems. J Royal Soc Interface 16(159):20190629
Weinans E et al (2021) Evaluating the performance of multivariate indicators of resilience loss. Sci Rep. https://doi.org/10.1038/s41598-021-87839-y
White PS, Picket STA (1985) Natural disturbances and patch dynamics: an introduction. In: Pickett STA, White PS (eds) The ecology of natural disturbance and patch dynamics. Academic Press, San Diego, pp 3–13
White JC et al (2017) A nationwide annual characterization of 25 years of forest disturbance and recovery for Canada using Landsat time series. Remote Sens Environ 194:303–321. https://doi.org/10.1016/j.rse.2017.03.035
White JC et al (2019) Assessing spectral measures of post-harvest forest recovery with field plot data. Int J Appl Earth Obs Geoinf 80:102–114. https://doi.org/10.1016/j.jag.2019.04.010
White JC et al (2022) Mapping, validating, and interpreting spatio-temporal trends in post-disturbance forest recovery. Remote Sens Environ 271:11904. https://doi.org/10.1016/j.rse.2022.112904
White JC, Hermosilla T, Wulder MA (2023) Pre-fire measures of boreal forest structure and composition inform interpretation of post-fire spectral recovery rates. For Ecol Manage 537:120948
Wiesenfeld K (1985) Noisy precursors of nonlinear instabilities. J Stat Phys 38:1071–1097. https://doi.org/10.1007/BF01010430
Wiesenfeld K, McNamara B (1986) Small-signal amplification in bifurcating dynamical systems. Phys Rev A 33:629–642. https://doi.org/10.1103/PhysRevA.33.629
Wissel C (1984) A universal law of the characteristic return time near thresholds. Oecologia 65:101–107. https://doi.org/10.1007/BF00384470
Wu M et al (2022) Drought legacy in sub-seasonal vegetation state and sensitivity to climate over the northern hemisphere. Geophys Res Lett. https://doi.org/10.1029/2022GL098700
Wulder MA et al (2019) Current status of Landsat program, science, and applications. Remote Sens Environ 225:127–147. https://doi.org/10.1016/j.rse.2019.02.015
Wuyts B et al (2017) Amazonian forest-savanna bistability and human impact. Nat Commun 8:15519. https://doi.org/10.1038/ncomms15519
Xiao C, Zaehle S, Yang H, Wigneron J-P, Schmullius C, Bastos A (2023) Land cover and management effects on ecosystem resistance to drought stress. Earth Syst Dynam 14:1211–1237. https://doi.org/10.5194/esd-14-1211-2023
Xiong X et al (2020) MODIS and VIIRS calibration and characterization in support of producing long-term high-quality data products. Remote Sens 12(19):3167
Yang X et al (2022) Detection and characterization of coastal tidal wetland change in the northeastern US using Landsat time series. Remote Sens Env 276:113047
Yi C, Jackson N (2021) A review of measuring ecosystem resilience to disturbance. Environ Res Lett 16:053008
Yin Z, Dekker SC, van den Hurk BJJM, Dijkstra HA (2014) Bimodality of woody cover and biomass across the precipitation gradient in West Africa. Earth Syst Dynam 5(257–270):2014. https://doi.org/10.5194/esd-5-257-2014
Yu X et al (2022) Contrasting drought legacy effects on gross primary productivity in a mixed versus pure beech forest. Biogeosci Discus 19:4315–4329
Zeileis A et al (2003) Testing and dating of structural changes in practice. Comp Stat Data Anal 44:109–123
Zhang J et al (2022) NIRv and SIF better estimate phenology than NDVI and EVI: Effects of spring and autumn phenology on ecosystem production of planted forests. Agric Forest Meteorol 315(15):108819. https://doi.org/10.1016/j.agrformet.2022.108819
Zhao Y, Li Y (2022) Impact of fisheries footprint on an early warning indicator of resilience reduction in marine net primary productivity. ICES J Mar Sci 2022(79):2741–2751. https://doi.org/10.1093/icesjms/fsac213
Zhu Z et al (2017) The effects of teleconnections on carbon fluxes of global terrestrial ecosystems. Geophys Res Lett 44(7):3209–3218. https://doi.org/10.1002/2016GL071743
Acknowledgements
This paper is an outcome of the Workshop: ‘Tipping Points and Understanding EO data needs for a Tipping Element Model Intercomparison Project’ held at the International Space Science Institute (ISSI) in Bern, Switzerland (10-14 October 2022). We thank the ISSI for the great hospitality and their distinct approach to hosting. C. S. acknowledges funding from the Fachagentur Nachwachsende Rohstoffe e.V. (FNR) through the ERA-Net cofound action ForestValue (project FORECO, project nr. 2221NR088X). A.B. was funded by the European Union (ERC StG, ForExD, grant agreement No. 101039567). S. L. would like to acknowledge funding from the Earth Commission which is hosted by Future Earth and is the science component of the Global Commons Alliance. W.D. acknowledges the CONSOLIDATION funded by the Austrian Science Fund (FWF). A.B. was funded by the European Union (ERC StG, ForExD, grant agreement No. 101039567). T.S acknowledges support from the DFG STRIVE project (SM 710/2-1). S.B. and N.B. have received funding from the Volkswagen Stiftung, the European Union’s Horizon 2020 research and innovation programme, and under the Marie Sklodowska-Curie grant agreement No. 956170, as well as from the Federal Ministry of Education and Research under grant No. 01LS2001A. This is ClimTip contribution #2; the ClimTip project has received funding from the European Union's Horizon Europe research and innovation programme under grant agreement No. 101137601, funded by the European Union. Views and opinions expressed are those of the authors only and do not necessarily reflect those of the European Union or the European Climate, Infrastructure and Environment Executive Agency (CINEA). Neither the European Union nor the granting authority can be held responsible for them.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no conflicts of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bathiany, S., Bastiaansen, R., Bastos, A. et al. Ecosystem Resilience Monitoring and Early Warning Using Earth Observation Data: Challenges and Outlook. Surv Geophys (2024). https://doi.org/10.1007/s10712-024-09833-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10712-024-09833-z