Abstract
The significant role of nonlinear wave–particle interactions in the macrodynamics and microdynamics of the Earth’s outer radiation belt has long been recognised. Electron dropouts during magnetic storms, microbursts in atmospheric electron precipitation, and pulsating auroras are all associated with the rapid scattering of energetic electrons by the whistler-mode chorus, a structured electromagnetic emission known to reach amplitudes of about \(1\%\) of the ambient magnetic field. Despite the decades of experimental and theoretical investigations of chorus and the recent progress achieved through numerical simulations, there is no definitive theory of the chorus formation mechanism, not even in the simple case of parallel (one-dimensional) propagation. Here we follow the evolution of these theories from their beginnings in the 1960s to the current state, including newly emerging self-consistent excitation models. A critical review of the unique features of each approach is provided, taking into account the most recent spacecraft observations of the fine structure of chorus. Conflicting interpretations of the role of resonant electron current and magnetic field inhomogeneity are discussed. We also discuss the interplay between nonlinear growth and microscale propagation effects and identify future theoretical and observational challenges stemming from the two-dimensional aspects of chorus propagation.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Article Highlights
-
A brief overview of the early history of chorus studies is provided, focusing on concepts still used in today’s research
-
A review of modern nonlinear growth theories of the parallel-propagating magnetospheric chorus emission is presented
-
Theoretical models do not fully agree on the role of resonance current and magnetic field inhomogeneity
-
Two-dimensional aspects of wave propagation interfere with predictions of one-dimensional nonlinear theories
1 Introduction
The whistler-mode chorus emissions (Storey 1953) are one of the major drivers of local acceleration in the Earth’s outer radiation belt (Thorne 2010), affecting its dynamics over a large range of temporal and spatial scales. On the timescales of hours and days, numerical simulations based on the quasilinear theory of wave–particle interactions have been very successful in modelling the evolution of the radiation belt electron content (Horne et al. 2005; Shprits et al. 2008; Subbotin et al. 2011). These models work with magnetospheric wave power distributions averaged over a broad range of frequencies and describe scattering as a stochastic process caused by successive impulses from small amplitude waves with random phases (Horne et al. 2003).
On the scale of minutes and below, the stochastic approach becomes insufficient. Discrete, high-amplitude structures in time–frequency spectrograms, a characteristic feature of chorus, cause significant perturbations to resonant electron trajectories, which lead to particle trapping and nonlocal transport (Allanson et al. 2021). Such processes require a full nonlinear treatment and may result in a much faster particle energisation and losses than those predicted by the diffusive Fokker–Planck equations of the quasilinear theory (Mourenas et al. 2018). However, the efficiency of nonlinear electron acceleration through cyclotron resonance with a parallel-propagating chorus is limited by amplitude modulations (Tao et al. 2013; Hiraga and Omura 2020) and phase decoherence (Zhang et al. 2020a) within wave packets.
Various theories have been proposed to explain the formation and properties of chorus elements, with the hope of better modelling the wave–particle interactions and understanding their impact on global radiation belt dynamics. In this review article, we start by going back to the early hypotheses on triggered whistler-mode emission (Sect. 2) to identify the fundamental principles of nonlinear chorus growth and to point out some intriguing yet imprecise concepts that have been since improved and incorporated into newer research. We then continue with a review of the three most widely used recent theories: the backward wave oscillator theory with a step-like discontinuity in the electron distribution (sBWO, Sect. 3.1), initially proposed by Trakhtengerts (1995); the nonlinear growth theory (NGTO, Sect. 3.2) developed in a series of papers starting with Omura et al. (2008); and the self-consistent framework for chorus excitation (SCCE, Sect. 3.3) described by Zonca et al. (2022) and qualitatively applied by Tao et al. (2021). Finally, in Sect. 4, we consider the effects of cold plasma density filamentations on two-dimensional (2D) propagation of whistler-wave packets and discuss the limitations of 1D nonlinear growth theories in explaining the fine structure of chorus.
The above-mentioned modern theories are all based on a common set of complex wave amplitude equations and similar ideas about the resonant electron current, yet they diverge in the use of mathematical notation. To avoid confusion, we spend the rest of the Introduction (Sects. 1.1 and 1.2) refreshing the basics of whistler-mode dispersion and resonant electron motion in order to establish a unified notation. The revised concepts also serve as prerequisites for the analysis of the propagation and growth of chorus emissions in Sects. 3 and 4.
For the sake of conciseness, chorus waves generated at large wave normal angles (WNA) are completely omitted from this article; interested readers can look into the observational paper by Santolík et al. (2009), or into the review by Shklyar and Matsumoto (2009) for a general description of electron interactions with highly oblique whistler waves. Regarding the growth mechanism of these emissions, some recent hypotheses can be found in Mourenas et al. (2015), Li et al. (2016), and Artemyev et al. (2016) and references therein.
1.1 Characterisation of the Whistler-Mode Chorus Emission
Chorus emissions propagate in the whistler mode, which is the right-hand polarised branch of the magnetised cold plasma dispersion relation (Gurnett and Bhattacharjee 2017) below the electron cyclotron and plasma frequencies, whichever is lower. For parallel-propagating waves, i.e., when the wave vector \(\varvec{k}\) is parallel or antiparallel to the ambient magnetic field \(\varvec{B_0}\), the refractive index \(\mu \) can be written as
Here, \(\omega \) stands for wave frequency, \(\varOmega _{\textrm{e}}\) for electron gyrofrequency, \(\omega _{\textrm{pe}}\) is the electron plasma frequency, and the motion of ions was neglected. The group velocity is found to be
where the second formula results from the approximation \(\omega _{\textrm{pe}}^2 \gg \omega (\varOmega _{\textrm{e}} - \omega )\). The phase velocity \(V_{\textrm{p}}\) becomes equal to \(V_{\textrm{g}}\) at \(\omega \approx \varOmega _{\textrm{e}}/2\), which is an interesting property with possible implications for the chorus power spectrum (Sauer et al. 2022).
When the wave normal angle \(\theta _{\textrm{k}} = \angle (\varvec{k},\varvec{B_0})\) becomes nonzero, the dispersion properties of whistler waves are best represented by 2D plots in the \((\omega ,\theta _{\textrm{k}})\) space, as shown in Fig. 1 for \(\omega _{\textrm{pe}}/\varOmega _{\textrm{e}} = 5\). Phase and group velocity (panels a and b) of parallel waves maximise at \(\omega = \varOmega _{\textrm{e}}/2\) and \(\omega = \varOmega _{\textrm{e}}/4\), respectively, and quickly decrease as the WNA gets close to the resonance cone. As shown in all panels, the R-mode becomes evanescent above the resonance cone defined by \(\theta _{\textrm{k}} = \theta _{\textrm{res}} \approx \arccos (\omega /\varOmega _{\textrm{e}})\). The polar angle of the Poynting vector, \(\theta _{\textrm{S}}\) (Fig. 1c), remains small everywhere except for high frequencies near the resonance cone, suggesting that whistler wave energy propagates almost along field lines even without the presence of waveguides (Storey 1953; Walker 1976). At the Gendrin angle \(\theta _{\textrm{G}} \approx \arccos (2\omega /\varOmega _{\textrm{e}})\), the Poynting vector stays parallel to the ambient magnetic field. The ellipticity of the magnetic field, \(E_{\textrm{B}}\) (ratio of the minor and major axis of the polarisation ellipse of the magnetic field), is equal to one across all \(\theta _{\textrm{k}}\) at the proton plasma frequency and remains close to unity at higher frequencies.
Propagation properties of whistler-mode waves in the frequency range from proton to electron gyrofrequency, \(\varOmega _{\textrm{p}}< \omega < \varOmega _{\textrm{e}}\). The plasma-to-cyclotron frequency ratio is set to \(\omega _{\textrm{pe}}/\varOmega _{\textrm{e}} = 5.0\). The plotted data were obtained by numerically solving the unapproximated cold electron-proton plasma dispersion relations from Stix (1992)
Due to the strong dependence of whistler-mode dispersion properties on the plasma density and the WNA, studying wave propagation analytically often proves difficult. In practice, the propagation path is obtained numerically by integrating the ray tracing equations resulting from Hamiltonian optics [Suchy (1981), Horne (1989), and Eqs. A1–A2 in the Appendix]. The (Hamiltonian) geometric optics is based on the eikonal approximation,Footnote 1 which requires the time scales and length scales of environmental variations to be substantially larger than \(1/\omega \) and 1/k, respectively, allowing for a plane-wave description (Bernstein 1975). For its convenience, the ray approximation represents an important step in the derivation of fundamental equations of the nonlinear chorus growth theories in Sect. 3. However, the eikonal approximation breaks down when we introduce thin density ducts into the plasma environment and has to be replaced by a full-wave approach to capture the effects of a strongly inhomogeneous medium (Sect. 4).
Electron density and wave spectrograms from a full orbit of Van Allen Probe A recorded on 29–30 August 2014, processed by the methods of Santolík et al. (2002), Santolík et al. (2003b) and Santolík et al. (2010). The panels show, in order: electron plasma density, magnetic power spectral density, electric power spectral density, the ellipticity of the magnetic field, planarity of the magnetic field, wave normal angle and polar Poynting angle. The upper line in the spectrogram marks half of the electron gyrofrequency; the lower line follows the proton gyrofrequency, which rises into the EMFISIS frequency range only at low altitudes. (1) Plasmatrough: region of tenuous plasma outside the plasmasphere (2) Plasmapause: outer boundary of the plasmasphere. (3) Plasmasphere: cold, dense plasma co-rotating with the Earth. (A) Whistler-mode chorus/exohiss. (B) Plasmaspheric hiss. (C) Equatorial noise. (D) Lightning generated whistlers, kHz radiation emitted from lightning strokes. (E) Instrument noise. Reprinted from Hanzelka (2022)
The defining characteristics of chorus waves, which differentiate them from other whistler-mode emissions, are their spectral features (Burtis and Helliwell 1969; Tsurutani and Smith 1974; Taubenschuss et al. 2015). In Fig. 2, we show a spectrogram of \(10\,\textrm{Hz}\) to \(10\,\textrm{kHz}\) electromagnetic emissions recorded during a full orbit of Van Allen Probe A. The two bands of intense emissions ranging from about \(0.1\varOmega _{\textrm{e0}}\) to \(0.5\varOmega _{\textrm{e0}}\) (lower band) and from \(0.5\varOmega _{\textrm{e0}}\) to \(0.8\varOmega _{\textrm{e0}}\) (upper band), denoted by the label “A”, represent the chorus emission or exohiss. A 6-second burst mode snapshot of magnetic wave power, taken during the orbit from Fig. 2, is presented in the form of a spectrogram in Fig. 3. Here we observe narrow-band spectral elements with chirping frequency (rising in this case), whose presence needs to be confirmed in the high-cadence burst mode data to avoid confusing chorus with exohiss.Footnote 2 Chorus is generated near the magnetic equator by nonlinear resonant interactions with energetic electrons, with wave seeds growing from anisotropy-driven instability of the hot electron distribution (Tsurutani and Smith 1974; Santolík 2008; Li et al. 2008).
Magnetic power spectral density from a 6-second burst mode snapshot taken during the orbit in Fig. 2, starting at 01:49:43.35 UT. It reveals narrow-band, rising-tone chorus elements in the lower frequency band, with weaker coherent emissions in the upper band. The emission band centred on 600 Hz is assumed to be the result of linear growth, while the discrete elements are a product of nonlinear interaction between electrons and whistler waves
Statistical results from the THEMIS, Cluster and Polar spacecraft have shown that chorus occurs predominantly in the dayside and morning sectors at L-shells ranging from the plasmapause to the magnetopause, with average wave power steeply decreasing above \(40^{\circ }\) of latitude (Li et al. 2009; Bunch et al. 2012; Santolík et al. 2014b). However, these studies did not use high-resolution data to confirm the presence of discrete, chirping structures in the spectrograms. Taubenschuss et al. (2014) analysed over 500 burst-mode snapshots gathered by the THEMIS satellite and found that the lower band was divided into two main populations based on the wave normal angle: quasiparallel waves below the Gendrin angle and weaker highly oblique waves near the resonance cone. The upper band showed no clear division and was sometimes connected to the lower band, i.e. the spectral gap at \(0.5\varOmega _{\textrm{e}}\) was not always present (Kurita et al. 2012; Teng et al. 2019; Gao et al. 2019). This gap is commonly associated with increased obliquity and Landau damping (Omura et al. 2009; Li et al. 2019; Sauer et al. 2022) and thus will not appear in the theories of parallel chorus wave growth described in this review. As established by many observational studies (Santolík et al. 2014b; Artemyev et al. 2016; Agapitov et al. 2018), the very oblique chorus waves are much less common than the parallel ones, and their origin is likely associated with nonlinear Landau resonant interaction near the resonance cone (Soto-Chavez et al. 2014; Mourenas et al. 2015) rather than with the cyclotron resonance. Furthermore, the oblique, lower-band chorus consists mainly of falling tones, while risers dominate the quasiparallel propagation (Taubenschuss et al. 2014).
Research focusing on lower-band waves reveals a very narrow average bandwidth of \(0.01\varOmega _{\textrm{e}}\) (Gao et al. 2014) and the frequency sweep rates ranging from about \(5 \cdot 10^{-6} \varOmega _{\textrm{e}}^2\) to \(10^{-4} \varOmega _{\textrm{e}}^2\) (Macúšová et al. 2010; Teng et al. 2017). The typical RMS magnetic field amplitudes range from \(0.01\,{\textrm{nT}}\) to \(0.3\,{\textrm{nT}}\) (Li et al. 2011), with some elements occasionally reaching peak amplitudes \(B_{\textrm{w}} > 1\,{\textrm{nT}}\) and \(B_{\textrm{w}}/B_0 > 0.01\) (Santolík et al. 2014a; Gao et al. 2014).
Waveforms and propagation properties of the highlighted chorus element from Fig. 3. A band-pass filter \(0.1\varOmega _{\textrm{e0}}< \omega < 0.49\varOmega _{\textrm{e0}}\) was applied before calculating the analytic signal from Hilbert transform, and we used the Savitzky–Golay filter to obtain the derivative of phase. a, b Perpendicular (\(B_{x}\)) and parallel (\(B_{z}\)) magnetic field components. c Amplitude envelopes of the two components from previous panels (red and blue lines) and the total magnetic field (black line). d Instantaneous frequency obtained from the analytic signal. e Wave normal angle computed with SVD methods (Santolík et al. 2003b). f Azimuthal angle of the wave vector, obtained with SVD methods
A unique feature of the lower-band chorus is the clear amplitude modulations of individual elements, which are called subpackets (Santolík et al. 2003a, 2014a). Figure 4a, b shows the time series of magnetic field components corresponding to the element highlighted by pink lines in Fig. 3. The statistical analysis conducted by Santolík et al. (2014a) shows that the lengths of subpackets exhibit a large variance, with most of them falling between \(5\,{\textrm{ms}}\) and a few tens of milliseconds. The rapid changes in instantaneous frequency near amplitude minima (Fig. 4c, d) hint at jumps in the wave phase. However, a smooth evolution of phase appears to be likely at the beginning of an element, as further demonstrated by Crabtree et al. (2017b) and Foster et al. (2021). Based on simulations of Nogi and Omura (2022), the character of subpackets might be strongly related to their distance from the source region. However, the source region has a field-aligned width of thousands of kilometres (Santolík et al. 2004), complicating the definition of distance travelled from the source. An extended discussion is provided in Sect. 3 (see especially the phenomenological model of Tao et al. (2021), reviewed in Sect. 3.3), but the detailed origin of the subpacket structure is currently still unclear.
Another interesting property of high-amplitude chorus subpackets is the variations in wave normal angle. In the source, Landau damping of waves with large \(\theta _{\textrm{k}}\) values has not acted long enough to suppress such features (Hsieh and Omura 2018), and as suggested in Sect. 4.2, damping formulas derived from the homogeneous plasma theory (Brinca 1972) may not even be appropriate. The spikes in obliquity arise from a mismatch in amplitude modulations of the perpendicular and the parallel magnetic field component, as seen in the right half of Fig. 4c, e. This suggests that a complete description of chorus formation requires a two-dimensional treatment, possibly with the inclusion of transverse density irregularities that modulate the field-aligned power distribution. Such theories are currently not available, but some progress has been made recently through full-wave simulations of ducted whistler-wave propagation, which are discussed in Sect. 4.
Finally, it should be mentioned that the well-behaved chorus elements, with a very narrow bandwidth and nearly constant chirping rate, are not the only form of chorus. Examples of chorus elements with diffuse features or with oscillating tones can be found, e.g., in Santolík et al. (2010), Li et al. (2012) and Gao et al. (2017). The evolution of such emissions cannot be described with the quasi-monochromatic wave approximation employed in all of the theories discussed in Sects. 2 and 3.
1.2 Basics of Resonant Electron Motion
A precise understanding of the phase space motion of resonant electrons is at the core of all theories of nonlinear chorus growth. Let us assume a parallel-propagating whistler-mode wave described by the following magnetic and electric wave fields:
An electron interacting with such wave is said to be in exact cyclotron resonance when its parallel velocity \(v_{\parallel }\) fulfils the condition
where \(V_{\textrm{R}}\) is the resonance velocity, \(k_{\parallel }\) is the parallel component of the wave vector and
is the Lorentz factor evaluated at the resonance velocity. Where convenient, we will replace velocities v by momenta divided by the electron mass m, that is, \(u = \gamma v\). The formulas for resonance momentum and Lorentz factor then read as
and
The full set of gyroaveraged equations of motion for the cyclotron-resonant electron takes the form
The newly introduced notation is defined as follows: \(\zeta \) is the angle between the gyrophase \(\varphi \) and wave magnetic field phase, \(\zeta = \varphi - \psi \); \(\varOmega _{\textrm{w}} = B_{\textrm{w}}e/m\) represents a normalised wave amplitude; and h is the distance along a magnetic field line measured from the equator. The last term in each of Eqs. 9 and 10 relates to the adiabatic motion in the inhomogeneous background magnetic field. In Eq. 11, the term with \(1/u_{\perp }\) becomes relevant only at low pitch angles, and is often neglected. A thorough analysis of these equations of motion can be found in numerous papers, starting with Roberts and Buchsbaum (1964).
Equations 5 and 7 can be solved for \(V_{\textrm{R}}\) and \(U_{\textrm{R}}\) to obtain the resonance velocity (momentum) curves
and
similar formulas with a different notation can be found in Summers et al. (2012). The curve \(V_{\textrm{R}}(v_{\perp })\) is plotted in red in Fig. 5a for \(\omega /\varOmega _{\textrm{e}} = 0.25\), \(\omega _{\textrm{pe}}/\varOmega _{\textrm{e}} = 5.0\), and has the shape of an elliptical arc which touches the \(v_{\parallel }^2 + v_{\perp }^2 = c^2\) circle at \(V_{\textrm{R}} = V_{\textrm{p}}\) (the \(+\) sign choice in Eq. 14 becomes unphysical beyond this point). In the momentum space, the curve takes on a hyperbolic shape; a portion of this curve is plotted in Fig. 5b.
a Resonance curve \(V_{\textrm{R}}(v_{\perp })\) based on Eq. 14 is plotted in red. Properties of the whistler wave are determined by wave frequency \(\omega /\varOmega _{\textrm{e}} = 0.25\) and plasma frequency \(\omega _{\textrm{pe}}/\varOmega _{\textrm{e}} = 5.0\). The grey region \(\pm V_{\textrm{tr}}/2\) shows the extent of the trapping potential and is based on Eq. 29 with \(\varOmega _{\textrm{w}}/\varOmega _{\textrm{e}} = 0.01\). The dashed curve represents the speed of light circle, and the dotted vertical line connects to the point at which the resonance velocity reaches the speed of light. The motion of resonant particles is restricted to curves given by Eq. 16, plotted in blue colour for exact-resonance energies \(34.6\,\textrm{keV}\) and \(85.7\,\textrm{keV}\). The grey patch represents the approximate extent of the trapping potential based on Eq. 29, magenta circles show the constant energy surface, and the red line represents the resonance curve. b) Same plots as in panel a, but in the \((u_{\parallel },u_{\perp })\) space
To better understand the electron’s three-dimensional motion in the momentum space, we first examine trajectories in the \((u_{\parallel },u_{\perp })\) space. Dividing Eq. 10 by Eq. 9, with the inhomogeneity terms removed, results in
This differential equation has a closed-form solution
where \(\gamma _0 = \sqrt{1 + u_{\parallel 0}^2/c^2}\) and \(u_{\parallel 0}\) denotes the \(u_{\parallel }\)-intercept. Curves from this family are ellipses with a minor (perpendicular) to major (parallel) axis ratio \(\sqrt{1-V_{\textrm{p}}^2/c^2}\) and with their centres shifted towards positive parallel momenta by
a representative plot is shown in Fig. 5. Notice that there is no \(\varOmega _{\textrm{w}}\) or \(\zeta \)-dependence, meaning that when an electron passes through a whistler wave packet, it will stay on one of these curves as long as the wave frequency and background magnetic field remain constant.
Since the particle trajectories in \((u_{\parallel },u_{\perp })\) space lie on curves described by the amplitude-independent Eq. 15, it comes as no surprise that there exists a relation to the linear growth formula for anisotropy-driven instability (Kennel and Petschek 1966)
where \(F_{\textrm{h}}\) is the hot electron distribution normalized by the total electron density and
is the pitch angle anisotropy in a low-velocity approximation. Under this approximation, the electron motion in the \((v_{\parallel },v_{\perp })\) space is described by
Let us compare this curve to the isolines of a bi-Maxwellian distribution with anisotropy A, given by a differential equation
Note that for the bi-Maxwellian distribution, temperature anisotropy and pitch-angle anisotropy are identical, i.e., \(A = T_{\perp }/T_{\parallel } - 1\). Equating the above two differential expressions gives
Putting \(v_{\parallel }\) at the exact resonance defined in Eq. 5 (with \(\gamma = 1\)), we arrive at
which is the marginal instability condition for anisotropy-driven whistler wave growth that appears in the linear growth formula from Eq. 18. This relation between the phase space motion of electrons and the linear theory has a clear physical meaning: electrons which oscillate on the isolines of the bi-Maxwellian do not change the velocity space distribution, the net change in particle energy is zero, and thus the waves cannot grow or be damped.
To analyse the evolution of relative phase \(\zeta \) near resonance, let us start with the simplified time evolution of \(\zeta \) as given by Eq. 11 with the \(1/u_{\perp }\) term removed, and define
The quantity \(\nu \) represents a parallel velocity shift with respect to the resonance velocity. As a next step, we take the time derivative of \(\nu \), using the homogeneous form of Eqs. 10 and 9 and
and obtain a pendulum-like equation
Here, it is a common approach to replace \(u_{\perp }\) by some constant mean value \(\langle u_{\perp } \rangle \), with \(\gamma \) being calculated for this mean perpendicular momentum at the exact resonance (Omura et al. 2008). We then proceed to make the expansion around the resonance by setting \(\nu = 0\), which leads to
where
is the trapping frequency (frequency of oscillations in the trapping potential). This resulting pendulum equation is sometimes called the second-order resonance equation and one of the first application of its non-relativistic version to chorus growth was provided by Sudan and Ott (1971). It describes a resonant electron in the gyrating frame, where the perpendicular velocity vector oscillates around \(-\varvec{B_{\textrm{w}}}\). As predicted by the resonance velocity formula (Eq. 14, Fig. 5a), the electrons propagate in the direction opposite to the whistler wave unless there is a substantial gyroperiod dilation (\(\gamma \gg 1\)). With plasma and wave parameters typical for the Earth’s outer radiation belt, we get \(\omega _{\textrm{tr}} \ll \omega \), which is an important scaling relation for chorus theories discussed in Sect. 3.
The expression for \(\omega _{\textrm{tr}}\) can be used to define the extent of the resonance region across parallel velocities
Unlike in Omura et al. (2015b), \(V_{\textrm{tr}}\) represents the full width of the resonance island. The \(\pm V_{\textrm{tr}}/2\) region is plotted in grey in Fig. 5. However, since we are using a fixed perpendicular momentum and calculating the Lorentz factor as \(\gamma _{\textrm{R}} = \sqrt{1 + U_{\textrm{R}}^2 + \langle u_{\perp } \rangle ^2}\), the grey areas have to be considered as an approximation of the full width of the trapping region, and it becomes very inaccurate at low pitch angles where the changes in \(u_{\perp }\) due to scattering become significant (Albert et al. 2021).
Moving to the inhomogeneous case, with the h-dependence of \(\varOmega _{\textrm{e}}\) and cold plasma density included, we can repeat the approximate calculation leading to the pendulum equation for resonance motion (Eq. 27). Notice first that unlike in the homogeneous case, \(\nu \) is now h-dependent through k(h) and \(\varOmega _{\textrm{e}}(h)\), but also through the adiabatic changes in \(u_{\parallel }\). For the purpose of analysing the second-order particle motion as a local process, we may neglect these slow changes as long as
This condition is always well satisfied for resonant electrons and chorus emissions in the Earth’s outer radiation belt. The extra terms coming from \(\partial k / \partial h\) and \(\partial \varOmega _{\textrm{e}}/\partial h\) are not \(\zeta \)-dependent, so we arrive at a pendulum equation with a torque
where we introduced the inhomogeneity factor
with
A detailed derivation of the relativistic inhomogeneity factor can be found in Omura et al. (2008), with the addition of the frequency change \(\partial \omega / \partial t\). We will return to chirping waves and the inhomogeneity factor in Sects. 2.1 and 3.2.
Phase portrait showing the behaviour of electrons near cyclotron resonance as described by Eq. 31 with a constant inhomogeneity factor \(S = -0.5\) (panel a) and \(S = -1.2\) (panel b). Particles in the trapping region (green arrow) oscillate around a constant phase \(\zeta _0\). Untrapped particles (red arrow) are not phase-locked
Let us examine the particle trajectories in \((\zeta ,\nu )\) space. If we assume that the electrons are travelling from \(h > 0\) towards \(h = 0\), where the magnetic field strength has a global minimum, and that density is also growing away from \(h = 0\), then S must be negative for \(U_{\textrm{R}}\) negative. In Fig. 6a, we plot the trajectories and trapping region for \(S = -0.5\). The trajectories can be expressed as a family of curves
where C is a real constant. The separatrix, which represents the boundary of the trapping region, has a function form
where \(\zeta _0 = \pi - \arcsin (-S)\) is at the stable point, \(\zeta _1 = \arcsin (-S)\) is at the saddle point, and \(\zeta _2\) is at the right-hand boundary of the separatrix. For \(|S |> 1\) (Fig. 6b), \(\textrm{d}\nu /\textrm{d}t\) never changes sign, and thus particles in a strongly inhomogeneous environment never become phase-locked. In total, we distinguish three populations of particles: trapped particles, which are found within the grey region of Fig. 6; untrapped particles that cross the exact resonance \(\nu = 0\) and become strongly scattered; and untrapped particles that do not cross the exact resonance and experience a slow scattering process called the nonresonant diffusion. A quantitative theory of this type of diffusion was presented by Chen et al. (2016) and An et al. (2022) for the case of electron interaction with electromagnetic ion cyclotron waves.
Before we conclude this section, we should emphasise that in practice, the interactions of charged particles with a realistic wave field must be investigated numerically. Test particle simulations enjoy great popularity due to their low computational cost and are commonly used to study scattering and energisation. They either solve the set of Eqs. 9–12 (or their Hamiltonian equivalent) to track trajectories of particles interacting with a plane wave (Bell 1984; Albert 1993; Bortnik et al. 2008), or they employ the Boris algorithm to solve the second-order equation of motion with Lorentz force under a more realistic wave model (Omura and Summers 2006; Hanzelka et al. 2021). However, to validate the theories of chorus growth, self-consistent simulations are needed, which rely on the particle-in-cell method (Hikishima et al. 2009; Tao et al. 2017) or other approaches based on the Vlasov equation (Nunn 1993; Harid et al. 2014; Pezzi et al. 2019). In such codes, the hot electron population is evolved together with the electromagnetic field, allowing for parametric studies of chirping and subpacket formation.
2 The History of Theoretical Chorus Studies
In the first half of the 20th century and up until the end of 1950s, theories on the origin of natural, audio-frequency electromagnetic emissions detected by receivers on ground stations were mostly focused on the lighting-generated whistlers (Burton and Boardman 1933; Storey 1953). While the dawn chorus was present among the studied “musical atmospherics”, they did not attract much attention until the discovery of the radiation belts (van Allen et al. 1958), which triggered a surge of interest in particle acceleration in the geospace. The importance of gyroresonant interaction between charged particles and circularly polarised electromagnetic waves was recognised by Helliwell and Bell (1960) and others, and their ideas were soon expanded into studies of whistler wave growth and damping due to cyclotron resonance with electrons.
In the following paragraphs we briefly review the theoretical efforts in the 1960s and 1970s that laid the foundation for modern theories of nonlinear chorus growth. Due to the sizeable amount of literature written on this topic, we direct our attention mostly towards physical concepts that have stood the test of time and are essential for our current understanding of chorus emissions. The preceding research on the nonlinear Landau resonance (O’Neil 1965; Al’tshul’ and Karpman 1966; Kruer et al. 1969), which influenced the development of mathematical descriptions of the cyclotron resonance, is omitted here.
2.1 Phase Bunching, Trapping and Helical Current
In one of the early theoretical papers focused solely on chorus, Dowden (1962) noted that bunches of electrons are needed to produce strong and coherent (quasi-monochromatic) radiation at frequencies described by the Doppler-shifted resonance condition (Eq. 5). He assumed that this bunching happens along the field line coordinate h and that the motion of electrons away from (or towards) the equator is responsible for the rising (or falling) frequency of the emitted whistler waves. Brice (1963), and later Bell and Buneman (1964), analysed the effect of the \(\varvec{v}\times \varvec{B_{\textrm{w}}}\) component of the Lorentz force and suggested that the relative phase of electrons \(\zeta \) will have a stable point and postulated phase-bunching in the gyrating frame as the dominant process that leads to coherent electromagnetic emissions. Effectively, the resonant electrons represent a current flowing through an end-fire array, or in other words, through a travelling-wave helical antenna (Kraus 1949; Stenzel 1976a). Unlike in Dowden’s model, this type of bunching keeps the plasma density unchanged. The feedback loop between electron bunching by whistler waves and emission of whistler waves by the bunched electrons represents the basic concept of backwards-wave oscillators, whose application to chorus generation will be reviewed in greater detail in Sect. 3.1. However, note that at this stage of theoretical development, the electron population was not divided into trapped and untrapped, a distinction that is essential in the modern understanding of chorus growth.
Building on the ideas of phase bunching and helical resonant current (travelling-wave antenna), Helliwell (1967) presented a comprehensive theory of triggered whistler-mode emissions. Despite stating that the “analysis is unrefined and is intended only to establish the reasonableness of the model”, Helliwell introduced and refined concepts that still influence modern analytical studies of chorus emission, as we will see in Sect. 3 (Hanzelka et al. 2020; Tao et al. 2021). The fundamental idea of Helliwell’s approach was the so-called consistent-wave condition, which simply required that within a finite interaction region, the spatially variable gyrophase of resonant electrons must match the Doppler-shifted frequency of the whistler wave. This condition ensured that the energy transfer from particles to waves was maximised by maximising the coupling time. It was further assumed that the triggering process could quickly reach an optimal state where wave amplitude and resonant current within the interaction region exhibit no temporal variations, keeping a steady amplitude profile along the field line.
To retrieve the frequency variation from the consistent-wave condition, we must find the differential of gyrofrequency, particle parallel velocity and phase velocity. A common approximation in chorus theory and particle simulations is to replace the dipole field with a parabolic Taylor expansion around the magnetic equator, leading to a gyrofrequency formula
where \(R_{\textrm{E}}\) is the Earth’s radius, and L denotes the L-shell. Nevertheless, for the purpose of generality, the magnetic field and its gradient will be kept implicit in most equations presented in this review. Using the refractive index from Eq. 1 with \(\omega _{\textrm{pe}} = \mathrm {const.}\) (in the high-density approximation), together with the conservation of the first adiabatic moment and energy of electrons, Helliwell (1967) arrived at a chirping rate
where \(\alpha \) was the electron pitch angle at the centre of the interaction region. Furthermore, the interaction region was allowed to drift, adding another component to the chirping rate that explained some uncommon spectral shapes of chorus like hooks or inverted hooks.
Due to a spread in \(v_{\parallel }\), the untrapped resonant electrons were supposed to become debunched on the order of \(T_{\textrm{tr}}/4\), where \(T_{\textrm{tr}}\) is a trapping period related to the motion in the potential well described by the Eqs. 27 and 28 in their nonrelativistic limit. Note that Helliwell (1967) did not consider the nonuniformity of velocity distribution near resonance or the effects of inhomogeneity on the shape of the trapping region (cf. Fig. 6), and assumed that the electrons start deep within the potential well and reach \(\zeta = \pi \) at approximately the same time, thus forming a bunch. For simplicity, the first half of the interaction region was said to be dominated by bunching and the second half by radiation. The length of the interaction region was taken to be only twice the distance covered by an unperturbed electron during its motion from \(\zeta = 0\) to \(\zeta = 2\pi \) (i.e., \(v_{\parallel } = V_{\textrm{R}}\) at the equator, but \(V_{\textrm{tr}}\) is taken to be negligibly small). The bandwidth of triggered waves was related to the variation of gyrofrequency across the interaction region and the spread of electron streaming velocity around the resonance velocity.
Due to limited knowledge of the hot electron velocity distribution and the exaggeration of the phase bunching effect (Dysthe 1971), we will skip most of the discussion related to resonant current and radiation power presented in Helliwell (1967). The two most important ideas are the increase of input power due to the broadening of the trapping region and the existence of a limiting amplitude, which is reached when the bunching time becomes shorter than a resonant electron’s time of flight through the interaction region. The first point is especially intriguing, as it portrays the growth of discrete whistler wave emissions as independent of anisotropy-driven instabilities, which are essential for quasilinear theories (Kennel and Petschek 1966). It is now well known that pitch-angle anisotropy is essential for the triggering process, as shown by numerical simulations and spacecraft observations (Burton 1976; Li et al. 2010; Tao 2014; Fu et al. 2014; Katoh et al. 2018). However, the highest linearly unstable frequency does not represent a strict upper limit for nonlinear frequency chirping, as demonstrated, e.g., by the simulations of Hikishima et al. (2009).
2.2 Wave Equations and Inhomogeneity Factor
As mentioned above, the trapped (phase-locked) electrons and the inhomogeneity of the plasma medium play a dominant role in the triggering of chorus emissions. This was recognised by Dysthe (1971) and Nunn (1971), who also presented a pendulum equation for oscillations around the exact second-order cyclotron resonance, similar to Eqs. 31–34.
In Nunn (1971) and the follow-up paper Nunn (1974), general formulas describing the nonlinear convective growth of whistler wave amplitude are derived that represent the basis for all chorus theories listed in Sect. 3. The derivation can be summarised as follows: Taking the Maxwell curl equations and the linearised equation of electron motion in a cold plasma fluid, we split the current that appears in Ampère’s law into its cold component \(\varvec{J_{\textrm{c}}}\) and hot resonant component \(\varvec{J_{\textrm{R}}}\) and solve for the complex magnetic wave field \({\tilde{B}}_{\textrm{w}}\) equivalent to Eq. 3. After applying a narrowband approximation, which enforces slow variation of the complex wave amplitudes and currents, we obtain
which can be split into
where \(J_{\textrm{E}}\) and \(J_{\textrm{B}}\) are components of the resonant current parallel to \(\varvec{E_{\textrm{w}}}\) and \(\varvec{B_{\textrm{w}}}\), respectively. Note that the equation for phase \(\psi _{\textrm{NL}}\) relates to nonlinear changes, which are much slower than the evolution of the “cold phase” \(\psi - \psi _{\textrm{NL}}\) dictated by the cold plasma dispersion relation. The right-hand side of Eq. 41 thus represents the convective variation of frequency due to nonlinear effects. See also Karpman et al. (1974) and references therein for an energy density formulation of these equations.
The transverse resonant current at distance h along the field line can be evaluated through the formula
where \(f_{\textrm{R}}\) is the phase space density (PSD) distribution perturbed due to wave–particle interactions and \(f_{0}\) is the initial gyrotropic distribution. Finding the shape of \(f_{\textrm{R}}\) and determining the contribution of trapped and untrapped particles to the resonant current is one of the most difficult and important tasks in nonlinear wave growth theories—this fact was not fully appreciated in the early descriptions of resonant particle dynamics discussed in Sect. 2.1. The effect of non-gyrotropy (i.e., the dependence of \(f_{\textrm{R}}\) on \(\zeta \)) on the dispersion relation will be briefly discussed in Sect. 2.3 in connection to the formation of sidebands. Based on numerical solutions of particle trajectories near the exact resonance, Nunn (1971) concluded that the current would be dominated by particles trapped deep within the potential well after a few trapping periods. This limits the spread of \(v_{\parallel }\) in the helical beam, which means that the electromagnetic emission will have a sharply defined wavelength. Along the particle stream, the environment changes slowly on scales of \(V_{\textrm{R}}T_{\textrm{tr}}\), and thus the nonlinear phase difference \(\psi _{\textrm{NL}}\) is expected to stay nearly constant. Finally, it is noted by Nunn (1974) that an instability driven by pitch-angle anisotropy is necessary to trigger nonlinear growth.
So far, all the theories we described focused on how the radiation from coherent phase-space structures drives wave amplitude growth and frequency change, but the effect of these changes on particles was not fully considered. Roux and Pellat (1978) noticed that chirping could change electron trajectories in the \((\zeta ,\nu )\)-space in a way that enhances or reduces the tear-drop deformation of the resonance island. Vomvoridis et al. (1982) derived an effective inhomogeneity ratio
where S was the nonrelativistic version of the inhomogeneity factor from Eq. 32. After finding an optimum value of S for amplitude growth, numerically or analytically, the corresponding chirp rate can be derived. Furthermore, chirping waves can maintain nonzero \(S_{\textrm{eff}}\) even at the equator where \(S = 0\), allowing for wave growth without magnetic field inhomogeneity. These were pivotal ideas, later used to develop a nonlinear growth theory of chorus growth in the form summarised by Omura (2021)—see Sect. 3.2 for details. For an extension of the quasi-monochromatic treatment of nonlinear whistler-mode wave growth to oblique propagation angles, see Shklyar and Matsumoto (2009).
2.3 Sideband Excitation Theories
As mentioned below Eq. 42, phase-bunching effects by both trapped and untrapped electrons introduce a gyrophase dependence into the perturbed hot electron distribution. Within the linear theory of whistler-mode wave instabilities in a homogeneous plasma, the analysis starts with the integration of the PSD distribution along unperturbed particle trajectories (Stix 1992; Ichimaru 2004), resulting in a zeroth-order term of the Vlasov equation that implicitly contains the gyrotropic condition (Gurnett and Bhattacharjee 2017). In quasilinear theories, the broadband character of the wavefield is expected to randomise phases, leading again to uniformity in \(\zeta \) (Kennel and Engelmann 1966; Lemons et al. 2009). However, since high-amplitude whistler waves heavily perturb the electron trajectories near the resonance curve, and because the chorus elements are narrowband, the effects of non-gyrotropy should be included in the nonlinear dispersion relation for the whistler mode.
Inspired by the artificial triggering of chorus by the dashes in a Morse code signal (Helliwell et al. 1964), Sudan and Ott (1971) provided a dynamical theory of whistler wave growth and chirping caused by non-gyrotropy. They assumed that a sufficiently long triggering signal at a constant frequency creates a population of strongly phase-correlated resonant electrons, emitting a secondary whistler wave—this is analogous to the end-fire helical antenna imagined by Brice (1963).Footnote 3 Under a simplified model of the correlated population, where the variation of PSD in phase is harmonic, they found instability in sidebands with frequency shifts \(\delta \omega \) in the order of \(\omega _{\textrm{tr}}\). Sudan and Ott (1971) further noted that the inhomogeneity of \(B_0\) is essential because as long as the correlated particles stay in resonance with the triggering wave, the radiated power will support amplitude growth of this primary wave instead of the sidebands (compare with Helliwell (1967) and their splitting of the interaction region into a phase-bunching half and a radiation-emitting half). The approximate formula for the sideband growth rate was found to be
With representative parameters \(\langle v_{\perp } \rangle /c = 0.4\) and \(\omega _{\textrm{pe}}/\varOmega _{\textrm{e}} = 4.2\), an estimated fraction of phase-correlated particles \(n_{\textrm{R}}/n_{\textrm{c}} \in [5\cdot 10^{-6},5\cdot 10^{-5}]\), and frequency \(\omega = 10^4\,{\mathrm{s^{-1}}}\), we get a wave growth estimate in the approximate range from \(10^{2}\,{\mathrm{s^{-1}}}\) to \(2\cdot 10^{2}\,{\mathrm{s^{-1}}}\). Sudan and Ott (1971) conclude that the numerical results obtained from Eq. 44 agree with the observations of Helliwell et al. (1964).
On the other hand, Karpman (1974) criticised the above-reviewed results on the sideband growth rate, pointing out that the perfect phase correlation assumed by Sudan and Ott (1971) (\(\delta \)-function in parallel velocities at \(V_{\textrm{R}}\) and a cosine distribution in phases) is unrealistic, and claimed that the sideband growth rate should be much closer to the linear growth rate \(\gamma _{\textrm{L}}\) from Eq. 18. They based their arguments on the analytical computations of Bud’ko et al. (1972), who in turn were inspired by the exact nonlinear Landau damping theory of O’Neil (1965) and assumed that the distribution of resonant particles reaches an ergodic state. Here, the term “ergodic” refers to the mixing property of the trapped particle evolution operator: for \(t/T_{\textrm{tr}} \rightarrow \infty \), a coarse-grained distribution is asymptotically constant along phase space trajectories for any mesh size, and its value at any point can be obtained by averaging the initial distribution. Based on energy conservation and the ergodic theorem, Bud’ko et al. (1972) conclude that the maximum growth rate of the sideband is about \(1.4\gamma _{\textrm{L}}\), which is typically much less than the predictions based on Eq. 44. Karpman (1974) also notes that the inhomogeneity of the background magnetic field introduces an asymmetry between the upper and lower sidebands, explaining the dominance of rising tone elements.
Denavit and Sudan (1975) proposed a more general distribution of resonant electrons expressed in the form of Fourier decomposition, yet it was still assumed to be initially strongly concentrated near \(\zeta \approx \pi \), leading to vanishing phase-correlation harmonics of order three and higher. Unlike Bud’ko et al. (1972), they worked with a set of secondary waves coupled to the primary wave instead of a single test wave. The shift between the mean velocity of resonant particles and the resonance velocity of the primary wave, which is responsible for the frequency shift of sidebands, came from the slope of the initial velocity distribution along \(v_{\parallel }\). The dispersion relation derived by Denavit and Sudan (1975) shows splitting of the whistler mode determined by the primary wave’s amplitude. Depending on the inhomogeneity of \(B_0\) and the shape of the initial velocity distribution, the excitation coefficient of one of the sidebands can increase, leading to a preferential rising-tone or falling tone structure. The resulting peak growth rate formula is
where the density of resonant particles \(n_{\textrm{R2}} \propto \omega _{\textrm{pR2}}^2\) corresponds only to the component of resonant current \(J_{\textrm{R}}\) that contributes to the instability of magnetic field perturbations; Denavit and Sudan (1975) estimate \(n_{\textrm{R2}}/n_{\textrm{c}} = 10^{-7}\). With this estimate and the values of frequencies and velocities defined below Eq. 44, we get a growth rate of \(1.4\cdot 10^2\,{\mathrm{s^{-1}}}\). Despite the different power-law coefficients, there is little quantitative change for the chosen representative values of input parameters.
Nunn (1986) sidestepped the difficulties of finding the analytical expression for the resonant particle distribution by performing a backward numerical integration of electron trajectories. However, as in all of the above-discussed approaches, the amplitude of the primary wave was slowly changing, and the amplitude of the secondary wave was supposed to be much smaller so as not to perturb the particle trajectories.
In a realistic scenario, the triggering wave (either artificial or naturally generated from anisotropy-driven instabilities) will experience fast growth, increasing \(\omega _{\textrm{tr}}\) and widening the spectral gap between the primary wave and the sidebands. Therefore, the power radiated by the phase-correlated electron should create a rising-frequency fluctuation spectrum, similar to the continuous frequency drift assumption (Eq. 78) made by Omura and Nunn (2011). Furthermore, overlapping trapping potentials of the triggered wave and the primary wave will result in loss of phase correlation before the ergodic state sets in, making the application of results from Bud’ko et al. (1972) to chorus growth questionable. Unfortunately, a self-consistent description of the frequency drift poses serious mathematical challenges which have yet to be fully resolved. One promising path towards a complete analytical description of the nonlinear chorus growth is reviewed in Sect. 3.3.
3 Modern Chorus Theories
At the beginning of this section, three points must be clarified. First, the word “modern” in the heading refers to the fact that the theories described below are still actively used in recent literature to explain observations from spacecraft and numerical experiments. Second, the three theories described below—the step-backwards-wave oscillator (sBWO) regime of chorus growth, the nonlinear growth theory of chorus by Omura et al. (NGTO), and the self-consistent chorus excitation (SCCE) framework—are those that we considered as the most prevalent in recent publications, and should by no means be considered as a comprehensive list. For example, the very rigorous self-consistent Hamiltonian theory of Crabtree et al. (2017a) was not included due to the limited number of its applications in the published literature. And third, despite calling these theories modern, they often rely on the concepts from the 1960s–1980s described in Sect. 2, which will be frequently referenced.
3.1 Backwards-Wave Oscillator Theory of Chorus Growth
In the inner magnetosphere, where field lines are closed, separate magnetic flux tubes can be viewed as resonant cavities, with the conjugate ionospheres acting as mirrors for electromagnetic waves (for unducted waves, magnetospheric reflections at higher altitudes may occur). Whistler wave packets bouncing between the mirrors experience amplification through interaction with trapped populations of energetic electrons. This concept is called the magnetospheric cyclotron maser and can explain the origin of certain types of electromagnetic emissions, e.g., the quasiperiodic hiss emissions (Trakhtengerts and Rycroft 2008). However, the predicted amplification is not fast enough to explain the growth of chorus emissions. To achieve large wave growth, the maser must operate in a backwards-wave oscillator (BWO) regime where the wave packets interact with a well-organised electron beam propagating in the opposite direction. In the theories of Brice (1963) and Helliwell (1967), the beam is equivalent to the helical current formed by phase bunching. The BWO concept has been known since the 1950s from laboratory experiments (Kompfner and Williams 1953; Chow and Pantell 1960).
As shown, e.g., by Trakhtengerts (1995), the BWO regime can also be achieved when a step-like deformation is present in the \(f(v_{\parallel })\) distribution of hot electrons, situated close to the cyclotron resonance velocity for a frequency on the bottom of the chorus band. Their calculations demonstrated that the presence of a hiss band could lead to the formation of coherent wavelets near the upper frequency bound of the noise. The basic equations of the BWO theory of chorus generation are the same as in most theories of nonlinear whistler-mode growth: the equations of motion for electrons in a parallel whistler wavefield (Eqs. 9, 10, and 11) and the complex amplitude equation 39, complemented with the conservation of phase space density of electrons (Liouville’s theorem). Assuming a low-efficiency operation of the oscillator, the resonant current is expected to be carried mainly by particles near \(V_{\textrm{R}}\), and the variation of \(v_{\parallel }\) can be neglected in the evaluation of the \(\partial /\partial t + v_{\parallel } \partial /\partial h\) operator of the Vlasov equation and is kept only for calculation of the resonance mismatch \(\nu \) from Eq. 24. The perturbation \(\delta f\) to the hot electron distribution can then be expressed in simple terms.
The salient features of the theory are expressed through the evolution of a reduced distribution (Demekhov and Trakhtengerts 2008)
The integral is to be taken over a region near the resonance velocity, and it is further assumed that the most important contribution to the phase space evolution happens near \(v_{\perp }\), and that the adiabatic changes in parallel and perpendicular velocity over the interaction region length can be neglected. These considerations justify removing the equation of motion for \(v_{\perp }\) and writing a reduced Vlasov equation for \(\Phi \):
Here \(V_{*}\) represents the absolute value of step velocity and \(\mathcal {F}\) is the smooth component of the initial distribution function
where b denotes the height of the step deformation, \(n_{\textrm{eq}}\) is the equatorial hot electron density and \(\Theta \) is the Heaviside function. The resonant current arising due to the perturbations can be expressed through \(\Phi \) as
where \(\zeta _{0}(\zeta ,t,h)\) is the initial relative phase angle. This expression is consistent with the definition of resonant current from Eq. 42 for \(\delta f = f_{\textrm{R}} - f_0\). The resonant current enters the amplitude equation 39, and together with the evolution of phase and parallel velocities (Eqs. 9 and 11 rewritten into a convective form in an inertial frame travelling at a velocity corresponding to the step-like deformation), we get a system of equations describing a self-consistent evolution of the electron distribution and whistler-mode waves. Finally, an estimate of the dimension of the interaction region is needed, which can be obtained by considering the distance travelled by electrons from the equator before the \(B_0\)-inhomogeneity and second-order resonance effects cause loss of phase correlation (Trakhtengerts 1999).
The step-BWO theory of chorus generation does not provide simple analytical estimates on the amplitudes and frequencies of chorus elements, and must be instead solved numerically as a nonlinear hyperbolic system of conservation laws (Demekhov and Trakhtengerts 2005). The nonlinear growth rate to which the numerical results are often compared (Demekhov and Trakhtengerts 2005; Demekhov 2017) is based on exact calculations of the trapped particle motion (monochromatic plane wave, homogeneous field) carried out by Bud’ko et al. (1972), resulting in
This relationship between growth rate and trapping frequency can be plugged into the formula for the effective inhomogeneity ratio (e.g., Eq. 43) to express the chirp rate, resulting in the qualitative relation
However, as discussed in Sect. 2.3 when dealing with the sideband instability, the above growth rate formula does not include the distortion of particle trajectories caused by sidebands/subpackets obtained from numerical solution of the sBWO reduced Vlasov equation 47. These simulation results can be successfully compared with direct satellite observations, as shown recently by Demekhov et al. (2020a).
The step-BWO theory and related simulations also successfully explained the repetition of chorus elements, which is a prediction outside of the scope of the theories discussed in Sects. 3.2 and 3.3.2, and Demekhov (2011) demonstrated the possibility of falling-tone chorus formation in off-equatorial sources. A major shortcoming of the BWO theory comes from the assumption of a step-like feature in \(f(v_{\parallel })\), which is supposed to be formed due to the cyclotron interaction of hot electrons with a hiss emission. The presence of low-frequency whistler-mode hiss, as seen at around \(600\,{\textrm{Hz}}\) in Fig. 3, does not always correlate with observations of chorus elements. Furthermore, the simulation results on step formation from the hiss emission by Trakhtengerts et al. (1996) have never been experimentally confirmed. However, as noted by Demekhov et al. (2017) and Hanzelka et al. (2021), phase space density depletions caused by interaction with a chorus subpacket form a step-like feature in the direction perpendicular to the curve \(V_{\textrm{R}}(v_{\perp })\) in \((v_{\parallel },v_{\perp })\) space, as is introduced by Eq. 14 and shown in Fig. 5a. This relates the electron hole formation described later in Sect. 3.2 to the BWO approach. Unfortunately, this notion can be applied only to later stages of the chorus growth when a strong wave packet has already been formed, leaving the PSD perturbation processes in the initial stage of chorus growth unexplained. Note that both the initial PSD perturbations in \((v_{\parallel },v_{\perp })\) space, as well as those linked to chorus subpackets still wait for a direct experimental confirmation, which might be achieved with a specialized design of electron analyzers (Hanzelka et al. 2021).
3.2 Nonlinear Growth Theory of Omura et al.
In a series of papers starting with Omura et al. (2008) and Omura et al. (2009), a theory was developed that attempts to simplify the description of frequency drift and amplitude growth of chorus emissions observed by spacecraft and in kinetic simulations. Applications of this approach have appeared in many papers from recent years: Hikishima et al. (2009), Nunn and Omura (2012), Summers et al. (2012), Kurita et al. (2012), Omura et al. (2015a), Foster et al. (2017), Katoh et al. (2018), Juhász et al. (2019), Hanzelka et al. (2020), and Zhang et al. (2021), to name a few. The description provided here reflects the current state of the theory as summarized by Omura (2021). Details concerning the oblique propagation of chorus (Omura et al. 2019) are left out.
3.2.1 Overview
In the NGTO, the effective inhomogeneity ratio (also called the inhomogeneity factor) introduced by Vomvoridis et al. (1982), Eq. 43, is derived in a relativistic form, similar to the formulation from Eqs. 32–34. Since the source region of chorus emissions is confined to about ten degrees of latitude within the equator (Santolík et al. 2004, 2005; Taubenschuss et al. 2016), the cold plasma density is often taken as constant, resulting in
with
The wave equations for complex amplitude are derived in a similar fashion to Nunn (1974) (see Eqs. 39–41 and the paragraph above them). However, the plane wave frequency and wave vector, defined as \(\omega = \partial \psi /\partial t\) and \(k = -\partial \psi /\partial h\), are plugged into to computation before removing higher-order derivatives, resulting in a whistler-mode dispersion dispersion relation with a nonlinear correction term (Omura et al. 2008)
We observe that the resonant current component \(J_{\textrm{E}}\) modifies the wave amplitude, and the \(J_{\textrm{B}}/B_{\textrm{w}}\) quantity modifies the dispersion relation. While Eq. 40 can be in principle solved numerically, given suitable initial conditions and knowledge of \(J_{\textrm{E}}\), Eq. 54 is more difficult to interpret. Omura and Nunn (2011) view the growth of chorus elements as a triggering process, where a strong initial wave of frequency \(\omega _0\) forms the resonant current and preserves its spatial structure given by a fixed wavenumber \(k_0\). Under this assumption, we can write in Eq. 54\(k = k_0\), \(\omega = \omega _0 + \delta \omega \), where \(\delta \omega \ll \omega _0\) is a small perturbation in frequency. Solving for \(\delta \omega \), we get
demonstrating a connection between chirping and \(J_{\textrm{B}}\). Nunn (1974) suggested that \(\omega _0\) must be changed periodically to reflect that a triggered wave has replaced the initial triggering wave at a higher frequency. Unfortunately, it is not obvious how to implement this stepping up in frequency. One approach to this issue was presented by Hanzelka et al. (2020) and is briefly discussed in Sect. 3.2.2. For implementation of the frequency stepping in self-consistent numerical simulations, see Nunn (1993) and Nunn et al. (2021).
A crucial part of each nonlinear growth theory of chorus in the evaluation of resonant current, which depends on the perturbed hot electron PSD distribution. Following Omura et al. (2009) and Summers et al. (2012), the initial equatorial distribution is chosen to be bi-Maxwellian in momenta,
where
is the number density of the hot population. We point out that this distribution is chosen mostly for convenient integration and works well in a weakly relativistic setting, but for higher values of \(\gamma \), a two-temperature generalisation of the Jüttner distribution should be used, as proposed, e.g., by Kuzichev et al. (2019). However, it should also be mentioned that we need to model the electron distribution only in the range of momenta where the interaction happens. Therefore we do not need to use a sum of Maxwellians or kappa distributions to represent both tail and core of the electron momentum distribution.
It is further assumed that a bi-Maxwellian can model the electron distribution along a magnetic field line at any distance h, within the limits of the interaction region. From Liouville’s theorem, we have
By substituting formulas for adiabatic evolution of electron momentum into Eq. 58 and comparing the result with Eq. 56, we obtain the off-equatorial thermal momenta and density
where
and \(A_0\) is the equatorial temperature anisotropy.
Another simplification in the NGTO comes from reducing the distribution \(f(u_{\parallel },u_{\perp },h)\) to
where K is a normalisation constant. Note that restricting the resonant population to a narrow region along a constant \(u_{\perp }\) or pitch angle \(\alpha \) is a common simplification in both analytical (Helliwell 1967; Denavit and Sudan 1975) and numerical (Nunn 1993; Demekhov and Trakhtengerts 2005) studies. By requiring that \(f_{\delta }(u_{\parallel },u_{\perp },h)\) and \(f(u_{\parallel },u_{\perp },h)\) both integrate to the same density, n(h), and that they have the same average perpendicular momentum, \(U_{\perp }(h)\), we get
with
To evaluate the components of resonant current \(J_{\textrm{E}}\), \(J_{\textrm{B}}\), a factorisation
is introduced, where the simplified perpendicular distribution from Eq. 64 is used. Factor \(Q \in [0,1]\) represents the depth of the depletion in the trapping region, \(g_{\textrm{tr}}\) is the trapped particle distribution and \(g_0\) is the unperturbed distribution.
As a next step, the trapped particle distribution \(g_{\textrm{tr}}\) is replaced by a constant \(G = f_{\delta }(U_{\textrm{R}},U_{\perp })\). This represents a crucial point in the simplification of the resonant current computation, which states that the phase space density inside the trapping region is taken to be perfectly mixed—in other words, a waterbag model of trapped electron distribution is used. Recalling the shape of the boundaries of the inhomogeneous electron trap from Eq. 36, the components of the resonant current can now be expressed as
with
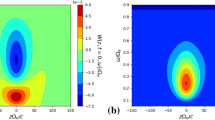
In Fig. 7, we show the plots of \(-J_{\textrm{E}}(S)\) and \(-J_{\textrm{B}}(S)\) as obtained from numerical integration of Eqs. 67 and 68. The quantity \(-J_{\textrm{E}}/J_0\) has a peak \(J_{\textrm{E,max}} \doteq 0.98\) at \(S \doteq -0.41 \equiv S_{\textrm{max}}\), and \(-J_{\textrm{B}}/J_0\) attains value \(J_{\textrm{B,max}} \doteq 1.29\) at \(S_{\textrm{max}}\). Note that \(-J_{\textrm{B}}\) has a maximum at \(S \doteq -0.07\), which is however not relevant for maximisation of wave power transfer. More importantly, \(J_{\textrm{B}}\) can be nonzero at \(S = 0\), indicating that variation of frequency is possible at the equator via Eq. 55. The change in frequency then shifts S away from zero, thus facilitating amplitude growth through \(J_{\textrm{E}}\) without the presence of spatial gradients of B(h); growth of chirping chorus elements in a homogeneous field has been recently successfully demonstrated with particle-in-cell (PIC) simulations (Fujiwara et al. 2023).
Unlike in Omura (2021), we allow here for G to be h-dependent, making it a constant in velocity space, but not in the positional space. This extension coming from Hanzelka et al. (2020) is important for NGTO-based wave simulations with drifting source region, and has impact on the boundary conditions represented by the chorus equations 71 and 74. The original equations can be easily recovered by setting \(h = 0\).
The NGTO further assumes that the frequency growth of each chorus element (or each subpacket of the element, see Sect. 3.2.2) happens locally at a single point along the chosen field line at \(h = h_0\). We call this point the source, and we assume that the transfer of energy from particles to waves maximises in the source, and thus \(J_{\textrm{E}} = J_{\textrm{E,max}}\), \(S = S_{\textrm{max}}\). By definition the strength of the ambient magnetic field minimises at \(h = 0\); in that case, the linear growth rate for parallel whistler waves reaches its maximum at the equator and serves as the energy source for the naturally generated, narrowband triggering wave (Omura et al. 2008). With no convective growth, the evolution equation for the wave frequency is simply
The chirp rate can be then expressed at the source point \(h_0\) as
where we switched to the normalised wave amplitude \(\varOmega _{\textrm{w}}\). The trapping frequency has been written out explicitly to highlight the dependence of frequency on amplitude. Let us remark that the wavenumber k depends not only on frequency but also on the position h through the gyrofrequency \(\varOmega _{\textrm{e}}(h)\). Equation 71 is the first of two chorus equations and serves as an initial boundary condition for the transport Eq. 70.
To obtain the growth factor for the absolute nonlinear instability in the source, the inhomogeneous transport equation for amplitude (Eq. 40) is rewritten as
\(\varGamma _{\textrm{N}}\) is the convective nonlinear growth rate. To proceed further, an estimate of the spatial gradient of the amplitude of a growing chorus subpacket is needed. Omura et al. (2009) propose that to achieve a self-sustaining nonlinear growth in the near-equatorial region, the spatial gradient of the wave amplitude should be approximately constant in space. Assuming that the chirp does not change much due to dispersion and propagation effects (the whistler wave group velocity from Eq. 2 remains approximately constant near the equator and in the frequency interval corresponding to the lower-band chorus), we can neglect their contribution to S at larger distances and make an estimate
where the parabolic approximation of \(\varOmega _{\textrm{e}}\) from Eq. 37 was used after the second equals sign. Here we must note that, in general, \(S = S_{\textrm{max}}\) does not have to hold further away from the source, which limits the precision of quantitative predictions of the nonlinear growth theory. Finally, the second chorus equation, i.e. the initial boundary value condition for amplitude growth, can be stated as
with
Here \(\langle u_{\perp } \rangle \) was substituted with \(\gamma _{\textrm{R}}V_{\perp 0}\), which is a common simplification in the treatment of the inhomogeneity factor under the NGTO. Equations 40, 70, 71 and 74 can be solved numerically to obtain the wavefield of a parallel propagating chorus element.
To complete the description of the nonlinear growth theory, two additional parameters are required: the threshold amplitude at which the growth rate becomes positive and the optimum amplitude at which the growth saturates. The condition on absolute instability is
and by inserting the expression from Eq. 73 on the right-hand side, the amplitude for which the marginal instability is encountered becomes
The threshold amplitude is meaningful only in the source, so all variables are assumed to be evaluated at \(h = h_0\).
Let us now return to the frequency perturbation related to \(-J_{\textrm{B}}/B_{\textrm{w}}\) stated in Eq. 55. Introducing the assumption that the actual frequency change within a single subpacket proceeds gradually, a nonlinear transition time \(T_{\textrm{N}}\) can be defined by equating
The ratio between the transition time and the trapping period is given by the dimensionless parameter
In the source, the left-hand side of Eq. 78 can be replaced with the chorus equation 71, and the \(J_{\textrm{B}}\) component of the resonant current can be calculated from Eqs. 67 and 68 with \(S = S_{\textrm{max}}\). After these substitutions, we can use Eq. 55 and express the normalised amplitude
Vlasov hybrid simulations (Omura and Nunn 2011) have shown that the optimum amplitude is close to the maximum amplitude at which the wave growth breaks down.
Together, the threshold amplitude and the optimum amplitude define a range of wave frequencies \(\omega : \varOmega _{\textrm{thr}}(\omega ) < \varOmega _{\textrm{opt}}(\omega )\), in which the nonlinear growth of chorus emissions becomes possible. In Fig. 8, we plot \(\varOmega _{\textrm{thr}}(\omega )\) and \(\varOmega _{\textrm{opt}}(\omega )\) for two pairs of the free parameters \(\tau \) and Q. For \((\tau ,Q) = (0.25,1.0)\), the lowest frequency at which the growth is possible is \(\omega = 0.12\varOmega _{\textrm{e0}}\), while for \((\tau ,Q) = (1.0,0.25)\), the limiting frequency increases to \(\omega = 0.16\varOmega _{\textrm{e0}}\). The characteristic amplitudes themselves can change by more than an order of magnitude in dependence on the two free parameters. In general, these parameters have to be estimated from simulations.
3.2.2 Source Drift and Subpackets
The chorus equations of the NGTO, together with the amplitude and frequency advection equations, can be used to model the wavefield of a parallel-propagating rising-tone chorus element near the magnetic equator (Summers et al. 2012). However, additional assumptions about the resonant current and the triggering process must be made to reproduce the subpacket structure (see Fig. 4) and to include the drift motion of source (Demekhov et al. 2020a). These modelling efforts serve two main purposes. First, they help us understand the parametric dependence of various chorus properties. Second, they provide a reasonable approximation of the real wavefield, which can be used as an input for test-particle studies of electron acceleration and scattering of resonant electrons.
a Flowchart of the generation mechanism of the subpacket structure of a whistler-mode chorus element. The initial stage is skipped in the numerical model. b Schematic representation of the sequential subpacket formation model. After the wave amplitude reaches the optimum amplitude \(\varOmega _{\textrm{opt}}\) at \((t_{\textrm{max},0},h_0) \sim \) Point 0, it starts decreasing until it reaches the threshold amplitude \(\varOmega _{\textrm{thr}}\) at \((t_{\textrm{end},0},h_0) \sim \) Point \(0^{\prime \prime }\) within a time period \(\delta t_0\). At this point the radiation emitted from \((t_1,h_1) \sim \) Point \(0^{\prime }\) arrives, where \(0^{\prime }\) corresponds with the peak resonant current which was released from Point 0. The new subpacket starts growing from Point \(0^{\prime }\). This generation process is then repeated with each subpacket (Points 1, \(1^{\prime }\), and \(1^{\prime \prime }\), etc.). Adapted from Hanzelka et al. (2020)
Hanzelka et al. (2020) presented a model based on the NGTO that utilised the sequential triggering process from Shoji and Omura (2013) and ideas about resonant current escaping upstreamFootnote 4 from the interaction region and emitting secondary waves Brice (1963); Helliwell (1967); Trakhtengerts et al. (2003). The complete scheme can be described as follows (see also Fig. 9): A coherent wave is formed near the frequency where anisotropy-driven linear growth maximises. Resonant current component \(J_{\textrm{B}}\) starts growing and introduces a nonlinear phase shift into the wave field. Frequency change related to the phase shift pushes S towards \(S_{\textrm{max}}\), \(J_{\textrm{E}}\) component of the resonant current becomes large and commences the rapid growth of the first subpacket. During the growth of a subpacket, the optimum amplitude is reached at one point, which also marks the peak of the resonant current \(J_{\textrm{E}}\). Following Kubota and Omura (2018), the sign of the nonlinear growth rate \(\varGamma _{\textrm{N}}\) is switched at this point, letting the wave damp until it encounters the threshold amplitude. This heuristic approach enforces the formation of subpackets with nearly symmetric envelopes, similar to those observed in self-consistent simulations and in spacecraft measurements. The 3D spatial distribution of the current has a helical shape, making the resonant electrons act as an antenna radiating whistler-mode waves at a frequency determined by the pitch of the helix and the cold plasma dispersion relation. Hanzelka et al. (2020) further postulated that the continuous radiation from the antenna cannot replace the previous subpacket until its normalised amplitude drops below \(\varOmega _{\textrm{thr}}\). This uniquely defines the source location \((t_{i+1},h_{i+1})\) of the new subpacket in time and space,
The interval between Points \((i+1)\) and \((i+1)''\) in Fig. 9b was denoted \(\delta t_{i} = t_{\textrm{end},i} - t_{\textrm{max},i}\); the times where the previous subpacket reaches its maximum and where it ends are called \(t_{\textrm{max},i}\) and \(t_{\textrm{end},i}\), respectively. Because the dispersive properties between source points of two adjacent subpackets do not change much, we use the resonance velocity and group velocity at \((t_{\textrm{max},i},h_i)\) in the calculation of the new source location. The drift velocity of the source can be expressed as
which is a strictly positive value. The triggering process repeats for each subpacket until an upper-frequency limit is reached.
Because of the overlap of resonance regions of high-amplitude subpackets, Hanzelka et al. (2021) introduced a resonant current suppression factor that results in more realistic values of \(B_{\textrm{w}}\). Numerical results from the model are shown in Fig. 10 for the following initial conditions and parameters: \(\omega _0 = 0.21\,\varOmega _{\textrm{e0}}\), \(\omega _{\textrm{f}} = 0.46\,\varOmega _{\textrm{e0}}\), \(B_{\textrm{surf}} = 2.52\cdot 10^{-5}\,{\textrm{T}}\), \(Q = 0.5\), \(\tau = 0.35\), \(\omega _{\textrm{pe}} = 4.2\,\varOmega _{\textrm{e0}}\), \(\omega _{\textrm{phe}} = 0.3\,\varOmega _{\textrm{e0}}\), \(V_{\perp 0} = 0.4\,c\), \(U_{\textrm{t}\parallel 0} = 0.16\,c\), \(L = 4.58\). In the numerical simulation, the linear growth stage is skipped, with each subpacket starting from an amplitude slightly above the threshold value \(\varOmega _{\textrm{thr}}\). An obvious shortcoming of the improved model is the lack of current suppression in the first subpacket, resulting from the sequential triggering scheme. Comparison of the average amplitude growth \(2\cdot 10^{2}\,{\mathrm{s^{-1}}}\) in the source of the first subpacket shows a good match with the prediction of sideband theory based on Eq. 44.
Chorus wavefield calculated from an improved model with resonant current suppression. Time evolution of the wave magnetic field amplitude \(B_{\textrm{w}}\) of a chorus element propagating along the magnetic field line towards positive h. Plotted for two values of latitude, \(\lambda _{\textrm{m}} = 0^{\circ }\) (red line) and \(\lambda _{\textrm{m}} = 10^{\circ }\) (blue line). b Evolution of amplitude in time and space. Dotted lines show the spatial cuts at \(0^{\circ }\) and \(10^{\circ }\) of latitude. The total wavefield was obtained as a superposition of the left- and right-propagating waves. Panels c and d show the wave frequency \(\omega \) and follow the format of panels a and b, with only the right-propagating element being plotted. Reprinted from Hanzelka et al. (2021)
Unfortunately, an in-depth comparison between the model and observations is not possible, mostly due to two reasons. First, certain input parameters cannot be observed with sufficient precision. As shown by Hanzelka et al. (2021), reliable measurements of phase space density in the resonance region on scales of \(T_{\textrm{tr}}\) are currently not feasible, and thus we cannot determine Q. The measurements of the hot electron distribution are also plagued with large uncertainties, limiting our knowledge of \(\omega _{\textrm{phe}}\), \(V_{\perp }\) and \(U_{\textrm{t},\parallel }\). Parameter \(\tau \) is related to the nonlinear transition time for the formation of the resonant current \(J_{\textrm{R}}\), and \(J_{\textrm{R}}\) can be directly determined only by precise measurements of phase space density near the electron hole. And second, the model has seven input parameters (nine when counting \(\omega _{0}\) and \(\omega _{\textrm{f}}\)), which makes the sampling of the full configuration space unfeasible.
The motion of the source can be compared to multipoint measurements from the Cluster spacecraft fleet (Santolík et al. 2004). It was shown that the source position fluctuates within 1000 to \(2000\,{\textrm{km}}\) of the geomagnetic equator, and the extent of the source ranges from 3000 to \(5000\,{\textrm{km}}\). The values of latitudinal drift shown in Fig. 10d and in Hanzelka (2022) amount to 900 to \(4600\,{\textrm{km}}\). However, the analysis of Santolík et al. (2004) relates to a large scale motion of the source, not its motion during the formation of a single element. This independent motion of the sources of each separate chorus element was indirectly proven by Demekhov et al. (2020a), who observed frequency differences in THEMIS observation of chorus elements near the equator and linked them to the bidirectional motion of their sources. The velocity of this upstream motion has been determined to be \(V_{\textrm{g}} + V_{\textrm{R}}\) based on PIC simulations (Nogi and Omura 2022; Harid et al. 2022), which, according to Eqs. 2 and 5, becomes positive for \(\omega \gtrsim \varOmega _{\textrm{e}}/2\). This result does not agree with Eq. 83. So far, there is no rigorous theoretical support for the conclusion of Nogi and Omura (2022), but the recent parametric analysis by Nogi and Omura (2023) suggests that the source drift and the character of amplitude modulations strongly depend on the resonant current formation process, which may have been oversimplified in the model of Hanzelka et al. (2020).
Analysing chorus subpackets (Santolík et al. 2003a, 2014a) with theoretical and semi-empirical models proves difficult because the exact origin of the amplitude modulations is still disputed. This lack of theoretical understanding becomes critical when comparing the instantaneous frequencies from spacecraft data with the numerical model. The jumps in frequency found between subpackets in Fig. 4 resemble the irregular chirp rate from the wave model in Fig. 10c; however, it is not apparent if these features come from the breakdown of the resonance island, as assumed in the sequential triggering model, or if they are a simple result of wave beating with a phase mismatch. It was discovered with Bayesian spectral analysis (Crabtree et al. 2017b) that the initial subpackets correspond to a single chirping plane wave, but the later amplitude modulations are better explained as a summation of multiple plane waves. Wavelet analysis of several RBSP observations (Tsurutani et al. 2020) even suggests that the subpackets have constant frequency and that the chirping comes from discrete jumps.
We suggest that future modelling efforts should focus on removing the free parameters \(\tau \) and Q, and the parallel theory should be updated to a quasiparallel version which could explain the frequency gap near \(\varOmega _{\textrm{e}}/2\) and allow to expand the model to higher latitudes. However, even such improvements might not resolve the questions about subpackets, which may originate not only from the nonlinear generation process but also from convective growth, superposition of multiple plane waves, and possibly from propagation effects in an inhomogeneous plasma (ducting) as well. Furthermore, a thorough statistical analysis of the subpacket structure is missing in current literature, limiting thus our ability to validate theoretical and numerical results.
3.2.3 Summary
The nonlinear growth theory of Omura et al. (2008, 2009, 2015a) provides an approximate formula for the calculation of resonant currents arising from the non-gyrotropy near the trapping region, and it assigns meaning to the nonlinear dispersion relation by postulating that the wavenumber remains constant within a single subpacket. Using further simplifications based on self-consistent simulations of the triggering process, four new features are introduced:
-
1.
Relativistic form of the inhomogeneity ratio S, improving on the previous results of Vomvoridis et al. (1982).
-
2.
Resonant current formation (and thus also the nonlinear wave growth and chirping) at the equator where the magnetic field gradient is zero.
-
3.
Threshold amplitude for the onset of the nonlinear growth.
-
4.
Optimum amplitude at which the resonant current saturates.
With these tools, a plane-wave model can be constructed that predicts the growth of amplitude and frequency of a triggered rising-tone chorus element.
The description of phase space perturbations provided by the NGTO may seem quite different from the sBWO theory, yet the fundamental physical concepts are the same. The step-like deformation assumed in Sect. 3.1 represents a local increase in pitch angle anisotropy, which serves as a free source of energy for the waves: electrons from high-density regions above the step lose energy, while electrons from the low-density region below the step gain energy, resulting in a net positive power transfer to electromagnetic fields. The step feature erodes during the evolution of a chorus element, accessing free energy stored in particles at lower parallel velocities. Similarly, the electron hole in the NGTO (which forms only when the initial distribution is sufficiently anisotropic) increases the local PSD gradient along the pitch angle, and the hole propagates towards lower velocities, akin to the step erosion. Additionally, a small hill/clump is formed at higher velocities, representing a minor gradient that was suggested to be the source of weak falling-tone emissions (Omura et al. 2015b; Nogi and Omura 2022).
A full description of fallers and oblique propagation is so far outside of the scope of the theory; however, the relativistic inhomogeneity ratio can be generalised to Landau and cyclotron resonance with oblique whistler waves, as shown by Omura et al. (2019). A calculation by Omura et al. (2009) tells us how the coherent and nonlinear damping through Landau resonance can contribute to creating the spectral gap at \(0.5 \varOmega _{\textrm{e}}\) during propagation away from the magnetic equator, but it cannot explain existence of the gap inside the source (Li et al. 2019). Nevertheless, the theory cannot be used in its current state to model wavefields of chorus elements with higher wave normal angles, and therefore we omitted the discussion of oblique propagation.
Overall, the NGTO brings more clarity to the discussion of the chorus triggering process, and it enables us to estimate the chirp rate and wave amplitudes based on the properties of cold and hot plasma in the generation region. However, it relies on a number of assumptions and approximations that neglect some potentially important properties of chorus emissions. First of all, the emission source is modelled by a single point at the equator, while observations (see the discussion of chorus properties in Sect. 1.1) show that the source region extends thousands of kilometres away from the \(B_0\)-minimum. The homogeneous phase space density distribution in the electron hole contradicts test-particle simulations and PIC simulations of the trapped particle population during the initial stage of wave growth. The applicability of the plane wave approximation has been challenged by some subpacket studies, e.g., Crabtree et al. (2017b), who suggest that a chorus element is best represented by a superposition of multiple plane waves. The reduction of the perpendicular momentum distribution of electrons to a delta function and the use of averaged \(\langle u_{\perp } \rangle \) in the second-order resonance complicates comparison with particle simulations and decreases the accuracy of quantitative predictions. Similarly, the inhomogeneity factor S may deviate from the fixed value of \(-0.41\) (Nunn et al. 2009), and thus the variations in the resonant current stemming from the dynamics of S are missing from the NGTO. Furthermore, the theory provides no description of the deformation/breakdown of the electron hole, which is expected to happen between subpackets in sequential triggering models (Shoji and Omura 2013; Hanzelka et al. 2020). The derivation of threshold amplitude is based on the assumption of constant field-aligned amplitude gradient \(\partial B_{\textrm{w}} / \partial h\), for which there is no clear support in self-consistent simulations. And finally, the NGTO does not provide any mechanism that would explain the repetition of elements, which is one of the defining features of the whistler-mode chorus.
In conclusion, it is evident that despite the advances in theoretical understanding of chorus through the NGTO, a more robust theory is needed to overcome the current limitations and refine our knowledge of the nonlinear growth process. The recent results of self-consistent particle and Vlasov simulations (Ke et al. 2017; Tao et al. 2017; Katoh et al. 2018; Nunn et al. 2021; Nogi and Omura 2023) should serve as guidance for such an improved theory.
3.3 Self-Consistent Theoretical Framework of Chorus Wave Excitation (SCCE)
The new self-consistent chorus excitation (SCCE) framework developed by Zonca et al. (2022) aims to provide a self-consistent analytical description of the interaction between a whistler-mode fluctuation spectrum and resonant electrons. This approach focuses on deriving the nonlinear response of hot electron distribution in a general “Dyson-like” form, which is subsequently reduced to demonstrate the salient features of chorus growth. Although this framework has been reviewed in detail by Chen and Zonca (2016) and the underlying physical and mathematical concepts go back to nonlinear Landau damping studies of O’Neil (1965) and Al’tshul’ and Karpman (1966), its application to chorus is very recent (Tao et al. 2017).
3.3.1 Overview
As a first step, Zonca et al. (2022) split the current density into cold and hot components, deriving a nonlinear dispersion relation equivalent to Eq. 54. Next, they formulate a complex wave equation analogous to Eq. 39. However, instead of the amplitude and phase of the wave magnetic field, they use the wave intensity
and arrive at
with
and
where W is the nonlinear phase shift, \(\varGamma \) is the convective growth rate, and the evaluation at k denotes that the given quantities correspond to the solution of the whistler-mode cold plasma dispersion relation \({\bar{D}}_{\textrm{w}}(h,k(h),\omega _k) = 0\) (see Eq. 1). Equation 85 given above corresponds to Equation (16) from Zonca et al. (2022), but we converted Gaussian units to SI units, switched from electric field representation to magnetic fields, and utilized the group velocity formula from Eq. A1. Since this form of the complex wave equation comes from the intensity/energy-density formulation, it retains the additional derivative of dispersion relation (Karpman 1974), but can be proven equivalent to the wave amplitude formulations used by the NGTO and the sBWO theories. The proof can be found in Zonca et al. (2021) and Zonca et al. (2022) and derives from the perturbed dispersion relation (modified here to fit our notation)
which stems from the same approximations (i.e., separable cold (=core) and hot (=perturbation) currents plus slowly-varying wave fields) that were used by Nunn (1974) to obtain Eq. 39.
Unlike in the sideband theory (Sect. 2.3) or the NGTO (Sect. 3.2), Zonca et al. (2022) do not assume a test wave at \(\omega +\delta \omega \) or a continuous shift in the frequency of a plane wave. Instead, they write the perturbation of the hot electron density \(\delta f\) as a response to a dense fluctuation spectrum, summing over all possible wavenumbers k. The spectral components are always assumed to approximately fulfil the whistler dispersion relation. Further, they use the Vlasov equation to derive an evolution equation of the background distribution (zeroth summation component) \(f_0\) in dependence on \(B_{\textrm{w}k}\) and \(\delta f_k\), and another evolution equation for \(\delta f_k\) in dependence on \(f_0\). By formal inversion of the evolution operators, \((\partial _t + v_{\parallel }\partial _h)f_0\) can be cast in a form similar to the Dyson equation, describing the emission and absorption of whistler-mode electromagnetic oscillators. The resulting Dyson-like equation captures the self-consistent evolution of the phase space structures and the chirping chorus element, accounting for self-interactions in the fluctuation spectrum.
In contrast to the sBWO theory as presented by Demekhov and Trakhtengerts (2008), the operator \(\partial _t + v_{\parallel }\partial _h\) includes the perturbations to the parallel velocity of resonant particles, thus capturing the full nonlinear response of the PSD distribution. However, Zonca et al. (2022) proceed to reduce the Dyson-like equation to a simpler form by assuming that the nonlinear response is dominated by electrons near the exact resonance, avoiding thus the need for numerical methods and restricting the analysis to narrowband emissions. Furthermore, it is assumed that the newly excited waves have such frequencies that the power transfer from electrons to waves is maximised; the importance of maximisation of power transfer was recognised already by Helliwell (1967) and later confirmed by self-consistent simulations (Katoh and Omura 2016).
Due to the complexity of the general framework presented by Zonca et al. (2022), we will not review the resulting equations in detail, and we will instead focus on the new concepts and their relation to older theories. The growth and chirping of chorus emissions are shown to be associated with the aforementioned maximisation of wave power transfer, in agreement with the NGTO. However, instead of the excitation of discrete whistler seeds, the chirping comes from the excitation of a noise spectrum, with the frequency of the dominant wavenumber continuously sliding towards higher values. Furthermore, the nonlinear phase shift is found to be directly associated with the wave intensity peak. This suggests that the connection between the continuous chirp rate \(\partial \omega / \partial t\) and the nonlinear frequency variation \(\delta \omega \) postulated in Eq. 78 is approximately correct; however, it should be understood as a result of the power transfer peak being nonlinearly shifted to higher frequencies and exciting different parts of the noise spectrum.
To take a closer look at the origin of chirping, the approach to nonlinear variations induced by \(J_{\textrm{R}}\) must be explained in more detail. In contrast to the NGTO, the SCCE formalism postulates that the nonlinear phase shift W causes perturbation to both frequency and wave number, which are linked through the cold plasma dispersion relation. This interpretation corresponds to a shift in resonance velocity
Here we introduced the dagger symbol to signify that the frequency variation \(\delta \omega \) from the NGTO (Eq. 55) is different from the variation \(\delta \omega ^{\dagger }\) introduced in the SCCE theory. The frequency of waves that resonate with \((V_{\textrm{R}} + \delta V_{\textrm{R}}^{\dagger })\) particles then grows at a rate
and the total change in frequency across a chorus element is given by
The integral is taken over a curve in \((\omega ,t)\) space where the partial time derivative of \(\delta \omega ^{\dagger }\) maximises; this curve, to a good approximation, follows the intensity peak curve of a chorus element. Such integration is not possible within the NGTO where there is a only a single value of frequency at each time at a given spatial point. The integrated change in frequency based on Eq. 91 agrees with the frequency change in intensity peak obtained from the numerical solution of the full SCCE equations (Appendix D in Zonca et al. (2022)). Considering Eqs. 86 and 41, SCCE and NGTO agree on the importance of \(J_{\textrm{B}}\) for the chirping of chorus elements.
The new theoretical framework also reveals the connection between the nonlinear growth rate, trapping period, and chirping: \(\gamma _{\textrm{NL}} \propto \omega _{\textrm{tr}}\), \(\partial \omega / \partial t \propto \gamma _{\textrm{NL}}^2\). These proportionalities can be found in the earlier sideband theories (Bud’ko et al. 1972; Trakhtengerts 1999), but here, they have been placed on a rigorous mathematical foundation. The reduced version of the Dyson-like equation can be treated analytically to retrieve
where the constant 1/2 defines the optimum value of the nonrelativistic version of the inhomogeneity factor S as derived by Vomvoridis et al. (1982). The theory of Zonca et al. (2022) thus provides a fully analytical derivation of chirping in both rising and falling elements, as indicated by the ± sign.
Another interesting feature of the new approach is the treatment of the magnetic field nonuniformity. It is shown that the nonuniform initial hot electron distribution provides the energy source for the nonlinear excitation and that the \(B_0\) field can be treated as homogeneous. This can be contrasted with the NGTO, where the wave growth can start without any nonuniformity (field or electron distribution). A similar conclusion was reached based on the laboratory experiments and Hamiltonian theory presented by Crabtree et al. (2017a), who further suggest that a discrete nature of the wave spectrum could influence the development of chirping tones in a homogeneous environment (compare to the sideband excitation models discussed in Sect. 2.3). Nevertheless, a nonuniform ambient magnetic field is a critical component of chorus formation since it contributes to the symmetry breaking between fallers and risers, as suggested by the simulations of Wu et al. (2020).
In summary, the new theoretical framework developed by Zonca et al. (2022) provides a rigorous rederivation of previous major results on the chorus growth mechanism and rejects the nonlinear phase shift as a source of frequency chirping. On top of that, it shows a one-to-one correspondence of chorus chirping with superradiance in free-electron lasers and indicates the possible application of the new description in the BWO mechanism (Chen and Zonca 2016). Nevertheless, at this point, wavefield calculations rely on a reduction of the Dyson-like equation and its numerical solution, which requires Savitzky-Golay filtering to prevent the loss of regularity in \(\partial _{\omega }\). And while the time–frequency spectrograms presented in Zonca et al. (2022) show repetition of elements and formation of subpackets, the large chirp rate (\(> 5\cdot 10^{-4}\varOmega _{\textrm{e0}}^2\)) and short duration (\(<5\cdot 10^{2}\varOmega _{\textrm{e0}}\)) of each element cannot be compared with observations (Teng et al. 2017) due to the high value of the magnetic field inhomogeneity parameter \(a = 8.62\cdot 10^{-5}\varOmega _{\textrm{e0}}^2c^{-2}\), which \(10^3\)-times larger than the dipole field value for \(L = 4\). The substantial spectral width of simulated elements also does not match well with observations (Gao et al. 2014); however, it is similar to the simulation results of Tao et al. (2017) in a \(B_0\)-field with strong inhomogeneity. Furthermore, the current description is nonrelativistic, assumes parallel propagation in a parabolic magnetic field (with the field inhomogeneity being neglected everywhere but in the initial distribution function), and cannot handle discrete steps in the frequency spectrum due to the continuous limit introduced in the reduced model. Therefore, the explanation of the origin of subpackets, defined in the sense of Santolík et al. (2003a), is currently beyond the reach of the reduced model.
3.3.2 Trap-Release-Amplify Model (TaRA)
The Trap-Release-Amplify phenomenological model of chorus waves (TaRA for short) presented by Tao et al. (2021) describes the growth of chorus elements based on the qualitative results of the SCCE framework and PIC simulations. It also utilises the antenna effect introduced by Helliwell (1967), which was considered in the NGTO-based numerical model of Hanzelka et al. (2020); see Sect. 3.2.2. The frequency drift in the TaRA model arises from the selective amplification of new emissions from the broadband whistler-wave spectrum due to the phase-locking condition (\(\textrm{d}^2\zeta /\textrm{d}t^2 \approx 0\)), which is connected with the maximisation of wave power transfer. The chirp is thus partially explained due to inhomogeneity of the ambient magnetic field in the upstream, as originally suggested by Helliwell (1967). This description differs from the analytical results of Zonca et al. (2022), who neglected \(\partial B_0/\partial h\) and recovered the frequency growth solely from the nonuniformity of the hot electron distribution. Since TaRA is a phenomenological model, the rate of detrapping in the upstream region due to decreasing amplitude and shrinking trapping region is not quantified—a detailed review of this process can be found in Artemyev et al. (2018).
Unlike in the theory of Helliwell (1967), the TaRA model also acknowledges the relation of frequency shift to the particle trapping and wave amplitude as prescribed by Eq. 43 (where \(B_{\textrm{w}}\) is hidden in the ratio S), thus taking into account the case when the \(s_{\omega }\) component of Eq. 52 dominates the \(s_{\textrm{c}}\) component near the equator (note that the TaRA model is presented in a nonrelativistic form, but the concepts easily translate to the equations of Sect. 3.2 based on relativistic particle motion). In total, three equations for the chirp rate are given: In the upstream,
which describes the physical origin of the chirp due to the inhomogeneity of the magnetic field. Electrons entering this region are already phase correlated from resonant interactions that have taken place further downstream. Near the equator, where \(\partial B_0/\partial h \approx 0\), the chirp rate can be expressed as
where \(S_{\textrm{max}} \approx -0.4\) according to the NGTO. While Eq. 94 provides the well-known relation between chirp and trapping frequency, which appears in the sBWO theory (Eq. 51, obtained from the results of Vomvoridis et al. (1982) and nonlinear evolution of f inside the trapping region) and SCCE framework (Eq. 92, obtained self-consistently from the reduced Dyson-like equation), the physical origin of chirp is due to the excitation of higher frequencies in the upstream region. This is consistent with the proposition of Helliwell (1967), who splits the interaction region into two parts, with radiation dominating the upstream and electron bunches forming downstream. Finally, after the whistler waves pass the equator, the field inhomogeneity and chirp have effects of similar magnitude, so
Notice that the extension of the NGTO presented in Hanzelka et al. (2020) uses a relativistic version of this chirp rate formula, given in Eq. 71, thus naturally incorporating this TaRA concept into numerical wave models, but applies it only in the source, with \(S = S_{\textrm{max}}\) to maximise the power transfer.
The explanation of the origin of subpackets differs significantly from the NGTO. Instead of considering each subpacket as the basic unit of wave excitation (which later becomes the new triggering wave), in TaRA, modes at all frequencies contribute to the generation of new emissions. Oscillations of resonant particles in the order of \(\omega _{\textrm{tr}}^{-1}\) modulate the wave power transfer (Tao et al. 2017), and this translates to amplitude modulations, which are further accentuated due to convective growth downstream. This description agrees with the conclusion of Nogi and Omura (2022), who conducted PIC simulations and observed a very stable electron hole in the source region, which produced a single, long, weakly modulated packet that split into subpackets during propagation. This poses difficulty for the spacecraft analysis of subpackets (Santolík et al. 2014a; Foster et al. 2017) by suggesting that multipoint measurements are required to capture the important convective evolution of the subpacket structure. Furthermore, wave superposition needs to be taken into account when analysing the fine structure of chorus (Santolík et al. 2004; Zhang et al. 2020b; Nunn et al. 2021). For further discussion of the possible origins of a complex subpacket structure, see Sect. 4.
We may conclude that while the TaRA model provides an interesting novel description of the chorus generation mechanism, there are still many contentious points, e.g., the role of wave superposition and the relative importance of \(\partial B_0 / \partial h\) versus hot electron distribution inhomogeneity. Despite the agreement between theory and simulations, careful comparison with spacecraft data will be needed to show whether the predictions of TaRA and SCCE provide better accuracy than sBWO and NGTO.
4 Ducted Propagation Affecting the Structure of Chorus
As shown in Fig. 4 and numerous literature (Santolík et al. 2003a, 2014a; Foster et al. 2017; Crabtree et al. 2017b), rising-tone chorus elements have a complex subpacket structure. The wave magnetic field exhibits amplitude modulations with highly variable length and depth whose structure can differ between the perpendicular components (\(B_{x,y}\)) and parallel component (\(B_z\)). These modulations are associated with irregularities in the instantaneous frequency and the wave normal angle. The convectively increasing modulation depth predicted by the TaRA model (Sect. 3.3.2) cannot well explain the amplitude drops down to zero, and the NGTO-based numerical wave model from Fig. 10 is too regular and relies on the electron hole breakdown assumption, which was not confirmed by self-consistent simulations (Tao et al. 2021; Nogi and Omura 2022).
One possible explanation for the inability to accurately describe the subpacket structure within theories from Sect. 3 is the reliance on a single plane wave model. As discussed by Crabtree et al. (2017b), the amplitude modulations of chorus elements may be better explained as a superposition of multiple chirping waves, especially at frequencies above \(\omega \approx \varOmega _{\textrm{e}}/4\). One-dimensional PIC simulations, Vlasov simulations and sBWO-based models can reproduce observations of fast subpacket amplitude modulations and frequency sweep rates (Nunn et al. 2021; Zhang et al. 2021) but cannot capture the evolution of the wave normal angle. Considering the significant obliquity displayed by some subpackets in Fig. 4e and the statistics of Santolík et al. (2014a), it is possible that two-dimensional theory and simulations are needed to fully describe the fine structure of chorus. As demonstrated with the kinetic simulations of Ke et al. (2017), the frequency growth in two-dimensional models can be more discrete, akin to the observational results of Tsurutani et al. (2020) or Foster et al. (2021). However, self-consistent simulations in more than one spatial dimension are computationally expensive, and the research in this area is still in the early stages.
Regarding the two-dimensional propagation of waves, we must also consider the effects of field-aligned density ducts on the chorus spectral structure. As was shown by cold electron fluid simulations of Katoh (2014) and kinetic simulations of Ke et al. (2021), a wide density enhancement can strongly modulate the spatial and temporal distribution of whistler-mode waves. Furthermore, it was shown by laboratory experiments (Stenzel 1976b) and theoretical analysis (Weibel 1977; Eliasson and Shukla 2004) that high-amplitude whistler waves can modify cold plasma density and induce self-focusation through the formation of thin filaments. Effects of wavelength-scale narrow ducts were numerically investigated by Zudin et al. (2019) for the case of ionospheric ducts and by Streltsov and Bengtson (2020) and Williams and Streltsov (2021) in the case of a homogeneous magnetic field near the equatorial region of the outer radiation belt. The difference between the wide and narrow ducting modes and their effects on the amplitude, frequency and propagation properties of chorus elements will be discussed in the following two sections.
4.1 Wide Density Ducts
As follows from cold plasma theory and spacecraft observations (Carpenter 1968; Walker 1976), whistler waves in the inner magnetosphere must be ducted to prevent attenuation due to Landau damping at higher wave normal angles (WNA), which was demonstrated by ray tracing simulations in hot plasma (Bortnik et al. 2011; Hanzelka and Santolík 2019). In these simulations, the ducts were assumed to have a characteristic width of multiple wavelengths, ensuring that the density background can be considered only weakly inhomogeneous and thus allowing for the use of ray optics. Observational proof of the existence of such wide ducts in the outer radiation belt and of their guiding effects was provided by Chen et al. (2021), with strong indications appearing in earlier studies (Angerami 1970; Koons 1989; Sonwalkar et al. 1994; Bell et al. 2009; Demekhov et al. 2020b). A statistical analysis by Gu et al. (2022) based on Van Allen Probes data shows a significant occurrence of density variations with characteristics scale \(< 1000\,\textrm{km}\) in regions with increased whistler wave activity, further emphasizing the importance of density inhomogeneities in whistler-mode propagation studies.
Let us first focus on the case of a homogeneous magnetic field. For simplicity and analytical tractability, we will assume that the duct is axially symmetric along \(\varvec{B}_0\), ray oscillations are small, and the peak of the density enhancement can be approximated by a parabolic profile as defined in Eq. A9. It can then be shown that the lateral ray position x (measured from the centre of the duct) and the perpendicular wave vector component \(k_x\) harmonically oscillate with frequency
where \(s_{\textrm{duct}} = -1\) represents density enhancement; see Appendix A for a detailed derivation. As an example, consider a whistler ray with frequency \(\omega = 0.25\varOmega _{\textrm{e}}\) in a plasma with \(\omega _{\textrm{p0}} = 5\varOmega _{\textrm{e0}}\) and a magnetic field \(B_0 = 300\,{\textrm{nT}}\), oscillating in a \(100\,{\textrm{km}}\) wide duct (\(w = 50\,{\textrm{km}}\)). The frequency from Eq. 96 then evaluates to \(\varOmega _{\textrm{HO}} = 1.1\cdot 10^{-2}\,\omega \). In this case, approximately 45 wavelengths (\(\lambda = 2\pi /k \approx 12\,{\textrm{km}}\)) will fit between two crossings of \(x = 0\), and the subpacket duration will be \(22\,{\textrm{ms}}\). To reach durations below \(10\,{\textrm{ms}}\), which are common in observations (Santolík et al. 2014a), the ratio \(\lambda /w\) would drop below 2, clearly violating the approximation of geometric optics. Also, note that while we assumed a parabolic density profile, corresponding to a Gaussian or other functions with a well-defined peak, ducts may have a more rectangular shape with strong density gradients near the boundaries, as considered by Williams and Streltsov (2021), which again rules out the application of ray optics.
Results of propagation simulation of a modulated chorus element, adapted from Hanzelka and Santolík (2022). The equatorial cold current source radiates ten chorus subpackets with frequency growing linearly in time from \(0.15 \varOmega _{\textrm{e0}}\) to \(0.50 \varOmega _{\textrm{e0}}\). The stationary density background in panel a shows a field-aligned density enhancement (duct) with relative density increase of \(10\%\), the standard deviation \(\sigma _{L}\) of the Gaussian profile is \(150\,{\textrm{km}}\) at the equator. The white and black stars show the position of probes that measured the waveforms in panels c and d, respectively. b A snapshot from the wave amplitude evolution. c Amplitude envelope as measured by the probe on the slope of the density duct, \(1\sigma _{L}\) away from the central field line. d Amplitude envelope as measured by the probe on the central field line. Stationary density background with field-aligned enhancement
In a curved magnetic field, the oscillations widen and waves start leaking out at higher latitudes. Ke et al. (2021) studied the effects of ducts on whistlers in 2D kinetic simulations and concluded that the waves remain quasiparallel and experience focusing effects, improving thus upon the simpler numerical models of ducted propagation by Katoh (2014) and Hanzelka and Santolík (2019). Hanzelka and Santolík (2022) used full-wave simulations in a linearised cold electron fluid to study the evolution of amplitude modulations and wave normal angle in a chirping wave with a predefined subpacket structure. They found that the WNA does not exhibit rapid variations to the same extent as a typical chorus element, but certain parts of the element can be seen by a probe as heavily attenuated. This effect is due to the frequency dependence of the Poynting flux direction, resulting in the concentration of certain frequencies along a path that does not cross the probe’s position. Examples are shown in Fig. 11. Such profound amplitude modulations along the element may affect analyses of multipoint spacecraft observations of chorus (Demekhov et al. 2020a), which explain the lack of low frequencies in the spectrum as an effect of source drift—compare with Fig. 10. Density-induced wave focusation could also explain sudden drops in the amplitude of neighbouring elements in a chorus train, as suggested by Hosseini et al. (2021) based on full-wave simulations with lentil-shaped density irregularities.
4.2 Thin Density Filaments
Theoretical and numerical analysis of whistler-mode propagation in narrow density filaments with rectangular profiles shows the emergence of a new, ducted mode with different dispersion properties. When the characteristic width of individual filaments drops to subwavelength scale, the wave energy propagates as if unducted until the walls of the filament bunch are reached (Zudin et al. 2019). However, when the duct width remains above this subwavelength threshold, the wave vector direction is significantly affected, as shown by the numerical simulation of lower-band chorus by Hanzelka and Santolík (2022) for the case of a 2D duct comb. The study also noted that the density irregularities cause a shift from circular towards elliptical polarisation, confirming the deviations from a homogeneous plasma whistler-mode dispersion relation (compare with Fig. 1, the ellipticity panel in particular). Note that since the eikonal approximation enters into the derivation of the complex wave equation 39, none of the chorus theories discussed in Sect. 3 (sBWO, NGTO and SCCE) could explain the behaviour around strong irregularities even if the theories were extended to two dimensions.
The EMHDFootnote 5 (Electron MagnetoHydroDynamics) simulations of Streltsov and Bengtson (2020) and Williams and Streltsov (2021) show formation of short subpackets in a homogeneous magnetic field within a smoothened rectangular duct. Hanzelka and Santolík (2022) investigated the propagation of a modulated chorus element in a dipole field with a comb of wavelength-scale Gaussian ducts, with a focus on the wave normal angle behaviour. It was shown that away from \(\omega = \varOmega _{\textrm{e}}/4\), where \(\partial V_{\textrm{g}}/\partial \omega = 0\), the subpacket structure can change drastically, and these new amplitude modulations are accompanied by large and rapid variations in WNA, similar to the spacecraft observation from Fig. 4. The loss of regularity in amplitude modulations towards higher frequencies agrees well with the case studies of Crabtree et al. (2017b) and Foster et al. (2021). Two waveforms detected by two closely separated probes from the Hanzelka and Santolík (2022) simulations, shown here in Fig. 12, reveal the strong spatial variability of fine structure, which can be compared to the multipoint Cluster spacecraft measurements presented by Santolík et al. (2003a). Note also the spectral width of the element displayed in Fig. 12—due to the subpackets being strongly localised in time, the spectrum shows a width comparable with experimental data, despite using a single-wave model.
Simulation of chorus wave propagation in multiple thin ducts, adapted from Hanzelka and Santolík (2022) and presented in a format similar to Fig. 11. The stationary density ducts in panel a have a relative density increase of \(3\%\), the standard deviation \(\sigma _{L}\) of the Gaussian profile is \(15\,\textrm{km}\) at the equator. The white and black stars show the position of probes that measured the waveforms in panels (b–d) and e-g), respectively. b Amplitude envelope as measured by the probe on the slope of the central density duct, \(1\sigma _{L}\) away from the central field line, \(\lambda _{\textrm{m}} = 4.75^{\circ }\). c Instantaneous frequency obtained from Hilbert transform of the complex amplitude. d Wave normal angle obtained by the SVD methods of Santolík et al. (2003b). e–g Similar to b–d, but for a waveform measured by a probe on the central field line, \(\lambda _{\textrm{m}} = 4.0^{\circ }\)
We may conclude that in the presence of thin ducts, the amplitude envelope and WNA exhibit significant spatio-temporal variations, which suggests that results on chorus fine structure obtained from 1D theories and simulations cannot be directly compared with spacecraft observations. Moreover, it is currently unknown if and how strong density irregularities modify the nonlinear wave growth in the source region. Because waves around \(\omega = \varOmega _{\textrm{e}}/2\) are not guided by either density enhancements of depletions, it was conjectured (Bell et al. 2009) that ducting effect may be behind the spectral gap that divides chorus into lower band and upper band. However, such hypothesis will have to be confirmed by 2D or 3D self-consistent simulations, which is still a very young research field.
5 Summary and Conclusions
We have reviewed the development of nonlinear chorus growth theory from 1960s up to the current date, with a focus on parallel-propagating lower-band rising-tone emissions. We have shown that many concepts that are important in modern theories have been known since the influential studies of Helliwell (1967) and Vomvoridis et al. (1982). Namely, the importance of phase-bunching and trapping, the helical antenna concept and source drift, and the relation between chirp rate and wave amplitude.
The three prominent theories discussed in Sect. 3 are all based on the same set of narrowband complex wave equations, but they take different approaches to the computation of phase space density perturbations and the associated resonant current. In the sBWO model, a step function in parallel velocities is postulated, and the evolution of phase space density is solved numerically, with simplifying assumptions about the role of trajectory perturbations and the velocity spread of resonant particles. The NGTO takes inspiration from kinetic simulations and assumes the formation of a homogeneous phase space density (PSD) hole in the trapping region, with the source region being replaced by a single point for simplicity. The relative importance of chirp rate and magnetic field inhomogeneity at different distance from the equator is used to define a threshold amplitude for the onset of nonlinear growth, and the nonlinear variation of frequency due to resonant current is directly linked to chirp rate to define an optimum amplitude, near which the growth saturates. Extension to a drifting source is possible by introducing a sequential triggering model based on the upstream flow of phase-correlated particles (the helical antenna concept).
The most recent of the three theories, the SCCE framework and the related TaRA phenomenological model, introduce some novel concepts. The nonlinear evolution of PSD in the resonance region is solved in a general form that assumes excitation of new whistler waves from a continuous spectrum. The general result, a Dyson-like equation, can be reduced to reveal the relation between chirp rate and amplitude from Vomvoridis et al. (1982). The chirping is linked to the spectral power peak sliding to higher frequencies in order to maximise power transfer, in agreement with the early ideas of Helliwell (1967). The TaRA model further attempts to explain the formation of subpackets through convective growth of shallow amplitudes modulations in the source which arise from the periodic motion of trapped electrons, as seen in 1D self-consistent simulations.
Despite the overall success in the explanation of chirp rate and amplitude growth, the experimentally observed large spatio-temporal variations in the subpackets structure escape the understanding provided by modern chorus theories. In Sect. 4, we explained the importance of ducting and two-dimensional effects for the formation of fine chorus structure. These findings are based on recent full-wave simulations (Zudin et al. 2019; Williams and Streltsov 2021; Hanzelka and Santolík 2022) and are currently not implemented in analytical theories of chorus growth.
We conclude that while the state-of-art theories and simulations provide a good explanation for the amplitude and frequency characteristic of quasiparallel chorus elements, further investigations are needed to fully understand the role of resonant current and the aspects of two-dimensional propagation and its effect on the nonlinear growth. And finally, we want to acknowledge and highlight the importance of rigorous mathematical frameworks such as the SCCE, which bring a much needed insight into the kinetic simulations that dominate the current research on nonlinear wave–particle interactions in the Earth’s inner magnetosphere.
Data Availability
The Van Allen Probe data are publicly available from the NASA’s Space Physics Data Facility, repository https://spdf.gsfc.nasa.gov/pub/data/rbsp/.
Code Availability
Not applicable.
Notes
Sometimes referred to as the WKB approximation, after G. Wentzel, H. A. Kramers and L. Brillouin, who however worked on quantum-mechanical waves.
Note that some authors, e.g., Meredith et al. (2003), use the term chorus for any whistler-mode emission in the lower or upper frequency band, regardless of the presence of narrow-band chirping wave packets.
In this article, the terms upstream and downstream always refer to the wave frame.
References
Agapitov OV, Mourenas D, Artemyev AV, Mozer FS, Hospodarsky G, Bonnell J, Krasnoselskikh V (2018) Synthetic empirical chorus wave model from combined Van Allen probes and cluster statistics. J Geophys Res Space Phys 123(1):297–314. https://doi.org/10.1002/2017JA024843
Albert JM (1993) Cyclotron resonance in an inhomogeneous magnetic field. Phys Fluids B: Plasma Phys 5(8):2744–2750. https://doi.org/10.1063/1.860715
Albert JM, Artemyev AV, Li W, Gan L, Ma Q (2021) Models of resonant wave-particle interactions. J Geophys Res Space Phys 126(6):e29216. https://doi.org/10.1029/2021JA029216
Allanson O, Watt CEJ, Allison HJ, Ratcliffe H (2021) Electron diffusion and advection during nonlinear interactions with whistler mode waves. J Geophys Res Space Phys 126(5):e28793. https://doi.org/10.1029/2020JA028793
Al’tshul’ LM, Karpman VI (1966) Theory of nonlinear oscillations in a collisionless plasma. Sov J Exp Theor Phys 22:361
An X, Artemyev A, Angelopoulos V, Zhang X, Mourenas D, Bortnik J (2022) Nonresonant scattering of relativistic electrons by electromagnetic ion cyclotron waves in earth’s radiation belts. Phys Rev Lett 129(13):135101. https://doi.org/10.1103/PhysRevLett.129.135101
Angerami JJ (1970) Whistler duct properties deduced from VLF observations made with the Ogo 3 satellite near the magnetic equator. J Geophys Res 75(31):6115–6135. https://doi.org/10.1029/JA075i031p06115
Artemyev A, Agapitov O, Mourenas D, Krasnoselskikh V, Shastun V, Mozer F (2016) Oblique whistler-mode waves in the earth’s inner magnetosphere: energy distribution, origins, and role in radiation belt dynamics. Space Sci Rev 200(1–4):261–355. https://doi.org/10.1007/s11214-016-0252-5
Artemyev AV, Neishtadt AI, Vainchtein DL, Vasiliev AA, Vasko IY, Zelenyi LM (2018) Trapping (capture) into resonance and scattering on resonance: summary of results for space plasma systems. Commun Nonlinear Sci Numer Simul 65:111–160. https://doi.org/10.1016/j.cnsns.2018.05.004
Bell TF (1984) The nonlinear gyroresonance interaction between energetic electron and coherent VLF waves propagating at an arbitrary angle with respect to the earth’s magnetic field. J Geophys Res 89(A2):905–918. https://doi.org/10.1029/JA089iA02p00905
Bell TF, Buneman O (1964) Plasma instability in the whistler mode caused by a gyrating electron stream. Phys Rev 133(5A):1300–1302. https://doi.org/10.1103/PhysRev.133.A1300
Bell TF, Inan US, Haque N, Pickett JS (2009) Source regions of banded chorus. Geophys Res Lett 36:L11101. https://doi.org/10.1029/2009GL037629
Bernstein IB (1975) Geometric optics in space- and time-varying plasmas. Phys Fluids 18:320–324. https://doi.org/10.1063/1.861140
Bortnik J, Thorne RM, Inan US (2008) Nonlinear interaction of energetic electrons with large amplitude chorus. Geophys Res Lett 35(21):L21102. https://doi.org/10.1029/2008GL035500
Bortnik J, Chen L, Li W, Thorne RM, Horne RB (2011) Modeling the evolution of chorus waves into plasmaspheric hiss. J Geophys Res Space Phys 116:A08221. https://doi.org/10.1029/2011JA016499
Brice N (1963) An explanation of triggered very-low-frequency emissions. J Geophys Res 68:4626. https://doi.org/10.1029/JZ068i015p04626
Brinca AL (1972) On the stability of obliquely propagating whistlers. J Geophys Res 77(19):3495–3507. https://doi.org/10.1029/JA077i019p03495
Bud’ko NI, Karpman VI, Pokhotelov OA (1972) Nonlinear theory of the monochromatic circularly polarized VLF and ULF waves in the magnetosphere. Cosm Electrodyn 3:147–164
Bunch NL, Spasojevic M, Shprits YY (2012) Off-equatorial chorus occurrence and wave amplitude distributions as observed by the polar plasma wave instrument. J Geophys Res Space Phys 117(A4):A04205. https://doi.org/10.1029/2011JA017228
Burtis WJ, Helliwell RA (1969) Banded chorus—a new type of VLF radiation observed in the magnetosphere by OGO 1 and OGO 3. J Geophys Res 74(11):3002. https://doi.org/10.1029/JA074i011p03002
Burton RK (1976) Critical electron pitch angle anisotropy necessary for chorus generation. J Geophys Res 81(25):4779. https://doi.org/10.1029/JA081i025p04779
Burton E, Boardman E (1933) Audio-frequency atmospherics. Proc Inst Radio Eng 21(10):1476–1494
Carpenter DL (1968) Ducted whistler-mode propagation in the magnetosphere; a half-gyrofrequency upper intensity cutoff and some associated wave growth phenomena. J Geophys Res 73(9):2919–2928. https://doi.org/10.1029/JA073i009p02919
Chen L, Zonca F (2016) Physics of Alfvén waves and energetic particles in burning plasmas. Rev Mod Phys 88(1):015008. https://doi.org/10.1103/RevModPhys.88.015008
Chen L, Thorne RM, Bortnik J, Zhang X-J (2016) Nonresonant interactions of electromagnetic ion cyclotron waves with relativistic electrons. J Geophys Res Space Phys 121(10):9913–9925. https://doi.org/10.1002/2016JA022813
Chen R, Gao X, Lu Q, Chen L, Tsurutani BT, Li W, Ni B, Wang S (2021) In situ observations of whistler mode chorus waves guided by density ducts. J Geophys Res Space Phys 126(4):e28814. https://doi.org/10.1029/2020JA028814
Chow KK, Pantell RH (1960) The cyclotron resonance backward-wave oscillator. Proc IRE 48(11):1865–1870. https://doi.org/10.1109/JRPROC.1960.287421
Crabtree C, Ganguli G, Tejero E (2017) Analysis of self-consistent nonlinear wave-particle interactions of whistler waves in laboratory and space plasmas. Phys Plasmas 24(5):056501. https://doi.org/10.1063/1.4977539
Crabtree C, Tejero E, Ganguli G, Hospodarsky GB, Kletzing CA (2017) Bayesian spectral analysis of chorus subelements from the van Allen probes. J Geophys Res Space Phys 122(6):6088–6106. https://doi.org/10.1002/2016JA023547
Demekhov AG (2011) Generation of VLF emissions with the increasing and decreasing frequency in the magnetosperic cyclotron maser in the backward wave oscillator regime. Radiophys Quantum Electron 53(11):609–622. https://doi.org/10.1007/s11141-011-9256-x
Demekhov AG (2017) Relationship between the parameters of the linear and nonlinear wave generation stages in a magnetospheric cyclotron maser in the backward-wave oscillator regime. Radiophys Quantum Electron 59(10):773–781. https://doi.org/10.1007/s11141-017-9746-6
Demekhov AG, Trakhtengerts VY (2005) Dynamics of the magnetospheric cyclotron ELF/VLF maser in the backward-wave-oscillator regime. I. Basic equations and results in the case of a uniform magnetic field. Radiophys Quantum Electron 48(9):639–649. https://doi.org/10.1007/s11141-005-0109-3
Demekhov AG, Trakhtengerts VY (2008) Dynamics of the magnetospheric cyclotron ELF/VLF maser in the backward-wave-oscillator regime. II. The influence of the magnetic-field inhomogeneity. Radiophys Quantum Electron 51(11):880–889. https://doi.org/10.1007/s11141-009-9093-3
Demekhov AG, Taubenschuss U, Santolík O (2017) Simulation of VLF chorus emissions in the magnetosphere and comparison with THEMIS spacecraft data. J Geophys Res Space Phys 122(1):166–184. https://doi.org/10.1002/2016JA023057
Demekhov AG, Taubenschuss U, Hanzelka M, Santolík O (2020a) Frequency dependence of very low frequency chorus poynting flux in the source region: THEMIS observations and a model. Geophys Res Lett 47(6):e86958. https://doi.org/10.1029/2019GL086958
Demekhov AG, Titova EE, Maninnen J, Pasmanik DL, Lubchich AA, Santolík O, Larchenko AV, Nikitenko AS, Turunen T (2020b) Localization of the source of quasiperiodic VLF emissions in the magnetosphere by using simultaneous ground and space observations: a case study. J Geophys Res Space Phys 125(5):e27776. https://doi.org/10.1029/2020JA027776
Denavit J, Sudan RN (1975) Whistler sideband instability. Phys Fluids 18(5):575–584. https://doi.org/10.1063/1.861173
Dowden RL (1962) Doppler-shifted cyclotron radiation from electrons: a theory of very low frequency emissions from the exosphere. J Geophys Res 67(5):1745–1750. https://doi.org/10.1029/JZ067i005p01745
Dysthe KB (1971) Some studies of triggered whistler emissions. J Geophys Res 76(28):6915–6931. https://doi.org/10.1029/JA076i028p06915
Eliasson B, Shukla PK (2004) Theoretical and numerical studies of density modulated whistlers. Geophys Res Lett 31(17):L17802. https://doi.org/10.1029/2004GL020605
Foster JC, Erickson PJ, Omura Y, Baker DN, Kletzing CA, Claudepierre SG (2017) Van Allen Probes observations of prompt MeV radiation belt electron acceleration in nonlinear interactions with VLF chorus. J Geophys Res Space Phys 122(1):324–339. https://doi.org/10.1002/2016JA023429
Foster JC, Erickson PJ, Omura Y (2021) Subpacket structure in strong VLF chorus rising tones: characteristics and consequences for relativistic electron acceleration. Earth Planets Space 73(1):140. https://doi.org/10.1186/s40623-021-01467-4
Fu X, Cowee MM, Friedel RH, Funsten HO, Gary SP, Hospodarsky GB, Kletzing C, Kurth W, Larsen BA, Liu K, MacDonald EA, Min K, Reeves GD, Skoug RM, Winske D (2014) Whistler anisotropy instabilities as the source of banded chorus: Van Allen probes observations and particle-in-cell simulations. J Geophys Res Space Phys 119(10):8288–8298. https://doi.org/10.1002/2014JA020364
Fujiwara Y, Omura Y, Nogi T (2023) Triggering of whistler-mode rising and falling tone emissions in a homogeneous magnetic field. J Geophys Res Space Phys 128(2):e2022JA030967. https://doi.org/10.1029/2022JA030967
Gao X, Li W, Thorne RM, Bortnik J, Angelopoulos V, Lu Q, Tao X, Wang S (2014) Statistical results describing the bandwidth and coherence coefficient of whistler mode waves using THEMIS waveform data. J Geophys Res Space Phys 119(11):8992–9003. https://doi.org/10.1002/2014JA020158
Gao Z, Su Z, Chen L, Zheng H, Wang Y, Wang S (2017) Van Allen Probes observations of whistler-mode chorus with long-lived oscillating tones. Geophys Res Lett 44(12):5909–5919. https://doi.org/10.1002/2017GL073420
Gao X, Chen L, Li W, Lu Q, Wang S (2019) Statistical results of the power gap between lower-band and upper-band chorus waves. Geophys Res Lett 46(8):4098–4105. https://doi.org/10.1029/2019GL082140
Gu W, Liu X, Xia Z, Chen L (2022) Statistical study on small-scale (\({{\le }}\)1,000 km) density irregularities in the inner magnetosphere. J Geophys Res Space Phys 127(7):e30574. https://doi.org/10.1029/2022JA030574
Gurnett DA, Bhattacharjee A (2017) Introduction to plasma physics: with space, laboratory and astrophysical applications. Cambridge University Press, Cambridge
Hanzelka M (2022) Nonlinear processes in space plasmas and their effects on the generation and propagation of electromagnetic waves. PhD thesis, Charles University, Faculty of Mathematics and Physics, Prague, Czech Republic
Hanzelka M, Santolík O (2019) Effects of ducting on whistler mode chorus or exohiss in the outer radiation belt. Geophys Res Lett 46(11):5735–5745. https://doi.org/10.1029/2019GL083115
Hanzelka M, Santolík O (2022) Effects of field-aligned cold plasma density filaments on the fine structure of chorus. Geophys Res Lett. https://doi.org/10.1029/2022GL101654
Hanzelka M, Santolík O, Omura Y, Kolmašová I, Kletzing CA (2020) A model of the subpacket structure of rising tone chorus emissions. J Geophys Res Space Phys 125(8):e28094. https://doi.org/10.1029/2020JA028094
Hanzelka M, Santolík O, Omura Y, Kolmašová I (2021) Measurability of the nonlinear response of electron distribution function to chorus emissions in the Earth’s radiation belt. J Geophys Res Space Phys 126(9):e29624. https://doi.org/10.1029/2021JA029624
Harid V, Gołkowski M, Bell T, Li JD, Inan US (2014) Finite difference modeling of coherent wave amplification in the Earth’s radiation belts. Geophys Res Lett 41(23):8193–8200. https://doi.org/10.1002/2014GL061787
Harid V, Gołkowski M, Hosseini P, Kim H (2022) Backward-propagating source as a component of rising tone whistler-mode chorus generation. Front Astron Space Sci 9:981949. https://doi.org/10.3389/fspas.2022.981949
Helliwell RA (1967) A theory of discrete VLF emissions from the magnetosphere. J Geophys Res 72(19):4773–4790. https://doi.org/10.1029/JZ072i019p04773
Helliwell RA, Bell TF (1960) A new mechanism for accelerating electrons in the outer ionosphere. J Geophys Res 65:1839. https://doi.org/10.1029/JZ065i006p01839
Helliwell RA, Katsufrakis J, Trimpi M, Brice N (1964) Artificially stimulated very low frequency radiation from the ionosphere. J Geophys Res 69(11):2391–2394. https://doi.org/10.1029/JZ069i011p02391
Hikishima M, Yagitani S, Omura Y, Nagano I (2009) Full particle simulation of whistler-mode rising chorus emissions in the magnetosphere. J Geophys Res Space Phys 114:A01203. https://doi.org/10.1029/2008JA013625
Hiraga R, Omura Y (2020) Acceleration mechanism of radiation belt electrons through interaction with multi-subpacket chorus waves. Earth Planets Space 72(1):21. https://doi.org/10.1186/s40623-020-1134-3
Horne RB (1989) Path-integrated growth of electrostatic waves—the generation of terrestrial myriametric radiation. J Geophys Res 94:8895–8909. https://doi.org/10.1029/JA094iA07p08895
Horne RB, Glauert SA, Thorne RM (2003) Resonant diffusion of radiation belt electrons by whistler-mode chorus. Geophys Res Lett 30(9):1493. https://doi.org/10.1029/2003GL016963
Horne RB, Thorne RM, Glauert SA, Albert JM, Meredith NP, Anderson RR (2005) Timescale for radiation belt electron acceleration by whistler mode chorus waves. J Geophys Res Space Phys 110(A3):A03225. https://doi.org/10.1029/2004JA010811
Hosseini P, Agapitov O, Harid V, Gołkowski M (2021) Evidence of small scale plasma irregularity effects on whistler mode chorus propagation. Geophys Res Lett 48(5):e92850. https://doi.org/10.1029/2021GL092850
Hsieh Y-K, Omura Y (2018) Nonlinear damping of oblique whistler mode waves via Landau resonance. J Geophys Res Space Phys 123(9):7462–7472. https://doi.org/10.1029/2018JA025848
Ichimaru S (2004) Statistical plasma physics: basic principles, 1st edn. CRC Press, Boca Raton
Juhász L, Omura Y, Lichtenberger J, Friedel RH (2019) Evaluation of plasma properties from chorus waves observed at the generation region. J Geophys Res Space Phys 124(6):4125–4136. https://doi.org/10.1029/2018JA026337
Karpman VI (1974) Nonlinear effects in the ELF waves propagating along the magnetic field in the magnetosphere. Space Sci Rev 16(3):361–388. https://doi.org/10.1007/BF00171564
Karpman VI, Istomin JN, Shklyar DR (1974) Nonlinear theory of a quasi-monochromatic whistler mode packet in inhomogeneous plasma. Plasma Phys 16(8):685–703. https://doi.org/10.1088/0032-1028/16/8/001
Katoh Y (2014) A simulation study of the propagation of whistler-mode chorus in the Earth’s inner magnetosphere. Earth Planets Space 66:6. https://doi.org/10.1186/1880-5981-66-6
Katoh Y, Omura Y (2016) Electron hybrid code simulation of whistler-mode chorus generation with real parameters in the Earth’s inner magnetosphere. Earth Planets Space 68:192. https://doi.org/10.1186/s40623-016-0568-0
Katoh Y, Omura Y, Miyake Y, Usui H, Nakashima H (2018) Dependence of generation of whistler mode chorus emissions on the temperature anisotropy and density of energetic electrons in the Earth’s inner magnetosphere. J Geophys Res Space Phys 123(2):1165–1177. https://doi.org/10.1002/2017JA024801
Ke Y, Gao X, Lu Q, Wang X, Wang S (2017) Generation of rising-tone chorus in a two-dimensional mirror field by using the general curvilinear PIC code. J Geophys Res Space Phys 122(8):8154–8165. https://doi.org/10.1002/2017JA024178
Ke Y, Chen L, Gao X, Lu Q, Wang X, Chen R, Chen H, Wang S (2021) Whistler mode waves trapped by density irregularities in the Earth’s magnetosphere. Geophys Res Lett 48(7):e92305. https://doi.org/10.1029/2020GL092305
Kennel CF, Engelmann F (1966) Velocity space diffusion from weak plasma turbulence in a magnetic field. Phys Fluids 9(12):2377–2388. https://doi.org/10.1063/1.1761629
Kennel CF, Petschek HE (1966) Limit on stably trapped particle fluxes. J Geophys Res 71:1–28. https://doi.org/10.1029/JZ071i001p00001
Kompfner R, Williams NT (1953) Backward-wave tubes. Proc IRE 41(11):1602–1611. https://doi.org/10.1109/JRPROC.1953.274186
Koons HC (1989) Observations of large-amplitude, whistler mode wave ducts in the outer plasmasphere. J Geophys Res 94:15393–15397. https://doi.org/10.1029/JA094iA11p15393
Kraus JD (1949) The helical antenna. Proc IRE 37:263–272
Kruer WL, Dawson JM, Sudan RN (1969) Trapped-particle instability. Phys Rev Lett 23(15):838–841. https://doi.org/10.1103/PhysRevLett.23.838
Kubota Y, Omura Y (2018) Nonlinear dynamics of radiation belt electrons interacting with chorus emissions localized in longitude. J Geophys Res Space Phys 123(6):4835–4857. https://doi.org/10.1029/2017JA025050
Kurita S, Katoh Y, Omura Y, Angelopoulos V, Cully CM, Le Contel O, Misawa H (2012) THEMIS observation of chorus elements without a gap at half the gyrofrequency. J Geophys Res Space Phys 117:A11223. https://doi.org/10.1029/2012JA018076
Kuzichev IV, Soto-Chavez AR, Park J, Gerrard A, Spitkovsky A (2019) Magnetospheric chorus wave simulation with the TRISTAN-MP PIC code. Phys Plasmas 26(7):072901. https://doi.org/10.1063/1.5096537
Lemons DS, Liu K, Winske D, Gary SP (2009) Stochastic analysis of pitch angle scattering of charged particles by transverse magnetic waves. Phys Plasmas 16(11):112306. https://doi.org/10.1063/1.3264738
Li W, Thorne RM, Meredith NP, Horne RB, Bortnik J, Shprits YY, Ni B (2008) Evaluation of whistler mode chorus amplification during an injection event observed on CRRES. J Geophys Res Space Phys 113(A9):A09210. https://doi.org/10.1029/2008JA013129
Li W, Thorne RM, Angelopoulos V, Bortnik J, Cully CM, Ni B, Le Contel O, Roux A, Auster U, Magnes W (2009) Global distribution of whistler-mode chorus waves observed on the THEMIS spacecraft. Geophys Res Lett 36(9):L09104. https://doi.org/10.1029/2009GL037595
Li W, Thorne RM, Nishimura Y, Bortnik J, Angelopoulos V, McFadden JP, Larson DE, Bonnell JW, Le Contel O, Roux A, Auster U (2010) THEMIS analysis of observed equatorial electron distributions responsible for the chorus excitation. J Geophys Res Space Phys 115:A00F11. https://doi.org/10.1029/2009JA014845
Li W, Thorne RM, Bortnik J, Shprits YY, Nishimura Y, Angelopoulos V, Chaston C, Le Contel O, Bonnell JW (2011) Typical properties of rising and falling tone chorus waves. Geophys Res Lett 38(14):L14103. https://doi.org/10.1029/2011GL047925
Li W, Thorne RM, Bortnik J, Tao X, Angelopoulos V (2012) Characteristics of hiss-like and discrete whistler-mode emissions. Geophys Res Lett 39(18):L18106. https://doi.org/10.1029/2012GL053206
Li W, Mourenas D, Artemyev AV, Bortnik J, Thorne RM, Kletzing CA, Kurth WS, Hospodarsky GB, Reeves GD, Funsten HO, Spence HE (2016) Unraveling the excitation mechanisms of highly oblique lower band chorus waves. Geophys Res Lett 43(17):8867–8875. https://doi.org/10.1002/2016GL070386
Li J, Bortnik J, An X, Li W, Angelopoulos V, Thorne RM, Russell CT, Ni B, Shen X, Kurth WS, Hospodarsky GB, Hartley DP, Funsten HO, Spence HE, Baker DN (2019) Origin of two-band chorus in the radiation belt of Earth. Nat Commun 10:4672. https://doi.org/10.1038/s41467-019-12561-3
Macúšová E, Santolík O, Décréau P, Demekhov AG, Nunn D, Gurnett DA, Pickett JS, Titova EE, Kozelov BV, Rauch JL, Trotignon JG (2010) Observations of the relationship between frequency sweep rates of chorus wave packets and plasma density. J Geophys Res Space Phys 115(A12):A12257. https://doi.org/10.1029/2010JA015468
Meredith NP, Horne RB, Thorne RM, Anderson RR (2003) Favored regions for chorus-driven electron acceleration to relativistic energies in the Earth’s outer radiation belt. Geophys Res Lett 30(16):1871. https://doi.org/10.1029/2003GL017698
Mourenas D, Artemyev AV, Agapitov OV, Krasnoselskikh V, Mozer FS (2015) Very oblique whistler generation by low-energy electron streams. J Geophys Res Space Phys 120(5):3665–3683. https://doi.org/10.1002/2015JA021135
Mourenas D, Zhang XJ, Artemyev AV, Angelopoulos V, Thorne RM, Bortnik J, Neishtadt AI, Vasiliev AA (2018) Electron nonlinear resonant interaction with short and intense parallel chorus wave packets. J Geophys Res Space Phys 123(6):4979–4999. https://doi.org/10.1029/2018JA025417
Nogi T, Omura Y (2022) Nonlinear signatures of VLF-triggered emissions: a simulation study. J Geophys Res Space Phys 127(1):e29826. https://doi.org/10.1029/2021JA029826
Nogi T, Omura Y (2023) Upstream shift of generation region of whistler-mode rising-tone emissions in the magnetosphere. J Geophys Res Space Phys 128(3):e2022JA031024. https://doi.org/10.1029/2022JA031024
Nunn D (1971) A theory of VLF emissions. Planet Space Sci 19(9):1141–1167. https://doi.org/10.1016/0032-0633(71)90110-3
Nunn D (1974) A self-consistent theory of triggered VLF emissions. Planet Space Sci 22(3):349–378. https://doi.org/10.1016/0032-0633(74)90070-1
Nunn D (1986) A nonlinear theory of sideband stability in ducted whistler mode waves. Planet Space Sci 34(5):429–451. https://doi.org/10.1016/0032-0633(86)90032-2
Nunn D (1993) A Novel Technique for the Numerical Simulation of Hot Collision-Free Plasma; Vlasov hybrid simulation. J Comp Phys 108(1):180–196. https://doi.org/10.1006/jcph.1993.1173
Nunn D, Omura Y (2012) A computational and theoretical analysis of falling frequency VLF emissions. J Geophys Res Space Phys 117(A8):A08228. https://doi.org/10.1029/2012JA017557
Nunn D, Santolik O, Rycroft M, Trakhtengerts V (2009) On the numerical modelling of VLF chorus dynamical spectra. Ann Geophys 27(6):2341–2359. https://doi.org/10.5194/angeo-27-2341-2009
Nunn D, Zhang XJ, Mourenas D, Artemyev AV (2021) Generation of realistic short chorus wave packets. Geophys Res Lett 48(7):e92178. https://doi.org/10.1029/2020GL092178
Omura Y (2021) Nonlinear wave growth theory of whistler-mode chorus and hiss emissions in the magnetosphere. Earth Planets Space 73(1):95. https://doi.org/10.1186/s40623-021-01380-w
Omura Y, Nunn D (2011) Triggering process of whistler mode chorus emissions in the magnetosphere. J Geophys Res Space Phys 116(A5):A05205. https://doi.org/10.1029/2010JA016280
Omura Y, Summers D (2006) Dynamics of high-energy electrons interacting with whistler mode chorus emissions in the magnetosphere. J Geophys Res Space Phys 111(A9):A09222. https://doi.org/10.1029/2006JA011600
Omura Y, Katoh Y, Summers D (2008) Theory and simulation of the generation of whistler-mode chorus. J Geophys Res Space Phys 113:A04223. https://doi.org/10.1029/2007JA012622
Omura Y, Hikishima M, Katoh Y, Summers D, Yagitani S (2009) Nonlinear mechanisms of lower-band and upper-band VLF chorus emissions in the magnetosphere. J Geophys Res Space Phys 114(A7):A07217. https://doi.org/10.1029/2009JA014206
Omura Y, Miyashita Y, Yoshikawa M, Summers D, Hikishima M, Ebihara Y, Kubota Y (2015a) Formation process of relativistic electron flux through interaction with chorus emissions in the Earth’s inner magnetosphere. J Geophys Res Space Phys 120(11):9545–9562. https://doi.org/10.1002/2015JA021563
Omura Y, Nakamura S, Kletzing CA, Summers D, Hikishima M (2015b) Nonlinear wave growth theory of coherent hiss emissions in the plasmasphere. J Geophys Res Space Phys 120(9):7642–7657. https://doi.org/10.1002/2015JA021520
Omura Y, Hsieh Y-K, Foster JC, Erickson PJ, Kletzing CA, Baker DN (2019) Cyclotron acceleration of relativistic electrons through Landau resonance with obliquely propagating whistler-mode chorus emissions. J Geophys Res Space Phys 124(4):2795–2810. https://doi.org/10.1029/2018JA026374
O’Neil T (1965) Collisionless damping of nonlinear plasma oscillations. Phys Fluids 8(12):2255–2262. https://doi.org/10.1063/1.1761193
Pezzi O, Cozzani G, Califano F, Valentini F, Guarrasi M, Camporeale E, Brunetti G, Retinò A, Veltri P (2019) ViDA: a Vlasov–DArwin solver for plasma physics at electron scales. J Plasma Phys 85(5):905850506. https://doi.org/10.1017/S0022377819000631
Roberts CS, Buchsbaum SJ (1964) Motion of a charged particle in a constant magnetic field and a transverse electromagnetic wave propagating along the field. Phys Rev 135(2A):381–389. https://doi.org/10.1103/PhysRev.135.A381
Roux A, Pellat R (1978) A theory of triggered emissions. J Geophys Res 83(A4):1433–1441. https://doi.org/10.1029/JA083iA04p01433
Santolík O (2008) New results of investigations of whistler-mode chorus emissions. Nonlinear Processes Geophys 15(4):621–630. https://doi.org/10.5194/npg-15-621-2008
Santolík O, Pickett JS, Gurnett DA, Storey LRO (2002) Magnetic component of narrowband ion cyclotron waves in the auroral zone. J Geophys Res Space Phys 107(A12):1444. https://doi.org/10.1029/2001JA000146
Santolík O, Gurnett DA, Pickett JS, Parrot M, Cornilleau-Wehrlin N (2003) Spatio-temporal structure of storm-time chorus. J Geophys Res Space Phys 108:1278. https://doi.org/10.1029/2002JA009791
Santolík O, Parrot M, Lefeuvre F (2003) Singular value decomposition methods for wave propagation analysis. Radio Sci 38:10–1. https://doi.org/10.1029/2000RS002523
Santolík O, Gurnett D, Pickett J (2004) Multipoint investigation of the source region of storm-time chorus. Ann Geophys 22:2555–2563. https://doi.org/10.5194/angeo-22-2555-2004
Santolík O, Gurnett DA, Pickett JS, Parrot M, Cornilleau-Wehrlin N (2004) A microscopic and nanoscopic view of storm-time chorus on 31 March 2001. Geophys Res Lett 31(2):L02801. https://doi.org/10.1029/2003GL018757
Santolík O, Gurnett DA, Pickett JS, Parrot M, Cornilleau-Wehrlin N (2005) Central position of the source region of storm-time chorus. Planet Space Sci 53(1–3):299–305. https://doi.org/10.1016/j.pss.2004.09.056
Santolík O, Gurnett DA, Pickett JS, Chum J, Cornilleau-Wehrlin N (2009) Oblique propagation of whistler mode waves in the chorus source region. J Geophys Res Space Phys 114(A12):A00F03. https://doi.org/10.1029/2009JA014586
Santolík O, Gurnett DA, Pickett JS, Grimald S, Décreau PME, Parrot M, Cornilleau-Wehrlin N, El-Lemdani Mazouz F, Schriver D, Meredith NP, Fazakerley A (2010) Wave-particle interactions in the equatorial source region of whistler-mode emissions. J Geophys Res Space Phys 115(15):A00F16. https://doi.org/10.1029/2009JA015218
Santolík O, Pickett JS, Gurnett DA, Menietti JD, Tsurutani BT, Verkhoglyadova O (2010) Survey of Poynting flux of whistler mode chorus in the outer zone. J Geophys Res Space Phys 115:A00F13. https://doi.org/10.1029/2009JA014925
Santolík O, Kletzing CA, Kurth WS, Hospodarsky GB, Bounds SR (2014) Fine structure of large-amplitude chorus wave packets. Geophys Res Lett 41:293–299. https://doi.org/10.1002/2013GL058889
Santolík O, Macúšová E, Kolmašová I, Cornilleau-Wehrlin N, Conchy Y (2014) Propagation of lower-band whistler-mode waves in the outer Van Allen belt: systematic analysis of 11 years of multi-component data from the cluster spacecraft. Geophys Res Lett 41:2729–2737. https://doi.org/10.1002/2014GL059815
Sauer K, Chen H, Dubinin E, Lu Q (2022) Frequency bands and gaps of magnetospheric chorus waves generated by resonant beam/plateau electrons. J Mod Phys 13(6):864–891. https://doi.org/10.4236/jmp.2022.136050
Shklyar D, Matsumoto H (2009) Oblique whistler-mode waves in the inhomogeneous magnetospheric plasma: resonant interactions with energetic charged particles. Surv Geophys 30(2):55–104. https://doi.org/10.1007/s10712-009-9061-7
Shoji M, Omura Y (2013) Triggering process of electromagnetic ion cyclotron rising tone emissions in the inner magnetosphere. J Geophys Res Space Phys 118(9):5553–5561. https://doi.org/10.1002/jgra.50523
Shprits YY, Subbotin DA, Meredith NP, Elkington SR (2008) Review of modeling of losses and sources of relativistic electrons in the outer radiation belt II: local acceleration and loss. J Atmos Sol-Terr Phys 70(14):1694–1713. https://doi.org/10.1016/j.jastp.2008.06.014
Smith RL, Helliwell RA, Yabroff IW (1960) A theory of trapping of whistlers in field-aligned columns of enhanced ionization. J Geophys Res 65:815. https://doi.org/10.1029/JZ065i003p00815
Sonwalkar VS, Inan US, Bell TF, Helliwell RA, Chmyrev VM, Sobolev YP, Ovcharenko OY, Selegej V (1994) Simultaneous observations of VLF ground transmitter signals on the DE 1 and COSMOS 1809 satellites: detection of a magnetospheric caustic and a duct. J Geophys Res 99(A9):17511–17522. https://doi.org/10.1029/94JA00866
Soto-Chavez AR, Wang G, Bhattacharjee A, Fu GY, Smith HM (2014) A model for falling-tone chorus. Geophys Res Lett 41(6):1838–1845. https://doi.org/10.1002/2014GL059320
Stenzel RL (1976) Antenna radiation patterns in the whistler wave regime measured in a large laboratory plasma. Radio Sci 11(12):1045–1056. https://doi.org/10.1029/RS011i012p01045
Stenzel RL (1976) Filamentation instability of a large amplitude whistler wave. Phys Fluids 19(6):865–871. https://doi.org/10.1063/1.861552
Stix T (1992) Waves in plasmas. American Institute of Physics, Melville
Storey LRO (1953) An investigation of whistling atmospherics. Philos Trans R Soc Lond 246(908):113–141. https://doi.org/10.1098/rsta.1953.0011
Streltsov AV, Bengtson MT (2020) Observations and modeling of whistler mode waves in the magnetospheric density ducts. J Geophys Res Space Phys 125(10):e28398. https://doi.org/10.1029/2020JA028398
Subbotin DA, Shprits YY, Ni B (2011) Long-term radiation belt simulation with the VERB 3-D code: comparison with CRRES observations. J Geophys Res Space Phys 116(A12):A12210. https://doi.org/10.1029/2011JA017019
Suchy K (1981) Real Hamilton equations of geometric optics for media with moderate absorption. Radio Sci 16(06):1179–1182. https://doi.org/10.1029/RS016i006p01179
Sudan RN, Ott E (1971) Theory of triggered VLF emissions. J Geophys Res 76(19):4463–4476. https://doi.org/10.1029/JA076i019p04463
Summers D, Omura Y, Miyashita Y, Lee D-H (2012) Nonlinear spatiotemporal evolution of whistler mode chorus waves in Earth’s inner magnetosphere. J Geophys Res Space Phys 117(A9):A09206. https://doi.org/10.1029/2012JA017842
Tao X (2014) A numerical study of chorus generation and the related variation of wave intensity using the DAWN code. J Geophys Res Space Phys 119(5):3362–3372. https://doi.org/10.1002/2014JA019820
Tao X, Bortnik J, Albert JM, Thorne RM, Li W (2013) The importance of amplitude modulation in nonlinear interactions between electrons and large amplitude whistler waves. J Atmos Solar Terr Phys 99:67–72. https://doi.org/10.1016/j.jastp.2012.05.012
Tao X, Zonca F, Chen L (2017) Identify the nonlinear wave-particle interaction regime in rising tone chorus generation. Geophys Res Lett 44(8):3441–3446. https://doi.org/10.1002/2017GL072624
Tao X, Zonca F, Chen L (2021) A “Trap-Release-Amplify’’ model of chorus waves. J Geophys Res Space Phys 126(9):e29585. https://doi.org/10.1029/2021JA029585
Taubenschuss U, Khotyaintsev YV, Santolík O, Vaivads A, Cully CM, Le Contel O, Angelopoulos V (2014) Wave normal angles of whistler mode chorus rising and falling tones. J Geophys Res Space Phys 119(12):9567–9578. https://doi.org/10.1002/2014JA020575
Taubenschuss U, Santolík O, Graham DB, Fu H, Khotyaintsev YV, Le Contel O (2015) Different types of whistler mode chorus in the equatorial source region. Geophys Res Lett 42(20):8271–8279. https://doi.org/10.1002/2015GL066004
Taubenschuss U, Santolík O, Breuillard H, Li W, Le Contel O (2016) Poynting vector and wave vector directions of equatorial chorus. J Geophys Res Space Phys 121(12):11,912-11,928. https://doi.org/10.1002/2016JA023389
Teng S, Tao X, Xie Y, Zonca F, Chen L, Fang WB, Wang S (2017) Analysis of the duration of rising tone chorus elements. Geophys Res Lett 44(24):12,074-12,082. https://doi.org/10.1002/2017GL075824
Teng S, Tao X, Li W (2019) Typical characteristics of whistler mode waves categorized by their spectral properties using van Allen probes observations. Geophys Res Lett 46(7):3607–3614. https://doi.org/10.1029/2019GL082161
Thorne RM (2010) Radiation belt dynamics: the importance of wave-particle interactions. Geophys Res Lett 37(22):L22107. https://doi.org/10.1002/2017GL075824
Trakhtengerts VY (1995) Magnetosphere cyclotron maser: backward wave oscillator generation regime. J Geophys Res 100(A9):17205–17210. https://doi.org/10.1029/95JA00843
Trakhtengerts VY (1999) A generation mechanism for chorus emission. Ann Geophys 17:95–100. https://doi.org/10.1007/s00585-999-0095-4
Trakhtengerts VY, Rycroft MJ (2008) Whistler and Alfvén mode cyclotron masers in space. Cambridge University Press, Cambridge
Trakhtengerts VY, Rycroft MJ, Demekhov AG (1996) Interrelation of noise-like and discrete ELF/VLF emissions generated by cyclotron interactions. J Geophys Res 101(A6):13293–13302. https://doi.org/10.1029/95JA03515
Trakhtengerts VY, Demekhov AG, Hobara Y, Hayakawa M (2003) Phase-bunching effects in triggered VLF emissions: antenna effect. J Geophys Res Space Phys 108(A4):1160. https://doi.org/10.1029/2002JA009415
Tsurutani BT, Smith EJ (1974) Postmidnight chorus: a substorm phenomenon. J Geophys Res 79(1):118–127. https://doi.org/10.1029/JA079i001p00118
Tsurutani BT, Chen R, Gao X, Lu Q, Pickett JS, Lakhina GS, Sen A, Hajra R, Park SA, Falkowski BJ (2020) Lower-band “monochromatic’’ chorus riser subelement/wave packet observations. J Geophys Res Space Phys 125(10):e28090. https://doi.org/10.1029/2020JA028090
van Allen JA, Ludwig GH, Ray EC, McIlwain CE (1958) Observation of high intensity radiation by satellites 1958 alpha and gamma. J Jet Propuls 28(9):588–592. https://doi.org/10.2514/8.7396
Vomvoridis JL, Crystal TL, Denavit J (1982) Theory and computer simulations of magnetospheric very low frequency emissions. J Geophys Res 87(A3):1473–1490. https://doi.org/10.1029/JA087iA03p01473
Walker ADM (1976) The theory of whistler propagation. Rev Geophys Space Phys 14:629. https://doi.org/10.1029/RG014i004p00629
Weibel ES (1977) Self channeling of whistler waves. Phys Lett A 61(1):37–39. https://doi.org/10.1016/0375-9601(77)90256-0
Williams DD, Streltsov AV (2021) Determining parameters of whistler waves trapped in high-density ducts. J Geophys Res Space Phys 126(12):e29228. https://doi.org/10.1029/2021JA029228
Wu Y, Tao X, Zonca F, Chen L, Wang S (2020) Controlling the chirping of chorus waves via magnetic field inhomogeneity. Geophys Res Lett 47(10):e87791. https://doi.org/10.1029/2020GL087791
Zhang XJ, Agapitov O, Artemyev AV, Mourenas D, Angelopoulos V, Kurth WS, Bonnell JW, Hospodarsky GB (2020) Phase decoherence within intense chorus wave packets constrains the efficiency of nonlinear resonant electron acceleration. Geophys Res Lett 47(20):e89807. https://doi.org/10.1029/2020GL089807
Zhang XJ, Mourenas D, Artemyev AV, Angelopoulos V, Kurth WS, Kletzing CA, Hospodarsky GB (2020) Rapid frequency variations within intense chorus wave packets. Geophys Res Lett 47(15):e88853. https://doi.org/10.1029/2020GL088853
Zhang XJ, Demekhov AG, Katoh Y, Nunn D, Tao X, Mourenas D, Omura Y, Artemyev AV, Angelopoulos V (2021) Fine structure of chorus wave packets: comparison between observations and wave generation models. J Geophys Res Space Phys 126(8):e29330. https://doi.org/10.1029/2021JA029330
Zonca F, Tao X, Chen L (2021) Nonlinear dynamics and phase space transport by chorus emission. Rev Mod Plasma Phys 5(1):8. https://doi.org/10.1007/s41614-021-00057-x. arXiv:2106.15026 [physics.plasm-ph]
Zonca F, Tao X, Chen L (2022) A theoretical framework of chorus wave excitation. J Geophys Res Space Phys 127(2):e2021JA029760. https://doi.org/10.1029/2021JA029760
Zudin IY, Zaboronkova TM, Gushchin ME, Aidakina NA, Korobkov SV, Krafft C (2019) Whistler waves’ propagation in plasmas with systems of small-scale density irregularities: numerical simulations and theory. J Geophys Res Space Phys 124(6):4739–4760. https://doi.org/10.1029/2019JA026637
Funding
Open access publishing supported by the National Technical Library in Prague. This work has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No. 870452 (PAGER). We further thank Craig Kletzing, Bill Kurth, George Hospodarsky, and other colleagues from the Van Allen Probes EMFISIS Waves team at the University of Iowa for their hard work on the development and operations of the instrument, whose data are used in Fig. 4. We also thank our colleague Ivana Kolmašová for her help with the initial selection of intense chorus events in the EMFISIS burst mode data set.
Author information
Authors and Affiliations
Contributions
Conceptualisation: MH, OS; methodology: MH, OS; formal analysis and investigation: MH; writing—original draft preparation: MH; writing—review and editing: OS, MH; funding acquisition: OS; resources: OS; supervision: OS.
Corresponding author
Ethics declarations
Conflict of interest
Authors declare no competing interests.
Ethics approval
Not applicable.
Consent to participate
Not applicable.
Consent for publication
Not applicable.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A. Derivation of Whistler-Mode Ray Oscillations in Density Ducts
Appendix A. Derivation of Whistler-Mode Ray Oscillations in Density Ducts
The general form of cold plasma ray tracing equations reads (Stix 1992)
where \({\bar{D}}(k,\omega ) = 0\) is the dispersion relation. To trace a two-dimensional trajectory of ducted rays propagating in a magnetised plasma, the Eqs. (A1) and (A2) must be solved numerically for some general functions of density \(n_{\textrm{e}}(x,z)\) and magnetic field \(\varvec{B}_0(x,z)\). However, with suitable approximations, the basic principles can be explained analytically on a homogeneous field case. Let us assume the simplified from of refractive index for oblique whistler waves
\(\varvec{B_{\textrm{0}}}\) directed along the z-axis and electron density \(n_{\textrm{e}}\) dependent on the x-coordinate only. The nonzero derivatives of the dispersion relation
are found to be
By introducing the small-angle approximation \(\sin \theta _{\textrm{k}} \approx \theta _{\textrm{k}}\), \(\cos \theta _{\textrm{k}} \approx 1\), we get \(k_z \approx \mathrm {const.}\), \(V_{\textrm{g}z} \approx \mathrm {const.}\), reducing the system to one dimension. The problem can be further simplified by using a parabolic density profile
where \(s_{\textrm{duct}} = -1\) stands for a density enhancement, \(s_{\textrm{duct}} = 1\) models a density depletion, and w represents a characteristic width of the duct. Finally, the ray evolution in the \((x,k_x)\) space reduces to an elliptical/hyperbolic motion,
where we used an additional simplification \((x/w)^2 \ll 1\) and denoted the plasma frequency at \(x = 0\) as \(\omega _{\textrm{p0}}\). Whether the ray will be guided depends on the sign of \(2\omega - \varOmega _{\textrm{e}}\) and \(s_{\textrm{duct}}\).
Recalling the group velocity definition from Eq. (A1) and combining it with the ducted propagation described by Eq. (A10) above, we can show that x(t) behaves like a harmonic oscillator. The oscillation frequency is found to be
which is the Eq. 96 from Sect. 4.1.
As a final note, we must point out the difference between ducts with small and large density variations. If the density gradients are small and the wave remains quasiparallel, positive density variations (crests) guide only lower-band waves, and negative density enhancements (troughs) guide only upper-band waves, as described here. However, as shown already by Smith et al. (1960), in deep troughs, the wave normal angle of lower-band waves may reach the Gendrin angle and reflect back towards the center of duct. Such troughs can therefore guide wave energy at all frequencies larger than the lower hybrid frequency, but the waves will experience stronger damping due to the oblique wave vectors.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hanzelka, M., Santolík, O. Theories of Growth and Propagation of Parallel Whistler-Mode Chorus Emissions: A Review. Surv Geophys 45, 1–54 (2024). https://doi.org/10.1007/s10712-023-09792-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10712-023-09792-x