Article Highlights

  • Applicability of Growth methodology to inversion of gravity changes in volcano gravimetry is investigated by synthetic case studies

  • Pros and cons of the Growth inversion approach are demonstrated on simulated thin elongated sources

  • Optimization of gravimetric monitoring networks based on Growth simulations and synthetic sources is proposed

1 Introduction

We focus here on the capability of the Growth inversion method (Camacho et al. 2021b) to correctly detect thin elongated source bodies of high density contrasts in cases when the input gravity data, given on the topographic surface, are sparse, low in number, and of poor signal-to-noise ratio. The Growth inversion belongs to inversion approaches that make no prior assumptions about the number and geometry of the sought sources, but seek sources in the form of agglomerates of populated cells of a subsurface partition (e.g., Last and Kubik 1983; Rene 1986; Barbosa and Silva 1994; Li and Oldenburg 1998; Boulanger and Chouteau 2001; Uieda and Barbosa 2012). The Growth inversion explores the model space and lets source bodies grow by populating prismatic cells in the volumetric domain below the topographic surface with positive and negative density contrasts during an iterative weighted adjustment process (Camacho et al. 2021b). Thin elongated sources of high density contrasts pose a great challenge to such inversion methods.

The Growth inversion methodology used here was originally developed for inverting point surface gravity data, the complete Bouguer anomalies (CBA), in order to obtain structural density models of the subsurface (Camacho et al. 1997, 2000, 2002, 2011a, 2011b, 2021a). Later it was modified to be applicable in volcano-gravimetric studies to inversion of spatiotemporal (time-lapse) microgravity changes which are typically observed as sparse data with low signal-to-noise ratio given on the topographic surface (Camacho et al. 2011c, 2021b). Inverting gravity changes has raised new challenges for the Growth approach in terms of severe under-sampling of the information about the sources due to a low number of observation points. Compared to inverting CBA data, in the case of gravity changes one deals with data of amplitudes at a few tens of μGals (1 μGal = 10−8 m/s2) with observational error at the level of 10 to 15 μGal, i.e., data with much higher level of noise.

Due to the limited number of input gravity data, the volcano-gravimetric studies usually opt for inversions based on assumed simple geometric source bodies, their gravitational effect being given by an analytical formula. In such inversions the number of sought source parameters is smaller than the number of input gravity data. The source parameters are then found by optimization methods such as the genetic algorithm. This approach might better suit cases where there is external evidence or justified reasoning for choosing the number of sought sources and their shapes, e.g., spheres, ellipsoids, cylinders, prism, etc. On the other hand, inversion methods which do not pre-constrain the number or shapes of sources are better suited in the absence of such externally justified assumptions and may identify the subsurface locations of the most significant density changes, indicate the nature of the sources, and shed light on the subsurface geodynamic process. We compared the two approaches in a case study at the Laguna del Maule volcanic field, Chile (Vajda et al. 2021). Spatiotemporal gravity changes observed on Ischia (Italy), related to the 2017 earthquake, were inverted and interpreted using the Growth approach (Berrino et al. 2021), too. We have also revisited the gravimetric interpretation of the volcanic unrest of 2004–2005 on Tenerife (Canary Islands, Spain) by applying the Growth inversion to the observed time-lapse gravity changes (Vajda et al. 2023).

Here we focus on another challenge posed to the Growth inversion approach by thin elongated sources of high differential densities, such as dikes or sills, and chimneys. The spatial resolution of the sought source bodies in Growth inversion is limited by the size of the cells (prisms), into which the subsurface is partitioned, which depends both on the volume of the model space domain and on the number of input data points. The bottom boundary of the model domain and the cell size are automatically determined by the Growth upon its execution, not to exceed available computer memory, as specified in the Growth code (its modification would require a new program compilation). In our case studies, the cell size is several tens to several hundred meters. Naturally, thin elongated sources that are several meters or several tens of meters thick will be sensed and reproduced by Growth as much thicker, more voluminous, and with correspondingly much lower differential densities. How well the Growth inversion approach can then cope with such sources, and how useful the Growth solutions respective to such sources will be for interpretation, is the subject of our presented work.

2 Growth Inversion Approach

The Growth inversion method used in our study, implemented as the GROWTH-dg tool (Camacho et al. 2021b) makes no apriori assumptions about the number and shapes of the sources. The inversion procedure first generates a 3D partition of the model space. It divides the subsurface volumetric domain into rectangular prismatic cells. Then the procedure explores and fills the cells by positive and negative differential densities via an automated iterative adjustment process. Differential densities are alternatively referred to as density contrasts. These densities can optionally vary from cell to cell, allowing heterogeneous models. The variety in heterogeneous models is incremental, facilitated by revisiting and refilling of cells. The adjustment process is mixed and weighted. It both minimizes the input data misfit and maximizes the structural simplicity and compactness of the model, i.e., the agglomerate of populated cells, in a balanced way. The minimization of data misfit is counter-acted by the maximization of model compactness. These two are balanced by means of a weighting factor called the balance factor (λ).

The Growth inversion methodology developed by Camacho et al. (1997, 2000, 2002) originally aimed at inversion of topographically corrected gravity anomalies/disturbances (Vajda et al. 2020) better known as complete Bouguer anomalies (CBA). The input CBA gravity data are given on the topographic surface, at points where the surface gravity is measured. The inversion of CBA data results in subsurface structural density models. The numerical realization of the inversion approach and the corresponding software applications were improved over time, resulting in the GROWTH-2 (Camacho et al. 2011a, 2011b) and GROWTH-3 (Camacho et al. 2021a) software tools, respectively. Next, the Growth method was modified (Camacho et al. 2021b) to suit the inversion of sparse spatiotemporal (time-lapse) gravity changes observed at the benchmarks of volcano-gravimetric networks, implemented in software application GROWTH-dg. While the inversion of gravity anomalies yields the subsurface distribution of density anomalies, commonly referred to as density contrasts, the inversion of temporal gravity changes results in subsurface distribution of temporal density changes, which we call here again simply density contrasts. Hence the product of the obtained model source body volume times its density contrast represents the subsurface time-lapse mass change.

The Growth inversion process and its implementation in the GROWTH-dg software tool has been described in detail and with due mathematical apparatus in (Camacho et al. 2021b). Therefore we do not repeat the description here. To follow our work presented here, it is essential that the reader gets acquainted with the cited paper first. We only briefly rephrase the concepts and highlight some key features of the inversion procedure in the next section.

2.1 Growth Inversion Process

As the name of this inversion method implies, it is based on a growth process of source bodies throughout a mixed weighted iterative adjustment process. The inversion process explores and gradually fills the cells of the subsurface partition by positive and negative density contrasts. As more and more cells are filled and aggregated, the source bodies grow. The growth process is not initiated from pre-specified seeds, it executes automatically.

The unknowns in the adjustment are the density contrasts of the individual subsurface cells. The observables are the gravity data at several points on the topographic surface. The design matrix is formed based on the gravitational effect of a rectangular prism. The density contrasts in the subsurface partition are not sought at once. Instead, they are sought in a model exploration and cell filling iterative process, in which only one cell is added to the aggregation of filled cells in each iteration. The iterative adjustment process aims at minimizing the data misfit, i.e., the residuals. To avoid blurry or messy solutions, a constraint is adopted to apply regularization. The minimization of data misfit is combined in the adjustment process with maximizing the structural model simplicity and compactness in terms of minimizing the total anomalous mass. The balance between minimizing the misfit residuals and minimizing the total anomalous mass of the model is weighted, controlled by the so-called balance factor (λ). The adjustment is therefore weighted mixed and based on least squares adjustment with L2 norm, cf. Eq. 5 in (Camacho et al. 2021b).

Parameter λ plays a key role. High λ values provide structurally simple models with only a few source bodies nicely compacted, yet with a poorer data fit. High λ values also force the bodies to assume rounder shapes. Conversely, low λ values produce models with small resulting misfit residuals in terms of root mean square (r.m.s.), referred to as “tight fit”. However, the use of low λ values results in fitting also the observational noise, which means translating observational noise into model noise. This is referred to as “overfitting”, as the resulting misfit r.m.s. is considerably lower than the level of noise in the input gravity data. Such models are messy, polluted with many artifacts in terms of a large portion of scattered filled cells. Also the source bodies in over-fitted models can grow too large and attain distorted shapes. The program provides a default value for λ upon its execution, estimated based on an analysis of the input gravity data. The user can change the default value prior to running the inversion procedure. Hints for choosing proper λ values can come from the autocorrelation analysis of the resulting gravity residual values (see Camacho et al. 2021b for more details). Practical advice recommends running the inversion several times with various λ values, to observe the behavior of the inversion solutions in response to the λ values, while watching the level of misfit in each solution.

The rationale of the Growth inversion approach dwells in how it operates with the density contrast in the cell filling process. This concept is essential for interpretation. The user must understand that from the nature of the Growth inversion it follows that the growth process cannot, in principle, determine the true density contrasts of the model sources. Both the volume and the density contrast of resulting source bodies remain ambiguously determined. This must be accounted for in the interpretation. Only the product of the volume and the density contrast of a source body, that is its mass, is determined realistically, if optimal values of the balance factor are adopted. Understanding how Growth approach works with density contrasts is thus vital. It is demonstrated in our work presented here by the synthetic case studies in real environments (see the multitude of inversion models in the online Supplement).

Growth can produce either homogenous or heterogeneous density contrast models. Homogenous models consist of positive and negative source bodies, all having the same value (in absolute sense) of the density contrast, which is constant throughout each body. This is achieved in the iterative exploration procedure by allowing exploring only empty cells and filling each cell only once. The cell filling is controlled by a target density contrast value, which is an inversion parameter preset prior to running the inversion process. Running the Growth process requires the use of relatively small target density contrasts. The higher the density contrast the smaller and rounder the source body of the inversion solution. Consequently, there is a limit for higher density contrasts, above which the inversion process would not run. This limit is governed by the amplitude of the input gravity data and by the average size of the cells of the subsurface partition. By allowing the procedure to explore also already filled cells, and to refill the cells repeatedly several times, heterogeneous source bodies can be obtained. The density contrasts among the aggregation of cells forming the source body differ from each other by incremental steps, depending on how many times the procedure allowed the cells to be refilled with a preset density contrast. At the beginning of the iterative adjustment process only one or very few cells are filled, therefore their density contrast is scaled up to a very high value. As the process advances, adding more and more filled cells, one by one, the density contrast in all the already filled cells is gradually scaled down. The down-scaling completes upon the termination of the process when the model density contrast arrives at or converges to the target density contrast pre-selected at the execution of the inversion run. There are two ways to pre-destine the final density contrasts of the obtained inversion solutions, in both the homogenous and the heterogeneous models.

The first option is to pre-set, prior to running the inversion process, the following inversion parameters, which is to be done by the user: the target average density contrast and the number of levels of the density contrasts (equal to 1 for homogenous models). The second option is an alternative to the first one. It dwells in pre-setting, prior to running the inversion process, the following inversion parameters, which is to be done again by the user: the portion (in %) of filled cells out of all cells of the subsurface partition, and the number of levels of the density contrasts (again equal to 1 for homogenous models). The inversion procedure then terminates when the portion of filled cells reaches the pre-specified level, affecting the final average density contrast reached upon termination. Again, the advice is to run the inversion repeatedly for several values of the pre-selected target average density contrast, or alternatively for several values (%) of the pre-selected portion of filled cells, for each single value of the balance factor (λ), while watching the evolution of the model along with its misfit residuals.

In addition, the Growth inversion procedure offers an optional adjustment of offset or linear trend in the input data, optional iterative reweighting (parameter B) to suppress the effect of outliers and gravity points with uncorrelated signal due to site effects, and optional depth weighting (parameter D). The iterative reweighting is achieved by a robust procedure based on iteratively reweighted least-squares solutions by successively assigning small weights to large residuals. The depth weighting compensates for an assumed increase of background density with depth, which has impact on the resulting density contrasts thus affected by depth, causing positive sources to be displaced or prolonged downwards and negative sources upwards. These features are described in detail in (Camacho et al. 2021b). These three features should be used with due care and awareness, exercised by running trial and error inversion runs with sensitively varied values of these inversion parameters. At the beginning of the online Supplement (sections B through G), we demonstrate, using synthetic gravity data, the response of the inversion solutions to the values of the individual inversion parameters. Another example of the model response to the depth weighting and to iterative reweighting for real data of the 2004–2005 unrest on Tenerife can be found in (Vajda et al. 2023).

Let us address once more the cell size of the subsurface partition, since it is related not only to the resolution of the resulting Growth model, but also to the highest applicable target density contrast of the model. Naturally, to achieve the highest possible resolution in the model, the smallest possible cell size is desired. There is a lower limit to the cell size though, below which the program would not run. With making the cell size smaller the number of subsurface cells grows rapidly. The number of subsurface cells depends on the volume of the model space, which is controlled by the horizontal size of the model space and its depth reach—both are selected automatically by the program: the horizontal size based on the horizontal extent of the input gravity data, the depth of the lower boundary based on the loss of sensitivity to the gravity signal with depth. The number of subsurface cells (in combination with the number of input gravity data points) governs the computer memory requirements. Of course the stronger the computer the greater the admissible number of subsurface cells and the smaller the admissible smallest cell size. But there always would be a limit, depending on the computer power. The limit is set in the present GROWTH-dg, which we use in this study, which is also publically available (cf. Camacho et al. 2021b) such that the program runs on common present day desktops in a reasonably short time, so that many repeated inversion runs with varying the inversion parameters can be obtained in a reasonable time. The limit of course can be changed in the FORTRAN code, which is also publically available (cf. Camacho et al. 2021b), and the program recompiled to run with higher number of cells of smaller sizes on more powerful computers.

The average cell size is automatically selected by the program and offered as default. It can be over-driven by the user, but typically towards higher values. There is a limit aiming towards smaller values. It is dictated by the size of the model space volume, hence by the number of the subsurface cells, as well as by the number of the input gravity data on the surface. The smallest applicable in the inversion (average) cell size also impacts the highest applicable in the inversion target (average) density contrast.

3 Case Studies Using Synthetic Gravity Data

We illustrate below, using synthetic case studies, how the Growth inversion detects and images thin elongated sources representing dykes, sills, flat chambers or conduits. The inversions are run on synthetic gravity data generated by simulated simple source bodies on the topographic surface in real volcanic environments of the Ischia island (Italy), the Laguna del Maule volcanic field of the southern Andes (Chile), and the central volcanic complex (CVC) of Tenerife, Canary Islands (Spain). The simulated source bodies, such as shallow or deep beam-like or plate-like thin prisms in sub-vertical or sub-horizontal positions, thin vertical cylinders or flat rotational ellipsoids, will mimic either the real sources of actual historical geodynamic events, or hypothetical presumed sources. To study the loss of information on the source when observing at benchmarks of existing gravimetric networks, caused by the sparseness of the data that may insufficiently sample the source signal, the inversions for synthetic data on gravity benchmarks are compared to inversions for data simulated on a relatively dense equidistant grid on the topographic surface. To study the effect of noise in the input gravity data, we contaminate the benchmark data by adding noise at the level of 35%.

Three kinds of Growth solutions are thus presented for each source in each case study region: (1) Growth models obtained for noise-free grid data, (2) those obtained for noise-free benchmark data, and (3) those obtained for noisy benchmark data. The Growth solutions that best reproduce some aspects of the simulated source body, such as its shape, depth, orientation or mass are referred to as best-recovery models. The noise-free grid data shall serve the purpose of identifying the best achievable reproducibility of a given source in the given settings using the Growth inversion. The noise-free benchmark data shall serve the purpose of analyzing the impact of the low number of benchmarks and of their spatial distribution on the reproducibility of a given source in the given settings using the Growth inversion. The noisy benchmark data shall serve the purpose of analyzing the combined effect of both the noise and the sparsity of the benchmark data on the reproducibility of a given source in the given settings using the Growth inversion.

The forward modelling is carried out in package Potent (Geophysical Software Solutions Pty. Ltd.). The noise-free synthetic gravity data are displayed, both for the grid and for the benchmarks, as fields, using the same interpolation method for both, namely kriging. They are presented as draped over the shaded relief in the study area, using package Surfer by Golden Software. Only point data on the topographic surface (in case of both grid and benchmarks) enter the Growth inversion, not interpolated data. The forward computed gravity data represent synthetic spatiotemporal gravity changes due to the simulated source bodies of density contrasts that represent temporal subsurface density changes. The Growth inversion solutions are presented as 3D models in terms of source bodies comprised of populated prism aggregations, visualized in 3D using an in-house MATLAB script. The original source is displayed in the model also, to visually assess the reproducibility of the source by the Growth model.

The Growth solutions are sensitive to the choice of the values of free tunable inversion parameters. This is illustrated on practical examples in sections B through G of the online Supplement. In our work presented here we run all the inversions with no offset or trend adjustment, no iterative reweighting, and no depth weighting. We run the inversions with the smallest possible average cell size of the subsurface partition that the program accepts, which is input data specific. We focus on how to vary and properly select the values of the two key inversion parameters, the balance factor (λ) and the target density contrast (Δρ). The proper selection is achieved by many trial-and-error inversion runs, usually starting with the λ value proposed by the program as default value and experimenting with the Δρ value. The proper selection of the combination of these two values is very case-sensitive, depending on the size, shape, relative location, depth, orientation and density contrast of the source, the relief of the study area, and the sampling of its gravity signal by the grid or benchmarks. Usually it takes running many trial-and-error inversions for the user to develop a proper feeling for the given situation under study. This is what we have done also. Many trial-and-error inversions were run. Only some of them are presented in the Supplement (sections H through J) to share experience and provide some guidance, to illustrate the process of selecting proper values for the two key inversion parameters. In the main paper only specific best-recovery solutions are presented out of those shown in the Supplement. Hence the reader is urged to carefully read and consider also the Supplement along with the main paper. One more comment: When we refer to the depth of the Growth solution source body, its depth is represented by the average depth of the populated cells.

3.1 Laguna Del Maule Volcanic Field (Chile)

The Laguna del Maule volcanic field (LdMvf), situated within the Andean Southern Volcanic zone, is a large silicic volcanic area underlain by a large magma reservoir (Miller et al. 2017b). A widespread deformation at rates greater than 20 cm/year has been observed at LdMvf since 2007 (Feigl et al. 2014; Le Mével et al. 2015, 2016). Deformation data were modelled and interpreted in terms of an inflating sill (Zhan et al. 2019) at about 5 km below surface, i.e., at depth 3 km below sea level (b.s.l.). Miller et al. (2017b) inverted complete Bouguer anomalies (CBA gravity data) in the area and interpreted the obtained structural density model as a shallow, crystal-poor, volatile-rich, silicic magma reservoir overlying the sill. This interpretation is supported also by seismic data (Wespestad et al. 2019; Bai et al. 2020). Numerous NE- to SW-trending fault, dome, and dike structures were identified above the magma reservoir by seismic, magnetic and geologic field studies (Peterson et al. 2020; Garibaldi et al. 2020).

Spatiotemporal gravity changes accompanying the ongoing inflation were observed by (Miller et al. 2017a) over three roughly annual periods spanning 2013–2016. Residual gravity changes, corrected for the gravitational effect of surface deformation using a local free-air effect (Miller et al. 2017a) and using a deformation-induced topographic effect (Vajda et al. 2019, 2021) were inverted and interpreted by Miller et al. (2017a) and Vajda et al. (2021), respectively. In both studies the spatiotemporal gravity changes are explained by upward risen hydrothermal fluids above the magmatic reservoir. The transport of the fluids is mediated by the faults, prevalently by the Troncoso fault.

Here we simulate synthetic gravity generated by (a) a shallow thin horizontal beam-like prism with positive density contrast simulating the rejuvenation of the Troncoso fault, (b) a deep thin sub-horizontal plate-like prism simulating the inflating inclined sill injected by fresh magma.

3.1.1 Troncoso Fault Brines Rejuvenation Simulation (Shallow, Thin, Horizontal, Beam-Like Prism)

First we simulate a brines-filled, porous, shallow, thin (43 m by 170 m), horizontally elongated (6.2 km long), beam-like prism representing the source body related to the Troncoso fault, inspired by the inversion solution to the spatiotemporal gravity changes observed at LdMvf from 2013–2014 by Miller et al. (2017a). The parameters (position, size, orientation, density contrast and mass) of this prism are listed in Table 1. This source is meant to simulate rejuvenation of a pathway for magmatic brines.

Table 1 The UTM coordinates (easting Xc, northing Yc) and elevation above sea level (a.s.l.) Zc of the center of the prism, its length (longer horizontal dimension), width (vertical dimension), thickness (shorter horizontal dimension), orientation (strike), volume, density contrast (temporal density change), and mass (mass change)
Full size table

Synthetic noise-free gravity data are forward computed for the prism, first at a regular grid on the topographic surface with spacing 500 m (Fig. 1, left), and next at the benchmarks of the gravimetric network at LdMvf (Miller et al. 2017a; Vajda et al. 2021), see Fig. 1 (right). Both the datasets are displayed as fields, using the same kriging interpolation. The topographic surface is represented by a down-sampled LiDAR DEM described in (Vajda et al. 2021).

Fig. 1
figure 1

Synthetic noise-free gravity on the grid (left) and at the benchmarks of the gravimetric network at LdMvf (right) due to the shallow thin horizontal beam-like prism simulating the rejuvenation of the Troncoso fault

Full size image

We have run Growth inversions of the grid data for a subsurface partition with cells of average size 250 m, which is the smallest that the program would accommodate. Many inversions were run for combinations of various values of the two key inversion parameters, the balance factor (λ) and the density contrast (Δρ), in a trial-and-error seeking approach. Several of those solutions are presented in the Supplement (section H.1). For noise-free grid data it is the solutions with relatively low λ values and low Δρ values that best reproduce not only the orientation and relative shape (horizontal elongation) of the simulated prism, but also its length and depth. The width and the vertical dimension of the reproduced source—thus its volume—are highly exaggerated in these solutions, depending on the Δρ value applied in the inversion. On the other hand, solutions with relatively low λ values along with relatively high Δρ values recover best, as good as possible, the thin dimensions (particularly the width) of the original source, though at the cost of the reproduced source being shaggy, meaning holey or scattered. The mass of the source is recovered correctly for optimal values of λ and Δρ. In this particular case the optimal values mean a range for λ from 5 to 50 for Δρ around 10 kg/m3, or a range for Δρ from 5 to 100 kg/m3 for λ around 5.

In the best-recovery solution adopting Δρ = 10 kg/m3 the width of the prism is recovered at about 500 m at best (compared to the original 43 m), and the vertical dimension at about 1250 m at best (compared to the original 170 m). Due to the much lower than original density contrast of the reproduced source, the volume of the reproduced source is exaggerated by multiples of ten (about 88 times for Δρ = 10 kg/m3). This is the price to be paid for using low density contrasts in the Growth solutions, which however guarantee the as successful as possible recovery of the orientation, relative shape, depth and mass of the original source. The best-recovery solution for the noise-free grid data adopting a low density contrast (Δρ = 10 kg/m3) is presented in Fig. 2 (left column). The mass of the prism in this solution is reproduced accurately, the depth is shifted slightly deeper, by 57 m. Green dots represent the grid data. The outline of the original prism is shown by black lines.

Fig. 2
figure 2

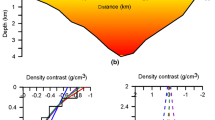
Best-recovery inversion model for noise-free grid data (left), noise-free benchmark data (middle) and noisy benchmark data (right). First row is 3D view (azimuth α =  − 11°, elevation z = 13°), second row shows the top view (α = 0°, z = 90°), the third row is lateral view (α = 0°, z = 0°), and the fourth row lists the inversion parameters and model parameters

Full size image

Next we invert the noise-free synthetic gravity given at the benchmarks of the LdMvf gravimetric network consisting of 29 stations (see Fig. 1, right). We run the Growth inversion as we did for the grid data, varying the values of λ and Δρ, with average cell size of the subsurface partition 300 m (see the Supplement, section H.1). The lesson learned from these inversion runs is that the depth of the prism is best reproduced (to within a few meters) with tight-fit solutions (around λ = 3) and fairly low Δρ values (around 10 kg/m3), even though such solutions produce scattered distorted source bodies (see Supplement, figure H.1.3.a). In such solutions, the mass is overdetermined, though, by about 8%. The mass is correctly recovered for slightly more compact source bodies (λ around 11, Δρ around 10 kg/m3), see (Supplement, figure H.1.3.b). In such solutions, the depth of the source is already overdetermined by about 300 m. The more compact the solution body (for higher λ values) the more distorted its reproduced shape, tending towards a vertical U-shape, the deeper its recovered depth, and the more under-determined its mass (see Supplement, figure H.1.3.c). With even higher λ values the recovered body becomes round (see Supplement, figures B.1.c and C.1.c). In Fig. 2 (middle column) we present the best-recovery solution for a relatively high density contrast (Δρ = 100 kg/m3) that best reproduces the mass of the source (to within 2.5%) and moderately overestimates its depth by about 370 m. For a similar best-recovery solution, yet with a low density contrast, see (Supplement, figure H.1.4).

We repeat the same procedure as above also for the noisy benchmark data with noise-to-signal ratio of 35%, i.e., noise with the amplitude of 10 μGal (see the Supplement, section H.1). The solutions behave similarly to those for noise-free benchmark data, except for the need to use higher λ values to filter out the data noise, and the solutions being slightly more distorted. The best-recovery solution for a low density contrast, which accurately reproduces the mass and over-estimates the depth by 788 m is shown in (Supplement, figure H.1.6, left). The best-recovery solution for a relatively high density contrast, which over-estimates the mass by 23% and over-estimates the depth by 340 m is presented in Fig. 2 (right column).

Comparing the best-recovery model obtained for noise-free gravity data at the benchmarks (Fig. 2, middle column) with that obtained for the noise-free grid data (Fig. 2, left column) we observe a distortion in the solution, i.e., in the reproduced source body due to the sparsity of the benchmarks. The reproduced source has a pronounced vertical U-shape, and is shifted downward by several hundred meters. The noise in the benchmark data at the level of 10 μGal, i.e., 35% of the studied signal, calls for applying slightly higher balance factor values, but does not cause additional severe distortions in the solution. Much more distortion is due to the benchmark sparsity than to the noise in the data.

Despite strong distortion in the vertical shape and the depth of the Growth image of the original prism, the solution still provides some hints that the source may be associated with the simulated Troncoso fault rejuvenation even with the given number and spatial distribution of the monitoring benchmarks and even with assuming noise in the input data at the level of 35%. However, it would be very difficult, nay impossible, to ascribe the reproduced source with its shape and depth to the original shallow thin horizontal prism, unless there were external reasons to lead such interpretation, compensating for the distortion in depth and shape in the source image.

3.1.2 Inflating Sill Magma Injection Simulation (Deep, Thin, Plate-Like, Sub-Horizontal Prism)

We simulate the injection of fresh magma into the inflating sill at LdMvf, inspired by the inversion solution of Feigl et al. (2014), see also (Zhan et al. 2019). The sill is represented by a thin inclined prism (9 km by 5.3 km) at the depth of 3 km b.s.l. (about 5 km below the surface). The parameters of this prism are listed in Table 2. Note that the fairly deep prism is very thin, its thickness being only 5 m.

Table 2 The UTM coordinates (Xc, Yc) and elevation Zc (a.s.l.) of the center of the prism, its width (shorter horizontal dimension), length (longer horizontal dimension), thickness, orientation, volume, density contrast and mass
Full size table

Noise-free synthetic gravity was forward computed for the sill-simulating prism, both on a regular grid on the topographic surface with spacing 1 km, and at the benchmarks of the LdMvf gravimetric network. Both datasets are presented in Fig. 3 as fields, using the same kriging interpolation. The crosses show the positions of the benchmarks. Horizontal projection of the sill-simulating prism is shown as hatched rectangle. Additional dataset was prepared by adding noise to the benchmark data at the level of 35%, i.e., with amplitude of about 5 μGal.

Fig. 3
figure 3

Synthetic noise-free gravity generated by the sill-simulating prism on regular grid with step 1 km (left) and on the benchmarks (right)

Full size image

Growth inversion solutions for various combinations of λ and Δρ values are presented for all three datasets in the Supplement (section H.2) along with comments on those solutions. Here we show (Fig. 4) the best-recovery solutions for all three datasets. This simulation demonstrates how very difficult, nay impossible, it is to gravimetrically reveal a deep thin plate-like sub-horizontal prism using the Growth inversion approach, even if noise-free gravity at a regular grid were available.

Fig. 4
figure 4

Best-recovery Growth models that accurately (to within 1%) reproduce the mass of the simulated sill, for noise-free grid data (left panels), noise-free benchmark data (middle panels), and noisy benchmark data (right panels), adopting low density contrasts. Top row is top view (α = 0, δ = 90), middle row is lateral view at the sill edge (α =  − 14, δ = 0), bottom row is 3D view perpendicular to the sill plane (α = 76, δ = 70)

Full size image

Examining the benchmark solutions that best (to within 1%) reproduce the mass of the sill (Fig. 4), we conclude that the Growth image of the deep thin sub-horizontal plate-like prism looks for both noise-free and noisy benchmark data more like a vertically elongated stump, resembling a diapir. Also the depth of the center of mass of the sill is over-determined by about 1 km. From these solutions it is not possible to hint that the original source is a thin inclined (at 20 degrees) plate-like prism.

3.2 CVC of Tenerife

The central volcanic complex (CVC) of Tenerife experienced an unrest starting in spring of 2004 and concluding late 2005. Apart for accompanying seismicity, fumarolic activity and degassing, it was manifested also by observed spatiotemporal gravity changes (Gottsmann et al. 2006). The time-lapse gravity changes observed at a network of 14 benchmarks indicated that the reactivation was accompanied by an addition to subsurface mass, which was not accompanied by any observable widespread surface deformation (Fernández et al. 2015). Gottsmann et al. (2006) attributed these gravity changes to the upward migration of hydrothermal fluids released from a deep reservoir, possibly coupled with a dike intrusion into the Santiago Rift, or magma injection into a conjugated fault system several km below the surface in May–July 2004. Mass injection was estimated at 11 × 1010 kg with the upper bound of 20 × 1010 kg.

These gravity changes were revisited by Prutkin et al. (2014), who interpreted the 2004/5 non-eruptive unrest as hybrid (rather than purely magmatic or purely hydrothermal), caused by an intrusion of magma (estimated at 15 × 1010 kg) to a depth of about 6 km b.s.l. at the centre of the NW seismogenic zone identified by Cerdeña Domínguez et al. (2011), roughly 5 km to the NNW of Pico Viejo. The intrusion allegedly triggered the upward release of hydrothermal brines (estimated at 2 × 1010 kg) through a network of permeable pathways or zones of least resistance into shallow-seated hydrothermal systems, causing the perturbation of the aquifers.

Vajda et al. (2023) reinterpreted the spatiotemporal gravity changes of the unrest using the Growth inversion approach. They also interpreted the unrest as hybrid due to a stalled magma intrusion and released upward-migrated volatiles, in accordance with previous studies. The intrusion, possibly in the form of a swarm of dikes or sills and dikes, arrived from depths below 8 km (b.s.l.) into the central part of the island just north of the Teide–Pico Viejo twin stratocones, causing a bulk density increase within this intruded volume related to a mass injection of 23 × 1010 kg. The intrusion propagated along the boundary between the basaltic core of the island, the Boca Tauce volcanic body, and the more permeable and less compacted lower-density volcanic rocks. The stalled intrusion released volatiles that disturbed the aquifer at the SW of the caldera rim (injected mass of 2.9 × 1010 kg).

Here we simulate gravity changes, both at a regular dense grid on the topographic surface and at the benchmarks of the original gravimetric network, due to synthetic sources such as a hypothetical conduit of the Teide volcano (thin vertical cylinder), and an assumed phonolitic magma chamber below the Teide volcano at 1.25 km b.s.l.

3.2.1 Simulated Chimney Injection of Teide Volcano (Shallow, Thin, Vertical Cylinder)

First we simulate a hypothetical conduit feeding the Teide summit, a chimney represented by shallow thin vertical cylinder with radius 50 m and density contrast 300 kg/m3. The cylinder has its base at sea level and ends 100 m short of the Teide summit (Table 3).

Table 3 Parameters of the simulated thin vertical cylinder. The Xc and Yc are UTM easting and northing, Zc is height (m a.s.l.) of the center of the top plane of the cylinder
Full size table

The simulated chimney does not generate any observable gravitational effect (above the 5 μGal threshold) on the benchmarks of the gravimetric network at CVC Tenerife. This implies that mass movement above sea level within an assumed central Teide conduit would remain undetected by the presently existing benchmarks of the gravimetric network. Therefore, we invert only the noise-free synthetic gravity data forward computed at the regular grid on the topographic surface on an area of 7 × 7 km2 with spacing 50 m (see Fig. 5). The gravity data are presented in the form of a field, using the kriging interpolation, which reaches amplitude of 210 μGal at the summit.

Fig. 5
figure 5

Synthetic noise-free gravity on a 50 m grid on the topographic surface generated by a thin vertical cylinder simulating the Teide volcano summit chimney of radius 50 m and density contrast 300 kg/m.3 (left). The Growth model reproducing the chimney to a depth of 800 m a.s.l. (right) and detailed summit top view (inset)

Full size image

By trial-and-error inversion runs for various Δρ values, seeking the optimal λ value (see the Supplement, figure I.1.2), we found the solution that best reproduces the simulated chimney. The best-recovery solution (λ = 23, Δρ = 100 kg/m3) reproduces very well the thin vertical cylinder down to the depth of about 800 m a.s.l., beyond which the solution is holey (Fig. 5, see also figure I.1.1 of the Supplement). Due to the preset density contrast of this solution, the reproduced chimney has roughly a triple volume compared to the original one, and is likewise thicker. The mass change of the injection is under-estimated by 6% which is due to not reproducing the cylinder at depths between sea level and 800 m a.s.l.

3.2.2 Simulated Phonolitic Magma Chamber Underneath Teide Volcano (Flat, Horizontal, Biaxial Ellipsoid)

By implication, explosive eruptions involve a shallow phonolitic magma chamber system at the centre of the island (Marti and Gudmundsson 2000). Petrological evidence indicates several coexisting isolated phonolitic reservoirs (Ablay et al. 1998; Martí and Geyer 2009; Andújar and Scaillet 2012; Andújar et al. 2010, 2013). Their location varied during the evolution of the CVC (Andújar 2007), spanning depths of about 1–2 km b.s.l. for the twin stratovolcanoes (Ablay and Martí 2000) and 1 km a.s.l. for Montaña Blanca and Roques Blancos (Andújar and Scaillet 2012; Andújar et al. 2013). Such a magma chamber system has not been firmly confirmed by geophysical methods, yet, though recent seismic studies may point to similar conclusions (Koulakov et al. 2023).

Here we simulate an assumed magma chamber represented by a flat horizontal biaxial ellipsoid at the depth (of its center) equal to 1.25 km b.s.l. horizontally aligned with the Teide summit, with major semi-axis (horizontal dimension) of 1200 m, minor semi-axis (vertical dimension) of 250 m, volume of 1.5 × 109 m3, density contrast of 180 kg/m3, and simulated mass injection equal to 27 × 1010 kg (Table 4).

Table 4 Parameters of the simulated flat, horizontal, biaxial ellipsoid representing the assumed magma chamber. The XC, YC (UTM easting and northing) and ZC (elevation a.s.l.) are the coordinates of the center of the ellipsoid
Full size table

Synthetic noise-free gravity was forward computed both at the regular grid on the topographic surface (step 300 m) and at the benchmarks of the gravimetric network, see Fig. 6. The gravity data are presented in the form of a field, using the kriging interpolation. The synthetic field due to this simulated chamber attains maximum values (about 90 μGal) on the slopes of the Teide cone, not at the summit, while at the benchmarks of the gravimetric network it has the highest value at benchmark MAJU (about 60 μGal) located about 2.5 km to the SE off the summit.

Fig. 6
figure 6

Synthetic noise-free gravity field (interpolated) generated by the flat rotational ellipsoid simulating a phonolitic magma chamber beneath the Teide volcano: (left) on a regular grid (on the topographic surface) with step 300 m and (right) on the benchmarks of the gravimetric monitoring network. The hatched circle shows the horizontal projection of the position and size of the chamber

Full size image

For the noise-free grid data inversion only data from a roughly circular area covering the caldera were used, i.e., data points from the grid with values above 15 μGal (see Fig. 6, left). This reduction of the number of input data allowed reducing the minimum adopted average cell size from 600 (respective to the whole grid) to 320 m. First we ran the inversion with a chosen density contrast of 180 kg/m3, which is the same as that of the original simulated source, and with λ = 15 (see Fig. 7, left column). This solution can be considered as best-recovery, since it exactly reproduced the mass of the chamber, and over-estimated its depth only by 136 m, which is only 3% of the depth of the chamber below the surface. The reproduced chamber in this solution is, however, round and does not reveal the relative shape, the horizontal flatness of the chamber. Since usually the solutions with very low density contrasts reveal the relative shape of the source better, we ran the inversion also with the same balance factor and the density contrast of 5 kg/m3 (see the Supplement, figure I.2.2b). Naturally, such inversion produces a large blown-up source body. Yet, the horizontal flatness of the simulated chamber was not revealed in the solution with very low Δρ value.

Fig. 7
figure 7

Best recovery Growth models for the noise-free grid data (left), the noise-free benchmark data (middle) and the noisy (35% / 20 μGal) benchmark data (right). A 3D view (top row), top view (middle row), and lateral view from south (bottom row)

Full size image

Next we ran the inversions for the noise-free benchmark data. For the density contrast of 180 kg/m3, which is the same as that of the simulated magma chamber source, and for λ = 2 (arrived at by trial-and-error inversion runs), we obtain the best-recovery solution (Fig. 7, middle column) with misfit r.m.s. of 1 μGal, exactly reproduced mass and exactly reproduced depth. The shape of the chamber is not reproduced correctly, it is thinner and vertically stretched, as well as slightly tilted. This is due to the sparsity and spatial distribution of the benchmarks sampling the gravity signal. As in the case of grid data, running the inversion with a very low density contrast of 5 kg/m3 did not help revealing the relative shape of the simulated chamber (see the Supplement, figure I.2.3b).

Finally we ran the inversions for the noisy benchmark data with noise at the level of 35% which corresponds to about 20 μGal noise amplitude. For the density contrast of 180 kg/m3, due to the presence of noise we have to raise the value of the balance factor to λ = 6 (arrived at by trial-and-error inversion runs), in order to obtain the best recovery solution exactly reproducing the mass (Fig. 7, right column), with misfit r.m.s. of 8 μGal, max misfit of 24 μGal, under-estimated depth by 320 m (which is 6% of the depth below the surface). The shape of the chamber is not reproduced adequately, it is even more vertically stretched and tilted. It resembles more of a dike than an ellipsoidal chamber. This is due to the sparsity and spatial distribution of the benchmarks, as well as their noise. Yet, the sparsity has more impact on the solution than the noise. We found a best-recovery solution, which reproduces the mass exactly, yet is slightly larger, also for a density contrast of 100 kg/m3 (see Supplement, figure G.2.4c).

3.3 Ischia

Ischia is one of the most evident cases of intra-calderic resurgence with uplift of about 900 m. The resurgent area has a polygonal shape resulting from the reactivation of regional faults and the activation of faults directly related to volcano-tectonism (Acocella and Funiciello 1999). Ischia experienced a destructive earthquake (magnitude Mw = 3.9) on 21 August 2017 located in the northern part of the island (DeNovellis et al., 2018; Berrino et al. 2021 and references therein). The earthquake was accompanied by co-seismic displacements detected by InSAR satellites. DeNovellis et al. (2018) inverted the SAR data and identified a fault plane respective to the earthquake. The earthquake was accompanied also by spatiotemporal gravity changes. These, however, were not observed as co-seismic. Though the observed time-lapse gravity changes cover the quake event, they relate to a period 29/05/2016 to 22/09/2017. Berrino et al. (2021) interpreted the gravity changes using the Growth inversion approach.

3.3.1 Hypothetical Fault Plane Opening (Shallow, Thin, Sub-Vertical, Plate-Like, Void Prism)

We simulate here a hypothetical fault plane opening, amounting to half a meter, of the fault plane respective to the Ischia 2017 earthquake, as interpreted by DeNovellis et al. (2018). The fault plane opening is represented by a void right-rectangular prism with the parameters listed in Table 5. It is 2 km long (E–W elongated), 1 km wide (vertical dimension with a southward dip of 70 arc-deg.), 50 cm thick, empty (density contrast relative to the surrounding rock environment, negative 2200 kg/m3), with its center at the depth of 570 m b.s.l., roughly 800 m below the earth surface with a simulated mass change of − 2.2 × 109 kg. Although such fault opening did not take place, we are interested in what gravity signal would it hypothetically produce and what is the capability of the Growth inversion method to detect and reproduce such a source body, i.e., a shallow extremely thin sub-vertical plate-like void prism, based on gravity observed at the gravimetric monitoring network of Ischia.

Table 5 The UTM coordinates of the center (Xc, Yc, Zc) of the prism, its width (vertical dimension), length (longer horizontal dimension), thickness (shorter horizontal dimension), orientation, volume, density contrast and mass
Full size table

We compute synthetic noise-free gravity both at a regular grid with spacing 300 m on the topographic surface (Fig. 8, left) and at the benchmarks of the Ischia gravimetric monitoring network (Berrino et al. 2021), see Fig. 8 (right). Both datasets are displayed in the form of fields using the same kriging interpolation. We also compute a dataset at benchmarks with added noise at the level of 35% of the signal.

Fig. 8
figure 8

Synthetic noise-free gravity (μGal) due to the void prism mimicking the 50 cm opening of the 2017 fault plane: on the 300 m grid on the topographic surface (left) and on the benchmarks (right). Solid line shows the projection of the top of the prism, dashed line its (southward dipping) bottom

Full size image

We have run the Growth inversions on the noise-free grid and benchmark data, as well as on the noisy benchmark data, for various combinations of the λ and Δρ values (see the Supplement, section J.1). The trial-and-error approach revealed that different combinations of the two key inversion parameters better reproduce different parameters of the original prism. For the noise-free grid data (Fig. 9, left column) the Growth inversion correctly reproduces the strike and the dip of the shallow thin sub-vertical prism. The shape and size of the sub-vertical plane of the prism are correctly reproduced with small density contrasts around − 5 kg/m3 and λ values around 10. Naturally, for such small density contrasts the volume of the prism is blown-up, magnified by a factor of about 440 (recall that the prism is only half a meter thick while the cell size of the subsurface partition is 80 m). The thickness of the reproduced source is magnified likewise. However, the mass change due to the simulated fault opening is reproduced accurately. Also the depth of the prism is reproduced correctly (only by 8 m shallower), and the vertical span is reproduced adequately also.

Fig. 9
figure 9

Best recovery Growth models for the noise-free grid data (left), the noise-free benchmark data (middle) and the noisy (35% / 7 μGal) benchmark data (right): (top row) top view (α = 0, δ = 90), (middle row) lateral view from roughly west, right at the edge of the prism ((α = -86, δ = 0), (bottom row) 3D view from roughly south, perpendicular at the prism plane (α = 4, δ = 30)

Full size image

For the noise-free benchmark data (Fig. 9, middle column) the same holds true as for the noise-free grid data, this time for density contrasts around − 3 kg/m3 and λ values around 6, only the image of the original prism being slightly more distorted and thicker. The mass change is this time reproduced correctly in solutions with λ = 8 and Δρ from − 4 to − 11 kg/m3. The depth of the prism is this time reproduced slightly shallower by 100 to 150 m, yet the depth reach is reproduced quite all right.

The inversion of the noisy benchmark data (Fig. 9, right column) requires higher λ values, which causes the image of the original prism to be even more distorted, rounder, thicker and shallower, with a shorter depth reach. The mass of the original prism is significantly underestimated, reproduced only at about a half of that of the original prism. Again, the solutions that better indicate the shape (except for the thickness) of the prism are those for lower density contrasts, such as Δρ =  − 2 kg/m3, this time requiring λ = 33 to filter out the impact of the data noise on the model. Despite the more pronounced distortions in the Growth image of the original prism, compared to the noise-free benchmark data, the correlation of the location, dip, size and shape of the sub-vertical plane with the fault plane solution obtained from DInSAR data gives enough hints that the simulated gravity changes are associated with the simulated fault plane. Comparing the solutions obtained for benchmark data with those obtained for the grid data, it is clear that the design of the monitoring network, i.e. the number and spatial distribution of the benchmarks is not optimal, yet sufficient to detect a presumed fault plane (respective to the 2017 earthquake) opening on Ischia.

4 Discussion

The inversions carried out on noise-free grid data on the topographic surface served for investigating the best achievable reproducibility, using the Growth inversion approach, of the simulated thin elongated sources that from a viewpoint of free-geometry inversion methods can be considered extremely difficult to recover due to their thin dimensions and also orientation. Our synthetic simulations revealed that with the assumed dense noise-free grid data the Growth inversion can quite successfully detect and reproduce horizontal thin beam-like shallow prism, shallow thin vertical prism or cylinder, and vertical or sub-vertical thin shallow plate-like prism.

By “quite successfully” we mean reproducing, to a certain degree of accuracy, most of the source parameters, such as horizontal position, depth, orientation in terms of strike and dip, relative shape (except for thickness), and mass. What cannot be reproduced correctly is the thickness of the thin dimensions, especially in the vertical direction, and hence the volume of the source. The thickness of these sources and their volumes are over-estimated by multiples of ten or even hundred, depending on the selected target density contrast adopted in the inversion.

On the other hand, the low density contrasts that cause the severe exaggeration of the volume and thickness of the thin dimensions, are needed for best reproducibility of the length of beam-like prisms or of the size and shape of the plane of the plate-like prisms. Again, the term “to a certain degree of accuracy” cannot be quantified, as it is very case- and source-specific. It depends on the dimensions and depth of the given source, its orientation, as well as its density contrast. Our study presented here gives some guidance and clues, but cannot be considered exhaustive or complete. It should motivate the practitioners to run their own simulations for sources of their interest.

The worst candidate for successful recovery is, as one would intuitively expect, the horizontal or sub-horizontal plate-like thin prism. Its reproduced shape is vertically stretched, attaining appearance more of a diapir or nearly a dyke. Also the moderately deep, moderately flat horizontal rotational ellipsoid masks its shape and pretends in the Growth inversion a thinner vertically elongated appearance and slightly shallower vertical position. On the other hand, the good reproducibility of the simulated thin shallow vertical conduit within the Teide strato-cone amazed us.

The inversions with noise-free benchmark data have demonstrated that the sparsity of benchmarks of gravimetric monitoring networks can more- or less-severely corrupt the Growth image of the source to be reproduced. The most affected aspects are the depth and the vertical shape (meaning laterally projected shape) of the source. Whether “more- “ or “less- “ depends on the number of the benchmarks and on their spatial distribution relative to the position of the source to be detected and reproduced. Again, the distortion cannot be quantified, as it is case- and source-specific.

The inversions with noisy benchmark data, arbitrarily opting for noise at the level of 35%, have demonstrated that the effect of data noise, combined with the sparsity of benchmarks, leads to even higher distortion in the Growth image of the sources to be reproduced. Again, the degree of distortion, due to the combined effect of noise and benchmark sparsity, cannot be quantified, as it is very case- and source-specific. These simulations give a taste of how much distortion can be expected in Growth images of real sources hunted for in the practice. This hopefully will motivate the practitioners to run their own simulations that are tailored to their specific investigative needs.

For the noise-free data, especially for grid data, the presented best-recovery Growth models are tight-fit (low λ values) solutions with misfit r.m.s., and often also with maximum misfit, approaching 0 μGal. The models for noise-free grid data, though representing unrealistic solutions, serve to show the limit of the best achievable source reproducibility using the Growth approach. The models for noise-free benchmark data represent also unrealistic solutions, and serve to show how much the source reproducibility deteriorates due to the sparsity of the benchmarks in the given network, disregarding the effect of noise present in real micro-gravity data. The deterioration due to benchmark sparsity is area-, network- and source-specific. It depends on the roughness of the relief in the study area, and on the design of the network, namely the number of benchmarks and their spatial distribution relative to the position and character of the given source. Consequently, simulations as those presented here can serve for testing the optimal design of gravimetric networks in a given monitored area using all sorts of simulated sources that can be assumed as potentially occurring in the given area.

In the light of experience discussed above, we recommend to run the Growth inversion first with very low density contrast (Δρ) values and various balance factor values (λ) and to find by a trial-and-error process a λ value that produces a solution at the verge between noisy and compact, i.e., tight-fit to slightly overfitting solutions. Too compact solutions bias the shape of the source towards too round, and bias the depth of the source towards greater depths (positive contrast bodies) or shallower depths (negative contrast bodies). We recommend running Growth inversions next with relatively higher λ values producing more compact bodies, yet not too round, to successfully reproduce the depth and mass of the source. These recommendations cannot be quantified, because they depend on the size and shape, orientation, depth and density contrast of the source body, the topographic relief, the number, spatial coverage and distribution of gravity benchmarks, as well as the relative level of noise in the input gravity data.

5 Conclusions

The Growth images, particularly in the case of sparse noisy benchmark data typically encountered in volcano-gravimetric practice, of thin elongated sources of high density contrasts, are to be expected as moderately to severely distorted. The actual sources of such shapes and contrasts, generating the observed surface gravity data, thus would not be readily recognizable in their Growth images. Despite this drawback, a trained user with experience may hint even on the thin elongated sources from their distorted images, if the user understands the nature of the distortions. Such experience can be gained only by running many synthetic simulations in the given study area for various suspected sources.

Our recommendation is to run, in addition to the inversion of the observed gravity data, also inversions for synthetic data due to simulated simple sources that potentially can occur in the given study area for the given geodynamic event, and to compare and correlate the Growth model obtained for the observed data with the Growth images of the simulated synthetic sources. And we recommend this be done for Growth solutions adopting very low density contrasts, and also as high as possible density contrasts, in each case with balance factor values that produce models at the verge between noisy scattered and compact. Such balance factor values are to be sought by a sensible trial-and-error process, repeatedly running multiple inversions.

As illustrated by the great diversity of the Growth solutions for combinations of various values of the inversion parameters, particularly the two key parameters (λ and Δρ, the interpretation of Growth models is a highly ambiguous endeavor, especially when working with sparse and noisy benchmark data, which is an inherent case in volcano gravimetry. The interpretation becomes meaningful only when assisted or backed up by external evidence, such as that from other geophysical methods, structural geological or tectonic controls, or volcanological cognition.