FormalPara Article Highlights

  • Numerical models provide insights into the seismic cycle, temporal and spatial earthquake clustering, and occurrences of large events

  • The geometry of faults and the direction of tectonic forces influence seismic productivity, magnitude of earthquakes, and their location

  • The recurrence time of large earthquakes should be carefully used in seismic hazard assessments accounting for its variation

1 Introduction

Earthquakes and induced tsunami, flooding, or landslides result in disasters, when the natural events “meet” physical and social vulnerability and exposed values. The disasters, in their turn, may lead to negative impacts on most of the United Nations Sustainable Development Goals (SDGs 1–4, 6–8, 10, 11, 16, and 17) by exacerbating poverty, threatening food security, increasing mortality and psychological well-being, affecting education by school building damages, contaminating shallow water resources due to tsunamis, disrupting energy supplies, significantly influencing an economic growth and provoking an economic recession, affecting vulnerable groups of people and human settlements, threatening global peace, security and partnership. The recorded economic losses (r.e.l.) due to earthquakes only for 1998–2017 are estimated to be USD 661 billion (CRED-UNISDR 2018). Earthquakes affected more than 125 million people and killed more people than any other type of natural hazards for the same time duration, with the cumulative death toll (d.t.) of more than 747,000 fatalities exacerbated by the vulnerability of poor and badly prepared populations exposed to the 2004 Indian Ocean earthquake and tsunami and to the 2010 Haiti earthquake (CRED-UNISDR 2018).

For the last two decades, earthquake-related disasters impacted tremendously the society at local to global levels. A few examples of the impacts follow: the 2004 Sumatra–Andaman magnitude M = 9.1 earthquake and tsunamis (227,898 d.t.; the d.t. numbers hereinafter are taken from USGS (2013)); the 2005 Kashmir M = 7.6 earthquake (86,000 d.t.); the 2008 Wenchuan M = 7.9 earthquake and induced landslides (87,587 d.t., and USD 96 billion r.e.l.; the numbers of r.e.l. are taken from CRED-UNISDR 2018); the 2010 Haiti M = 7.0 earthquake (~ 316,000 d.t.) that damaged significantly the national infrastructure including the public sanitation system and hence created conditions for the cholera outbreak in nine months after the earthquake (Orata et al. 2014); the 2010 Chili M = 8.8 earthquake and tsunamis, followed by food scarcity; the 2011 Great East Japan M = 9.0 earthquake (the Tohoku earthquake) and concatenated tsunamis, flooding, and a nuclear power plant incident (USD 228 billion r.e.l.); and the 2015 Nepal M = 7.8 earthquake and avalanches.

Disasters influence profoundly all countries, economically well or less developed, and almost all sectors of economy (Ismail-Zadeh 2018). The vulnerability to earthquakes is growing essentially because of globalisation, concentration of people in and around earthquake-prone regions, physical and social vulnerability, and the increase in values exposed to earthquake hazards. “Today an earthquake may affect several hundred thousand lives and cause significant damage up to hundred billion dollars. A large earthquake may trigger an ecological catastrophe, if it occurs in close vicinity to a nuclear power plant” (Ismail-Zadeh 2014, 2018). Scientific knowledge on natural (e.g., seismic) hazards and vulnerabilities, as well as risk assessments, contributes to disaster risk reduction and develops a foundation for sustainable development (Cutter et al. 2015; Kontar et al. 2021). Meanwhile, this knowledge and evidence-based options for actions in reducing disaster risks should be delivered to decisionmakers and to the society in a way to be usable, useful, and used (Boaz and Hayden 2002; Ismail-Zadeh et al. 2017; Berkman 2020; Ismail-Zadeh 2021a).

Although vulnerability and exposure are main drivers of earthquake-related disasters, earthquakes are triggers of the disasters, and hence understanding of occurrences and spatial–temporal distributions of extreme seismic events could enhance hazard assessment and contribute to preparedness for a significant reduction in earthquake impacts (Ismail-Zadeh 2021b). In this paper, we review advances in modelling of lithosphere dynamics and earthquake occurrences focusing on a block-and-fault dynamics model (BAFD model) developed by Gabrielov et al. (1990). In doing so, we improve our understanding on localisation of large earthquakes in a system of major regional faults and on the recurrence time of these earthquakes, keeping in mind that the information is vitally important for disaster risk management. Even though we do not know the exact time, place and magnitude of a future regional earthquake, the information on the area, where large earthquakes might occur (not necessarily where they did occur in the recorded history), together with improved seismic hazard assessments in the area can help in undertaking relevant preventive measures to reduce risks in earthquake-prone regions (Ismail-Zadeh and Takeuchi 2007).

In the next section, we review models of lithosphere dynamics, stress generation, fault slips, and earthquake occurrences. The basic principles and features of the BAFD model are discussed in Sect. 3. Then, we review in Sect. 4 the BAFD models developed for several earthquake-prone regions, namely Carpathians, Caucasus, Tibet-Himalaya, and Sunda arc. In Sect. 5, we consider a spherical BAFD model applied to analysis of the global tectonic plate dynamics. In Sect. 6, we discuss implications of earthquake modelling for seismic hazard assessment, forecasting, and recurrence of large earthquakes, as well as model limitations and outlook, before presenting concluding remarks in Sect. 7.

2 Models of the Lithosphere Dynamics, Stress Building and Earthquakes

The lithosphere presents a hierarchy of blocks, where the largest blocks are the major lithospheric plates (Keilis-Borok 2003). Coupled to the hotter and rheologically weaker asthenosphere, colder and stronger lithospheric plates are involved in relative movement leading to tectonic stress localisation mainly along fault zones and to stress release in earthquakes. The plates split into smaller blocks (e.g., mountain belts, plateaus, shields) by thin fault planes whose width by several orders of magnitude smaller than the characteristic size of the blocks they separate (Keilis-Borok 2003). The fault planes are relatively flat surfaces along which adjacent blocks move under control of friction and plate motion (Rice 1993; Rice et al. 2001). They slip along the surfaces, where displacements are discontinuous (as earthquakes), and the slips are essentially realised through formation of failures on the surfaces and their subsequent healing (e.g., Rice and Ben-Zion 1996; Keilis-Borok et al. 2001; Ben-Zion 2008; Ismail-Zadeh 2012a). The movements “turn the lithosphere into a nonlinear hierarchical dissipative system, where strong earthquakes are the critical phenomena” (Keilis-Borok 2003). The lithosphere dynamics evolves over time and space from a steady state to a catastrophe (e.g., Keilis-Borok 1990; Sornette and Sammis 1995; Turcotte 1999; Ismail-Zadeh et al. 2012a).

The lithospheric blocks are locked normally during decades and centuries by friction along the faults separating them, and over these periods, elastic strain builds up with a tectonic stress growth. When stresses reach a certain strength level, which the blocks cannot withstand, and the amount of strain exceeds the frictional forces preventing slip, blocks on both sides of the fault slide rapidly as the elastic strains are relieved, generating a fault rupture (an earthquake). Although there are (slow) earthquakes releasing energy over hours to months, in this work, we consider the earthquakes caused by a sudden slip along a fault. The fault slip and resulting earthquake are related to a stress drop and followed by stress redistribution and viscoelastic healing. After that, elastic strains start to build up again and the process (called a seismic cycle) repeats on a given part of a fault. Therefore, the seismic cycle consists of three slip phases: inter-seismic (steady accumulation of elastic strain coinciding with frictional locking of a fault), co-seismic slip (a sudden rupture or earthquake), and post-seismic slip (characterised by aseismic ‘afterslip’ occurring around the rupture zone and viscoelastic relaxation of the earthquake-induced stress) followed by relocking the fault (e.g., Thatcher and Rundle 1984; Cohen 1999).

A progress has been made for the last decades in understanding of the lithosphere dynamics and in computational geodynamics and seismology, particularly, in modelling of geodynamical processes including stress localisation (e.g., Ismail-Zadeh et al. 2005, 2010) and stress redistribution (e.g., Stein 1999; Pollitz and Sacks 2002); coupling geodynamic and seismic processes (e.g., Ismail-Zadeh et al. 1999; van Dinther et al. 2013; Sobolev and Muldashev 2017); earthquake dynamics (e.g., Soloviev and Ismail-Zadeh 2003; Ismail-Zadeh et al. 2012a, 2018); deformations around faults, rupture processes and seismic wave propagations along complex faults and fault networks (e.g., Barbot et al. 2009; Jiang and Lapusta 2016; Kyriakopoulos et al. 2019); and comprehensive seismic hazard analysis (e.g., Graves et al. 2011; Sokolov and Ismail-Zadeh 2015, 2016). Quantitative models of stress evolution and earthquake dynamics can be split into three types according to Ismail-Zadeh et al. (2012a) and Ismail-Zadeh et al. (2018): (I) models of stress generation, localisation, and transfer; (II) models of dynamic systems reproducing basic features of seismicity, and (III) models of fault dynamics and seismicity.

Type-I models help to identify the areas of high stress localisations in an earthquake-prone region, and/or static, viscoelastic, and dynamic Coulomb failure stress changes after an earthquake to forecast the potential sites of subsequent earthquakes (Ismail-Zadeh et al. 2012a). For example, stress generation and its localisation in the lithosphere were studied in several earthquake-prone regions such as Carpathians and Apennines (e.g., Ismail-Zadeh et al. 2005, 2010; Aoudia et al. 2007) and in the Marmara Sea region (e.g., Hergert and Heidbach 2010). King et al. (1994) analysed how Coulomb failure stress changes are associated with an earthquake and whether the changes may trigger aftershocks. Particularly, it was shown that the main aftershock activity match well the area of positive values of the Coulomb failure stress change (Stein 1999). The seismicity-inferred Coulomb failure stress change models constrained by geodetic and structural seismology models provide better understanding of earthquake triggering scenarios (e.g., Becker et al. 2018). Although type-I models provide an insight into stress localisation and its changes before future earthquakes, these models do not allow yet to study nonlinear dynamics of earthquake occurrences in much detail as type-II models do.

The type-II generic models of seismicity analyse occurrences, clustering, and frequencies of synthetic earthquakes. Earthquake simulations rely heavily on the elastic rebound theory (Reid 1910), according to which elastic stresses accumulate due to tectonic plate movements, and the stresses are released when they exceed the tensile strength. The elastic rebound model produces a periodic sequence of equal magnitude earthquakes linking the Reid’s theory with the concept of the seismic cycle, although real sequences of earthquakes are more complicated (e.g., Thatcher 1990; Soloviev and Maksimov 2001). Particularly, a large earthquake is followed by a period of seismic activation and sometimes by another strong earthquake as it was shown by a deterministic nonlinear model for seismicity (e.g., Newman and Knopoff 1982).

Based on laboratory experiments, Dieterich (1972, 1978) introduced a model with a time-dependent friction law, and the model was further developed by Ruina (1983), Cao and Aki (1986), and others. This model gives an adequate description of pre-seismic, co-seismic and post-seismic slip on a fault (Tse and Rice 1986). Soloviev and Maksimov (2001) mentioned that a challenging point of the model is its applicability to real fault zones, because it is unclear how to scale the empirical parameters of the friction law for real faults, and the fault dynamics in the model is sensitive to small variations in the parameter values. A spatial inhomogeneity (e.g., asperities and barriers) of the strength distribution in the fault plane was considered to be important in modelling of earthquake sequences. For example, asperities and barriers are strong patches that do not permit further propagation of a fracture and break during a strong earthquake (Das and Aki 1977; Kanamori and Steward 1978).

Some type-II models suggest the possibility of chaotic earthquake sequences with a power law distribution of their magnitudes. Burridge and Knopoff (1967) proposed a simple model for earthquake simulations, which was composed of blocks connected to each other via springs. Each model block interacts with other blocks, and the force driving the block dynamics depends on the distances of the blocks from their equilibrium position and on a friction force. Several models based on the spring-block interaction (e.g., Narkounskaia et al. 1992), cellular automata (e.g., Nakanishi 1991; Rundle and Klein 1993), scaling organisation of fracture tectonics (Allègre et al. 1995; Shebalin et al. 2002), colliding cascades (e.g., Zaliapin et al. 2003), epidemic-type aftershock sequence (ETAS) (Ogata 1988), and branching aftershock sequence (Turcotte et al. 2007) were developed later to reproduce general properties of observed seismicity (Ismail-Zadeh et al. 2018).

A cellular automaton-type (‘sandpile’) model introduced by Bak and Tang (1989) was composed of a lattice of threshold elements with random loading and a simple deterministic rule of stress release and nearest-neighbour redistribution, where a sequence of consecutive breaks in the stress redistribution generates an avalanche (earthquake). The sandpile model reveals an important property of self-organised criticality, that is, it evolves to a critical state from any initial state, and this state is characterised by a power law distribution of the earthquake magnitudes (Gabrielov and Newman 1994; Soloviev and Maksimov 2001).

Although the models of type-II are rather abstract and sometimes oversimplified, they allow for understanding important features of seismicity. Meanwhile, only models of type-III dealing with fault dynamics allow for simulating realistic earthquakes (Ismail-Zadeh et al., 2018). For example, several models were developed in the case of a large heterogeneous fault (e.g., Ben-Zion and Rice 1993; Lyakhovsky et al. 2001; Zöller et al. 2005; Lapusta and Liu 2009; Nodal and Lapusta 2010) and in the case of a system of faults (e.g., Gabrielov et al. 1990, 2007; Ward 1992, 1996, 2000; Robinson and Benites 1996, 2001; Panza et al. 1997; Fitzenz and Miller 2001; Soloviev and Ismail-Zadeh 2003; Rundle et al. 2006; Zhou et al. 2006; Ismail-Zadeh et al. 2007, 2012a; Peresan et al. 2007; Zöller and Hainzl 2007; Pollitz 2009; Bielak et al. 2010; Vorobieva et al. 2014, 2019, 2021). The results of the modelling improved significantly our understanding of earthquake occurrences and seismic hazards.

Over the past few decades, space geodesy has revolutionised our understanding of the dynamics of lithospheric deformation associated with earthquakes. Numerical models of fault kinematics based on geodetic data have provided a better insight into the mechanics of the earthquake cycle (e.g., Kaneko et al. 2010; Barbot et al. 2012; Jiang and Lapusta 2016). These models described processes along a fault interface, although they neglected inelastic properties of the surrounding domain. Mechanical coupling between the brittle and ductile regions was shown to be important during post- or inter-seismic deformation (e.g., Johnson and Segall 2004; Lambert and Barbot 2016). Particularly, a model that couples fault slip and viscoelastic deformation to simulate fault dynamics in the lithosphere-asthenosphere system was developed to determine dynamic rupture propagation, as well as afterslip, slow-slip events, and the modulation of a strain rate incurred in the ductile regions (Lambert and Barbot 2016).

Lithospheric deformation is controlled by the short-term (second to years) and long-term (centuries to millions of years) viscoelastic behaviour of the mantle (Wang et al 2012). To understand the interplay between mantle dynamics and associated tectonic stresses on the one hand and fault slips and earthquakes on the other, several numerical approaches have been developed to accommodate two different time scales: million years down to seconds. Ismail-Zadeh et al. (1999) used two linked models—a finite-element model of viscous mantle flow induced by a sinking lithospheric slab (Ismail-Zadeh et al. 2000) and a viscoelastic model of the lithospheric slab-and-fault dynamics—to analyse how an earthquake pattern of the intermediate-depth seismicity in the Vrancea region is influenced by the lithosphere-mantle dynamics. Bridging the long-term geodynamic processes and short-term seismic processes in one model is a challenging numerical problem associated with a fine time discretisation, which is computationally expensive. For example, van Dinther et al. (2013) used a geodynamic model of subduction and incorporated the rate-weakening friction law at the subduction plate interface allowing simulations of seismic cycles. However, the rupture processes in the model took a significant time compared to natural occurrences of earthquake (seconds to minutes). Sobolev and Muldashev (2017) developed a sophisticated approach (similar to that developed by Ismail-Zadeh et al. 1999) by combining long-term and short-term models. They took the geometry of the long-term geodynamic model of the lithosphere subduction as an initial setup for the modelling of the seismic cycles and modified the rheology of the crust and mantle in the short-term model to consider transient creep processes and earthquake sequences.

Soloviev and Ismail-Zadeh (2003) highlighted difficulties related to a detection of the impact of a single factor on the dynamics of seismicity using seismic observations, because seismicity is impacted by an assemblage of factors some of which may be more significant than that under consideration. It is also difficult (if not impossible) to single out the impact of an isolated factor by using seismic observations. These difficulties may be partly resolved by an employment of catalogues of the synthetic seismicity generated by realistic earthquake simulations (e.g., Gabrielov and Newman 1994; Soloviev and Ismail-Zadeh 2003).

3 Lithosphere Block-and-Fault Dynamics Model

A prominent feature of the lithosphere as a nonlinear hierarchical complex system is the persistent recurrence of abrupt overall changes or critical transitions, i.e. earthquakes whose magnitudes depend on the lithosphere volume. The lithosphere dynamics is controlled by a variety of physical and chemical mechanisms (e.g., stress corrosion, nonlinear filtration, rock dissolution, petrochemical transitions, mechanical processes, impact of pressure and temperature) influencing the lithospheric strength, strain-and-stress in fault systems, and earthquake occurrences (Keilis-Borok 2003). Statistical and phenomenological studies of seismicity based on historical and observed earthquakes have a disadvantage because of the extremely short history of instrumental observations. These observations cover a period of about hundred years compared to the time of the tectonic processes resulting in stress localisation and earthquake occurrences (Soloviev and Ismail-Zadeh 2003). Earthquake catalogues generated by numerical modelling cover much longer duration of time allowing for analysis of seismicity features, putting forward hypotheses, and finding their statistical significance (e.g., Ismail-Zadeh et al. 2018).

Seismicity and seismic properties differ from one to another earthquake-prone region, and these differences, among other factors, can be attributed to tectonic structures (such as faults) and main driving forces determining the regional dynamics. An active tectonic region developed through the geological history can be presented by a number of interacting lithospheric blocks separated by faults. Although tectonic energy is stored in the entire volume of the lithosphere, energy release in earthquakes takes place to a significant extent along relatively thin fault zones. A block-and-fault dynamics (BAFD) model features a hierarchical structure of the lithosphere as a set of blocks separated by faults forming a network, where tectonic forces present the loading mechanism, and stress drops (failures) imitate earthquakes. The BAFD model analyses how the observed dynamics of earthquakes (namely, the seismic cycle, intermittency in the seismic regime, the earthquake frequency-magnitude distribution, long-range interaction between synthetic earthquakes, and clustering of earthquakes in space and time), as well as fault slip rates, depend on the lithosphere structure and driving tectonic forces. The basic principles of the model were proposed by Gabrielov et al. (1990). As the BAFD model’s mathematical description, its numerical discretisation, and the solution method have been reviewed by Ismail-Zadeh et al. (2018), we refer a reader to the paper for details and present here an essential description of the model.

The BAFD model presents a seismic region as a structure of perfectly rigid (upper crustal or lithospheric) blocks separated by relatively thin, weak, and less rigid fault planes. The assumption, that the lithosphere is modelled by perfectly rigid blocks, is based on the fact that the effective elastic moduli in the fault zones are much lower than those inside the blocks. The block-and-fault structure considered in the model is a bounded and simply connected part of a layer limited by two horizontal planes (Fig. 1). Model faults are defined as the intersection lines of model fault planes with the upper horizontal plane approximating the surface topography. Dip angles of the fault planes are specified in the model based on the knowledge of the deep structure of the region under study.

Fig. 1
figure 1

A block-and-fault structure in BAFD models

Full size image

The blocks interact with each other and with the underlying medium, which can be either the lower ductile crust, if blocks represent the upper crust, or the asthenosphere in the case of the lithospheric blocks. The motions of the blocks are assumed to be horizontal and are a consequence of the given motions of the boundary of the block structure and the underlying medium. As the blocks are perfectly rigid, all deformations are assumed to take place in the fault planes and at the block bottoms of the model. Relative displacements of the blocks occur only along the fault planes. The model displacements lead to stress localisation in the fault planes similar to that caused by plate boundary deformations. The displacements are assumed to be infinitely small compared to the geometric dimensions of blocks, and hence, the geometry of the block structure does not change during numerical simulations. The block displacements are determined so that the model structure is in quasi-static equilibrium state at each model time step.

The model blocks interact visco-elastically along the fault planes. The effective viscosity of the fault zone is considered to be either constant featuring linear fault slip (Soloviev and Ismail-Zadeh 2003) or strain rate-dependent featuring nonlinear fault slip (Vorobieva et al. 2019). Vorobieva et al. (2019) showed that the rate of inelastic displacements in BAFD models is small and almost constant within inter-seismic phases, and hence, there is no significant difference between the strain rate-dependent fault slip and the linear slip in the model during these phases of the seismic cycle. After an earthquake, however, the rate of inelastic displacements increases resulting in lowering the effective viscosity, and this rate decreases gradually during further numerical simulations to its values that were before the earthquake (Vorobieva et al. 2019).

Earthquakes in the BAFD model are simulated using the Coulomb stress failure criterion and the dry friction law (King et al. 1994). When stresses reach the critical strength level in some part of a fault plane, a stress drop occurs according to the dry friction law, and it follows by a stress discharge on the fault plane, which can cause stress drops in other parts of the fault plane. The stress drops at the model fault plane produce synthetic earthquakes. The earthquake magnitudes are estimated using the empirical relationship between the magnitude and its rupture area (Wells and Coppersmith 1994). Immediately after the earthquake, the areas of the fault plane affected by the stress drop exhibit creeping, which is characterised by a rapid growth of inelastic displacements until the stress falls below a certain stress level. Thus, the BAFD model generates synthetic earthquakes. Different features of the BAFD model seismicity have been analysed in detail by Keilis-Borok et al. (1997), Maksimov and Soloviev (1999), Keilis-Borok et al. (2001), Soloviev and Ismail-Zadeh (2003), Vorobieva and Soloviev (2005), Soloviev (2008), and Ismail-Zadeh et al. (2018).

Keilis-Borok et al. (1997) studied the dependence of synthetic earthquake occurrences in the model on the structure fragmentation and the boundary movement and showed that the number of small magnitude events increases with the fragmentation of a block structure, whereas the number of large events may decrease and increase depending on the boundary movement. Statistical methods were used to analyse clustering (Maksimov and Soloviev 1999; Soloviev and Ismail-Zadeh 2003) and long-range interaction between synthetic events (Soloviev and Ismail-Zadeh 2003; Vorobieva and Soloviev 2005) in the model. Particularly, it was shown that earthquake clustering depends on the geometry of a block-and-fault structure and on the rheological parameters of fault zones, and there is the long-range interaction of synthetic earthquakes depending on the relative positions of fault segments and on movements specified in the model. The b-value, characterising earthquake size distribution in the frequency-magnitude (Gutenberg-Richter) plots, becomes smaller before large synthetic events (Soloviev 2008).

4 BAFD Model Applications

The BAFD model was applied to study seismicity and statistics of earthquakes in several earthquake-prone areas, such as the south-eastern Carpathians (Panza et al. 1997; Soloviev et al. 1999; Ismail-Zadeh et al. 1999), the central Alpine-Himalayan belt (Sobolev et al. 1999), the western Alps (Vorobieva et al. 2000; Soloviev and Ismail-Zadeh 2003), Sunda island arc (Soloviev and Ismail-Zadeh 2003), Tibet-Himalaya (Ismail-Zadeh et al. 2007; Vorobieva et al. 2017, 2021), Italy and its surroundings (Peresan et al. 2007), Kachchh rift zone (Vorobieva et al. 2014), and Caucasus (Soloviev and Gorshkov 2017; Vorobieva et al. 2019). Here, we overview the application of the BAFD model to the orogenic regions, such as Carpathians, Caucasus, and Tibet-Himalaya, as well as to the Sunda arc, associated with the Indo-Australian plate subduction, which have been subjects to earlier surveys (Soloviev and Ismail-Zadeh 2003; Ismail-Zadeh et al. 2012a, b; Ismail-Zadeh et al. 2018). Except for recent applications of the BAFD model, which we add to this overview, the novelty of this study is related to an analysis of how large earthquakes are localised in the fault networks and what the recurrence times of the large events are.

4.1 Carpathians

Large intermediate-depth earthquakes occur in the Vrancea region at the bend of the south-eastern Carpathians causing destruction in Romania and shaking central and eastern European cities several hundred kilometres away from the event hypocentres. The earthquake hypocentres are localised in the mantle within a volume of about 110(deep) × 70 × 30 km3. These earthquakes are likely to be associated with tectonic stress releases within the relic part of the oceanic lithosphere descending beneath Vrancea (e.g., Petrescu et al., 2021). Geology, geodynamics, and seismicity of the Vrancea region were reviewed by Ismail-Zadeh et al. (2012b).

The BAFD model was used to analyse the lithosphere dynamics and intermediate-depth large earthquakes in the Vrancea region (Panza et al. 1997; Soloviev et al. 1999, 2000; Ismail-Zadeh et al. 1999). Figure 2 (model 1; panels a–c) illustrates the location of Vrancea, the BAFD structure used by Panza et al. (1997) to model seismicity in the region, the driving forces, the observed and synthetic seismicity. Panza et al. (1997) tuned the parameters of the BAFD model to match epicentres of synthetic seismicity to the epicentres in the Vrancea seismicity, as well as to get the slope of the frequency-magnitude curve of synthetic earthquakes closer to the slope of the Gutenberg-Richter curve for the Vrancea seismicity. The catalogue of synthetic seismicity obtained by Panza et al. (1997) contained events computed for the period of 7,000 years. The maximum magnitude of synthetic earthquakes was 7.6, close to the magnitude of the 1940 Vrancea Mw = 7.7 earthquake. Model 1, consisting of a few lithospheric blocks, reproduced the main features of the observed seismicity in space and showed some irregularities in the temporal distribution of strong synthetic events (Fig. 2c). The strong events were grouped in temporal (about 100–200 years long) clusters, and these groups appeared with an average return period of about 300–350 years within the time intervals from about 500 to 3000 years and 4000 to 7000 years. However, within the interval from 3,000 to 4,000 years, a large earthquake occurs once for about 100 years, rather periodically.

Fig. 2
figure 2

BAFD models for the Vrancea region. Model 1: panels a–c (by Panza et al. 1997). a Maps of observed seismicity in Vrancea for 1900–1995 and (b) modelled strong seismicity (5.0 < M < 7.6) for 7,000 years. Grey areas are the projections of fault planes on the upper plane, and red arrows indicate the movements of blocks in the model. Cyan lines (in panel b) are the model fault segments separating three blocks: the Intra-Alpine, Moesian, and Black Sea sub-plates. c Temporal distribution of large synthetic earthquake events. Model 2: panels d–f (by Ismail-Zadeh et al. 1999). d The block-and-fault structure of the lithosphere containing a descending slab (the right block), where the hypocentres of observed seismicity in Vrancea are projected onto the vertical plane along the NW–SE direction (violet line AB in panel a). Green arrows stand for the average rate of movement of the block boundaries derived from the lithosphere-mantle dynamics model by Ismail-Zadeh et al. (2000). Panels (e) and (f) feature large synthetic earthquake events associated with the slab block for two numerical experiments: e no slab rollback, i.e. no counter clockwise rotation of the right block, and (f) with slab rollback. Modified after Soloviev and Ismail-Zadeh (2003) with permission from Springer Nature

Full size image

Soloviev et al. (1999) carried out a sensitivity analysis of synthetic earthquakes with respect to the parameters of the BAFD model by Panza et al. (1997) and showed how variations of the model parameters influence the spatial distribution of epicentres, the slope of the Gutenberg-Richter curve, the level of seismic activity, and the maximum magnitude of synthetic earthquakes. Focal mechanisms of earthquakes generated by the BAFD model for Vrancea were analysed by Soloviev et al. (2000). The mechanisms of the largest synthetic events were found to be thrust faulting like the mechanisms of the three strongest Vrancea earthquakes.

Ismail-Zadeh et al. (1999) used a mantle flow pattern as a driving mechanism for another BAFD model of the Vrancea region (model 2; see Fig. 2d–f). The rate and the direction of the lithosphere movement were prescribed on the basis of numerical model calculations of the mantle flow induced by a descending slab beneath the Vrancea region (Ismail-Zadeh et al. 2000). It was shown that small changes in the dip angle of the lithospheric slab control a pattern of seismicity. Namely, if the distribution of M > 6.8 events in Fig. 2e seems to be in a good agreement with the observed seismicity pattern (Fig. 2d) at the right side of the modelled slab, a small change in the direction of slab movement results in a significant change in the localisation of earthquakes reducing the magnitude of the events (Fig. 2f). Similarly, Press and Allen (1995) found from the seismic observation in the southern California that small changes in the direction of plate motion influence the pattern of seismic release.

4.2 Caucasus

The Caucasus region is a remarkable site of moderate to strong seismicity, where devastating earthquakes caused significant losses of lives and livelihood (Ismail-Zadeh et al. 2020). The earthquakes are associated with the ongoing continental collision between the Eurasian and Arabian plates. Lithospheric deformations in the Caucasian region occur mainly within the Greater and Lesser Caucasus mountains in a response to lateral transport and rotation of crustal blocks (e.g., Reilinger et al. 2006). The deformations and stress localisations result in destructive earthquakes, such as the 1902 Shamakha (Azerbaijan) M = 6.9 ± 0.2, the 1988 Spitak (Armenia) M = 6.9, and the 1991 M = 7.0 Racha (Georgia) earthquakes. Geology, geodynamics, and seismicity of the Caucasus were reviewed by Ismail-Zadeh et al. (2020).

The BAFD model was applied to study the dynamics of the crustal blocks and seismicity in the Caucasus (Soloviev and Gorshkov 2017; Vorobieva et al. 2019). Using the morphostructural zoning, Soloviev and Gorshkov (2017) developed a hierarchical network of lineaments for the Caucasus correlating with the major active faults mapped in the region (Trifonov et al. 1994; Karakhanyan et al. 2004; Ismail-Zadeh et al. 2020). The movement of the block structure was in agreement with regional geodynamic models and geodetic measurements (Philip et al. 1989; Reilinger et al. 2006). The BAFD model experiments were performed for the time interval of 8,000 years. Although the pattern of synthetic seismic events showed a general agreement with that of the regional seismicity, some events occurred at faults segments where no earthquakes have been previously recorded (Soloviev and Gorshkov 2017).

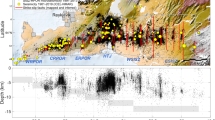
Another BAFD model (Fig. 3) was developed for the Transcaucasian region (Vorobieva et al. 2019), and the model’s catalogue covered synthetic seismic events for 10,000 years. The model results showed that synthetic strong earthquakes mimicked well the regional seismicity (Fig. 3a); the slope of the frequency-magnitude plot for synthetic events showed a good agreement with that for observed regional seismicity in the magnitude range from 5 to 7.5 (Fig. 3b); and the focal mechanisms of synthetic seismicity confirmed the regional stress state pattern (Vorobieva et al., 2019).

Fig. 3
figure 3

A BAFD model of the Transcaucasian region. a Map presenting the block model (brown lines). Instrumentally recorded earthquakes are marked by red dots (magnitude M4.5 +), by small red stars (M6 +), and big red stars (M7 +) (ANSS catalogue for the period of 1974–2017). Historical strong earthquakes as well as instrumentally recorded seismicity for the period from 1000 to 1973 are marked by small yellow stars (M6 +) and big yellow stars (M7 +) (Ulomov and Medvedeva 2014). Synthetic seismicity (M > 6) imposed on the map of observed seismicity: blue stars are the events of magnitude M7 + , blue circles M6.5 + events, and light blue dots M6 + events. (b; inserted in panel a) Frequency-magnitude relationship for earthquakes: the blue curve represents the data from the ANSS earthquake catalogue; the red dashed curve represents the data from Ulomov and Medvedeva (2014) since 1800, M ≥ 6.0; and the black bold curve corresponds to the synthetic events. Lower panels present synthetic earthquake magnitudes versus time for three faults segments, where (c) the 1991 Racha earthquake, (d) the 1902 Shamakha earthquakes, and (e) the 1988 Spitak earthquake occurred as well as for (f) the Nakhichevan fault. Modified after Vorobieva et al. (2019) with permission from Elsevier

Full size image

Vorobieva et al. (2019) demonstrated also that the average recurrence time (ART) intervals of strong synthetic events in the Transcaucasian region are consistent with those derived from observations. For example, fault segment 1 (Fig. 3c) associated with the 1991 Racha earthquake produced synthetic earthquakes of magnitude 7 + (the maximum magnitude of 7.5) with the ART of about 300 years. Fault segment 2 (Fig. 3d) related to the site of strong earthquakes in Shamakha in 1667, 1859, and 1902 (M = 6.9 ± 0.2) also generated earthquakes of magnitude 7 + (the same maximum magnitude of 7.5) with the ART of about 200 years. Fault segment 3 (Fig. 3e), which was associated with the rupture zone of the 1988 Spitak earthquake, produced strong (M = 6.5 +) earthquakes with the ART of about 1000 years. The BAFD model predicted M7 + earthquakes to occur at segment 4 associated with the Nakhichevan fault (Fig. 3f), where the ART of strong synthetic seismic events was estimated to be about 700 years. Occurrences of the strong earthquakes are rather periodic at fault segments 1, 2, and 3, but they are irregular at segment 4, presenting an example of nonlinear complex dynamics of the blocks-and-faults structure. Vorobieva et al. (2019) noticed that the Nakhichevan fault presents a serious hazard to Yerevan, the capital city of Armenia, and to the city Nakhichevan of Azerbaijan.

4.3 Tibet-Himalaya

The seismic activity in the Tibet Plateau and Himalaya is associated with the still ongoing convergence between the Indian and Eurasian plates (e.g., Barazangi and Ni 1982; Le Pichon et al. 1992). Earthquakes in the region occur mainly in response to the crustal movement, deformations, and stress localisation along major regional faults. A BAFD model of seismicity was used to study seismicity of the Tibet-Himalayan region (Ismail-Zadeh et al. 2007). The block structure of the model consisted of six major blocks (Fig. 4) delineated by Replumaz and Tapponnier (2003) that were pushed by the Indian plate at a rate of about 4.2 cm yr−1 (Bilham et al. 1997). Several sets of numerical experiments were performed to analyse the distribution of synthetic earthquakes, the frequency-magnitude relationships, earthquake focal mechanisms, and the relative velocities of block displacements along faults. BAFD-generated catalogues contained seismic events for the time interval of 4,000 years.

Fig. 4
figure 4

Maximum magnitudes of the synthetic earthquakes generated by the BAFD model for the Tibet-Himalayan region (Ismail-Zadeh et al. 2007). The model consists of six major crustal blocks: Indo-Pakistan, Qiangtang, Qaidam, Songpan, and West and East Lhasa Himalaya. Major regional faults separate the blocks (fault names are in italic). The black arrow indicates the motion of India relative to Eurasia. Modified after Sokolov and Ismail-Zadeh (2015) with permission from Elsevier

Full size image

The epicentres of large synthetic earthquakes are located on fault segments associated with the Himalaya, as well as on some internal faults of Tibet (Fig. 4). The largest synthetic events in this model occur along the left and right parts of the Himalayan Frontal Trust, the Karakorum, the northern part of the Karakorum-Jiali, and Xiamshui He faults, as well as the Gulu rift. The BAFD model by Ismail-Zadeh et al. (2007) identified large synthetic events (M = 7.6–8.0) along the Longmen Shan fault, where the Wenchuan M = 7.9 earthquake occurred in 2008. The 2015 Nepal M = 7.8 earthquake was associated with the central part of the Himalayan Frontal Thrust but occurred outside of the modelled fault system. Several great earthquakes with normal-fault mechanisms identified by the model were associated with the Gulu rift zone, and the recurrence time of these events varied from about 1200 to 50 years (Ismail-Zadeh et al. 2007).

The slope of the frequency-magnitude plot for synthetic earthquakes in several BAFD experiments was close to the slope of this plot for the observed seismicity. It was shown that variations in the frequency-magnitude relationship depend on changes in the block movements. Particularly, variations in the rheological properties of fault zones affect the rates of crustal block displacements and relative displacements along faults, and this may influence the recurrence time of large events (Ismail-Zadeh et al 2007).

4.4 Sunda Arc

The seismicity of many earthquake-prone regions is associated with the interaction of continents with oceanic plates along subduction zones. Statistical properties of earthquakes and the localisation of large earthquakes may vary from one segment to another segment of a subduction arc, and the source of the variations is not well understood. The Sunda island arc is an active convergence boundary formed via the subduction of the Indian and Australian plates beneath the Burma and Sunda plates (Widiyantoro and van der Hilst 1996). Large earthquakes of the arc, including the 2004 Aceh-Sumatra great M = 9.1 earthquake, are basically associated with the tectonic deformation and related stress localisation in the Sunda trench.

Soloviev and Ismail-Zadeh (2003) analysed the seismicity of the Sunda island arc using a BAFD model. A one-block structure with ten faults approximating the Sunda island arc was considered in the model, and the dynamics of seismicity was simulated for two hundred years. The model events follow the pattern of regional earthquakes (Fig. 5a). The cumulative frequency-magnitude curve for the synthetic catalogue matches rather well that for the observed seismicity except the parts of the curves corresponding to magnitudes greater than 8 (Fig. 5b). Note that, the work we review here was published in 2003, and if the 2004 M = 9.1 Aceh-Sumatra and the 2005 M = 8.6 Nias-Simeulue earthquakes (marked in Fig. 5b by stars) are added to the statistics of earthquakes, the misfit between two curves would be smaller at the tails of the curves. Ismail-Zadeh et al. (2018) mentioned that “the BAFD model for the Sunda arc predicted (in advance to the great events of the 21st century in the region) a considerable deviation of the frequency-magnitude curve (in the range of magnitudes from 8 to 9 +) between the observed (1900–1999) and modelled seismic events”.

Fig. 5
figure 5

BAFD model for the Sunda island arc. a Maps of observed M > 6 seismicity (red open circles) for 1900–1999 and synthetic M > 7 seismicity (black open circles) for 200 years; the model block is marked by solid line. b Cumulative frequency-magnitude plots for the observed seismicity of the Sunda Arc (solid curve 1) and for the synthetic seismicity with magnitudes reduced by 1 (dashed curve 2). Two black stars mark the magnitude of the 2004 Aceh-Sumatra M = 9.1 and the 2005 Nias-Simeulue M = 8.6 earthquakes (their epicentres are shown in panel a and marked by red-in-green stars). Modified after Soloviev and Ismail-Zadeh (2003) with permission from Springer Nature

Full size image

Soloviev and Ismail-Zadeh (2003) identified two areas prone to large seismicity: (i) one in the eastern part of the Sunda arc, and (ii) another in its north-western part, where the 2004 Aceh-Sumatra earthquake occurred (Fig. 5a). They showed that small change in the plate movement influences the slope of the cumulative frequency-magnitude curve for the synthetic events, changing the number of small events, as well as decreasing the maximum earthquake magnitude. Similarly, a minor change in the model geometry at the same plate motion may result in a major change of the seismicity pattern.

Before 2004, nobody realised that an earthquake with a magnitude more than 9 could occur in the Sunda arc region. According to Ruff and Kanamori (1980), the magnitude of an earthquake in the region could not be more than 8.5 considering the convergence rate of about 6.7 cm yr−1 and the age of the subducting lithosphere of about 80 Myr. Earthquakes of magnitude 9 could happen within a younger (up to 50 Myr) lithosphere subducting at much higher rate of 9–12 cm yr−1. Meanwhile, Soloviev and Ismail-Zadeh (2003) showed that one can expect seismic events in the region with M > 8.5, if two other factors—the geometry of the subduction zone and the direction of the plate convergence—that influence earthquake magnitudes and their locations are considered. Numerical models of seismic cycles for subduction zones showed also that low‐angle subduction and thick sediments in the subduction channel could be additional factors controlling huge tectonic stress releases in giant earthquakes (Muldashev and Sobolev 2020).

5 Spherical BAFD Model: Simulating Dynamics of Tectonic Plates

To study the dynamics of major tectonic plates, a spherical BAFD model was introduced by Digas et al. (1999) and further developed by Melnikova et al. (2004), Rozenberg et al. (2005), Melnikova and Rozenberg (2007), and others. The lithosphere was split into several tectonic plates, which motion was assumed to follow the plate velocity model (e.g., HS3-NUVEL1; Gripp and Gordon 2002). As a response to the movement, tectonic stresses were generated, accumulated, localised, and released in earthquakes along the major fault zones of the model. Initially, the lithosphere was considered as a thin layer, since the thickness of the lithosphere is significantly less than the linear dimensions of the lithospheric plates. Although this simplified spherical model reduced the cost of computations, it was unable to introduce spatial dimensions and dip angle of fault planes, which are among essential parameters in determining seismicity patterns. Later, the model was modified allowing a spherical layer (Fig. 6a) to approximate the lithosphere (Rozenberg et al. 2005) and to consider varying thickness of lithospheric plates and their blocks, as well as depth-dependence viscoelastic properties of fault planes (Melnikova and Rozenberg 2007). These modifications of the model permitted studies of the dynamics of the thick continental and thin oceanic lithospheric plates.

Fig. 6
figure 6

Spherical BAFD model. a An example of model structure; red blocks present a part of the spherical layer approximating the lithosphere; the Earth’s projection is imaged by NASA. b A map of synthetic seismicity produced by the spherical model showing epicentres of strong M ≥ 6 earthquakes occurred for 100 years, where brown circles indicate shallow seismicity (depth < 50 km) and red circles deeper seismicity (50 km < depth < 100 km). Largest synthetic events are marked by white stars, and the largest earthquakes occurred for 1900–2019 (NEIC earthquake catalogue) by yellow stars. The topography and synthetic seismicity are plotted using the SeismicEruption software. c The cumulative number of earthquakes versus magnitude for the earthquakes (solid line) and synthetic events (dashed line) for the same time interval (based on Rozenberg 2020)

Full size image

Rozenberg (2020) used a spherical BAFD model to analyse dynamics of earthquakes and occurrences of large events. The model was represented by fifteen major tectonic plates: Africa, Antarctica, Arabia, Australia, Caribbean, Cocos, Eurasia, India, Juan de Fuca, Nazca, North America, Pacific, Philippines, Somalia, and South America (Fig. 6b). The synthetic seismicity covered well two main seismic belts—the Circum-Pacific and Alpine-Himalayan—where most of large earthquakes occur. The largest events in the model occurred on several fault segments approximately at the same locations as in the reality. For example, three great earthquakes occurred in Chile (the 1960 Great Chilean M = 9.5, the 2010 Maule M = 8.8, and the 2015 Illapel M = 8.3) are well captured by the model. Similarly, synthetic earthquakes fit rather well the area of the 2004 Aceh-Sumatra M = 9.1 and the 2005 Nias-Simeulue M = 8.6 earthquakes. Meanwhile, the model could not reproduce large events at some faults located at the northern and eastern parts of the African plate.

The frequency-magnitude plot for the global seismicity shows almost linear curve, and its slope is close to one (Fig. 6c). Meanwhile, for the synthetic events, the cumulative number of low magnitude events is smaller, and the maximum magnitude earthquake is about half of a magnitude lower than those in the real seismicity catalogue. The number of low magnitude events in the synthetic catalogues is likely to be associated with the discretisation of the model: the finer is fault plane discretisation, the smaller events can be produced but at a higher computational cost (Ismail-Zadeh et al. 2007; Soloviev 2008). Therefore, a further development of the model is indeed required. Particularly, a stochastic component was introduced into the forces acting on the lithospheric blocks or in the physical properties of faults of the spherical BAFD models. This modification improved the earthquake dynamics to some extent (Melnikova and Rozenberg 2015). However, to reproduce important regularities observed in recorded seismicity, a calibration of the model by tuning model parameters to fit observations would be necessary (e.g., Rozenberg 2020).

A spherical block-and-fault structure complicates numerical simulations compared to polygonal structures of blocks. Numerical experiments using the spherical BAFD model showed that the model computations are almost intractable on a single computer processor requiring a huge memory and enormous computational time. For example, a model with 15 tectonic plates and about 200 major fault planes requires computations employing about 4 millions cells, which discretise fault segments and plate bottoms (Melnikova et al. 2017). The most time consuming numerical procedures are the computations of inelastic displacements and tectonic stresses in model cells. Computational time and memory increase with a larger number of blocks and faults, and with a sufficiently fine spatial discretisation to allow smaller magnitude seismic events to be produced in the model. Meanwhile, basic computations related to each cell are performed independently from each other, and therefore, computational jobs can be distributed rather uniformly among processors of a parallel (super)computer. Therefore, a parallelisation of the computer code for the spherical BAFD model is essential to reduce the computational cost. Particularly, Rozenberg (2020) showed that parallel computations using 50 computer cores reduce the computational time by a factor of 20 compared to that performed on a single core processor.

6 Discussion

While a comprehensive theory of seismotectonic processes is still to be developed, various properties of the lithosphere (e.g., spatial heterogeneity, hierarchical block structure, rheology, fault slip) are correlated with the properties of earthquake sequences (e.g., Keilis-Borok 2003; Ammon et al. 2021). Quantitative modelling of lithosphere dynamics and earthquakes in different regions show that the lithosphere can be considered as a large dissipative system, whose dynamic behaviour exhibits abrupt transitions from a steady state to earthquakes.

In this paper, we have overviewed numerical models of earthquake dynamics with the particular emphasis on the dynamics of lithospheric blocks and faults. The BAFD model provides a tool for solving a broad range of geodynamical and seismological problems, such as tectonic processes and seismicity, large seismicity within a fault network, and seismic hazard assessment.

6.1 Implications for Seismic Hazard Assessment and Earthquake Forecasting

Instrumentally recorded earthquakes and historical information about seismicity (e.g., written stories, archaeological findings, and paleo-seismological evidence on large seismic events in the geological past) provide the basis for studies in seismology and seismic hazard assessments (SHAs). However, the information about large but rare earthquakes in a particular region is incomplete. Therefore, only recorded large earthquakes and a few historical damaging events are normally accounted in SHAs because of the lack of information about historical large events and their recurrence time. Earthquake simulators allow overcoming the difficulties in SHAs by using instrumentally recorded, historical, and simulated earthquakes.

Particularly, using observed earthquakes and large magnitude synthetic events generated by a BAFD model, Sokolov and Ismail-Zadeh (2015) developed a data-enhanced approach to a probabilistic Monte-Carlo SHA (DESHA). They applied this approach to assess seismic hazard in the Tibet-Himalayan region. For this, several catalogues of synthetic events generated by the BAFD model for 4,000 years (Ismail-Zadeh et al. 2007; see also Sect. 4.3) were used in the regional SHA. The catalogues were chosen based on the best match between the observed and simulated fault slip rates, GPS-velocities, earthquake focal mechanisms, the annual rate of earthquake occurrence, and the slopes of the Gutenberg-Richter (earthquake magnitude-frequency) curves.

Ground motion model predictions based on the standard probabilistic SHA (GSHAP model; Giardini et al. 1999) and on the DESHA (Sokolov and Ismail-Zadeh 2015) differ significantly in several areas, including the 2008 Wenchuan earthquake zone. The zone surrounding the seismogenic source of this earthquake was characterised by the peak ground acceleration (PGA) at rock sites below 2 m s−2 for a 475-year return period, both in the GSHAP model and the Chinese local SHA model, while the DESHA model results showed that the PGA values may be more than 3 m s−2 for the same area, closer to the recorded acceleration accounting for the site conditions (Sokolov and Ismail-Zadeh 2015). Hence, the DESHA model, incorporating BAFD-modelled earthquakes into probabilistic SHAs, provides better understanding of ground (Ismail-Zadeh 2018). The BAFD and other earthquake simulators can provide important information about the location and the magnitude of possible earthquakes with maximum credible magnitudes.

The DESHA model accounting for extreme seismic events, which may occur in study regions, helps to identify the zones characterised by a high ground motion level using the deaggregation method (e.g., Bazzurro and Cornell 1999). Simulations of the ground shaking from these scenario earthquakes can allow constraining the reasonably expected level of maximum ground motion, providing information for “planning of emergency response and recovery, for seismic risk mitigation and reinsurance, and for the structural design” (Sokolov and Ismail-Zadeh 2015). Although the simulated data account for large earthquakes, which occur during several thousand years, peak ground motion values should be evaluated considering the design limits of ordinary building structures. This corresponds to the ground motion with probability 0.1 of exceedance the specified PGA value at least once in 50 years leading to the average return period 475 years (Sokolov and Ismail-Zadeh 2015). In the case of especially important building structures, such as nuclear power plants or large dams, the probability 0.005 of exceedance the PGA in 50 year (the average return period 10,000 years, resulting in the highest design limits) should be considered.

Synthetic events which occurred over a time window of several thousand years can be used to interpret the seismic cycle behaviour. Assuming that a segment of the catalogue of synthetic events accurately approximates the observed seismic sequence, the part of the catalogue immediately following this segment might be used to forecast future large earthquakes (Soloviev and Ismail-Zadeh 2003). The BAFD model can also help to detect and analyse foreshocks in the vicinity of eventual large earthquakes, and hence, it could serve as a short-term earthquake forecasting of large events (e.g., Kato and Ben-Zion 2021). Meanwhile, the forecasting possibility of the BAFD model should not be overstated as it does not predict the time and the probability of occurrence of future large events but indicates their possible locations. The model can indicate a premonitory pattern determined prior to large synthetic events.

6.2 Implications for Recurrence of Large Earthquakes

Being a nonlinear hierarchical system, the lithosphere displays a number of intricate features, including high sensitivity of earthquake productions and their localisation to external perturbations (e.g., driving forces of lithospheric plates), and the response on the perturbations may depend on the complexity of faults, their rheological and frictional properties. The impact of perturbations can influence the stability of fault dynamics in a sense that the external stimuli may either advance the seismic productivity or delay it postponing next large earthquakes (e.g., Franović et al. 2016). The duration of seismic cycles derived from BAFD models should be carefully analysed to assess the recurrence of large earthquakes. A deeper understanding of spatio-temporal interactions of fault networks as well as the role of fluids (e.g., Gabrielov et al. 2007) and relevant pore pressure and stress perturbations on fault slip dynamics is required to unravel the geophysical processes and regional seismic hazards.

An analysis of recurrence time of large events in the BAFD model shows that the time between large events may vary considerably. This implies that an average recurrence time should be used cautiously in hazard assessment. A time interval between two consecutive large earthquakes in a regional fault network may be much shorter than the average recurrence time of the large regional events. For example, the 2015 Nepal M = 7.8 earthquake occurred in 81 years after the 1934 Bihar-Nepal M = 8.0 earthquake, although the recurrence time of great earthquakes in eastern Nepal since Late Holocene were estimated to be between 750 ± 140 and 870 ± 350 years on the basis of geological, paleo-seismological, geophysical, and geodetic observations (Bollinger et al. 2014; Baro et al. 2020).

The Saint–Venant’s compatibility condition (Muskhelishvili 1975) applied to lithosphere block-and-fault structures assumes that the relative fault slips can be realised through the block movements. However, the geometry of lithospheric block-and-fault structures is often incompatible with tectonic movements. The BAFD model exhibits properties of kinematic and geometric incompatibilities (e.g., when one fault moves, and stresses are accumulated on other faults) leading to heterogeneous stress localisation and their release in earthquakes along fault segments of the model (McKenzie and Parker 1967; Gabrielov et al. 1996; Keilis-Borok 2003). This paper presents quantitative manifestations of the geometric and kinematic incompatibilities of the lithosphere block-and-fault structures on a wide range of timescales—from seismicity (seconds) to neotectonics (thousands of years).

6.3 BAFD Model Limitations and Outlook

Studies performed using the BAFD model show the model’s effectiveness as a tool to analyse the nonlinear dynamics of the lithosphere and seismicity. Although the BAFD model reproduces basic features of observed seismicity, it has several limitations, which we discuss here briefly (see Ismail-Zadeh et al. 2018 for detail). Lithospheric blocks are considered to be rigid, although the blocks can deform at the geological time scale. Meanwhile the deformation of blocks at the time scale of BAFD models (several thousand years) is small compared to their size, and hence the model assumes a fixed geometry not changing with time. While model displacements are infinitely small compared with the typical size of lithospheric blocks, the relative displacement of the blocks can vary from about 10 m to 100 m for one thousand years, if the blocks move with a rate of 1–10 cm yr−1. The BAFD model accounts only for a horizontal motion of lithospheric plates as a stress-building mechanism, although the gravitational potential energy contributes also to stress generation in the lithosphere (e.g., Aoudia et al. 2007; Ismail-Zadeh et al. 2005, 2010). BAFD model parameters cannot be still determined uniquely, because regional geodetic, geophysical, and geological observations are usually incomplete and/or have limited accuracy and/or their interpretations are sometimes inconsistent. Changes in the parameters of the model (e.g., prescribed driving forces and rheological properties of fault zones) will influence its results (Ismail-Zadeh et al. 2018).

The BAFD models should employ data assimilation approaches to fit better observed and synthetic seismic patterns and fault slip rates and to forecast future seismicity. The physics of earthquakes should be integrated into BAFD models to improve numerical models of earthquake occurrences. Seismological, geophysical, geodetic, geochemical, and geological data can be assimilated in the numerical models to enhance their capacities in forecasting extreme seismicity (e.g., Van Aalsburg et al. 2007; Werner et al. 2011). Precise geodetic measurements related to GNSS-velocities of lithospheric block movements and lower crustal flow orientations derived from seismic anisotropy studies would help to assess block dynamics and fault slip rates. The BAFD models can provide better understanding of the relationship between the geometrical and rheological properties of fault zones and spatial–temporal distribution of large earthquakes (Ismail-Zadeh et al. 2018).

7 Concluding Remarks

The model of the lithospheric block-and-fault dynamics provides an insight into the seismic cycle, clustering of earthquakes in space and time, localisation of large seismic events, and their recurrence. The BAFD model has revealed that the geometry of a lithospheric block-and-fault structure, as well as the direction of driving tectonic forces, significantly influences seismic productivity, magnitude of earthquakes, and their location. The BAFD model allows for viscoelastic and strain rate-dependent nonlinear fault slip. An optimisation of the misfit between observed and modelled fault slips by tuning rheological parameters of model fault planes can assist in forecasting future seismicity within natural lithospheric block-and-fault structures. The recurrence time of large earthquakes should be considered with a great caution as the time interval between consecutive large seismic events can vary significantly, both in the model and in natural seismicity. The recurrence time should be hence carefully used in seismic hazard assessments accounting for its variation.

Although a common approach to seismic hazard assessment is based on the knowledge of recorded and some historical data for a few hundred years, what such an analysis entails is an inability to assess the hazards of extreme seismic events, which are rare (and hence not recorded in many cases), but their consequences are huge. We have shown that earthquake simulations can provide a reliable source of information on extreme events within a network of regional faults and enhance hazard assessment. All this will require continued improvements of earthquake simulations and forecasts by the BAFD model, and of seismic hazard assessments. Interdisciplinary analysis of data-enhanced seismic hazard combined with data on physical and social vulnerability and exposure will undoubtedly reveal new surprises about seismic risk and safety.