1 Introduction

In the previous paper (Elliott 2020), we reviewed the different Earth Observing systems for measuring solid Earth processes and discussed at what stages they could contribute to improving the assessment of earthquake hazard, risk and disaster management. We consider earthquake hazard to constitute damaging seismic events that lead to loss of life, and the economic and social damages that can occur to exposed vulnerable populations. We aim to mitigate these losses by improving our understanding of the physical processes that generate the earthquake hazard, as well as the characteristics of the sources of earthquakes in terms of faulting. The examples presented here do not aim to measure the direct earthquake hazard of strong ground motion (such as peak ground acceleration) that is the primary concern for engineering solutions designed to mitigate earthquake losses. Instead, we aim to improve hazard assessment by measuring and understanding the deformation of the Earth’s crust to illuminates the location, potency and rate of major earthquake-generating sources—information and knowledge that can be subsequently used to better estimate future strong ground motion when combined with other sources of information and models. Here we provide examples of the use of Earth Observation (EO) and associated geophysical datasets (airborne and ground based), to measure the deformation associated with failure of the crust on faults, a consequence of the earthquake cycle.

The earthquake cycle encapsulates our current understanding of the physical solid Earth process of earthquake generation in terms of deformation (Savage and Prescott 1978) measurable with geodetic techniques using satellite systems. The cycle comprises an increase in strain across faults occurring in the interseismic period, often taking hundreds or thousands of years to build up, depending on the tectonic environment and faulting. This may result in only millimetres of relative displacement across distances of hundreds of kilometres on either side of a major fault over the course of a year (e.g., Bell et al. 2011). However, this very small gradient of displacement is detectable from Earth Observation satellites using Interferometric Synthetic Aperture Radar (InSAR) and the Global Navigation Satellite System (GNSS) (Wright 2002). The accumulation of strain continues until the resulting stress on the fault overcomes the friction resisting it, leading to the initiation of earthquake rupture (termed the coseismic period, lasting seconds to minutes). This coseismic period involves the relative displacement of large volumes of crustal material across the fault in the short time of an earthquake rupture. For a large earthquake, these displacements may be many metres in the near-field close to the fault, and they decay away to centimetres and millimetres at tens to hundreds of kilometres away in the far-field. The fault trace itself may also be many tens or hundreds of kilometres long, so the total area over which the permanent ground deformation is measurable with sensitive satellite observations for even a moderate earthquake maybe as much as 100–100,000 sq. km. This coseismic phase is immediately followed by the postseismic period, in which deformation continues to occur around and below the fault zone and may last (and be detectable) for months to decades (Bürgmann and Dresen 2008). This period involves both seismic processes (in the form of a decaying prevalence and magnitude of aftershocks), and aseismic processes (Wright et al. 2013) comprising afterslip and deeper viscoelastic relaxation (e.g., Hearn et al. 2002), and potentially poroelastic rebound (e.g., Jónsson et al. 2003). Postseismic deformation is typically some fraction of the coseismic deformation but is at a higher rate than the long-term interseismic rates normally observed. For major earthquakes, this postseismic deformation may be visible from Earth Observing systems, particularly after time series analysis of satellite data corrected for atmospheric noise (e.g., Li et al. 2009). The cycle for the given fault then returns to the background rate of strain accumulation during the next interseismic period. Each of these stages of deformation (when onshore) is measurable by Earth Observing systems. InSAR/GNSS data are applicable to observing and modelling all three parts of the cycle, whilst optical imagery is predominately used when large coseismic offsets have occurred.

EO derived measurements of coseismic ground deformation (coupled with other a priori constraints from seismological, optical, topographic and field mapping) can be used as inputs for geophysical inverse models (e.g., Elliott et al. 2016). These models aim to approximate the Earth, typically as an elastic medium in a half-space, from which the parameters of the earthquake source (Okada 1985) such as fault location and orientation (e.g., Bagnardi and Hooper 2018) and the distribution of slip are determined (e.g., Simons et al. 2002; Feng et al. 2010; Amey et al. 2018). More complicated models can include other rheologies such as viscoelastic processes (e.g., Pollitz et al. 2000), in particular when looking at postseismic deformation (e.g., Deng et al. 1998). From these models, further calculations of stress transfer through the crust can be made (e.g., Barnhart et al. 2019b), as well as interpretations of active tectonic process such as the growth of geological structures and the deformation of the continents.

The study of earthquake sources and their relationship to the active fault structures seen at the surface has made a significant contribution to our understanding of plate tectonics, as well as determining where strain is currently building up in the crust. Geodetic systems are particularly suited to determining how much of a fault surface is locked and accumulating strain, as opposed to releasing it aseismically (a ratio termed the degree of fault coupling). Establishing this is a critical constraint in assessing the seismic potential for a fault system (Avouac 2015). The relatively new field of seafloor geodesy is opening up our ability to use GNSS to observe deformation underwater (Bürgmann and Chadwell 2014), which is particularly important for the Earth’s subduction zones that cause the largest earthquakes and associated tsunamis (e.g., Lay et al. 2005; Watanabe et al. 2014). Seafloor multibeam bathymetric surveys also offer the chance to capture the displacement associated with major earthquakes, although areas with sufficient pre-existing high-resolution coverage, such as the Japan trench (Fujiwara et al. 2011), are limited due to the expense of acquisition.

In terms of both earthquake hazard and risk, there is a contrast between coastal areas exposed to subduction zone events (those at plate boundaries) versus those in continental interiors (within deforming “plates”). The location of fault interfaces for subduction zones are relatively well determined (Hayes et al. 2018). The shallow, up-dip part of these faults is located offshore where there is no population exposure to generate a risk. By the time the earthquake rupture is beneath land on the down-dip portion of the fault, the slip interface is typically located relatively deep, affecting the type of shaking experienced in earthquakes. Such faults tend to rupture relatively frequently as the fault interfaces accumulate strain more rapidly, and they are often relatively well studied as a fault system and seismic cycle, such as along the Chilean subduction zone (e.g., Chlieh et al. 2004), although the potential size and chances of major events may not be recognised (Kagan and Jackson 2013). Conversely, the locations of faults onshore are not always well known, and their relatively infrequent rupture means that less information can be drawn from past events and their recurrence. The immediate proximity of onshore (shallow) faults to population centres results in earthquakes in continental interiors causing more fatalities despite being smaller (England and Jackson 2011). There is also a contrast in what EO data can offer in these two domains. In the case of subduction zones, EO normally only provides measurements onshore and therefore of the far-field effects of deformation associated with these types of convergent areas. Conversely, for continental earthquakes (in particular for large or shallow processes), EO provides information on the detail of near-field deformation right at, or above, the fault. In terms of preparedness there are therefore some differences in the EO approaches to assessing the hazard applied to these two contrasting domains. For subduction zones, the potential for major hazard is more widely recognised and the location of the fault that is going to host the big earthquakes is more of a known quantity. The priorities are to determine the degree of interface coupling and the mechanical behaviour of the zone, as well as seismic gaps left behind from previous events to characterise the hazard (e.g., Métois et al. 2012), as well as the distribution of earthquake magnitudes and maximum credible size of rupture. The identification of these characteristics is made more tractable by much (but by no means all) of the accumulating strain being released on the single dominant offshore fault structure. Conversely for continental interiors, the fault that will eventually break in an earthquake will not necessarily have been identified before the event, as many active faults are not identified until they rupture due to their hidden or subtle expression in the landscape geomorphology. The continental lithosphere is much older than oceanic crust and hence much more complicated in terms of inherited structures, fabrics and weaknesses. Furthermore, the way in which the strain in the crust is eventually partitioned onto the array of distributed faults is not fully understood. However, where there are interactions between both subduction fault interfaces and upper crustal faults, the earthquake and rupture pattern can result in extremely complicated displacement patterns, as was the case in the 2016 Kaikoura earthquake in New Zealand (e.g., Hamling et al. 2017; Furlong and Herman 2017).

In this article, we present some individual examples of the use of such Earth Observation data (some current imaging systems are provided in Table 1) for understanding earthquakes, using satellite radar for a recent small earthquake in western Turkey (2019) and optical systems for the large Palu earthquake (Sulawesi) in 2018 and Sichuan earthquake (China) in 2008. These examples illustrate EO measurements for an earthquake at the limit of detectability with InSAR, as compared to a pair of major earthquakes with very large geodetic signals and a major human impact. None of this work can be done in isolation without an understanding of the local context: in situ geophysical and field measurements can be critical in interpreting or constraining satellite observations. To this end we present an example of seismic risk from triggered earthquakes at a reservoir and dam in Koyna (India) that additionally makes use of non-Earth Observation data. We finish with conclusions on the recent and potential for use of EO in better constraining the sources of earthquake hazards, in particular the use of EO for measurements of long-term strain accumulation.

Table 1 Imaging characteristics of the main satellite systems illustrated within this paper for measuring earthquake deformation (or their newer active equivalent)
Full size table

2 InSAR Observations and Modelling of an Earthquake

Measurements of tectonic deformation have increased dramatically over the past two decades from the growth in, and quality of, satellite-geodetic measurements, which have in turn improved our understanding of active faulting. Prior to the emergence of EO data, the predominant constraint on earthquakes was from seismological measurements and field observations. By combining multiple sets of observations (e.g., Fielding et al. 2013), it is possible to better constrain shallow continental earthquake locations, fault segmentation and ruptures. These are all critical parameters for the assessment of seismic hazard because they capture the characteristics of potential seismic sources and the relative positions of fault structures likely to generate strong motion.

A large number of small and shallow earthquakes have occurred beneath the continents in the time window of Sentinel-1 radar satellite imaging (October 2014–present). With systematic and regular coverage we expect to capture with EO data most of the continental earthquakes with magnitude greater than moment magnitude (Mw) 5.5 that are shallow (< 20 km), something that was less achievable with previous Synthetic Aperture Radar (SAR) systems (Lohman and Simons 2005) due to the lack of data. However, it is not always clear whether these earthquakes are readily visible in interferograms produced over the epicentral areas or not (Funning and Garcia 2018), as the ground deformation can be masked by atmospheric noise for these small events, or their magnitude and depth are beyond the ability of the imaging systems to detect them. Phase decorrelation associated with vegetation also means that the longer-wavelength L-band data is more suitable at equatorial latitudes to capture earthquake deformation signals (Morishita 2019) than the C-band of Sentinel-1, but the volume of data (in terms of both temporal and spatial coverage) is not yet as great at this longer SAR wavelength. However, by using atmospheric corrections and time series approaches (Hooper et al. 2012), modelling of an increasing number of earthquakes should be possible using EO techniques (Tian et al. 2018). Other signal processing approaches such as Independent Component Analysis (ICA) can extract masked signals from InSAR data (Ebmeier 2016) for improved detection of even smaller seismic and aseismic events (Maubant et al. 2020). Machine learning also offers the prospect to improve detection of hidden or slowly deforming events within large data sets of automatically processed InSAR products (Anantrasirichai et al. 2018).

From such an analysis, the locations of active faults can be better identified based upon precise locations of seismic activity, especially in regions of low seismological instrumentation, where solutions can be biased in terms of earthquake location and depth (e.g., Elliott et al. 2010). Links can then be established between geodetically derived fault locations and the expression of the active fault in the geomorphology of the surface. Here, we illustrate this workflow by providing our analysis of a specific example from a recent small earthquake in Turkey and demonstrate the use of other satellite-derived data such as digital elevation models from stereo optical imagery to supplement the interpretation made with Sentinel-1 InSAR data.

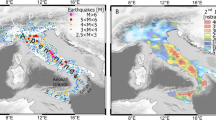
On the 20 March 2019, a moment magnitude (Mw) 5.7 earthquake struck the south-west corner of Turkey, 10 km east of the town of Acipayam (population ~ 11,000) and just west of Lake Salda (Fig. 1). This normal faulting event occurred in a region of distributed deformation, with rates of extension across the whole region of 20 mm/yr according to GNSS measurements (Aktug et al. 2009). Major earthquakes have also occurred in the area, the largest of which was the 1914 magnitude 7.0 event 80 km to the east near the city of Burdur, which killed 4000 people (Ambraseys 1988). Other major normal faulting earthquakes in the past half century (Fig. 1) were the 1971 magnitude 6.2 earthquake sequence also near Burdur (Taymaz and Price 1992), the 1995 Mw 6.2 Dinar earthquake (Wright et al. 1999) and the 2017 Mw 6.6 Kos-Bodrum earthquake (Karasözen et al. 2018). These earthquakes are the release of extensional strain that accumulated over centuries. Major normal faulting scarps are visible in the geomorphology across the whole region, and large mountains strike approximately perpendicular to the extensional direction.

Fig. 1
figure 1

a Map of SW Turkey with past earthquakes overlaid on hillshaded topography. Focal mechanisms of shallow (< 40 km) earthquakes of magnitude 5 + from 1976 to 2020 from the Global Centroid Moment Tensor (GCMT) catalogue are denoted by the blue and white circles and demonstrate the extension of the upper crust by normal faulting. Major faults from the Global Earthquake Model (GEM) Active Fault Database are denoted by red lines, based largely in this region upon Woessner et al. (2015). Seismicity prior to 1976 is from the USGS, based upon the International Seismological Centre ISC-GEM Global Instrumental Earthquake Catalogue (Storchak et al. 2013). Seismic catalogue locations of the 2019 Mw 5.7 mainshock and Mw 5.1 aftershock near Acipayam are denoted for GCMT and USGS. Dashed box indicates the extent of the area show in b–g. Earthquake deformation observations: b–c example of InSAR data from Sentinel-1 interferograms (displacement of the Earth’s surface relative to the satellite in the line of sight, with negative motion (blue) indicating motion away from the satellite (predominately subsidence in this case) and d, e modelling of a small earthquake—20 March 2019 Mw 5.7 earthquake at Acipayam, Turkey. InSAR data are available in b ascending (track 58) and c descending (track 138) directions (Az indicate direction of satellite, los is the line of sight look direction). These data are then modelled as elastic dislocations to determine the best fitting fault parameters, and the residual difference between these two datasets f, g indicates the noise in the interferograms and any mis-modelling of the data from the simplified assumptions of modelling a fault as a single rectangular dislocation of constant slip. The area of slip on the two possible fault planes is indicated by the rectangles and the up-dip projections of these faults to the surface are indicated by the lines (with the ticks indicating the down-dip direction). There remains a focal ambiguity where it is not possible to determine if the fault dips to the east (black outline) or west (grey outline) as both these solutions yield almost the same pattern of deformation at the surface (the east dipping solution is shown here in the model). This ambiguity is because the fault slip is buried at depth and there is no surface rupture to resolve this. The red stars indicate the epicentral location reported by the USGS (37.408° N, 29.531° E) and centroid location by GCMT (37.37° N, 29.38° E). The black dashed rectangle indicates the spatial extent of Fig. 3

Full size image

Sentinel-1 imagery over Turkey are acquired by the European Space Agency (ESA) every 6 days (achieved using both identical copies of Sentinel 1A and 1B currently in orbit). This occurs along ground tracks (numbered by orbit) that are normally about 250 km wide (Table 1) imaged from a low Earth orbit at about 700 km altitude (at the boundary of the Earth’s outermost pair of atmospheric layers of the thermosphere and exosphere). As the satellites are launched into a near-polar orbit, they image the Earth in two directions on every orbit—in the ascending direction when travelling south-to-north and in the descending direction when completing the orbit north to south. We use data from both the ascending and descending tracks to better constrain the surface deformation. This is because multiple look directions are differently sensitive to the ground motion in the vertical and horizontal (both look directions image vertical uplift as a shortening in range, but eastward motion is measured with opposite signs). This can be particularly useful in constraining some earthquake fault parameters, which can easily trade-off against each other in fault inversions if only a single component of displacement is measured (Funning et al. 2005).

The short interval between data acquisitions of 6 days (due to imaging from both Sentinel-1A and 1B) from immediately before (17 March 2019) and after the earthquake (23 March 2019) means the interferometric results are coherent even in regions of dense vegetation or intensive cultivation. Additionally, the sooner after the earthquake the second image is acquired, the less postseismic deformation contaminates the coseismic signal, which can often be a disadvantage of the latency of the EO polar satellites for InSAR. The regular repeat also helps to separate out any potential additional deformation from aftershocks, such as the Mw 5.1 that occurred in the same area on the 31 March 2019. The earthquake deformation is visible in the processed InSAR data with 3–4 cm of motion away from the satellite (Fig. 1), which indicates elastic subsidence typical of normal faulting (as the sign of the signal is the same in both look directions from ascending and descending passes, this indicates predominantly vertical motion). The smoothness of the signal demonstrates that the faulting did not reach to the surface and that the slip remains buried at depth. If there had been surface faulting or fissuring, then discontinuities in the signal would be visible in the InSAR data. Such signals provide a useful method for identifying off-fault deformation (Xu et al. 2016) or other active fault strands that may have been induced (Fialko et al. 2002) and triggered in the main earthquake (Xu et al. 2020), as well as any triggered landsliding (e.g., Kargel et al. 2016; Huang et al. 2017; Delorme et al. 2020). The regular pattern or ‘blotchy’ signal in the data (particularly for ascending track 58, Fig. 1) is indicative of atmospheric noise due to the difference in tropospheric path delays between the two SAR image dates and most likely due to variations in water vapour (Jolivet et al. 2014a). This is one of the main limiting factors for detecting small tectonic signals as it can often obscure the geophysical ground displacement. Further corrections to such data could be made using weather model data, such as from the European Centre for Medium-Range Weather Forecasts (ECMWF) which removes part of the atmospheric noise (e.g., Jolivet et al. 2011; Yu et al. 2018). An improved signal-to-noise ratio improves subsequent elastic dislocation modelling that is often implemented on such data and in turn this will reduce uncertainties in the derived fault parameters.

The next step is to downsample the data in order to exclude redundant data points and speed up the subsequent modelling analysis. The very high resolution of the InSAR data (typical pixel spacing less than 100 m) is not required to characterise most features of deformation especially in this case of a small buried event such as this. In this case, 750 datapoints for each interferogram are sufficient to capture the magnitude, shape and displacement gradient within the data. Modelling the surface deformation data points is usually achieved with a form of elastic dislocation (e.g., Okada 1985) code to solve for the fault parameters of location, depth and orientation, as well as magnitude of slip. A large range of modelling software and approaches have been developed to estimate sub-surface fault parameters based upon inversions of surface displacement data (e.g., Jónsson et al. 2002; Funning et al. 2007; Barnhart and Lohman 2010; Minson et al. 2013). Here we use the Geodetic Bayesian Inversion Software (GBIS) to perform inversions of the InSAR data using a Markov-chain Monte Carlo algorithm that finds the posterior probability distribution of the fault location (x, y, depth), size (length, width), orientation (strike, dip) and slip (Bagnardi and Hooper 2018). Therefore, not only do we find a model that fits the data well, but we also get a sense of the range of uncertainty and trade-offs between the various fault parameters based upon how noisy the input datasets are assessed to be (Table 2).

Table 2 Fault parameters from the geodetic solution from both the east dipping nodal plane solution (NP1) and for the westward dipping solution (NP2)
Full size table

The fault parameter modelling results (Figs. 1, 2) indicate that the fault strikes NNW-SSE and is predominately normal dip-slip. This corroborates the seismological solutions in terms of fault orientation (Table 2), but the location of the earthquake from the InSAR modelling (denoted by the rectangles in Fig. 1) is more towards the town of Acipayam than in the USGS seismological solution (USGS 2019) by almost 8 km (indicated by the red star in Fig. 1). As the fault slip remains buried, a focal plane ambiguity remains (as it does for the seismological solution), in which it is not possible to discriminate whether the fault dips to the ENE or WSW (Fig. 2a). If the rupture were to dip eastwards, the model indicates the fault would project up to the surface near to the town of Acipayam (2 km to the west of it). If the fault instead dips westwards, the up-dip projection of the fault plane is about halfway between Acipayan and Lake Salda. Further time series analysis may be able to resolve this ambiguity, but usually local seismic networks and relocated seismicity are needed when there is no evidence of surface rupture (de Michele et al. 2013; Elliott et al. 2015). The recent study of this earthquake by Yang et al. (2020), favours the eastward dipping solution based upon the supplementary evidence from aftershock locations and reported field observations. An additional issue that arises when modelling buried fault slip in small earthquakes in that it is possible to fit the data as equally well with a near line source as a finite fault plane. Therefore, what typically happens in such cases is that the estimated fault slip (Fig. 2e) increases and trades off with a narrowing of the fault width (Fig. 2g) leaving both poorly constrained (but still maintaining approximately the same earthquake moment—Fig. 2i). The surface projection of the fault planes at depth then appear nearly as lines in map view (Fig. 1d, e). In this case the optimal slip is very high (3 metres) for such a small earthquake, and the estimated fault width is very narrow (400 m) given the fault length is over 8 km (Table 2), so stress drops would become unreasonably large. When such a trade-off occurs, an option is to constrain the prior in the Bayesian modelling approach within what is considered physically reasonable bounds (Bagnardi and Hooper 2018), or alternatively one of the fault parameters such as the fault width could be fixed (Yang et al. 2020).

Fig. 2
figure 2

a Schematic diagram of the relative location of the two possible fault plane solutions for the Acipayam earthquake. In one solution, the fault plane dips steeply to the ENE, in the other it dips more shallowly to the WSW (solid red lines). The up-dip projections of the fault planes to the surface are denoted by dashed red lines. As the modelled slip increases, the width of these fault lines collapse to approximately the same point in the modelling due to trade-offs between these two parameters for buried sources. The relative locations of the seismological solutions are indicated by red stars. b–k Modelling results for fault parameters (location, size, orientation and slip) and parameter uncertainties (posterior probability distributions) through Bayesian analysis using GBIS (Bagnardi and Hooper 2018) for the eastward dipping fault plane solution based upon the data in Fig. 1. The best fit fault model for each parameter is shown by the red line, with the histogram of the distributions of solutions shown in blue for 800,000 model iterations (Table 2 has the best fit model and range of solutions). The fault plane location (upper midpoint of slip area) is given relative to a reference point 29.531° E, 37.408° N which is the USGS epicentre

Full size image

An interplay exists between the active tectonics associated with faulting and the subsequent change in topography, erosion and deposition that is revealed in the analysis of the tectonic geomorphology of a landscape, which can be useful in earthquake-prone areas to identify the location of active fault structures (Burbank and Anderson 2009). Combining geodetic observations of earthquake cycle deformation with geomorphic observations of faulting can be important for assessing seismic hazard, in particular in regions with large, infrequent earthquakes (Hodge et al. 2015). To augment the analysis performed here with the Sentinel-1 InSAR data and the subsequent modelling, we also examine the topography in the area to try to link any surface geomorphic features with the causative fault plane. The availability and resolution of topographic data are highly variable globally, but it often acts as an important underlying dataset for geomorphic analysis of active faulting (e.g., Arrowsmith and Zielke 2009) and for landscape evolution in mountainous terrain (e.g., Boulton and Stokes 2018). Open global datasets from the Shuttle Radar Topography Mission (SRTM) (Farr and Kobrick 2000) provide 30 m (1 arc second) topographic data (Fig. 3b) for most of the mid and low latitude areas of the world (60 degrees north to 56 degrees south, Farr et al. 2007) and these are typically used in the InSAR processing chain to correct for topography (originally prior to 2015 only 90 m (3 arc second) data was available outside of the USA—Fig. 3c). Higher-resolution datasets exist commercially or may be available from national agencies but are not openly available. Here we compare the hierarchy of both SAR derived and optically stereo-derived Digital Elevation Models (DEMs) for this region (Fig. 3).

Fig. 3
figure 3

Examples of Digital Elevation Models (DEMs) of the topography of the earthquake epicentral area derived from radar (left column a–c) and optical stereo imagery (right column d–f) depicted as hillshaded relief illuminated from the southeast. The rows go from high resolution (top) to lower-resolution datasets (bottom). g Depicts a Sentinel-2 RGB image over the same region. The town of Acipayam is in the lower left corner of each panel. The white arrows in a denote the edge of a step in topography, most likely associated with the edge of a fan. The white lines in d indicate the surface trace (ticks indicating direction of dip) and subsurface fault plane of the east-dipping solution found in the modelling of the InSAR data (Fig. 1). h Profile of topography perpendicular to the surface projection of the fault trace (X–X′ and Y–Y′) for the east-dipping solution shown in d. The profiles are taken through the TanDEM-X and SPOT DEMs and highlight the differences in resolution but also the greater noise present in the photogrammetrically derived SPOT DEM (note 3 m was subtracted from the SPOT DEM height to align it)

Full size image

Low-resolution topographic datasets (often in conjunction with interpreting optical satellite imagery from Landsat) have been useful in the past for mapping out major fault structures (Taylor and Yin 2009) and can contribute towards building databases across the globe of active fault traces (Styron et al. 2010). However, for more subtle geomorphic traces of activity, high-resolution datasets are required (with Light Detection and Ranging (LiDAR) being the best (Prentice et al. 2009), but least available). The Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) GDEM (Fig. 3f) offers 30 m resolution near-globally as well as the freely available Advance World 3-Dimensional (AW3D) (Fig. 3e) based upon the Panchromatic Remote sensing Instrument for Stereo Mapping (PRISM). These openly available relatively low-resolution topography datasets enable analysis of major tectonic features, but it is more difficult to discriminate subtle features such as those within the basin in this case (Fig. 3).

Many modern optical imaging satellite instruments are multispectral with relatively narrow spectral bands across visible Red, Green, Blue (RGB) as well as wider bands at Near-Infrared (NIR) and beyond. However, they commonly also have a wider band that crosses most of the visible spectrum in a single channel termed the panchromatic, which is usually double the resolution (half the pixel size/spacing) of the visible multi-spectral bands. This band is typically used to derive topography because of its higher resolution, and usually is done when acquired as an in-track stereo mode when two images are taken in quick succession (as opposed to cross track which is separated in space and in time). The baseline separation of images (often a couple of hundreds of kilometres apart) yields different perspectives of the Earth’s surface from which a digital elevation model can be derived from using the process of photogrammetry (Noh and Howat 2015). Satellite systems that are able to acquire in-track panchromatic imagery at medium and high resolutions, and that have been applied to active tectonic faulting observations include the WorldView series (Barnhart et al. 2019a), the pair of Satellite Pour l’Observation de la Terre (SPOT6/7) systems (Zhou et al. 2016) and the two Pleiades satellites (Zhou et al. 2015; Hodge et al. 2019).

Using panchromatic stereo imagery (1.5 m) from SPOT6, it is possible to derive relatively high-resolution topography at about 3 m spacing, albeit with some high-frequency noise and artefacts (Fig. 3d, h), especially over flat-lying areas. Commercially available TanDEM-X WorldDEM data (Krieger et al. 2007) provides good quality topography at 12 m resolution (Fig. 3a, h). In both these latter two datasets, the streets and buildings within the town of Acipayam start to become visible, as well as more subtle fluvial features. The potential location of the projection of the east-dipping fault that is inferred to be immediately up-dip of the modelled InSAR data is 2 km east of the town of Acipayam and is approximately aligned with north–south running step in topography that is visible in the hill-shaded higher-resolution DEMs. However, the topographic step associated with this potential fault uplift is subtle at less than 10 m (Fig. 3h) and such features can often be difficult to discriminate between relative footwall uplift and terrace edges due to fluvial incision from the drainage in this valley or from alluvial fans out washing from the mountains. Improved quality DEMs are required to be able to better interrogate the landscape geomorphology and its interaction with tectonics. However, such ambiguities highlight the necessity to supplement EO data with field observations to improve the robustness of remotely inferred interpretations. Whilst for many major onshore shallow earthquakes EO data captures the deformation and topography of an area well, it is still important to combine this remotely derived data with other seismological and geophysical datasets as well as field observations to fully constrain and understand the earthquake deformation process and potential for future hazard (Hamling 2019).

The requirements for high-resolution DEMs also highlight the discrepancy of the closed nature of such datasets versus the more open policies for recently acquired optical and SAR imagery, which are much more freely available and regularly updated at 10 m. In contrast, topography datasets are more often static (infrequently updated) and not openly available at such resolutions of 10 metres. Most aspects of active landscape evolution involve changes in the Earth’s topography, be it migrating fluvial systems and knickpoints, retreating glacial streams, uplifting landscapes associated with earthquake faulting or landsliding resulting from seismic shaking. Additionally, the changing built environment associated with urbanisation also alters the local topography and is an important measure of the exposure and potential vulnerability of a population to a hazard. The lack of high-resolution topography that keeps pace with this rate of change presents a challenge to understanding the processes driving the evolving shape of our Earth and the parts of our society exposed to hazards.

The initial seismological epicentre from the USGS (USGS 2019) placed the earthquake further to the east than found here, amongst the high topography southwest of Lake Salda (Fig. 1). Without further information and investigation, such events might be attributed to one of the obvious major faults in the area that has been previously mapped (Emre et al. 2013). However, seismological locations of earthquakes (determined teleseismically) can be incorrect by many kilometres to tens of kilometres, although this can be greatly reduced with local networks and earthquake relocation techniques (e.g., Elliott et al. 2015). The geodetic data and modelling in this particular case indicate the faulting is further to the west but not along the major known fault immediately south and west of Acipayam (Emre et al. 2013, 2018). Comparison of the modelled fault location with the subtle surface geomorphology expressed in the higher-resolution topographic data, points to a previously unidentified active fault within the basin as a likely candidate for this earthquake, much nearer the town of Aipayam than suggested by the original USGS epicentre location. The main topography in the east runs north–south (Fig. 3), whereas the fault plane solution indicates a fault striking more NNW-SSE (Fig. 1). Whilst there appears to be a subtle raised portion of topography on the western edge of the basin with a similar strike (Fig. 3a–f), and a line of greener vegetation that may be associated with a spring line running along the proposed fault (Fig. 3g), the nonlinear shape of this feature along strike (Fig. 3a) indicates more likely that the step in topography is associated with the edge of an alluvial fan emanating from the mountains west of Acipayam, rather than a fault scarp, despite the surface projection of the modelled fault running approximately along this line of topography (Fig. 3d). The profiles through the highest resolution elevation data (Fig. 3h) do not show a consistent step in topography at the location of the surface projection of the fault trace, indicating that the fault plane has not accumulated significant enough cumulative offset that has propagated to shallow depths to present a clear scarp in the geomorphology. Robustly identifying the location of such active faults near to towns and cities is an important part of improving our knowledge of the seismic hazard. The proximity of the fault to the exposed buildings affects the estimated magnitude of ground accelerations and the subsequent calculated losses (Hussain et al. 2020). Knowing the location of particular scarps is also important at a local scale to avoid building infrastructure that straddles a fault. In this particular case, the surface projection of the fault plane is 2 km further into the basin (Fig. 3d) than the existing mapped fault that is behind the town of Acipayam, and is an example of the spatial migration of activity that might be associated with the breakup of a hanging wall block (e.g., Biggs et al. 2010). Furthermore, examining the faulting related to such minor earthquakes (as done here) acts as a motivator for targeting both future research and also raising societal awareness of the active faulting in the area that may be capable of hosting much larger earthquakes from ruptures on the previously identified major faults.

3 Sub-pixel Cross-Correlation of SAR-Amplitude Imagery and Optical Imagery

Sub-pixel correlation of both radar amplitude and optical images is now a commonly used technique for the measurement of surface deformation. It has been proven complementary to InSAR in several geophysical studies (e.g., Klinger et al. 2006; de Michele and Briole 2007; de Michele et al. 2010). Subpixel offsets of optical data, along with Synthetic Aperture Radar (SAR) and InSAR, are also used to constrain models of neo-rifting episodes (e.g., Barisin et al. 2009; Grandin et al. 2010).

In the Radar domain, the cross-correlation method was proven reliable with SAR amplitude data by Michel et al. (1999). A SAR system sends radar pulses to the ground and measures both the amplitude and the phase of the backscattered signal. The phase is used to perform the synthetic aperture. The phase difference is used to construct differential interferograms (DInSAR, InSAR) as used in the previous section, while the radar amplitude data can be used to map subpixels offsets following the correlation methodology firstly described in Michel et al. (1999). These methods, often called “offset tracking” complement InSAR particularly when the ground displacement is larger than half an interferometric fringe per pixel. This was the case for the major 2008 Mw 7.9 Sichuan earthquake, China, due to large slip of a fault that ruptured all the way to the surface (Fig. 4). At this rate of ground deformation, interferometric fringes become indistinguishable and the InSAR signal becomes incoherent, thus unusable. This is one of the main reasons why SAR offset tracking is today a widely used technique for retrieving coseismic surface displacements of large earthquakes (e.g., Peltzer et al. 2001; Fialko et al. 2005; Pathier et al. 2006; de Michele et al. 2009, 2010; Yan et al. 2013; Hamling et al. 2017). Additionally, the use of a SAR system presents multiple other advantages. Firstly, SAR pulses penetrate through clouds. Secondly, they are independent of solar illumination, since the SAR antenna emits his own source of illumination. Thirdly, correlograms obtained from SAR-amplitude images contain different sets of information with respect to optical correlograms; since a SAR system acquires data along the Line of Sight direction of the satellite (LoS) whilst travelling in the azimuthal direction of the satellite, the SAR amplitude correlogram contains contributions from both horizontal (in the azimuth direction) and vertical (in LoS direction) ground motion. Significant East–West horizontal motion is recorded in the LoS component as well. This information, both from ascending and descending orbits, can be combined to calculate the 3D displacement field of an earthquake, such as that obtained for the Mw 7.9 Sichuan earthquake (de Michele et al. 2010), shown in Fig. 4.

Fig. 4
figure 4

Modified from de Michele et al. 2010

The three dimensional displacement field of the Sichuan earthquake (2008 Mw 7.8, China) retrieved by cross-correlation of SAR data.

Full size image

The use of cross-correlation to measure displacement fields of the Earth’s surface was first conceptualised by Crippen and Blom (1991, 1992) and Crippen (1992) and applied to optical spaceborne imagery. They called the method “imageodesy” and applied it to measure the displacement field of the Landers earthquake (1992 Mw 7.2, California) and the displacement field of a landslide with CNES (Centre National d’Etude Spatiales—French Space Agency) SPOT satellite imagery. The method assumes that image distortions due to mass movements can be measured with high precision as “errors” in the resampling field between orthorectified pre- and post-event images. The application of the methodology in earthquake studies was further developed in Michel (1997) and published in Van Puymbroeck et al. (2000), using SPOT data. The authors successfully implemented the methodology and applied it to measure the displacement field of the Landers Earthquake. In the method, images acquired before and after a deforming event are first resampled to a common geometry, typically using a Digital Elevation Model (DEM). Offsets are commonly calculated by differentiating the phases of the Fast Fourier Transforms on a moving window basis. Then, subpixel offset is achieved by interpolating the correlation peak within the moving window. The residual offset between the two images is expected to be due to surface deformation that occurred within the images’ acquisition period. The theoretical precision is 1/10 of the pixel size, but this value largely depends on the image noise.

The method has been widely used, alone or as a complement to other geodetic techniques, to improve our knowledge of how the Earth’s crust deforms. It is typically called either offset tracking, image-correlation or offset method but it relies on the same principles. There are many studies using the method and its subsequent modifications. As an example, Michel and Avouac (2002) applied the offsets method to measure the displacement field of the Izmit Earthquake (1999, Mw 7.5, Turkey) using SPOT satellite. Dominguez et al. (2003) used SPOT to measure the horizontal displacement field of the Chi–Chi earthquake (1999, Mw 7.6, Taiwan). Coupling their results with an elastic dislocation model (Okada 1985), they understood that the deeper portion of the fault was not activated during the Chi–Chi earthquake.

Klinger et al. (2006) used cross-correlated SPOT data before and after the Kokoxili earthquake (2002, Mw 7.8, Tibet) to extract features suggesting a rupture model with fault segments separated by strong persistent geometric barriers. Michel and Avouac (2006) used sub-metric resolution aerial photographs to precisely map the coseismic displacement field of the Landers earthquake (1992, Mw 7.3, California) and studied in detail the Kickapoo step over. The use of aerial photographs was crucial to measure volcano deformation at Piton de La Fournaise (La Reunion Island) by de Michele and Briole (2007). The method is further used in Leprince et al. (2007), Ayoub et al. (2009) and also in Milliner et al. (2015). Avouac et al. (2006) analyzed the 2006 Mw 7.6 Kashmir earthquake by modelling both seismic waveforms and using sub-pixel offset of the Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) images to measure ground deformation. SPOT is used to map the horizontal displacement field of the Denali earthquake (2002, Mw 7.9, Alaska) by Taylor et al. (2008). If the images are not acquired from exactly the same point of view, the methodology requires that the pre- and post-event images be perfectly resampled to the same geometry by means of a Digital Elevation Model (DEM). This requires a robust sensor focal plane model. If in the case that the latter information is undisclosed (which is often the situation for commercial satellites), then de Michele et al. (2008) suggested a method to extract the displacement field of an earthquake from non-orthorectified images coming from different image sources, by means of Principal Component Analyses. This concept of avoiding the use of a DEM to extract the displacement field of an earthquake is further expressed into the Perpendicular to Epipolar Offset method (Hollingsworth et al. 2012; Ayoub 2014).

In the past two decades, the subpixel correlation technique has become indispensable to map the surface ruptures associated with major earthquakes. The earthquake rupture geometry at the surface can be used as a hint for understanding rupture style and velocity at depth. Jointly with InSAR, GPS and seismological data, Konca et al. (2010) reveal a supershear behaviour of the 1999 Duzce earthquake (Mw 7.1, Turkey). On the other hand, sometimes the surface rupture geometry is particularly simple with respect to the complex source geometry, as highlighted by Wei et al. (2011) for the 2010 El Mayor Cucapah earthquake (Mw 7.2, Mexico). Potentially, if we could acquire images at very high frequency from space, from a geostationary telescope, subpixel offsets could be used as a seismometer, provided that the images’ geometry is exactly the same, as highlighted in Michel et al. (2012). The advent of a new generation of satellites, with improved repetition frequency, allows more and more studies of earthquake ruptures from space. For instance, Landsat 8 has been used by Jolivet et al. (2014b) and Avouac et al. (2014) to show that a geological thrust fault can respond to neo-tectonic stress by slipping with a strike slip mechanism during the Balochistan earthquake (2013, Mw 7.7). In this earthquake, Vallage et al. (2015, 2016) used cross-correlation of SPOT5 images to precisely map the fault rupture at the surface, inferring non-elastic properties of the shallow fault section and structural control on its geometry. In the study of Xu et al. (2016), subpixel offsets of optical data have been used as a hint to challenge a well-established model (the “shallow slip deficit”) pointing out the impact of data resolution on fault process analyses. During the 2016 Mw 7.8 Kaikōura earthquake, New Zealand, Hollingsworth et al. (2017) and Hamling et al. (2017) used Landsat 8, Sentinel 1 and ALOS2 respectively to map the intricate surface ruptures and the displacement field of this complex earthquake. Klinger et al. (2018) derived coseismic horizontal displacements in the Papatea–Jordan–Kekerengu triple junction area using high resolution optical satellite image correlation, with Pleiades and SPOT6. They found evidence for significant off-fault deformation. With this earthquake, Zinke et al. (2019) pushed the methodology further by combining cross-correlation and ray tracing to stereo World View images to retrieve the detailed 3D displacement field, without having to differentiate pre- and post-earthquake DEMs, thus increasing the precision of the measurements. Optical image correlation and SAR offset tracking are today well-established and robust techniques. The advent of the EU Copernicus Sentinel program (particularly Sentinel 1 and 2) brings an unprecedented amount of data, available with high repetition frequency (2 satellites per mission, between 5 and 12 day image acquisitions) and available at no cost. This improves the chances of imaging an earthquake with the offset-tracking methods. At the time of writing, the methodology is routinely used alone (as shown in Fig. 5), where the Palu earthquake (2018, Mw 7.5, Soulawesi) ruptured the surface generating a pluri-metric displacement field (e.g., Scott et al. 2019; Bacques et al. 2020), and in combination—or as a complement—with InSAR (e.g., Marchandon et al. 2018; Scott et al. 2019).

Fig. 5
figure 5

Modified after Bacques et al. (2020)

The displacement field of the Palu earthquake (2018, Mw 7.3, Sulawesi) from Sentinel 2. Ground displacement is presented here as sub-pixel offsets i.e. a fraction of the Sentinel-2 pixel size (plus or minus 5 m in the North–South direction and in the East–West direction (a and b respectively). c A zoom on the Palu city area; offsets are shown as displacement vectors in an area where the North–South displacement is very sharp, indicating the surface trace of the fault rupture. Contains modified Copernicus data.

Full size image

4 Artificial Water Reservoir-Triggered Earthquakes

Earth Observation data typically allow for wide area coverage and measurements of major deformation events, as illustrated in the previous examples. However, in many cases, the geophysical phenomena of interest are small in magnitude, or the background rates from which we try to detect a deviation are themselves small. Thus in situ and local measurements made using sensitive ground-based instruments are often required to fully characterised the evolution of the geophysical process. Additionally, the kind of information sought may require inferences of subsurface structures, which are more suited to be determined from airborne data using differing geophysical tools than perhaps that available from high altitude orbiting satellites. For this case study, we highlight a range of remotely derived observations as applied to understanding the potential for triggering of earthquakes from artificial reservoirs. Artificial water reservoirs are created all over the world for flood control, irrigation and power generation. Under certain geological conditions, the filling of these reservoirs can trigger earthquakes. To date, at least four sites globally have experienced triggered earthquakes exceeding magnitude 6 (Hsingfengkiang in China, Kariba on the Zambia–Zimbabwe border, Kremasta in Greece and Koyna in India). Koyna, located near the west coast of India, is a classic example of such reservoir-triggered seismicity (RTS), whereby triggered earthquakes started soon after the impoundment of the Koyna Dam in 1962. The creation of another (Warna dam), just 20 km south of Koyna in 1985 gave further rise to RTS. So far in the last 57 years, 22 earthquakes of magnitude M ≥ 5, some 200 earthquakes of M ≥ 4 and several thousand smaller earthquakes have occurred in the region (Fig. 6). Detailed studies of RTS events carried out in 1970s has led to the identification of certain characteristics of RTS sequences that delineate them from normal earthquake sequences. The association between water level changes and RTS in Koyna–Warna region is well established. However, the part played by reservoirs in the triggering of earthquakes is not well understood due to the lack of near field studies. The earthquakes are shallow (mostly 2 to 9 km depth), confined to a region of some 30 km by 20 km, and moreover, there is no other source of earthquakes within 100 km of Koyna Dam. To better characterise these processes, the suitability of the Koyna region for setting up a deep borehole laboratory was examined during the International Continental Drilling Program (ICDP) workshop held at Hyderabad and Koyna in 2011. However, prior to committing to an expensive project, a range of datasets were acquired to assess the tectonics of the region to enable the suitable design and deployment of a deep borehole. These included airborne gravity, gravity gradient and magnetic surveys and LiDAR coverage of the Koyna region, amongst several others (Gupta 2017, 2018). A 3 km deep pilot borehole has so far been drilled, with observations currently being made to design the final ~ 7 km deep borehole laboratory.

Fig. 6
figure 6

Location of the Koyna Warna region in the vicinity of west coast of India; epicentres of the 10 December 1967 M 6.3, earthquakes of M 5.0 to 5.9 and smaller events for the period August 2005 to December 2017; locations of surface and bore-well seismic stations; the Western Ghat Escarpment is shown by the green line. (Inset) Location of Koyna in western India. (inset II) Epicentres of M ≥ 3.7 earthquakes during 1967–2015 (USGS) within 50 km (inner) and 100 km (outer circle) of the Koyna Dam. There are almost no seismic events detected outside the Koyna region. Modified from Gupta (2017). The Donachiwada Fault that hosted the 10 December 1967 earthquake and several M ~ 5 and smaller earthquakes is shown by parallel black lines

Full size image

Airborne gravity-gradient and magnetic (AGGM) surveys provide measurements from which density structures and magnetic anomalies can be delineated. Using such surveys, we unravelled the sub-surface structure in the Koyna–Warna region to address the potential controls on the pattern and distribution of observed RTS in the area. The region covered is shown in Fig. 6 and is at a draped surface about 120 m above ground level at an interval of ~ 1 km. The magnetic anomalies are predominately caused by the basaltic layer, which varies in thickness from 400 to 1600 m (Gupta et al. 2016; Mishra et al. 2017). The magnetic data were filtered with a cut-off wavelength of 10 km to focus on the deeper sources of these anomalies. The resulting map broadly depicts the subsurface structure (Fig. 7). It is characterised by a prominent NW–SE trend in the southern region and a NNE-SSW trend in the centre, flanked by a prominent negative anomaly. This anomaly is centred close the Udgiri borehole (Figs. 6, 7). An east–west trend of the anomaly is observed close to the southern end of the Koyna Dam. It has been also found that this east–west trending anomaly disappears when data are filtered with a higher cut-off wavelength leading to the inference of the source of these anomalies being shallower compared to the north–south and northwest–southeast trending anomalies. The northwest-southeast and north–south trending features are prominently identified in the central area of RTS in the filtered anomaly plots. This is consistent with the earthquake cluster in the vicinity of the Western Ghat Escarpment. The subsurface structure below the Donachiwada fault (considered to be the main causative fault of RTS at Koyna) has been inferred using the AGGM data as depicted in Fig. 8. It corresponds to a low in the observed GDD (Vertical Gravity Gradient) and magnetic field, as the top most layer is basalt with high magnetic susceptibility and density increases with depth. The delineated vertical block structure is consistent with the fault inferred from earthquake data.

Fig. 7
figure 7

Location of geophysical investigations in the Koyna–Warna region. These included deployment of 6 borehole seismometers; airborne gravity-gradient—magnetic surveys (green lines), LiDAR coverage (orange polygon), the western limit of LiDAR surveys coinciding with the Western Ghat Escarpment; magneto-telluric profiling. Epicentres of earthquakes of M ≥ 3 for the period August 2005 through December 2015 are also depicted (after Gupta et al. 2016)

Full size image
Fig. 8
figure 8

Low-pass filtered magnetic anomaly map of the region (location of the Koyna and Warna reservoirs are indicated by black outlines). M ≥ 2 earthquakes for the period 2005–2015 are shown by blue dots. AB is a section across the most prominent magnetic anomalies. CD is section across the Donachiwada causative fault (green lines)

Full size image

Topographic data acquired at very high resolutions using LiDAR (Light Detection and Ranging) has become a fundamental remote sensing tool for the Earth sciences (Krishnan et al. 2011). LiDAR data are particularly useful for fault ruptures and for identification of geomorphic markers associated with active faulting (Zielke and Arrowsmith 2012), especially in the presence of forest canopy and vegetation cover that can obscure the subtle geomorphology from observation by optical satellite imagery. There were surface traces of the faulting caused by the Koyna earthquake of 10 December 1967 (Gupta et al. 1999). However, neither the M 5.8 earthquake of 13 September 1967, nor the later M ~ 5 earthquakes in the Koyna–Warna region, provided any surface evidence of faulting at depth. One question that remained unanswered was whether the faulting was confined to the basement only or propagated through the basalt cover as well. A combination of rugged topography and dense vegetation makes fieldwork looking for possible traces of faulting difficult. To overcome this difficulty LiDAR surveys were carried out in the area covering the region of RTS in the Koyna–Warna area. The area covered 1064 sq. km and is shown in Fig. 9 where LiDAR and orthophotograph data were acquired in April 2014 (Arora et al. 2017). A total of 21 ground control points were established before acquisition of multiple return and waveform LiDAR and orthophotograph data. The NNE-SWW trending lineament, starting just south of the Koyna Reservoir and running through the Warna Reservoir is the surface expression of the Donachiwada Fault responsible for most of RTS in the region, including the 10 December 1967 M 6.3 Koyna main earthquake.

Fig. 9
figure 9

LiDAR hillshade DEM of the Koyna region. A major regional north–south fracture across the seismic region and three NNE-SSW trending fracture zones (red lines) are seen from south of the Koyna Reservoir to north of the ridge to the left of the Warna Reservoir. The western most NNE-SSW trend coincides with the trend of the Donachiwada fault (after Gupta et al. 2016)

Full size image

The 1967 earthquake occurred more than two decades before the first observations of ground deformation associated with major seismic events were possible with SAR satellites. However, the magnitude 5 events in 2009 occurred in the era of ALOS SAR data and were just large enough to have surface deformation associated with them. Arora et al. (2018) have focused on the lineaments within the Deccan Traps in the area of RTS in the Koyna Warna region and have shown their connection with the subsurface basement using LiDAR and Synthetic Aperture Radar (SAR) interferometry. Interferometric measurements conducted for the Koyna–Warna region indicated displacement associated with two M ~ 5 earthquakes that occurred on 14 November 2009 and 12 December 2009. Both these earthquakes had normal faulting dominated movement. The size of these events is beyond the detectability limit of InSAR data using single interferograms (as used in the earlier section) and instead a time series approach is required to use larger data volumes before and after the earthquakes to reduce the noise due to atmosphere in the data. As depicted in Fig. 10, a LoS displacement of up to ~ 12 mm between March 2009 and September 2010 was observed. Arora et al. (2018) note that incremental LoS displacement calculated for the total time period of SAR coverage from 12 January 2007 to 10 March 2011 shows that all the displacement occurred within the period March 2009 to September 2010 (i.e. from just before to just after the occurrence of two M ~ 5 RTS events). Direct evidence of faulting was also provided by the slicken sides in the deep bore holes drilled in the region for various scientific investigations and setting up of the borehole seismic network. Arora et al. (2018) conclude that their work supports an inheritance model for basement faulting with repeated earthquakes causing upward propagation of faulting, which in turn causes fractures permitting water from the reservoirs to percolate into faults and consequently triggering earthquakes.

Fig. 10
figure 10

Comparison of total line of sight (LoS) displacements (coloured points, dm) estimated by the Advanced Land Observation Satellite Phased-Array-type L-band Synthetic Aperture Radar (ALOS-PALSAR) images in the Warna area from ascending track 536 (frame 330) for the period from March 2009 to September 2010 with synthetic LoS displacements (isolines, in dm) calculated using fault-plane models of the two M ≥ 5 earthquakes. Positive LoS displacements are directed towards the satellite. Direction of flight and LoS are shown by arrows below the figure. Rectangles are projections to the surface of the fault planes. The asterisks show the epicentres of the two earthquakes (after Arora et al. 2018)

Full size image

Near-field investigations are of utmost importance to comprehend the initiation of an earthquake in a fault zone and observe what proceeds and follows the nucleation process. For these near field studies, it is crucial to locate a suitable place for setting up the necessary near field observation laboratory. At Koyna, India, due to a thick basalt cover and dense vegetation, it was very difficult to trace the surface manifestation of the causative fault of the 1967 M 6.3 earthquake and the continued RTS in the Koyna–Warna region. By combining a range of datasets we have shown that a range of remotely sensed data from airborne gravity-gradient and magnetic surveys, through to LiDAR and SAR Interferometry have provided evidence for the nature the subsurface structure in the Koyna–Warna region. This has helped in tracing the causative Donachiwada fault, and the association of gravity and magnetic anomalies with hypocenters, and that the basement faulting extends to the surface. These inputs have been helpful in locating the site for placing the 3 km deep Pilot Borehole, which was completed in June 2017 (Gupta 2018). Drilling of this Pilot Borehole confirmed that the inferred location of the Donachiwada fault is correct. The work at this Pilot Borehole is in progress and will provide the necessary inputs for designing the ~ 7 km deep main Borehole laboratory.

5 Conclusions

The recent increase in the number of Earth Observation satellites has expanded the use of such data in characterising earthquake deformation. The large data volumes and an open data policy of the Sentinel missions have been an important development for accessibility, and this change has democratised the application and exploitation of such datasets. It has widened the uptake from users for both scientific and commercial use, and it has increased the range of scientific questions that can be addressed, as well as the number of environmental, commercial and industrial applications. Here we have selected a few examples where the data coverage, quality and availability have been optimal to make for good case studies. However, sometimes there is a suboptimal response to an earthquake in terms of coverage for the longer-term postseismic phase, as well as a lack of regular data for a complete time series to look at long-term deformation processes for slowly straining areas. (These recommendations have been discussed in the previous paper, Elliott 2020.)

For the past two and a half decades, SAR satellites have been used to measure surface displacements associated with major earthquakes by an increasing number of research groups using interferometry. Much systematic exploitation using newer Sentinel-1 SAR data has already occurred and this has typically been on focused on larger deformation signals from significant earthquakes (e.g., Lindsey et al. 2015; Floyd et al. 2016; Grandin et al. 2016; Xu et al. 2020), although this is expanding to cover ever-increasing smaller events (Funning and Garcia 2018). As the data coverage and ease of access has improved, the number of potential events to study has greatly expanded. Here we have shown an example of measuring deformation associated with a small earthquake in Turkey and its relationship with the surrounding geomorphology. Whilst the earthquake itself did not pose a particular major shaking hazard to the region, it illuminates a potential source fault in an area that previously contained only a few identified active fault traces. Although ambiguities in interpreting remotely derived datasets still remain, such observations provide an impetus to carefully study an area in terms of the active tectonics. Combining InSAR observations with remotely derived high-resolution topography will continue to improve our assessment for the potential of earthquake shaking near cities. We also described examples of making surface observations using pixel offsets from both optical EO systems and from SAR using the technique of sub-pixel cross-correlation. This method is complementary to InSAR and is particularly suited to observing large offsets associated with major surface rupturing continental earthquakes. Using ever-increasing high-resolution imagery from optical satellites, it is possible to provide huge amounts of detail of the fault rupture at the surface. Important questions of the amount of on and off fault deformation can start to be addressed, as well as to determine the differing behaviour of the crust in terms of elastic and non-elastic behaviour (Diederichs et al. 2019). Finally, we illustrated the importance of combining space-based EO with other airborne remotely derived datasets using an example of triggered seismicity from Konya, India. Using a single source of remotely sensed data is unlikely to give the complete overview of a geophysical process; as is the case here in understanding the impact of reservoir loading on the evolution of seismicity. The importance of a complete synthesis is highlighted for determining the controls and interaction of the subsurface geology and surface loads with the locations and rates of subsequent seismicity.

Improvements in our understanding of earthquakes and faulting will enable better assessments of the locations of future earthquake hazards, as well as help constrain estimates of the sizes and characteristics of shaking sources. Understanding the relative location, depth and extent of earthquake-generating sources near cities is particularly relevant when determining the risk, as the ground accelerations quickly drop off with distance from the fault. Whilst identifying new active fault traces is an important outcome, it is also necessary to identify which portions of a fault did not rupture in a given earthquake because those portions may now be prone to future failure. Here we have focused on illustrating the use of EO with examples of the deformation associated with earthquakes (i.e. the process at the end of the earthquake cycle). However, where newer satellite systems such as Sentinel-1 offer a game-changing approach is in understanding the other parts of the earthquake cycle (Salvi et al. 2012) described in the introduction—in particular that of the long-term strain accumulation building up to earthquakes. Whilst studies of strain rates using Sentinel-1 have focused on deformation over a few 100’s km scale (Shirzaei et al. 2017; Morishita et al. 2020), and have begun to encompass whole countries such as Iceland (Drouin and Sigmundsson 2019), large (1000’s km +) systematic attempts to do so are now only beginning to be achieved (Weiss et al. 2020) as the archive of data becomes suitably long to improve the signal to noise ratio. To make accurate measurements of small deformation signals over long wavelengths requires a continuity of data that is important for establishing a long time series. Also, widespread, consistent coverage is required, with almost all the tectonic zones now being covered regularly by Sentinel-1 offering the chance to capture whole continent-scale deformation. This ability to measure solid Earth processes will be greatly enhanced with the upcoming joint NASA-ISRO SAR mission (NISAR) in a couple of years which will image land surface changes globally.