Abstract
During the last 20 years, geophysicists have developed great interest in using gravity gradient tensor signals to study bodies of anomalous density in the Earth. Deriving exact solutions of the gravity gradient tensor signals has become a dominating task in exploration geophysics or geodetic fields. In this study, we developed a compact and simple framework to derive exact solutions of gravity gradient tensor measurements for polyhedral bodies, in which the density contrast is represented by a general polynomial function. The polynomial mass contrast can continuously vary in both horizontal and vertical directions. In our framework, the original three-dimensional volume integral of gravity gradient tensor signals is transformed into a set of one-dimensional line integrals along edges of the polyhedral body by sequentially invoking the volume and surface gradient (divergence) theorems. In terms of an orthogonal local coordinate system defined on these edges, exact solutions are derived for these line integrals. We successfully derived a set of unified exact solutions of gravity gradient tensors for constant, linear, quadratic and cubic polynomial orders. The exact solutions for constant and linear cases cover all previously published vertex-type exact solutions of the gravity gradient tensor for a polygonal body, though the associated algorithms may differ in numerical stability. In addition, to our best knowledge, it is the first time that exact solutions of gravity gradient tensor signals are derived for a polyhedral body with a polynomial mass contrast of order higher than one (that is quadratic and cubic orders). Three synthetic models (a prismatic body with depth-dependent density contrasts, an irregular polyhedron with linear density contrast and a tetrahedral body with horizontally and vertically varying density contrasts) are used to verify the correctness and the efficiency of our newly developed closed-form solutions. Excellent agreements are obtained between our solutions and other published exact solutions. In addition, stability tests are performed to demonstrate that our exact solutions can safely be used to detect shallow subsurface targets.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Gravity exploration methods try to identify the anomalous mass bodies in the Earth (Blakely 1996). Gravity signals such as gravity fields and gravity gradient tensors are measured using gravimeters and gravity gradiometers, which can be located on the air–Earth interface, in boreholes, or be carried by marine ships and aircraft, and even by satellites (Nabighian et al. 2005). The amplitudes of the gravity field are inversely proportional to the square of the distance (R) between the observation site and the causative body, that is \(O(R^{-2})\). As for the gravity gradient tensor, its amplitude is inversely proportional to the third power of distance, that is \(O(R^{-3})\). Therefore, compared to the gravity field, gravity gradient tensor signals are more sensitive to the shallow anomalous structures in the Earth (Droujinine et al. 2007; Beiki and Pedersen 2010; Martinez et al. 2013; Beiki et al. 2014; Gutknecht et al. 2014; Li 2015; Ramillien 2017). Mathematically, both gravity field and gravity gradient tensor signals can be formulated as volume integrals over the causative body. When the observation site is located inside the mass body, a local spherical coordinate system can be introduced at the observation site, so that a factor of distance squared (\(R^{2}\)) would be introduced (such as \(\mathrm{d}v=R^2 \sin \theta \mathrm{d}r \mathrm{d}\theta \mathrm{d}\phi\), Blakely 1996), which can further weaken the singularity appearing in the integrands of the gravity signals (Jin 2002). Therefore, from the mathematical point of view, the gravity field can be evaluated without mathematical singularities, as \(O(R^{-2}\times R^{2})=O(1)\), but the mathematical singularities always remain in the gravity gradient tensor formulation, when observation sites approach the causative body, that is \(O(R^{-3}\times R^{2})=O(R^{-1})\).
Designing gravity gradiometers for measuring gravity gradient tensor signals is a difficult task. The gravity gradient tensor is a \(3\times 3\) symmetrical tensor with each entry being the second derivatives of the gravitational potential (or the first derivatives of the gravity field or the gravity acceleration). In terms of differential measurements, accelerations of at least two spatially separated masses were generally used to estimate the components of the gravity gradient tensor. Depending on the accuracies of the available gradiometers, gravity gradient tensor signals can be applied in geodesy (0.01 Eötvös to 0.1 Eötvös), autonomous navigation (0.1 Eötvös to 1 Eötvös) and oilfield and mineral exploration geophysics (1 Eötvös to 10 Eötvös) (Evstifeev 2017). In exploration geophysics, the cause of the increased interest in gravity gradiometers is that, compared to gravity anomalies measured by gravimeters, gravity gradient tensor signals contain more detailed information about the subsurface structures (Chapin 1998; Nabighian et al. 2005). Furthermore, compared to gravity field data, gravity gradient tensor anomaly maps generally provide more contrasting and clearer edge delineations, such as those arising from salt domes in oil and gas prospecting (Pedersen and Rasmussen 1990). Up to now, several gravity gradiometers have been adopted in realistic exploration geophysical problems, such as the 3D FTG (full tensor gradiometer) system by Bell Geospace (Bell and Hansen 1998; Bell et al. 1997; Brewster 2016; Abtahi et al. 2016) and the Falcon AGG airborne gravity gradiometer by BHP Billiton (Australia) (Lee 2001).
To invert measured gravity gradient tensor (GGT) signals, we need an accurate forward solver. In general, GGT forward modelling can be performed either numerically or analytically. Using numerical methods such as Gaussian quadrature approaches (Talwani and Ewing 1960), Fourier domain methods (Parker 1973; Wu and Chen 2016), finite-element methods and finite-difference methods (Cai and Wang 2005; Farquharson and Mosher 2009; Jahandari and Farquharson 2013), the GGT signals caused by a mass body can be straightforwardly evaluated. However, the accuracies of numerical GGT signals can be seriously reduced by these numerical methods. For instance, using finite-element and finite-difference methods, improper translation of the computed gravitational potential to its second-order derivatives can lead to serious numerical errors. These undesired precision loss issues can be completely avoided by analytic approaches, which offer highly accurate GGT signals in terms of exact solutions.
Due to early limitations in the considered model geometries, the simple rectangular prismatic element has been widely accepted as a basic element in gravity forward modelling. Using these prismatic elements, the mass distributions in the Earth were simply approximated conceding a certain loss of geometrical accuracy. As for this basic element, several exact solutions of the gravity gradient tensor signals were developed (Forsberg 1984; Li and Chouteau 1998; Montana et al. 1992; Nagy and Papp 2000; Holstein et al. 2013; De Stefano and Panepinto 2016). However, it is difficult to accurately approximate a complex body using prisms. Polyhedral elements are endowed with great flexibility in presentation of 3D mass sources with complex geometries. Compared to prismatic elements, discretisations in terms of polyhedrons need lower numbers of elements to represent complicated mass bodies (Petrović 1996). Several analytical solutions have been successfully derived for the gravity gradient tensor signals of a homogeneous polyhedral body (Okabe 1979; Götze and Lahmeyer 1988; Kwok 1991; Petrović 1996; Werner and Scheeres 1996; Tsoulis and Petrović 2001; Holstein 2002; Tsoulis 2012; Holstein et al. 2013; D’Urso 2014a). Closed-form solutions of the gravity gradient tensor were also derived for other homogeneous simple geometries, such as pyramids (Sastry and Gokula 2016) and cylinders (Rim and Li 2016).
Seeking simplicity, geophysicists often assume that the Earth is composed of 3D anomalies in a layered medium or a succession of strata with horizontally undulating interfaces (e.g., sedimentary basins and underlying bedrock). In each layer, the rock mass density predominantly exhibits depth-dependent variations. To approximate the density variations in sedimentary basins, several closed-form solutions of gravity signals were derived for depth-dependent mass contrast functions, such as exponential functions (Cordell 1973; Chai and Hinze 1988; Chappell and Kusznir 2008), hyperbolic functions (Litinsky 1989; Rao et al. 1995), parabolic functions (Chakravarthi et al. 2002), quadratic polynomials (Rao 1985, 1990; Gallardo-Delgado et al. 2003) and cubic polynomials (García-Abdeslem 2005). Compared to these depth-dependent functions, polynomials offer a more flexible way to approximate arbitrarily variable density distributions. Very recently, Jiang et al. (2017) have given a detailed performance comparison between polynomial mass contrast functions and depth-dependent mass contrast functions for the capability of approximating complicated density distributions in the Earth. The result clearly demonstrates the superiority of polynomial mass contrast functions over the depth-dependent mass contrast functions. As the real Earth has complicated mass density distributions, it is important to deal with a general polynomial mass contrast function, which not only varies in depth (vertical direction), but also varies in the horizontal direction.
For general polynomial functions, Pohánka (1998), Holstein (2003), Hansen (1999), D’Urso (2014b) and Ren et al. (2017a) have successfully derived closed-form solutions for the gravity field of a polyhedral body, in which the mass contrast linearly varies in both horizontal and vertical directions. Quite recently, analytical expressions for the gravity field of a polyhedral body with cubic polynomial density contrast in both horizontal and vertical directions were derived by D’Urso and Trotta (2017) and Ren et al. (2018). Nevertheless, only Holstein (2003) and D’Urso (2014b) have successfully derived closed-form solutions for gravity gradient tensor of a polyhedral body, in which the mass contrast varies linearly in both horizontal and vertical directions. To the best of our knowledge, closed-form solutions for gravity gradient tensor signals of a polygonal body with high-order polynomial mass contrasts (such as quadratic and cubic orders) varying in both horizontal and vertical directions have not been previously reported.
To overcome this both theoretically and practically important issue, we have successfully derived closed-form solutions for modelling the gravity gradient tensor of the above cases in this study. Inside the polyhedral body, its density contrast is approximated by a general polynomial function (currently, a maximum order up to and including three is considered). The polynomial mass contrast function can vary in both horizontal and vertical directions. Therefore, it has the capability to approximate complicated mass contrasts in realistic Earth models. To begin with, we apply the Gaussian gradient theorem to transform the volume integrals of GGT signals into surface integrals over the faces of polyhedra. Then, we apply the surface divergence theorem to further transform these surface integrals into a sequence of line integrals along the edges of the polyhedra. In the process of reducing the integral dimension, several vector or dyadic identities are employed to reduce the orders of the density polynomials and of the singularities in R in the integrands. The line integrals along the edges of the polyhedra are evaluated in terms of known analytical expressions (e.g., Gradshteyn and Ryzhik 2007).
To verify the accuracies of our new analytical solutions, a right rectangular prism with depth-dependent density contrasts, an irregular polyhedron with linear density contrast and a tetrahedral element with horizontally and vertically varying density contrast are tested. For the prism model, its reference solution for the gravity gradient tensor is computed from the derivatives of García-Abdeslem’s (2005) analytical solution for the gravity field. The analytical solution derived by Holstein (2003) is used as reference for the irregular polyhedral model. Results from high-order Gaussian quadrature are used as reference solutions for the tetrahedron model.
2 Theory
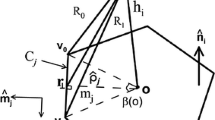
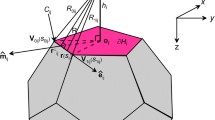
Illustration of the geometry of a polyhedral body H and the associated geometric quantities on face \(\partial H_i\) with their definitions given in Table 5
For an arbitrary interior point \({\mathbf {r}}\) of the polyhedral body (see Fig. 1, Appendix A and Table 5), let \(\lambda ({\mathbf {r}})\) denote the density contrast in the polyhedral mass target at that point. The difference between two points denotes a vector, for example, the vector from a source point \({\mathbf {r}}\) to the observation point \({\mathbf {r}}'\) is denoted by \({\mathbf {r}}-{\mathbf {r}}'\). The gravitational acceleration field at the observation point \({\mathbf {r}}^\prime\) is (Ren et al. 2018)
where \(G=6.673\times 10^{-11}\, {\text {m}}^3\,{\text {kg}}^{-1}\,{\text {s}}^{-2}\) is Newton’s gravitational constant, \(\nabla _{\mathbf {r}}\) is the gradient operator on point \({\mathbf {r}}\), \(R=|{\mathbf {r}}-{\mathbf {r}}'|\) is the distance from the observation site to the running integral point in the source polyhedral body H, and the gradient theorem (Tai 1997) is applied.
Using Eq. (1) for the gravity field, the gravity gradient tensor \({\mathbf {T}}\) can be derived as follows:
where \(\nabla _{{\mathbf {r}}^\prime }\) denotes the gradient operator on point \({\mathbf {r}}^\prime\) and the relation \({\nabla _{{\mathbf {r}}}}\frac{1}{R} = -{\nabla _{\mathbf {r'}}}\frac{1}{R}\) is used.
Using the following vector identity (Tai 1997):
where \(\mathbf {A}\) can be a scalar or a vector, setting \(\varphi = \frac{1}{R}\) and \(\mathbf {A}= \nabla \lambda\) and using the gradient theorem (Tai 1997), the volume integral term \(\iiint _H {({\nabla _{{\mathbf {r}}}}\frac{1}{R})({\nabla _{{\mathbf {r}}}}\lambda ) \mathrm{d}v}\) in Eq. (2) can be further transformed as
Setting \(\varphi = \frac{1}{R}\) and \(\mathbf {A} = \lambda\) in Eq. (3), the surface integral \(\iint _{\partial {H_i}} {\lambda {\nabla _{{\mathbf {r}}}}\frac{1}{R}{\mathrm{d}}s}\) in Eq. (2) can be transformed as
where the surface gradient theorem (Tai 1997) is used. The symbol \(\nabla _{s}\) denotes the surface gradient operator, where the subscript s means it is an operator on a 2D surface. In the above, the definition (A.3) of the number \(h_i\), constant over facet plane i, as the projection onto the facet normal \(\mathbf {n}_i\) of the position vector of a planar point \({\mathbf {r}}\) relative to the observation point \({\mathbf {r}}'\) and the following vector identity were used:
where f is an arbitrary scalar function and \({\hat{\mathbf {n}}}\) is the outward pointing normal unit vector of the considered surface. In Eq. (5), we set \(f=\frac{\lambda }{R}\).
Substituting Eqs. (4) and (5) into Eq. (2), we obtain the following expression for the gravity gradient tensor of a polyhedral body H with arbitrary mass contrast function \(\lambda ({\mathbf {r}})\):
The density function \(\lambda\) is defined as a general polynomial function. It allows for the density variations in both horizontal and vertical directions, which is defined as:
where P is the maximum polynomial order, and \(\lambda _{d}\) are the d-th order density terms. For instance, the zero (constant), first (linear), quadratic and cubic order density terms are given as:
where \(a_{klm}\) are known coefficients which can be estimated by fitting measured gravity field data (Blakely 1996). The total gravity signal is the sum of the individual contributions from different mass densities, such as \(\lambda _0\), \(\lambda _1\), \(\lambda _2\) and \(\lambda _3\).
Substituting the density contrast in Eqs. (8) into (7), we get the final gravity gradient tensor:
where \({\mathbf {T}}_{d}\) denotes the individual contribution from the d-th order density contrast. In this study, we only consider the cases \(0 \le P \le 3\). For simplicity, we denote x, y and z by \(x_p (p=1, 2, 3)\) in the following sections, that is
2.1 Constant Density Contrast
For the constant term, substituting \(\lambda _0=a_{000}\) and \(\nabla _{{\mathbf {r}}}\lambda _0=0\) into Eq. (7), we get \({\mathbf {T}}_0\) as follows:
Detailed derivations of expressions for the line integral \(\int\nolimits _{C_{ij}} \frac{1}{R}{\mathrm{d}}l\) and the surface integral \(\iint \nolimits _{\partial {H_i}} {\frac{1}{{{R^3}}}{\mathrm{d}}s}\) are given in Appendix B.
2.2 Linear Density Contrast
As for the linear terms in the polynomial density contrast, we set \(\lambda _1=\mathbf {a}\cdot {\mathbf {r}}\), where \(\mathbf {a}=(a_{100}, a_{010}, a_{001})\) and \({\mathbf {r}}=(x,y,z)\). Substituting \(\lambda =\lambda _1=\mathbf {a}\cdot {\mathbf {r}}\) and \(\nabla _{\mathbf {r}}\lambda =\nabla _{\mathbf {r}}\lambda _1=\mathbf {a}\) and \(\nabla _{\mathbf {r}}\nabla _{\mathbf {r}}\lambda _1=\mathbf {0}\) into Eq. (7), we get
The above equation consists of one kind of line integral, i.e., \(\int _{C_{ij}} {\frac{{\mathbf {r}}}{R}{\mathrm{d}}l}\) and two kinds of surface integrals, i.e., \(\iint _{\partial {H_i}}\) \({\frac{{\mathbf {r}}}{R^3}{\mathrm{d}}s}\) and \(\iint _{\partial H_i}\frac{1}{R}{\mathrm{d}}s\), with their detailed derivations given in Appendix C.
2.3 Quadratic Density Contrast
As for the quadratic term in the polynomial density contrast in Eq. (11), its gradient is
The second derivative of \(\lambda _2\) is
Substituting \(\lambda _2\) and its derivatives \(\nabla _{{\mathbf {r}}}\lambda _2\) and \(\nabla _{{\mathbf {r}}}\nabla _{{\mathbf {r}}}\lambda _2\) into the general expression of the gravity gradient tensor in Eq. (7), four kinds of integrals need to be considered (their detailed derivations are given in Appendix D), which are the line integral term \(\int _{C_{ij}}\frac{x_px_q}{R}{\mathrm{d}}l\), the surface integral term \(\iint _{\partial H_i}\frac{x_px_q}{R^3}{\mathrm{d}}s\), the surface integral term \(\iint _{\partial H_i}\frac{x_p}{R}{\mathrm{d}}s\) and the volume integral term \(\iiint _H\frac{1}{R}\mathrm{d}v\), where, using \(p, q=1,2,3\), the notations in Eq. (14) are adopted, and the product \(x_px_q\) represents an arbitrary quadratic monomial.
2.4 Cubic Density Contrast
Finally, we discuss the gravity gradient tensor due to the cubic density terms given in Eq. (12). For the first- and second-order derivatives in Eq. (7), we have
and
Substituting \(\lambda _3\), \(\nabla _{\mathbf {r}}\lambda _3\) and \(\nabla _{\mathbf {r}}\nabla _{\mathbf {r}}\lambda _3\) into the expression of the gravity gradient tensor in Eq. (7), we find that we only need to deal with four types of integrals (their detailed derivations are given in Appendix E) to get the final closed-form solutions of \({\mathbf {T}}_{3}\) in Eq. (13). These four types of integrals are the line integral \(\int _{C_{ij}}\frac{x_px_qx_t}{R}{\mathrm{d}}l\), the surface integral \(\iint _{\partial H_i}\frac{x_px_qx_t}{R^3}{\mathrm{d}}s\), the surface integral \(\iint _{\partial H_i}\frac{x_px_q}{R}{\mathrm{d}}s\) and the volume integral \(\iiint _H\frac{x_p}{R}\mathrm{d}v\), with \(p,q,t=1,2,3\). Here, the notations in Eq. (14) are used, such that \(x_px_q\) and \(x_px_qx_t\) represent arbitrary quadratic and cubic monomials, respectively.
2.5 Comparison with Other Solutions
The previously published analytical solutions of gravity gradient tensors for different geometries and mass density contrasts are listed in Table 1. Most of these solutions were designed for rectangular prisms with constant density contrasts (Forsberg 1984; Montana et al. 1992; Li and Chouteau 1998; Nagy and Papp 2000; Rim and Li 2016) and for polyhedra (or cylinders) with constant density contrasts (Okabe 1979; Götze and Lahmeyer 1988; Kwok 1991; Werner and Scheeres 1996; Holstein 2002; Holstein et al. 2007a, b; Tsoulis and Petrović 2001; Tsoulis 2012; D’Urso 2014a). Only a few studies have been carried out for linear mass density contrasts (Holstein 2003; D’Urso 2014b; Sastry and Gokula 2016). Using our new findings, we successfully derive a set of analytical expressions of the gravity gradient tensor signals for a general polyhedron with constant, linear, quadratic and cubic polynomial mass functions. Our closed-form solutions for constant and linear polynomial mass functions may have different forms from the previously published solutions, but they should produce the same results. In addition, we were not only the first to find the exact solutions for the quadratic and cubic cases, but also our solutions allow for mass contrasts varying simultaneously in both horizontal and vertical directions. However, it is difficult to derive closed-form solutions of the GGT for higher-order polynomial density contrasts, simply because analytical expressions cannot be found for 1D edge integrals in terms of the existing integral tables (Gradshteyn and Ryzhik 2007).
3 Verification
Three models were used to validate our closed-form solutions. The first one is a rectangular prism model (Fig. 2), for which the derivatives of closed-form solutions for the gravity field in García-Abdeslem (2005) were taken as references. The second model is an irregular polyhedron with linear density contrast, taken from Holstein (2003), for which a comparison with Holstein’s (2003) solution is given. The third model is a relatively complicated tetrahedral body (Fig. 5). As there are no reference solutions for the GGT of polyhedral mass bodies with quadratic and cubic density contrasts, we have used high-order Gaussian quadrature rules (such as 512 × 512 × 512 = 124,217,728 quadrature points) to calculate GGT reference solutions. Additionally, we allowed the density in the tetrahedral body to vary in both horizontal and vertical directions. We should mention that because our formulae require the observation site to be located at the origin of the Cartesian coordinate system, for each observation site, a coordinate translation must be performed to move the observation site to the origin.
3.1 A Prismatic Body with Depth-Dependent Density Contrast
The prism is located in a Cartesian coordinate system with the z-axis downward. In Fig. 2a, the coordinate ranges of the prismatic body are \(x=[10,20]\) km, \(y=[10,20]\) km and \(z=[0,8]\) km. The density function is a depth-dependent cubic polynomial which is taken from García-Abdeslem (2005):
where the density contrast is in \({\text {kg}}/{\text {m}}^{3}\) and z is in km.
a García-Abdeslem’s (2005) prism model. b The prism in the left panel is decomposed into two polyhedral bodies
In the García-Abdeslem’s (2005) work, an analytic formula for the vertical gravity field caused by a rectangular prism with density contrast varying as a depth-dependent cubic polynomial was derived. Therefore, we took the derivatives of García-Abdeslem’s solution (i.e., \(T_{xz}\), \(T_{yz}\), \(T_{zz}\)) as references to verify our solution for the gravity gradient tensor. Furthermore, to verify our solution for an arbitrary polyhedral body, we decomposed the original rectangular prism into two polyhedra (as shown in Fig. 2b). These two polyhedra share the plane with vertices 1, 3, 8 and 9. Note, this test requires points 1, 3, 8 and 9 to be co-planar. If they were not co-planar, the surface (1, 3, 8, 9) would need to be divided into two triangles (1, 3, 8) and (3, 8, 9). The values of \(T_{xz}\), \(T_{yz}\) and \(T_{zz}\) were computed at two observation sites. One is located at point (12, 12, − 0.001) km with a 1-m offset right above the top face of the prismatic body, whereas the other one is located at point (20, 10, − 0.001) km, that is near a corner of the rectangular prism.
The results computed by our closed-form solution and by derivatives of García-Abdeslem’s (2005) gravity field solution are compared in Table 2. We compare GGT elements \(T_{xz}\), \(T_{yz}\), \(T_{zz}\), because only \(g_z\) is given in García-Abdeslem (2005). Excellent agreement is obtained between these two approaches, with relative errors on the order of \(10^{-13}\%\) at site (12, 12, − 0.001) km and relative errors \(10^{-6}\)–\(10^{-7}\%\) at site (20, 10, − 0.001) km. The tensor trace \(T_{xx}+T_{yy}+T_{zz}=\nabla ^{2}_{{\mathbf {r}}'}U\) is a useful tool for indicating numerical error. Using the Poisson equation \(\nabla ^2_{{\mathbf {r}}'}U=-4\pi G\lambda\) for the gravitational potential U, the tensor trace vanishes outside the source body and is \(-4\pi G\lambda\) inside the source body. Since our observation points are outside the source body, we have calculated the relative errors shown in Table 2 as \(|T_{xx}+T_{yy}+T_{zz}|/(|T_{xx}|+|T_{yy}|+|T_{zz}|)\). The relative error of the tensor trace is \(2.74\times 10^{-13}\%\) at the location above the top face and \(3.77\times 10^{-11}\%\) above the corner. Both our solution and García-Abdeslem’s (2005) solution for the GGT are singular, when observation sites are located on edges and corners. When the observation site gets close to the corner, the mathematical singularity becomes stronger, and this is, why the relative error is larger at site (20, 10, − 0.001) km.
In summary, the excellent agreement of the different solutions has successfully verified the accuracy of our new closed-form solutions for a polyhedral body with depth-dependent polynomials up to and including cubic order.
3.2 An Irregular Polyhedron with Linear Density Contrast
An irregular polyhedron is tested to compare our solution with Holstein’s (2003) solution for linear media. The target model is composed of 8 faces and 10 points (Fig. 3), originally designed by Holstein et al. (1999, Appendix A). The linear density contrast inside the target body is taken from Holstein (2003, Appendix C), that is
where the density \(\lambda\) is in \(\mathrm {kg}/\mathrm {m}^3\), coordinates are given in km. First, we compute the gravity gradient tensor at two test points, an outer point with coordinates of (0, 0, 0) km and an interior point at the centroid \(\bar{\mathbf {R}}=\frac{1}{88}(40,250,-1541)\) km. The results are shown in Table 3. An excellent agreement is obtained between our closed-form solution and Holstein (2003)’s solution.
Irregular polyhedral model described in Holstein et al. (1999, Appendix A). \((x,\;y,\;z)\) coordinates of the vertices are 1 \((10, 10, -12)\) km, 2 \((10, -10, -12)\) km, 3 \((-10, -10, -12)\) km, 4 \((-10, 10, -12)\) km, 5 \((-20, 30, -12)\) km, 6 \((30, 30, -12)\) km, 7 \((20, 20, -22)\) km, 8 \((20, -30, -22)\) km, 9 \((-20, -30, -22)\) km and 10 \((-20, 20, -22)\) km. Two test points for comparison with Holstein’s (2003) solution are marked by blue stars. A vertical profile is marked by a red dotted line
Second, the gravity gradient anomalies are evaluated on a vertical profile passing through the target body, in order to validate our formulas by the well-known Poisson equation \(\nabla ^2_{{\mathbf {r}}'}U=-4\pi G\lambda\), where U is the gravitational potential. The vertical profile is from a point with coordinates of \((0, 0, -\,34)\) km to a point with coordinates of (0, 0, 0) km, with observation points placed at a uniform vertical (z) spacing of 1 km. Due to the discontinuity of the gradient tensor signals on the boundary, we only perform tests at two points which are very close to the boundary (with a small distance of \(\pm \,10^{-10}\) km). The value of \(-4\pi G\lambda\) is used as the reference. The relative errors are calculated using the formula \(\frac{(T_{xx}+T_{yy}+T_{zz})+4\pi G\lambda }{|T_{xx}|+|T_{yy}|+|T_{zz}|}\) and shown in Fig. 4. The maximum absolute relative error is \(3.08389\times 10^{-13}\%\).
a Comparison of the Laplacian term \(T_{xx}+T_{yy}+T_{zz}\) calculated by our new closed-form solution to the reference value of \(-4\pi G \lambda\) for the causative body in Fig. 3. b Relative errors calculated as \(\frac{(T_{xx}+T_{yy}+T_{zz})+4\pi G\lambda }{|T_{xx}|+|T_{yy}|+|T_{zz}|}\)
3.3 A Tetrahedral Mass Body with Horizontal and Vertical Density Contrasts
In practical gravity exploration, the underground mass bodies can have complicated shapes. To calculate their GGT signals, we generally need to discretise the underground mass bodies into sets of disjoint elements with different shapes, such as structured hexahedral or prismatic elements and unstructured tetrahedral elements. Compared to regular prismatic elements, unstructured tetrahedral elements can well approximate arbitrarily complicated anomalies. Using recent Delaunay triangulation techniques (e.g., Si 2015), geophysicists can easily set up discretised triangulated grids to represent complicated anomalous targets. Therefore, unstructured grid techniques have been widely used in the geophysical community, not only in gravity exploration (Jahandari and Farquharson 2013; Ren et al. 2017c), but also in the electromagnetic induction community (Li and Key 2007; Schwarzbach et al. 2011; Ren et al. 2013) and the seismic imaging field (Lelièvre et al. 2011). Testing a single tetrahedral mass body not only aims to test the performance of our new closed-from solutions for complicated density contrasts (horizontal and vertical density contrasts), but also demonstrates its compatibility with other codes developed for unstructured grids. This verification is an important step towards joint inversion for multiple parameters, such as magnetisation vector, conductivity, velocity and mass density on the same unstructured gird.
The geometry of the tetrahedron is shown in Fig. 5. We used the density contrast as given in D’Urso and Trotta (2017, equation 166), which includes horizontal variation of the density contrast
where the unit of the density is kg /m\(^3\) and the units of the coordinates are km.
A tetrahedron with cubic polynomial density contrast. The coordinates of the vertices are (0, 0, 0.02) km for vertex 1, \((-\,0.05,0.01,0.1)\) km for vertex 2, (0.05, 0.05, 0.08) km for vertex 3 and \((0.05,-0.05,0.05)\) km for vertex 4. The measuring plane is marked by red colour and located at \(x=[-0.16, 0.16]\) km, \(y=[-0.16, 0.16]\) km and \(z=0\) km. The red dashed line marks a profile passing through the interior
A measuring plane is located above the tetrahedron in a range of \(x=[-\,0.16, 0.16]\) km, \(y=[-\,0.16, 0.16]\) km and \(z=0\,\)km. On the measuring plane, the gravity gradient tensors were computed using our closed-form solution and a Gaussian quadrature rule with \(512\times 512\times 512\) points. The high-order Gaussian quadrature rule was built by projecting the tetrahedral element into a hexahedral element (Rathod et al. 2006) and then applying the standard Gauss Legendre Quadrature rule (Golub and Welsch 1969). Since there are no published results of GGTs for high-order polynomial density contrasts, we compare to results computed by high-order Gaussian quadrature as the reference solutions. The six components of the gravity gradient tensor are shown in Fig. 6 for our analytical solutions and in Fig. 7 for Gaussian quadrature solutions. The relative errors with regard to the Gaussian quadrature solution are shown in Fig. 8. Clearly, the results from our analytical solution agree quite well with those computed by the Gaussian quadrature rule, with absolute relative errors less than \(2\times 10^{-7}\%\). The computation time for the analytical solution is about 0.9 s, and the computation time for \(512\times 512\times 512\) points Gaussian quadrature is about 3.7194 h.
Similar to Fig. 6, but for solutions calculated by Gaussian quadrature with \(512\times 512\times 512\) points
Furthermore, the sums of the diagonal entries \(T_{xx}+T_{yy}+T_{zz}\) were computed using the analytical solution. When the observation site is outside the source region, as in our example, these three diagonal entries satisfy the Laplace equation, that is \(\nabla ^2U=T_{xx}+T_{yy}+T_{zz}=0\), thus providing an independent means of verification of our closed-form solutions. As shown in Fig. 9, the relative error \(|T_{xx}+T_{yy}+T_{zz}|/(|T_{xx}|+|T_{yy}|+|T_{zz}|)\) has a maximum value of \(3.26\times 10^{-12}\%\). Therefore, the condition of \(\nabla ^2U=T_{xx}+T_{yy}+T_{zz}=0\) is satisfied by our solutions.
a Absolute values of tensor traces \(T_{xx} +T_{yy} +T_{zz}\) of our closed-form solution for a tetrahedral anomaly and observation sites distributed on a plane (Fig. 5). The density contrast is given in Eq. (23). b Relative errors of tensor traces \(T_{xx} +T_{yy} +T_{zz}\) calculated as \(|T_{xx}+T_{yy}+T_{zz}|/(|T_{xx}|+|T_{yy}|+|T_{zz}|)\)
Next, with the aim of testing the case of cross-varying mass contrasts, the following density contrast and the same tetrahedral body as shown in Fig. 5 were used:
where the unit of density is kg /m\(^3\) and the units of the coordinates are km. This density contrast function simultaneously varies in both horizontal and vertical directions, ranging from about \(-300\) to 400 kg/m\(^3\). A measurement profile is positioned at \(x=[-0.2, 0.2]\) km, \(y=0\) km and \(z=0\) km. The six components of the gravity gradient tensor were calculated by our analytical formulae and Gaussian quadrature with \(512\times 512\times 512\) points as shown in Fig. 10. The relative errors of our solutions with respect to the Gaussian quadrature solutions are shown in Fig. 11. Note, that the maximum absolute relative errors are less than \(5\times 10^{-8}\)%. Therefore, the results computed by our analytical solution have excellent agreement with those computed by high-order Gaussian quadrature, for this case where the density contrast simultaneously varies in both horizontal and vertical directions. Furthermore, a test was conducted with observations sites located on a path at \(x=[-0.05,0.05]\) km, \(y=0\) km, \(z=0.04\) km crossing the interior. For this setup, the tensor elements and traces \(T_{xx}+T_{yy}+T_{zz}\) were calculated. An excellent agreement between the computed traces of the gravity gradient tensor and the reference value of \(-4\pi G\lambda\) (see Fig. 12) is obtained, which clearly verifies our closed-form solution.
Gravity gradient tensors of the tetrahedron model (Fig. 5) along the profile at \(x=[-0.2, 0.2]\) km, \(y=0\) km and \(z=0\) km calculated by our analytical method (solid lines) and the high-order Gaussian quadrature rule with \(512\times 512\times 512\) points (circles). The mass contrast is given in Eq. (24)
a Comparison of the Laplacian term \(T_{xx}+T_{yy}+T_{zz}\) calculated by our new closed-form solution to the reference value of \(-4\pi G \lambda\) for the tetrahedral body in Fig. 5. b Relative errors calculated as \(\frac{(T_{xx}+T_{yy}+T_{zz})+4\pi G\lambda }{|T_{xx}|+|T_{yy}|+|T_{zz}|}\). As shown in Fig. 5, the measuring profile passes through the interior with coordinates of \(x=[-0.05, 0.05]\) km, \(y=0\) km and \(z=0.04\) km
3.4 Numerical Stability
Theoretically, closed-form solutions should be accurate. However, due to the limitations of floating point arithmetics, these solutions contain inevitable rounding errors, when the amplitudes of the gravity signals approach zero. This phenomenon has been observed in previous studies (Holstein and Ketteridge 1996; Holstein 2003; Holstein et al. 2007a), which shows that the relative error of the gravity field will grow, when the distance between the mass target and the observation site approaches infinity. We use relative error here to avoid discussion of anomaly magnitude and instrument-dependent measurement accuracy. Beyond a certain distance, gravity anomalies can even be totally corrupted by floating point errors. Assuming that the mass body has a size of \(\alpha\) and the site-to-target distance is denoted by \(\delta\), the growth of the relative error \(\eta\) satisfies the following formula (Holstein and Ketteridge 1996; Holstein 2003; Holstein et al. 2007a):
where \(\gamma\) is defined as \(\gamma =\alpha /\delta\), \(\gamma ^{-1}\) is referred to as the dimensionless target distance, the exponent \(\kappa\) indicates the speed of error growth, and \(\varepsilon\) is the relative error when \(\frac{1}{\gamma }=1\), identified in these papers as the floating point machine precision constant. On a log–log scale plot, Eq. (25) is a linear error growth curve \(\lg (\eta )=\kappa \lg \left( \frac{1}{\gamma }\right) +\lg (\varepsilon )\).
We present an experiment, in which the tetrahedron shown in Fig. 5 was used to recover the above linear error growth curve. The size of the tetrahedron was set to the diameter of its circumscribed sphere, that is \(\alpha =0.134\) km. The starting point for the profile is located at the centre of the circumscribed sphere of the tetrahedral model. The measuring profile is formulated as \(x=y, z=0\) km.
Following Holstein et al. (2007a), the equivalent mass point approach was adopted as the reference solution, by which the tetrahedral body is approximated by a point source located at the centre of the circumscribed sphere. The anomalies calculated by our new closed-form expressions and by the equivalent point-mass approach are denoted by T and \({T}_{\mathrm{point}}\), respectively. In addition, the relative errors \(\eta =\left| {T}-{T}_{\mathrm{point}}\right| /\left| {T}_{\mathrm{point}}\right|\) were computed. Four polynomial density contrasts of different orders were used for the stability test:
where the unit of the density contrast is kg/m\(^3\) and the units of the coordinates are km. The ranges of density contrasts are about 200–1800 kg/m\(^3\) for the linear case, about 40–2200 kg/m\(^3\) for the quadratic case and about 10–2250 kg/m\(^3\) for the cubic case.
The relative error curves are shown in Fig. 13 for the above four density contrasts. In Fig. 13, at low dimensionless target distances \(\gamma ^{-1}\), the relative errors decrease with increasing \(\gamma ^{-1}\), because the tetrahedron is better approximated as a mass point with increasing distance. However, the gravity anomalies are progressively corrupted with increasing target distance, and when the dimensionless target distance (\(\gamma ^{-1}\)) is beyond a critical value, the rounding error in the unstable calculations exceeds the solution difference, resulting in a rising trend of the relative errors (cf. Holstein 2003). We reconstructed the entire error growth curves by extrapolating the ascending parts back to \((\gamma ^{-1}=1,\;\eta =\varepsilon )\). In Fig. 13, the reconstructed curves are denoted by blue dashed lines. We observe that there are two linear error growth trends for each polynomial density contrast, that is \(T_{zx}\) and \(T_{zy}\) share the same error growth behaviour, and \(T_{xx}\), \(T_{yy}\), \(T_{zz}\) and \(T_{yx}\) share the same error growth behaviour. The estimated values of \(\kappa\) are shown in Table 4. Using the estimated \(\kappa\), the critical dimensionless target distances were calculated from that value of \(\gamma ^{-1}\) where the rising part of the error curve indicates a relative error of 1 (Holstein and Ketteridge 1996; Holstein 2003; Zhou 2010) in Eq. (25), which are also shown in Table 4.
As shown in Table 4, for the linear density case, \(\kappa\) is about 4.31 for \(T_{xx}\), \(T_{yy}\), \(T_{zz}\) and \(T_{xy}\) and about 5.28 for \(T_{xz}\) and \(T_{yz}\), which agrees with previously estimated values of 4 and 5 given by Holstein (2003), respectively. As \(\kappa\) indicates the error growth speed, Table 4 and Fig. 13 also show that the higher the order of the density contrast polynomial is, the faster the errors accumulate. At the critical dimensionless target distance, the accumulated rounding error has the same amplitude as the true anomaly. Therefore, to safely use our exact solution, we should require our observation sites to be located in a range, which is less than the critical value \(\frac{1}{\gamma _{\mathrm{crit}}}\). Finally, interested readers are referred to Table 4 for the specific dimensionless site-target distances for the constant, linear, quadratic and cubic density cases.
4 Conclusions
In the presented work, we have derived a set of closed-form solutions for the gravity gradient tensor of an arbitrary polyhedral body. The density contrast of the polyhedral body is represented as a polynomial function of up to and including third order. The polynomial function allows density contrasts to simultaneously vary in both horizontal and vertical directions. To our best knowledge, this is the first time that analytical solutions of the gravity gradient tensor are derived for an arbitrary polyhedral body with polynomial orders up to three. Three synthetic models (a prismatic body, an irregular polyhedron and a tetrahedral body) were used to test the correctness and the efficiency of our newly developed closed-form solutions. By comparing to published closed-form solutions and high-order Gaussian quadrature solutions, the high accuracies of our solutions with deviations of less than \(2\times 10^{-7}\)% from the Gaussian quadrature solutions were demonstrated. The computation time used by our analytical solution is significantly less than that of the high-order Gaussian quadrature.
The numerical stability tests show that, when dealing with cubic density contrast, our closed-form solutions would generate inaccurate solutions, if the dimensionless target distance, which is defined as the ratio of the distance between the observation site and the causative body to the dimension of the causative body, is larger than about 282 for \(T_{xx}\), \(T_{yy}\), \(T_{zz}\), \(T_{yx}\) components, and 137 for \(T_{zx}\), \(T_{zy}\) components, on a profile with \(x=y\) and \(z=0\,{\text {m}}\). This inaccuracy problem is caused by the limited precision of floating point operations, when the amplitudes of the gravity gradient tensors are very close to zero. However, since most applications of gravity gradient tensors aim at detecting anomalous bodies in the very shallow subsurface of the Earth, this problem of precision loss should not cause a serious problem in practical situations, and our closed-form solutions are very safe to be applied in exploration geophysics.
For the cases of constant, linear, second and cubic polynomial order, there are systematic recurrences of previously evaluated integrals as well as occurrences of new types of integrals, when going to higher polynomial order. We assume that this is a trend even for higher polynomial orders (\(P>3\)). However, extending our work to higher polynomial orders will be a nontrivial task as more and more complicated integrals need to be considered. By contrast, using the analytical expressions presented in this study, closed-form solutions for the magnetic field can be derived easily.
References
Abtahi SM, Pedersen LB, Kamm J, Kalscheuer T (2016) Consistency investigation, vertical gravity estimation and inversion of airborne gravity gradient tensor data—a case study from northern Sweden. Geophysics 81(3):B65–B76
Beiki M, Pedersen LB (2010) Eigenvector analysis of gravity gradient tensor to locate geologic bodies. Geophysics 75(6):I37–I49
Beiki M, Keating P, Clark DA (2014) Interpretation of magnetic and gravity gradient tensor data using normalized source strength—a case study from McFaulds Lake, Northern Ontario, Canada. Geophys Prospect 62(5):1180–1192
Bell RE, Hansen RO (1998) The rise and fall of early oil field technology: the torsion balance gradiometer. Lead Edge 17(1):81–83
Bell RE, Anderson R, Pratson L (1997) Gravity gradiometry resurfaces. Lead Edge 16(1):55–59
Blakely RJ (1996) Potential theory in gravity and magnetic applications. Cambridge University Press, Cambridge
Brewster J (2016) Comparison of gravity gradiometer designs using the 3D sensitivity function. SEG Tech Progr Expand Abstr 2016:1583–1587
Cai Y, Wang C (2005) Fast finite-element calculation of gravity anomaly in complex geological regions. Geophys J Int 162(3):696–708
Chai Y, Hinze WJ (1988) Gravity inversion of an interface above which the density contrast varies exponentially with depth. Geophysics 53(6):837–845
Chakravarthi V, Raghuram H, Singh S (2002) 3-D forward gravity modeling of basement interfaces above which the density contrast varies continuously with depth. Comput Geosci 28(1):53–57
Chapin D (1998) Gravity instruments: past, present, future. Lead Edge 17(1):100–100. https://doi.org/10.1190/1.1437806
Chappell A, Kusznir N (2008) An algorithm to calculate the gravity anomaly of sedimentary basins with exponential density-depth relationships. Geophys Prospect 56(2):249–258
Cordell L (1973) Gravity analysis using an exponential density-depth function—San Jacinto Graben, California. Geophysics 38(4):684–690
De Stefano M, Panepinto S (2016) On the approximation of the potential fields when using right rectangular prisms. Geophys Prospect 65:1366
Droujinine A, Vasilevsky A, Evans R (2007) Feasibility of using full tensor gradient (FTG) data for detection of local lateral density contrasts during reservoir monitoring. Geophys J Int 169(3):795–820
D’Urso M (2014a) Analytical computation of gravity effects for polyhedral bodies. J Geod 88(1):13–29
D’Urso M (2014b) Gravity effects of polyhedral bodies with linearly varying density. Celest Mech Dyn Astron 120(4):349–372
D’Urso MG, Trotta S (2017) Gravity anomaly of polyhedral bodies having a polynomial density contrast. Surv Geophys 38(4):781–832
Evstifeev MI (2017) The state of the art in the development of onboard gravity gradiometers. Gyroscopy Navig 8(1):68–79
Farquharson CG, Mosher CRW (2009) Three-dimensional modelling of gravity data using finite differences. J Appl Geophys 68(3):417–422
Forsberg R (1984) A study of terrain reductions, density anomalies and geophysical inversion methods in gravity field modelling. Technical report, Ohio State University, Columbus Department of Geodetic Science and Surveying
Gallardo-Delgado LA, Pérez-Flores MA, Gómez-Treviño E (2003) A versatile algorithm for joint 3D inversion of gravity and magnetic data. Geophysics 68(3):949–959
García-Abdeslem J (2005) The gravitational attraction of a right rectangular prism with density varying with depth following a cubic polynomial. Geophysics 70(6):J39–J42
Golub GH, Welsch JH (1969) Calculation of Gauss quadrature rules. Math Comput 23(106):221–230
Götze HJ, Lahmeyer B (1988) Application of three-dimensional interactive modeling in gravity and magnetics. Geophysics 53(8):1096–1108
Gradshteyn IS, Ryzhik IM (2007) Table of integrals, series, and products, 7th edn. Academic Press, New York
Gutknecht BD, Goetze HJ, Jahr T, Jentzsch G, Mahatsente R, Zeumann S (2014) Structure and state of stress of the chilean subduction zone from terrestrial and satellite-derived gravity and gravity gradient data. Surv Geophys 35(6):1417–1440
Hansen R (1999) An analytical expression for the gravity field of a polyhedral body with linearly varying density. Geophysics 64(1):75–77
Holstein H (2002) Gravimagnetic similarity in anomaly formulas for uniform polyhedra. Geophysics 67(4):1126–1133
Holstein H (2003) Gravimagnetic anomaly formulas for polyhedra of spatially linear media. Geophysics 68(1):157–167
Holstein H, Ketteridge B (1996) Gravimetric analysis of uniform polyhedra. Geophysics 61(2):357–364
Holstein H, Schrholz P, Starr AJ, Chakraborty M (1999) Comparison of gravimetric formulas for uniform polyhedra. Geophysics 64(5):1438–1446
Holstein H, Sherratt E, Anastasiades C (2007a) Gravimagnetic anomaly formulae for triangulated homogeneous polyhedra. In: 69th EAGE conference and exhibition incorporating SPE EUROPEC 2007
Holstein H, Sherratt EM, Reid AB (2007b) Gravimagnetic field tensor gradiometry formulas for uniform polyhedra. SEG Technical Program Expanded Abstracts 2007:750–754. https://doi.org/10.1190/1.2792522
Holstein H, Fitzgerald D, Stefanov H (2013) Gravimagnetic similarity for homogeneous rectangular prisms. In: 75th EAGE conference and exhibition incorporating SPE EUROPEC 2013
Jahandari H, Farquharson CG (2013) Forward modeling of gravity data using finite-volume and finite-element methods on unstructured grids. Geophysics 78(3):G69–G80
Jiang L, Zhang J, Feng Z (2017) A versatile solution for the gravity anomaly of 3D prism-meshed bodies with depth-dependent density contrast. Geophysics 82(4):G77–G86
Jin J (2002) The finite element method in electromagnetics. Wiley-IEEE Press, New York
Kwok YK (1991) Gravity gradient tensors due to a polyhedron with polygonal facets. Geophys Prospect 39(3):435–443
Lee JB (2001) FALCON gravity gradiometer technology. Explor Geophys 32(3/4):247–250
Lelièvre PG, Farquharson CG, Hurich CA (2011) Computing first-arrival seismic traveltimes on unstructured 3-D tetrahedral grids using the fast marching method. Geophys J Int 184(2):885–896
Li X (2015) Curvature of a geometric surface and curvature of gravity and magnetic anomalies. Geophysics 80(1):G15–G26
Li X, Chouteau M (1998) Three-dimensional gravity modeling in all space. Surv Geophys 19(4):339–368
Li Y, Key K (2007) 2D marine controlled-source electromagnetic modeling: Part 1—an adaptive finite-element algorithm. Geophysics 72(2):WA51–WA62
Litinsky VA (1989) Concept of effective density: key to gravity depth determinations for sedimentary basins. Geophysics 54(11):1474–1482
Martinez C, Li Y, Krahenbuhl R, Braga MA (2013) 3D inversion of airborne gravity gradiometry data in mineral exploration: a case study in the Quadrilátero Ferrífero, Brazil. Geophysics 78(1):B1–B11
Montana CJ, Mickus KL, Peeples WJ (1992) Program to calculate the gravitational field and gravity gradient tensor resulting from a system of right rectangular prisms. Comput Geosci 18(5):587–602
Nabighian MN, Ander ME, Grauch VJS, Hansen RO, LaFehr TR, Li Y, Pearson WC, Peirce JW, Phillips JD, Ruder ME (2005) Historical development of the gravity method in exploration. Geophysics 70(6):63ND–89ND
Nagy D, Papp G, Benedek J (2000) The gravitational potential and its derivatives for the prism. J Geodesy 74(7):552–560
Okabe M (1979) Analytical expressions for gravity anomalies due to homogeneous polyhedral bodies and translations into magnetic anomalies. Geophysics 44(4):730–741
Parker R (1973) The rapid calculation of potential anomalies. Geophys J Int 31(4):447–455
Pedersen LB, Rasmussen TM (1990) The gradient tensor of potential field anomalies: some implications on data collection and data processing of maps. Geophysics 55(12):1558–1566
Petrović S (1996) Determination of the potential of homogeneous polyhedral bodies using line integrals. J Geodesy 71(1):44–52
Pohánka V (1998) Optimum expression for computation of the gravity field of a polyhedral body with linearly increasing density. Geophys Prospect 46(4):391–404
Ramillien GL (2017) Density interface topography recovered by inversion of satellite gravity gradiometry observations. J Geodesy 91(8):881–895
Rao DB (1985) Analysis of gravity anomalies over an inclined fault with quadratic density function. Pure Appl Geophys 123(2):250–260
Rao DB (1990) Analysis of gravity anomalies of sedimentary basins by an asymmetrical trapezoidal model with quadratic density function. Geophysics 55(2):226–231
Rao CV, Raju M, Chakravarthi V (1995) Gravity modelling of an interface above which the density contrast decreases hyperbolically with depth. J Appl Geophys 34(1):63–67
Rathod H, Venkatesudu B, Nagaraja K (2006) Gauss Legendre quadrature formulas over a tetrahedron. Numer Methods Partial Differ Equ 22(1):197–219
Ren Z, Kalscheuer T, Greenhalgh S, Maurer H (2013) A goal-oriented adaptive finite-element approach for plane wave 3-D electromagnetic modelling. Geophys J Int 194(2):700–718
Ren Z, Chen C, Pan K, Kalscheuer T, Maurer H, Tang J (2017a) Gravity anomalies of arbitrary 3D polyhedral bodies with horizontal and vertical mass contrasts. Surv Geophys 38(2):479–502
Ren Z, Chen C, Tang J, Chen H, Hu S, Zhou C, Xiao X (2017b) Closed-form formula for full magnetic gradient tensor of a homogeneous polyhedral body: a tetrahedral grid example. Geophysics 82(6):WB21–WB28
Ren Z, Tang J, Kalscheuer T, Maurer H (2017c) Fast 3-D large-scale gravity and magnetic modeling using unstructured grids and an adaptive multilevel fast multipole method. J Geophys Res Solid Earth 122(1):79–109
Ren Z, Zhong Y, Chen C, Tang J, Pan K (2018) Gravity anomalies of arbitrary 3D polyhedral bodies with horizontal and vertical mass contrasts up to cubic order. Geophysics 83(1):G1–G13
Rim H, Li Y (2016) Gravity gradient tensor due to a cylinder. Geophysics 81(4):G59–G66
Sastry RG, Gokula A (2016) Full gravity gradient tensor of a vertical pyramid model of flat top and bottom with depth-wise linear density variation. In: Symposium on the application of geophysics to engineering and environmental problems 2015. Society of Exploration Geophysicists and Environment and Engineering Geophysical Society, pp 294–301
Schwarzbach C, Börner RU, Spitzer K (2011) Three-dimensional adaptive higher order finite element simulation for geo-electromagnetics—a marine CSEM example. Geophys J Int 187(1):63–74
Si H (2015) TetGen, a Delaunay-based quality tetrahedral mesh generator. ACM Trans Math Softw 41(2):11:–11:36
Tai C (1997) Generalized vector and dyadic analysis: applied mathematics in field theory. IEEE Press, New York
Talwani M, Ewing M (1960) Rapid computation of gravitational attraction of three-dimensional bodies of arbitrary shape. Geophysics 25(1):203–225
Tsoulis D (2012) Analytical computation of the full gravity tensor of a homogeneous arbitrarily shaped polyhedral source using line integrals. Geophysics 77(2):F1–F11
Tsoulis D, Petrović S (2001) On the singularities of the gravity field of a homogeneous polyhedral body. Geophysics 66(2):535–539
Werner RA, Scheeres DJ (1996) Exterior gravitation of a polyhedron derived and compared with harmonic and mascon gravitation representations of asteroid 4769 Castalia. Celest Mech Dyn Astron 65(3):313–344
Wilton D, Rao S, Glisson A, Schaubert D, Al-Bundak O, Butler C (1984) Potential integrals for uniform and linear source distributions on polygonal and polyhedral domains. IEEE Trans Antennas Propag 32(3):276–281
Wu L, Chen L (2016) Fourier forward modeling of vector and tensor gravity fields due to prismatic bodies with variable density contrast. Geophysics 81(1):G13–G26
Ylä-Oijala P, Taskinen M (2003) Calculation of CFIE impedance matrix elements with RWG and n \(\times\) RWG functions. IEEE Trans Antennas Propag 51(8):1837–1846
Zhou X (2010) Analytic solution of the gravity anomaly of irregular 2D masses with density contrast varying as a 2D polynomial function. Geophysics 75(2):I11–I19
Acknowledgements
This study was supported by Grants from the National Basic Research Program of China (973 - 2015CB060200), the National Science Foundation of China (41574120), the Natural Science Foundation of Hunan Province of China (2016JJ2139), the State High-Tech Development Plan of China (2014AA06A602), the Project of Innovation-driven Plan in Central South University (2016CX005), and an award for outstanding young scientists by Central South University (Lieying program 2013) and the Fundamental Research Funds for the Central Universities of Central South University (1053320171677). YL was supported by Pioneer Hundred Talents Program, Chinese Academy of Sciences. Deep thanks are given to H. Holstein and H. Götze and an anonymous reviewer for critical and helpful comments which significantly improved the quality of this article.
Author information
Authors and Affiliations
Corresponding authors
Appendices
Appendix A: Geometric Symbols
The target body H is a polyhedron bounded by N polygonal faces, the geometric quantities of which and their definitions are given in Fig. 1 and Table 5, respectively. The i-th face \(\partial H_i\) of H is composed of \(M_i\) edges of which the j-th edge is denoted by \(C_{ij}\). Symbol \({\mathbf {r}}_{ij}\) denotes a point on the j-th edge of face \(\partial H_i\) of the polyhedral body H. The symbol \(\hat{\mathbf {{n}}}_i\) denotes the outward pointing unit normal vector of face \(\partial H_i\). The vertices on face \(\partial H_i\) are arranged in an anticlockwise order around the unit vector \(\hat{\mathbf {n}}_i\). The starting point and ending point on edge \(C_{ij}\) are denoted by \(\mathbf {v}_{0ij}\) and \(\mathbf {v}_{1ij}\), respectively. Thus, the tangential unit vector \(\hat{\mathbf {e}}_{ij}\) along edge \(C_{ij}\) is calculated as:
Furthermore, the outward pointing unit vector \(\mathbf {m}_{ij}\) of edge \(C_{ij}\) and face \(\partial H_i\) is calculated as:
Let us establish a local Cartesian coordinate system, the origin of which is located at the observation point \({\mathbf {r}}^\prime\), that is \({\mathbf {r}}^\prime =(0,0,0)\). Symbol \({\mathbf {r}}=(x,\,y,\,z)\) represents an arbitrary source point in the polyhedron, and \(R=|{\mathbf {r}}-\mathbf {r'}|\) is the distance from a source point to the observation point. The three unit vectors \(\hat{\mathbf {n}}_i\), \(\hat{\mathbf {m}}_{ij}\) and \(\hat{\mathbf {e}}_{ij}\) form a natural orthonormal basis on edge \(C_{ij}\) so that projections of vector \(({\mathbf {r}}-{\mathbf {r}}^\prime )\) along these three unit vectors yield a set of local coordinates \((m_{ij},\,s_{ij},\,h_i)\) on edge \(C_{ij}\), which are calculated as:
In Fig. 1, point \(\mathbf {p}_{ij}\) is the projection of \({\mathbf {r}}^\prime\) onto edge \(C_{ij}\). Vector \(\mathbf {L}_{ij}=\mathbf {p}_{ij}-{\mathbf {r}}^\prime\) is pointing from the observation site \({\mathbf {r}}^\prime\) to point \(\mathbf {p}_{ij}\) with its magnitude being denoted by \(L_{0ij}\). Since \({\mathbf {r}}-{\mathbf {r}}^\prime =\mathbf {L}_{ij}+({\mathbf {r}}-\mathbf {p}_{ij})\) and \(\mathbf {L}_{ij}\cdot \hat{\mathbf {e}}_{ij}=0\), the 1D parametrised local coordinate \(s_{ij}\) along edge \(C_{ij}\) can also be calculated as \(s_{ij}=({\mathbf {r}}-\mathbf {p}_{ij})\cdot \hat{\mathbf {e}}_{ij}\). Thus, any source point on edge \(C_{ij}\) can be denoted by this local coordinate \(s_{ij}\):
Using the fact that \({\mathbf {r}}^\prime =(0, 0, 0)\), the above equation becomes:
Meanwhile, the distance \(R=|{\mathbf {r}}-{\mathbf {r}}'|\), from any source point on edge \(C_{ij}\) to the observation site, is parametrised as
The distances from \(\mathbf {r'}\) to the vertices \(\mathbf {v}_{0ij}\) and \(\mathbf {v}_{1ij}\) are defined as
where \(s_{0ij}\) and \(s_{1ij}\) are the parametrised coordinates of the vertices \(\mathbf {v}_{0ij}\) and \(\mathbf {v}_{1ij}\), respectively.
In addition, in Fig. 1, \(\mathbf {o}_i\) is the projection of the observation site \({\mathbf {r}}^\prime\) on the i-th face \(\partial H_i\), and \(\varvec{\hat{\rho }}_{ij}^ \bot = \frac{\mathbf {p}_{ij} - \mathbf {o}_i}{\left| {\mathbf {p}_{ij} - \mathbf {o}_i} \right| }\) is the unit vector which points from point \(\mathbf {o}_i\) to point \(\mathbf {p}_{ij}\). The direction of \(\varvec{\hat{\rho }}_{ij}^ \bot\) can be either identical or opposite to the direction of the outward normal vector \(\mathbf {m}_{ij}\) on edge \(C_{ij}\). \(\rho _i=|{\mathbf {r}}-\mathbf {o}_i|\) is the distance between the projection centre \(\mathbf {o}_i\) and a source point \({\mathbf {r}} \in \partial H_{i}\).
Appendix B: Gravity Gradient Tensor due to Constant Density Contrast
Using the local coordinate \(s_{ij}=({\mathbf {r}}-{\mathbf {r}}^\prime )\cdot \hat{\mathbf {e}}_{ij}\) along edge \(C_{ij}\) and using Eq. (A.6), the line integral in (15) can be converted into a definite integral:
where \({\mathrm{d}}s_{ij}\) is a differential of variable \(s_{ij}\). The values of \(s_{ij}\) at the vertices \(\mathbf {v}_{0ij}\) and \(\mathbf {v}_{1ij}\) are \(s_{0ij}\) and \(s_{1ij}\), respectively. The analytical solution of the above definite integral can be looked up in integral tables (equation 2.261 in Gradshteyn and Ryzhik 2007):
When the observation site lies on the extension of edge \(C_{ij}\) (\(L_{0ij} = 0\) and \({s_{1ij}} \cdot {s_{0ij}} >0\)), the integrand function is reduced to \(\frac{1}{|s_{ij}|}\) which leads to the second formula of Eq. (B.2). We should note that when the observation site \({\mathbf {r}}^\prime\) is located within the edge \(C_{ij}\) (\(L_{0ij} = 0\) and \({s_{1ij}} \cdot {s_{0ij}} \le 0\)), the linear integral term \(\int \nolimits _{{C_{ij}}} {\frac{1}{R}{\mathrm{d}}l}\) has a weak logarithmic singularity. Therefore, we cannot compute gravity gradient tensors, when the observation site is located on an edge of the polyhedral body.
The analytic expression for the surface integral term \(\iint _{\partial {H_i}} {\frac{1}{R^3}{\mathrm{d}}s}\) in Eq. (15) can be derived using the result from Ylä-Oijala and Taskinen (2003) and Ren et al. (2017b)
where
where the variables \(m_{ij}\), \(s_{1ij}\), \(s_{0ij}\), \(L_{0ij}\), \(h_{i}\), \(R_{1ij}\) and \(R_{0ij}\) are shown in Fig. 1 and all can be calculated in terms of the coordinates of the vertices of the polyhedral body. In Eq. (B.3), the observation site cannot be located on the surface \(\partial H_{i}\) of the polyhedral body. In the case that the observation site is located on the surface of the polyhedral body, \(\mathbf {r'}\in \partial H_i\), the gravity gradient tensor is singular, which is an inherent feature of gravity gradient tensor (Li and Chouteau 1998; Holstein 2003).
Appendix C: Gravity Gradient Tensor due to Linear Density Contrast
First, we consider the line integral term \(\int _{{C_{ij}}} {\frac{{{\mathbf {r}}}}{R}{\mathrm{d}}l}\) in Eq. (16). Using the parametrisation in Eq. (A.5), it can be changed to
where
The analytic solution for the first linear integral in Eq. (C.1) has been given in Eq. (B.2).
Second, we deal with the surface integral term \(\iint _{\partial H_i}\frac{{\mathbf {r}}}{R^3}{\mathrm{d}}s\). Using the identity \(\nabla _{\mathbf {r}}\frac{1}{R}=\frac{{\mathbf {r}}^\prime -{\mathbf {r}}}{R^3}\), our previous assumption \({\mathbf {r}}^\prime =(0, 0, 0)\), and Eq. (6) (setting \(f=\frac{1}{R}\)), we have
where \(\nabla _{s}\) denotes the surface gradient operator, and the surface gradient theorem is used (Tai 1997). According to Eq. (A.3), \(h_i=({\mathbf {r}}-{\mathbf {r}}')\cdot \hat{\mathbf {n}}_i\). Analytic expressions for the line integral term \(\int _{{C_{ij}}} {\frac{{1}}{R}{\mathrm{d}}l}\) and the surface integral term \({h_i}\iint _{\partial {H_i}} {\frac{1}{{{R^3}}}{\mathrm{d}}s}\) have been presented in Eqs. (B.1) to (B.2) and Eqs. (B.3) to (B.4), respectively.
Third, the surface integral term \(\iint _{\partial H_i}\frac{1}{R}{\mathrm{d}}s\) can be evaluated using the result of Ren et al (2017a, equation 33),
where as shown in Fig. 1, \(\mathbf {o}_i\) is the projection point of the observation site onto the plane containing the face \(\partial H_i\), \(\rho _i=\left| {\mathbf {r}}-\mathbf {o}_i\right|\), \({\mathbf {r}}\) is a running integral point on edge \(C_{ij}\), i.e., \({\mathbf {r}} \in C_{ij}\). Using the geometrical variables given in Fig. 1, we have (Ren et al. 2017a):
When \(m_{ij}\rightarrow 0\), the limit of Eq. (C.5) exists and is equal to zero. Therefore, there is no singularity in Eq. (C.5). As demonstrated in Fig. 14, \(\alpha (\mathbf {o}_i)\) is the angular extent of the arc region lying within a plane containing surface \(\partial H_i\) and centred at \(\mathbf {o}_i\). Note that the projection point \(\mathbf {o}_i\) can be located inside, outside or on edges of the surface \(\partial H_i\). The value of the extent angle \(\alpha (\mathbf {o}_i)\) depends on the geometrical relation between \(\mathbf {o}_i\) and the polygon \(\partial H_i\). When point \(\mathbf {o}_i\) is located inside \(\partial H_i\), \(\alpha (\mathbf {o}_i)=2\pi\); when point \(\mathbf {o}_i\) is located on an edge of the polygon \(\partial H_i\) but not at a vertex, \(\alpha (\mathbf {o}_i)=\pi\); when point \(\mathbf {o}_i\) is located at a vertex, \(\alpha (\mathbf {o}_i)\) is the angle enclosed by its two adjacent edges. To avoid judgement of the geometrical relation between point \(\mathbf {o}_i\) and the polygon \(\partial H_i\) and facilitate programming, the angle \(\alpha (\mathbf {o}_i)\) can be expressed as a sum of the angles subtended by each edge of the polygon \(\partial H_i\) (Wilton et al. 1984, page 278):
where the contribution of each edge is calculated as
and \({\varvec{\hat{\rho }}}_{ij}^ \bot = \frac{\mathbf {p}_{ij} - \mathbf {o}_i}{\left| \mathbf {p}_{ij} - \mathbf {o}_i \right| }\) is the unit vector from point \(\mathbf {o}_i\) to point \(\mathbf {p}_{ij}\). The contribution \(\alpha _{ij}\) of edge \(C_{ij}\) to the angular extent \(\alpha (\mathbf {o}_i)\) vanishes, when point \(\mathbf {o}_i\) is on the edge \(C_{ij}\) or on its extension, and otherwise the sign of \(\alpha _{ij}\) depends on whether unit vector \({\varvec{\hat{\rho }}}_{ij}^ \bot\) is identical or opposite to unit normal vector \(\hat{\mathbf {m}}_{ij}\).
Finally, the closed-form solution for gravity gradient tensor \({\mathbf {T}}_1\) in Eq. (13) caused by a linear density contrast can be obtained by substituting Eqs. (C.4), (C.3) and (C.1) into Eq. (16).
Appendix D: Gravity Gradient Tensor due to Quadratic Density Contrast
First, using Eqs. (A.5) and (14), the line integral \(\int _{C_{ij}}\frac{x_px_q}{R}{\mathrm{d}}l\) is transformed as
Using the integral table (Equation 2.264.3 in Gradshteyn and Ryzhik 2007), we obtain
Analytic solutions for the remaining second and third line integrals in Eq. (D.1) have been derived in Eqs. (C.2) and (B.2), respectively. Thus, we have successfully derived the analytic expressions for the line integral \(\int \nolimits _{{C_{ij}}} {\frac{{{x_p}{x_q}}}{R}{\mathrm{d}}l}\) in Eq. (D.1).
Second, we consider the surface integral \(\iint _{\partial H_i}\frac{x_px_q}{R^3}{\mathrm{d}}s,~(p,q=1,2,3\)). In view of the assumption that \({\mathbf {r}}^\prime =(0, 0, 0)\), we have
Using the above equation and the following divergence vector identity:
\(\frac{x_p x_q}{R^3}\) can be transformed as (setting \(\mathbf {A}=x_p{\hat{\mathbf {x}}}_q\) and \(\varphi =\frac{1}{R}\)):
Integrating the above equation over the face \(\partial H_i\) and applying the surface divergence theorem (Tai 1997), we have
where \(\int _{C_{ij}} \frac{x_p}{R}{\mathrm{d}}l=\hat{\mathbf {x}}_p\cdot \int _{C_{ij}}\frac{{\mathbf {r}}}{R}{\mathrm{d}}l\) and \(\iint _{\partial H_i} \frac{x_p}{R^3}{\mathrm{d}}s=\hat{\mathbf {x}}_p\cdot \iint _{\partial H_i}\frac{{\mathbf {r}}}{R^3}{\mathrm{d}}s\). The analytic solutions for the linear integral \(\int _{C_{ij}}\frac{{\mathbf {r}}}{R}{\mathrm{d}}l\) and for the surface integral \(\iint _{\partial H_i}\frac{{\mathbf {r}}}{R^3}{\mathrm{d}}s\) have already been given in Eqs. (C.1) and in (C.3), respectively. Furthermore, the surface integral term \(\iint _{\partial {H_i}} {\frac{1}{R}{\mathrm{d}}s}\) has been derived in Eq. (C.4).
Third, the surface integrals \(\iint _{\partial H_i}\frac{x_p}{R}{\mathrm{d}}s\) for \((p=1,2,3)\) are the three components of the vector surface integral \(\iint _{\partial H_i}\frac{{\mathbf {r}}}{R}{\mathrm{d}}s\), that is \(\iint _{\partial H_i}\frac{x_p}{R}{\mathrm{d}}s=\hat{\mathbf {x}}_p\cdot \iint _{\partial H_i} \frac{{\mathbf {r}}}{R}{\mathrm{d}}s\). Using our assumption \({\mathbf {r}}^\prime =(0,0,0)\), Eq. (6) (setting \(f=R\)) and the surface gradient theorem (Tai 1997), the integral \(\iint _{\partial H_i} \frac{{\mathbf {r}}}{R}{\mathrm{d}}s\) can be calculated as (Ren et al. (2017a), equation 34)
The analytic solution of the surface integral \(\iint _{\partial H_i}\frac{1}{R}{\mathrm{d}}s\) in Eq. (D.7) has been presented in Eq. (C.4), and the remaining line integral \(\int _{C_{ij}}R{\mathrm{d}}l\) in Eq. (D.7) can be computed according to integral tables (equation 2.262.1 in Gradshteyn and Ryzhik 2007),
It is easy to see that the limit of the logarithmic term in Eq. (D.8) is zero when \(L_{0ij}\rightarrow 0\) (Ren et al. 2018).
Fourth, the volume integral term \(\iiint _H\frac{1}{R}\mathrm{d}v\) can be calculated as (equation 18, Ren et al. 2018):
where the analytic solution for the integral term \(\iint _{\partial {H_i}} {\frac{1}{R}{\mathrm{d}}s}\) has been given in Eq. (C.4).
In conclusion, the gravity gradient tensor \({\mathbf {T}}_2\) in Eq. (13) of a polyhedral body with quadratic density contrast \(\lambda _2\) in Eq. (11) can be evaluated in terms of closed-form solutions by substituting Eqs. (11), (D.7), (D.9), (D.1) and (D.6) into Eq. (7).
Appendix E: Gravity Gradient Tensor due to Cubic Density Contrast
First, we deal with the line integral \(\int _{C_{ij}}\frac{x_px_qx_t}{R}{\mathrm{d}}l\). In terms of the definition of the local coordinate \(s_{ij}\), which is given in Eq. (A.5), we obtain
Using the integral table (Gradshteyn and Ryzhik (2007), equation 2.264.3), we get
Here, the integrals \(\int _{s_{0ij}}^{s_{1ij}} \frac{1}{\sqrt{{s_{ij}^2} + L_{0ij}^2} } {\mathrm{d}}s_{ij}\), \(\int _{s_{0ij}}^{s_{1ij}} \frac{s_{ij}}{\sqrt{{s_{ij}^2} + L_{0ij}^2} } {\mathrm{d}}s_{ij}\) and \(\int _{s_{0ij}}^{s_{1ij}} \frac{s_{ij}^2}{\sqrt{{s_{ij}^2} + L_{0ij}^2} } {\mathrm{d}}s_{ij}\) can be analytically evaluated using Eqs. (B.2), (C.2) and (D.2), respectively. Finally, this gives the closed-from solution for the line integral \(\int _{C_{ij}}\frac{x_px_qx_t}{R}{\mathrm{d}}l\) in Eq. (E.1).
Second, we will deal with the surface integral \(\iint _{\partial H_i}\frac{x_px_qx_t}{R^3}{\mathrm{d}}s\). Similar to Eq. (D.5), the integrand \(\frac{x_px_qx_t}{R^3}\) can be transformed as follows:
Integrating the above equation over the face \(\partial H_i\) and applying the surface divergence theorem (Tai 1997) to the first term on the right-hand side, we get
where the line integral \(\int _{C_{ij}} \frac{x_px_q}{R}{\mathrm{d}}l\) can be analytically evaluated using Eq. (D.1), the values of the surface integrals \(\iint _{\partial H_i}\frac{x_px_q}{R^3}{\mathrm{d}}s\) and \(\iint _{\partial H_i}\frac{x_p}{R}{\mathrm{d}}s\) can be analytically calculated using Eqs. (D.6) and (D.7), respectively.
Third, using the result from (Ren et al. 2018, equation 26), the surface integral \(\iint _{\partial {H_i}} {\frac{{{x_p}{x_q}}}{R}{\mathrm{d}}s}\) can be calculated as
where the closed-form solution for surface integral \(\iint _{\partial H_i}\frac{x_p}{R}{\mathrm{d}}s\) is given in Eq. (D.7). The line integral \(\int _{C_{ij}}x_pR{\mathrm{d}}l=\hat{\mathbf {x}}_p\cdot \int _{C_{ij}}{\mathbf {r}}R{\mathrm{d}}l\). Using Eq. (A.5) and the integral table Gradshteyn and Ryzhik (2007, equations 2.262.1–2.262.2), \(\int _{C_{ij}}{\mathbf {r}}R{\mathrm{d}}l\) is calculated as
The surface integral \(\iint _{\partial {H_i}} {R{\mathrm{d}}s}\) in Eq. (E.5E.6) can be calculated using the result of Ren et al. (2017a, equation 33). This means
where the calculation of the angular extent \(\alpha (\mathbf {o}_i)\) has been presented in Eq. (C.6), and
When \(m_{ij}\) approaches zero, the last two terms in Eq. (E.9) approach zero.
Fourth, volume integral \(\iiint _H\frac{x_p}{R}\mathrm{d}v\) can be calculated from Ren et al. (2018, equation 24)
where the surface integral \(\iint _{\partial H_i}R{\mathrm{d}}s\) is given in Eq. (E.8).
To conclude, substituting Eqs. (12), (E.10), (E.5E.6), (E.4) and (E.1) into Eq. (7), we can obtain the solution of the gravity gradient tensor \({\mathbf {T}}_3\) in Eq. (13) due to a cubic density contrast.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Ren, Z., Zhong, Y., Chen, C. et al. Gravity Gradient Tensor of Arbitrary 3D Polyhedral Bodies with up to Third-Order Polynomial Horizontal and Vertical Mass Contrasts. Surv Geophys 39, 901–935 (2018). https://doi.org/10.1007/s10712-018-9467-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10712-018-9467-1