Abstract
Measurements of the splitting or birefringence of seismic shear waves that have passed through the Earth’s mantle yield constraints on the strength and geometry of elastic anisotropy in various regions, including the upper mantle, the transition zone, and the D″ layer. In turn, information about the occurrence and character of seismic anisotropy allows us to make inferences about the style and geometry of mantle flow because anisotropy is a direct consequence of deformational processes. While shear wave splitting is an unambiguous indicator of anisotropy, the fact that it is typically a near-vertical path-integrated measurement means that splitting measurements generally lack depth resolution. Because shear wave splitting yields some of the most direct constraints we have on mantle flow, however, understanding how to make and interpret splitting measurements correctly and how to relate them properly to mantle flow is of paramount importance to the study of mantle dynamics. In this paper, we review the state of the art and recent developments in the measurement and interpretation of shear wave splitting—including new measurement methodologies and forward and inverse modeling techniques,—provide an overview of data sets from different tectonic settings, show how they help us relate mantle flow to surface tectonics, and discuss new directions that should help to advance the shear wave splitting field.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Knowledge of present-day dynamical processes taking place within the Earth’s mantle is crucial to our understanding of the workings of our planet’s interior and how it has evolved through time. Important aspects of mantle dynamics that remain poorly understood include what controls patterns of mantle flow, how this flow interacts with the surface plates, and how the lithospheric mantle deforms as a result of plate boundary interactions. Ample observations of deformational processes in the upper crust are available to us from geology, but our knowledge of mantle deformation is limited to more indirect observations and comes chiefly from seismic waves that pass through the mantle and are recorded at the surface. In particular, elastic anisotropy in the mantle results from deformation, so measurement of seismic anisotropy represents perhaps the best tool available to geophysicists to directly probe patterns of deformation at depth. It was recognized early on by seismologists that regions of the Earth’s mantle are anisotropic (e.g., Hess 1964; Forsyth 1975), and it is now clearly established that seismic anisotropy is present at several depth ranges in the mantle. Because of the relationships between seismic anisotropy and past and present deformation, the delineation and interpretation of anisotropy has become an integral part of studying dynamic processes in the Earth’s mantle.
Elastic anisotropy manifests itself in the seismic wavefield in many ways, and anisotropy affects the propagation of body and surface waves as well as the free oscillations of the Earth (for a recent review of wave propagation in anisotropic media, see Maupin and Park 2007). One of the most clear-cut manifestations of anisotropy in seismic data is shear wave splitting, which is analogous to the optical birefringence of minerals under polarized light. Upon propagation through an anisotropic region of the Earth, a shear wave is split into two orthogonally polarized components and accumulates a delay time between the fast and slow (quasi-) shear pulses. The splitting parameters, ϕ, δt, are measured from seismic records; these correspond to the orientation of the fast quasi-S phase and the time delay between the fast and slow components, respectively. Since early studies by, e.g., Keith and Crampin (1977), Kosarev et al. (1979), Ando et al. (1983), Vinnik et al. (1984), Fukao (1984), and Silver and Chan (1988) shear wave splitting has emerged as a popular tool for characterizing anisotropy in the Earth, most notably in the crust, upper mantle, and in the D″ region directly above the core-mantle boundary (CMB). With the increasing availability of broadband seismic data, there are now hundreds of published studies that examine shear wave splitting and interpret it in terms of mantle anisotropy. A major advantage of the shear wave splitting technique is that splitting is unambiguously due to anisotropic structure somewhere along the raypath; however, because it is, like travel time, a path-integrated measurement, with a single measurement it is impossible to tell where along the path the anisotropy lies without additional information. Because anisotropic regions are typically sampled with near-vertical ray paths, splitting measurements have poor depth resolution (e.g., Babuska and Cara 1991).
Along with the rapid progress in shear wave splitting techniques and methodologies and the increasing availability of broadband seismic data, progress in experimental mineral physics over the past two decades has allowed seismologists to relate shear wave splitting measurements to mantle deformation more accurately. In the upper mantle, seismic anisotropy is a result of the crystallographic or lattice preferred orientation (LPO) of intrinsically anisotropic mantle minerals, primarily olivine. In the transition zone and lower mantle, other minerals likely play a role in generating anisotropy, including wadsleyite and/or ringwoodite in the transition zone and perovskite, post-perovskite, and/or ferropericlase in D″. Additionally, a contribution to anisotropy from shape preferred orientation (SPO) might be present if materials with elastically distinct properties, such as melt, align preferentially. In the upper mantle it is generally thought that anisotropy is generated when an aggregate of crystals of mantle minerals, mainly olivine, undergoes deformation to high strains and develops an LPO (e.g., Christensen 1984; Zhang and Karato 1995). Recent mineral physics results indicate that anisotropic fabric can be affected by the stress, temperature, and pressure conditions and by volatile content (e.g., Jung and Karato 2001; Mainprice 2007; Karato et al. 2008; Jung et al. 2009). These new experimental results open the possibility that seismological characterization of mantle anisotropy may help us to understand the physical conditions present in the Earth’s mantle; however, they also introduce potential ambiguities in the interpretation of shear wave splitting measurements.
With the extensive number of published shear wave splitting studies from a wide variety of tectonic settings now available in the literature, with new innovations in shear wave splitting methodologies such as the introduction of shear wave splitting tomography, with increasing attention being paid to observations of anisotropy in D″ and other remote regions of the mantle, and with other exciting developments, an assessment of the shear wave splitting field is important and timely, and we hope that this paper will contribute to that assessment. The ever-increasing availability of data from different regions is allowing for comparisons among shear wave splitting studies and for their amalgamation into global datasets which, on interpretation, are yielding exciting and often surprising results. The aim of this paper is to review the state of the art and discuss new advances relating to shear wave splitting measurements and their interpretation in terms of mantle processes. Our aim is not to provide a detailed history of the development of the shear wave splitting field, nor is it to provide an exhaustive compilation of the entire shear wave splitting literature. Rather, our goal is to concentrate on the present state of the field, with an emphasis on the recent literature and exciting new research directions.
2 Shear Wave Splitting Methodologies
2.1 Making the Measurement
2.1.1 Broadband Teleseismic and Local Data
Shear wave splitting manifests itself over a range of frequencies and exhibits a range of sensitivities to structures on different length scales in different parts of the Earth, depending on the type of data used. For the purpose of characterizing anisotropy and deformation in the Earth’s mantle, the type of data that is most often used is that from broadband seismic stations. For the common case in which the delay time, δt, accumulated between the fast and slow shear waves (for upper mantle anisotropy, this is generally on the order of about 1 s) is much smaller than the dominant period, T, of the wave under study, the fast and slow components will not achieve a full separation in time on the seismogram, and their measurement is not straightforward, particularly in the case of noisy data or complex anisotropic structure.
A variety of measurement methods (and subsequent variations) have been developed to measure shear wave splitting parameters from broadband seismic data and the most common of these are reviewed briefly here. These methods generally entail processing steps such as filtering, rotating the seismogram components, identifying records with high signal-to-noise ratio, choosing a time window for the analysis, and the visual and/or statistical examination of the resulting diagnostic plots and error estimates. While there have been several efforts to partially or fully automate the process of making shear wave splitting measurements (e.g., Teanby et al. 2004; Evans et al. 2006), most shear wave splitting analysts continue to rely on visual inspection of individual waveforms as a final check of the data.
As discussed in Sect. 2.2, a variety of seismic phases are suitable for characterizing mantle anisotropy with shear wave splitting, depending on which region of the mantle is under study. In particular, core phases such as SKS, SKKS, and PKS as well as direct S waves from either local (just below the receiver) or teleseismic (Δ = 40–80°) distances are useful. From a measurement perspective, core phases such as SKS provide several advantages over direct S phases; in particular, the initial polarization of the shear wave (before it has passed through an anisotropic medium) is controlled by the P-to-S conversion at the CMB and is therefore known. In addition, this conversion constrains the observed splitting to be on the receiver side of the path. Several common measurement methods, such as transverse component minimization and the multichannel method, require knowledge of the incoming polarization azimuth. This can either be assumed (for SKS, for example, this corresponds to the backazimuth), predicted from the source mechanism, if it is known, measured directly from the seismogram (as long as δt ≪ T, the initial polarization direction is preserved in the uncorrected particle motion; e.g., Vidale 1986), or estimated along with the splitting parameters.
2.1.1.1 The Transverse Component Minimization Method
The transverse component minimization method, introduced by Silver and Chan (1991), is perhaps the most commonly used splitting measurement method for broadband data. This method utilizes a grid search approach to identify the pair of splitting parameters (ϕ, δt) which best minimizes the amount of energy on the transverse component (equivalently, which best linearizes the corrected particle motion) when the effect of splitting is accounted for. The method can be applied either to the horizontal components, rotated into a radial (R) and transverse (T) coordinate system (where the so-called radial component corresponds to the backazimuthal direction for core phases or to the initial polarization direction for direct S waves), or to the Q–T components in a ray-coordinate based L–Q–T coordinate system (Sileny and Plomerova 1996; Vecsey et al. 2008). For perfectly vertical incidence, the two coordinate systems are equivalent.
The transverse component minimization method is based upon the principle that a shear wave is linearly polarized in the absence of anisotropy, and that passage through an anisotropic medium will result in significant energy on the transverse component and an elliptical particle motion, which is diagnostic of shear wave splitting. The method performs a grid search over all possible values of ϕ and δt (up to a reasonable maximum delay time value, usually ~4 s), rotates and time-shifts the horizontal components appropriately, and measures the amount of energy on the corrected transverse component, producing a contour plot of transverse component energy for all possible pairs of splitting parameters. The best-fitting parameters correspond to the minimum on this contour plot; formal errors on the measurements are estimated using an F test formulation (Silver and Chan 1991). A slight variation on the transverse component minimization method involves a minimization not of the transverse component energy but of the smaller eigenvalue of the corrected covariance matrix (or using a similar eigenvalue-based measure of linearity); identifying the most nearly-singular time-domain covariance matrix is equivalent to identifying the most linear particle motion (Vidale 1986; Silver and Chan 1991). The eigenvalue method may be used even when the initial polarization of the shear wave is unknown (Silver and Chan 1991; Savage 1999). An example of a shear wave splitting measurement using the transverse component minimization method, using the SplitLab software of Wüstefeld et al. (2007), is shown in Fig. 1. The case in which the shear wave is not significantly split—that is, there is little or no energy on the uncorrected transverse component, and the initial particle motion is linear or nearly so—is referred to as a “null” measurement. This may be diagnostic of no anisotropy along the path traversed by the shear wave, or it may indicate that the initial polarization of the phase is (nearly) parallel to either a fast or slow direction of symmetry of the anisotropic medium. These two possibilities can be distinguished by making an additional measurement using another (non-orthogonal) initial polarization.
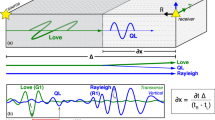
Example shear wave splitting measurements on an SKS phase using the transverse component minimization (shown on plot as “minimum energy”) and the cross-correlation (shown on plot as “rotation-correlation”) methods carried out using the SplitLab software (Wüstefeld et al. 2007). Data are from station OR093 of the High Lava Plains seismic experiment in eastern Oregon (Long et al. in review) for an event (Mw = 6.4) on August 20, 2007 located in the western Pacific Ocean at an epicentral distance of 103° and a backazimuth of 291°. Data have been filtered to retain periods between 8 and 25 s. Top left panel the radial (dashed blue line) and transverse (solid red line) components of the seismogram are shown; the window used in the splitting analysis is shown in gray. Thin dotted lines indicate the expected arrival times for SKS (left) and SKKS (right) from the iasp91 Earth model. Middle row of panels Diagnostics for the cross-correlation method are shown, including the corrected fast (dashed blue line) and slow (solid red line) components (far left panel), the corrected radial (dashed blue line) and transverse (solid red line) components (center left panel), the initial particle motion (dashed blue line) and the corrected particle motion (solid red line) once the effect of splitting is removed (center right panel), and the contour plot of the correlation coefficient (far right panel) with the best-fitting splitting parameters (ϕ, δt) shown with the crossed lines and the 95% confidence region indicated in gray. Bottom row corresponding diagnostic plots for the transverse component minimization method. The methods yield the following best-fitting splitting parameters: ϕ = 85°, δt = 2.2 s (cross-correlation); ϕ = 83°, δt = 2.1 s (transverse component minimization). The two measurement methods agree very well; however, as indicated by the contour plots and by the formal errors on the measurements (center, top), the transverse component minimization measurement is much better constrained than the cross-correlation measurement
The transverse component minimization method is most often applied to individual seismograms, and individual measurements of (ϕ, δt) are then averaged, sometimes weighted by the individual errors on each measurement, to obtain best-fitting splitting parameters for a given station. However, other methods of obtaining average splitting parameters for a given station that rely on stacking procedures have also been developed. For example, Wolfe and Silver (1998) proposed a method of stacking error surfaces obtained from splitting measurements for phases measured at a variety of backazimuths; a similar stacking technique has been proposed by Restivo and Helffrich (1999). Such stacking methods have the advantage of compensating for noisy data or poor waveform clarity, and making explicit use of null observations. This can yield increased confidence in average splitting-parameter estimates. Stacking procedures, however, implicitly assume that the anisotropy consists of a single homogeneous layer beneath the station, since it assumes that all seismograms share the same set of splitting parameters. If this assumption is violated, then the resulting measurement will be difficult to interpret and potentially valuable information about vertically heterogeneous anisotropy (see Sect. 2.3) is lost.
2.1.1.2 The Cross-Correlation Method
The cross-correlation method was used in early studies by Fukao (1984), Bowman and Ando (1987), and others and is similar in principle to the transverse component minimization method. It also utilizes a grid-search approach to identifying the best-fitting splitting parameters by rotating and time-shifting the horizontal components (or the Q, T components in a ray-centered coordinate system). Like the transverse-component-minimization method, the cross-correlation method operates upon the principle that, after propagation through an anisotropic medium, a shear wave is split into orthogonally polarized fast and slow components with identical pulse shapes. The method therefore seeks to maximize the cross-correlation between the corrected horizontal components, which is mathematically equivalent to maximizing the determinant of the time-domain covariance matrix (e.g. Silver and Chan 1991; Levin et al. 1999). As with the transverse component minimization method, the measurement is classified as a “null” if the shear phase has not undergone splitting and displays a linear initial particle motion. An example of a measurement using the cross-correlation method is shown in Fig. 1 along with the transverse component minimization measurement for the same SKS phase; the two methods yield nearly identical results for this particular arrival. Although typically used at long period, both the transverse-component-minimization and cross-correlation methods can be utilized at high frequency as well.
2.1.1.3 The Multichannel (Splitting Intensity) Method
The multichannel method was introduced by Chevrot (2000) (based on earlier work by Vinnik et al. 1989b) as an alternative to single-record methods such as transverse component minimization and cross-correlation. This method takes advantage of the predicted variation in the amount of energy on the uncorrected transverse component with incoming polarization angle (equivalent to the backazimuth for SKS-type phases) for a single, horizontal layer of anisotropy. The actual quantity measured on individual seismograms in the splitting intensity, S, which is defined as the amplitude of the transverse component relative to the time derivative of the radial component; this quantity can be measured either by simple projection of the components or by a singular value decomposition (SVD) procedure (Chevrot 2000). In particular, the predicted radial and transverse components for a vertically propagating shear wave that has undergone passage through a single layer of anisotropy with a horizontal axis of transversely isotropic (TI) symmetry can be written at long period (δt ≪ T) as (Silver and Chan 1988; Vinnik et al. 1989b; Chevrot 2000):
where β is the angle between the fast axis ϕ and the incoming polarization direction. Thus, S = δt sin 2β. If the azimuthal dependence of the splitting intensity (referred to as the splitting vector) is measured, the best-fitting splitting parameters (ϕ, δt) can be retrieved by fitting a sin(2β) curve to the splitting vector. The delay time δt corresponds to the amplitude of the sinusoid and the fast axis ϕ can be inferred from the phase of the sinusoid at the origin. The splitting intensity measurements can either be stacked in azimuthal bins to improve signal-to-noise ratio (Chevrot 2000) or used individually (Long and van der Hilst 2005b). An example of a multichannel measurement from a broadband station in Japan (Long and van der Hilst 2005a) is shown in Fig. 2.
Example measurements using the multichannel method. a An illustration of an individual splitting intensity measurement from the splitting data set of Long and van der Hilst (2005a) using data from station TKA the F-net array in Japan. An SKS arrival is shown; the data have been filtered to retain periods between 8 and 50 s and rotated to show the radial (bottom trace) and transverse (middle trace) components. The waveforms have been standardized by deconvolution with the radial component (Chevrot 2000). The top trace shows the time derivative of the radial component overlain with the transverse component; the splitting intensity is measured from their relative amplitudes by simple projection. The vertical bars indicate the time window used in the analysis. b The splitting vector measured at F-net station AMM using SKS, SKKS, and direct teleseismic S phases is shown. Individual splitting intensity measurements (circles) are plotted with their 2σ error bars. The best-fitting sinusoid is shown with a black line. The best-fitting splitting parameters obtained from this fit are ϕ = 46°, δt = 0.65 s
Because the multichannel method requires good coverage in incoming polarization angle, its utility is limited by the backazimuthal coverage in seismicity if only core phases are used, and published azimuthal coverage maps (Chevrot 2000) indicate that many regions have very poor backazimuthal coverage in the distance range at which SKS phases are usually measured. However, the coverage can be dramatically improved if direct teleseismic S phases from deep events are included, as long as any potential contribution from source-side anisotropy is accounted for and minimized (Long and van der Hilst 2005a). Perhaps because of the limitations imposed by the requirement of good incoming polarization angle coverage, the multichannel method has only been applied to a limited number of data sets, including single stations in Brazil and the Central African Republic (Chevrot 2000) and array data in Japan (Long and van der Hilst 2005a), Tibet (Lev et al. 2006), and the eastern Alps (Kummerow and Kind 2006).
2.1.1.4 The Cross-Convolution Method
The transverse component minimization, cross-correlation, and multichannel measurement methods all rely upon the assumption that the shear wave under consideration has undergone splitting due to a single layer of anisotropy with a horizontal axis of symmetry. However, in the real Earth, shear waves may pass through multiple regions of anisotropy and have dipping axes of anisotropic symmetry (and may also have lower symmetry systems than the transversely isotropic geometry that is often assumed). In order to surmount some of the problems posed by the possible presence of complex anisotropy at depth, Menke and Levin (2003) proposed a cross-convolution method. (See also use of ‘apparent’ splitting parameters in the presence of complex structure, Sect. 2.3.1.) The actual computation consists of convolving the observed radial and tangential component seismograms with the impulse responses predicted by a hypothetical Earth model, and then varying the model to minimize the misfit between observed and predicted seismograms. Tests on synthetic and real data (Menke and Levin 2003) indicate that the cross-convolution method yields similar results to traditional methods in the presence of a single horizontal layer of anisotropy, and may do a better job of distinguishing whether complex anisotropic models are required by a given data set. An example of a cross-convolution measurement on synthetic waveforms is shown in Fig. 3.
An example of a cross-convolution measurement, modified from Menke and Levin (2003). Top traces: synthetic radial and transverse component seismograms are generated for a two-layer anisotropic model. The cross-convolution diagnostic is then performed using a one-layer model (middle) and the correct two-layer model (bottom). The cross-convolution traces contain information about both the model and the synthetic data and are obtained by cross-convolving the (synthetic) radial and transverse traces with the predicted horizontal impulse response functions for the earth model being tested (for further details, see Menke and Levin 2003). Visual inspection of the cross-convolution traces confirms that the two-layer fit is substantially better than the fit obtained for a one-layer model, as expected
2.1.1.5 Comparisons Among Measurement Methods
As described above, a variety of splitting measurement methods, each with their own assumptions, biases, preprocessing steps, and error estimation procedures, are in wide use in the seismological community. Comparisons among different measurement methods are, therefore, instructive. For the case of a single layer of TI with a horizontal axis of symmetry and no lateral heterogeneity, sampled by a vertically propagating shear wave measured on a noise-free seismogram, all of the measurement methods described above should yield identical estimates of the shear wave splitting parameters. However, for the more realistic case of noisy data and complex anisotropic structure, different measurement methods often do yield different splitting parameter estimates, as has been documented for several data sets (e.g., Levin et al. 2004; Long and van der Hilst 2005a, b; Wüstefeld and Bokelmann 2007). Additionally, substantial differences in preprocessing steps such as filtering and windowing exist among disparate studies, and measurement methods may respond differently to discrepancies in preprocessing procedures.
Several studies that seek to compare measurement methods for both synthetic and real data have been published. Long and van der Hilst (2005b) carried out a comparison of the transverse component minimization, cross-correlation, and multichannel methods for SKS and direct teleseismic S phases at two stations in Japan, one of which has a relatively simple splitting pattern, and one of which overlies more complex anisotropy. They found that the transverse component minimization method and cross-correlation methods were much more likely to disagree at the station with the more complex splitting pattern. They also found that the multichannel method yielded more usable measurements when more restrictive filtering schemes were used. Wüstefeld and Bokelmann (2007) carried out a comparison of the transverse component minimization method and the cross-correlation method with a focus on identifying null measurements and correctly characterizing splitting for phases whose incoming polarization directions are close (within 10–15°) to the null directions. They highlight the observation that the cross-correlation method yields ϕ estimates that are nearly 45° off when the incoming polarization is very close to a null direction; this problem is exacerbated for noisy data (Wüstefeld and Bokelmann 2007). The transverse component minimization method is also known to yield inaccurate estimates (often with unreasonably large δt values) in this situation (e.g., Savage 1999; Long and van der Hilst 2005b; Vecsey et al. 2008). Finally, Vecsey et al. (2008) recently carried out a study of synthetic and real SKS data comparing the transverse component minimization method, the closely related eigenvalue method, and the cross-correlation method. They argue that the transverse component minimization method is most robust for noisy data and recommend a set of best practices related to each measurement method.
Each of the measurement methods described above has pros and cons, and in practice a combination of methods increases the confidence that individual measurements are robust and may help to distinguish complex anisotropy beneath a station (e.g., Levin et al. 2004; Long and van der Hilst 2005a, b; Lev et al. 2006). Some workers have concluded that the transverse component minimization method is the most robust method for noisy data, but any advantage may only persist for SKS-type phases, where the initial polarization corresponds to the backazimuth (assuming that the polarization has been unaffected by other factors, such as extreme lateral heterogeneity); for direct S phases, the initial polarization must either be modeled from the (imperfectly known) source mechanism or estimated from the seismogram along with the splitting parameters. Additionally, the transverse component minimization method seems to be more affected by complex anisotropy beneath a station (Long and van der Hilst 2005b). Using a combination of the transverse component minimization and the cross-correlation methods for SKS and direct teleseismic S phases may increase confidence in individual measurements and avoid the problems posed by phases whose incoming polarization directions are near the null directions (e.g., Levin et al. 2004; Long 2009). Relative to the single-record methods, multiple-record methods (namely stacking with transverse-component-minimization and multichannel methods) have several distinct advantages. First, they easily deal with null or near-null splitting and therefore avoid subjectivity in characterizing null measurements. Second, they are generally much more robust than measurements of (ϕ, δt) from individual seismograms (Wolfe and Silver 1998; Chevrot 2000; Long and van der Hilst 2005b). One disadvantage of the multichannel method is that it discards much of the information available in the seismogram (at least two records are required to obtain splitting parameters) and thus requires a more complete range of initial polarization angle in order to find the best-fitting splitting parameters (ϕ, δt), which can be difficult to achieve. This disadvantage ends up being a significant advantage in performing splitting tomography, since the splitting intensity, unlike the actual splitting parameters, can be treated like a travel time (see Sect. 2.4.2).
2.1.2 High-Frequency Data
In this paper, we focus on the use of shear wave splitting to characterize mantle anisotropy and deformation and therefore focus on measurement methods for broadband data where the intent is to measure splitting associated with delay times that are much smaller than the dominant period of the signal. However, higher-frequency data can also be useful for splitting analysis, and in particular, often contains information about near-surface anisotropy. The measurement and interpretation of crustal anisotropy is, of course, an important topic in its own right (see, e.g., Crampin 1984; Kaneshima 1990; Crampin and Chastin 2003; Cochran et al. 2003; Gerst and Savage 2004) and can yield valuable information about the state of stress in the upper crust and temporal changes in that stress state. From the point of view of characterizing anisotropy in the Earth’s mantle, the presence of anisotropy in the crust is a potential contaminant in the shear wave splitting signal. It is usually argued (e.g., Silver 1996; Savage 1999) that the typical delay time value for crustal anisotropy is perhaps ~0.1–0.2 s, and that this represents a small contribution to typical delay times measured from broadband data and attributed to mantle anisotropy, which are typically on the order of ~1 s for most raypath geometries (e.g., Silver 1996; Fouch and Rondenay 2006). Therefore, any crustal contribution to long-period data is usually ignored; however, the use of higher-frequency data to characterize crustal anisotropy beneath a station could potentially allow for explicit “crustal corrections” of broadband splitting measurements. Additionally, several studies have demonstrated that, at higher frequencies, splitting measurements tend to be biased towards near-surface structure in the presence of vertically varying anisotropy (e.g., Rümpker and Silver 1998; Saltzer et al. 2000). This sounds a note of caution for studies that use very high-frequency data to characterize upper mantle anisotropy; for example, Nakajima and Hasegawa (2004) measured shear wave splitting beneath northern Tohoku from earthquakes originating in the subducting Pacific slab at frequencies between 2 and 8 Hz and found average delay times of ~0.1 s, which they attributed to anisotropic structure in the mantle wedge.
2.1.3 Array Data
Unlike many seismological analysis techniques, shear wave splitting is a single-station measurement. Because the technique does not require array data it has been widely applied to isolated stations to obtain local estimates of upper mantle anisotropy (e.g., Vinnik et al. 1989a; Ansel and Nataf 1989; Silver and Chan 1991; Barruol and Hoffmann 1999). However, the increasing availability of data from permanent and temporary broadband arrays has led to a corresponding increase in shear wave splitting studies that have the ability to examine variations in anisotropic structure over large regions (and at short length scales) using array data. These types of studies contribute not only to our understanding of anisotropy and mantle flow on regional scales in different types of tectonic environments, but also to our ability to understand the length scales over which anisotropic structures may change and to make individual measurements more accurately.
For example, array studies of shear wave splitting in subduction zones have led to the detailed characterization of splitting patterns in the mantle wedge above subducting slabs, which typically show dramatic lateral variations (e.g., Fischer et al. 1998; Smith et al. 2001; Levin et al. 2004; Pozgay et al. 2007). Analysis of the length scales over which splitting changes can also provide insight about the processes that produce short-scale changes in anisotropic structure, and about the lateral and vertical sensitivity of shear wave splitting measurements. Small-scale variations in splitting parameters for densely spaced arrays have been characterized for several regions (e.g., Wolfe and Vernon 1998; Fouch et al. 2004; Harmon et al. 2004; Ryberg et al. 2005) and the length scales over which splitting parameters can change due to lateral changes in anisotropic structure at depth have been explored using numerical modeling (Rümpker and Ryberg 2000; Chevrot et al. 2004; Fischer et al. 2005, Levin et al. 2007). The availability of array data can also improve the reliability of individual splitting measurements, because it enables the visual inspection of radial and transverse waveforms for a given SKS arrival across the entire array (e.g., Fouch 2007). This allows the analyst to evaluate possible measurement errors at individual stations due to noise contamination or cycle skipping. Finally, shear wave splitting measurements for densely spaced arrays are beginning to allow for the implementation of tomographic inversion methods for splitting data, as discussed in Sect. 2.4.2. For a host of reasons, therefore, the availability of array data is crucial to our ability to resolve anisotropic structure at depth, even though shear wave splitting is usually thought of as a single-station technique.
2.2 Which Seismic Phases are Useful?
2.2.1 Characterizing Upper Mantle Anisotropy
The phases that are commonly used to probe anisotropic structure in the upper mantle are shown in Fig. 4. SKS and other core phases (e.g., SKKS, PKS) are, by far, the most popular phase used in shear wave splitting studies. They provide several advantages over other shear phases; in addition to the fact that its unperturbed polarization is controlled by the P-to-S conversion at the CMB, which is important from a measurement point of view, this conversion also means that any observed splitting must be due to anisotropic structure on the receiver side between the CMB and the surface. The nearly vertical propagation of SKS through the upper mantle also means that the incidence angle will be well within the so-called shear wave window (shear phases that have incidence angles larger than ~35° at the surface may be affected by nonlinear shear particle motion in the absence of anisotropy; e.g., Savage 1999).
Some of the most commonly used phases to probe upper mantle anisotropy (a) and D″ anisotropy (b). In the upper mantle, these include SK(K)S phases at epicentral distances greater than ~88° and direct teleseismic S phases from deep events at distances between ~40° and 80° (a). For D″, useful phases include SKS-SKKS pairs at distances between ~110° and 120°, which can be examined for splitting discrepancies, S and/or ScS phases at distances between ~85° and 95°, and Sdiff phases beyond ~100° (b)
From a ray theoretical point of view, SKS may be affected by anisotropic structure anywhere along the receiver side of its mantle ray path. However, SKS splitting is nearly always interpreted in terms of upper mantle anisotropy, and a potential contribution from the lower mantle is ignored. There are a few lines of evidence to support this interpretation; one argument makes use of splitting measurements for pairs of phases that sample the upper mantle in a similar way but the rest of the mantle differently, such as SKS and SKKS (Niu and Perez 2004; Restivo and Helffrich 2006) or SKS and deep local S (Meade et al. 1995). In the overwhelming majority of cases, splitting measurements for such pairs agree, implying that the source of the splitting is in the upper mantle There are, however, notable exceptions. For example, Long (2009) documented significant SKS-SKKS splitting discrepancies in western North America that require a contribution from the lower mantle.
A second line of argument comes from array studies of SKS splitting. If the earthquake distribution used at each station is similar, then any variations in splitting across the array are likely due to upper mantle anisotropy beneath the receiver, since the lower mantle is being sampled in a similar way at all stations. Similarly, it is often assumed that the contribution to SKS splitting from the crust (thought to be on the order of ~0.1 s; e.g., Savage 1999) is much smaller than the upper mantle contribution, usually on the order of ~1 s (Silver 1996; Fouch and Rondenay 2006). The approximation usually made in SKS splitting studies that the primary source of the anisotropy is in the upper mantle is probably valid in most cases, but important exceptions have been documented. For example, Mattatall and Fouch (2007) argue for a significant effect of crustal anisotropy on SKS measurements near Parkfield, CA.
In addition to the popular S(K)KS phases, other shear phases are useful for characterizing upper mantle anisotropy, including direct S waves at local and teleseismic distances, converted phases such as P660s, and reflected phases such as SS or sS. The splitting of local, direct S waves in subduction zone settings, where deep earthquakes are usually plentiful, has been used extensively to characterize anisotropy in the mantle wedge, and a large body of literature on local splitting above subducting slabs exists (see Sect. 4.1.5). Direct S phases at teleseismic distances can also be used to probe upper mantle anisotropy, but their use is not as straightforward as that of SKS (both from a measurement and an interpretation point of view). Because the incidence angle at the surface cannot exceed ~35°, epicentral distances (Δ) greater than ~40° must be used, and beyond ~80° there may be contamination from other shear phases in the seismogram. Because the initial polarization of direct S is not fixed by the backazimuth, it must be predicted from the focal mechanism, measured directly from the seismogram, or treated as an unknown in the measurement process. If the analyst wishes to probe upper mantle anisotropy beneath the receiver, then care must be taken to minimize any contamination from source-side anisotropy in the upper mantle beneath the earthquake. The use of deep events (>200–300 km) can help to minimize any contribution for anisotropy near the source. However, when direct teleseismic S phases are used to characterize receiver-side anisotropy, it is imperative to test for a significant source-side contribution by examining splitting from individual events at a range of stations (e.g., Long and van der Hilst 2005a). Conversely, direct teleseismic S (or phases such as ScS) can be used to probe source-side anisotropy (e.g., Kaneshima and Silver 1992; Russo and Silver 1994; Müller et al. 2008), as long as anisotropy beneath the receiver is properly accounted for.
Converted phases (e.g., Kosarev et al. 1984; Girardin and Farra 1998; Iidaka and Niu 1998) or phases that have undergone an underside surface reflection (e.g., SS; Wolfe and Silver 1998, or sS; Anglin and Fouch 2005) can be useful for upper mantle anisotropy studies, although, again, some caution must be exercised. Converted phases may have low signal-to-noise ratio that makes accurate splitting measurements difficult; this can be improved by stacking, but then information about complex anisotropy may be lost. For phases that contain an underside reflection, the phase shift associated with the reflection must be properly accounted for as well as complex structure near the bounce point, such as the oceanic Moho. Finally, P-to-S conversions from the Moho can be used to isolate the crustal contribution to splitting that is always combined with the splitting in teleseismic shear waves. As with SKS, the conversion fixes the polarity to be radial. The primary disadvantage of this approach is that the converted phase (usually measured on receiver functions rather than raw seismograms) is weak, leading to large uncertainty. In addition, there are other contributions from converted/reflected phases in the crust that can mask this particular arrival. Nevertheless, this is an often-utilized procedure (e.g., McNamara and Owens 1993; Iidaka 2003; Rai et al. 2008) that continues to yield consistent characteristics for crustal splitting, namely delay times averaging about 0.2 s.
2.2.2 Characterizing Anisotropy in the Transition Zone, Lower Mantle, and D″
The majority of published shear wave splitting studies focus on anisotropy in the upper mantle; however, a variety of shear phases can be used to probe the transition zone, the lower mantle, and the D″ region directly above the CMB. SK(K)S phases propagate through the entire mantle, sampling all of these regions in addition to the upper mantle and crust beneath the receiver, but there have only been a few studies that have identified a contribution to SK(K)S from the transition zone or lower mantle. For example, Iidaka and Niu (1998) compared the splitting of SKS and P600s waveforms and found evidence for a contribution from anisotropy beneath the upper mantle. In addition to waveform comparisons between SK(K)S and other phases, direct S waves from deep earthquakes can be used to probe the uppermost lower mantle and transition zone; Wookey et al. (2002) found evidence for mid-mantle anisotropy in the vicinity of the Tonga-Kermadec subduction zone using regional S phases. At these short epicentral distances, however, care must be taken to account correctly for the effects of S-to-P conversions near the surface (Saul and Vinnik 2003; Wookey et al. 2003; Wookey and Kendall 2004).
Discrepancies in shear wave splitting for SKS and SKKS phases from the same event-station pair can also provide evidence for a contribution from anisotropy beneath the upper mantle, since SKS and SKKS have very similar raypaths in the upper mantle and their paths only diverge significantly in the lower mantle. SKS-SKKS splitting discrepancies were first documented by James and Assumpçao (1996) for stations located in Brazil, and have since been found at a limited number of stations. While global studies of SKS-SKKS differential splitting have demonstrated that measured splitting parameters for SKS and SKKS agree in 95% of cases (Niu and Perez 2004), a few studies have identified isolated examples of SKS-SKKS splitting discrepancies (Niu and Perez 2004; Restivo and Helffrich 2006; Long 2009) and attributed them to anisotropy in the lower mantle.
Seismic anisotropy in the D″ layer can be probed using a variety of phases; in addition to SKS-SKKS splitting discrepancies, which can be produced by certain styles of anisotropy in D″ (Hall et al. 2004), phases that propagate nearly horizontally through D″ are often used to interrogate D″ anisotropy (e.g., Maupin 1994; Kendall and Silver 1996; Lay et al. 1998; Moore et al. 2004; Wookey and Kendall 2007; Fig. 4). These include direct S phases that turn in the lowermost mantle, ScS phases at relatively large epicentral distances (greater than ~65°), and shear waves that have been diffracted along the core-mantle boundary (Sdiff). The “combined” S + ScS phase at epicentral distances greater than ~85°, where S and ScS arrive simultaneously, has also been subjected to shear wave splitting measurements to infer D″ anisotropy. Phases that propagate horizontally through D″ are often examined for a time separation between the SV and SH components, which correspond to vertically and horizontally polarized waves, or more sophisticated measurement techniques can be brought to bear (e.g., Garnero et al. 2004a; Wookey et al. 2005; Wookey and Kendall 2008) that can allow for a more complete description of the geometry of anisotropy, including the dip of the symmetry axis.
2.3 Diagnosing Complex Anisotropic Structure
It is important to understand the impact of complex anisotropic structure on both the measurement and interpretation of measurements. In some cases, the measurements are meaningful, even in the presence of complex structure, while in others the results are simply wrong. For example, single-record measurements (e.g. transverse-component-minimization or cross-correlation) are meaningful for a homogeneous layer with arbitrary symmetry. In the presence of vertical heterogeneity, the resulting ‘apparent’ splitting parameters (namely, measurements made under the assumption of a single homogeneous layer when multiple layers are present) can still be related to anisotropic properties in a straightforward manner. In contrast, multi-record stacks, the averaging of individual measurements, or use of a sin(2β) fit to the splitting intensity implicitly assume all rays have passed through a single homogeneous region with horizontal symmetry axis. In this case rays with arbitrary polarization and for a limited range of incidence angles and backazimuths should all yield the same splitting parameters. The violation of these assumptions can lead to measurements that are not meaningful. Thus, a critical, although sometimes neglected, aspect of shear wave splitting studies is to examine splitting data from individual records for diagnostics of complex anisotropic structure at depth. In the presence of such complex structure, extreme care must be taken to relate measurements to anisotropy at depth properly, and perform appropriate averaging. Here we will focus on the case of complex anisotropy (multiple layers, dipping axis of symmetry, small-scale lateral heterogeneity) in the upper mantle beneath a seismic station, but complex structure may be present in other parts of the mantle (e.g., D″) as well.
2.3.1 Backazimuthal Variations in Apparent Splitting Parameters
It has long been recognized that the presence of complex anisotropy will result in variations in apparent splitting parameters with backazimuth and/or (in the case of direct teleseismic S phases) with incoming polarization azimuth. For the case of multiple layers of anisotropy, this backazimuthal variation takes the form of a periodic variation in both ϕ and δt measurements with a π/2 periodicity (Silver and Savage 1994). A dipping axis of symmetry, in contrast, will manifest itself as a π periodicity for the case of TI symmetry (e.g., Chevrot 2000). Forward modeling studies (e.g. Brechner et al. 1998) have shown that in the case of multiple layers of anisotropy with dipping symmetry axes, the backazimuthal variations in apparent splitting parameters can be quite complicated. Whatever form the complex anisotropy takes, variations in apparent splitting parameters with incoming polarization azimuth are a valuable diagnostic for complex anisotropic structure at depth, and a sign that average splitting parameters at the station cannot be simply related to the mantle flow direction at depth. Backazimuthal variations in splitting have been identified by numerous studies in a variety of tectonic settings including, for example, transform faults such as the San Andreas (Savage and Silver 1993; Özalaybey and Savage 1994, 1995; Liu et al. 1995; Polet and Kanamori 2002), triple junctions such as the Mendocino (Hartog and Schwartz 2000), collision zones such as Tibet (e.g., Lev et al. 2006), mantle upwellings such as Hawaii (Walker et al. 2001), and subduction zones (e.g., Long and van der Hilst 2005a, b). An example of backazimuthal variations in splitting parameters observed at a station in the western US is shown in Fig. 5.
An example of a station that exhibits a complex splitting pattern that may be diagnostic of complex anisotropic structure beneath the station. SKS splitting measurements obtained using the transverse component minimization method at Transportable Array station G05A are plotted as a function of backazimuth (circles indicate “good" quality measurements; squares indicate “fair”). There is some variation with backazimuth in the measured splitting parameters, particularly in ϕ. Bottom panel: Individual splitting measurements are plotted with respect to backazimuth and incidence angle; again, the backazimuthal variation can be seen. Measurements are from the dataset of Long et al. (in review)
2.3.2 Complex Behavior of the Splitting Vector
If the multichannel measurement method (Chevrot 2000) is used and individual splitting intensity measurements are plotted with respect to the incoming polarization azimuth, then complex anisotropic structure can be diagnosed by looking for complex behavior of the splitting vector. As discussed in Sect. 2.1, in the case of a single anisotropic layer, the splitting vector will take the form of a sin(2β) curve and the delay time δt and the fast direction ϕ can be obtained from the amplitude and phase, respectively, of the sinusoid. Because the splitting intensity is a commutative measurement and the cumulative effect of anisotropy on the measured splitting intensity along a raypath can be represented as a sum of each layer, in the case of two distinct layers of anisotropy, the splitting vector will still take the form of a sin(2β) curve; this is analogous to an “apparent” splitting parameter obtained using a single-record method. By itself, therefore, the splitting vector cannot be used to diagnose multiple (horizontal) layers of anisotropy, and this method should be used in conjunction with apparent splitting parameter measurements or the cross-convolution method to characterize (or rule out) this type of complex structure. However, other forms of complex anisotropy will cause the splitting vector to deviate from a perfect sin(2β) curve; in particular, if the axis of symmetry deviates from the horizontal, the splitting vector will have a sin(β) term and the discrete Fourier transform of the splitting vector will have energy in the n = 1 azimuthal harmonic (Chevrot 2000). Lateral variations in anisotropy, including contributions from the crust, can also result in the deviation of the splitting vector from a perfect sin(2β) curve. The multichannel method has been used in conjunction with apparent splitting measurements to diagnose complex anisotropy in Japan (Long and van der Hilst 2005a, b) and Tibet (Lev et al. 2006); an example of a complex splitting vector measured at a station in Japan is shown in Fig. 6.
An example of a complex splitting pattern obtained using the multichannel method, diagnostic of complex anisotropy beneath the station. Individual splitting intensity measurements made at F-net station TMR in Japan are plotted with respect to incoming polarization azimuth. In contrast to the splitting vector plotted in Fig. 2, the pattern is more complicated than a simple sin(2) dependence. Measurements are from the data set of Long and van der Hilst (2005a)
2.3.3 Frequency Dependence of Splitting Measurements
It has been demonstrated using forward modeling techniques that apparent splitting parameters will depend on frequency in the presence of multiple layers of anisotropy and that higher frequency measurements are generally biased towards near-surface layers (Silver and Savage 1994; Rumpker and Silver 1998; Saltzer et al. 2000). From a finite-frequency point of view (discussed further in Sect. 2.4.2), the sensitivity kernels for shear wave splitting measurements depend on the frequency content of the waves under study and, in general, the size of the first Fresnel zone (where most of the sensitivity is concentrated) will increase with decreasing frequency. Because the sensitivity kernels are frequency dependent, in the presence of laterally or vertically varying anisotropic structure, splitting measurements will be frequency dependent as well. Any dependence on frequency can therefore be interpreted as evidence for complex anisotropic structure at depth (see also Saltzer et al. 2000; Fouch and Rondenay 2006). Frequency dependent splitting has been identified in several regions, including New Zealand (Marson-Pidgeon and Savage 1997), Australia (Clitheroe and van der Hilst 1998), the Marianas (Fouch and Fischer 1998), the Kaapvaal craton (Fouch et al. 2004), and Japan (Long and van der Hilst 2005b, 2006; Wirth and Long 2008); an example is illustrated in Fig. 7.
An example of strongly frequency-dependent splitting of local S phases from the data set of Wirth and Long (2008). a Individual splitting measurements using the cross-correlation method are plotted at the midpoint between the event and station; data were filtered to retain energy at periods between 8 and 50 s. Bars are scaled to the delay time and the color indicates the delay time range: δt > 1.7 (red), 1.7 > δt > 1.2 (yellow), δt < 1.2 (green). b Same as (a), but the data have been filtered to retain energy at periods between 2 and 8 s
2.3.4 Small-Scale Lateral Variations
Yet another manifestation of complex anisotropic structure in shear wave splitting data sets can be found by exploiting the dense station spacing that is a feature of many broadband seismic arrays. In particular, variations in splitting parameters over short length scales are an indicator of lateral heterogeneity in anisotropic structure. (Conversely, similarity in splitting parameters measured at adjacent stations can be used to place depth constraints on the source of the anisotropy, via a Fresnel zone argument, as in Alsina and Snieder 1995.) The effect of lateral anisotropic variations at depth on splitting measurements can be subtle; several studies have demonstrated that in the vicinity of sharp lateral transitions in anisotropic structure the effect of the boundaries on the shear waveforms can be complex (e.g., Ryberg and Rümpker 2000), Chevrot et al. 2004; Fischer et al. 2005). Lateral variations in splitting parameters can also be used to place depth constraints on complex anisotropy; for example, variations over short length scales are often interpreted as being due to lateral heterogeneity in shallow anisotropy. Observations of short-scale lateral variations in splitting parameters have been exploited to infer information about anisotropic heterogeneity at depth in several regions and particularly striking examples have been documented in studies by Fouch et al. (2004) for the Kaapvaal Craton and by Mattatall and Fouch (2007) for the San Andreas Fault near Parkfield. Using the extremely dense broadband PASO-DOS array, Mattatall and Fouch (2007) found splitting variations over distances of just a few km and interpreted them as being due to anisotropy in the shallow crust. They further argued that such extreme small-scale variations indicate a larger contribution to broadband splitting measurements from the crust than is usually accounted for.
2.3.5 Discrepancies Among Different Measurement Methods
Another important diagnostic for the presence of complex anisotropy at depth is the existence of discrepancies in measured apparent splitting parameters when different measurement methods are used, as discussed in Sect. 2.1.1. As pointed out by, e.g., Menke and Levin (2003), complex anisotropy will result in correspondingly complex waveforms that do not conform to the predictions of the single, horizontal layer of anisotropy that is implicitly assumed by the transverse component minimization method or the cross-correlation method. Because these different measurement methods may respond differently to such complexity, discrepancies between splitting parameters measured with different methods (within the measurement errors) on the same waveform may be diagnostic of complex anisotropic structure at depth. For example, Levin et al. (2004) measured splitting of local S waves in Kamchatka with both the transverse component minimization and cross-correlation methods and identified a substantial population of S arrivals for which the two methods yielded individually well constrained but discrepant splitting parameters.
2.3.6 The Importance of Diagnosing Complex Anisotropy
As described above, there are several strategies for recognizing the effect of complex anisotropy in shear wave splitting patterns, and it is imperative for shear wave splitting practitioners to do the best job possible of diagnosing complex anisotropy through a combination of the methods described above. Not only does a more complete description of complex anisotropy allow the analyst to do a better job of relating shear wave splitting observations to mantle processes at depth, but properly accounting for the possibility of complicated anisotropic structure can help to avoid serious errors in interpretation. Of course, many of the diagnostics described above require dense arrays and/or years of data in order, for example, to obtain sufficient coverage in incoming polarization azimuth (equivalent to backazimuth for core phases), and in some cases data limitations preclude this type of analysis. In these cases, it is important for shear wave splitting practitioners to be candid about the limitations of a particular data set and to be cautious about its interpretation.
2.4 Extracting Information About Complex Structure
2.4.1 Forward Modeling
One method for characterizing complex anisotropic structure at depth once it has been diagnosed from the patterns of shear wave splitting measured at the surface is to carry out forward modeling studies to try to match observed splitting patterns with predicted ones. A well-known example of this is the techniques that have been developed to model multiple layers of (horizontal) anisotropy at depth. Analytical expressions that describe the variation in measured apparent (ϕ, δt) values in the presence of two (or more) anisotropic layers were developed by Savage and Silver (1993) and Silver and Savage (1994) and many studies have attempted to match backazimuthal variations in splitting parameters using two-layer modeling (e.g., Özalaybey and Savage 1994, 1995; Levin et al. 1999; Polet and Kanamori 2002; Walker et al. 2005a, b). Other techniques for predicting apparent shear wave splitting parameters for complex anisotropic structures include those based on particle motion perturbation methods (e.g., Rümpker and Silver 1998; Fischer et al. 2000; Abt and Fischer 2008), the cross-convolution method (Menke and Levin 2003; Yuan et al. 2008) or those based on pseudospectral waveform simulations (e.g., Chevrot et al. 2004; Abt and Fischer 2008).
Another class of forward modeling studies includes work towards evaluating predicted shear wave splitting patterns for geodynamical models of mantle processes, which can both narrow the class of plausible anisotropic models that are consistent with splitting data and shed light on the geodynamical processes responsible for generating anisotropy in different tectonic settings. Many of these studies have focused on mantle flow in subduction zones, particularly in the mantle wedge (e.g., Fischer et al. 2000; Hall et al. 2000; Long et al. 2007b; Kneller and van Keken 2007; Kneller et al. 2008), but other tectonic settings such as mid-ocean ridges (e.g., Blackman and Kendall 2002; Nippress et al. 2007), and continental collisional zones (e.g. Davis et al. 1997) have also been examined. Geodynamical modeling studies have used a variety of approaches for approximating the relationship between strain and anisotropy, including those that assume that the fast axis of olivine aligns locally with the finite strain ellipse (e.g., Fischer et al. 2000; Hall et al. 2000). This approach, however, ignores possible complexities such as olivine fabric transitions and does not realistically model the development of LPO or take into account the timescale over which LPO develops (Kaminski and Ribe 2002). Various other approaches to model directly fabric development using schemes such as D-Rex (Kaminski et al. 2004) or viscoplastic self-consistent modeling (e.g., Tommasi et al. 2000) have also been implemented (see, e.g., Lev and Hager 2008a). Because these geodynamical models contain (hopefully) realistic anisotropic geometries, including lateral heterogeneity, they represent a useful tool for characterizing shear wave splitting patterns that result from complex anisotropy. A recent overview of efforts to integrate mineral physics constraints into geodynamical models in order to predict seismological observables such as shear wave splitting is provided by Blackman (2007).
2.4.2 Inverse Modeling: Shear Wave Splitting Tomography
One of the more exciting developments in recent years in the realm of interpreting shear wave splitting measurements for mantle anisotropy has been the development and application of techniques for the tomographic inversion of shear wave splitting measurements for anisotropic structure at depth. Shear wave splitting tomography has lagged considerably behind isotropic wavespeed tomography, for several reasons. First, dense seismic networks are needed in order to achieve the good coverage in backazimuth and incidence angle required for tomography. This challenge is always present for tomographic inversions of geophysical data, but is more acute for shear wave splitting tomography because individual splitting measurements are far more difficult to make than simple traveltime measurements. A second challenge comes from the fact that 21 elastic parameters are needed fully to describe the most general elastic tensor, in contrast to the single parameter needed to describe isotropic wavespeed; this means that inverting for laterally varying general anisotropy is much more ill-posed than traditional seismic tomography inversions. Of course, the parameter space can (and must) be substantially reduced in order to make shear wave splitting tomography feasible, but it is important to be sure that the assumptions made in reducing the number of parameters that describe anisotropy are reasonable.
Early work on the inversion of shear wave splitting parameters, in combination with P wave travel time residuals, was done by Síleney and Plomerová (1996) and Plomerová et al. (1996), who inverted data from the western US and Fennoscandia for a set of parameters that describe a homogeneous anisotropic media with a dipping axis of either hexagonal or orthorhombic symmetry. These early studies solved for a homogenous anisotropic structure at depth, but the availability of dense array data is beginning to allow for the development of techniques to solve for laterally and vertically heterogeneous anisotropy at depth using tomographic methods. For example, Rümpker et al. (2003) and Ryberg et al. (2005) developed a method to invert SKS splitting observations across a very dense network of short-period sensors across the Dead Sea transform fault for a 6-block anisotropic model at depth.
In the past few years, theoretical and practical developments towards carrying out full tomographic inversions of splitting measurements have proceeded along two parallel tracks. One of these (Abt and Fischer 2008; Abt et al. 2009) has focused on carrying out local splitting tomography using a ray theoretical approach, with application to data sets acquired in subduction zone settings using earthquakes located in the subducting slab to obtain a set of crossing rays that sample the mantle wedge. The inversion approach described by Abt and Fischer (2008) utilizes measurements made by the transverse component minimization method (Silver and Chan 1991) and the model space is described using a 3-D block parameterization which allows for axes of symmetry that are described by an azimuth and a dip. The partial derivatives of the measured apparent splitting parameters with respect to the model space parameters are calculated by carrying out ray tracing for individual rays and progressively applying a rotation and time-shift to an idealized input wavelet for each model block that approximates the effect of splitting. The inversion itself uses an iterative, linearized, damped least-squares approach to solve for changes to the starting model to converge upon a solution. The technique has been applied to a set of local S measurements from the TUCAN experiment in Central America.
Another approach to the tomographic inversion of shear wave splitting uses a different type of data, namely measurements of the teleseismic shear wave splitting intensity (Chevrot 2000), and incorporates finite-frequency effects into the inversion framework. Analytical expressions for finite-frequency sensitivity kernels for shear wave splitting intensity were developed by Favier and Chevrot (2003) and Favier et al. (2004), and these studies provided the first theoretical framework for considering full finite-frequency effects on shear wave splitting measurements. Subsequent studies have explored various aspects of incorporating finite-frequency sensitivity kernels into a tomographic framework (Chevrot 2006; Long et al. 2008) and on numerically calculating sensitivity kernels using an adjoint approach (Sieminski et al. 2008) or in realistic, heterogeneous starting models (Long et al. 2008).
The shear wave splitting intensity measurement introduced by Chevrot (2000) is, in many ways, better suited to imaging anisotropic structure through tomographic inversion than single-record measurement methods which measure “apparent” splitting parameters (ϕ, δt) in complex media. From a measurement point of view, the splitting intensity is a more robust measurement (Chevrot 2000) that is less affected by subjective choices on the part of the analyst such as filtering or windowing (Long and van der Hilst 2005b) and also deals better with waveforms that exhibit null or near-null splitting. Finally, the splitting intensity is commutative, unlike the so-called splitting operator (Silver and Chan 1991; Silver and Savage 1994), which means that it can be summed along a ray (or throughout a sensitivity kernel volume) and can be treated similarly to a traveltime delay in traditional wavespeed tomography, as it can be linearly related to anisotropic perturbations at depth (Chevrot 2006; Long et al. 2008; Sieminski et al. 2008).
Computations of full wave-equation sensitivity kernels for the splitting intensity are similar in philosophy to finite-frequency kernels for isotropic travel times measured by cross-correlation (e.g., Dahlen et al. 2000; de Hoop and van der Hilst 2005), and the kernels are then used to set up a linearized tomographic inversion for a carefully chosen set of anisotropic parameters. Splitting intensity sensitivity kernels are obtained by solving the partial differential equations (PDEs) that govern wave-equation splitting tomography; the kernel expressions can then be evaluated approximately (using single-scattering Born theory) either analytically (Chevrot 2006) or numerically (Long et al. 2008), in some cases by utilizing adjoint computations (Sieminski et al. 2008). An example of 2-D splitting intensity sensitivity kernels for an SKS arrival for the parameterization used by Long et al. (2008) is shown in Fig. 8.
Example of 2-D finite-frequency sensitivity kernels for SKS waves, after Long et al. (2008). The kernels are calculated with respect to two parameters: the anellipticity parameter, which represents the strength of anisotropy, and the dip of the symmetry axis from the horizontal. Green colors indicate zero sensitivity, while red and blue indicate strong sensitivity (positive or negative). The kernels are calculated with respect to a homogeneous background model with a horizontal axis of symmetry; for further details, see Long et al. (2008)
3 Linking Shear Wave Splitting to Mantle Processes
Seismic anisotropy in the Earth’s mantle is a consequence of deformation, whether through LPO or SPO, and it is this link between mantle flow and the geometry and strength of anisotropy that drives much of the scientific interest in shear wave splitting as a geophysical technique. Recent overviews of experimental mineral physics results relating to mantle anisotropy have been published by Mainprice (2007), Karato et al. (2008) (for upper mantle anisotropy), and Yamazaki and Karato (2007) (for D″ anisotropy), and for a more detailed review of the mineral physics literature we refer the reader to these publications. Here, we provide a brief overview of the experimental constraints on the relationship between deformation and the resulting anisotropy and a general summary of recent advances relevant to the interpretation of shear wave splitting measurements.
3.1 The Upper Mantle
It is generally agreed that LPO in olivine makes the primary contribution to upper mantle anisotropy; it is volumetrically most important and has a single-crystal shear wave anisotropy of ~18% (see, e.g., Mainprice 2007). Most of the constraints we have on the relationships between deformation and the resulting LPO come from experiments done on olivine aggregates or from the petrographic analysis of mantle-derived rocks. It is generally thought that deformation in the dislocation creep regime is required to produce LPO; in contrast, diffusion creep does not produce LPO and in fact efficiently wipes out any preexisting fabric (e.g., Karato and Wu 1993). The discussion of upper mantle LPO that follows therefore focuses on experiments that have been carried out in the dislocation creep regime. Recent experimental results, however, have provided some evidence that deformation in the diffusion creep regime can produce LPO in anhydrous two-phase aggregates deformed at low stresses (Sundberg and Cooper 2008), and such a mechanism may potentially be applicable to some regions of the mantle.
Until recently, a very simple relationship was used to infer upper mantle flow beneath a seismic station from shear wave splitting measurements, based on measurements of LPO in naturally deformed peridotite rocks (e.g., Christensen 1984; Nicolas and Christensen 1987) and in samples deformed in the laboratory in simple shear (e.g., Zhang and Karato 1995). These studies suggested that the fast axis of olivine tends to align with the maximum shear direction for large strains (~100% or greater), which implies that the fast splitting direction measured at a seismic station for nearly vertically propagating S phases roughly corresponds to the direction of (horizontal) maximum shear beneath that station. (For the case of vertical shear, the fast direction would align vertically and for a TI medium, there would be no splitting of vertically propagating S waves.) However, a series of experiments by Jung and Karato (2001) produced a dramatically different result: when olivine samples that contained a significant amount of water incorporated into the crystal structure (~200–1,200 ppm) were deformed at high stresses and relatively low temperatures, the fast direction tended to align 90° away from the flow direction. They termed this geometry “B-type” olivine fabric and suggested that it might explain, for example, observations of trench-parallel fast directions in the mantle wedge above subducting slabs (discussed further in Sect. 4.1.5).
Since the work of Jung and Karato (2001), subsequent experiments have shown that LPO geometry in deformed olivine aggregates depends strongly on the experimental conditions, namely on stress, temperature, and water content. Studies by Katayama et al. (2004), Jung et al. (2006), and Katayama and Karato (2006) mapped out the occurrence of five different olivine fabric types (the original A-type plus B-, C-, D-, and E-types). Karato et al. (2008) suggested that that the asthenospheric upper mantle may generally be dominated by E- or C-type olivine rather than the traditionally assumed A-type. Natural occurrences of each of the olivine fabric types recognized in the laboratory have been identified, notably B-type fabric from convergent boundaries (e.g., Mizukami et al. 2004; Skemer et al. 2006) and C-type fabric from deep mantle samples (see, e.g., Katayama and Karato 2006). However, global databases of fabric types for natural peridotite samples (Ben Ismail and Mainprice 1998) show that B-, C-, and E-type fabrics make up very small percentages of the global population (approximately 7, 7, and 2%, respectively; Mainprice 2007), and most samples are A- or D- type. Of course, there is potentially a sampling bias in the geological record (since samples come from unusual locales such as kimberlite pipes and ophiolites), so this may not accurately reflect the statistical distribution of fabric types in the mantle. From the point of view of interpreting shear wave splitting measurements, the only fabric type that dramatically changes the geometrical relationship between flow and fast splitting direction is B-type. Based on experimental results and natural samples (Jung and Karato 2001; Mizukami et al. 2004; Katayama and Karato 2006; Karato et al. 2008) and geodynamical modeling (Kneller et al. 2005, 2008), B-type fabric has been thought to be restricted to limited regions of the upper mantle, namely the forearc corner of some subduction zone mantle wedges.
While the dependence of olivine fabric on stress, temperature, and water content has been fairly well established, its possible dependence on pressure has been a topic of some debate. A few studies have claimed experimental support for a pressure-induced fabric transition in olivine, including Couvy et al. (2004), Mainprice et al. (2005), and Raterron et al. (2007). However, it has been debated whether the observed transitions were in fact due to pressure or if they were influenced by other factors, such as stress or water content (Karato et al. 2008). A recent study by Jung et al. (2009) on dry olivine reported a transition from A-type to B-type fabric at ~3GPa, which corresponds to a depth of ~90 km in the mantle. Taken at face value, these experimental results would suggest that B-type fabric might dominate the upper mantle below 90 km. However, as Jung et al. (2009) point out, their work covers a limited set of experimental conditions and, as discussed below, the applicability of this set of experiments to the upper mantle remains uncertain.
The presence of small amounts of partial melt can also affect the anisotropic properties of a volume of mantle rock. Melt can affect anisotropy through an SPO effect; because its elastic properties are dramatically different from the surrounding matrix, deformation may produce alignment of melt into sheets, tubules, disks, or other configurations, leading to SPO-related anisotropy (e.g., Zimmerman et al. 1999). It has also been suggested (Holtzman et al. 2003) that the presence of partial melt can alter olivine LPO development in the polycrystalline matrix, changing by 90° the relationship between the shear direction and the fast splitting direction. There has, however, been some debate about the applicability of the experimental geometry used by Holtzman et al. (2003) to the Earth’s mantle (Karato et al. 2008). Partial melt is only present in the Earth’s mantle in very specific and localized tectonic settings (i.e., directly beneath island arcs, mid-ocean ridges, and actively extending rift zones), and while melt has been invoked to explain shear wave splitting patterns in a few localized regions (e.g., the East African Rift; Kendall et al. 2004), models invoking only olivine LPO development due to solid-state mantle flow have successfully explained splitting observations even in a mid-ocean ridge setting where partial melt is present (Blackman and Kendall 2002; see also Mainprice 2007). It is thus likely that LPO in olivine is the dominant source of anisotropy in the upper mantle, with SPO playing at most a minor role. This is in marked contrast to the crust, where fluid-filled cracks appear to be the dominant source of anisotropy.
With all of the new experimental mineral physics results on the olivine LPO “fabric diagram,” where does this leave shear wave splitting practitioners? From a splitting point of view, the only olivine fabric type that changes the expected relationship between mantle flow and the resulting fast splitting direction is B-type, although other seismological observables such as surface waves may be used to distinguish between, for example, A-, C-, or E-type fabric in the asthenospheric mantle (Karato et al. 2008). Because experimental work has suggested that B-type fabric is associated with significant water content, low temperatures, and high stresses, its possible occurrence has been thought to be limited to the mantle wedge above subduction zones (Karato et al. 2008). Outside of the mantle wedge, the traditional relationship that the measured fast polarization direction corresponds to the mantle maximum shear direction has generally held up (e.g., Mainprice 2007; Karato et al. 2008; Becker et al. 2003; Behn et al. 2004; Conrad et al. 2007).
A pressure-induced transition to B-type fabric at upper mantle depths, as suggested by Jung et al. (2009), would call that assumption into question. However, the suggestion that the mantle may be dominated by B-type fabric below ~80–90 km, as implied by the Jung et al. (2009) experiments, is difficult to reconcile with both seismological observations and with the rock record. For example, models of upper mantle flow that take into account plate motion and mantle density heterogeneity have been extremely successful at explaining observations of anisotropy beneath ocean basins with an A-type fabric assumption; this is true for both shear wave splitting measurements (e.g., Behn et al. 2004; Conrad et al. 2007) and models of anisotropy from surface waves (e.g. Becker et al. 2003; Becker 2008). Global surface wave models of the depth distribution of azimuthal anisotropy (e.g., Debayle et al. 2005) do not show evidence for a drastic change in olivine fabric type at upper mantle depths. Additionally, the observation that only ~7% of natural mantle peridotites have B-type fabric (Mainprice 2007) is difficult to reconcile with an upper mantle that is dominated by B-type olivine, and there are observations of sheared mantle lherzolites from depths of 150–200 km that exhibit A-type fabric (Karato et al. 2008). However, the experiments of Jung et al. (2009) are important in establishing laboratory evidence for a pressure-induced olivine fabric transition, and the extension of such high-pressure deformation experiments to a larger range of temperature and stress conditions, as well as to samples with significant water content, will shed further light on the applicability of these results to the Earth’s mantle. (We note that the deviatoric stresses in the Jung et al. experiments were significantly higher than those than would be expected for the asthenospheric upper mantle.) The shear wave splitting community awaits further experimental results on a pressure-induced fabric transition with great interest, but until the applicability of such experiments to the Earth’s mantle is more firmly established, the A-type fabric assumption is likely to remain the dominant relationship for interpreting shear wave splitting measurements in most tectonic settings.
3.2 The Transition Zone and Lower Mantle
In contrast to the large amount of published literature available on olivine LPO, there is a dearth of experimental constraints on deformation and LPO of transition zone and lower mantle minerals, mainly due to the challenges involved with performing deformation experiments at the pressures associated with the transition zone and lower mantle. There is some observational evidence for anisotropy in the transition zone, mainly from surface wave and normal mode observations (e.g., Trampert and van Heijst 2002; Beghein and Trampert 2004; Beghein et al. 2008). By contrast, comparisons of shear wave splitting from core phases and deep local S phases or converted phases do not generally turn up evidence for splitting associated with transition zone anisotropy, with only a few exceptions (e.g., Fouch and Fischer 1996; Iidaka and Niu 1998). The development of LPO in wadsleyite, which has an intrinsic shear wave anisotropy of ~13% (Mainprice 2007) has been simulated using polycrystalline plasticity modeling by Tommasi et al. (2004). Overall, however, there is very little experimental data on LPO development in transition zone materials (Karato 2008). Beneath the transition zone, it is generally inferred that there is little or no contribution to shear wave splitting from lower mantle anisotropy. Based on the observation of apparent lower mantle isotropy (with the exception of D″, discussed in the next section), it has been suggested that the lower mantle may be deforming via diffusion creep rather than a dislocation creep mechanism and therefore no LPO is produced (e.g., Karato and Li 1992; Karato et al. 1995). Some experimental results, however, provide support for dislocation creep in the uppermost lower mantle (Cordier et al. 2004) and there are a few observational studies that claim evidence for a contribution to shear wave splitting from anisotropy in this depth range (e.g., Wookey et al. 2002).
3.3 The D″ Region
In contrast to the overlying lower mantle, observations of seismic anisotropy in the D″ layer at the base of the mantle are abundant, and both SPO- and LPO-type models have been proposed (e.g., Kendall and Silver 1998; Lay et al. 1998; Karato 1998). Models that invoke SPO as a mechanism for generating anisotropy in D″ rely on the presence of a material in the lowermost mantle with elastic properties that sharply contrast with the surrounding matrix. This could take the form of partial melt, which is often invoked as the cause of that ultra-low velocity zones (ULVZs) that are intermittently observed at the base of the mantle, of compositionally distinct subducted materials that have made their way to the CMB, or of infiltrated Fe from the core (e.g. Kendall and Silver 1998). Most of the work that has been done to address the feasibility of SPO-type models has used equivalent medium theory or other forward modeling techniques to predict the bulk elastic constants of SPO media and to evaluate the effect of the resulting anisotropy on shear waveforms (e.g., Kendall and Silver 1998; Moore et al. 2004; Hall et al. 2004). The consensus from these studies is that SPO-type models generally do a good job of matching the seismological constraints.
Models that invoke the LPO of lowermost mantle minerals can also plausibly explain splitting observations in D″ if deformation is being accommodated via dislocation creep (e.g., Karato 1998). A recent review of experimental constraints on LPO in lowermost mantle minerals can be found in Yamazaki and Karato (2007) and we provide only a brief summary here. The mineral phases that could contribute to LPO-induced anisotropy in D″ include perovskite, ferropericlase, and the recently discovered post-perovskite phase. (Mg,Fe)O ferropericlase, although it makes up perhaps 20–25% of the lower mantle by volume, has a very large intrinsic shear wave anisotropy (~50% or more) at depth; perovskite is considerably less anisotropic (e.g., Karki et al. 1999; Wentzcovitch et al. 2006; Mainprice 2007; Marquardt et al. 2009). The single-crystal elasticity of post-perovskite is not yet well understood; several different sets of elastic constants obtained from first-principles calculations have been published (Iitaka et al. 2004; Stackhouse et al. 2005; Wentzcovitch et al. 2006) but discrepancies among studies exist.
While there are some data available on LPO development in lowermost mantle minerals, the experiments are nearly always done at pressure and/or temperature conditions that are far removed from those found at the CMB, or, in the case of post-perovskite, done on analog materials. Fabric development in (Mg,Fe)O aggregates at large shear strains has been explored by several different studies (Yamazaki and Karato 2002; Merkel et al. 2002; Heidelbach et al. 2003; Long et al. 2006) and the experimentally determined LPO patterns, in combination with single-crystal elastic constants at D″ pressures, generally result in shear wave splitting predictions that are consistent with seismological observations. Specifically, the LPO of (Mg,Fe)O appears to correctly predict dominantly V SH > V SV anisotropy for horizontally propagating phases and little or no splitting of more vertically propagating phases such as SK(K)S (e.g., Long et al. 2006). Deformation experiments on post-perovskite analogs have been performed by Yamazaki et al. (2006) on CaTiO3 and by Merkel et al. (2006) on MgGeO3. Merkel et al. (2007) carried out deformation experiments on MgSiO3 post-perovskite and found that the predicted shear wave splitting patterns do a generally poor job of matching the seismological constraints, although there is a great deal of uncertainty about the application of experiments done at ambient temperature to the Earth’s mantle. Experiments on analog materials at high temperatures (e.g., Yamazaki et al. 2006) may in fact be more relevant (Karato 2008), and shear wave splitting predicted from the experimentally determined LPO patterns of Yamazaki et al. (2006) for CaTiO3 post-perovskite are more consistent with the observations (Wookey and Kendall 2007). The LPO data for lowermost mantle phases remain incomplete, but it is likely that both ferropericlase and post-perovskite contribute to any LPO-induced anisotropy, and if regions dominated by perovskite exist in the D″ layer, there may be a contribution from perovskite as well (Mainprice et al. 2008).
4 Measurements and Interpretation in Different Tectonic Settings
With the measurement methods examined in Sect. 2 and the experimental mineral physics constraints discussed in Sect. 3 in mind, we now turn our attention to shear wave splitting measurements obtained in a variety of regions and their interpretation in terms of mantle flow/deformation. We focus our discussion on the upper mantle and the D″ region, because constraints on transition zone and lower mantle anisotropy from shear wave splitting are sparse and several studies have found that these regions generally make little or no contribution to splitting observations (with a few notable exceptions). An exhaustive compilation of every shear wave splitting study in the published literature is far beyond the scope of this paper, and for additional references and discussion we refer the reader to recent overviews of splitting observations in different settings, such as those of Fouch and Rondenay (2006) for continental interiors, Long and Silver (2008) for subduction zones, and Wookey and Kendall (2007) for D″.
4.1 Upper Mantle Anisotropy
4.1.1 Ocean Basins
Because of the paucity of broadband seismic stations located in ocean basins, the availability of shear wave splitting constraints in the oceans is limited (e.g., Conrad et al. 2007). Individual splitting measurements can be difficult to carry out for noisy stations located in an oceanic environment and stacking techniques are often useful (e.g., Wolfe and Silver 1998). It is instructive to examine shear wave splitting patterns in the ocean basins away from spreading centers, upwellings, and subduction zones, as mantle flow in the ocean basins is likely controlled by simple shear within the asthenospheric mantle. The ocean basins therefore provide an excellent test case for whether simple geodynamical models of mantle flow can match splitting observations, and what assumptions about olivine LPO are required to do so. Sparse shear wave splitting datasets can be augmented with constraints on azimuthal anisotropy from surface wave inversions (e.g. Debayle et al. 2005), which have better spatial coverage (though poorer lateral resolution) than splitting measurements and which provide the additional advantage of placing depth constraints on anisotropic structure.
Constraints on azimuthal anisotropy beneath the ocean basins are best evaluated in the context of the predictions made by geodynamical models. Recent modeling studies by Behn et al. (2004) and Conrad et al. (2007) have attempted to match observed shear wave splitting patterns in the ocean basins with instantaneous flow calculations that take into account both plate motions and active mantle flow due to density heterogeneities at depth (inferred from tomographic models). Behn et al. (2004) carried out splitting measurements for a group of stations in the Atlantic and Indian Oceans surrounding Africa, and found that models incorporating plate motions and large-scale upwelling due to the African Superplume matched the observations well. A similar study by Conrad et al. (2007) found an excellent match between shear wave observations in ocean basins and the predictions from global numerical models of mantle flow (Fig. 9). Complementary studies by, e.g., Becker et al. (2003) and Maggi et al. (2006) have had similar success in predicting the distribution of upper mantle azimuthal anisotropy (as constrained by surface waves) using global models of mantle flow and/or plate motions. Because these studies assumed an A-type (or similar) olivine fabric geometry, the success of these modeling studies in matching observations of azimuthal anisotropy suggests that the traditional relationship between strain and anisotropy (that the fast splitting direction roughly corresponds to the upper mantle direction of maximum shear) is the correct one for interpreting splitting beneath ocean basins. Although shear wave splitting constraints in ocean basins are sparse, the measurement and interpretation of splitting in this simple tectonic regime is very important to our understanding of how to relate splitting observations to mantle flow, because the observations are well-matched by large-scale geodynamical models that predict flow and the resulting anisotropy.
Comparison between splitting observations in the Atlantic Ocean basin a Pacific Ocean basin b and model predictions from the work of Conrad et al. (2007). Splitting observations are shown in blue and the splitting predictions from a flow model that takes into account both plate-driven flow and flow driven by density heterogeneities in the mantle are shown with black bars. The root-mean-square misfit is ~21° for the Atlantic and ~11° for the Pacific, roughly on the order of (or smaller than) the measurement errors. The assumption of A-type (or similar) olivine fabric was used in this study, demonstrating that the splitting observations are not compatible with the upper mantle being dominated by B-type fabric at asthenospheric depths
4.1.2 Continental Regions
Another region where shear wave splitting can provide important constraints on mantle structure and dynamics is in the study of continents. There are two basic problems that can be addressed by these data. The first is assessing the existence and character of a mechanical asthenosphere that concentrates shear. As noted above, anisotropy in the ocean basins is dominated by asthenospheric flow, demonstrating the existence of a well-developed asthenosphere there. It has been debated for decades whether such an asthenosphere is present beneath continents as well and, if so, whether its nature is different from the sub-oceanic asthenosphere (e.g., Froidevaux and Schubert 1975; Schmeling and Bussod 1996; Schutt and Humphreys 2001; Rychert et al. 2007). The other problem relates to the role of the lithospheric mantle in orogenic deformation. Geological observations have provided an excellent characterization of the crustal response to this deformation, but it remains controversial what the mantle’s role is and this issue can be addressed by studying mantle seismic anisotropy. In general, anisotropy beneath the continents is more challenging to study than anisotropy beneath the oceans, primarily because there can be anisotropic contributions from both the lithosphere and asthenosphere, and the lithospheric component shows strong spatial variability (e.g., Silver 1996; Savage 1999; Fouch and Rondenay 2006). On the other hand, there are extensive splitting data for the continents. Indeed, the vast majority of splitting observations sample anisotropy in the subcontinental mantle. Most encouraging, the recent deployment of large arrays of stations in areas of geologic interest, along with Global Positioning System (GPS) measurements to provide a characterization of the surface deformation, have permitted at least a partial resolution of these issues, and consequently progress in our understanding of the mantle’s role in continental dynamics.
Rather than present an exhaustive review of continental anisotropy from splitting (see Fouch and Rondenay 2006 for a review of splitting in stable continental regions), we discuss two actively deforming plate boundary zones that exhibit end-member behaviors regarding the relative contributions of the lithosphere and asthenosphere: westernmost North America and Central Asia. These regions also illustrate methods of using quantitative hypothesis tests to assess the primary cause of the anisotropy. They are also characterized by having the extensive coverage in terms of splitting observations, helped by recent large-array deployments in both areas as well as extensive GPS data sets. This allows for a joint analysis (e.g. Holt 2000) of the splitting and GPS data sets which permits the quantitative evaluation of both asthenospheric and lithospheric contributions to mantle anisotropy.
In the case of asthenospheric flow, it is assumed that the GPS surface velocity field constitutes a velocity boundary condition at the top of the asthenosphere (i.e., the velocity at the top of the asthenosphere is equal to the velocity at the surface) and that the bottom of the asthenosphere is assumed to translate at a constant velocity. The asthenospheric shear is then assumed to be parallel to the local vectorial difference between the top and bottom of the asthenosphere, and it is usually further assumed that the a-axis of olivine and, for vertically propagating shear waves, the splitting fast polarization direction is oriented parallel to this direction. As long as the surface field is laterally varying, a unique minimum misfit solution for subasthenospheric velocity can be obtained (Silver and Holt 2002).
Another important endmember case is more appropriate to describe lithospheric deformation. Consider lithospheric deformation where the crust and mantle components of the lithosphere deform coherently. This style of deformation is termed vertically-coherent deformation (e.g. Silver 1996) and is assumed to occur when making the so-called thin-viscous-sheet approximation. In this case the finite strain field of the crust and mantle will be identical. Thus a simple test for this style of lithospheric deformation is that the surface field, inferred from GPS, can be used to predict the mantle field and ultimately the splitting fast polarization direction. As in the asthenospheric case, the corresponding misfit between modeled and measured fast polarization directions is a measure of the success of this model. Compared to the asthenospheric case, the lithospheric deformation case is more complex, because there is a broader range of finite strain geometries. For asthenospheric flow, the mantle deforms by progressive simple shear with a horizontal shear plane. The GPS velocity is used to define the azimuth of the horizontal shear. In the case of lithospheric deformation, the mantle can deform by simple shear, either right- or left-lateral pure shear, or intermediate cases. As discussed by Wang et al. (2008), it is nevertheless possible to address this problem if it can be assumed that the mantle deforms by either simple shear or pure shear (excluding intermediate cases), in which case the instantaneous maximum shear directions are invariant for simple shear, and the instantaneous maximum extension direction is invariant for pure shear. It is possible to distinguish between simple shear (right or left lateral) and pure shear by utilizing the rotational component of the velocity gradient tensor, after a correction has been made for rigid-body rotation (Wang et al. 2008) using the line-rotation method (e.g., Holt and Haines 1993). If the surface field is a good predictor of the mantle field, this is termed vertically coherent deformation. In addition to lithospheric anisotropy produced by vertically coherent deformation, a possible contribution to the splitting signal from anisotropy “frozen” into the lithosphere as a result of past tectonic processes must also be accounted for (e.g. Silver 1996; Savage 1999).
4.1.2.1 Westernmost North America
Shear wave splitting beneath the westernmost part of the United States has been extensively studied (e.g., Savage and Silver 1993; Özalaybey and Savage 1995; Savage and Sheehan 2000; Schutt and Humphreys 2001; Polet and Kanamori 2002; Fouch 2007; Long et al. in review) and there have been several recent attempts to link these observations to active flow processes in the mantle in the context of various models (e.g., Silver and Holt 2002; Becker et al. 2006; Fouch 2007; Zandt and Humphreys 2008). With the ongoing Transportable Array (TA) component of USArray, the picture of shear wave splitting and anisotropy beneath the continental United States should improve dramatically in the near future, and determinations of the splitting patterns at TA stations in the westernmost US are beginning to appear (e.g. Fouch 2007). There is little obvious correspondence between shear wave splitting measurements and surface geology, which tends to argue that active mantle flow in the asthenosphere is the likely source of the anisotropy. Several workers have invoked asthenospheric flow models to explain the western US splitting pattern. For example, Silver and Holt (2002) found that simple asthenospheric flow provides an excellent fit to the observations in westernmost North America, with an eastward subasthenospheric velocity of a few cm/year. This eastward flow is well explained by density heterogeneity produced by the sinking of the Farallon slab (Silver and Holt 2002; Becker et al. 2006).
The pattern of anisotropy in the western US (Fig. 10) suggests that the simple flow model proposed by Silver and Holt (2002) fails further to the East, where splitting orientations rotate around to be nearly orthogonal to observations in the West. This characteristic change has been has been explained in a variety of ways that argue for a perturbation in the mantle flow field. For example, Savage and Sheehan (2000) attributed this pattern to a mantle upwelling beneath central Nevada. More recently, Zandt and Humphreys (2008) have argued that this flow field is more likely related to toroidal flow around the southern edge of the descending Gorda-Juan de Fuca slab, because there is no evidence for a plume. This is an intriguing hypothesis, and in many ways is similar to the 3-D flow field observed in other subduction zones (Long and Silver 2008). However, this circular pattern is really defined by a few stations in the eastern Basin and Range, and a more quantitative test of this hypothesis is desirable, where the instantaneous flow model is actually used to predict splitting, as in Becker et al. (2006). [Zandt and Humphreys (2008) compare splitting to the predicted velocity field for this model, but the anisotropic geometry is in fact controlled by the finite strain, as noted above.] An alternate hypothesis to explain the circular pattern of fast directions in the western US and, in particular, the small delay times observed beneath central Nevada in the Great Basin has been recently proposed by West et al. (2009), who invoke a localized downwelling due to lithospheric delamination. As with the Zandt and Humphreys (2008) model, further evidence for or against this scenario will likely come from detailed forward modeling studies. Another important task is to evaluate the model of Silver and Holt (2002) for newly augmented data sets to assess in detail the misfit of the simple asthenospheric flow model; such an exercise would pinpoint more precisely the regions where additional mechanisms are needed.
SKS splitting parameters (red lines indicate orientation of the fast axis and the length of the bar is proportional to delay time) observed in the western US from the compilation of Zandt and Humphreys (2008). These authors interpret the observed pattern as evidence for toroidal flow around the southern edge of the Juan de Fuca slab; however, other interpretations are possible (e.g., Silver and Holt 2002; Becker et al. 2006; Fouch 2007)
4.1.2.2 Tibetan Plateau and Surrounding Regions
The Tibetan Plateau is the quintessential continent–continent collision. It has been an object of scientific study for at least the past century and, since the advent of plate tectonic theory, has been used as a textbook illustration of the success of the Wilson Cycle in explaining the mountain-building process (e.g. Silver 2007). While both the exceptional topography of Tibet and its thickened crust have been well-explained by the collision of two plates, there remains a long-standing controversy as to the behavior of the lithospheric mantle during this collision. This is most clearly illustrated by the wide range of properties attributed to the mantle in current models. While some models predict homogeneous thickening and shortening of the Tibetan Lithosphere (e.g. England and Houseman 1986), others predict mantle behavior that is distinctly different from the crustal deformation, by, for example, advocating delamination of thickened mantle lithosphere by a convective instability (e.g., Molnar et al. 1993) or by the complete decoupling of crust and mantle by channelized flow in a low viscosity crust (e.g., Royden et al. 1997; Clark and Royden 2000). The question of whether or not the crust and mantle components of the lithosphere exhibit vertically coherent deformation during orogeny thus constitutes an important diagnostic in determining the actual style of continental deformation. Equally important, it is also unclear whether the dominant contribution to the splitting signal is from the asthenosphere or lithospheric mantle. As discussed above, this test can be performed by using a joint analysis of splitting and GPS.
Shear wave splitting at stations located on the Tibetan Plateau and its margins has been studied extensively (e.g. McNamara et al. 1994; Huang et al. 2000; Flesch et al. 2005; Lev et al. 2006; Sol et al. 2007; Wang et al. 2008) and a wealth of data is now available to carry out the type of hypothesis testing described above. The two end-member models of asthenospheric flow and vertically coherent deformation were evaluated by Wang et al. (2008), making use of nearly 200 splitting observations and 2000 GPS observations in a joint analysis. It was found that the vertically coherent deformation model provided an excellent fit to the data (Fig. 11) and that this fit was much better than a model invoking asthenospheric flow. This result suggests that (1) the mantle lithosphere dominates the anisotropic signal in Tibet, and (2) that the crust and mantle deform coherently during the building of the Tibetan Plateau. Given the importance of gravitational relaxation in driving deformation it can be further inferred that the crust and mantle are mechanically coupled (Wang et al. 2008). This places a first-order constraint on deformation style for Tibet and points to the importance of this joint splitting and crustal deformation analysis in studying continental dynamics.
A map of shear wave splitting observations and model predictions from the surface deformation field from Wang et al. (2008) for the Tibetan Plateau. The splitting observations are shown as blue bars and model predictions for left-lateral simple shear (red), right-lateral simple shear (yellow), or pure shear (green). The model used at a given station depends on the value of the kinematic vorticity number, as shown in the legend. Note the strong correlation between the model predictions and the splitting observations
4.1.3 Mid-Ocean Ridges
As with the case of the ocean basins, the available shear wave splitting data in the vicinity of mid-ocean ridges is fairly limited due to the difficulty and expense of deploying OBS instrumentation. Splitting observations gleaned from the MELT experiment at the East Pacific Rise (Wolfe and Solomon 1998) represent the most detailed picture available of splitting due to mantle flow beneath an oceanic spreading center. A study of shear wave splitting for the GLIMPSE experiment (Harmon et al. 2004), deployed directly to the West of the MELT study area, provides a complementary picture of asthenospheric flow beneath young seafloor adjacent to a mid-ocean ridge. Wolfe and Solomon (1998) found that measured fast directions at all MELT stations are oriented approximately parallel to the spreading direction (that is, perpendicular to the strike of the ridge). Although the observed fast directions were very uniform, they found more spatial variation in δt, with delay times being generally higher (by ~0.5–1 s) to the West of the ridge than to the East. The observed pattern of fast directions is generally consistent with anisotropy controlled by olivine alignment in a 2-D corner flow field, but contrary to the predictions made by a model in which anisotropy is controlled by vertically aligned melt-filled cracks, which would predict ridge-parallel fast directions close to the ridge (Wolfe and Solomon 1998). Because a melt-rich olivine texture such as that observed in laboratory experiments of Holtzman et al. (2003) would also predict ridge-parallel fast splitting directions for a 2-D corner flow model, it is apparently unnecessary to invoke a contribution from melt to the anisotropy inferred from the MELT splitting data set. In order to explain the MELT observations, Wolfe and Solomon (1998) invoke two layers of anisotropy, both with a ridge-perpendicular fast axis: one due to spreading-induced corner flow, and a second, deeper layer due to return flow. Further to the West in the GLIMPSE study area, observations of ϕ continue to be dominated by spreading-parallel fast directions, but there is a large variability in δt (~1.2–2.2 s) that is interpreted as evidence for lateral heterogeneity in upper mantle LPO, perhaps due to the onset of small-scale convection beneath young seafloor (Harmon et al. 2004).
Although the availability of splitting constraints from mid-ocean ridges is limited, the available data suggest that mantle flow beneath ridges (and the associated upper mantle anisotropy) generally conforms to the expectations of a simple, 2-D corner flow-type model. This has been borne out by subsequent modeling studies that invoke 2-D corner flow-type models to explain the MELT observations (e.g., Nippress et al. 2007), sometimes in combination with dynamically driven flow (from the Pacific superswell) or a passive thermal anomaly (e.g., Blackman and Kendall 2002; Conder et al. 2002; Conder 2007). In contrast, splitting observations from an extensional rift setting in Ethiopia have been interpreted as having a significant contribution from melt-induced anisotropy (Kendall et al. 2004). Generally speaking, continental rift zones do not exhibit the extension-parallel fast directions observed in the vicinity of mid-ocean ridges (e.g., Gao et al. 1997), as borne out by observations from the Rio Grande (Gök et al. 2002) and Baikal (Gao et al. 1994) rift zones as well as eastern Africa (Kendall et al. 2004).
4.1.4 Mantle Upwellings
Several studies of shear wave splitting in the vicinity of putative zones of mantle upwelling, including Hawaii (Walker et al. 2001), Yellowstone (Walker et al. 2004; Waite et al. 2005), Iceland (Bjarnson et al. 2002), the Eifel hotspot (Walker et al. 2005a), and the Society hotspot near French Polynesia (Russo and Okal 1998; Fontaine et al. 2007), have been carried out. The pattern of splitting in and surrounding the Great Basin in central Nevada (and, in particular, the dominance of null splitting or very low delay times in the central Great Basin) has been interpreted as evidence for the interaction between North American plate motion and a large-scale mantle upwelling (e.g., Savage and Sheehan 2000; Walker et al. 2005b), but has more recently been interpreted as evidence for a localized downwelling due to lithospheric delamination (West et al. 2009). Shear wave splitting in the vicinity of supposed mantle upwellings have typically been understood in the context of interactions between vertical upwelling flow and simple shear between the lithospheric mantle and the asthenosphere, a consequence of absolute plate motion (APM). For example, Walker et al. (2001) examined shear wave splitting around the Hawaii hotspot and noted a spatial pattern in fast directions that they explained in terms of a parabolic asthenospheric flow model, in which a plume impinges on a moving lithospheric plate [see also Vinnik et al. (2003) and Walker et al. (2003)]. Similar models have been invoked to explain a semicircular pattern of fast directions in the vicinity of the Eifel hotspot (Walker et al. 2005a, b) and to explain the spatial distribution of fast directions in the eastern Snake River Plain adjacent to the putative Yellowstone hotspot (Walker et al. 2004). Waite et al. (2005) interpreted measured fast directions in the Yellowstone region as being generally consistent with APM, although the effect of aligned melt was invoked to explain the observed splitting at a few stations. A model that combines the effect of mantle upwelling with APM, resulting in parabolic flow in the asthenosphere, has been successful at explaining splitting patterns in some regions associated with mantle upwelling, but has proved less successful in regions such as Iceland (Bjarnason et al. 2002; Walker et al. 2005b) or Afar (Gashawbeza et al. 2004; Walker et al. 2005b). In particular, the splitting patterns observed in Iceland appear to be best explained by mid-ocean ridge spreading along with northward motion of the subasthenospheric mantle in a hot spot reference frame (Bjarnason et al. 2002).
4.1.5 Subduction Zones
Subduction zones have been among the most popular targets for shear wave splitting studies, and since early work by, e.g., Ando et al. (1983), Fukao (1984), and Bowman and Ando (1987), a plethora of splitting studies using data from subduction regions has become available (for an overview, see Long and Silver 2008). A typical example of splitting patterns observed in a subduction zone setting from Japan is shown in Fig. 12. Subduction zones are among the most complicated tectonic settings on Earth and the interaction of the mantle flow field with downgoing slabs remains poorly understood, which makes subduction zone regions an exciting scientific target for shear wave splitting practitioners. However, because the structure of subduction zones is complicated, the contributions from anisotropy from various parts of the subduction system (the overriding plate, the mantle wedge, the subducting slab, and the sub-slab mantle) to splitting measurements must be properly accounted for. An astonishing diversity in splitting patterns has been identified in different regions from both local S phases (from earthquakes originating in the slab) and teleseismic phases such as SKS and direct S, including both trench-parallel and trench-perpendicular fast directions (with some oblique directions as well) and widely variable δt values. A variety of models has been proposed to explain shear wave splitting observations in specific regions, including those that invoke 2-D corner flow (e.g., Fischer et al. 2000; Hall et al. 2000), B-type olivine fabric (e.g., Nakajima and Hasegawa 2004; Long et al. 2007b; Kneller et al. 2008; Jung et al. 2009), trench-parallel flow above (e.g., Smith et al. 2001; Conder and Wiens 2007; Hoernle et al. 2008) or below (Russo and Silver 1994; Long and Silver 2008) the slab, foundering of lower crust beneath the island arc (Behn et al. 2007), transpression due to oblique subduction (Mehl et al. 2003), anisotropy due to aligned hydrated faults in the slab (Faccenda et al. 2008), or some combination of these mechanisms. It has proven difficult, however, to identify a unique, synoptic model for subduction zone anisotropy that can explain the global variability in splitting observations.
An example of spatial variations in splitting patterns in a subduction zone region, after Long and van der Hilst (2005a). Average splitting parameters for teleseismic shear phases are plotted at the station locations; stations which exhibit significant splitting but very complex splitting patterns are shown with a triangle. Dashed lines show the contours of the subducting Pacific and Philippine Sea plates at 100 km intervals
Elucidating the processes that lead to the complex splitting patterns observed in Japan (Fig. 12) and elsewhere can be difficult, but one promising approach to the study of flow patterns in subduction zones is to look at average splitting parameters found globally in subduction regions and to try to identify correlations with other parameters that describe subduction. Because several dozen splitting studies have been carried out in subduction zone settings, there is a wealth of data available and such a global approach is feasible. Long and Silver (2008) constructed a global data set of average splitting parameters (ϕ, δt) for both the wedge region (from local S splitting) and for the sub-wedge region, which comprises the subducting slab and the sub-slab mantle (from a comparison of teleseismic and local splitting in addition to source-side splitting). Identifying average splitting parameters for different subduction zones (or subduction zone segments) involves considerable simplifying assumptions and does not take into account the full spatial heterogeneity observed in many regions, but the aim of such an exercise is to determine the first-order properties of the global splitting signal and the associated mantle flow field.
Long and Silver (2008) found that the sub-wedge splitting signal is relatively simple, and an updated version of the global database that includes constraints from source-side S splitting measurements confirms this observation. The sub-wedge splitting signal is overwhelmingly dominated by trench-parallel fast directions, with only a few exceptions (most notably Cascadia; Currie et al. 2004). The global sub-wedge splitting signal appears to be simple, but the preponderance of trench-parallel fast directions and the wide range of observed delay times are contrary to the expectations of a simple 2-D entrained flow model if A-type (or similar) olivine fabric is assumed. Long and Silver (2008) carried out comparisons between the average sub-wedge split time and a host of other parameters that describe subduction, such as convergence velocity, slab dip, and obliquity angle, and identified a clear correlation between sub-wedge delay time and the absolute value of the trench migration velocity in a hot spot reference frame [V t ] (Fig. 13). We interpret the sub-wedge signal as being mainly due to anisotropy beneath the slab, for several reasons: in particular, we do not observe any correlation between delay time and slab age (thickness), and the geometry of the anisotropy appears to be controlled by the geometry of the trench and does not correlate with fossil spreading directions. There is no obvious mechanism to explain the global variation in sub-wedge delay times with a model invoking anisotropy within the slab; we instead interpret the correlation between δt and |V t | as evidence that the sub-wedge splitting signal is controlled by trench-parallel sub-slab mantle flow induced by trench migration.
a Plots demonstrating the relationships between average sub-slab and wedge delay times and trench migration rates, after Long and Silver (2008). Left panel: average sub-slab δt vs. the absolute value of trench migration velocity, |V t|, for different subduction zones or subduction zone segments. Middle panel: average wedge δt vs. the normalized trench migration velocity (that is, |V t| normalized by the convergence velocity V c. The legend is shown in the right panel. b A schematic diagram summarizing some of the mantle flow processes, inferred from shear wave splitting measurements, that may be operating in subduction zones, according to a model proposed by Long and Silver (2008)
In contrast to the relatively simple sub-slab splitting signal, splitting patterns in the mantle wedge from local S splitting are much more variable. As with the sub-slab case, large variability in average δt values are observed, with some mantle wedges appearing nearly isotropic (e.g., Indonesia; Hammond et al. 2006) and others exhibiting split times of up to ~1 s or more (e.g., Tonga; Smith et al. 2001). There is also a great deal of heterogeneity in measured fast directions. A transition from trench-parallel splitting close to the trench to trench-perpendicular further in the backarc has been observed in several regions (e.g., northern Honshu; Nakajima and Hasegawa 2004), but the opposite transition has been observed in a few regions, including Kamchatka (Levin et al. 2004). In some wedges, the spatial pattern of fast directions is extremely complicated, such as central Japan (Salah et al. 2008; Wirth and Long 2008). As with the sub-slab case, the pattern that would be predicted for a simple corner flow model with A-type olivine fabric—dominantly trench-perpendicular fast directions—is virtually absent from the global database. Arc-parallel flow in localized channels (e.g., Pozgay et al. 2007), the presence of B-type fabric in the forearc wedge (e.g., Nakajima and Hasegawa 2004), complex slab morphology (Kneller and van Keken 2007), and the foundering of lower crust (Behn et al. 2007) have all been invoked to explain the complex splitting patterns associated with anisotropy in the wedge. As with the sub-slab case, Long and Silver (2008) compared average wedge δt values to other subduction-related parameters, and again found a correlation with trench migration velocity: when δt is plotted against the absolute value of the trench migration velocity normalized by the convergence velocity, a clear pattern emerges (Fig. 13). Subduction systems that are dominated either by downdip motion of the slab or by trench migration tend to have large split times, while systems which have comparable convergence and trench migration rates tend to have smaller δt.
Based on these observed correlations, Long and Silver (2008) proposed a model in which mantle flow in subduction systems is strongly influenced by the migration of trenches with respect to the underlying mantle. A sketch of this model is shown in Fig. 13. While the Long and Silver (2008) model appears to explain the first-order features of the global splitting dataset, alternative models have also been proposed. These include a recent model by Faccenda et al. (2008) that invokes the hydration of generally trench-parallel faults in subducting slabs as a mechanism for generating trench-parallel SKS splitting. Jung et al. (2009) have also suggested the possibility that the sub-slab mantle is dominated by B-type olivine fabric, which would imply that the observed trench-parallel fast directions beneath slabs are due not to trench-parallel flow but to entrained flow. As discussed in Sect. 3.1, however, the upper mantle beneath ocean basins appears to be dominated by A-type or similar fabric, and it is likely that the same relationship between strain and anisotropy holds beneath subducting slabs.
Many fundamental questions remain about the character of the mantle flow field associated with subducting slabs and the proper interpretation of shear wave splitting measurements in a subduction zone environment. Ambiguities remain, for example, about which olivine fabric types are important in different parts of the subduction system and under what conditions B-type olivine fabric might exist in the mantle wedge (e.g., Karato et al. 2008) and perhaps beneath the slab (Jung et al. 2009). From a measurement point of view, it is difficult to distinguish between anisotropy in the subducting slab versus anisotropy in the sub-slab mantle and therefore arguments about whether the data are better fit by models that invoke anisotropy in the slab or in the sub-slab region are indirect (e.g., Long and Silver 2008; Faccenda et al. 2008). Further progress in characterizing and understanding the contribution to splitting measurements from active mantle flow will likely come from comparing splitting measurements from raypaths that sample the slab, wedge, and sub-slab mantle in different combinations (from the measurement side) and from fully 3-D geodynamical modeling studies (numerical and analog) that take into account effects such as trench migration, complex slab morphology, and the extent of mechanical coupling between the slab and the surrounding mantle (from the modeling side).
4.2 The D″ Region
Since early suggestions that the lowermost mantle may be anisotropic (e.g., Doornbos et al. 1986; Cormier 1986), a plethora of studies has been carried out using shear phases that pass through the D″ region. Most of these studies have turned up evidence that there is significant anisotropy in D″, although its strength and geometry vary dramatically from region to region. As discussed in Sect. 2.2.2, anisotropy in D″ is usually inferred from the splitting of phases that propagate nearly horizontally at the base of the mantle, such as S, ScS, and Sdiff, or (less often) by comparing splitting from phases that sample the upper mantle in a similar way but have very different raypaths in the lower(most) mantle, such as SKS-SKKS. In any case, studies that seek to isolate the contribution to shear wave splitting from D″ must account for the contribution to splitting from upper mantle anisotropy beneath the receiver and any contribution from source-side anisotropy. Particularly in the presence of complex anisotropy in the upper mantle beneath a seismic station, this correction can be tricky, and this serves as an additional source of error in the characterization of D″ splitting.
A recent survey of studies of D″ anisotropy can be found in Wookey and Kendall (2007); here we provide a brief overview of the first-order constraints provided by these studies. Many studies of D″-associated shear wave splitting, after correcting the waveforms for the effect of upper mantle anisotropy beneath the receiver (and possibly near the source), rotate the horizontal seismogram components into the radial-transverse coordinate system, pick the arrival times for the SV and SH components, and then measure the traveltime difference between the two. Very often, the SH component is found to lead the SV component and V SH > V SV anisotropy is inferred. Measurements of differential traveltimes of SV and SH components provide only limited information about the geometry of anisotropy, but the simplest possible medium that can explain such discrepancies, namely transverse isotropy with a vertical axis of symmetry (VTI), is often assumed. More sophisticated measurement methods have been proposed which place tighter constraints on the geometry of anisotropy; Wookey et al. (2005) proposed a method for measuring differential S-ScS splitting which allows the dip of the symmetry axis in D″ to be constrained. The possibility of anisotropy with a non-VTI symmetry has also been explored through waveform modeling approaches, e.g. beneath the Caribbean (Garnero et al. 2004a).
The two most studied regions of D″, popular because of favorable source-receiver distribution, are located beneath the central Pacific and beneath the Caribbean. Beneath the central and southeastern Pacific, anisotropy has been shown to be highly spatially variable (e.g., Russell et al. 1999; Ford et al. 2006), with some studies finding evidence that D″ is isotropic (Kendall and Silver 1996) and others finding evidence for V SV > V SH (e.g., Ritsema et al. 1998) or V SH > V SV (e.g., Fouch et al. 2001) anisotropy. Beneath the Caribbean, several studies have found evidence for V SH > V SV anisotropy (e.g., Rokosky et al. 2004) and recent work has shown that anisotropy in this region is variable on very short length scales (e.g., Rokosky et al. 2006) and has a significant non-VTI component (e.g., Garnero et al. 2004a; Maupin et al. 2005). Beneath Alaska, D″ anisotropy has been studied by, e.g., Matzel et al. (1996) and Garnero and Lay (1997) and these studies infer V SH > V SV anisotropy. Beneath the Atlantic, the D″ layer appears to be isotropic or nearly so (Garnero et al. 2004b). Additional studies that find evidence for V SH > V SV anisotropy have been performed beneath the Indian Ocean (Ritsema 2000), the Antarctic Ocean (Usui et al. 2005), and Siberia (Thomas and Kendall 2002). Finally, observational evidence for a dipping axis of anisotropic symmetry in D″ has been identified beneath the northwest Pacific (Wookey et al. 2005) and beneath Siberia (Wookey and Kendall 2008). Delay times attributed to anisotropy in D″ range from ~1 s up to ~10 s, corresponding (depending on the path length of the phases of interest) to up to 5% shear wave anisotropy. While studies of D″-associated shear wave splitting in horizontally propagating shear waves have been very successful at supplying observational evidence for D″ anisotropy, in generally they suffer from fundamental limitations on raypath coverage, dictated by the distribution of sources and receivers at the Earth’s surface. In practice this means that only limited regions of D″ have been studied so far using shear wave splitting, and for those that have been studied, the azimuthal coverage is poor.
Based on these observations, it is possible to provide a picture of the first-order anisotropic characteristics of D″ (e.g., Karato 1998; Kendall and Silver 1998; Long et al. 2006; Wookey and Kendall 2007). In most regions, V SH > V SV anisotropy appears to predominate, particularly beneath the Caribbean, Alaska, Siberia, Indian Ocean, and southwest Pacific regions (Wookey and Kendall 2007). These regions correlate with regions possessing higher-than-average S wavespeed velocities from tomographic models; this suggests that this style of anisotropy may be related to the presence of paleoslab material directly above the CMB. This may be due to the increased probability of the presence of post-perovskite in such regions (e.g., Hernlund et al. 2005), to large-scale regions of high-strain deformation in the dislocation creep regime associated with the impingement of a slab upon the CMB (e.g., McNamara et al. 2002), or to oriented melt pockets in the low-melting-point (e.g. basaltic) portion of the slab (Kendall and Silver 1998). In other regions of D″, there is evidence for isotropy or very weak anisotropy; e.g., beneath the Atlantic (Garnero et al. 2004b) or parts of the central and southeastern Pacific (Kendall and Silver 1996, 1998). In general, D″ beneath the central and southeastern Pacific region shows highly spatially variable anisotropy, with evidence for both V SH > V SV and V SH > V SV (e.g., Russell et al. 1998, 1999; Ford et al. 2006) and variations in observed splitting over short length scales. Phases such as SK(K)S, which have more vertical raypaths in D″ than phases such as S, Sdiff, and (at teleseismic distances) ScS, generally appear to be unaffected by anisotropy in D″; there is a general lack of splitting (or splitting less than ~0.2 s) of SK(K)S phases due to anisotropy beneath the upper mantle in the global dataset (e.g., Meade et al. 1995; Niu and Perez 2004). This observation is generally consistent with VTI symmetry. However, studies of SKS-SKKS splitting discrepancies indicate that localized regions of D″ may contribute to SK(K)S splitting (e.g., Niu and Perez 2004; Wang and Wen 2007; Long 2009), sometimes with delay times up to ~3 s (Long 2009).
What does this first-order picture of D″ anisotropy tell us about the responsible mechanism and about dynamical processes at the base of the mantle? As pointed out by Karato (1998), Long et al. (2006), Wookey and Kendall (2007), and others, the first-order picture of D″ anisotropy is consistent with both SPO- and LPO-type mechanisms, and it remains difficult to discriminate between these two different types of anisotropy from the available data. The relative contributions to possible LPO-induced anisotropy from different mineral phases, including (post)-perovskite and (Mg,Fe)O, also remain poorly understood. Because of these uncertainties, we have not yet reached the point where observations of D″-associated shear wave splitting can be interpreted in terms of local mantle flow processes and/or the physical and chemical conditions present locally in D″, as can observations of upper mantle anisotropy. However, there are several promising strategies for increasing our understanding of D″ anisotropy and the responsible mechanism(s), including seismological observations, geodynamical models, and mineral physics experiments, and we discuss some of these strategies in Sect. 5.2.2.
5 Outlook, Challenges, and New Directions
Recent progress in characterizing mantle anisotropy from shear wave splitting measurements and in understanding the dynamical processes that operate to produce that anisotropy has been exciting and rapid. However, many questions about the characterization of complex anisotropic structures in the mantle and the relationships between mantle flow and the resulting anisotropy persist, and even first-order questions about the mechanisms responsible for anisotropy and about the details of mantle flow processes in different tectonic settings remain unanswered. With the ongoing explosion in the availability of broadband seismic data, particularly from dense arrays, and with the recent progress in splitting methodologies and in understanding how anisotropic fabrics form under laboratory conditions, we expect that significant progress on many of these fundamental questions will be made in the near future. In this section, we outline some of the avenues for progress we see as particularly promising for shear wave splitting studies and for the integration of shear wave splitting results with other geophysical constraints.
5.1 Methodologies
5.1.1 Measurement Methods
The increasingly common application of a wide variety of shear wave splitting measurement methods to broadband data provides avenues for integrating different measurement methods to provide a fuller picture of anisotropic structure at depth. As discussed in Sect. 2.1, different measurement methods have different strengths and weaknesses, and a combination of measurement methods can not only help to investigate the possibility of complex anisotropy (which may cause discrepancies among measurement methods), but to provide increased confidence in individual measurements for noisy data or in the presence of complex structure. It is becoming increasingly common for shear wave splitting practitioners to use more than one measurement method on individual data sets (e.g., Levin et al. 2004; Long and van der Hilst 2005a; Lev et al. 2006; Long 2009); similar results with different methods provide increased confidence in the findings, while discrepancies are a red flag that the measurements must be examined with great care, as they may be diagnostic of complex anisotropy (Long and van der Hilst 2005b) or of near-null splitting (Wüstefeld and Bokelmann 2007). The availability of shear wave splitting modeling codes such as SplitLab (Wüstefeld et al. 2007) that explicitly include multiple measurement methods is a positive development. Increased use of measurement strategies such as the cross-convolution method (Menke and Levin 2003; Yuan et al. 2008) that do not make (or that vary) a priori assumptions about the geometry of anisotropy beneath the station is also promising. We note, finally, that the multichannel measurement method introduced by Chevrot (2000) provides a very useful complement to single-record measurement strategies. The multichannel method provides several advantages over traditional single-record measurements (Chevrot 2000; Long and van der Hilst 2005b) and its disadvantages can be ameliorated by its combination with more traditional single-record measurements. Of particular note is the utility of individual splitting intensity measurements for imaging using wave-equation tomography methods (Chevrot 2006; Long et al. 2008). The further application of the multichannel method to different data sets will therefore open doors for new work on imaging mantle anisotropy at depth.
5.1.2 Shear Wave Splitting Tomography
The development and application of methodologies for tomographic inversion of shear wave splitting measurements represents a very promising avenue for future progress in understanding seismic anisotropy and the mantle flow processes from which anisotropy results. Progress in this area has been (and will continue to be) enabled by both the increasing availability of dense array data and by the theoretical development of frameworks for splitting tomography. Both local ray theoretical tomography (Abt and Fischer 2008; Abt et al. 2009) and teleseismic splitting intensity tomography using finite-frequency kernels (Chevrot 2006; Long et al. 2008) each have pros and cons and have different data and computational requirements, but both are likely to find a variety of useful applications in the future.
The incorporation of finite-frequency effects into the interpretation of shear wave splitting measurements, both from a forward modeling and a tomographic inversion point of view, holds promise for several reasons. Because many shear wave splitting studies are carried out at relatively long periods (~8–10 s or more), finite-frequency effects become important and the interpretation of splitting measurements with finite-frequency sensitivity kernels allows for a more accurate mapping of splitting observed at the surface to anisotropic structure at depth. The analysis of shear wave splitting from a wave-equation point of view also allows for better depth resolution; as demonstrated by Chevrot (2006), even perfectly vertical SKS waves can be used for tomographic imaging if finite-frequency effects are taken into account, because SKS sensitivity kernels will overlap at depth if the station spacing is small enough. The theoretical development of finite-frequency sensitivity kernels for splitting intensity measurements has progressed a great deal, and includes work on accounting for near-surface effects (Favier et al. 2004), benchmarking sensitivity kernel computations against spectral element waveform simulations (Chevrot et al. 2004), computing kernels using an adjoint formulation (Sieminski et al. 2008) and with respect to background models that include realistic heterogeneity derived from geodynamical models (Long et al. 2008), and incorporating sensitivity kernel computations into tomographic inversions (Chevrot 2006; Long et al. 2007a; Fig. 8).
Finally, the integration of constraints from numerical modeling studies into tomographic inversions represents a very promising avenue for progress in understanding how complex anisotropy results from mantle flow. The choice of a starting model in tomographic inversions is important in general, but is particularly crucial in very underdetermined problems such as shear wave splitting tomography (e.g., Abt and Fischer 2008; Long et al. 2008). Long et al. (2007b, 2008) argued that several of the problems associated with inverting for anisotropic structure at depth can be mitigated by using realistic starting models obtained from geodynamical modeling studies and used 2-D models of mantle wedge flow as starting models for sensitivity kernel computations (and thus for splitting intensity inversions). This can be taken a step further by using geodynamical constraints directly in the tomographic inversion problem: for example, Long et al. (2007a) use a suite of geodynamical models directly to invert splitting intensity measurements for geodynamical model parameters. Utilizing a priori constraints from geodynamical modeling studies allows for both the computation of sensitivity kernels in realistic background media and for the identification, through tomographic inversion, of anisotropic models that both fit the splitting intensity data and are geodynamically plausible. The integration of geodynamical models with shear wave splitting tomography, therefore, represents a promising avenue of future research.
5.2 Data, Measurement, and Interpretation Strategies
5.2.1 The Use of Reflected and Converted Phases
In addition to the phases commonly used in shear wave splitting studies (such as SKS, SKKS, and direct S), there are a variety of shear phases that traverse anisotropic regions of the mantle with different raypath geometries. Of particular interest from the point of view of characterizing upper mantle anisotropy are phases that sample the upper mantle far away from either the source or receiver, such as SS. Using traditional analysis methods, shear wave splitting analysts are limited to characterizing upper mantle anisotropy in the vicinity of seismic stations or seismic sources; however, if splitting for the upper mantle legs of SS near the bounce point can be properly analyzed, then it is theoretically possible to probe anisotropy far away from both sources and receivers. This would vastly increase our ability to image anisotropy beneath, for example, ocean basins where station coverage is sparse. Early attempts at measuring splitting from SS phases, however, have encountered some difficulties (e.g., Wolfe and Silver 1998) that are likely due to complex wave propagation effects. In particular, the phase shift at the SS bounce point must be properly accounted for, as well as converted phases from the Moho (especially for oceanic bounce points). While further theoretical development is needed to properly measure splitting due to anisotropy in the vicinity of the SS bounce point, this is a promising avenue for further research, as a reliable methodology for SS splitting would allow for a better characterization of shear wave splitting beneath the oceans. Along the same line, reflected phases such as sS can be used to characterize upper mantle anisotropy far away from the receiver (e.g., Anglin and Fouch 2005).
Another type of phase that holds promise for shear wave splitting practitioners is converted phases (e.g., Girardin and Farra 1998; Vinnik et al. 2002), including those converted at seismic discontinuities such as the Moho, or the 410 and 660 km transition zone discontinuities. Converted phases are already used to detect sharp changes in anisotropic structure by looking for backazimuthal variations in transverse component receiver functions that are the manifestations of so-called P-to-SH conversions at shallow (crust or uppermost mantle) depths beneath a station (e.g., Levin and Park 1998; Park et al. 2004). However, if converted phases such as Ps, P410s, or P660s with good waveform clarity and high signal-to-noise ratio (SNR) can be indentified on seismic records, they can be subjected to splitting analysis and the results can be used to place some depth constraints on the responsible anisotropy. Of course, detection of such phases with sufficient SNR can be difficult, but a few studies have looked at splitting above the Moho or above the 660 km transition using converted phases (e.g., Iidaka and Niu 1998; Iidaka 2003) have been carried out. Measurements of shear wave splitting on phases converted at the Moho provide constraints on crustal anisotropy at the frequencies of interest (e.g., McNamara et al. 1994; Herquel et al. 1995; Ozacar and Zandt 2004), which is not only interesting in its own right, but can also be used to “correct” shear wave splitting measurements for the effect of crustal anisotropy and isolate the contribution from the mantle. A great deal of care, however, must be taken to account for other sources of seismic energy that may interfere with the direct conversed phases on the seismogram, such as crustal reverberations; this can be a significant source of error if not properly accounted for.
5.2.2 New Strategies for D″ Anisotropy
While observations of D″ anisotropy from shear wave splitting are abundant, the mechanism(s) which generates anisotropy at the base of the mantle remains poorly understood, in part because the raypath distribution used in studies of D″-associated splitting is very limited (e.g., Kendall and Silver 1998). Of course, the raypath geometry of phases which sample the D″ layer is limited by the distribution of sources and receivers at the surface. We suggest, however, that combining constraints from different types of phases that sample the same region of D″ in different geometries is a promising (although challenging) avenue of inquiry. For example, a limited number of regions of D″ that appear to contribute to SK(K)S splitting have been identified (e.g., Wang and Wen 2007; Long 2009) and, if those regions can also be probed with (nearly) horizontally propagating waves such as S or ScS, then the constraints can be combined to produce a fuller picture of the anisotropic geometry. Constraints from different types of horizontally propagating phases can also be combined. For example, Long et al. (2006) suggested that anisotropy due to the LPO of (Mg,Fe)O should result in azimuthal variations in the amount of splitting, while most SPO-based models should not, and that studies of azimuthal anisotropy could be used to discriminate between LPO- and SPO-type models for D″ anisotropy. If specific regions of D″ can be probed using different phases propagating along a variety of azimuthal paths, the resulting tighter constraints on the geometry of anisotropy should be very helpful in discriminating among different classes of models. Finally, constraints on lowermost mantle anisotropy provided by global models derived from normal mode data (e.g. Panning and Romanowicz 2004) can be combined with constraints from body waves, although the length scales over which anisotropy can be discriminated are different for different types of observations.
In addition to progress on the observational side, future progress in understanding D″ anisotropy will almost certainly come from studies in the mineral physics and geodynamics realms as well. Ongoing efforts to characterize LPO in lowermost mantle minerals (or their low-pressure analogs) are likely to result in a better understanding of the active slip systems in (post-) perovskite and ferropericlase at lowermost mantle conditions. In particular, the extension of recent work on possible LPO geometries (and predicted splitting patterns) in D″ (e.g., Yamazaki and Karato 2002; Long et al. 2006; Yamazaki et al. 2006; Merkel et al. 2006, 2007) to higher pressures, more realistic temperatures, and to experiments on polyphase aggregates should yield a more complete picture of possible anisotropic geometries that might result from LPO processes. Another area of ongoing research that is likely to yield fruit is the integration of realistic flow models with mineral physics results and the comparison of the predictions from such studies with seismological observations. Many of the geodynamical modeling efforts focused on D″ anisotropy to date have used models of downgoing slabs impinging upon the CMB (e.g., McNamara et al. 2002; Wenk et al. 2006), but many other flow geometries are possible and there is a great deal of progress to be made in the integration of constraints from seismology, mineral physics, and geodynamics to study anisotropy in D″ and its causative mechanisms.
5.3 Global Integration of Splitting Data Sets
With the ever-increasing popularity of shear wave splitting as a seismological analysis technique, there are now literally hundreds of published shear wave splitting studies in the scientific literature using a range of phases and measurement methods that cover a variety of tectonic settings and regions of the Earth’s mantle. It is timely, therefore, to take advantage of this wealth of splitting data and to undertake comparative studies of shear wave splitting in different types of tectonic regimes. For example, the global compilation of Long and Silver (2008) was enabled by the availability of several dozen splitting studies that have been undertaken to date in subduction zone settings; the abundance of shear wave splitting measurements now available may enable similar studies for other regions. Of course, caution must be exercised when splitting measurements from different studies are combined into a global database. Differences among studies in measurement methods, preprocessing steps, frequency content, phases used, and other choices on the part of the analyst must be carefully accounted for in global compilations. Additionally, compilations that rely on average splitting parameters, such as that of Long and Silver (2008) do not fully capture the complexity of shear wave splitting data and only reflect the first-order picture of anisotropy (and therefore the first-order controls on the mantle flow field). Despite these limitations, however, global compilations of shear wave splitting measurements can be very useful, and comparisons of splitting behavior among different regions with similar tectonic regimes can help us to understand which of the many processes that may contribute to anisotropy in a given tectonic setting are, in fact, operating.
5.4 Integration with Other Seismological Constraints
We also view the integration of shear wave splitting data sets with other seismological observables that are sensitive to mantle anisotropy, such as surface waves (e.g., Debayle et al. 2005), normal modes (e.g., Beghein et al. 2008), and body wave travel times (e.g., Grésillaud and Cara 2007), as a promising avenue for progress in the near future in understanding mantle anisotropy. There has been some theoretical progress on how to relate shear wave splitting to P wave traveltime residuals (e.g., Plomerová et al. 1996; Schulte-Pelkum and Blackman 2003) and to surface wave observations (e.g. Montagner et al. 2000). Extreme care must be taken, however, to properly account for the effect of vertically varying anisotropy and in particular for the fact that the shear wave splitting operator is non-commutative (Silver and Savage 1994; Wolfe and Silver 1998); some schemes for predicting shear wave splitting in common use may fail for vertically varying anisotropy. In particular, the method of Montagner et al. (2000) utilizes simplifying assumptions that do not account for the non-commutivity of the splitting operator at long periods. Integrating splitting observations with other seismological observables remains a significant challenge, because different observables are sensitive to anisotropy at different depths and on different length scales and properly integrating them is usually non-trivial. Inferences about mantle anisotropy using different observables has often led to conflicting pictures of anisotropy and mantle processes (e.g., Maupin and Park 2007; Montagner 2007). For example, calculations of shear wave splitting from surface-wave-derived models of azimuthal anisotropy in the upper mantle often poorly predict splitting measurements (e.g., Simons et al. 2002).
One very promising line of research in this realm is the development of techniques for joint inversions of shear wave splitting measurements and other seismological observables such as surface waves. For example, Panning and Nolet (2008) recently proposed a method for inverting surface wave observations for azimuthal anisotropy in the upper mantle with a parameterization scheme that reduces the number of parameters needed to describe the anisotropic medium reasonably, and suggest that this tomographic scheme can be modified to incorporate observations of splitting intensity to perform joint inversions. A joint inversion of surface waveforms and splitting data was carried out by Marone and Romanowicz (2007) to produce a model for upper mantle anisotropy beneath North America. We note, however, that there is a discrepancy in the shear wave splitting literature regarding the commutivity of the splitting operator in the low-frequency limit. Several theoretical studies have claimed that the splitting operators do not commute even at low frequency (e.g., Savage and Silver 1993; Wolfe and Silver 1998), while other workers have asserted that in the low-frequency limit the higher-order terms that lead to this non-commutivity can be discarded (Montagner et al. 2000). Until this discrepancy is resolved, results based on the assumption of commutivity should be treated with some caution. In any case, there continue to be positive developments in the development of joint tomographic inversion frameworks for splitting observations and other seismological observables, and we expect rapid progress along this line in the near future.
5.5 Integration with Other Geophysical Constraints
We note, finally, that the interpretation of shear wave splitting measurements in the context of other geophysical data sets and various forward modeling techniques also represents a promising way forward in our quest to understand splitting and the mantle processes that generate the anisotropy responsible for it. A great deal of attention is being paid to the prediction of seismic anisotropy from geodynamical models of mantle flow (e.g., Becker et al. 2003; Behn et al. 2004; Conrad et al. 2007; Long et al. 2007b; Kneller et al. 2008; Lowman et al. 2007; Becker 2008) and, in particular, in utilizing techniques for properly modeling the development of LPO in olivine (and other minerals) incorporating the latest results from mineral physics experiments (e.g., Tommasi et al. 2000; Kaminski et al. 2004; Lev and Hager 2008a). New work on rheological anisotropy in the Earth’s mantle, which may provide constraints complementary to those on elastic anisotropy, is currently ongoing (e.g., Lev and Hager 2008b) and integrating constraints on rheological and elastic anisotropy may provide additional insight into mantle flow processes in the future. In addition to constraints on mantle anisotropy available from geodynamical models and mineral physics, other geophysical and geological observables can be combined with shear wave splitting measurements to gain insight into active mantle flow processes. For example, the crustal deformation field as determined from GPS measurements can be compared to the upper mantle flow field inferred from shear wave splitting to evaluate the extent of crust-mantle coupling (e.g., Holt 2000; Flesch et al. 2005; Wang et al. 2008). Other indicators of crustal processes such as the geometry of faults or other major geological structures can also be compared to shear wave splitting observations (e.g., Silver 1996; Fouch and Rondenay 2006; Lev et al. 2006) to infer the depth distribution of seismic anisotropy and/or the extent of mechanical coupling between the crust and mantle. We view the integration of shear wave splitting data sets with other geological and geophysical observations as an important future direction for research on the causes and consequences of upper mantle anisotropy.
6 Summary
Because of the causative link between mantle deformation and elastic anisotropy, measurements of shear wave splitting yield some of the most direct constraints available to us on the pattern of mantle flow and deformation and on the processes that generate and control this pattern. Techniques for measuring and interpreting shear wave splitting have been part of the toolkit of observational seismologists for several decades, but there have been significant advances in splitting methodologies in recent years, and the ever-increasing availability of broadband data, particularly from dense arrays, is yielding tighter constraints on the character of anisotropy in different tectonic settings. Along with progress on the observational side, new experimental mineral physics results on LPO formation in upper and lowermost mantle materials are creating exciting new avenues for the interpretation of splitting measurements, but also introducing potential ambiguities into the analysis. Despite the advances made in understanding shear wave splitting, both from a measurement and an interpretation point of view, many fundamental uncertainties remain about how properly to relate inferences about the geometry and strength of anisotropy to mantle flow processes at depth, and even first-order questions about the geometry of mantle flow in different tectonic regions remain open. With the advances summarized in this paper relating to measurement methodologies and strategies for shear wave splitting tomography, the amalgamation of splitting measurements into global data sets, the integration of results from geodynamical modeling and mineral physics experiments into the interpretation of splitting measurements, and the assimilation of constraints from splitting with other seismological and geophysical observables, we anticipate rapid progress on these fundamental questions in the near future.
References
Abt DL, Fischer KM (2008) Resolving three-dimensional anisotropic structure with shear-wave splitting tomography. Geophys J Int 173:859–886
Abt DL, Fischer KM, Abers GA, Strauch W, Protti JM, Gonzalez V (2009) Shear-wave anisotropy beneath Nicaragua and Costa Rica: implications for flow in the mantle wedge. Geochem Geophys Geosyst 173:859–886
Alsina D, Snieder R (1995) Small-scale sublithospheric continental mantle deformation: constraints from SKS splitting observations. Geophys J Int 123:431–448
Ando M, Ishikawa Y, Yamazaki F (1983) Shear wave polarization anisotropy in the upper mantle beneath Honshu, Japan. J Geophys Res 88:5850–5864
Anglin KD, Fouch MJ (2005) Seismic anisotropy in the Izu-Bonin subduction system. Geophys Res Lett 32. doi:10.1029/2005GL022714
Ansel V, Nataf H-C (1989) Anisotropy beneath 9 stations of the Geoscope broadband network as deduced from shear-wave splitting. Geophys Res Lett 16:409–412
Babuska V, Cara M (1991) Seismic anisotropy in the Earth. Kluwer Academic Publishers, Dordrecht
Barruol G, Hoffmann R (1999) Upper mantle anisotropy beneath the geoscope stations. J Geophys Res 104:10757–10773
Becker TW (2008) Azimuthal seismic anisotropy constrains net rotation of the lithosphere. Geophys Res Lett 35. doi:10.1029/2007GL032928
Becker TW, Kellogg JB, Ekström G, O’Connell RJ (2003) Comparison of azimuthal seismic anisotropy from surface waves and finite-strain from global mantle-circulation models. Geophys J Int 155:696–714
Beghein C, Trampert J (2004) Probability density functions for radial anisotropy: implications for the upper 1200 km of the mantle. Earth Planet Sci Lett 217:151–162
Beghein C, Resovsky J, van der Hilst RD (2008) The signal of mantle anisotropy in the coupling of normal modes. Geophys J Int 175:1209–1234
Behn MD, Conrad CP, Silver PG (2004) Detection of upper mantle flow associated with the African superplume. Earth Planet Sci Lett 224:259–274
Behn MD, Hirth G, Keleman PB (2007) Trench-parallel anisotropy produced by foundering of arc lower crust. Science 317:108–111
Ben Ismail W, Mainprice D (1998) An olivine fabric database: an overview of upper mantle fabrics and seismic anisotropy. Tectonophysics 296:145–157
Bjarnason IT, Silver PG, Rümpker G, Solomon SC (2002) Shear wave splitting across the Iceland hot spot: Results from the ICEMELT experiment. J Geophys Res 107. doi:10.1029/2001JB000916
Blackman DK (2007) Use of mineral physics, with geodynamic modeling and seismology, to investigate flow in the Earth’s mantle. Rep Prog Phys 70:659–689
Blackman DK, Kendall J-M (2002) Seismic anisotropy in the upper mantle, 2: predictions for current plate boundary flow models. Geochem Geophys Geosyst 3. doi:10.1029/2001GC000247
Bowman JR, Ando M (1987) Shear-wave splitting in the upper-mantle wedge above the Tonga subduction zone. Geophys J Roy Astr Soc 88:25–41
Brechner S, Klinge K, Krüger F, Plenefisch T (1998) Backazimuthal variations of splitting parameters of teleseismic SKS phases observed at the broadband stations in Germany. Pure Appl Geophys 151:305–331
Chevrot S (2000) Multichannel analysis of shear wave splitting. J Geophys Res 105:21579–21590
Chevrot S (2006) Finite-frequency vectorial tomography: a new method for high-resolution imaging of upper mantle anisotropy. Geophys J Int 165:641–657
Chevrot S, Favier N, Komatitsch D (2004) Shear wave splitting in three-dimensional anisotropic media. Geophys J Int 159:711–720
Christensen NI (1984) The magnitude, symmetry, and origin of upper mantle anisotropy based on fabric analyses of ultramafic tectonites. Geophys J R Astron Soc 76:89–111
Clark MK, Royden LH (2000) Topographic ooze: building the eastern margin of Tibet by lower crustal flow. Geology 28:703–706
Clitheroe G, van der Hilst RD (1998) Complex anisotropy in the Australian lithosphere from shear-wave splitting in broad-band SKS records. In: Braun J et al (eds) Structure and evolution of the Australian Continent. American Geophysical Union, Washington, DC, pp 73–78
Cochran ES, Vidale JE, Li Y G (2003) Near-fault anisotropy following the Hector Mine earthquake. J Geophys Res 108. doi:10.1029/2002JB002352
Conder JA (2007) Dynamically driven mantle flow and shear wave splitting asymmetry across the EPR, MELT area. Geophys Res Lett 34. doi:10.1029/2007GL030832
Conder JA, Wiens DA (2007) Rapid mantle flow beneath the Tonga volcanic arc. Earth Planet Sci Lett 264:299–307
Conder JA, Forsyth DW, Parmentier EM (2002) Asthenospheric flow and asymmetry of the East Pacific rise, MELT area. J Geophys Res 107. doi:10.1029/2001JB000807
Conrad CP, Behn MD, Silver PG (2007) Global mantle flow and the development of seismic anisotropy: differences between the oceanic and continental upper mantle. J Geophys Res 112. doi:10.1029/2006JB004608
Cordier P, Ungár T, Zsoldos L, Tichy G (2004) Dislocation creep in MgSiO3 perovskite at conditions of the Earth’s uppermost lower mantle. Nature 428:837–840
Cormier VF (1986) Synthesis of body waves in transversely isotropic earth models. Bull Seism Soc Am 76:231–240
Couvy H, Frost DJ, Heidelbach F, Krisztián N, Ungár T, Mackwell S, Cordier P (2004) Shear deformation experiments of forsterite at 11 GPa—1400°C in the multianvil apparatus. Eur J Miner 16:877–889
Crampin S (1984) Effective anisotropic elastic constants for wave propagation through cracked solids. Geophys J R Astron Soc 76:135–145
Crampin S, Chastin S (2003) A review of shear-wave splitting in the crack-critical crust. Geophys J Int 155:221–240
Currie CA, Cassidy JF, Hyndman R, Bostock MG (2004) Shear wave anisotropy beneath the Cascadia subduction zone and western North American craton. Geophys J Int 157:341–353
Dahlen FA, Hung S-H, Nolet G (2000) Fréchet kernels for finite-frequency traveltimes–I. theory. Geophys J Int 141:157–174
Davis P, England P, Houseman GA (1997) Comparison of shear wave splitting and finite strain from the India-Asia collision zone. J Geophys Res 102:27511–27522
De Hoop MV, van der Hilst RD (2005) On sensitivity kernels for ‘wave-equation’ transmission tomography. Geophys J Int 160:621–633
Debayle E, Kennett B, Priestly K (2005) Global azimuthal seismic anisotropy and the unusual plate-motion deformation of Australia. Nature 433:509–512
Doornbos DJ, Spilopoulos S, Stacey FD (1986) Seismological properties of D″ and the structure of the thermal boundary layer. Phys Earth Planet Int 41:225–239
England P, Houseman G (1986) Finite strain calculations of continental deformation: 2. Comparison with the India-Asia collision zone. J Geophys Res 91:3664–3676
Evans MS, Kendall J-M, Willemann RJ (2006) Automated SKS splitting and upper-mantle anisotropy beneath Canadian seismic stations. Geophys J Int 165:931–942
Faccenda M, Burlini L, Gerya TV, Mainprice D (2008) Fault-induced seismic anisotropy by hydration in subducting oceanic plates. Nature 455:1097–1100
Favier N, Chevrot S (2003) Sensitivity kernels for shear wave splitting in transverse isotropic media. Geophys J Int 153:213–228
Favier N, Chevrot S, Komatitsch D (2004) Near-field influences on shear wave splitting and traveltime sensitivity kernels. Geophys J Int 156:467–482
Fischer KM, Fouch MJ, Wiens DA, Boettcher MS (1998) Anisotropy and flow in Pacific subduction zone back-arcs. Pure Appl Geophys 151:463–475
Fischer KM, Parmentier EM, Stine AR, Wolf ER (2000) Modeling anisotropy and plate-driven flow in the Tonga subduction zone back arc. J Geophys Res 105:16181–16191
Fischer KM, Li A, Forsyth DW, Hung S-H (2005) Imaging three-dimensional anisotropy with broadband seismometer arrays. In: Levander A, Nolet G (eds) Seismic Earth: array analysis of broadband seismograms. American Geophysical Union, Washington, DC, pp 99–106
Flesch LM, Holt WE, Silver PG, Stephenson M, Wang C-Y, Chan WW (2005) Constraining the extent of crust-mantle coupling in central Asia using GPS, geologic, and shear-wave splitting data. Earth Planet Sci Lett 238:248–268
Fontaine FR, Barruol G, Tommasi A, Bokelmann GHR (2007) Upper-mantle flow beneath French Polynesia from shear wave splitting. Geophys J Int 170:1262–1288
Ford SR, Garnero EJ, McNamara AK (2006) A strong lateral shear velocity gradient and anisotropy heterogeneity in the lowermost mantle beneath the southern Pacific. J Geophys Res 111. doi:10.1029/2004JB003574
Forsyth DW (1975) The early structural evolution and anisotropy of the oceanic upper mantle. Geophys J R Astron Soc 43:103–162
Fouch MJ (2007) Asthenospheric dynamics of the Pacific northwestern United States. Earthscope national meeting, abstract 108
Fouch MJ, Fischer KM (1996) Mantle anisotropy beneath northwest Pacific subduction zones. J Geophys Res 101:15987–16002
Fouch MJ, Fischer KM (1998) Shear wave anisotropy in the Mariana subduction zone. Geophys Res Lett 25:1221–1224
Fouch MJ, Rondenay S (2006) Seismic anisotropy beneath stable continental interiors. Phys Earth Planet Int 158:292–320
Fouch MJ, Fischer KM, Wysession ME (2001) Lowermost mantle anisotropy beneath the Pacific: imaging the source of the Hawaiian plume. Earth Planet Sci Lett 190:167–180
Fouch MJ, Silver PG, Bell DR, Lee JN (2004) Small-scale variations in seismic anisotropy near Kimberley, South Africa. Geophys J Int 157:764–774
Froidevaux C, Schubert G (1975) Plate motion and structure of the continental asthenosphere: a realistic model of the upper mantle. J Geophys Res 80:2553–2564
Fukao Y (1984) Evidence from core-reflected shear waves for anisotropy in the earth’s mantle. Nature 309:695–698
Gao S, Davis PM, Liu H, Slack PD, Zorin YA, Mordvinova VV, Kozhevnikov VM, Meyer RP (1994) Seismic anisotropy and mantle flow beneath the Baikal rift zone. Nature 371:149–151
Gao S, Davis PM, Liu H, Slack PD, Rigor AW, Zorin YA, Mordvinova VV, Kozhevnikov VM, Logatchev NA (1997) SKS splitting beneath continental rift zones. J. Geophys Res 102:22781–22797
Garnero EJ, Lay T (1997) Lateral variations in mantle shear wave anisotropy beneath the north Pacific and Alaska. J Geophys Res 102:8121–8135
Garnero EJ, Maupin V, Lay T, Fouch MJ (2004a) Variable azimuthal anisotropy in Earth’s lowermost mantle. Science 306:259–261
Garnero EJ, Moore MM, Lay T, Fouch MJ (2004b) Isotropy or weak vertical transverse isotropy in D″ beneath the Atlantic Ocean. J Geophys Res 109. doi:10.1029/2004JB003004
Gashawbeza EM, Klemperer SL, Nyblade AA, Walker KT, Keranen KM (2004) Shear-wave splitting in Ethiopia: precambrian mantle anisotropy locally modified by Neogene rifting. Geophys Res Lett 31. doi:10.1029/2004GL020471
Gerst A, Savage MK (2004) Seismic anisotropy beneath Ruapehu Volcano: a possible eruption forcasting tool. Science 306:1543–1547
Girardin N, Farra V (1998) Azimuthal anisotropy in the upper mantle from observations of P-to-S converted phases: application to southern Australia. Geophys J Int 133:615–629
Gök R, Ni JF, West M, Sandvol E, Wilson D, Aster R, Baldridge WS, Grand S, Gao W, Tillmann F, Semken S (2002) Shear wave splitting and mantle flow beneath LA RISTRA. Geophys Res Lett 30. doi:10.1029/2002GL016616
Grésillaud A, Cara M (2007) Anisotropy and P-wave tomography: a new approach for inverting teleseismic data from a dense array of stations. Geophys J Int 126:77–91
Hall C, Fischer KM, Parmentier EM, Blackman DK (2000) The influence of plate motions on three-dimensional back arc mantle flow and shear wave splitting. J Geophys Res 105:28009–28033
Hall SA, Kendall J-M, van der Baan M (2004) Some comments on the effects of lower-mantle anisotropy on SKS and SKKS phases. Phys Earth Planet Int 146:469–481
Hammond JOS, Kaneshima S, Wookey J, Inoue H, Yamashina T, Harjadi P (2006) Shear wave splitting beneath Indonesia: evidence for slab anisotropy. Eos Trans AGU 87, fall meet suppl, abstract MR23A-07
Harmon N, Forsyth DW, Fischer KM, Webb SC (2004) Variations in shear-wave splitting in young Pacific seafloor. Geophys Res Lett 31. doi:10.1029/2004GL020495
Hartog R, Schwartz SY (2000) Subduction-induced strain in the upper mantle east of the Mendocino triple junction, California. J Geophys Res 105:7909–7930
Heidelbach F, Stretton I, Langenhorst F, Mackwell S (2003) Fabric evoluition during high shear strain deformation of magnesiowustite (Mg0.8,Fe0.2)O. J Geophys Res 108(B3):2154. doi:10.1029/2001JB001632
Hernlund JW, Thomas C, Tackley PJ (2005) A doubling of the post-perovskite phase boundary and structure of the Earth’s lowermost mantle. Nature 434:882–886
Herquel G, Wittlinger G, Guilbert J (1995) Anisotropy and crustal thickness of northern Tibet: new constraints for tectonic modeling. Geophys Res Lett 22:1925–1928
Hess HH (1964) Seismic anisotropy of the uppermost mantle under oceans. Nature 203:629–630
Hoernle K, Abt DL, Fischer KM, Nichols H, Hauff F, Abers GA, van der Bogaard P, Heydolph K, Alvarado G, Protti M, Strauch W (2008) Geochemical and geophysical evidence for arc-parallel flow in the mantle wedge beneath Costa Rica and Nicaragua. Nature 451:1094–1098
Holt WE (2000) Correlated crust and mantle strain fields in Tibet. Geology 28:67–70
Holt WE, Haines AJ (1993) Velocity fields in deforming Asia from the inversion of earthquake-released strains. Tectonics 12:1–20
Holtzman BK, Kohlstedt DL, Zimmerman ME, Heidelbach F, Hiraga T, Hustoft J (2003) Melt segregation and strain partitioning: implications for seismic anisotropy and mantle flow. Science 301:1227–1230
Huang W-C, Ni J, Tilman F, Nelson D, Guo J, Zhao W, Mechie J, Kind R, Saul J, Rapine R, Hearn T (2000) Seismic polarization anisotropy beneath the central Tibetan Plateau. J Geophys Res 105:27979–27989
Iidaka T (2003) Shear-wave splitting analysis of later phases in southwest Japan—a lineament structure detector inside the crust. Earth Planets Space 55:277–282
Iidaka T, Niu F (1998) Evidence for an anisotropic lower mantle beneath eastern Asia: comparison of shear-wave splitting data from SKS and P660s. Geophys Res Lett 25:675–678
Iitaka T, Hirose K, Kawamura K, Murakami M (2004) The elasticity of the MgSiO3 post-perovskite phase in the Earth’s lowermost mantle. Nature 430:442–445
James DE, Assumpçao M (1996) Tectonic implications of S-wave anisotropy beneath SE Brazil. Geophys J Int 126:1–10
Jung H, Karato S (2001) Water-induced fabric transitions in olivine. Science 293:1460–1463
Jung H, Katayama I, Jiang Z, Hiraga T, Karato S (2006) Effects of water and stress on the lattice preferred orientation in olivine. Tectonophysics 421:1–22
Jung H, Mo W, Green HW (2009) Upper mantle seismic anisotropy resulting from pressure-induced slip transition in olivine. Nature Geosci 2:73–77
Kaminski É, Ribe NM (2002) Timescales for the evolution of seismic anisotropy in mantle flow. Geochem Geophys Geosyst 3. doi:10.1029/2001GC000222
Kaminski É, Ribe NM, Browaeys JT (2004) D-Rex, a program for calculation of seismic anisotropy due to crystal lattice preferred orientation in the convective upper mantle. Geophys J Int 158:744–752
Kaneshima S (1990) Origin of crustal anisotropy: shear wave splitting studies in Japan. J Geophys Res 95:11121–11133
Kaneshima S, Silver PG (1992) A search for source-side anisotropy. Geophys Res Lett 19:1049–1052
Karato S (1998) Some remarks on the origin of seismic anisotropy in the D″ layer. Earth Planets Space 50:1019–1028
Karato S (2008) Deformation of Earth materials: an introduction to the rheology of the solid Earth. Cambridge University Press, Cambridge
Karato S, Li P (1992) Diffusion creep in perovskite: implications for the rheology of the lower mantle. Science 255:1238–1240
Karato S, Wu P (1993) Rheology of the upper mantle: a synthesis. Science 260:771–778
Karato S, Zhang S, Wenk H (1995) Superplasticity in the Earth’s lower mantle: evidence from seismic anisotropy and rock physics. Science 270:458–461
Karato S, Jung H, Katayama I, Skemer P (2008) Geodynamic significance of seismic anisotropy of the upper mantle: new insights from laboratory studies. Annu Rev Earth Planet Sci 36:59–95
Karki BB, Wentzcovitch RM, de Gironcoli S, Baroni S (1999) First-principles determination of elastic anisotropy and wave velocities of MgO at lower mantle conditions. Science 286:1705–1707
Katayama I, Karato S (2006) Effects of temperature on the B- to C-type fabric transition in olivine. Phys Earth Planet Int 157:33–45
Katayama I, Jung H, Karato S (2004) New type of olivine fabric at modest water content and low stress. Geology 32:1045–1048
Keith CM, Crampin S (1977) Seismic body waves in anisotropic media: synthetic seismograms. Geophys J R Astron Soc 49:225–243
Kendall J-M, Silver PG (1996) Constraints from seismic anisotropy on the nature of the lower mantle. Nature 381:409–412
Kendall J-M, Silver PG (1998) Investigating causes of D″ anisotropy. In: Gurnis M et al (eds) The core-mantle boundary region. American Geophysical Union, Washington, DC, pp 97–118
Kendall J-M, Stuart GW, Ebinger CJ, Bastow ID, Keir D (2004) Magma-assisted rifting in Ethiopia. Nature 433:146–148
Kneller EA, van Keken PE (2007) Trench-parallel flow and seismic anisotropy in the Marianas and Andean subduction systems. Nature 450:1222–1225
Kneller EA, van Keken PE, Karato S, Park J (2005) B-type olivine fabric in the mantle wedge: insights from high-resolution non-Newtonian subduction zone models. Earth planet Sci Lett 237:781–797
Kneller EA, Long MD, van Keken PE (2008) Olivine fabric transitions and shear-wave anisotropy in the Ryukyu subduction system. Earth Planet Sci Lett 268:268–282
Kosarev GL, Makeyeva LI, Savarensky YF, Chesnokov YM (1979) Influence of anisotropy under a seismograph station on the records of body waves. Izvestiya Phys Solid Earth 15:102–110
Kosarev GL, Makeyeva LI, Vinnik L (1984) Anisotropy of the mantle inferred from observations of P to S converted waves. Geophys J R Astron Soc 76:209–222
Kummerow J, Kind R (2006) Shear wave splitting in the Eastern Alps observed at the TRANSALP network. Tectonophysics 414:177–195
Lay T, Williams Q, Garnero EJ, Kellogg L, Wysession ME (1998) Seismic wave anisotropy in the D″ region and its implications. In: Gurnis M et al (eds) The core-mantle boundary region. American Geophysical Union, Washington, DC, pp 299–318
Lev E, Hager BH (2008a) Prediction of anisotropy from flow models: a comparison of three methods. Geochem Geophys Geosyst 9. doi:10.1029/2008GC002032
Lev E, Hager BH (2008b) Rayleigh-Taylor instabilities with anisotropic lithospheric viscosity. Geophys J Int 173:806–814
Lev E, Long MD, van der Hilst RD (2006) Seismic anisotropy in eastern Tibet from shear wave splitting reveals changes in lithospheric deformation. Earth Planet Sci Lett 251:293–304
Levin V, Park J (1998) P-SH conversions in layered media with hexagonally symmetric anisotropy: a cookbook. Pure Appl Geophys 151:669–697
Levin V, Menke W, Park J (1999) Shear wave splitting in the Appalachians and the Urals: a case for multilayered anisotropy. J Geophys Res 104:17975–17993
Levin V, Droznin D, Park J, Gordeev E (2004) Detailed mapping of seismic anisotropy with local shear waves in southeastern Kamchatka. Geophys J Int 158:1009–1023
Levin V, Okaya D, Park J (2007) Shear wave birefringence in wedge-shaped anisotropic regions. Geophys J Int 168:275–286
Liu H, Davis PM, Gao S (1995) SKS splitting beneath southern California. Geophys Res Lett 22:767–770
Long MD (2009) Azimuthal anisotropy in D″ beneath the eastern Pacific from SKS-SKKS splitting discrepancies. Earth Planet Sci Lett 285:181–189
Long MD, Silver PG (2008) The subduction zone flow field from seismic anisotropy: a global view. Science 319:315–318
Long MD, van der Hilst RD (2005a) Upper mantle anisotropy beneath Japan from shear wave splitting. Phys Earth Planet Int 151:206–222
Long MD, van der Hilst RD (2005b) Estimating shear-wave splitting parameters from broadband recordings in Japan: a comparison of three methods. Bull Seism Soc Am 95:1346–1358
Long MD, van der Hilst RD (2006) Shear wave splitting from local events beneath the Ryukyu arc: trench-parallel anisotropy in the mantle wedge. Phys Earth Planet Int 155:300–312
Long MD, Xiao X, Jiang Z, Evans B, Karato S (2006) Lattice preferred orientation in deformed polycrystalline (Mg, Fe)O and implications for seismic anisotropy in D″. Phys Earth Planet Int 156:75–88
Long MD, de Hoop MV, van der Hilst RD, Hager BH (2007a) Shear wave splitting intensity tomography beneath southwestern Japan and coupling with numerical flow models. Eos Trans AGU 88, fall meet suppl, abstract S31E-01
Long MD, Hager BH, de Hoop MV, van der Hilst RD (2007b) Two-dimensional modeling of subduction zone anisotropy and application to southwestern Japan. Geophys J Int 170:839–856
Long MD, de Hoop MV, van der Hilst RD (2008) Wave-equation shear wave splitting tomography. Geophys J Int 172:311–330
Long MD, Gao H, Klaus A, Wagner LS, Fouch MJ, James DE, Humphreys ED (in review) Shear wave splitting and the pattern of mantle flow beneath eastern Oregon. Earth Planet Sci Lett
Lowman JP, Piñero-Feliciangeli LT, Kendall J-M, Shahnas MH (2007) Influence of convergent plate boundaries on upper mantle flow and implications for seismic anisotropy. Geochem Geophys Geosyst 8. doi:10.1029/2007GC001627
Maggi A, Debayle E, Priestley K, Barruol G (2006) Azimuthal anisotropy of the Pacific region. Earth Planet Sci Lett 250:53–71
Mainprice D (2007) Seismic anisotropy of the deep Earth from a mineral and rock physics perspective. In: Schubert G (ed) Treatise on geophysics, vol 2. Elsevier, Oxford, pp 437–492
Mainprice D, Tommasi A, Couvy H, Cordier P, Frost DJ (2005) Pressure sensitivity of olivine slip systems: implications for the interpretation of seismic anisotropy of the Earth’s upper mantle. Nature 433:731–733
Mainprice D, Tommasi A, Cordier P, Carrez P, Ferre D (2008) Predicted glide systems and crystal preferred orientation of polycrystalline silicate Mg-perovskite at mantle pressures: implications for the seismic anisotropy of the lower mantle. Earth Planet Sci Lett 271:135–144
Marone F, Romanowicz B (2007) The depth distribution of azimuthal anisotropy in the continental upper mantle. Nature 447:198–201
Marquardt H, Speziale S, Reichmann HJ, Frost DJ, Schilling FR, Garnero EJ (2009) Elastic shear anisotropy of ferropericlase in Earth’s lower mantle. Science 324:224–226
Marson-Pidgeon K, Savage MK (1997) Frequency-dependent anisotropy in Wellington, New Zealand. Geophys Res Lett 24:3297–3300
Mattatall LR, Fouch MJ (2007) Small-scale variations in SKS splitting near Parkfield, California. Eos Trans AGU 88, fall meet. Suppl, abstract T53C-02
Matzel E, Sen MK, Grand SP (1996) Evidence for anisotropy in the deep mantle beneath Alaska. Geophys Res Lett 23:2417–2420
Maupin V (1994) On the possibility of anisotropy in the D″ layer as inferred from the polarization of diffracted S waves. Phys Earth Planet Int 87:1–32
Maupin V, Park J (2007) Theory and observations—wave propagation in anisotropic media. In: Schubert G (ed) Treatise on geophysics vol 1. Elsevier, Amsterdam, pp 289–321
Maupin V, Garnero EJ, Lay T, Fouch MJ (2005) Azimuthal aniosotropy in the D″ layer benath the Caribbean. J Geophys Res 110. doi:10.1029/2004JB003506
McNamara DE, Owens TJ (1993) Azimuthal shear wave velocity anisotropy in the Basin and Range province using Moho Ps converted phases. J Geophys Res 98:12003–12017
McNamara DE, Owens TJ, Silver PG, Wu FT (1994) Shear wave anisotropy beneath the Tibetan plateau. J Geophys Res 99:13655–13665
McNamara AK, van Keken PE, Karato S (2002) Development of anisotropic structure by solid-state convection in the Earth’s lower mantle. Nature 416:310–314
Meade C, Silver PG, Kaneshima S (1995) Laboratory and seismological observations of lower mantle isotropy. Geophys Res Lett 22:1293–1296
Mehl L, Hacker BR, Hirth G, Keleman PB (2003) Arc-parallel flow within the mantle wedge: evidence from the accreted Talkeetna arc, south central Alaska. J Geophys Res 108. doi:10.1029/2002JB002233
Menke W, Levin V (2003) The cross-convolution method for interpreting SKS splitting observations, with application to one and two-layer anisotropic earth models. Geophys J Int 154:379–392
Merkel S, Wenk H-R, Shu J, Shen G, Gillet P, Mao H-K, Hemley RJ (2002) Deformation of polycrystalline MgO at pressures of the lower mantle. J Geophys Res 107. doi:10.1029/2001JB000920
Merkel S, Kubo A, Miyagi L, Speziale S, Duffy TS, Mao H-K, Wenk H-R (2006) Plastic deformation of MgGeO3 post-perovskite at lower mantle pressures. Science 311:644–646
Merkel S, McNamara AK, Kubo A, Speziale S, Miyagi L, Meng Y, Duffy TS, Wenk H-R (2007) Deformation of (Mg, Fe)SiO3 post-perovskite and D″ anisotropy. Science 316:1729–1732
Mizukami T, Wallis SR, Yamamoto J (2004) Natural examples of olivine lattice preferred orientation patterns with a flow-normal a-axis maximum. Nature 427:432–436
Molnar P, England P, Martinod J (1993) Mantle dynamics, uplift of the Tibetan Plateau, and the Indian monsoon. Rev Geophys 31:357–396
Montagner J-P (2007) Deep earth structure—upper mantle structure: global istropic and anisotropic elastic tomography. In: Schubert G (ed) Treatise on geophysics, vol 1. Elsevier, Amsterdam, pp 559–589
Montagner J-P, Griot-Pommera DA, Lavé J (2000) How to relate body wave and surface wave anisotropy? J Geophys Res 105:19015–19027
Moore MM, Garnero EJ, Lay T, Williams Q (2004) Shear wave splitting and waveform complexity for lowermost mantle structures with low-velocity lamellae and transverse isotropy. J Geophys Res 103. doi:10.1029/2003JB002546
Nakajima J, Hasegawa A (2004) Shear-wave polarization anisotropy and subduction-induced flow in the mantle wedge of northern Japan. Earth Planet Sci Lett 225:365–377
Nicolas A, Christensen NI (1987) Formation of anisotropy in upper mantle peridotites - a review. In: Fuchs K, Froideveaux C (eds) Composition, structure and dynamics of the lithosphere-asthenosphere system. American Geophysical Union, Washington, DC, pp 111–123
Nippress SEJ, Kusznir NJ, Kendall J-M (2007) LPO predicted seismic anisotropy beneath a simple model of a mid-ocean ridge. Geophys Res Lett 34. doi:10.1029/2006GL029040
Niu F, Perez AM (2004) Seismic anisotropy in the lower mantle: a comparison of waveform splitting of SKS and SKKS. Geophys Res Lett 31. doi:10.1029/2004GL0211196
Ozacar AA, Zandt G (2004) Crustal seismic anisotropy in central Tibet: Implications for deformational style and flow in the crust. Geophys Res Lett 31. doi:10.1029/2004GL021096
Özalaybey S, Savage MK (1994) Double-layer anisotropy resolved from S phases. Geophys J Int 117:653–664
Özalaybey S, Savage MK (1995) Shear-wave splitting beneath western United States in relation to plate tectonics. J Geophys Res 100:18135–18149
Panning MP, Nolet G (2008) Surface wave tomography for azimuthal anisotropy in a strongly reduced parameter space. Geophys J Int 174:629–648
Panning MP, Romanowicz B (2004) Inferences on flow at the base of Earth’s mantle based on seismic anisotropy. Science 303:351–353
Park J, Yuan H, Levin V (2004) Subduction zone anisotropy beneath Corvallis, Oregon: a serpentinite skid mark of trench-parallel terrane migration? J Geophys Res 109. doi:10.1029/2003JB002718
Plomerová J, Sileny J, Babuska V (1996) Joint interpretation of upper-mantle anisotropy based in teleseismic P-travel time delays and inversion of shear-wave splitting parameters. Phys Earth Planet Int 95:293–309
Polet J, Kanamori H (2002) Anisotropy beneath California: shear wave splitting measurements using a dense broadband array. Geophys J Int 149:313–327
Pozgay SH, Wiens DA, Conder JA, Shiobara H, Sugioka H (2007) Complex mantle flow in the Mariana subduction system: evidence from shear wave splitting. Geophys J Int 170:371–386
Rai A, Rai SS, Gaur VK (2008) Crustal stress patterns: analysis of Ps splitting for seismic anisotropy. Curr Sci 94:911–915
Raterron P, Chen J, Li L, Weidner DJ, Cordier P (2007) Pressure-induced slip system transition in forsterite: single-crystal rheological properties at mantle pressure and temperature. Am Miner 92:1436-1445
Restivo A, Helffrich G (1999) Teleseismic shear wave splitting meaurements in noisy environments. Geophys J Int 137:821–830
Restivo A, Helffrich G (2006) Core-mantle boundary structure investigated using SKS and SKKS polarization anomalies. Geophys J Int 165:288–302
Ritsema J (2000) Evidence for shear velocity anisotropy in the lowermost mantle beneath the Indian Ocean. Geophys Res Lett 27:1041–1044
Ritsema J, Lay T, Garnero EJ, Benz H (1998) Seismic anisotropy in the lowermost mantle beneath the Pacific. Geophys Res Lett 25:1229–1232
Rokosky JM, Lay T, Garnero EJ, Russell S (2004) High-resolution investigation of shear wave anisotropy in D″ beneath the Cocos Plate. Geophys Res Lett 31. doi:10.1029/2003GL018902
Rokosky JM, Lay T, Garnero EJ (2006) Small-scale lateral variations in azimuthally anisotropic D″ structure beneath the Cocos plate. Earth Planet Sci Lett 248:411–425
Royden LH, Burchfiel BC, King W, Wang E, Chen Z, Shen F, Liu Y (1997) Surface deformation and lower crustal flow in Eastern Tibet. Science 276:788–790
Rümpker G, Ryberg T (2000) New “Fresnel-Zone” estimates for shear-wave splitting observations from finite-difference modeling. Geophys Res Lett 27:2005–2008
Rümpker G, Silver PG (1998) Apparent shear-wave splitting parameters in the presence of vertically-varying anisotropy. Geophys J Int 135:790–800
Rümpker G, Ryberg T, Bock G, DESERT Seismology Group (2003) Boundary-layer mantle flow under the Dead Sea transform fault inferred from seismic anisotropy. Nature 425:497–501
Russell S, Lay T, Garnero EJ (1999) Small-scale lateral shear velocity and anisotropy heterogeneity near the core-mantle boundary beneath the central Pacific imaged using broadband ScS waves. J Geophys Res 104:12183–12199
Russo RM, Okal EA (1998) Shear wave splitting and upper mantle deformation in French Polynesia: evidence for small-scale heterogeneity related to the Society hotspot. J Geophys Res 103:15089–15107
Russo RM, Silver PG (1994) Trench-parallel flow beneath the Nazca plate from seismic anisotropy. Science 263:1105–1111
Ryberg T, Rümpker G, Haberland C, Stromeyer D, Weber M (2005) Simultaneous inversion of shear wave splitting observations from seismic arrays. J Geophys Res 110. doi:10.1029/2004JB003303
Rychert CA, Rondenay S, Fischer KM (2007) P-to-S and S-to-P imaging of a sharp lithosphere-asthenosphere boundary beneath eastern North America. J Geophys Res 112. doi:10.1029/2006JB004619
Salah MK, Seno T, Iidaka T (2008) Upper mantle anisotropy beneath central and southwest Japan: an insight into subduction-induced mantle flow. J Geodyn 46:21–37
Saltzer RL, Gaherty J, Jordan TH (2000) How are vertical shear wave splitting measurements affected by variations in the orientation of azimuthal anisotropy with depth? Geophys J Int 141:374–390
Saul J, Vinnik L (2003) Earth science (communication arising): mantle deformation or processing artefact? Nature 422:136
Savage MK (1999) Seismic anisotropy and mantle deformation: what have we learned from shear wave splitting? Rev Geophys 37:65–106
Savage MK, Sheehan AF (2000) Seismic anisotropy and mantle flow from the Great Basin to the Great Plains, western United States. J Geophys Res 105:13715–13734
Savage MK, Silver PG (1993) Mantle deformation and tectonics: constraints from seismic anisotropy in western Unites States. Phys Earth Planet Int 78:207–227
Schmeling H, Bussod GY (1996) Variable viscosity convection and partial melting in the continental asthenosphere. J Geophys Res 101:5411–5423
Schulte-Pelkum V, Blackman DK (2003) A synthesis of seismic P and S anisotropy. Geophys J Int 154:166–178
Schutt DL, Humphreys ED (2001) Evidence for a deep asthenosphere beneath North America from western United States SKS splits. Geology 29:291–294
Sieminski A, Paulssen H, Trampert J, Tromp J (2008) Finite-frequency SKS splitting: measurement and sensitivity kernels. Bull Seism Soc Am 98:1797–1810
Sileny J, Plomerova J (1996) Inversion of shear-wave splitting parameters to retrieve three-dimensional orientation of anisotropy in continental lithosphere. Phys Earth Planet Int 95:277–292
Silver PG (1996) Seismic anisotropy beneath the continents: probing the depths of geology. Annu Rev Earth Planet Sci 24:385–432
Silver PG (2007) Riding the Wilson cycle. Geotimes 52:30–33
Silver PG, Chan WW (1988) Implications for continental structure and evolution from seismic anisotropy. Nature 335:34–39
Silver PG, Chan WW (1991) Shear wave splitting and subcontinental mantle deformation. J Geophys Res 96:16429–16454
Silver PG, Holt WE (2002) The mantle flow field beneath western North America. Science 295:1054–1057
Silver PG, Savage MK (1994) The interpretation of shear-wave splitting parameters in the presence of two anisotropic layers. Geophys J Int 119:949–963
Simons FJ, van der Hilst RD, Montagner J-P, Zielhuis A (2002) Multimode Rayleigh wave inversion for heterogeneity and azimuthal anisotropy of the Australian upper mantle. Geophys J Int 151:738–754
Skemer P, Katayama I, Karato S (2006) Deformation fabrics of a peridotite from Cima di Gagnone, central Alps, Switzerland: evidence of deformation under water-rich condition at lower temperatures. Contrib Miner Petrol 152:43–51
Smith GP, Wiens DA, Fischer KM, Dorman LM, Webb SC, Hildebrand JA (2001) A complex pattern of mantle flow in the Lau Backarc. Science 292:713–716
Sol S, Meltzer A, Burgmann R, van der Hilst RD, King R, Chen Z, Koons PO, Lev E, Liu YP, Zeitler PK, Zhang X, Zhang J, Zurek B (2007) Geodynamics of the southeastern Tibetan Plateau from seismic anisotropy and geodesy. Geology 35:563–566
Stackhouse S, Brodholt JP, Wookey J, Kendall J-M, Price GD (2005) The effect of temperature on the seismic anisotropy of the perovskite and post-perovskite polymorphs of MgSiO3. Earth Planet Sci Lett 230:1–10
Sundberg M, Cooper RF (2008) Crystallographic preferred orientation produced by diffusional creep of harzburgite: effects of chemical interactions among phases during plastic flow. J Geophys Res 113. doi:10.1029/2008JB005618
Teanby NA, Kendall J-M, van der Baan M (2004) Automation of shear-wave splitting measurements using cluster analysis. Bull Seism Soc Am 94:453–463
Thomas C, Kendall J-M (2002) The lowermost mantle beneath northern Asia: II. Evidence for lower-mantle anisotropy. Geophys J Int 151:296–308
Tommasi A, Mainprice D, Canova G, Chastel Y (2000) Viscoplastic self-consistent and equilibrium-based modeling of olivine lattice preferred orientations: implications for the upper mantle seismic anisotropy. J Geophys Res 105:7893–7908
Tommasi A, Mainprice D, Cordier P, Thoraval C, Couvy H (2004) Strain-induced seismic anisotropy of wadsleyite polycrystals and flow patterns in the mantle transition zone. J Geophys Res 109. doi:10.1029/2004JB003158
Trampert J, van Heijst HJ (2002) Global azimuthal anisotropy in the transition zone. Science 296:1297–1299
Usui Y, Hiramatsu Y, Furumoto M, Kanao M (2005) Thick and anisotropic D″ layer beneath Antarctic Ocean. Geophys Res Lett 32:doi:10.1029/2005GL022622
Vecsey L, Plomerová J, Babuska V (2008) Shear-wave splitting measurements—problems and solutions. Tectonophysics 462:178–196
Vidale JE (1986) Complex polarization analysis of particle motion. Bull Seism Soc Am 71:1511–1530
Vinnik LP, Kosarev GL, Makeyeva LI (1984) Lithospheric anisotropy as indicated by SKS and SKKS waves. Doklady Earth Sci Sect 278:39–43
Vinnik LP, Farra V, Romanowicz B (1989a) Azimuthal anisotropy in the Earth from observations of SKS at GEOSCOPE and NARS broadband stations. Bull Seism Soc Am 79:1542–1558
Vinnik LP, Kind R, Kosarev GL, Makeyeva L (1989b) Azimuthal anisotropy in the lithosphere from observations of long-period S-waves. Geophys J Int 99:549–559
Vinnik L, Peregoudov D, Makeyeva L, Oreshin S, Roecker S (2002) Towards a 3-D fabric in the continental lithosphere and asthenosphere: the Tien Shan. Geophys Res Lett 29. doi:10.1029/2001GL014588
Vinnik L, Montagner J-P, Girardin N, Dricker I, Saul J (2003) Comment on “Shear-wave splitting to test mantle deformation models around Hawaii” by Kristoffer T. Walker, Götz H. R. Bokelmann, and Simon L. Klemperer. Geophys Res Lett 30. doi:10.1029/2002GL015751
Waite GP, Schutt DL, Smith RB (2005) Models of lithosphere and asthenosphere anisotropic structure of the Yellowstone hot spot from shear wave splitting. J Geophys Res 110. doi:10.1029/2004JB003501
Walker KT, Bokelmann GHR, Klemperer SL (2001) Shear-wave splitting to test mantle deformation models around Hawaii. Geophys Res Lett 28:4319–4322
Walker KT, Bokelmann GHR, Klemperer SL (2003) Reply to “Shear wave splitting to test mantle deformation models around Hawaii” by Vinnik et al. Geophys Res Lett 30: doi:10.1029/2002GL016712
Walker KT, Bokelmann GHR, Klemperer SL (2004) Shear-wave splitting beneath the Snake River plain suggests a mantle upwelling beneath eastern Nevada, USA. Earth Planet Sci Lett 222:529–542
Walker KT, Bokelmann GHR, Klemperer SL, Bock G (2005a) Shear-wave splitting around the Eifel hotspot: evidence for a mantle upwelling. Geophys J Int 163:962–980
Walker KT, Bokelmann GHR, Klemperer SL, Nyblade A (2005b) Shear-wave splitting around hotspots: evidence for upwelling-related mantle flow? In: Foulger G et al (eds) Plates. Plumes & Paradigms, Geological Society of America, pp 171–192
Wang Y, Wen L (2007) Complex seismic anisotropy at the border of a very low velocity province at the base of the Earth’s mantle. J Geophys Res 112. doi:10.1029/2006JB004719
Wang C-Y, Flesch LM, Silver PG, Chang L-J, Chan WW (2008) Evidence for mechanically coupled lithosphere in central Asia and resulting implications. Geology 36:363–366
Wenk H-R, Speziale S, McNamara AK, Garnero EJ (2006) Modeling lower mantle anisotropy development in a subducting slab. Earth Planet Sci Lett 245:302–314
Wentzcovitch RM, Tsuchiya T, Tsuchiya J (2006) MgSiO3 postperovskite at D″ conditions. Proc Natl Acad Sci USA 103:543–546
West JD, Fouch MJ, Roth JB, Elkins-Tanton LT (2009) Vertical mantle flow associated with a lithospheric drip beneath the Great Basin. Nature Geosci 2:439–444
Wirth E, Long MD (2008) Frequency dependent shear wave splitting beneath Japan and implications for the mantle wedge. Eos Trans AGU, fall meet suppl, 89, abstract V31A-2115
Wolfe CJ, Silver PG (1998) Seismic anisotropy of oceanic upper mantle: shear-wave splitting observations and methodologies. J Geophys Res 103:749–771
Wolfe CJ, Solomon SC (1998) Shear-wave splitting and implications for mantle flow beneath the MELT region of the East Pacific Rise. Science 280:1230–1232
Wolfe CJ, Vernon FL (1998) Shear-wave splitting at central Tien Shan: evidence for rapid variation of anisotropic patterns. Geophys Res Lett 25:1217–1220
Wookey J, Kendall J-M (2004) Evidence of mid-mantle anisotropy from shear-wave splitting and the influence of shear-coupled P-waves. J Geophys Res. 109. doi:10.1029/2003JB002871
Wookey J, Kendall J-M (2007) Seismic anisotropy of post-perovskite and the lowermost mantle. In: Hirose K et al (eds) Post-perovskite: the last mantle phase transition. American Geophysical Union, Washington, DC, pp 171–189
Wookey J, Kendall J-M (2008) Constraints on lowermost mantle mineralogy and fabric beneath Siberia from seismic anisotropy. Earth Planet Sci Lett 275:32–42
Wookey J, Kendall J-M, Barruol G (2002) Mid-mantle deformation inferred from seismic anisotropy. Nature 415:777–780
Wookey J, Kendall J-M, Barruol G (2003) Earth science (communication arising (reply)): mantle deformation or processing artefact? Nature 422:136
Wookey J, Kendall J-M, Rümpker G (2005) Lowermost mantle anisotropy beneath the North Pacific from differential S-ScS splitting. Geophys J Int 161:829–838
Wüstefeld A, Bokelmann G (2007) Null detection in shear-wave splitting measurements. Bull Seism Soc Am 97:1204–1211
Wüstefeld A, Bokelmann G, Barruol G, Zaroli C (2007) Splitlab: a shear-wave splitting environment in Matlab. Comp Geosci 34. doi:10.1016/j.cageo.2007.1008.1002
Yamazaki D, Karato S (2002) Fabric devlopment in (Mg, Fe)O during large strain, shear deformation: implications for seismic anisotropy in Earth’s lower mantle. Phys Earth Planet Int 131:251–267
Yamazaki D, Karato S (2007) Lattice-preferred orientation of lower mantle materials and seismic anisotropy in the D″ layer. In: Hirose K et al (eds) Post-perovskite: the last mantle phase transition. American Geophysical Union, Washington, DC, pp 69–78
Yamazaki D, Yoshino T, Ohfuji H, Ando J, Yoneda A (2006) Origin of seismic anisotropy in the D″ layer inferred from shear deformation experiments on post-perovskite phase. Earth Planet Sci Lett 252:372–378
Yuan H, Deuker K, Schutt DL (2008) Testing five of the simplest upper mantle anisotropic velocity parameterizations using teleseismic S and SKS data from the Billings, Montana PASSCAL array. J Geophys Res 113. doi:10.1029/2007JB005092
Zandt G, Humphreys E (2008) Toroidal mantle flow through the western US slab window. Geology 36:295-298
Zhang S, Karato S (1995) Lattice preferred orientation of olivine aggregates deformed in simple shear. Nature 415:777–780
Zimmerman ME, Zhang S, Kohlstedt DL, Karato S (1999) Melt distribution in mantle rocks deformed in simple shear. Geophys Res Lett 26:1505–1508
Acknowledgments
We thank Jeff Gu for his efforts towards putting together this Special Issue and for the invitation to write this paper. We acknowledge with thanks the assistance of Erin Wirth and Mark Behn with the construction of Figs. 7 and 9, respectively. We thank George Zandt, Gene Humphreys, Bill Menke, and Vadim Levin for graciously granting permission to reproduce or adapt figures from their papers. We thank the Geological Society of America for their generous policy regarding fair use reproduction of figures from their journals; Figs. 10 and 11 are both reproduced from papers that appeared in Geology. Data from the F-net, Transportable Array (TA), and High Lava Plains Seismic Experiment networks were used to make figures in this paper. We thank the authors of publicly available splitting analysis codes for making them available to the community.
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License (https://creativecommons.org/licenses/by-nc/2.0), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Long, M.D., Silver, P.G. Shear Wave Splitting and Mantle Anisotropy: Measurements, Interpretations, and New Directions. Surv Geophys 30, 407–461 (2009). https://doi.org/10.1007/s10712-009-9075-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10712-009-9075-1