Abstract
We prove that the space of holomorphic p-forms on the moduli space \(\overline{\mathcal {M}}_{g,n}\) of stable curves of genus g with n marked points vanishes for \(p=14, 16, 18\) unconditionally and also for \(p=20\) under a natural assumption in the case \(g=3\). This result is consistent with the Langlands program and it is obtained by applying the Arbarello–Cornalba inductive approach to the cohomology of moduli spaces.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The moduli space \(\overline{\mathcal {M}}_{g,n}\) parameterizing stable curves of genus g with n marked points is a projective compactification with a beautiful geometric structure: all its boundary components are (products of) moduli spaces of the same kind but with smaller invariants. This remarkable property was employed by Enrico Arbarello and Maurizio Cornalba to perform an elegant inductive computation of the first few rational cohomology groups of \(\overline{\mathcal {M}}_{g,n}\). In particular, in [1] they proved that \(H^1(\overline{\mathcal {M}}_{g,n}) = H^3(\overline{\mathcal {M}}_{g,n}) = H^5(\overline{\mathcal {M}}_{g,n}) = 0\) and established an inductive approach to reduce the vanishing of odd cohomology (so long as it vanishes, since it is well known that \(H^{11,0}(\overline{\mathcal {M}}_{1,11}) \ne 0\)) to a finite number of explicit verifications in low genus.
A few years later, in [4] Gilberto Bini and the author pointed out that the same inductive procedure implies also the vanishing of the spaces of holomorphic p-forms \(H^{p,0}(\overline{\mathcal {M}}_{g,n})\) for \(0< p < 11\). More recently, a renewed interest in the Arbarello-Cornalba method is witnessed by the papers [3] by Jonas Bergström, Carel Faber, and Sam Payne, where they compute that \(H^7(\overline{\mathcal {M}}_{g,n}) = H^9(\overline{\mathcal {M}}_{g,n}) = 0\), and [5] by Samir Canning, Hannah Larson, and Sam Payne, where they prove inductively that the cohomology group \(H^k(\overline{\mathcal {M}}_{g,n})\) is pure Hodge-Tate (hence, in particular, \(H^{k,0}(\overline{\mathcal {M}}_{g,n})=0\)) for any even \(k \le 12\). This is consistent with the Langlands program, predicting that \(H^k(\overline{\mathcal {M}}_{g,n})\) should be pure Hodge-Tate for all even \(k \le 20\).
Here we move a small step forward along the same path by obtaining the following result:
Theorem 1
We have
for every g and n with \(2g-2 + n > 0\).
Furthermore, if \(H^{20,0}(\overline{\mathcal {M}}_{3,15}) = H^{20,0}(\overline{\mathcal {M}}_{3,16}) = 0\) then \(H^{20,0}(\overline{\mathcal {M}}_{g,n}) = 0\) for every g and n with \(2g-2 + n > 0\).
Once again, the crucial ingredient is a minor variant of the Arbarello-Cornalba inductive approach (see Lemma 1). Of course, the statement of Theorem 1 arises the following natural question:
Question 1
Is \(H^{20,0}(\overline{\mathcal {M}}_{3,15}) = H^{20,0}(\overline{\mathcal {M}}_{3,16}) = 0\)?
We work over the complex field \({\mathbb {C}}\).
2 The proofs
Lemma 1
Let \(0 < p \le 21\) and assume \(h^{p,0}(\overline{\mathcal {M}}_{g',n'})=0\) for every \(g', n'\) such that \(p \ge 2g'-2+n' > 0\). Then \(h^{p,0}(\overline{\mathcal {M}}_{g,n})=0\) for every g and n with \(2g-2 + n > 0\).
Proof
By double induction on g and n. Let \(d(g,n)=2g-2+n>0\).
If \(d(g,n)=1\) we have either \(g=0\) and \(n=3\), or \(g=1\) and \(n=1\), and in both cases the claim is obvious.
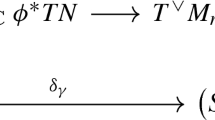
Let now \(d(g,n)>1\). If \(p \ge d(g,n)\) then the claim holds by assumption, hence let \(p < d(g,n)\). In the long exact sequence of cohomology with compact supports:
we have \(H^k_c(\mathcal {M}_{g,n}) =0\) for \(k < d(g,n)\) by [7]. Since the morphism
is compatible with the Hodge structures (see [1], p. 102), for \(p < d(g,n)\) there is an injection
Next we use the fact that each irreducible component of the boundary \(\partial \overline{\mathcal {M}}_{g,n}\) is the image of a map from \({\overline{{\mathcal {M}}}}_{g-1, n+2}\) or \({\overline{{\mathcal {M}}}}_{h,m+1} \times {\overline{{\mathcal {M}}}}_{g-h, n-m+1}\), where \(0 \le h \le g\) and both \(2\,h-2+m+1\) and \(2(g-h)-2+n-m+1\) are positive. By the analogue of Lemma (2.6) in [1] and the Hodge-Künneth formula, the map
is injective whenever the map (1) is. The right hand side involves the terms \(H^{p,0}({\overline{{\mathcal {M}}}}_{g-1,n+2})\) and \(H^{p,0}({\overline{{\mathcal {M}}}}_{g-h, n-m+1})\) with either \(h \ge 1\) or \(h=0\) and \(m \ge 2\), hence vanishing by induction, and products of two terms which have \(1 \le q \le 10\), since \(p \le 21\). Therefore by [4], Theorem 1, stating that \(H^{q,0}(\overline{\mathcal {M}}_{g,n}) =0\) for \(0< q < 11\), we obtain \(H^{p,0}(\overline{\mathcal {M}}_{g,n})=0\).
\(\square \)
Remark 1
The assumption of Lemma 1 is not satisfied for every \(11 \le p \le 21\): in particular, as it is well known \(H^{11,0}(\overline{\mathcal {M}}_{1,11}) \ne 0\) (see for instance [6], Section 2.3) and also \(H^{17,0}(\overline{\mathcal {M}}_{2,14}) \ne 0\) (see [6], Section 3.5).
Proof of Theorem 1
In order to apply Lemma 1 we have to fix an even integer p with \(14 \le p \le 20\) and check that \(H^{p,0}(\overline{\mathcal {M}}_{g',n'})=0\) for every \(g', n'\) such that \(p \ge 2g'-2+n' > 0\).
If \(g'=0\) then all cohomology is tautological (hence algebraic) by [8].
If \(g'=1\) then all even cohomology is tautological by [10].
If \(g'=2\) then all even cohomology is tautological for \(n' < 20\) by [11].
If \(g'=3\) then \(\overline{\mathcal {M}}_{g',n'}\) is unirational (hence \(H^{p,0}(\overline{\mathcal {M}}_{g',n'})=0\) for every \(p > 0\)) for \(n' \le 14\) by [9], Theorem 7.1 (notice that this range completely covers the case \(p \le 18\), while for \(p=20\) we need the additional assumption in the statement).
The same Theorem 7.1 in [9] yields the unirationality of \(\overline{\mathcal {M}}_{g',n'}\) also for \(g'=4\) and \(n' \le 15\), \(g'=5\) and \(n' \le 12\), \(g'=6\) and \(n' \le 15\), \(g'=7\) and \(n' \le 11\), \(g'=9\) and \(n' \le 8\), \(g'=11\) and \(n' \le 10\).
Finally, by [2], Theorem B., \(\overline{\mathcal {M}}_{g',n'}\) is unirational for \(g'=8\) and \(n' \le 11\) and \(g'=10\) and \(n' \le 3\), thus covering the last missing cases.\(\square \)
References
Arbarello, E., Cornalba, M.: Calculating cohomology groups of moduli spaces of curves via algebraic geometry. Inst. Hautes Études Sci. Publ. Math. 88, 97–127 (1998)
Ballico, E., Casnati, G., Fontanari, C.: On the birational geometry of moduli spaces of pointed curves. Forum Math. 21, 935–950 (2009)
Bergström, J., Faber, C., Payne, S.: Polynomial point counts and odd cohomology vanishing on moduli spaces of stable curves. Ann. Math. (to appear)
Bini, G., Fontanari, C.: Moduli of curves and spin structures via algebraic geometry. Trans. Amer. Math. Soc. 358, 3207–3217 (2006)
Canning, S., Larson, H., Payne, S.: The eleventh cohomology group of \(\overline{\cal{M} }_{g, n}\). Forum Math. Sigma 11(e62), 1–18 (2023)
Faber, C., Pandharipande, R.: Tautological and non-tautological cohomology of the moduli space of curves. Handbook of moduli. vol. I, pp. 293–330, Adv. Lect. Math. (ALM), 24, Int. Press, Somerville, MA, (2013)
Harer, J.: The virtual cohomological dimension of the mapping class group of an orientable surface. Invent. Math. 84, 157–176 (1986)
Keel, S.: Intersection theory of moduli space of stable \(n\)-pointed curves of genus zero. Trans. Amer. Math. Soc. 330, 545–574 (1992)
Logan, A.: The Kodaira dimension of moduli spaces of curves with marked points. Amer. J. Math. 125, 105–137 (2003)
Petersen, D.: The structure of the tautological ring in genus one. Duke Math. J. 163, 777–793 (2014)
Petersen, D.: Tautological rings of spaces of pointed genus two curves of compact type. Compos. Math. 152, 1398–1420 (2016)
Acknowledgements
The author is member of GNSAGA of the Istituto Nazionale di Alta Matematica “F. Severi”. This research project was partially supported by PRIN 2017 “Moduli Theory and Birational Classification”.
Funding
Open access funding provided by Università degli Studi di Trento within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Fontanari, C. Holomorphic differential forms on moduli spaces of stable curves. Geom Dedicata 218, 4 (2024). https://doi.org/10.1007/s10711-023-00851-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10711-023-00851-6