Complex hyperbolic orbifolds and hybrid lattices

Abstract

A class of complex hyperbolic lattices in PU(2, 1) called the Deligne-Mostow lattices has been reinterpreted by Hirzebruch (see [1, 10] and [24]) in terms of line arrangements. They use branched covers over a suitable blow up of the complete quadrilateral arrangement of lines in $\mathbb {P}^2$ to construct the complex hyperbolic surfaces over the orbifolds associated to the lattices. In [18] and [19], fundamental domains for these lattices have been built by Pasquinelli. Here we show how the fundamental domains can be interpreted in terms of line arrangements as above. This parallel is then applied in the following context. Wells in [25] shows that two of the Deligne-Mostow lattices in PU(2, 1) can be seen as hybrids of lattices in PU(1, 1). Here we show that he implicitly uses the line arrangement and we complete his analysis to all possible pairs of lines. In this way, we show that three more Deligne-Mostow lattices can be given as hybrids.

1 Introduction

The complex hyperbolic space ${{\textbf {H}}}^n_\mathbb {C}$ is the complex equivalent to the real hyperbolic space. It is defined starting from a Hermitian form of signature (n, 1) on $\mathbb {C}^{n+1}$ (which from now on will be chosen to be diagonal) and it contains the projectivisation of points of $\mathbb {C}^{n+1}$ which are negative for the product induced by the Hermitian form. Its isometry group is generated by the complex conjugation and the group PU(n, 1) of the projective matrices which preserve the Hermitian form.

An important problem in complex hyperbolic geometry is the study of lattices in PU(n, 1). To produce lattices, it is quite standard to use number theory to construct arithmetic lattices. Finding non-arithmetic lattices is an important and difficult problem.

In the real case, Gromov and Piatetski-Shapiro in [9] constructed infinitely many non-arithmetic lattices in any dimension, using a construction called hybridisation. It consists in getting a new non-arithmetic lattice by cutting and gluing pieces of arithmetic orbifolds along common totally geodesic hypersurfaces. In the complex case, the exact same construction is not possible, because there are no totally geodesic real hypersurfaces to cut and glue along. So far, very few examples of non-arithmetic complex hyperbolic lattices are known. In dimension 2, the only examples are the 9 commensurability classes coming from the Deligne-Mostow lattices (see below for more details) and the 13 examples from Deraux, Parker and Paupert in [6] and [7]. In dimension 3, one example comes from the Deligne-Mostow construction and a second example was constructed by Couwenberg, Heckman and Looijenga in [2] (recently identified as being the second example by Deraux in [4]). These are the only examples known in low dimension. The existence of non-arithmetic complex hyperbolic lattices is still an open question for $n \ge 4$.

The first examples of lattices were given by Picard using monodromy of hypergeometric functions. Those lattices were studied, among others, by Deligne and Mostow (see, for example, [12, 5]). We refer to the list in [5] as Deligne-Mostow lattices. In [23], Thurston gave a geometric interpretation of the same lattices. He started with cone metrics on a sphere with N prescribed cone angles and area one. He proved that the area is a Hermitian form of signature $(N-3,1)$ and that the metric completion of the moduli space of such cone metrics has a complex hyperbolic structure of finite volume. Using automorphisms of the sphere he then got an explicit list of cone singularities for which one can get a lattice. In this way, he produced a list of lattices containing the ones from the Deligne-Mostow initial construction. More precisely, he gives an integrality condition on the cone angles, which is equivalent to the $\Sigma$INT condition introduced by Mostow in [13], which generalised the INT condition from [5]. Note that the full list of Deligne-Mostow lattices also includes some lattices which do not satisfy the $\Sigma$INT condition, but are also discrete and which are commensurable to some of the lattices satisfying the integrality condition. These cases are not included in this work and more details about them can be found in [17].

Using Thurston’s work, in [18] and [19], Pasquinelli generalised a construction introduced by Parker in [16] to build explicit fundamental domain for all of the Deligne-Mostow lattices in PU(2, 1) with 3- and 2-fold symmetry respectively. This means that 3 (resp. 2) of the 5 cone points have the same cone angle. All of the Deligne-Mostow lattices in dimension 2 have either 2- or 3-fold symmetry.

These lattices also have a third interpretation, introduced by Hirzebruch (see, for example, [10]) for one case and generalised in [1] (see also [24]) for all of them. This construction is explained in Section 2.1. Hirzebruch considers four points in $\mathbb {P}^2$ such that no three of them lie on the same line. This configuration determines six lines passing through pairs of those four points. In this way one defines an arrangement of six lines in $\mathbb {P}^2$ with four points of triple intersection and three points of double intersection (see Figure 2). One then blows up the points of triple intersection in $\mathbb {P}^2$ and denote this space as $\widehat{\mathbb {P}^2}$. We will now have ten lines, the six lines in $\mathbb {P}^2$ mentioned above and four more lines, called exceptional divisors, coming from the blow up. One then defines a branched cover of $\widehat{\mathbb {P}^2}$, ramified along the ten lines with an appropriately chosen ramification index (see Table 1). A computation of the first and second Chern classes $c_1$ and $c_2$ of the branched cover shows that certain branched covers are complex hyperbolic surfaces. This is done using the equality case in Bogomolov-Miyaoka-Yau inequality, which guarantees that a compact complex surface of general type (which is our case), satisfying $c_1^2-3c_2=0$, is complex hyperbolic. In fact, one proves ( [1]) that the surface is the quotient of (a torsion-free subgroup of) a Deligne-Mostow lattice, denoted as (p, k) or $(p,k,p')$ for 3- or 2-fold symmetry (see Section 2.2 for more details).

This construction and the fact that the fundamental domains are very explicit allows us to understand the combinatorial structure of the fundamental domains in the blow up of $\mathbb {P}^2$. This is described in Section 2.3. In particular, we will prove the following description:

Theorem 1.1

Let $\Gamma$ be a Deligne-Mostow lattice. Then there exists a holomorphic map from ${{\textbf {H}}}^2_\mathbb {C}/\Gamma$ to $\widehat{\mathbb {P}^2}$ (with the arrangement of lines and branching data given in table 1) such that the fundamental domains in ${{\textbf {H}}}^2_\mathbb {C}$ constructed in [19] project to $\widehat{\mathbb {P}^2}$ satisfying the following conditions:

• 1. Its 0-skeleton projects to the intersection points of the arrangement of lines.

• 2. Its 1-skeleton projects to segments contained in the arrangement of lines.

• 3. The 2-facets which are contained in complex lines, project to triangles which are contained in the arrangement of lines.

In Section 4 we explain an application of this construction to a possible complex equivalent to the hybridisation of Gromov and Piatetski-Shapiro [9]. In the complex hyperbolic case, such a construction is impossible, since there are no totally geodesic real hypersurfaces along which to glue the lattices.

The first attempt of a complex hyperbolic equivalent of hybridisation was explored by Paupert following private correspondence with Hunt. Paupert showed in [20] that some hybrids of non-commensurable arithmetic groups are not discrete. In [25], Wells then modifies this definition into the one we use here (see Definition 4.1) and uses it to show that two of the Deligne-Mostow lattices in PU(2, 1) with 3-fold symmetry and of a certain type can be written as hybrids of two lattices in PU(1, 1), arithmetic and non-commensurable. One of the difficulties in his work is to choose a pair of totally geodesic hypersurfaces intersecting orthogonally.

Using line arrangements, we obtain natural candidates along which to hybridise. In this way, we show that

Theorem 1.2

The lattices (3, 8), (4, 6), (5, 4), (6, 4) and (3, 4, 4) are hybrids of two non-commensurable arithmetic lattices in PU(1, 1).

Note that the two cases (4, 6) and (5, 4) were already treated in [25]. Section 4 is devoted to proving this by a case by case analysis on all of the non-arithmetic lattices, searching for orthogonal complex lines, looking at their stabilisers and checking that these are triangle groups generating the lattice.

2 Background

2.1 Branched covers of line arrangements

In this section we will explain Hirzebruch’s construction (for a complete introduction to the subject see [1] and [24]). We consider an arrangement of lines in $\mathbb {P}^2$ and construct branched covers. For certain ramification orders these covers are complex hyperbolic ball quotients.

In order to verify if a given branched covering is complex hyperbolic one uses Miyaoka-Yau inequality. We state it in the simplest case when the surface is compact.

Theorem 2.1

(Miyaoka-Yau inequality) If Y is a compact surface of general type then $3c_2(Y)-c_1^2(Y)\ge 0$, with equality if and only if Y is complex hyperbolic.

When the surface is not compact a similar statement still holds. The surfaces we will construct in the rest of this section will always be of general type (see [24], Section 6.5).

In [10] Hirzebruch started the construction of branched covers and computed Chern numbers using the combinatorial data of the cover. In [1] (see also [24]) Hirzebruch’s construction is generalized. One defines ramification orders at the complex lines and supposing that a branched cover Y of $\widehat{\mathbb {P}^2}$ exists, one looks at ramification orders such that $3c_2(Y)-c_1^2(Y)$ satisfies the correct equality so that Y is a smooth complex hyperbolic surface. One then has to prove the existence of the appropriate branched covering (see [1, 11]).

Let $l_1,\cdots , l_k$ be a set of k distinct lines in $\mathbb {P}^2$. The intersection points with more than 2 lines are denoted by $p_j$ (called singular points) and the intersection points with only two lines by $q_i$. Blowing up the points $p_j$ we obtain a complex surface X with a configuration of divisors (with only normal crossings) which consists of the proper transforms of the lines, noted $D_i$, together with the exceptional divisors over the points $p_j$ (the copies of $\mathbb {P}^1$ obtained by the blow up process), noted $E_j$. For the exceptional divisors we have $E_j\cdot E_j=-1$ and for the proper transforms we have $D_i\cdot D_i=1-\sigma _i$, where $\sigma _i$ is the number of singular points of the arrangement on $D_i$. Note then that if $\sigma _i=2$ the proper transform $D_i$ is an exceptional divisor.

One constructs branched coverings $\pi : Y\rightarrow X$ with ramification $m_j$ along $E_j$ and $n_i$ along $D_i$. We will always consider branched covers of degree N satisfying the following conditions:

• 1. For each point $x\in D_i$ which is not contained in another divisor, $\pi ^{-1}(x)$ has $N/n_i$ points. Analogously, for each point $x\in E_j$ which is not contained in another divisor, $\pi ^{-1}(x)$ has $N/m_j$ points.

• 2. For each point $x\in D_i\cap D_j$ with $i \ne j$, $\pi ^{-1}(x)$ has $N/n_in_j$ points. Analogously, for each point $x \in D_i\cap E_j$, $\pi ^{-1}(x)$ has $N/n_im_j$ points.

In Tretkoff [24], the degree of the cover N remains implicit throughout the work. In fact, the only need for N is that we calculate $1/N (c_1^2-3c_2)$ and we show that it is equal 0, so the exact value of N is not relevant for our analysis.

The arrangement we consider here is the complete quadrilateral (also called $\overline{Ceva(1)}$ or Ceva(2)). It is obtained by taking four points in $\mathbb {P}^2$ in general position and by considering the lines connecting each pair. This will give six lines with three double intersections and four triple intersections exactly at the initial points. Together with the four blown-up points which are intersections of three lines we obtain the arrangement of 10 exceptional divisors. In suitable coordinates, we can take points

$$\begin{aligned} p_1&=[1:0:0],&p_2&=[0:1 :0],&p_3&=[0 :0 :1],&p_4&=[1 :1:1] \end{aligned}$$

and hence the six lines

$$\begin{aligned} l_{ij}&:z_i-z_j=0{} & {} \textit{ with }&i,j&\in \{0,1,2,3\},{} & {} i<j{} & {} \textit{ and }&z_0&=0. \end{aligned}$$

(1)

The line arrangement (see Figure 1) is then defined by

$$\begin{aligned} z_1z_2z_3(z_2-z_1)(z_3-z_2)(z_1-z_3)=0. \end{aligned}$$

Fig. 1

The complete quadrilateral arrangement

The ramification index at the exceptional divisors $E_j$ (which is the blow up of the point $p_j$) is set to be the value $m_j$ satisfying the following equation

$$\begin{aligned} \frac{2}{m_j}+\sum _{i=1}^{r}\frac{1}{n_i}={r_j}-2, \end{aligned}$$

(2)

where $r_j$ is the number of lines of the arrangement passing through the point $p_j$ and the sum is over these lines (in our case all the $r_j$ are equal to a same number $r=3$). This is a sufficient condition to guarantee that the Chern classes satisfy the equality in Miyaoka-Yau 2.1 (see [24], Section 5.5), when the ramification indices belong to the list of branched covers of ${\widehat{\mathbb {P}}}^2$ in Table 1.

Historically, the first case that was treated by Hirzebruch was that of $n_i=m_j=5$ (i.e. all the lines in the complete quadrilateral arrangement have same ramification order equal 5). In [10], he shows that the equality in Miyaoka-Yau is satisfied. This means that Y is a complex hyperbolic surface. In [26], Yamazaki and Yoshida determine the lattice $\Gamma$ in PU(2, 1) such that $\widehat{\mathbb {P}^2}$ is the quotient of ${{\textbf {H}}}^2_\mathbb {C}$ by $\Gamma$ and the surface Y is the quotient of ${{\textbf {H}}}^2_\mathbb {C}$ by the (torsion-free) subgroup $[\Gamma ,\Gamma ]$. In fact, this is a well known lattice, as we will see in Section 2.2.

The general case was then treated in [1]. In Table 1 (see [1] and [24]) we give a list of the ramification orders at the ten exceptional divisors which give complex hyperbolic manifolds . We also include a column stating the arithmeticity (A) or non-arithmeticity (NA) of the lattice and we identify to which Deligne-Mostow lattice it corresponds. The way we identify the Deligne-Mostow lattices is explained in Section 2.2 and one can recover the hypergeometric exponents from the ramification orders using Equation 4.

Table 1 Deligne-Mostow lattices and ramification orders

Note that some of the ramification orders are negative, or infinite. A negative order at a blown-up point corresponds to a branched cover where, over an exceptional divisor E, exceptional divisors appear again. To obtain a complex hyperbolic surface one needs to blow down these rational curves and singularities appear. The orbifold subgroup preserving E is a finite triangle group. In other words, instead of looking at branched covers of the blow up of $\mathbb {P}^2$, we are looking at branched covers of a blow down of $\widehat{\mathbb {P}^2}$. On the other hand, if the ramification order at E is infinite, E is covered by elliptic curves. Now, the complex hyperbolic surface of finite volume will be the complement of the elliptic curves, the branched covering being a compactification of the complex hyperbolic surface. In the following, we will always denote by $\widehat{P^2}$ the blow up of $\mathbb {P}^2$, after blowing down the lines with negative ramification index and removing the points which are images of the elliptic curves when the ramification index is infinite. This situation is explained in detail in Section 5.6 of [24].

Fig. 2

The ramification orders on the line arrangement for the 3- and 2-fold symmetry lattices

2.2 The Deligne-Mostow lattices

The branched covers Y over the orbifolds $\widehat{\mathbb {P}^2}$ constructed in section 2.1 actually correspond to quotients by (torsion free subgroups of) some well known lattices called the Deligne-Mostow lattices in PU(2, 1).

Those were introduced by Mostow and then studied by Deligne and Mostow in multiple papers in the 80’s using monodromy of hypergeometric functions. The 2-dimensional lattices are parametrised by 5 real numbers $\mu =(\mu _0, \dots \mu _4)$ with $0<\mu _i<1$ and $\sum \mu _i=2$. One thus obtains a finite list of values of $\mu$ for which one can obtain a lattice. The list grew longer with the subsequent works ([5, 12, 13]). The final list includes all ball quintuples satisfying an integrality condition called $\Sigma$INT, which generalises the condition INT introduced by Mostow in his first work. There are ten more lattices for which Mostow could not prove that the monodromy was not discrete and which were proven to be discrete later on, the so-called accidental lattices. They are commensurable to lattices satisfying the integrality condition and so they are usually not considered in the list of Deligne-Mostow lattices and we will do the same in this paper. For more details see [17]. The Deligne-Mostow lattices in PU(2, 1) are divided in two classes, the lattices with 2- and 3-fold symmetry. This means that respectively 2 and 3 of the 5 parameters have the same value. The condition on the sum and the symmetry means that the lattices with 2- (resp. 3-) fold symmetry can actually be identified using only 3 (resp. 2) parameters.

For the 3-fold symmetry case, up to permuting the weights, we assume that the three with the same value are $\mu _1=\mu _2=\mu _3$. This means that we can identify the lattice using two parameters p and k chosen in such a way that

$$\begin{aligned} \mu _0&=\frac{1}{2}+\frac{1}{p}-\frac{1}{k},&\mu _1=\mu _2=\mu _3&=\frac{1}{2} -\frac{1}{p},&\mu _4=\frac{2}{p}+\frac{1}{k}. \end{aligned}$$

Then we will denote the lattice determined by the parameters p and k as (p, k). Note that in the literature it is also sometimes denoted as $\Gamma _{(p,k)}$. We will then also be interested in the parameters

$$\begin{aligned} \frac{1}{l}&=\frac{1}{2}-\frac{1}{p}-\frac{1}{k},&\frac{1}{d}&=\frac{1}{2} -\frac{3}{p}. \end{aligned}$$

(3)

For the 2-fold symmetry case, again up to permuting the weights, we assume that the ones with the same values are $\mu _1=\mu _2$. This time we will need three parameters p, k and $p'$ chosen so that

$$\begin{aligned} \mu _0&=\frac{1}{2}+\frac{1}{p'}-\frac{1}{k},&\mu _1=\mu _2&=\frac{1}{2}-\frac{1}{p'},&\mu _3&=\frac{1}{2}+\frac{1}{p'}-\frac{1}{p},&\mu _4&=\frac{1}{p}+\frac{1}{k}. \end{aligned}$$

We will denote the lattice determined in this way as $(p,k,p')$. Again, in the literature, it is also sometimes denoted as $\Gamma _{(p,k,p')}$. To the lattice $(p,k,p')$ we will also associate the parameters

$$\begin{aligned} \frac{1}{l}&=\frac{1}{2}+\frac{1}{p'}-\frac{1}{p}-\frac{1}{k},&\frac{1}{k'}&=\frac{1}{p}+\frac{1}{k}-\frac{2}{p'}, \\ \frac{1}{l'}&=\frac{1}{2}-\frac{1}{p'}-\frac{1}{k},&\frac{1}{d}&=\frac{1}{2}-\frac{1}{p'}-\frac{1}{p}. \end{aligned}$$

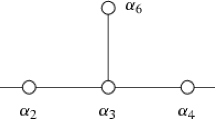
Tretkoff (see [24] Section 5.7, Tables 5.12 and 5.13) shows the list of the Deligne-Mostow lattices in PU(2, 1) is exactly the list that she obtains with the branched covers (see Section 2.1). This correspondence is given by using the parameters p, k, l, d for the 3-fold symmetry case and $p,p',k,k',l,l',d$ for the 2-fold symmetry case defined above as the ramification indices as in Figure 2. In fact, the relation between $\mu$ and the ramification indices is given by

$$\begin{aligned} \mu _\alpha +\mu _\beta =1- \frac{1}{n_{\alpha \beta }}, \end{aligned}$$

(4)

where $n_{\alpha \beta }$ is the weight associated to the line $l_{\alpha \beta }$, for $\alpha , \beta =0,1,2,3$, $\alpha <\beta$. At the blow up points, we have the associated weight $n_{*\beta }$, with Equation (4) still holding for $\beta =0,1,2,3$ and defining $\mu _*=\mu _4$ and obtained by $\sum \mu _i=2$.

Remark 2.2

Note that, following [13], the Deligne-Mostow lattices can be several possible groups $\Gamma _{\mu , \Sigma }$, where $\Sigma \subset S_5$ is a subgroup of the permutation of the elements of the ball 5-uple which are equal. In other words they are quotients of $\Gamma _{\mu ,\{e\}}$, which is the group associated to the ball 5-uple $\mu$ without keeping into account any symmetry given by equal elements of $\mu$. While these groups are commensurable, they are different groups. Here we will always consider $\Sigma$ to be $S_3 \subset S_5$ or $S_2 \subset S_5$ in the 3- and 2-fold symmetry cases respectively. Sometimes, the full symmetry group of $\mu$ is bigger. Our choice follows [19]. Tretkoff chooses instead the groups $\Gamma _{\mu , \{e\}}$. This is why the list in Table 1 only contains the lattices in the Deligne-Mostow list with p (for the 3-fold symmetry lattices) and $p'$ (for the 2-fold symmetry lattices) even. As mentioned by Tretkoff (see [24], Section 5.5, page 106), one could quotient the line arrangement by the symmetry given by the lines with same ramification orders, before taking the branched cover. The group of symmetries is (a subgroup, in the 2-fold symmetry case, of) ${\mathcal {S}}_3$, the permutations on three elements. This would allow to take odd values for the ramification orders and hence obtain the full list of Deligne-Mostow lattices satisfying the integrality condition. Below are the tables that completes the list of Deligne-Mostow lattices missing in Table 1 for the 3- and 2-fold symmetry cases. Together, the three tables form the complete list of Deligne-Mostow lattices.

(p, k)	p	k	l	d	A/NA
(3,4)	3	4	-12	-2	A
(3,5)	3	5	-30	-2	A
(3,6)	3	6	$\infty$	-2	A
(5,2)	5	2	-5	-10	A
(5,5/2)	5	5/2	-10	-10	A
(5,3)	5	3	-30	-10	A
(3,7)	3	7	42	-2	NA
(3,8)	3	8	24	-2	NA
(3,9)	3	9	18	-2	A
(3,10)	3	10	15	-2	NA
(3,12)	3	12	12	-2	A
(5,4)	5	4	20	-10	NA
(5,5)	5	5	10	-10	A
(7,2)	7	2	-7	14	A
(9,2)	9	2	-9	6	NA
(7,3)	7	3	42	14	NA
(9,3)	9	3	18	6	A
(7,7/2)	7	7/2	14	14	A
(9,9/2)	9	9/2	6	6	NA

Lattice $(p,k,p')$	p	k	$p'$	$k'$	l	$l'$	d	A/NA
(6,6,3)	6	6	3	-3	2	$\infty$	$\infty$	A
(10,10,5)	10	10	5	-5	2	5	5	A
(18,18,9)	18	18	9	-9	2	3	3	A
(4,4,3)	4	4	3	-6	3	-12	-12	A
(4,4,5)	4	4	5	10	5	20	20	NA
(3,6,3)	3	6	3	-6	3	$\infty$	-6	A
(2,4,3)	2	4	3	12	12	-12	-3	A
(2,3,3)	2	3	3	6	$\infty$	-6	-3	A

2.3 Fundamental domains

In [23], Thurston reinterpreted the Deligne-Mostow lattices in terms of moduli spaces of cone metrics on a sphere with a fixed number of cone singularities of a fixed angle and area 1. This space can be parametrised using $N-3$ projective coordinates in $\mathbb {C}$, where N is the number of cone points and forms a vector space on $\mathbb {C}$ (see below for an explicit description). Thurston shows that the area of the cone metric is a Hermitian form of signature $(N-3,1)$ on this moduli space and hence gives a complex hyperbolic structure on it. Moreover, he notices that this space is not complete, as one could take a sequence of cone metrics where two cone points get closer and closer. The limit, which is the cone metric where the two cone points have collapsed, is not in the moduli space, as the number of cone singularities was fixed, but it is in the metric completion. He considers the automorphisms of the sphere swapping cone points with same cone angles and those swapping twice cone points with different cone angles. The latter correspond to Dehn twists along a curve around the two cone points. In this way, Thurston finds a finite list of initial cone angles for which the metric completion of the moduli space is an orbifold, i.e. a quotient of complex hyperbolic space by a discrete group generated by the maps swapping cone points. Up to finite index, these groups are isomorphic to the ones from the Deligne-Mostow construction.

Here we will be interested in cone metrics with 5 cone points, which give a 2-dimensional complex hyperbolic structure. The 2- and 3-fold symmetry lattices come from cone metrics where respectively 2 and 3 of the 5 cone points have same angle.

For the lattice with 3-fold symmetry (p, k), denote $\frac{2\pi }{p}$ and $\frac{\pi }{k}$. Starting with the cone metric on the sphere with angles

$$\begin{aligned} (\pi -\theta +2\phi , \pi +\theta , \pi +\theta , \pi +\theta , 2\pi -2\theta -2\phi ), \end{aligned}$$

one can associate to it three complex coordinates in the way described in Section 4 of [18] and summarised below.

Denote the cone points as $v_*, v_0, v_1, v_2, v_3$, where $v_i$ for $i=1,2,3$ have the same cone angle. Now one can cut along geodesics from $v_0$ to $v_1, v_2, v_3$ and $v_*$ and flatten out the sphere in $\mathbb {C}$. We choose to place $v_*$ at the origin and choose coordinates ${{\textbf {t}}} = \begin{pmatrix} t_1 \\ t_2 \\ t_3 \end{pmatrix}\in \mathbb {C}^3$ so that the cone points in $\mathbb {C}$ are in the following positions:

$$\begin{aligned} v_*&=0, \nonumber \\ v_0&=-i\frac{\sin \theta }{\sin \left( \theta + \phi \right) } t_3 +i \frac{\sin \theta }{\sin \phi + \sin \left( \theta - \phi \right) } t_1, \nonumber \\ v_1&=i e^{-i \phi } t_1 -i \frac{\sin \theta }{\sin (\theta + \phi )}t_3, \nonumber \\ v_2&=-i e^{-i \phi } t_2+i \frac{ e^{-i \theta -i \phi } \sin \phi }{\sin (\theta +\phi )}t_3,\nonumber \\ v_3&=-i e^{-i \theta -i \phi }t_2+i \frac{ e^{-i \theta - i \phi } \sin \phi }{\sin (\theta +\phi )}t_3. \end{aligned}$$

(5)

See Figure 3 of [18] for the geometric meaning of the coordinates in terms of the cone points.

The area of the cone metric can then be written in terms of the coordinates as:

$$\begin{aligned} {{\,\textrm{Area}\,}}&=\frac{\sin \theta \sin \phi }{\sin (\theta + \phi )} |t_3|^2 -\sin \theta |t_2|^2-\frac{\sin \theta \sin \phi }{(\sin \phi + \sin (\theta - \phi ))}|t_1|^2 \nonumber \\&={{\textbf {t}}}^* H {{\textbf {t}}}, \end{aligned}$$

(6)

where H is the matrix of signature (1, 2) given by

$$\begin{aligned} H=\sin \theta \begin{bmatrix} -\frac{\sin \phi }{\sin \phi +\sin (\theta -\phi )}&{} 0 &{} 0 \\ 0 &{} -1 &{} 0 \\ 0 &{} 0 &{} \frac{\sin \phi }{\sin (\theta +\phi )} \end{bmatrix}. \end{aligned}$$

(7)

By asking for the area to be positive and considering the cone metric only up to rescaling, one can show that the space of configurations has a complex hyperbolic structure given by

$$\begin{aligned} {{\textbf {H}}}^2_\mathbb {C}=\mathbb {P}({\{ {{\textbf {t}}} \in \mathbb {C}^3 : \langle {{\textbf {t}}}, {{\textbf {t}}} \rangle = {{\textbf {t}}}^* H {{\textbf {t}}} > 0 \}}). \end{aligned}$$

Now, following Section 5 of [18], we consider the automorphisms of the sphere $R_1$ (swapping cone points $v_2$ and $v_3$), $R_2$ (swapping cone points $v_1$ and $v_2$) and $A_1$ (swapping twice cone points $v_0$ and $v_1$). One can then show that the Deligne-Mostow group (p, k) is isomprphic, up to finite index, to the group $\Gamma$ generated by $R_1$, $R_2$ and $A_1$ and that the space of cone metrics on the sphere can be identified to ${{\textbf {H}}}^2_\mathbb {C}/ \Gamma$. This is done by describing the quotient as the fundamental domain

$$\begin{aligned} D= \left\{ \begin{bmatrix} t_1 \\ t_2 \\ 1 \end{bmatrix}=P\left( \begin{bmatrix} s_1 \\ s_2 \\ 1 \end{bmatrix}\right) :\begin{array}{l l} \arg (t_1) \in (-\phi ,0), &{} \arg (t_2) \in (0,\theta ),\\ \arg (s_1) \in (0,\phi ), &{} \arg (s_2) \in (0,\theta ) \end{array} \right\} \end{aligned}$$

(8)

modulo the identifications given by the side pairings $R_1$, $R_2$, $P=R_1 R_2$, $J=R_1 R_2 A_1$. Section 8 of [18] gives a presentation for $\Gamma$ as

$$\begin{aligned} \Gamma =\left\langle J,P,R_1,R_2 :\begin{array}{l l} J^3=P^{3d}=R_1^p=R_2^p=(P^{-1}J)^k=(R_2R_1J)^l={{\,\textrm{Id}\,}}, \\ R_2=P R_1P^{-1}=JR_1J^{-1}, \ P=R_1R_2 \end{array} \right\rangle , \end{aligned}$$

(9)

Part of the strategy to build the fundamental domain is to look at the subspaces where two cone points collapse to a single one. These are complex lines in ${{\textbf {H}}}^2_\mathbb {C}$, each intersecting the fundamental polyhedron only in a triangular ridge on its boundary. Moreover, if $T_{ij}$ is the map swapping the cone points $v_i$ and $v_j$, then $T_{ij}$ is a complex reflection with mirror the complex line $L_{ij}$ where $v_i$ and $v_j$ collapse.

Using the notation above for the group generators, the complex reflections $T_{ij}$ at each of the complex lines considered are

$L_{ij}$	$T_{ij}$	order	$L_{ij}$	$T_{ij}$	order	$L_{ij}$	$T_{ij}$	order
12	$R_2$	p	01	$A_1$	k	*1	$R_2R_1J$	l
13	$R_1R_2R_1^{-1}$	p	02	$R_2A_1R_2^{-1}$	k	*2	$R_1JR_2$	l
23	$R_1$	p	03	$R_1R_2A_1R_2^{-1}R_1^{-1}$	k	*3	$JR_2R_1$	l
0	$P^3$	d

The reader looking for more details on the origin of this notation and the connection with hypergeometric functions, could look at yet another of Mostow’s papers, namely [14].

Now, for some of the lattices, the parameters l and d are negative or infinite, so what we explained so far seems to not make sense any more. This is because the combinatorial structure of the fundamental polyhedra depends on the parameters p, k, l, d from Section 2.2, which are the ramification orders at the $l_{ij}$ and (when >0) the order of the complex reflection $T_{ij}$ with mirror $L_{ij}$. When the parameter associated to one of these complex reflection is negative (resp. infinite), the (one or more) 2-facets corresponding to the parameter are substituted with a point (resp. a point on the boundary) as in Figure 3. More details about this can be found in [18], Section 9. The facets collapsing are the triangular ridges contained in the line $L_{ij}$. This is the exact equivalent of the behaviour described in Section 2.1, when the ramification orders are negative or infinite.

Fig. 3

The intersection of the line $L_{ij}$ with the polyhedron, when the $n_{ij}$ associated is positive (on the left) and when it is negative or infinite (on the right)

Remark 2.3

Note that whenever only two of the complex lines $L_{ij}$ meet at a point, they are orthogonal and if the intersection is a vertex of the polyhedron, it is not obtained by collapsing a facet. On the other hand, when a vertex is obtained by the collapsing of a ridge, it is at the intersection of three of the complex lines $L_{ij}$ which are then not orthogonal any more.

The sides of the polyhedra described in [18] all have (before collapsing if necessary) the same combinatorial structure. Moreover, they are all contained in bisectors, which are hypersurfaces equidistant from two given points (see [8]). A bisector is determined by its spine, which is the equidistant geodesic between the points in the complex disc containing both points. Bisectors are foliated in two ways by totally geodesic subspaces. First of all, by complex discs (called slices) orthogonal to the spine. Moreover, the union of totally real totally geodesic discs containing the spine (called meridians) forms the bisector. The structure of a side is given in Figure 5 where each two dimensional facet is explicitly contained in either a slice or a meridian except for the hexagonal facet which is in the intersection of three bisectors (called a Giraud disc).

Remark 2.4

Remark 2.2 can also be interpreted in terms of the $T_{ij}$. When building the fundamental domains, we consider the 3- and 2- fold symmetry, so we quotient $\Gamma _{\mu , \{e\}}$ by $S_3$ and $S_2$. In terms of the cone points, this is equivalent to say that instead of swapping two cone points with the same cone angle, we ignore that the cone angle is the same and we swap them twice (like we already do with cone points with different come angles). This is equivalent to taking the map $T_{ij}^2$ and it is what Tretkoff considers in general. Since, if p/2 is the order of $T_{ij}^2$, then p is the order of $T_{ij}$, quotienting by the symmetry allows to consider the cases when p is odd.

The same procedure can be done for the 2-fold symmetry case. How to associate coordinates to a cone metric can be found in Section 3A of [19], the automorphisms of the sphere considered are in Section 3B and the polyhedron is described in Section 4B. A presentation for the group $(p,k,p')$ is then given by

$$\begin{aligned} \Gamma =\left\langle \begin{array}{l l} K,Q,B_1, \\ B_2,R_0,A_0 \end{array} :\begin{array}{l l l l} B_1^p=B_2^p=\mathbb {R}_0^{p'}=A_0^{k'}=(Q^{-1}K)^k= (R_0K)^l={{\,\textrm{Id}\,}}, \\ (A_0 B_2 B_1)^{l'}=Q^{2d}={{\,\textrm{Id}\,}}, \quad Q=B_1R_0=R_0B_2=B_2^{-1}QB_1, \\ R_0^{-1}A_0R_0=A_0=K^{-2}, \quad B_2 K=K B_1 \end{array} \right\rangle , \end{aligned}$$

(10)

Fig. 4

The line arrangement with the corresponding vertices of the polyhedron

3 Line arrangements and fundamental domains

The main result of this section is that the line arrangement from the previous section and the fundamental domains are strongly related. We will explain the details only in the 3-fold symmetry case, as in the 2-fold symmetry case the construction works in the same way. The idea to keep in mind is that the complex lines $L_{ij}$ obtained by collapsing two cone points combinatorially intersect in the same way as the configuration of lines $l_{ij}$ defined by $z_i=z_j$ in $\widehat{\mathbb {P}^2}$, which form the complete quadrilateral arrangement in Figure 4. If $L_{ij}$ is the mirror of a certain complex reflection $T_{ij}$, then the ramification order at the corresponding $l_{ij}$ is the order of $T_{ij}$. Each vertex of the polyhedron is at the intersection of two of the ten complex lines.

More precisely:

Theorem 3.1

Let $\Gamma$ be a Deligne-Mostow lattice. Then there exists a holomorphic map from ${{\textbf {H}}}^2_\mathbb {C}/\Gamma$ to $\widehat{\mathbb {P}^2}$ (with the arrangement of lines and branching data given in table 1) such that the fundamental domains in ${{\textbf {H}}}^2_\mathbb {C}$ constructed in [19] project to $\widehat{\mathbb {P}^2}$ satisfying the following conditions:

• 1. Its 0-skeleton projects to the intersection points of the arrangement of lines.

• 2. Its 1-skeleton projects to segments contained in the arrangement of lines.

• 3. The 2-facets which are contained in complex lines, project to triangles which are contained in the arrangement of lines.

Proof of Theorem 3.1

Let $Q_5$ be the quotient of $(\mathbb {P}^1)^5$ by the diagonal action of ${{\,\textrm{Aut}\,}}(\mathbb {P}^1)$ in the sense of geometric invariant theory (see, for example [5] and [3]). Then one can consider the map

$$\begin{aligned} Q_5&\rightarrow \widehat{\mathbb {P}^2} \nonumber \\ (v_0,v_1,v_2,v_3,v_*)&\mapsto \left[ \frac{\det (v_1,v_0)}{\det (v_1,v_*)} : \frac{\det (v_2,v_0)}{\det (v_2,v_*)} : \frac{\det (v_3,v_0)}{\det (v_3,v_*)} \right] \end{aligned}$$

(11)

where $(v_1, \cdots , v_5)$ denote non-zero vectors in $\mathbb {C}^2$ representing points in $\mathbb {P}^1$. This map is an isomorphism (see again [3]).

By Thurston’s work, we can see ${{\textbf {H}}}^2_\mathbb {C}/\Gamma$ as the set of certain configurations of flat cone metrics on a sphere as decribed in Section 2.3. In other words, we can see it as the set of possible configurations of points on the sphere, respecting the restrictions given by the cone angles.

This means that we can look at the map in (11) and see how it acts on the cone points. By identifying ${{\textbf {H}}}^2_\mathbb {C}/\Gamma$ to $Q_5$ as described in Section 2.3, we look at the map

$$\begin{aligned} {{\textbf {H}}}^2_\mathbb {C}/\Gamma&\rightarrow \widehat{\mathbb {P}^2} \nonumber \\ (v_0,v_1,v_2,v_3,v_*)&\mapsto \left[ \frac{v_1-v_0}{v_1-v_*} : \frac{v_2-v_0}{v_2-v_*} : \frac{v_3-v_0}{v_3-v_*} \right] \end{aligned}$$

(12)

Recall that the lines of the line arrangement are given in Equation (1). Whenever the cone points $v_i$ are distinct, the image of the configuration is a point $[z_1 : z_2 : z_3 ]\in \mathbb {P}^2$, outside of the line arrangement. The image of the complex line $L_{ij}$ for $i \ne j$ and $i,j \in \{1,2,3\}$ has coordinates $z_i=z_j$ and hence is the line $l_{ij}$ in the arrangement. Similarly, the line $L_{i0}$ for $i \in \{1,2,3\}$ is defined by $v_i=v_0$ and hence its image satisfies $z_i=0$. Recalling from Equation (1) that we used the convention $z_0=0$, we have again that the image of $L_{i0}$ for $i \in \{1,2,3\}$ is the line $l_{i0}$ in the arrangement. The same can be seen for $L_{*i}$ for $i \in \{0,1,2,3\}$ by taking coordinates of the blow up (see, for example, Appendix A.1 of [3]). Here let us just remark that the line $L_*i$ projects in $\mathbb {P}^2$ to one of the points of triple intersection of the arrangement.

Let us now look at the 0-skeleton, which is formed by the vertices. In the non-degenerate configuration, where all the ramification orders are positive and finite, each vertex is at the intersection of two complex lines. When we blow down some complex lines, a ridge collapses to a vertex (see Figure 3). In the line arrangement, this vertex will be at the intersection of three complex lines now (the blown down point). This is descibed in Remark 2.3.

The vertices of the fundamental polyhedron are exactly at the intersection of two of these complex lines, so we can “see” them inside the line arrangement as being at each (double) intersection of two lines. Every ridge contained in a complex line is a triangular 2-facet of the fundamental domain and indeed every line in the arrangement intersects exactly three other lines in three distinct points.

Now to find all the sides of the polyhedron, one proceeds as follows. First, we need to find a pair of complex lines giving the top and bottom triangular ridges. To do this, choose your favourite exceptional divisor, i.e. a complex line $L_{*i}$ in the arrangement in $\widehat{\mathbb {P}^2}$. Now look at all the lines of the complete quadrilateral arrangement disjoint from it. They will be $L_{ij}$ for $j\in \{0,1,2,3\}$ and $j \ne i$.

Recalling Remarks 2.2 and 2.4 (see [24], Section 5.5, page 106) and comparing Figures 2 and 4, there is a 3- or 2-fold symmetry of the line arrangement which identifies lines $l_{12}$, $l_{13}$ and $l_{23}$ and also $l_{01}$, $l_{02}$ and $l_{03}$.

Similarly the three lines $L_{13}, L_{23}$ and $L_{12}$ are identified by the order three symmetry of the cone points. In other words, since the three lines $L_{ij}$ with $i, j \in \{1,2,3\}$ are identified by the symmetry, we will need only two of them (identified by a side pairing map) in the boundary of a fundamental domain. Similarly, the lines $L_{0i}$ for $i \in \{1,2,3\}$ are identified. Because of this, the intersection of $L_{13}$ with $L_{02}$ is outside the fundamental domain and hence does not correspond to a vertex.

We hence do not consider $L_{13}$ and $L_{02}$, noting that exactly one of them appears for each $L_{*i}$. This gives 8 pairs of complex lines. Each complex line contains three vertices and for each pair $L_{*i}$ and $L_{ij}$ as above, there will be two vertices (one in each line) that belong to a third line $L_{kl}$ with $k,l \ne i,j$. Note that since i, j, k, l all belong to $\{0,1,2,3\}$ and are distinct, the line $L_{kl}$ is uniquely determined by $L_{*i}$ and $L_{ij}$. The other two vertices on $L_{*i}$ are determined by the intersections with $L_{jk}$ and $L_{jl}$. Similarly, the other two vertices on $L_{ij}$ are determined by the intersections with $L_{*k}$ and $L_{*l}$. Then the last two edges in the side are the ones pairwise connecting these four vertices (one on each line $L_{*i}$ and $L_{ij}$) passing through the lines $L_{jk}$ and $L_{*l}$ in one case and through the lines $L_{jl}$ and $L_{*k}$ in the other case. An example is shown in Figure 5. $\square$

Fig. 5

The combinatorial structure of a side and the side B(P), as seen inside the line arrangement

4 Complex hybridisation

One of the main open problems in complex hyperbolic geometry is the relation between lattices and arithmeticity. In fact, as explained in the Introduction, while arithmetic groups are always lattices, few examples of non-arithmetic lattices are known and only in dimension 2 and 3. In dimension 4 or higher, existence of non-arithmetic lattices is still an open question. The hope for the existence comes from the parallel with the real hyperbolic space, in which infinitely many non-arithmetic lattices exist in any dimension. This has been proved in [9] by Gromov and Piatetski-Shapiro using a technique called hybridisation. It consists in taking two arithmetic lattices of dimension n and producing a new lattice by “glueing” along a hypersurface. When the two lattices are non-commensurable, the resulting lattice is shown to be non-arithmetic.

Since in complex hyperbolic space there are no totally geodesic real hypersurfaces, an immediate analogue of the hybridisation construction is not possible. Nonetheless, possible analogues have been explored first by Hunt, Paupert (see [20]) and Wells (see [25]). Here we will use Wells’ definition, which is the following.

Definition 4.1

Let $\Gamma _1, \Gamma _2 <PU(n,1)$ be lattices. The hybrid of $\Gamma _1$ and $\Gamma _2$ is the group $H=H(\Gamma _1,\Gamma _2)=\langle \Lambda _1, \Lambda _2 \rangle$ generated by $\Lambda _1$ and $\Lambda _2$, where $\Lambda _1, \Lambda _2 <PU(n+1,1)$ are two discrete subgroups which stabilise totally geodesic (complex) hypersurfaces $\Sigma _1$ and $\Sigma _2$ which are orthogonal. Moreover, we require that $\Gamma _i=\Lambda _i |_{\Sigma _i}$ and that the intersection $\Lambda _1 \cap \Lambda _2< PU(n-1,1)$ is a lattice.

Here the notation $\Gamma _i=\Lambda _i |_{\Sigma _i}<PU(n,1)$ means that $\Gamma _i$ is the restriction of $\Lambda _i \subset {{\,\textrm{Stab}\,}}\Sigma _i$ acting on ${\Sigma _i}$.

Note that when $n=2$, as in the case we are dealing with in this work, the last condition is empty.

In his paper, Wells proves that two of the non-arithmetic Deligne-Mostow lattices can be given as hybrids (in this sense) of two non-commensurable arithmetic lattices in PU(1, 1).

We now want to use the relation between Hizebruch’s construction and the fundamental domains from Section 2.3 to prove that the procedure from Wells can be extended to more of the 2-dimensional Deligne-Mostow lattices. In fact, Wells did not have explicit fundamental domains available and so there was the extra difficulty of finding suitable orthogonal subspaces along which to hybridise. The fundamental domains suggest which pairs of complex lines are orthogonal and using Hirzebruch’s construction we will show that it is immediate to see which are the triangle groups associated to them. We will use the parameters (p, k) and $(p,k,p')$ as in Section 2.2 to describe the lattices.

There are 9 commensurability classes in the 2-dimensional Deligne-Mostow lattices. Of these, two have been treated by Wells. They are (4, 6) (commensurable to (4, 4, 6)), and (5, 4). Here we will show that more of them can be given as hybrids. Moreover, no other of the Deligne-Mostow lattices can be given as a hybrid of the groups related to a line of our arrangement.

Theorem 4.2

The lattices (3, 8), (4, 6), (5, 4), (6, 4) and (3, 4, 4) are hybrids of two non-commensurable arithmetic lattices in PU(1, 1).

The strategy of the proof is the following. First, we will look at each complex line corresponding to a line in the arrangement by Theorem 3.1 and identify which triangle group is its stabiliser. Since Takeuchi [22] classified all arithmetic triangle groups in PU(1, 1), we record arithmeticity and commensurability class of each triangle group. This information is conveniently summarised in the table page 418 of [15]. Then we inspect in which case we can find two non-commensurable arithmetic lattices associated to two intersecting lines. Finally, we will show that the two stabilisers generate the whole group.

4.1 Proof of Theorem 4.2

We will denote $\Delta (a,b,c)$ as the triangle group in PU(1, 1) generated by two rotations of order a and b such that the product is of order c.

The first step is to use the results in [18] and [19] to write down the stabilisers of the complex lines that contain ridges of D. They are recorded in the following tables.

Table 2 The triangle groups stabilising the complex lines for 3-fold symmetry lattices

Table 3 The triangle groups stabilising the complex lines for 2-fold symmetry lattices

Note that we are only considering the triangle groups up to commensurability. In particular, when we have a triangle group with two equal angles, we can reduce the triangle to its half. This means to consider another triangle group commensurable to the first one. Then the order at the apex of the triangle doubles and from $\Delta (i,i,j)$ we get $\Delta (2,i,2j)$.

Moreover, we remark that one can “read off” the triangle groups from the line arrangement too. In fact, the triangle group that is the stabiliser of a line is $\Delta (a,b,c)$ where a, b and c are the ramification orders of the three lines of the arrangement intersecting the line of the arrangement corresponding to the given complex line.

Now for each non-arithmetic lattice, we look at the triangle group associated to each line. We then compare them to the table page 418 of [15], which gives arithmeticity and commensurability classes of triangle groups. In particular, one can find there 19 commensurability classes of arithmetic lattices. The following table records the triangle groups associated to each non-arithmetic lattice and whether it is non-arithmetic (NA) or arithmetic (A), in which case it also records which of the 19 commensurability classes it belongs to. When the corresponding parameter is negative or infinite, the facet collapse to a point and hence we do not find any triangle group corresponding to it. This is denoted in the table as –.

Table 4 The triangle groups associated to 3-fold symmetry NA lattices

Table 5 The triangle groups associated to the 2-fold symmetry NA lattices

By inspection of the 3-fold symmetry table, one can see that (3,8), (4,6), (5,4), (6,4) and (8,3) contain two non-commensurable arithmetic lattices coming from two orthogonal lines. Similarly, for the 2-fold symmetry table, it is the case for (4,4,6) and (3,4,4). Now, note that (4,4,6) is commensurable to (4,6) and (8,3) is commensurable to (3,8), which is why we omitted them in the theorem. This just means that we can see some of the lattices as hybrids in several different ways. Note also that whenever we have exactly two complex lines in D which intersect, they are orthogonal. This follows by calculating the hermitian product on the equations for the lines in [18].

The final step is to show that the triangle groups generate the whole group. The next section shows the step by step calculations for each of the groups in the theorem and the final step to the proof.

4.1.1 3-fold symmetry cases

Let us look at the orthogonal complex lines $L_{*3}$ and $L_{01}$. Note that the lattices (3, 8) and (6, 4) both belong to the lattices of second type, so the lines $L_{*i}$ for $i=1,2,3$ do not collapse (i.e. blow down), while the line $L_{*0}$ collapses to a point inside ${{\textbf {H}}}^2_\mathbb {C}$ in the first case and on the boundary in the second case. This means that we can always look at the two lines $L_{*3}$ and $L_{01}$.

The subgroups preserving a line $L_{ij}$ is generated by the complex reflections whose mirrors intersect $L_{ij}$. Moreover, two of these are enough, because the other will be a combination of these. So the stabiliser of $L_{*3}$ is generated by, for example, $J^{-1}P$ and $R_2$, which have $L_{01}$ and $L_{12}$ as mirrors, respectively. The stabiliser of $L_{01}$ is now generated by $JR_2R_1$ and $R_1$, which have $L_{*3}$ and $L_{23}$ as mirrors, respectively. For (3, 8), they are triangle groups $\Delta (2,3,24)$ and $\Delta (2,3,8)$, which are both arithmetic and non-commensurable (cfr table page 418 of [15]). For (6, 4) they are $\Delta (2,6,12)$ and $\Delta (2,4,6)$, which are again both arithmetic and non-commensurable.

Let us hence look at the hybrid group of these two $\Gamma =\langle J^{-1}P,R_2,JR_2R_1, R_1 \rangle < \Gamma _{(p,k)}$. By simple manipulations of the presentation of $\Gamma _{(p,k)}$ given in Equation (9), we can see that $R_1$, $R_2$ and J are enough to generate the full group. But now $J= J^{-1}PR_2^{-1}R_1^{-1}$ and hence the two groups are the same.

This means that the two non-arithmetic Deligne-Mostow lattices with 3-fold symmetry in PU(2, 1), (3, 8) and (6, 4) can be given as hybrids of two non-commensurable arithmetic lattices in PU(1, 1).

4.1.2 2-fold symmetry case

In the 2-fold symmetry case we have more choices of orthogonal lines, since the lines arrangement has fewer symmetries. Here we will choose $L_{03}$ and $L_{02}$, although multiple other choices would give similar hybridisation results. Recall that a presentation for the 2-fold symmetry groups is given in Equation (10).

The lines intersecting $L_{01}$ are $L_{*3}$, $L_{23}$ and $L_{*2}$, which have ramification orders l, $p'/2$ and l respectively. The stabiliser of $L_{01}$ is hence a triangle group $\Delta (2,p',l)$. Now $L_{*3}$ is the mirror of $R_0K$ and $L_{23}$ is the mirror of $R_0$.

Similarly, the lines intersecting $L_{*3}$ are $L_{01}$, $L_{12}$ and $L_{02}$, which have ramification orders k, p and $k'$ respectively. The stabiliser of $L_{*3}$ is hence a triangle group $\Delta (k,p,k')$. Now $L_{01}$ is the mirror of $Q^{-1}K=A_1$ and $L_{12}$ is the mirror of $B_2$.

Let us now look at $\Gamma =\langle R_0K, R_0, A_1, B_2 \rangle <\Gamma _{(p,k,p')}$. We want to show that $\Gamma$ is the full $\Gamma _{(p,k,p')}$. Now, using the presentation in [19], we can see that $\Gamma _{(p,k,p')}$ is generated by $B_1$, $R_0$ and $A_1$, so all we need is to express $B_1$ in terms of the generators of $\Gamma _{(p,k,p')}$. But from the presentation we can see that $B_1=R_0B_2R_0^{-1}$ and hence we are done.

Now for the lattice (4, 4, 6), we have that $\Delta (2,p',l)=\Delta (2,6,6)$ and $\Delta (k,p,k')=\Delta (4,4,6)$ are both arithmetic and non-commensurable. Similarly, for the lattice (3, 4, 4), we have that $\Delta (2,p',l)=\Delta (2,4,6)$ and $\Delta (k,p,k')=\Delta (4,3,12)$ are both arithmetic and non-commensurable. This proves the theorem.

Note that (4, 4, 6) is commensurable to (4, 6) so this just gives another way to see it as a hybrid.

4.2 Relation with Wells’ cases

In [25], Wells looks at subspaces $e_i^\perp$ and $v_{ijk}^\perp$, which are the mirrors of $R_i$ and $J^{\pm }R_jR_k$, with $k \equiv i \pm 1 (\hbox {mod }3)$, respectively. Note that his notation for the generators is standard and it is the same used in [18]. This means that we can use the presentation given with the fundamental domain to determine which ridges (2-facets, hence which complex lines in the arrangement) correspond to Wells’ subspaces.

He chooses subspaces $v_{312}^\perp$ and $v_{321}^\perp$ as orthogonal complex lines along which to hybridise. The first one is the mirror of $J^{-1}R_1R_2=J^{-1}P$, which is the cycle transformation of the ridge F(P, J), which is contained in $L_{01}$. The second one is the mirror of $JR_2R_1$, which is the cycle transformation associated to $F(R_1,J^{-1})$, which is contained in $L_{*3}$.

Looking at Figure 2, first we remark that the values considered are only for $p<6$, so $d<0$ and hence $L_{*0}$ is blown down to a single point. Moreover, $L_{*3}$ and $L_{01}$ are indeed orthogonal by Remark 2.3. Recall that if we look at the stabiliser of the complex line corresponding by Theorem 3.1 to a line in the arrangement, we are looking at the triangle group $\Delta (i,j,k)$, where i, j, k are the ramification orders of the three complex lines intersecting the initial line. So, (up to commensurability) the stabiliser of $v_{312}^\perp$ and hence $L_{01}$ will be $\Delta (2,p,l)$ because $L_{01}$ intersects $L_{*3}$ and $L_{*2}$, which both have ramification order l, and also $L_{23}$, which has ramification order p/2. Similarly, the stabiliser of $v_{321}^\perp$ and hence $L_{*3}$ will be $\Delta (2,p,k)$. These are indeed the values given by Wells in Tables 2, 3 and 4.

4.3 Triangle groups and ball 5-uples

There is another way to recover these triangle groups starting from the ball 5-tuples. Following Deligne and Mostow in [5], one can modify the ball 5-tuple $\mu$ by replacing two of the exponents $\mu _j$ and $\mu _k$ by the sum $\mu _j+\mu _k$, Then one can associate a triangle group $\Delta (a,b,c)$ to each ball 4-uple $(\mu _1',\mu _2',\mu _3', \mu _4')$ using the following formulae:

$$\begin{aligned} 1-\frac{1}{a}&=\mu _1'+\mu _2',&1-\frac{1}{b}&=\mu _1'+\mu _3',&1-\frac{1}{c}&=\mu _2'+\mu _3'.&\end{aligned}$$

Now, following Section 2.2, we can write the ball 5-tuple as

$$\begin{aligned} \mu =(\mu _0,\mu _1,\mu _2,\mu _3,\mu _*)= \left( \frac{1}{2}+\frac{1}{p}-\frac{1}{k}, \frac{1}{2}-\frac{1}{p}, \frac{1}{2}-\frac{1}{p}, \frac{1}{2}-\frac{1}{p}, \frac{2}{p}+\frac{1}{k}\right) . \end{aligned}$$

Then the ball 4-uples and the triangle groups obtained by this procedure are listed in the following table.

$\mu _j$, $\mu _k$	$\mu '$	$\Delta (a,b,c)$
01/02/03	$\left( 1-\frac{1}{k}, \frac{1}{2}-\frac{1}{p}, \frac{1}{2}-\frac{1}{p}, \frac{2}{p}+\frac{1}{k} \right)$	$\Delta (p/2,l,l)=\Delta (2,p,l)$
1/*2/*3	$\left( \frac{1}{2}+\frac{1}{p}-\frac{1}{k}, \frac{1}{2}-\frac{1}{p}, \frac{1}{2}-\frac{1}{p}, \frac{1}{2}+\frac{1}{p}+\frac{1}{k} \right)$	$\Delta (p/2,k,k)=\Delta (2,p,k)$
0	$\left( \frac{1}{2}-\frac{1}{p}, \frac{1}{2}-\frac{1}{p}, \frac{1}{2}-\frac{1}{p}, \frac{1}{2}+\frac{3}{p} \right)$	$\Delta (p/2,p/2,p/2)=\Delta (2,p,p/2)$
12/13/23	$\left( \frac{1}{2}+\frac{1}{p}-\frac{1}{k}, \frac{1}{2}-\frac{1}{p}, 1-\frac{2}{p}, \frac{2}{p}+\frac{1}{k} \right)$	$\Delta (k,d,l)$