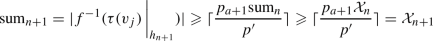Abstract
We characterise when there exists a quasiisometric embedding between two solvable Baumslag–Solitar groups. This extends the work of Farb and Mosher on quasiisometries between the same groups. More generally, we characterise when there can exist a quasiisometric embedding between two treebolic spaces. This allows us to determine when two treebolic spaces are quasiisometric, confirming a conjecture of Woess. The question of whether there exists a quasiisometric embedding between two treebolic spaces turns out to be equivalent to the question of whether there exists a bilipschitz embedding between two symbolic Cantor sets, which in turn is equivalent to the question of whether there exists a rough isometric embedding between two regular rooted trees. Hence we answer all three of these questions simultaneously. It turns out that the existence of such embeddings is completely determined by the boundedness of an intriguing family of integer sequences.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In his speech to the ICM in 1983 [1], Gromov proposed the vast project of classifying finitely generated groups up to quasiisometry. His line of thought leads to the question of whether an algebraic property P of finitely generated groups can be characterised by some other geometric (i.e. quasiisometry invariant) property. If this is the case then we say that the class of groups satisfying P is quasiisometrically rigid. It suggests that the algebraic property P in fact corresponds to some geometric feature of the groups. For example, Gromov [2] proved that virtual nilpotency is invariant under quasiisometries and corresponds to the geometric property of polynomial growth. In contrast, Erschler [3] proved that virtual solvability is not geometric; there exist groups G and H where G is solvable and H is not virtually solvable such that G and H have a common Cayley graph. Nevertheless, we can limit our focus to subclasses of solvable groups. Farb and Mosher [4] proved that the solvable Baumslag–Solitar groups BS(1, m) exhibit a fascinating rigidity; BS(1, m) is quasiisometric to BS(1, n) if and only if m, n are powers of a common integer (which holds if and only if they are commensurable). This paper generalises this result in two ways. First, the result is extended to the treebolic spaces HT(p, q); in their paper, Farb and Mosher utilise the fact that BS(1, m) acts cocompactly and isometrically on HT(m, m). Treebolic spaces were introduced by Bendikov, Saloff–Coste, Salvatori and Woess in [5] and they developed the theory further in [6, 7]. We characterise when treebolic spaces are quasiisometric (Theorem 2), confirming a conjecture of Woess [8]. Second, we study a stronger notion of rigidity by providing necessary and sufficient conditions for the existence of a quasiisometric embedding of one treebolic space into another (Theorem 1). In particular, we prove that BS(1, m) quasiisometrically embeds into BS(1, n) if and only if m, n are powers of a common integer.
1.1 Statement of results
Let \(p \in {{\mathbb {N}}}_{\geqslant 2}\) and let \(q > 1\). We are primarily interested in three classes of metric space: regular rooted trees R(p, q), symbolic Cantor sets \({{\mathbb {Z}}}(p,q)\) and treebolic spaces HT(p, q). These can be described as follows.
-
Let R(p, q) denote the rooted metric tree with all edges of length \(\log (q)\) and with valency \(p+1\) at every vertex apart from the basepoint which has valency p.
-
Let \({{\mathbb {Z}}}(p,q) = \{ 0, 1, \ldots , p-1 \}^{{{\mathbb {N}}}}\) be the space of infinite sequences on p letters. \({{\mathbb {Z}}}(p,q)\) admits a metric \(\rho \) making it a metric space of diameter 1. See Sect. 2.
-
Let T(p, q) be the metric tree with all edges of length \(\log (q)\) and with valency \(p+1\) at every vertex. Roughly speaking, the treebolic space HT(p, q) is formed by fixing height functions on T(p, q) and on the hyperbolic plane \({{\mathbb {H}}}^2\) and then gluing horostrips of \({{\mathbb {H}}}^2\) onto every edge of T(p, q) in a height-preserving manner. One can also think of HT(p, q) as being composed of infinitely many copies of \({{\mathbb {H}}}^2\) glued together along horoballs into the shape of a tree. See Sect. 2 for a rigorous definition.
We will be interested in three different types of embedding between these metric spaces: rough isometric embeddings, bilipschitz embeddings and quasiisometric embeddings. Fix a pair of metric spaces X, Y and a pair of constants \(K \geqslant 1\), \(C \geqslant 0\). We define (K, C)-quasiisometric embeddings and (K, C)-quasiisometries in the usual manner. A (K, 0)-quasiisometric embedding \(f : X \rightarrow Y\) is a K-bilipschitz embedding. A (K, 0)-quasiisometry \(f: X \rightarrow Y\) is a K-bilipschitz homeomorphism. A (1, C)-quasiisometric embedding \(f: X \rightarrow Y\) is a C-rough isometric embedding. A (1, C)-quasiisometry \(f: X \rightarrow Y\) is a C-rough isometry.
We will simultaneously answer three closely connected questions: when does there exists a rough isometric embedding \(R(p,q) \rightarrow R(p',q')\)? When does there exists a bilipschitz embedding \({{\mathbb {Z}}}(p,q) \rightarrow {{\mathbb {Z}}}(p',q')\)? And, finally, when does there exist a quasiisometric embedding \(HT(p,q) \rightarrow HT(p',q')\)? Remarkably, the existence of these embeddings is intimately related to the boundedness of a certain integral sequence \({\mathcal {X}}= {\mathcal {X}}(p,q,p',q')\) which can be defined as follows.
-
Consider the non-negative number line \({{\mathbb {R}}}_{\geqslant 0}\) and imagine marking each non-negative multiple of \(\log (q)\) in blue and each non-negative multiple of \(\log (q')\) in red. We begin with a single pebble in our hand. We then imagine walking forwards along the number line from 0 obeying the following rule as we go: each time we pass a blue, we multiply the amount of pebbles in our possession by p; each time we pass a red, we divide our pebbles evenly into \(p'\) groups and keep only one of the larger groups (e.g. if \(p' = 3\) then we divide 8 pebbles into 3,3,2 and keep only 3 pebbles); if we pass a red and a blue simultaneously then we first multiply our pebbles by p and only then do we divide them by \(p'\) and keep one of the larger groups as before. The changing quantity of pebbles in our possession as we walk along the number line forms the integral sequence \({\mathcal {X}}(p,q,p',q')\). For a formal definition, see the definition of the more general class of sequences \({\mathcal {X}}((p_n),(q_n),(p_n'),(q_n'))\) in Sect. 3.
Consider the following pair of number theoretic conditions on \(p,q,p',q'\).
-
(C1)
\(\log (p)/\log (q) < \log (p')/\log (q')\);
-
(C2)
\(\log (p)/\log (q) = \log (p')/\log (q')\) and \(p, p'\) are powers of a common integer.
We prove the following series of equivalences.
Theorem 1
The following are equivalent.
-
(A1)
Either (C1) or (C2) holds;
-
(A2)
\({\mathcal {X}}(p,q,p',q')\) is bounded;
-
(A3)
There exists a rough isometric embedding \(R(p,q) \rightarrow R(p',q')\);
-
(A4)
There exists a bilipschitz embedding \({{\mathbb {Z}}}(p,q) \rightarrow {{\mathbb {Z}}}(p',q')\);
-
(A5)
There exists a quasiisometric embedding \(HT(p,q) \rightarrow HT(p',q')\).
Without much added difficulty, we also obtain the following.
Theorem 2
The following are equivalent.
-
(B1)
(C2) holds;
-
(B2)
R(p, q) is rough isometric to \(R(p',q')\);
-
(B3)
\({{\mathbb {Z}}}(p,q)\) is bilipschitz homeomorphic to \({{\mathbb {Z}}}(p',q')\);
-
(B4)
HT(p, q) is quasiisometric to \(HT(p',q')\).
Remark
Some of the implications of Theorem 2 follow from Theorem 1. If R(p, q) is rough isometric to \(R(p',q')\) then there exist rough isometric embeddings \(R(p,q) \rightarrow R(p',q')\) and \(R(p',q') \rightarrow R(p,q)\). Similar statements hold if \({{\mathbb {Z}}}(p,q)\) is bilipschitz homeomorphic to \({{\mathbb {Z}}}(p',q')\) or HT(p, q) is quasiisometric to \(HT(p',q')\). Hence, it follows from Theorem 1 that (B2), (B3), (B4) all imply (B1).
The equivalence of (B1) and (B4), i.e. the quasiisometric classification of treebolic spaces, was conjectured by Woess (Question 2.15 [8]).
Corollary 3
HT(p, q) is quasiisometric to \(HT(p',q')\) if and only if \(\log (p)/\log (q) = \log (p')/\log (q')\) and \(p, p'\) are powers of a common integer.
The treebolic space HT(p, q) is an example of a horocyclic product (for a definition see Sect. 2 of [8]). Other examples include the Diestel–Lieder graphs \(\text {DL}(p,q)\) (introduced in [9]) and the Lie groups \(\text {Sol}(p,q)\). The quasiisometric classifications of the Diestel–Lieder graphs and the Sol groups were provided by Eskin, Fisher and Whyte [10, 11].
Recall that, when \(m \in {{\mathbb {N}}}_{\geqslant 2}\), the treebolic space HT(m, m) is quasiisometric to the solvable Baumslag-Solitar group \(BS(1,m) = \langle a,t | tat^{-1} = a^m \rangle \) with some word metric (see, for example, Sect. 3 of [4]). It follows from Corollary 3 that BS(1, m) is quasiisometric to BS(1, n) if and only if m, n are powers of a common integer; this result was originally proved by Farb and Mosher [4]. Indeed, the proof in this paper that (A5) implies (A4) essentially follows from their work; the only meaningful change required is to the proof of Lemma 5.1 of their paper. Theorem 1 gives us the following result, proving that the solvable Baumslag–Solitar groups obey an even stronger rigidity.
Corollary 4
There exists a quasiisometric embedding \(BS(1,m) \rightarrow BS(1,n)\) if and only if m, n are powers of a common integer.
Remark
The content of Theorem 1 and Theorem 2 intersects with the work of Deng, Wen, Xiong and Xi [12]. Indeed, the metric space \({{\mathbb {Z}}}(p,q)\) is a self-similar set satisfying the strong separation condition and is of Hausdorff dimension \(\log (p) / \log (q)\). Theorem 1 of their paper then immediately gives us that (C1) implies (A4). Further, Theorem 2 of their paper gives us the following: if \(\log (p) / \log (q) = \log (p') / \log (q')\) then (A4) holds if and only if (B3) holds. Now, Cooper proves in the appendix of [4] that if \({{\mathbb {Z}}}(m,m)\) is bilipschitz homeomorphic to \({{\mathbb {Z}}}(n,n)\) then m, n are powers of a common integer. Consequently, once we have proved that (A5) implies (A4), Corollary 4 follows from [12] and [4].
Theorem 1 tells us that unboundedness of the sequence \({\mathcal {X}}(p,q,p',q')\) is an obstruction to the existence of a rough isometric embedding \(R(p,q) \rightarrow R(p',q')\). It is possible to partially generalise this result to a far larger class of trees.
-
Suppose we have sequences \((p_n)_{n \in {{\mathbb {N}}}}\), \((q_n)_{n \in {{\mathbb {N}}}}\) such that \(p_n \in {{\mathbb {N}}}_{\geqslant 2}\) and \(q_n \in {{\mathbb {R}}}_{>1}\). Suppose also that \(p_n\) and \(q_n\) are bounded sequences and that \(\inf _n q_n > 1\). We can construct a rooted metric tree \(R = R((p_n), (q_n))\) as follows. We start with a basepoint b. The basepoint b has \(p_1\) edges emanating from it of length \(\log (q_1)\). The terminal vertices of these edges have \(p_2\) edges emanating from them of length \(\log (q_2)\). Then the terminal vertices of those edges have \(p_3\) edges emanating from them of length \(\log (q_3)\). Continuing in this way we will have constructed an infinite rooted tree \(R((p_n),(q_n))\). We call a rooted tree constructed in this manner spherically homogeneous. The regular rooted tree R(p, q) is precisely the spherically homogeneous tree associated to the constant sequences \(p_n = p\), \(q_n = q\).
Given sequences \((p_n), (q_n), (p_n'), (q_n')\), one can define an integral sequence \({\mathcal {X}}= {\mathcal {X}}((p_n), (q_n), (p_n'), (q_n'))\) analogous to the sequence \({\mathcal {X}}(p,q,p',q')\) defined above (see Sect. 3). In Sect. 3 we will also introduce a simple property, which we call (P), on integer sequences. We have the following.
Theorem 5
Suppose we have a pair of spherically homogeneous trees \(R((p_n), (q_n))\), \(R((p_n'), (q_n'))\) such that \((p_n')\) satisfies property (P). If \({\mathcal {X}}((p_n), (q_n), (p_n'), (q_n'))\) is unbounded then there does not exist a rough isometric embedding \(R((p_n),(q_n)) \rightarrow R((p_n'),(q_n'))\).
The set of bounded integer sequences taking values satisfying property (P) is a strict subset of the set of all bounded integer sequences, but contains (and is strictly larger than) the set of all periodic integer sequences. Hence,
Corollary 6
Suppose we have a pair of spherically homogeneous trees \(R((p_n), (q_n))\), \(R((p_n'), (q_n'))\) such that \((p_n')\) is periodic. If \({\mathcal {X}}((p_n), (q_n), (p_n'), (q_n'))\) is unbounded then there does not exist a rough isometric embedding \(R((p_n),(q_n)) \rightarrow R((p_n'),(q_n'))\).
1.2 Structure of the paper
Section 2 provides relevant details on the metric spaces \({{\mathbb {Z}}}(p,q)\) and HT(p, q). Section 3 focusses on embedding spherically homogeneous trees; in it we will prove Theorem 5, thereby proving that (A3) \(\implies \) (A2). In Sect. 4, by studying the sequence \({\mathcal {X}}(p,q,p',q')\), we will prove that (A2) \(\implies \) (A1). In Sect. 5 we find rough isometric embeddings between regular rooted trees when either (C1) or (C2) hold; it covers the implications (A1) \(\implies \) (A3) and (B1) \(\implies \) (B2). Finally, Sect. 6 considers how embeddings of regular rooted trees R(p, q), symbolic Cantor sets \({{\mathbb {Z}}}(p,q)\) and treebolic spaces HT(p, q) all relate to each other; we will prove (A5) \(\implies \) (A4) \(\implies \) (A3) \(\implies \) (A5), (B2) \(\implies \) (B3) and (B2) \(\implies \) (B4).
2 Preliminaries
2.1 Notation
Given a metric space X, a subset \(A \subset X\) and a constant \(r \geqslant 0\), we use the notation \(\mathcal {N}_r(A)\) to denote the r-neighbourhood of A. That is,
If we have another subset \(B \subset X\), we use the notation \(d_H(A,B)\) to denote the Hausdorff distance between A and B. This is defined to be the (possibly infinite) quantity
2.2 Symbolic Cantor sets
Let \({{\mathbb {Z}}}(p,q) = \{ 0, 1, \ldots , p-1 \}^{{{\mathbb {N}}}}\) be the space of infinite sequences on p letters. We can put a metric \(\rho \) on \({{\mathbb {Z}}}(p,q)\): given \((a_n), (b_n) \in {{\mathbb {Z}}}(p,q)\) set \(\rho ((a_n), (b_n)) = q^{-N}\) where \(a_n = b_n\) for \(n \leqslant N\) and \(a_{N+1} \ne b_{N+1}\).
2.3 Treebolic spaces
Let T(p, q) be the metric tree with all edges of length \(\log (q)\) and with valency \(p+1\) at every vertex. Let \(\gamma : [0,\infty ) \rightarrow T(p,q)\) be some geodesic ray based at a vertex b of T(p, q). The ray \(\gamma \) induces a height function \(h: T(p,q) \rightarrow {{\mathbb {R}}}\) on T(p, q) via
where \(\gamma _x\) is the geodesic segment from b to x. Now consider the upper half plane model of the hyperbolic plane: \({{\mathbb {H}}}^2 = \{ (x,y) \in {{\mathbb {R}}}\times {{\mathbb {R}}}_{>0} \}\) with the metric \(ds^2 = \frac{dx^2 + dy^2}{y^2}\). We can put a height function on this model of \({{\mathbb {H}}}^2\) via
Note that both these height functions coincide with the classical notion of a Busemann function (see Definition 8.17 [13]). By a horostrip in \({{\mathbb {H}}}^2\) we mean a subset of the form \(\{ (x,y) \in {{\mathbb {H}}}^2 : h(x,y) \in [a,b] \}\) for some real interval [a, b]. The space HT(p, q) is formed by gluing horostrips onto every edge of T(p, q) in a height-preserving manner. More precisely, let \(HT(p,q) = T(p,q) \times {{\mathbb {R}}}\) as a set. Let \(e = [v,w]\) be some edge of T(p, q) such that \(h(v) < h(w)\). We can put a metric on \(e \times {{\mathbb {R}}}\) by identifying it with the horostrip
If we do this for every edge of T(p, q) then we will have produced a metric on the whole of HT(p, q) by taking the shortest path metric. The key to understanding the geometry of HT(p, q) is the following fact. Let \(\pi : HT(p,q) \rightarrow T(p,q)\) be the projection. Let \(L: (-\infty , \infty ) \rightarrow T(p,q)\) be a height-increasing bi-infinite geodesic in T(p, q). Then \(\pi ^{-1}(L) \subset HT(p,q)\) is an isometrically embedded copy of \({{\mathbb {H}}}^2\). Hence we use the following terminology. A horocycle in HT(p, q) is a preimage \(\pi ^{-1}(x)\) where \(x \in T(p,q)\). A branching horocycle in HT(p, q) is a preimage \(\pi ^{-1}(v)\) where v is a vertex of T(p, q). For more details on treebolic spaces see Sect. 2B of [8].
3 Embeddings of spherically homogeneous trees
Let R be some spherically homogeneous tree with basepoint b. We can put a height function \(h: R \rightarrow {{\mathbb {R}}}_{\geqslant 0}\) on R via \(h(x) = d(b,x)\). We will also put an orientation on the edges of R: we orient the edges such that the initial vertex is closer to b than the terminal vertex.
Definition
Given some \(x \in R\), we define its tree of descendants \(\tau (x)\) to be the subset of R that is the union of x and all points that can be reached from x by paths that are in agreement with the orientation on R. Similarly, given a subset \(B \subseteq R\), we can define
Some notation.
-
V(R) denotes the vertex set of R.
-
Given a subset \(B \subseteq R\) and some height \(h \geqslant 0\) we use the notation
 to denote the set of all points in B of height h; this is always a finite set.
to denote the set of all points in B of height h; this is always a finite set. -
Suppose \(x,y \in R\). Let \(x \wedge y\) denote the point of \(\{ z \in R: x \in \tau (z), y \in \tau (z) \}\) of maximal height.
We now give a further series of definitions.
Definition
Let \(A \geqslant 0\). We say that a map \(f: R \rightarrow R'\) between two spherically homogeneous trees is A-coarsely height-preserving if \(\sup _{x \in R} {|}h(x) - h(f(x)){|} \leqslant A\).
Definition
Let \(b,b'\) denote the basepoints of \(R,R'\) respectively. A map \(f: R \rightarrow R'\) is a waterfall map if \(f(b) = b'\) and  is an isometry for all geodesic rays \(\gamma \) based at b.
is an isometry for all geodesic rays \(\gamma \) based at b.
Definition
We say that a map \(f: R \rightarrow R'\) between spherically homogeneous trees is order-preserving if the following implication holds:
That is, if y descends from x then f(y) descends from f(x).
Note that the following statements are equivalent: \(f: R \rightarrow R\) is a waterfall map; f is height-preserving and continuous; f is height-preserving and order-preserving.
Definition
Given a vertex \(v \in V(R)\) we denote by \(\mathcal {C}(v)\) the set of children of v. That is, \(\mathcal {C}(v) = \{ w_1, \ldots , w_p \}\) where \(w_1, \ldots , w_p\) are the vertices connected by a single edge to v such that \(h(w_i) > h(v)\).
A waterfall map \(f: R \rightarrow R'\) can be very far from any notion of injectivity. For example, it could map every geodesic ray based at b onto one single geodesic ray based at \(b'\). We will say that a waterfall map is distributive if it makes as much effort as possible to be injective; if it divides itself evenly at the vertices of \(R'\).
Definition
Suppose \(f: R \rightarrow R'\) is a waterfall map and suppose we have a vertex \(w \in V(R')\) such that \(f^{-1}(w)\) is non-empty. Write \(f^{-1}(w) = \{ x_1, \ldots , x_m \}\). If the \(x_i\) are vertices, then set \(p = {|}\mathcal {C}(x_i){|}\), the number of edges emanating outwards from a single \(x_i\). If the \(x_i\) are not vertices, then set \(p = 1\). Similarly, let \(p' = {|}\mathcal {C}(w){|}\), the number of edges emanating outwards from the vertex w. Consider the subsets
and choose \(\epsilon \) small enough that \(B_\epsilon (w)\) is isometric to a star with \(p'\) arms and \(B_\epsilon (x_i)\) is isometric to a star with p arms. Let \(P = mp\). Since f is a waterfall map, an arm emanating from some \(x_i\) is mapped isometrically onto one of the \(p'\) arms emanating from w. Thus, we get a map from a set of cardinality P (the set of arms emanating from the \(x_i\)) to a set of cardinality \(p'\) (the set of arms emanating from w). We say that f is distributive if at most \(\lceil \frac{P}{p'} \rceil \) arms emanating from the \(x_i\) can be mapped to the same arm emanating from w.
One could say that \(f: R \rightarrow R'\) is distributive if it takes \(b \mapsto b'\) and then lets R expand like a gas within \(R'\). The notion of a distributive waterfall map should generalise naturally to the case of maps between \({{\mathbb {R}}}\)-trees. Further, applying the result of Kerr [14] which states that quasi–trees are rough isometric to \({{\mathbb {R}}}\)-trees, there should be a well-defined notion of a distributive waterfall map between quasi-trees (i.e. one that is conjugate to a distributive waterfall map between two associated \({{\mathbb {R}}}\)-trees).
Definition
Suppose we two spherically homogeneous trees \(R = R((p_n), (q_n))\) and \(R' = R((p_n'), (q_n'))\). For the ease of the following definition, we also define \(q_0\) and \(q_0'\) to be 1. Then, we have the sets of vertex heights
Now let \(\mathcal {H} = \mathcal {H}(R) \cup \mathcal {H}(R')\) and write \(\mathcal {H} = \{ h_0, h_1, h_2, \ldots \}\) such that \(h_n < h_{n+1}\) for \(n \in {{\mathbb {N}}}_0\). We can now define the infinite integral sequence \({\mathcal {X}}= {\mathcal {X}}((p_n),(q_n),(p_n'),(q_n')): {{\mathbb {N}}}_{\geqslant 0} \rightarrow {{\mathbb {N}}}\). Set \({\mathcal {X}}_0 = 1\). If \({\mathcal {X}}_n\) has already been defined then we set
Note that in the case when the sequences have constant values \(p_n = p, q_n = q, p_n' = p', q_n' = q'\) then we recover the sequence \({\mathcal {X}}(p,q,p',q')\) described in the introduction.
This sequence is perhaps easier to understand geometrically. If we have a distributive waterfall map \(f: R \rightarrow R'\) between spherically homogeneous trees, the sequence \({\mathcal {X}}_n\) captures the maximum cardinality of preimages of points \(x \in R'\). More precisely, \({\mathcal {X}}_n\) takes the values of the piecewise constant function

as h increases.
Remark
Another definition of the sequence \({\mathcal {X}}_n\) can be found by observing that the progression of the sequence \({\mathcal {X}}_n\) depends only on the order of the multiples of \(\log (q)\) and \(\log (q')\) within the sequence \((h_n)\) rather than on the values themselves. Hence, we could replace \(\mathcal {H}\) with the set
where \(h_n = \log (s_n)\) and \({\mathcal {X}}_n\) would not change.
A first step towards understanding these sequences would be to know the following.
Question
Does the boundedness of the sequence \({\mathcal {X}}((p_n),(q_n),(p_n'),(q_n'))\) depend upon its initial value? In other words, if we changed \({\mathcal {X}}_0 = 1\) to \({\mathcal {X}}_0 = x_0\) for some \(x_0 \in {{\mathbb {N}}}\), could the sequence move from being bounded to unbounded or vice-versa?
Definition
Let \((a_n)_{n \in {{\mathbb {N}}}}\) be an integer sequence. We say that \((a_n)\) satisfies property (P) if there exists a partition
such that
-
(1)
\(S_i\) is “connected”: if \(x,y \in S_i\) then so is every integer between x and y;
-
(2)
There exists a fixed constant \(A \in {{\mathbb {Z}}}\) such that \(\prod _{n \in S_i} a_i = A\) for all i.
In other words, a sequence has property (P) if it can be decomposed into connected subsequences that have the same product.
Clearly, periodic sequences satisfy (P).
Theorem 5
Suppose we have a pair of spherically homogeneous trees \(R((p_n), (q_n))\), \(R((p_n'), (q_n'))\) such that \((p_n')\) satisfies (P). If \({\mathcal {X}}((p_n), (q_n), (p_n'), (q_n'))\) is unbounded then there does not exist a rough isometric embedding \(R((p_n),(q_n)) \rightarrow R((p_n'),(q_n'))\).
It is clear that if \({\mathcal {X}}\) is unbounded then a waterfall map \(R \rightarrow R'\) cannot be a rough isometric embedding since points \(x \in R'\) would have preimages of arbitrarily large cardinality and of the same height as x. If we could show that an arbitrary rough isometric embedding \(f: R \rightarrow R'\) is at bounded distance from a waterfall map then Theorem 5 would follow immediately and we would no longer need the requirement that \((p_n')\) satisfies property (P).
Question
Is every rough isometric embedding \(R \rightarrow R'\) between spherically homogeneous trees at bounded distance from a waterfall map?
Recall that a waterfall map is a height-preserving and order-preserving map \(R \rightarrow R'\). We will see that a rough isometric embedding \(R \rightarrow R'\) is at bounded distance from a height-preserving map (Lemma 7) and at bounded distance from an order-preserving map (Proposition 16 and Proposition 17). The curse is that this does not imply it is at bounded distance from a height-preserving and order-preserving map \(R \rightarrow R'\). However, the idea of the proof of Theorem 5 is to show that a rough isometric embedding \(R \rightarrow R'\) is at bounded distance from a height-preserving and coarsely order-preserving map \(f: R \rightarrow R'\): f can’t send a pair of siblings too far away from each other - the siblings will become k’th cousins where k depends only on the rough isometry constant of f. This will do.
Lemma 7
A rough isometric embedding \(f: R \rightarrow R'\) between spherically homogeneous trees is coarsely height-preserving and at bounded distance from a height-preserving rough isometric embedding.
Proof
Suppose f is an A-rough isometric embedding. Let \(x \in R\). We have that
where \(B = d(b',f(b)) + A\). So f is B-coarsely height-preserving.
We will now define a height-preserving map \(g: R \rightarrow R'\) at bounded distance from f. We have three cases.
-
(1)
If \(h(f(x)) = h(x)\) then set \(g(x) = f(x)\).
-
(2)
If \(h(f(x)) > h(x)\) then let g(x) be the unique point of height h(x) such that \(f(x) \in \tau (g(x))\). Then \(d(f(x), g(x)) = h(f(x)) - h(x) \leqslant B\).
-
(3)
If \(h(f(x)) < h(x)\) then let g(x) be any element of \(\tau (f(x))\) (there could be many) of height h(x). Then \(d(f(x), g(x)) = h(x) - h(f(x)) \leqslant B\).
Thus we see that g is height-preserving and \(d(f, g) \leqslant B\). Since g is at bounded distance from a rough isometric embedding, g is itself a rough isometric embedding. \(\square \)
Proof of Theorem 5
We will first prove the result for when \((p_n')\) is a constant sequence. This will constitute the majority of the proof. At the end, in Step 4, we will deduce the full result for when \((p_n')\) satisfies (P).
So suppose \((p_n')\) has constant value \(p' \in {{\mathbb {N}}}_{\geqslant 2}\). Write \(R = R((p_n), (q_n))\) and \(R' = R((p_n'), (q_n'))\) and denote by \(b,b'\) the basepoints of \(R,R'\) respectively. Let \(P \in {{\mathbb {N}}}_{\geqslant 2}\) be an upper bound for \((p_n)\) and let \(\epsilon , M > 0\) be such that \(\log (q_n) \in [\epsilon , M]\). Similarly, let \(\epsilon ', M' > 0\) be such that \(\log (q_n') \in [\epsilon ', M']\). Suppose there exists an A-rough isometric embedding \(f: R \rightarrow R'\) for some constant \(A \geqslant 0\). By the lemma above, we can assume that f is height-preserving.
Step 1: The plan. Let \(N \in {{\mathbb {N}}}\) be chosen such that \((N-1)\epsilon ' \geqslant A\). The plan is to inductively define an infinite sequence of vertices \(w_n \in V(R')\) that induce an infinite sequence of nested subtrees of \(R'\)
such that
-
(T1)
 has cardinality at most \((p')^N\);
has cardinality at most \((p')^N\); -
(T2)
If
 has cardinality less than \((p')^N\) then \(w_n = b'\);
has cardinality less than \((p')^N\) then \(w_n = b'\); -
(T3)
 .
.
Once we have defined a sequence of trees \(\tau _n\) satisfying properties (T1) and (T3) then we are done. The logic is this. By (T3), if \({\mathcal {X}}_n\) is unbounded then \(\text {sum}_n\) must be unbounded too. But, by (T1), \(\text {sum}_n\) is the preimage under f of a set of cardinality at most \((p')^N\) and so we can conclude that preimages of single points under f can have arbitrarily large cardinality. Since f is height-preserving, preimages of single points must all have the same height in R, i.e. they are contained in some set  . Further, since f is an A-rough isometry, they must all be contained in some ball of radius A. However, there is a fixed upper bound on the cardinality of balls of radius A in a level set
. Further, since f is an A-rough isometry, they must all be contained in some ball of radius A. However, there is a fixed upper bound on the cardinality of balls of radius A in a level set  . Hence if \({\mathcal {X}}_n\) is unbounded there cannot exist a rough isometric embedding of R into \(R'\).
. Hence if \({\mathcal {X}}_n\) is unbounded there cannot exist a rough isometric embedding of R into \(R'\).
The significance of property (T2) is given after the following crucial observation.
Claim
Suppose we have some \(w \in V(R')\) inducing a subtree \(\tau (w)\) and a pair of heights \(h < H\) such that  has cardinality at least \((p')^{N}\). Then
has cardinality at least \((p')^{N}\). Then

What is this saying? It says (assuming that w is more than N generations above points of height h) that if a point x of height h is mapped into \(\tau (w)\) then a descendant y will be too, and that the converse also holds: if y is mapped into  then it must descend from some x that is mapped into
then it must descend from some x that is mapped into  . In other words, the points of R which map into
. In other words, the points of R which map into  are precisely the descendants of those points of R which map into
are precisely the descendants of those points of R which map into  . The numerical condition \((N-1)\varepsilon ' \geqslant A\) ensures that the distance from x to w is at least A.
. The numerical condition \((N-1)\varepsilon ' \geqslant A\) ensures that the distance from x to w is at least A.
Property (T2) combined with the above claim implies that we have the equality

for each of the (yet to be defined) subtrees \(\tau _n\).
Step 2: The base case. Set \(w_0 = b'\). Then \(\tau _0 = \tau (b') = R'\). We need to verify that (T1), (T2) and (T3) hold. Since \(h_0 = 0\),  has cardinality 1, which is evidently less than \((p')^N\). Then (T1) and (T2) hold since \(w_0 = b'\). Finally note that
has cardinality 1, which is evidently less than \((p')^N\). Then (T1) and (T2) hold since \(w_0 = b'\). Finally note that
and so (T3) holds as well.
Step 3: The induction. Suppose \(\tau _n\) has been defined. We will now define \(\tau _{n+1}\). We have three cases to consider.
-
(1)
Suppose \(h_n \in \mathcal {H}(R) \setminus \mathcal {H}(R')\). That is, \(h_n\) is a vertex height for R but not \(R'\). In this case we set \(\tau _{n+1} = \tau _n\). Then
 will have the same cardinality as
will have the same cardinality as  since \(R'\) has no vertices with height in the interval \([h_n, h_{n+1})\). So \(\tau _{n+1}\) satisfies properties (T1) and (T2). Further, by (1) we have that $$\begin{aligned} \text {sum}_{n+1} = p_{a+1} \text {sum}_n \end{aligned}$$
since \(R'\) has no vertices with height in the interval \([h_n, h_{n+1})\). So \(\tau _{n+1}\) satisfies properties (T1) and (T2). Further, by (1) we have that $$\begin{aligned} \text {sum}_{n+1} = p_{a+1} \text {sum}_n \end{aligned}$$where \(h_n = \sum _{i=0}^a \log (q_i)\). By induction, we can assume that \(\text {sum}_n \geqslant {\mathcal {X}}_n\) and so
$$\begin{aligned} \text {sum}_{n+1} = p_{a+1} \text {sum}_n \geqslant p_{a+1} {\mathcal {X}}_n = {\mathcal {X}}_{n+1} \end{aligned}$$ -
(2)
We divide into two subcases.
-
(a)
Suppose \(h_n \in \mathcal {H}(R') \setminus \mathcal {H}(R)\) and
 has cardinality less than \((p')^N\) (and so in fact it has cardinality at most \((p')^{N-1}\)). By induction, \(w_n = b'\). Note also that the cardinality of
has cardinality less than \((p')^N\) (and so in fact it has cardinality at most \((p')^{N-1}\)). By induction, \(w_n = b'\). Note also that the cardinality of  is \(p'\) times larger than the cardinality of
is \(p'\) times larger than the cardinality of  . Set \(\tau _{n+1} = \tau _n\). Then it is clear that (T1) and (T2) hold. Note that
. Set \(\tau _{n+1} = \tau _n\). Then it is clear that (T1) and (T2) hold. Note that  since R does not branch in the interval \([h_n, h_{n+1}]\). Hence $$\begin{aligned} \text {sum}_{n+1} = \text {sum}_n \geqslant {\mathcal {X}}_n \geqslant \lceil \frac{{\mathcal {X}}_n}{p'} \rceil = {\mathcal {X}}_{n+1} \end{aligned}$$
since R does not branch in the interval \([h_n, h_{n+1}]\). Hence $$\begin{aligned} \text {sum}_{n+1} = \text {sum}_n \geqslant {\mathcal {X}}_n \geqslant \lceil \frac{{\mathcal {X}}_n}{p'} \rceil = {\mathcal {X}}_{n+1} \end{aligned}$$and so (T3) holds.
-
(b)
Suppose \(h_n \in \mathcal {H}(R') \setminus \mathcal {H}(R)\) and
 has cardinality \((p')^N\). In this case,
has cardinality \((p')^N\). In this case, 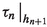 has cardinality \((p')^{N+1}\). Let \(\{ v_1, \ldots , v_{p'}\} = \mathcal {C}(w_n)\).
has cardinality \((p')^{N+1}\). Let \(\{ v_1, \ldots , v_{p'}\} = \mathcal {C}(w_n)\).  can be partitioned into \(p'\) sets of cardinality \((p')^N\) each:
can be partitioned into \(p'\) sets of cardinality \((p')^N\) each: 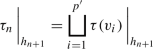
And so, using (1), we get a partition

Again, since R does not branch in the interval \([h_n, h_{n+1}]\), the cardinality of the above set is precisely \(\text {sum}_n\) and so there must exist some \(1 \leqslant j \leqslant p'\) such that

Set \(w_{n+1} = v_j\). It is clear that (T1) and (T2) hold and

and so (T3) holds.
-
(a)
-
(3)
Again, we divide into two subcases.
-
(a)
Suppose \(h_n \in \mathcal {H}(R) \cap \mathcal {H}(R')\) and
 has cardinality less than \((p')^N\). As before we set \(\tau _{n+1} = \tau _n\) and (T1) and (T2) hold. We have that $$\begin{aligned} \text {sum}_{n+1} = p_{a+1} \text {sum}_n \geqslant p_{a+1} {\mathcal {X}}_n \geqslant \lceil \frac{p_{a+1} {\mathcal {X}}_n}{p'} \rceil = {\mathcal {X}}_{n+1} \end{aligned}$$
has cardinality less than \((p')^N\). As before we set \(\tau _{n+1} = \tau _n\) and (T1) and (T2) hold. We have that $$\begin{aligned} \text {sum}_{n+1} = p_{a+1} \text {sum}_n \geqslant p_{a+1} {\mathcal {X}}_n \geqslant \lceil \frac{p_{a+1} {\mathcal {X}}_n}{p'} \rceil = {\mathcal {X}}_{n+1} \end{aligned}$$where \(h_n = \sum _{i=0}^a \log (q_i)\). So (T3) holds.
-
(b)
Finally suppose that \(h_n \in \mathcal {H}(R) \cap \mathcal {H}(R')\) and
 has cardinality \((p')^N\). Again we write \(\{ v_1, \ldots , v_{p'}\} = \mathcal {C}(w_n)\) and we have
has cardinality \((p')^N\). Again we write \(\{ v_1, \ldots , v_{p'}\} = \mathcal {C}(w_n)\) and we have 
The cardinality of the above set is \(p_{a+1} \text {sum}_n\) where \(h_n = \sum _{i=0}^a \log (q_i)\). Hence, there exists some \(1 \leqslant j \leqslant p'\) such that

and we set \(w_{n+1} = v_j\). (T1) and (T2) hold as before and
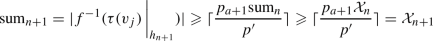
and so (T3) holds as well.
-
(a)
This completes our proof of the result in the case when \((p_n')\) is constant.
Step 4: The general case. Suppose \((p_n')\) satisfies (P). Let \({{\mathbb {N}}}= \bigsqcup _{i \in {{\mathbb {N}}}} S_i\) be the associated partition and suppose that \(\prod _{n \in S_i} p_n' = p'\) for some fixed constant \(p'\). Consider the spherically homogeneous tree \(R'' = R((p_n''),(q_n''))\) where
We claim that \(R'\) is rough isometric to \(R''\). Let \({\tilde{V}} \subset R'\) consist of all vertices in \(R'\) of height \(\sum _{i \leqslant k} \sum _{n \in S_i} \log (q_n')\) for \(k \in {{\mathbb {N}}}_0\). We can define a rough isometry \(g: {\tilde{V}} \rightarrow R''\) inductively. Let \(b'\) map to the basepoint of \(R''\). Let \(k \in {{\mathbb {N}}}_0\) and suppose that g is already defined on vertices of height \(h = \sum _{i \leqslant k} \sum _{n \in S_i} \log (q_n')\). If \(x \in R'\) has height h, then x has precisely \(p'\) descendants of height \(H = h + \sum _{n \in S_{k+1}} \log (q_n')\). Similarly, g(x) has precisely \(p'\) children with height H. We map  bijectively onto
bijectively onto  . The map constructed this way gives a rough isometry \(g: {\tilde{V}} \rightarrow R''\). Since \({\tilde{V}}\) is coarsely dense within \(R'\), precomposition of this map with the nearest point projection \(R' \rightarrow {\tilde{V}}\) will give a rough isometry \(R' \rightarrow R''\).
. The map constructed this way gives a rough isometry \(g: {\tilde{V}} \rightarrow R''\). Since \({\tilde{V}}\) is coarsely dense within \(R'\), precomposition of this map with the nearest point projection \(R' \rightarrow {\tilde{V}}\) will give a rough isometry \(R' \rightarrow R''\).
Suppose now that \({\mathcal {X}}= {\mathcal {X}}((p_n),(q_n), (p_n'), (q_n'))\) is unbounded. We want to show that \({\tilde{{\mathcal {X}}}} = {\mathcal {X}}((p_n),(q_n), (p_n''), (q_n''))\) is also unbounded. To see why this is the case, it is necessary to come up with a more visual understanding of the sequence \({\mathcal {X}}\). Imagine marking the non-negative number line with a blue dash for each of the sums \(\sum _{i = 0}^a \log (q_i)\). Similarly, imagine marking it with a red dash for each sum \(\sum _{i = 0}^b \log (q_i')\). The sequence \({\mathcal {X}}\) is formed by walking forwards along the number line and multiplying your previous value when you hit a blue dash (i.e. multiplying by \(p_{a}\)) and by applying a "ceiling-division" each time you hit a red dash (i.e. applying the function \(x \mapsto \lceil \frac{x}{p_b'} \rceil \)). If a blue dash and a red dash are placed at the same point, then we can just think of this as a blue dash followed by a red dash. The sequence \({\tilde{{\mathcal {X}}}}\) is formed from \({\mathcal {X}}\) by grouping together ceiling-divisions: for each i we gather all the red dashes corresponding to the set \(S_i\) together. Let \(D_i\) denote the red dash corresponding to \(\min S_i\). We can break down the transformation of \({\mathcal {X}}\) into \({\tilde{{\mathcal {X}}}}\) into two moves: (1) if \(b \in S_i\) and b does not correspond to \(D_i\) then move the corresponding red dash such that it sits to the right of \(D_i\) but to the left of the first blue dash following \(D_i\) (2) once all the red dashes corresponding to \(S_i\) have been gathered together, merge them into a single red dash positioned where \(D_i\) was and let the new dash correspond to the ceiling-division \(x \mapsto \lceil \frac{x}{\prod _{n \in S_i} p_n'} \rceil \). Now, both move (1) and move (2) can be broken down into smaller submoves. Move (1) can be achieved by repeatedly moving red dashes leftwards over either blue dashes or red dashes. Moving a red dash leftwards over a blue dash corresponds to the numerical transformation
where l is the multiplication value corresponding to the blue dash, k is the division value corresponding to the red dash, and x is the value of the sequence prior to these dashes. Similarly, moving a red dash leftwards over another red dash corresponds to the transformation
where k is the division value corresponding to the first red dash and \(k'\) is the division value corresponding to the second red dash. Finally, move (2) can be broken down into the merging of pairs of red dashes, i.e. the transformation
Since \(\lceil \frac{lx}{k} \rceil \leqslant l \lceil \frac{x}{k} \rceil \), \(\Big \lceil \frac{\lceil \frac{x}{k} \rceil }{k'} \Big \rceil = \Big \lceil \frac{\lceil \frac{x}{k'} \rceil }{k} \Big \rceil \) and \(\Big \lceil \frac{\lceil \frac{x}{k} \rceil }{k'} \Big \rceil = \lceil \frac{x}{kk'} \rceil \), these submoves never decrease the value of the sequence that follows the dashes. Further, since both multiplication and ceiling-division are non-decreasing functions, these submoves never decrease any of the sequence values that follow the dashes in question.
Let \(K \in {{\mathbb {N}}}\) be arbitrary and let \({\mathcal {X}}_n\) be some value of the sequence for which \({\mathcal {X}}_n \geqslant K\). Without loss of generality, we can assume that \({\mathcal {X}}_n\) is the value that the sequence takes just before a red dash \(D_i\) corresponding to some \(\min S_i\). This is because, walking onwards from \({\mathcal {X}}_n\), there is a uniform upper bound on how many dashes the sequence can pass before it reaches the first red dash corresponding to some \(\min S_i\), and the sequence \({\mathcal {X}}\) can only decrease by a factor of at most \(\sup _n p_n'\) for each dash it passes. Given such an \({\mathcal {X}}_n\), we can transform it into a value of the sequence \({\tilde{{\mathcal {X}}}}\) by applying moves (1) and (2) to all the dashes to the left of D. This is a finite number of moves, none of which decrease the value of \({\mathcal {X}}_n\). It follows that \({\tilde{{\mathcal {X}}}}_m \geqslant K\) for some \(m \in {{\mathbb {N}}}\) and hence \({\tilde{{\mathcal {X}}}}\) is unbounded.
Since \({\tilde{{\mathcal {X}}}}\) is unbounded, it follows from our work above that there is no rough isometric embedding \(R \rightarrow R''\) and hence, since \(R'\) is rough isometric to \(R''\), there is no rough isometric embedding \(R \rightarrow R'\). \(\square \)
Naturally, one hopes that the requirement that \((p_n')\) satisfies property (P) is unnecessary.
Conjecture
Suppose we have two spherically homogeneous trees \(R = R((p_n), (q_n))\) and \(R' = R((p_n'), (q_n'))\). If \({\mathcal {X}}((p_n), (q_n), (p_n'), (q_n'))\) is unbounded then there does not exist a rough isometric embedding of R into \(R'\).
One might suspect the converse holds: that if \({\mathcal {X}}_n\) is bounded then there exists a rough isometric embedding of R into \(R'\). This seems plausible since if \({\mathcal {X}}_n\) is bounded then a distributive waterfall map from R into \(R'\) would have bounded point preimages.
Question
If \({\mathcal {X}}_n((p_n), (q_n), (p_n'),(q_n'))\) is bounded, does there exist a rough isometric embedding \(R((p_n),(q_n)) \rightarrow R((p_n'),(q_n'))\)?
However, as the following example shows, we can find pairs of spherically homogeneous trees for which \({\mathcal {X}}_n\) is bounded and for which none of the distributive waterfall maps are rough isometric embeddings.
Example
Let \(R = R((p_n),(q_n))\) where \(p_1 = 6\), \(q_1 = 2\) and \(p_n = 3\), \(q_n = 4\) for \(n \geqslant 2\). Let \(R' = R((p_n'),(q_n'))\) where \(p_n' = 3\), \(q_n' = 4\) (equivalently \(R' = R(3,4)\)). Let \(b,b'\) denote the basepoints of \(R,R'\) respectively. The associated sequence \({\mathcal {X}}_n((p_n), (q_n), (p_n'), (q_n'))\) is bounded; indeed, \({\mathcal {X}}_n \leqslant 6\). Suppose that f is a distributive waterfall map of R into \(R'\). We will find two distinct geodesic rays, \(\gamma _B\) and \(\gamma _Y\), based at b which have the same image under f. We first need to establish a combinatorial fact.
Suppose we have 6 objects such that 3 are coloured blue and 3 are coloured yellow. If we want to partition the objects into 3 groups of size 2 then there must be a group which contains a blue and a yellow.
6 arms emanate from b which are divided between the 3 arms emanating from \(b'\). Thus, pairs of arms emanating from b are crushed together by f. Consider a fixed pair of arms emanating from b that are crushed together under f. We will say that descendants of the first arm are blue and descendants of the second arm are yellow. Consider the terminal vertex \(w_1 \in R'\) of the edge onto which the blue and yellow arm are crushed. The preimage of this vertex consists of 6 points, 3 blue and 3 yellow. By the statement above, we know that a blue arm and a yellow arm must be crushed onto the same edge emanating from \(w_1\). Let \(w_2\) be the terminal vertex of this edge. Again, we know that the preimage of \(w_2\) consists of 3 blue and 3 yellow points and we know that a blue arm and a yellow arm must be crushed onto some edge emanating from \(w_2\). Continuing in this way, we get a sequence of vertices \(b, w_1, w_2, w_3, \ldots \) such that if \(\eta \) is the geodesic which joins them all together then \(f^{-1}(\eta )\) contains a blue geodesic ray \(\gamma _B\) and a yellow geodesic ray \(\gamma _Y\). Points on \(\gamma _B\) and \(\gamma _Y\) of the same height have the same image under f even though they may be arbitrarily far away in R. So f is not a rough isometric embedding.
Note, however, that there does nonetheless exist a rough isometric embedding \(R \rightarrow R'\); if we crush \(\{ x \in R : h(x) \leqslant \log (2) \}\) to a point then we get 6 copies of R(3, 4) glued together; if we crush \(\{ y \in R' : h(y) \leqslant 2\log (4)\}\) to a point then we get 9 copies of R(3, 4) glued together.
4 The sequence \({\mathcal {X}}(p,q,p',q')\)
The sequence \({\mathcal {X}}(2,2,3,3)\) can be understood as follows. We start with the number line \(\mathbb {R}_{\geqslant 1}\) (a long pebbly beach perhaps). We begin with a single pebble in our hand. We then imagine walking along the number line playing the following game as we go: each time we pass a power of 2, we multiply the amount of pebbles in our possession by 2; each time we pass a power of 3, we divide our pebbles into 3 groups as evenly as possible and then keep only one of the larger groups. See Fig. 1. The question is whether there exists some fixed upper bound on the number of pebbles in our possession as we play this game.
In this section we prove that (A2) implies (A1). That is, we prove that if \({\mathcal {X}}(p,q,p',q')\) is bounded then either \(\log (p)/\log (q) < \log (p')/\log (q')\) (this is condition (C1)) or \(\log (p)/\log (q) = \log (p')/\log (q')\) and \(p, p'\) are powers of a common integer (condition (C2)). We need the following lemma.
Lemma 8
Suppose that \(\log (q')/\log (q)\) is irrational. Let \(a \log (q)\) be a multiple of \(\log (q)\) and let \(b \log (q')\) be the least multiple of \(\log (q')\) that is greater than \(a \log (q)\). Then there exists \(a' > a\) such that, if \(b' \log (q')\) is the least multiple of \(\log (q')\) greater than \(a' \log (q)\), we have
Proof
Write \(d = b \log (q') - a \log (q)\). Consider the metric space \(X = {{\mathbb {R}}}/ (\log (q) {{\mathbb {Z}}})\). Let \(\theta : X \rightarrow X\) be rotation by \(\log (q')\)

We can think of X as a circle with circumference \(\log (q)\) such that as x increases, [x] moves anticlockwise around the circle. We have a bilipschitz map
given by
\(\theta \) is conjugate under \(\eta \) to the map \(\theta ' = \eta \theta \eta ^{-1}: {{\mathbb {R}}}/ {{\mathbb {Z}}}\rightarrow {{\mathbb {R}}}/ {{\mathbb {Z}}}\)

which has dense orbits since \(\frac{\log (q')}{\log (q)}\) is irrational. Consequently, \(\theta \) has dense orbits. In particular, we can find arbitrarily large \(b'\) such that the anticlockwise distance from [0] to \(\theta ^{(b')}([0]) = [b' \log (q')]\) is less than d. If we choose \(a'\) such that \(a' \log (q)\) is the largest multiple of \(\log (q)\) less than \(b' \log (q')\), and if we choose \(b'\) large enough that \(a' > a\), then \(a'\) and \(b'\) satisfy the desired properties. \(\square \)
Theorem 9
If \({\mathcal {X}}(p,q,p',q')\) is bounded then either (C1) or (C2) holds.
Proof
First, suppose that \(\frac{\log (p)}{\log (q)} > \frac{\log (p')}{\log (q')}\). Let \(\beta = \frac{\log (q')}{\log (q)}\). So \(p^{\beta } > p'\). Consider the sequence defined by \(\mathcal {Y}_0 = 1\) and
Suppose \(h_n = a\log (q)\). We have that
The right-hand side of the above goes to infinity as a goes to infinity and hence \(\mathcal {Y}_n\) is unbounded. Thus \({\mathcal {X}}_n\) is also unbounded since \({\mathcal {X}}_n \geqslant \mathcal {Y}_n\) for all \(n \in {{\mathbb {N}}}_0\).
Now suppose that \(\frac{\log (p)}{\log (q)} = \frac{\log (p')}{\log (q')}\) and \(p, p'\) are not powers of a common integer. This implies that \(\log (q')/\log (q)\) is irrational. Let \(h_l = a\log (q)\) be some arbitrary element of \(\mathcal {H}(R)\). Let \(b \log (q')\) be the least multiple of \(\log (q')\) greater than \(a \log (q)\). By Lemma 8 we can find some \(a' > a\) such that if \(b' \log (q')\) is the least multiple of \(\log (q')\) greater \(a' \log (q)\) then
which rearranges to
If \(h_m = a'\log (q) \in \mathcal {H}(R)\) then
So \({\mathcal {X}}_m > {\mathcal {X}}_l\). But both \({\mathcal {X}}_m\) and \({\mathcal {X}}_l\) are integral and so in fact \({\mathcal {X}}_m \geqslant {\mathcal {X}}_l + 1\). We have shown that given \(l \in {{\mathbb {N}}}_0\) such that \(h_l \in \mathcal {H}(R)\) we can find \(m > l\) such that \(h_m \in \mathcal {H}(R)\) and \({\mathcal {X}}_m \geqslant {\mathcal {X}}_l + 1\). Repeating this process gives arbitrarily large values of \({\mathcal {X}}_n\) and so the sequence is unbounded. \(\square \)
5 Embeddings of regular rooted trees
Proposition 10
If (C2) holds then R(p, q) is rough isometric to \(R(p',q')\).
Proof
Write \(R = R(p,q)\) and \(R' = R(p',q')\). Let \(b,b'\) denote the basepoints of \(R,R'\) respectively. First, suppose that there exists some \(t \in {{\mathbb {N}}}\) such that \(p' = p^s\) and \(q' = q^s\). In this case, an identical argument to that given at the start of Step 4 of the proof of Theorem 5 shows that R is rough isometric to \(R'\) (we choose \(S_i = \{ (i-1)s + 1, (i-1)s + 2, \ldots , is\}\)).
In the general case, write \(p = r^s\), \(p' = r^t\) where \(r \in {{\mathbb {N}}}_{\geqslant 2}\). Then \(q' = q^{\frac{t}{s}}\). By the above, we know that \(R = R(p,q)\) is rough isometric to \(R(r, q^{\frac{1}{s}})\) which is rough isometric to \(R(r^t, q^{\frac{t}{s}}) = R(p', q') = R'\). So R is rough isometric to \(R'\). \(\square \)
Proposition 11
If (C1) holds then there exists a rough isometric embedding \(R(p,q) \rightarrow R(p',q')\).
Proof
We will first show that if \(p = p'\) and \(q > q'\) then there exists a rough isometric embedding \(f: R(p,q) \rightarrow R(p',q')\). We will first define f on the vertex set V of R(p, q). Set \(f(b) = b'\). If \(v \in V\) and f(v) is already defined then we define f on \(\mathcal {C}(v)\) as follows. Write \(\mathcal {C}(v) = \{ v_1, \ldots , v_p \}\). We know that  has cardinality \(p^k\) for some \(k \in {{\mathbb {N}}}\). Map \(\mathcal {C}(v)\) into this set injectively. If we precompose this map \(V \rightarrow R(p',q')\) with the nearest point projection \(R(p,q) \rightarrow V\) then we get a rough isometric embedding \(R(p,q) \rightarrow R(p',q')\).
has cardinality \(p^k\) for some \(k \in {{\mathbb {N}}}\). Map \(\mathcal {C}(v)\) into this set injectively. If we precompose this map \(V \rightarrow R(p',q')\) with the nearest point projection \(R(p,q) \rightarrow V\) then we get a rough isometric embedding \(R(p,q) \rightarrow R(p',q')\).
Now suppose the general case holds, i.e. \(\frac{\log (p)}{\log (q)} < \frac{\log (p')}{\log (q')}\). Say \(\frac{\log (p')}{\log (q')} = (1+ \xi ) \frac{\log (p)}{\log (q)}\) where \(\xi > 0\). Evidently, we can find \(a, b \in {{\mathbb {N}}}\) such that
Then
and so \(a \log (q) > b \log (q')\), or, equivalently, \(q^a > (q')^b\). By Theorem 10, we know that R(p, q) is rough isometric to \(R(p^a, q^a)\). Further, it is clear there exists an isometric embedding of \(R(p^a, q^a)\) into \(R((p')^b, q^a)\) since, by (2), \((p')^b \geqslant p^a\). Then, by our work above, there exists a rough isometric embedding of \(R((p')^b, q^a)\) into \(R((p')^b, (q')^b)\) since \(q^a > (q')^b\). Finally, we know that \(R((p')^b), (q')^b)\) is rough isometric to \(R(p', q')\). So there exists a rough isometric embedding of R(p, q) into \(R(p',q')\). \(\square \)
6 Equivalence of the embeddings
6.1 Generalising Farb–Mosher
In this section we will prove that (A5) \(\implies \) (A4).
Definition
Let \({{\mathbb {Q}}}(p,q)\) denote the set of bi-infinite sequences \((a_n)_{n \in {{\mathbb {Z}}}}\) on the alphabet \(\{0, \ldots , p-1\}\) such that \(a_n = 0\) for all sufficiently small n. We can put a metric on \({{\mathbb {Q}}}(p,q)\) by setting \(\rho ((a_n), (b_n)) = q^{-N}\) where \(a_n = b_n\) for \(n \leqslant N\) and \(a_{N+1} \ne b_{N+1}\). A clone of \({{\mathbb {Q}}}(p,q)\) is a subset consisting of all words beginning with some fixed word w. Every clone in \({{\mathbb {Q}}}(p,q)\) is bilipschitz homeomorphic to \({{\mathbb {Z}}}(p,q)\).
Let \(\partial ^u HT(p,q)\) denote the set of hyperbolic planes in HT(p, q). Via the projection map \(\pi : HT(p,q) \rightarrow T(p,q)\), the set \(\partial ^u HT(p,q)\) is in bijection with the set of height-increasing bi-infinite geodesics in T(p, q). This, in turn, can be seen to be in bijection with \({{\mathbb {Q}}}(p,q)\). We can put a metric on \(\partial ^u HT(p,q)\) as follows. If \(Q_1, Q_2 \in \partial ^u HT(p,q)\) then set \(d(Q_1, Q_2) = e^{-h(\sigma )}\) where \(\sigma \) is the horocycle \(\partial (Q_1 \cap Q_2)\). With this metric \(\partial ^u HT(p,q)\) is isometric to \({{\mathbb {Q}}}(p,q)\). Let \(m,n \in {{\mathbb {N}}}_{\geqslant 2}\) and suppose \(f: HT(m,m) \rightarrow HT(n,n)\) is a quasiisometry. In the paper of Farb and Mosher [4] (Proposition 4.1) they prove that if \(Q \in \partial ^u HT(m,m)\) then there exists a unique \(Q' \in \partial ^u HT(n,n)\) such that \(d_H(f(Q), Q') < \infty \) and they write \(f^u(Q) = Q'\). They also prove that, with respect to the metrics on \(\partial ^u HT(m,m)\) and \(\partial ^u HT(n,n)\), \(f^u\) is a bilipschitz homeomorphism (Theorem 6.1 of [4]). So a quasiisometry \(f: HT(m,m) \rightarrow HT(n,n)\) induces a bilipschitz homeomorphism \(f^u: {{\mathbb {Q}}}(m,m) \rightarrow {{\mathbb {Q}}}(n,n)\). Let \(C \subset {{\mathbb {Q}}}(m,m)\) be some clone. Since \(f^u\) is a bilipschitz homeomorphism and C has finite diameter, \(f^u(C)\) also has finite diameter and hence is contained in some clone \(C' \subset {{\mathbb {Q}}}(n,n)\). Thus, since C is bilipschitz homeomorphic to \({{\mathbb {Z}}}(m,m)\) and \(C'\) is bilipschitz homeomorphic to \({{\mathbb {Z}}}(n,n)\), we have an induced bilipschitz embedding \({{\mathbb {Z}}}(m,m) \rightarrow {{\mathbb {Z}}}(n,n)\). In summary, Farb and Mosher prove that a quasiisometry \(HT(m,m) \rightarrow HT(n,n)\) induces a bilipschitz embedding \({{\mathbb {Z}}}(m,m) \rightarrow {{\mathbb {Z}}}(n,n)\).
We would like to generalise this result in two ways. First, we would like to show that it holds if we no longer require f to be coarse surjective. That is, we assume only that f is a quasiisometric embedding. Second, we would like to show that it holds if we replace HT(m, m) with HT(p, q) and HT(n, n) with \(HT(p',q')\). Put concisely: we would like to prove that a quasiisometric embedding \(HT(p,q) \rightarrow HT(p',q')\) induces a bilipschitz embedding \({{\mathbb {Z}}}(p,q) \rightarrow {{\mathbb {Z}}}(p',q')\). Therefore, we need to analyse - up until the conclusion of the proof of Theorem 6.1 - all the instances when Farb and Mosher use the coarse surjectivity of f and all the instances when they use the fact that \(p = q\) and \(p' = q'\). One of these questions is easy to answer: the proof never once uses the fact that \(p = q\) and \(p' = q'\) so we can replace HT(m, m) with HT(p, q) and HT(n, n) with \(HT(p',q')\). The coarse surjectivity of f is used once, in the proof of Lemma 5.1. Thus we will need to reprove this lemma without ever using coarse surjectivity. This is the content of Lemma 12 below.
Remark
It is important to note that Theorem 7.2 of the Farb–Mosher paper is not actually proved as it is written. Theorem 7.2 says that if there is a bilipschitz embedding \({{\mathbb {Z}}}(m,m) \rightarrow {{\mathbb {Z}}}(n,n)\) then m, n are powers of a common integer. However, in the paper Cooper actually proves Corollary 10.11: that if there is a bilipschitz embedding \({{\mathbb {Z}}}(m,m) \rightarrow {{\mathbb {Z}}}(n,n)\) onto a clopen then m, n are powers of a common integer. Indeed, the proof relies on the fact that the image is a clopen set in \({{\mathbb {Z}}}(n,n)\). They can assume this extra condition since they have proved that \(f^u: {{\mathbb {Q}}}(m,m) \rightarrow {{\mathbb {Q}}}(n,n)\) is a bilipschitz homeomorphism (which follows from the coarse surjectivity of f) and hence the image of \(C \subset {{\mathbb {Q}}}(m,m)\) will be clopen in \(C' \subset {{\mathbb {Q}}}(n,n)\). In our case, when f is not coarse surjective, we know only that \(f^u\) is a bilipschitz embedding. However, it follows from the equivalence of (A4) and (A1) proved in this paper that Theorem 7.2 is nonetheless true.
So suppose we have some (K, C)-quasiisometric embedding \(f: HT(p,q) \rightarrow HT(p',q')\). For simplicity of notation, write \(HT(p,q) = X\), \(HT(p',q') = X'\). A generalisation of Proposition 4.1 in Farb–Mosher implies that there exists a constant \(A \geqslant 0\), only depending on K and C, such that for all \(Q \in \partial ^u X\) there exists some unique \(Q' \in \partial ^u X'\) such that \(d_H(f(Q), Q') \leqslant A\). We write \(f^u(Q) = Q'\). We can use the map \(f^u\) to define a map \(\theta _f: T(p,q) \rightarrow T(p',q')\) as follows (here we are identifying T(p, q) with the set of horocycles in \(X = HT(p,q)\) and similarly for \(T(p',q')\)). Suppose we have some horocycle \(\sigma \subset HT(p,q)\). Let \(\mu \) be the first branching horocycle above \(\sigma \); say \(\mu = \partial (Q_1 \cap Q_2)\) where \(Q_1, Q_2 \in \partial ^u X\). Let \(Q_i' \in \partial ^u X'\) have bounded Hausdorff distance from \(f(Q_i)\). Then we set \(\theta _f(\sigma ) = \partial (Q_1' \cap Q_2')\). The following lemma removes the coarse surjectivity requirement of Lemma 5.1 of Farb–Mosher.
Lemma 12
Given \(K \geqslant 1\), \(C \geqslant 0\), there exists a constant \(\lambda \geqslant 0\) such that if \(f:X \rightarrow X'\) is a (K, C)-quasiisometric embedding, then for each horocycle \(\sigma \subset X\) we have
Proof
In the proof of Lemma 5.1 of Farb–Mosher, they prove that there exists a constant \(\lambda _1 = \lambda _1(K,C) \geqslant 0\) such that for each horocycle \(\sigma \subset X\) we have
where \(\sigma ' = \theta _f(\sigma )\). In order to show that there exists some \(\lambda _2 = \lambda _2(K,C) \geqslant 0\) such that \(\sigma ' \subset \mathcal {N}_{\lambda _2}(f(\sigma ))\), Farb and Mosher use the coarse inverse of f which we no longer have. However, we can apply an alternative argument.
Let \(z \in \sigma '\). Let \(\mu \) be the branching horocycle above \(\sigma \) such that \(\theta _f(\sigma ) = \theta _f(\mu )\). Let \(Q_1, Q_2 \subset X\) be the two hyperbolic planes in X such that \(\mu = \partial (Q_1 \cap Q_2)\) and let \(Q_1', Q_2' \subset X'\) be the two hyperbolic planes in \(X'\) such that \(\sigma ' = \partial (Q_1' \cap Q_2')\). Recall that for \(i = 1,2\) we have
where A only depends on K, C. Let \(z_1\) be the unique point of \(Q_1' \setminus Q_2'\) satisfying \(d(z_1, z) = d(z_1, \sigma ') = d(z_1, Q_2') = 2A + 1\). Similarly, Let \(z_2\) be the unique point of \(Q_2' \setminus Q_1'\) satisfying \(d(z_2, z) = d(z_2, \sigma ') = d(z_2, Q_1') = 2A + 1\). We know there exists some \(x_i \in Q_i\) such that \(d(f(x_i), z_i) \leqslant A\). Thus, \(d(f(x_1), Q_2') \geqslant A+1\) and \(d(f(x_2), Q_1') \geqslant A+1\). Hence, \(x_1 \in Q_1 \setminus Q_2\) and \(x_2 \in Q_2 \setminus Q_1\). Also,
and so
which implies that
Let \(w_i\) be the unique point of \(\sigma \) realising \(d(\sigma , x_i)\). Then \(d(w_i, x_i) \leqslant d(x_i, \mu ) + \log (q)\). We know that
and so
and so we are done. \(\square \)
The rest of Farb and Mosher’s argument goes through almost verbatim - one only has to change m and n to \(p,q,p',q'\) as appropriate. It follows that if \(f: HT(p,q) \rightarrow HT(p',q')\) is a quasiisometric embedding then \(f^u: {{\mathbb {Q}}}(p,q) \rightarrow {{\mathbb {Q}}}(p',q')\) is a bilipschitz embedding. Let \(C \subset {{\mathbb {Q}}}(p,q)\) be some clone. We know that \(f^u(C)\) has finite diameter and hence is contained in some clone \(C' \subset {{\mathbb {Q}}}(p',q')\). We know that C and \(C'\) are bilipschitz homeomorphic to \({{\mathbb {Z}}}(p,q)\) and \({{\mathbb {Z}}}(p',q')\) respectively. So we have proved the following.
Proposition 13
If there exists a quasiisometric embedding \(HT(p,q) \rightarrow HT(p',q')\) then there exists a bilipschitz embedding \({{\mathbb {Z}}}(p,q) \rightarrow {{\mathbb {Z}}}(p',q')\).
6.2 Functors
In this section we will prove that (A4) \(\iff \) (A3) and (B3) \(\iff \) (B2). Much of this section is simply an application of the ideas contained in the paper of Bonk and Schramm [15] on the functors \(\partial \) and \(\text {Con}\) between Gromov-hyperbolic metric spaces and their boundary. However, for the purposes of this paper, it is simpler to ‘start from scratch’ as opposed to translating their more general work over to the needs of our specialised situation.
Suppose for every vertex v of R(p, q) we arbitrarily label the edges emanating from v with the letters \(\{ 0, \ldots , p-1 \}\). This edge labelling provides a natural identification of \({{\mathbb {Z}}}(p,q)\) with the set of geodesic rays based at the basepoint b of R(p, q). Throughout this section we make this identification. We begin with definitions.
Definition
Suppose we have a pair of maps \(f, g: R(p,q) \rightarrow R(p',q')\) between regular rooted trees. We say that f and g are roughly equivalent if \(d(f,g) < \infty \). We denote by [f] the rough equivalence class of some map f between regular rooted trees.
Definition
Let \(\mathcal {C}\) be the category consisting of regular rooted trees R(p, q) and rough isometric embeddings between them up to rough equivalence.
Definition
Let \(\mathcal {D}\) denote the category of symbolic Cantor sets \({{\mathbb {Z}}}(p,q)\) and bilipschitz embeddings between them.
We have the following theorem whose proof will be the content of this section.
Theorem 14
There exists a category isomorphism \(\partial : \mathcal {C} \rightarrow \mathcal {D}\) with inverse functor \(\Delta : \mathcal {D} \rightarrow \mathcal {C}\).
Evidently, Theorem 14 implies that (A4) \(\iff \) (A3) and (B3) \(\iff \) (B2). We begin by defining \(\partial : \mathcal {C} \rightarrow \mathcal {D}\).
Definition
We set \(\partial R(p,q) = {{\mathbb {Z}}}(p,q)\). Let \(f: R(p,q) \rightarrow R(p',q')\) be a rough isometric embedding. Let \(\gamma \in {{\mathbb {Z}}}(p,q)\). It follows from the Morse Lemma that there exists some \(\gamma ' \in {{\mathbb {Z}}}(p',q')\) with \(d_H(f(\gamma ), \gamma ') < \infty \). Indeed, such a \(\gamma '\) must be unique since distinct geodesic rays in \(R(p',q')\) have infinite Hausdorff distance. We set \(\partial [f] (\gamma ) = \gamma '\).
One needs to check that \(\partial [f]\) is well-defined: if f is roughly equivalent to g then \(d_H(f(\gamma ), g(\gamma )) < \infty \) and so \(\gamma '\) must be the same in both cases. It is also simple to check that \(\partial \) is functorial. Some notation.
-
Suppose \(\gamma , \eta \in {{\mathbb {Z}}}(p,q)\). Let \(\gamma \wedge \eta \) denote the point of \(\gamma \cap \eta \subset R(p,q)\) of maximal height.
Proposition 15
Let \(f: R(p,q) \rightarrow R(p',q')\) be a rough isometric embedding. Then \(\partial [f]: {{\mathbb {Z}}}(p,q) \rightarrow {{\mathbb {Z}}}(p',q')\) is a bilipschitz embedding.
Proof
Write \(g = \partial [f]\). Let \(\rho \) denote the metric on \({{\mathbb {Z}}}(p,q)\) and let \(\rho '\) denote the metric on \({{\mathbb {Z}}}(p',q')\). Let \(\gamma , \eta \in {{\mathbb {Z}}}(p,q)\) and write \(\gamma ' = g(\gamma ), \eta ' = g(\eta )\). By Lemma 7, we know that f is D-coarsely height-preserving for some constant \(D \geqslant 0\). We also know the following
Similarly,
So we just need to show that \({|}h(\gamma \wedge \eta ) - h(\gamma ' \wedge \eta '){|} \leqslant C\) where C is some constant that does not depend on \(\gamma , \eta \). We know that there exists some constant \(B \geqslant 0\) such that \(d_H(f(\gamma ), \gamma ') \leqslant B\) and \(d_H(f(\eta ), \eta ') \leqslant B\). Let \(x \in \gamma \), \(y \in \eta \) be such that \(d(f(x), \gamma ' \wedge \eta ') \leqslant B\) and \(d(f(y), \gamma ' \wedge \eta ') \leqslant B\). Then \(d(f(x), f(y)) \leqslant 2B\) and so \(d(x,y) \leqslant 2B + A\) where A is the rough isometry constant of f. Consequently, \(d(x, \gamma \cap \eta ) \leqslant 2B + A\) and so
Now let \(w \in \gamma '\), \(z \in \eta '\) be such that \(d(w, f(\gamma \wedge \eta )) \leqslant B\) and \(d(z, f(\gamma \wedge \eta )) \leqslant B\). Then \(d(w,z) \leqslant 2B\) and so \(d(w, \gamma ' \cap \eta ') \leqslant 2B\). Hence
and we are done. \(\square \)
Before defining \(\Delta : \mathcal {D} \rightarrow \mathcal {C}\), we need some more terminology.
-
By a clone in \({{\mathbb {Z}}}(p,q)\) we mean a subset \(C \subseteq {{\mathbb {Z}}}(p,q)\) consisting of all words beginning with some fixed word. Suppose we have some subset \(S \subseteq {{\mathbb {Z}}}(p,q)\). The minimal clone containing S is the clone containing S of minimal diameter.
-
Using an arbitrary edge labelling of R(p, q), we can identify a vertex v of R(p, q) with a finite word u in the alphabet \(\{ 0, \ldots , p-1\}\). Denote by C(v) the clone consisting of all words beginning with u. In this manner, we have a bijection between the vertices of R(p, q) and the clones of \({{\mathbb {Z}}}(p,q)\).
Definition
We set \(\Delta {{\mathbb {Z}}}(p,q) = R(p,q)\). Suppose we have a bilipschitz embedding \(g: {{\mathbb {Z}}}(p,q) \rightarrow {{\mathbb {Z}}}(p',q')\). Let \(v \in V(R)\) be some vertex of R(p, q). We have that \(gC(v) \subseteq {{\mathbb {Z}}}(p',q')\) is contained in some minimal clone \(C(w) \subseteq {{\mathbb {Z}}}(p',q')\) where \(w \in V(R')\). We set \(f(v) = w\). Thus, we have constructed a map \(f: V(R) \rightarrow R(p',q')\). Precomposition with the nearest point projection map gives us a map \(f: R(p,q) \rightarrow R(p',q')\). We set \([f] = \Delta g\).
Proposition 16
Retaining the notation from the previous definition, \(f: V(R) \rightarrow R(p',q')\) is an order-preserving rough isometric embedding.
Proof
A preliminary observation: given a vertex v of R, we have that \({{\,\textrm{diam}\,}}(gC(v)) = {{\,\textrm{diam}\,}}(C(f(v)))\). This follows from the minimality of \(C(f(v)) \supseteq gC(v)\).
We now prove that f is order-preserving. Suppose \(v, v'\) are vertices of \(R = R(p,q)\) such that \(v'\) descends from v. We want to show that \(f(v')\) descends from f(v). Write \(w = f(v)\) and \(w' = f(v')\). Since \(C(v') \subseteq C(v)\) we have that \(gC(v') \subseteq gC(v)\). Therefore \(gC(v') \subseteq C(w)\). Thus, by the minimality of \(C(w')\), we have \(C(w') \subseteq C(w)\). So \(w'\) descends from w. Hence, f is order-preserving.
We will now show that f is a rough isometric embedding. Let \(v, v' \in V(R)\) and, as before, write \(w = f(v)\), \(w' = f(v')\). We have three cases to consider: \(v'\) descends from v, v descends from \(v'\) or neither descends from the other. The first two cases are evidently symmetrical and so we only consider the first and the third. Suppose \(v'\) descends from v. Say, \(d(b,v) = k \log (q)\) and \(d(b,v') = l\log (q)\) where k, l are non-negative integers with \(k \leqslant l\). Then \(d(v,v') = (l-k)\log (q)\). We also know that \({{\,\textrm{diam}\,}}(C(v)) = q^{-k}\) and \({{\,\textrm{diam}\,}}(C(v')) = q^{-l}\). Thus
Similarly, since \(w'\) descends from w, we have that
By the observation, we know that \({{\,\textrm{diam}\,}}(C(w')) = {{\,\textrm{diam}\,}}(gC(v'))\) and \({{\,\textrm{diam}\,}}(C(w)) = {{\,\textrm{diam}\,}}(gC(v))\). Therefore
and similarly
Here we have used the fact that g is \(\lambda \)-bilipschitz and so only changes diameters by factors in the interval \([\lambda ^{-1}, \lambda ]\). So we are done in the case when \(v'\) descends from v. Now suppose that neither descends from the other. Let \(W = f(v \wedge v')\). We have that
Similarly, \({{\,\textrm{diam}\,}}(C(w \wedge w')) \geqslant \lambda ^{-2} {{\,\textrm{diam}\,}}(C(W))\). Since \(w \wedge w'\) descends from W this implies that
Also, note that our work on the case when \(v'\) descends from v implies that \(d(w,W) - d(v,v \wedge v')\) and \(d(W,w') - d(v \wedge v', v')\) are also both contained in the interval \([-2\log (\lambda ), 2\log (\lambda )]\). Therefore
Similarly, \(d(w,w') \geqslant d(v,v') - 8\log (\lambda )\). Therefore f is an \(8\log (\lambda )\)-rough isometric embedding. \(\square \)
The following proposition proves Theorem 14.
Proposition 17
\(\partial : \mathcal {C} \rightarrow \mathcal {D}\) and \(\Delta : \mathcal {D} \rightarrow \mathcal {C}\) are mutually inverse functors.
Proof
Let \(g: {{\mathbb {Z}}}(p,q) \rightarrow {{\mathbb {Z}}}(p',q')\) be a bilipschitz embedding and let \([f] = \Delta g\). Suppose that f has rough isometry constant A. We will first show that \(\partial [f] = g\). Let \((a_n) \in {{\mathbb {Z}}}(p,q)\), let \(\gamma \) be the corresponding geodesic ray and suppose that \((v_n)\) is the sequence of vertices traversed by \(\gamma \). Write \(w_n = f(v_n)\). We know that \((a_n) \in C(v_n)\) and \(C(v_n) \supseteq C(v_{n+1})\) for all n. Hence \(g((a_n)) \in gC(v_n)\) for all n. Further, \(gC(v_n) \subseteq C(w_n)\) and so \(g((a_n)) \in C(w_n)\) for all n. So we have
where we have used the fact that f preserves order. We know that \({{\,\textrm{diam}\,}}(C(v_n)) \rightarrow 0\) and so \({{\,\textrm{diam}\,}}(C(w_n)) = {{\,\textrm{diam}\,}}(gC(v_n)) \rightarrow 0\) since g is a bilipschitz embedding. Therefore \(g((a_n))\) is contained in a decreasing sequence of clones; there can only be one element contained in all of them. Let \(\gamma '\) be the geodesic ray joining together the vertices \(w_n\). We claim that \(d_H(f(\gamma ), \gamma ') < \infty \). It is clear that \(f(\gamma )\) is contained in a finite neighbourhood of \(\gamma '\). To see that \(\gamma '\) is contained in a finite neighbourhood of \(f(\gamma )\), note that \(d(w_n, w_{n+1}) \leqslant \log (q) + A\) for all n. It follows that some \(y \in \gamma '\) is at distance at most \(\max (\log (q) + A, d(b', w_1))\) from an element of \(f(\gamma )\). So \(\partial [f](\gamma ) = \gamma '\). But \(\gamma ' \in C(w_n)\) for all n and so \(\gamma ' = g((a_n))\). Hence \(\partial \Delta g = g\).
We will now prove that if we have an A-rough isometric embedding \(f: R(p,q) \rightarrow R(p',q')\) then \(\Delta \partial [f] = [f]\). By Lemma 7, we know that f is D-coarsely height-preserving for some constant \(D \geqslant 0\). Let \(v \in V(R)\). Suppose C(w) is the minimal clone such that \((\partial [f]) C(v) \subseteq C(w)\). Then \(\Delta (\partial [f]) (v) = w\). We want to show that w is at some uniformly bounded distance from f(v). By the minimality of w, there must exist \(\gamma , \eta \in C(v)\) such that \(\gamma \wedge \eta = v\) and \(\gamma ' \wedge \eta ' = w\) where \(\gamma ' = \partial [f](\gamma )\), \(\eta ' = \partial [f] (\eta )\). By the same argument as in Proposition 15, it follows that \({|}h(v) - h(w){|}\) is uniformly bounded. Let \(z \in \gamma '\) be such that \(d(z, f(v)) \leqslant B\). Then \({|}h(z) - h(v){|} \leqslant B + D\). So
which is uniformly bounded.
Finally, observe that \(\Delta \) is a functor because \(\partial \) is
\(\square \)
6.3 From trees to treebolic spaces
In this section we will prove that (A3) \(\implies \) (A5) and (B2) \(\implies \) (B4). Recall that T(p, q) is the infinite regular tree with vertex valency \(p+1\) and edge length \(\log (q)\). We can view T(p, q) as two copies of R(p, q) connected together at the basepoints by a line of length \(\log (q)\). With this in mind, write \(T(p,q) = R_1 \sqcup R_2 \sqcup L\) where \(R_1,R_2\) are isometric to R(p, q) and L is the open line of length \(\log (q)\). We let \(b_1\) denote the basepoint of \(R_1\) and let \(b_2\) denote the basepoint of \(R_2\). We can also write \(T(p',q') = R_1' \sqcup R_2' \sqcup L'\) where \(R_1', R_2',L',b_1',b_2'\) are defined similarly.
Proposition 18
A rough isometric embedding \(R(p,q) \rightarrow R(p',q')\) induces a rough isometric embedding \(T(p,q) \rightarrow T(p',q')\). Further, if R(p, q) is rough isometric to \(R(p',q')\) then T(p, q) is rough isometric to \(T(p',q')\).
Proof
Suppose we have an \(A-\)rough isometric embedding \(f: R(p,q) \rightarrow R(p',q')\). Let V(T) be the vertex set of T(p, q), let \(V_1\) be the vertex set of \(R_1\), let \(V_2\) be the vertex set of \(R_2\) and let V be the vertex set of R(p, q). We define a map \(F: V(T) \rightarrow T(p',q')\) as follows. If \(v \in V_1\) then set \(F(v) = f(v)\) where we have identified \(V_1\) with V and \(R(p',q')\) with \(R_1'\). If \(v \in V_2\) then set \(F(v) = f(v)\) where we have now identified \(V_2\) with V and \(R(p',q')\) with \(R_2'\). We need to prove that F is a rough isometric embedding. If \(v,w \in V_1\) or \(v,w \in V_2\), then F roughly preserves the distance between v and w since f does. Write \(\kappa = d(b', f(b))\). If \(v \in V_1\) and \(w \in V_2\) then we have that
Similarly, \(d(F(v), F(w)) \geqslant d(v,w) - 2\kappa - 2A\). So F is a rough isometric embedding. Note that if f is a rough isometry then so is F. \(\square \)
Proposition 19
Suppose we have some fixed height functions on T(p, q) and \(T(p',q')\) determined by the geodesic rays \(\gamma \) and \(\gamma '\) respectively. If there exists an A-rough isometric embedding \(f: T(p,q) \rightarrow T(p',q')\) then there exists a coarsely height-preserving A-rough isometric embedding \(g: T(p,q) \rightarrow T(p',q')\). Further, if f is a rough isometry then so is g.
Proof
Suppose \(\gamma \) has basepoint b and \(\gamma '\) has basepoint \(b'\). Let \(b''\) be the vertex of \(T(p',q')\) closest to f(b). By the Morse lemma, there exists a unique geodesic ray \(\gamma ''\) based at \(b''\) such that \(d_H(\gamma '', f(\gamma )) \leqslant B\) where \(B \geqslant 0\). Let \(\psi : T(p',q') \rightarrow T(p',q')\) be some isometry taking \(\gamma ''\) to \(\gamma '\). We claim that \(g = \psi f\) is coarsely height-preserving. Let \(x \in T(p,q)\). We have that
Similarly, \(d(b,x) \geqslant d(b',g(x)) - A - \log (q')\). Let \(\eta \) denote the geodesic segment from b to x. Let \(\xi \) denote the geodesic segment from \(b'\) to g(x). We have that \(d_H(\xi , g(\eta )) \leqslant C\) for some uniform constant \(C \geqslant 0\) by the Morse Lemma. Let \(\gamma \wedge \eta \) denote the point of \(\gamma \cap \eta \) of furthest distance from b and let \(\gamma ' \wedge \xi \) be defined similarly. Since \(g(\gamma )\) is uniformly close to \(\gamma '\) and \(g(\eta )\) is uniformly close to \(\xi \), identical arguments to those in the proof of Proposition 15 show that the difference between \(d(b, \gamma \wedge \eta )\) and \(d(b', \gamma ' \wedge \xi )\) is uniformly bounded. Since
and
it follows that g is coarsely height-preserving. \(\square \)
Recall that topologically \(HT(p,q) = T(p,q) \times {{\mathbb {R}}}\). Let \(\pi : HT(p,q) \rightarrow T(p,q)\) be the projection onto the first factor and let \(\zeta : HT(p,q) \rightarrow {{\mathbb {R}}}\) be the projection onto the second factor. We choose a height function on HT(p, q) that agrees with the height function on T(p, q): i.e. \(h(\pi x) = h(x)\) for all \(x \in HT(p,q)\).
Suppose we have a coarsely height-preserving rough isometric embedding \(f: T(p,q) \rightarrow T(p',q')\). Let \({\hat{f}}\) be the product map \(f \times \text {id}: HT(p,q) \rightarrow HT(p',q')\). We call \({\hat{f}}\) the horocyclic extension of f. We want to show that \({\hat{f}}\) is a quasiisometric embedding. Consider the function
given by
where \(y' = (\pi x, \zeta y)\) and \(x' = (\pi y, \zeta x)\). Two key observations are that for \(x,y \in HT(p,q)\)
-
\(d(x,y) \geqslant d(\pi x, \pi y)\);
-
\(d(x,y) \leqslant d(\pi x, \pi y) + D(x,y)\).
We can also claim that \(d(x,y) \geqslant D(x,y)\). Without loss of generality suppose that \(D(x,y) = d(x,y')\). This implies that \(h(x) \geqslant h(y)\). Let \(\mathcal {P}\) be the map which collapses HT(p, q) onto a hyperbolic plane containing x and \(y'\) (see, for example, the map \(\rho _j\) described at the start of the proof of Theorem 6.1 in [4]). \(\mathcal {P}\) preserves the length of paths and so it must be distance-contracting. So \(d(x,y) \geqslant d(x, \mathcal {P}(y))\). Further, \(d(x, \mathcal {P}(y)) \geqslant d(x, y')\) since \(y, \mathcal {P}(y)\) are contained in the same hyperbolic plane and \(h(y') \geqslant h(\mathcal {P}(y))\). Hence, \(d(x,y) \geqslant D(x,y)\).
Proposition 20
If \(f: T(p,q) \rightarrow T(p',q')\) is a B-coarsely height-preserving A-rough isometric embedding then the horocyclic extension \({\hat{f}}: HT(p,q) \rightarrow HT(p',q')\) is a \((2, A + 2B)\)-quasiisometric embedding. Further, if f is a rough isometry then \({\hat{f}}\) is a quasiisometry.
Proof
First observe that \({\hat{f}}\) is also B-coarsely height-preserving:
Claim
D is coarsely preserved by \({\hat{f}}\). That is, \({|}D(x,y) - D({\hat{f}}x, {\hat{f}}y){|} \leqslant 2B\).
Proof of claim
Let \(x,y \in T(p,q)\). Suppose \({|}h(x) - h({\hat{f}}x){|} = \delta \leqslant B\). There exists a quadrilateral in \({{\mathbb {H}}}^2\) with vertices \(v_1, v_2, v_3, v_4\) such that \(d(v_1, v_2) = d(x,y')\), \(d(v_3, v_4) = d({\hat{f}}x, {\hat{f}}y')\) and \(d(v_2, v_3) = d(v_4, v_1) = \delta \). Hence
Similarly,
and so \({|}D(x,y) - D({\hat{f}}x, {\hat{f}}y){|} \leqslant 2B\). \(\square \)
We have that
and
and so \({\hat{f}}\) is a \((2, A+2B)\)-quasiisometric embedding. Suppose now that f is also A-coarse surjective and let \(z \in HT(p',q')\). Let \(x \in T(p,q)\) be such that \(d(f(x), \pi z) \leqslant A\). Let \(y \in HT(p,q)\) satisfy \(\pi y = x\) and \(\zeta y = \zeta z\). Then \(d({\hat{f}}(y), z) \leqslant A\) since \({\hat{f}}(y)\) and z have the same depth. So \({\hat{f}}\) is also coarse-surjective. \(\square \)
The implications (A3) \(\implies \) (A5) and (B2) \(\implies \) (B4) follow from Proposition 18, Proposition 19 and Proposition 20.
Data Availability
The MATLAB code used to generate Fig. 1 is available from the author on reasonable request.
References
Gromov, M.: Infinite groups as geometric objects. In: Proceedings of the International Congress of Mathematicians August 16–24 1983 Warszawa, pp. 385–392. PWN - Polish Scientific Publishers (1984)
Gromov, M.: Groups of polynomial growth and expanding maps (with an appendix by Jacques tits). Publications Mathématiques de l’IHÉS 53, 53–78 (1981)
Dyubina, A.: Instability of the virtual solvability and the property of being virtually torsion-free for quasi-isometric groups. Int. Math. Res. Not. 2000(21), 1097–1101 (2000)
Farb, B., Mosher, L.: A rigidity theorem for the solvable Baumslag-Solitar groups. Inventiones Mathematicae 131, 419–451 (1998)
Bendikov, A., Saloff-Coste, L., Salvatori, M., Woess, W.: The heat semigroup and Brownian motion on strip complexes. Adv. Math. 226, 03 (2009)
Bendikov, A., Saloff-Coste, L., Salvatori, M., Woess, W.: Brownian motion on treebolic space: escape to infinity. Revista Matematica Iberoamericana 31, 935–976 (2012)
Bendikov, A., Saloff-Coste, L., Salvatori, M., Woess, W.: Brownian motion on treebolic space: positive harmonic functions. Annales de l’Institut Fourier 66(4), 1691–1731 (2016)
Woess, W.: What is a horocyclic product, and how is it related to lamplighters?, Internationale Mathematische Nachrichten 224, 1–27 (2013)
Diestel, R., Leader, I.: A conjecture concerning a limit of non-cayley graphs. J. Algebraic Comb. 14, 17–25, 01 (2001)
Eskin, A., Fisher, D., Whyte, K.: Quasi-isometric rigidity of solvable groups. In: Proceedings of the International Congress of Mathematicians 2010, vol. 3, p. 12. ICM 2010 (2005)
Eskin, A., Fisher, D., Whyte, K.: Coarse differentiation of quasi-isometries i: Spaces not quasi-isometric to Cayley graphs. Ann. Math. 176, 08 (2006)
Deng, J., Wen, Z.-Y., Xiong, Y., Xi, L.: Bilipschitz embedding of self-similar sets. Journal d’Analyse Mathématique 114, 63–97, 09 (2011)
Bridson, M., Haefliger, A.: Metric Spaces of Non-positive Curvature, vol. 319, p. 1. Springer, New York (2009)
Kerr, A.: Tree approximation in quasi-trees. arXiv preprint arXiv:2012.10741 (2020)
Bonk, M., Schramm, O.: Embeddings of Gromov hyperbolic spaces. Geomet. Funct. Anal. 10, 243–284 (2000)
Acknowledgements
I would like to thank my supervisor Cornelia Druţu for reading early drafts of this paper and providing helpful advice. I would also like to thank the referee for their insightful comments.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Nairne, P.S. Embeddings of trees, cantor sets and solvable Baumslag–Solitar groups. Geom Dedicata 217, 13 (2023). https://doi.org/10.1007/s10711-022-00745-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10711-022-00745-z


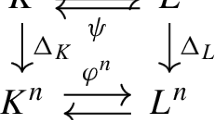
 to denote the set of all points in B of height h; this is always a finite set.
to denote the set of all points in B of height h; this is always a finite set. has cardinality at most
has cardinality at most  has cardinality less than
has cardinality less than  .
. will have the same cardinality as
will have the same cardinality as  since
since  has cardinality less than
has cardinality less than  is
is  . Set
. Set  since R does not branch in the interval
since R does not branch in the interval  has cardinality
has cardinality 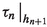 has cardinality
has cardinality  can be partitioned into
can be partitioned into 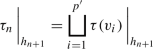



 has cardinality less than
has cardinality less than  has cardinality
has cardinality