Geometry of the Wiman–Edge pencil and the Wiman curve

Abstract

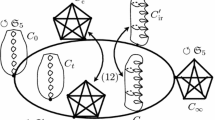
The Wiman–Edge pencil is the universal family $C_t, t\in {\mathcal {B}}$ of projective, genus 6, complex-algebraic curves admitting a faithful action of the icosahedral group $\mathfrak {A}_5$. The curve $C_0$, discovered by Wiman in 1895 (Ueber die algebraische Curven von den Geschlecht $p=4,5$ and 6 welche eindeutige Transformationen in sich besitzen) and called the Wiman curve, is the unique smooth, genus 6 curve admitting a faithful action of the symmetric group $\mathfrak {S}_5$. In this paper we give an explicit uniformization of ${\mathcal {B}}$ as a non-congruence quotient $\Gamma \backslash \mathfrak {H}$ of the hyperbolic plane $\mathfrak {H}$, where $\Gamma <{{\,\mathrm{PSL}\,}}_2(\mathbb {Z})$ is a subgroup of index 18. We also give modular interpretations for various aspects of this uniformization, for example for the degenerations of $C_t$ into 10 lines (resp. 5 conics) whose intersection graph is the Petersen graph (resp. $K_5$). In the second half of this paper we give an explicit arithmetic uniformization of the Wiman curve $C_0$ itself as the quotient $\Lambda \backslash \mathfrak {H}$, where $\Lambda$ is a principal level 5 subgroup of a certain “unit spinor norm” group of Möbius transformations. We then prove that $C_0$ is a certain moduli space of Hodge structures, endowing it with the structure of a Shimura curve of indefinite quaternionic type.