Equivariant cohomology of moduli spaces of genus three curves with level two structure

Abstract

We study the cohomology of the moduli space of genus three curves with level two structure and some related spaces. In particular, we determine the cohomology groups of the moduli space of plane quartics with level two structure as representations of the symplectic group on a six dimensional vector space over the field of two elements. We also make the analogous computations for some related spaces such as moduli spaces of genus three curves with a marked point and strata of the moduli space of Abelian differentials of genus three.

1 Introduction

The purpose of this note is to compute the de Rham cohomology of various moduli spaces of curves of genus 3 with level 2 structure. The group $\mathrm {Sp} \left( 6,\mathbb {F}_2 \right)$ acts on the set of level 2 structures of a curve. This action induces actions on the various moduli spaces under consideration which in turn yields actions on the cohomology groups. The cohomology groups thus become $\mathrm {Sp} \left( 6,\mathbb {F}_2 \right)$-representations and our goal is to describe these cohomology groups as representations together with their mixed Hodge structure.

The moduli spaces under consideration are essentially of three different types. First of all, we have the moduli space $\mathcal {M}_3[2]$ of genus 3 curves with level 2 structure and some natural loci therein. This will be our main object of study. Secondly we will consider the moduli space $\mathcal {M}_{3,1}[2]$ of genus 3 curves with level 2 structure and one marked point and some of its subspaces. Thirdly, we have the moduli space of genus 3 curves with level 2 structure marked with a holomorphic (i.e. Abelian) differential and some related spaces, e.g. the moduli space of genus 3 curves marked with a canonical divisor. There are many constructions, some classical and some new, relating the various spaces and which will provide essential information for our cohomological computations.

1.1 Outline

The plan of the paper is as follows. In Sect. 2 we give the basic definitions and sketch some of the classical theory around genus 3 curves and their level 2 structures. In particular, we recall the important Theorem 2 relating the moduli space of plane quartics with level 2 structure both to a space of certain configurations of points in the projective plane as well as to the moduli space of geometrically marked Del Pezzo surfaces of degree 2.

In Sect. 3 we sketch a construction, due to Looijenga [19], which expresses some natural loci in $\mathcal {M}_{3,1}[2]$ in terms of arrangements of tori and hyperplanes. We also discuss how one can use these complex geometrical descriptions, via a combination of combinatorial methods due to Fleischmann and Janiszczak [9] and algebraic methods due to Eisenbud and Sturmfels [8], to compute the cohomology groups of these loci.

Hyperelliptic curves will be somewhat peripheral in this note but we give a discussion in Sect. 4. In particular, we give the cohomology groups of the relevant moduli spaces. This has been done before by several authors - we briefly recall one method and give references to several others.

In Sect. 5 we recall some constructions and results regarding strata of moduli spaces of Abelian differentials, essentially due to Kontsevich and Zorich [18], and we make cohomological computations of these strata in genus 3, using our work from Sect. 3.

The core of the paper is Sect. 6 where we compute the cohomology of the moduli space $\mathcal {Q}[2]$ of plane quartics with level 2 structure as a representation of $\mathrm {Sp} \left( 6,\mathbb {F}_2 \right)$. This is done by comparing the results obtained previously in this paper to the arithmetic results of Bergvall [3] via standard comparison maps as well as some new constructions. The cohomology is given in Table 9 and is arguably the main result of this paper.

Finally, in Sect. 7 we make some comments around the cohomology of $\mathcal {M}_3[2]$ and, in particular, compute its $\mathrm {Sp} \left( 6,\mathbb {F}_2 \right)$-equivariant Euler characteristic, given below (see Sect. 1.2 for notation).

Theorem 1

The $\mathrm {Sp} \left( 6,\mathbb {F}_2 \right)$-equivariant weighted Euler characteristic of $\mathcal {M}_3[2]$ is

$$\begin{aligned} \mathrm {Eul}(\mathcal {M}_3[2],u)= & {} \phi _{1a} + \phi _{1a}u^2 - (\phi _{27a}+\phi _{35b}+\phi _{168a})u^4 + (2\phi _{120a}\\&+\,\phi _{168a}+\phi _{210a}+2\phi _{280b}+\phi _{405a}+\phi _{512a})u^6 \\&-\, (\phi _{21a}+\phi _{105b}+\phi _{105c}+\phi _{120a}+\phi _{168a}+2\phi _{189a} \\&+\,2\phi _{210a}+\phi _{210b}+\phi _{216a}+2\phi _{280b}+\phi _{315a}+\phi _{336a} \\&+\,2\phi _{378a}+4\phi _{405a}+2\phi _{420a}+\phi _{512a})u^8 \\&+\, (\phi _{70a}+\phi _{84a}+2\phi _{105c}+\phi _{120a}+2\phi _{168a}+2\phi _{189a} \\&+\, \phi _{189b}+\phi _{189c}+2\phi _{210a}+2\phi _{210b}+\phi _{216a}+3\phi _{280a} \\&+\, 2\phi _{280b}+2\phi _{315a}+3\phi _{336a}+3\phi _{378a}+4\phi _{405a}+4\phi _{420a} \\&+\, 5\phi _{512a})u^{10} + (\phi _{1a}+\phi _{15a}+\phi _{35b}+\phi _{84a} - \phi _{105a}-\phi _{168a}\\&-\,\phi _{189a}-\phi _{189b}-\phi _{189c}-\phi _{210a} -\, \phi _{210b}-\phi _{216a}-\phi _{280a}-2\phi _{280b}\\&-\,2\phi _{315a}-2\phi _{336a} - 2\phi _{378a}-2\phi _{405a}-2\phi _{420a}-3\phi _{512a})u^{12}. \end{aligned}$$

The main results of this note are Tables 1–10 giving the cohomology groups of various spaces occuring throughout the paper as representations of $\mathrm {Sp} \left( 6,\mathbb {F}_2 \right)$. For convenience (and for readers not interested in the representation structure of the cohomology) we also give some results in the form of Poincaré polynomials, for instance in Theorems 6, 7 and 11. We also remark that the results presented in Tables 1–10 give $\mathrm {Sp} \left( 6,\mathbb {F}_2 \right)$-equivariant point counts over finite fields of characteristic $\ge 3$ for the various moduli spaces occurring via Lefschetz trace formula (see, for instance, [3] for a detailed discussion on how to extract this information from Tables 1–10).

This paper relies heavily on the work of Looijenga [19] –indeed, already in the introduction of his paper Looijenga alludes to the possibility of making computations such as the ones have done here. Our work yields the results found in [13] and [19], arguably in a more natural way, and extends them by considering also level 2 structures (level structures are present already in Looijenga’s work but not in his cohomological results). A major difference between the work of Looijenga and the present paper is that the spaces considered by Looijenga have very few non zero cohomology groups while the spaces considered in this paper have lots of cohomology in every degree (even after splitting up the cohomology groups according to the representations occurring). This has the effect that where Looijenga can use nice and simple comparison maps and Gysin sequences we need to use more elaborate methods (and even after this, we are not able to patch together the cohomology of $\mathcal {M}_3[2]$ as he obtained the cohomology of $\mathcal {M}_{3}$).

1.2 Notations and conventions

Throughout the paper we shall encounter quite a large number of moduli spaces which will interact in various ways. Since it can be challenging to keep track of the notation of all these spaces we provide a list containing the most important ones below. We will not always need all the data in the notation below and at such instances we will leave out the unnecessary parts—e.g. $\mathcal {M}_{g}[l]$ will denote the moduli space $\mathcal {M}_{g,0}[l]$. At times we will add an overline to denote the closure of the space (in an appropriate ambient space). To stress that these closures are not compact, we place the line only over the data specifying the subspace and not over the entire symbol.

List of moduli spaces
$\mathcal {M}_{g,n}[l]$	The moduli space of curves of genus g with n marked points and level l structure, see Sects. 2.1 and 3.1
	The moduli space of hyperelliptic curves of genus g with n marked points and level l structure, see Sects. 2.2 and 4
$\mathcal {P}^2_{n}$	The moduli space of n points in general position in $\mathbb {P}^{2}$, see Sect. 2.3
${\mathcal {DP}}_{d,\mathrm {a}}^{\mathrm {gm}}$	The moduli space of geometrically marked Del Pezzo surfaces of degree d marked with an anticanonical curve, see Sects. 2.4 and 3.2
	The moduli space of curves of genus g marked with a holomorphic differential and level l structure, see Sect. 5
	The locus in consisting of curves marked with a holomorphic differential of type $\lambda$, see Sect. 5
$\mathcal {Q}[2]$	The moduli space of plane quartics with level 2 structure, see Sect. 2.2
$\mathcal {Q}_1[2]$	The moduli space of plane quartics with level 2 structure and one marked point, see Sect. 3.1
$\mathcal {Q}_{\mathrm {ord}}[2]$	The locus in $\mathcal {Q}_1[2]$ consisting of curves marked with an ordinary point, see Sect. 3.1
$\mathcal {Q}_{\mathrm {flx}}[2]$	The locus in $\mathcal {Q}_1[2]$ consisting of curves marked with a flex point, see Sect. 3.1
$\mathcal {Q}_{\mathrm {btg}}[2]$	The locus in $\mathcal {Q}_1[2]$ consisting of curves marked with a (genuine) bitangent point, see Sect. 3.1
$\mathcal {Q}_{\mathrm {hfl}}[2]$	The locus in $\mathcal {Q}_1[2]$ consisting of curves marked with a hyperflex point, see Sect. 3.1

Most of the paper will consider various cohomological computations and we therefore take this opportunity to establish some notation and recall some facts about cohomology of varieties. Throughout the paper we shall only consider de Rham cohomology with rational coefficients and we therefore use the simplified notation $H^{i} (X)$ for the cohomology group $H^{i} (X;\mathbb {Q})$ of a variety X.

The Poincaré polynomial of X, defined as

$$\begin{aligned} P(X,t) = \sum _{i \ge 0} \mathrm {dim}(H^{i} (X))t^k, \end{aligned}$$

encodes the dimensions of these $\mathbb {Q}$-vector spaces. The group $H^{i} (X)$ carries a mixed Hodge structure, i.e. $H^{i} (X)$ carries a weight filtration$W_{\bullet }$

$$\begin{aligned} \cdots \subseteq W_jH^{i} (X) \subseteq W_{j+1}H^{i} (X) \subseteq \cdots H^{i} (X) \end{aligned}$$

and a Hodge filtration$F^{\bullet }$

$$\begin{aligned} H^{i} (X) \supseteq \cdots F^pH^{i} (X) \supseteq F^{p+1}H^{i} (X) \supseteq \cdots \end{aligned}$$

such that $F^{\bullet }$ induces a pure Hodge structure of weight j on $\mathrm {gr}^W_jH^{i} (X)$. The Tate Hodge structure$\mathbb {Z}(1)$ is the unique Hodge structure on $\mathbb {Z}$ of pure weight $-2$. For a positive integer n we let $H^{i} (X)(n)$ denote the tensor product $H^{i} (X)\otimes \mathbb {Z}(1)^{\otimes n}$. Similarly, we let $H^{i} (X)(-n)$ denote $H^{i} (X)\otimes \mathbb {Z}(-1)^{\otimes n}$, where $\mathbb {Z}(-1)$ is the dual of $\mathbb {Z}(1)$. Tensor products with powers of the Tate Hodge structure or its dual are called Tate twists and have the effect of lowering the weights with 2n.

The following lemma will be used repeatedly. For a proof, see [19].

Lemma 1

Let X be a variety of pure dimension and let $Y \subset X$ be a hypersurface. Assume furthermore that both X and Y are rational homology manifolds. Then there is a Gysin exact sequence of mixed Hodge structures

$$\begin{aligned} \cdots \rightarrow H^{k-2} (Y)(-1) \rightarrow H^{k} (X) \rightarrow H^{k} (X{\setminus } Y) \rightarrow H^{k-1} (Y)(-1) \rightarrow \cdots \end{aligned}$$

The irreducible representations of $\mathrm {Sp} \left( 6,\mathbb {F}_2 \right)$ are denoted as $\phi _{dx}$ where the subscripts follow the conventions of [4], i.e. d denotes the dimension of the representation and the letter x is used to distinguish different representations of the same dimension. The letters used here are the same as in [4].

In Table 1–10 we consider the cohomology groups of various spaces as representations of $\mathrm {Sp} \left( 6,\mathbb {F}_2 \right)$ and decompose them into irreducible representations. More precisely, the rows of these tables represent the cohomology groups and the columns correspond to irreducible representations. Thus, a number n in the row indexed by $H^i$ and column indexed by $\phi _{dx}$ means that the irreducible representation $\phi _{dx}$ occurs with multiplicity n in $H^i$.

2 Background

In this section we recall some material related to curves, level structures and some related objects. Particular attention is given to plane quartics and their bitangents. For more information about this classical topic, see for instance Chapter 6 of [6], the paper [14] or Chapter 2 and 3 of [1].

We work over over the field of complex numbers.

2.1 Level structures

Let C be a smooth and irreducible curve of genus g and let $\mathrm {Jac}(C)$ denote its Jacobian. For any positive integer l there is an isomorphism

$$\begin{aligned} \mathrm {Jac}(C)[l] \cong \left( \mathbb {Z}/l\mathbb {Z} \right) ^{2g}, \end{aligned}$$

where $\mathrm {Jac}(C)[l]$ denotes the subgroup of l-torsion elements in $\mathrm {Jac}(C)$. A symplectic level l structure on C is an ordered basis $(D_1, \ldots , D_{2g})$ of $\mathrm {Jac}(C)[l]$ such that the Weil pairing has matrix of the form

$$\begin{aligned} \left( \begin{array}{cc} 0 &{} I_g \\ -I_g &{} 0 \end{array} \right) \end{aligned}$$

with respect to this basis, where $I_g$ denotes the identity matrix of size $g \times g$. We will often drop the adjective “symplectic” and simply say “level l structure”. There is a moduli space of curves of genus g with level l structure which we denote by $\mathcal {M}_{g}[l]$. For $n \ge 3$ it is fine but not for $n=2$ since a level 2 structure on a hyperelliptic curve is preserved by the hyperelliptic involution. The symplectic group $\mathrm {Sp}(2g,\mathbb {Z}/l\mathbb {Z})$ acts on $\mathcal {M}_{g}[l]$ by changing the level l structure.

2.2 Curves of genus three

Suppose that C is of genus 3. If C is not hyperelliptic, then a choice of basis of its space of global sections gives an embedding of C into the projective plane as a curve of degree 4. As is easily seen via the genus-degree formula, every smooth plane quartic curve is of genus 3 and we thus have a decomposition

where $\mathcal {Q}[l]$ denotes the quartic locus and denotes the hyperelliptic locus.

From now on we shall specialize to the case $l=2$. The locus $\mathcal {Q}[2]$ is by far the more complicated of the two loci and its investigation will therefore take up most of this note, but we will also consider hyperelliptic curves in Sect. 4.

There is a close relationship between level 2 structures on a plane quartic and its bitangents. More precisely, if $C \in \mathbb {P}^2$ is a plane quartic curve and $B \in \mathbb {P}^2$ is a bitangent line of C, then $C \cdot B = 2P + 2Q$ for some points P and Q on C. Thus, if we set $D=P+Q$ then $2D = K_C$. Divisors D with the property that $2D=K_C$ are called theta characteristics. A theta characteristic D is called even or odd depending on whether $h^0(D)$ is even or odd and it can be shown that there is a bijective correspondence between the set of odd theta characteristics of C and the set of bitangents of C given by the construction above.

Given two theta characteristics D and $D'$ we obtain a 2-torsion element by taking the difference $D-D'$. This gives the set $\Theta$ of theta characteristics on C the structure of a $\mathrm {Jac}(C)[2]$-torsor. The union $V=\mathrm {Jac}(C)[2] \sqcup \Theta$ is thus a vector space over $\mathbb {F}_2= \mathbb {Z}/2\mathbb {Z}$ of dimension 7. Alternatively, we can describe V as the 2-torsion subgroup of $\mathrm {Pic}(C)/\mathbb {Z}K_C$.

Let $\theta$ be an ordered basis of V consisting of odd theta characteristics. If D is a theta characteristic, then the number c of non zero coordinates of D relative to $\theta$ is an odd number. If the expression

$$\begin{aligned} h(D) \quad \mathrm {mod} \, 2 \end{aligned}$$

only depends on the residue class $c \, \mathrm {mod} \, 4$, we say that $\theta$ is an ordered Aronhold basis.

Proposition 1

There is a bijection between the set of ordered Aronhold bases on C and the set of level 2 structures on C.

For a proof, see either [7] or the paper [14]. We will see, in Theorem 2, that this bijection can be chosen to work well in families.

Thus, we may think of a level 2 structure on C as an ordered Aronhold basis of odd theta characteristics on C. Since odd theta characteristics are cut out by bitangents we can also think about level 2 structures in terms of ordered sets of seven bitangents (but we must then bear in mind that not every ordered set of seven bitangents corresponds to a level 2 structure).

2.3 Point configurations in the projective plane

Let $P_1, \ldots , P_7$ be seven points in $\mathbb {P}^2$. We say that the points are in general position if there is no “unexpected” curve passing through any subset of them, i.e. if

• no three of the points lie on a line and

• no six of the points lie on a conic.

We denote the moduli space of ordered septuples of points in general position in $\mathbb {P}^2$ up to projective equivalence by $\mathcal {P}^2_7$.

Given seven points in general position in $\mathbb {P}^2$ there is a net $\mathcal {N}$ of cubics passing through the points. The set of singular members of $\mathcal {N}$ is a plane curve T of degree 12 with 24 cusps and 28 nodes. The dual $T^{\vee } \subset \mathcal {N}^{\vee } \cong \mathbb {P}^2$ is a smooth plane quartic curve. Another way to obtain a genus 3 curve is by taking the set S of singular points of members of $\mathcal {N}$. The set S is a sextic curve with ordinary double points precisely at $P_1, \ldots , P_7$. From this information it is easy to see, via the genus-degree formula, that S has geometric genus 3. One can also show that the map $\sigma$ sending a point P in S to the unique member of $\mathcal {N}$ with a singularity at P is a birational isomorphism from S to T.

2.4 Del Pezzo surfaces of degree two

Recall that a Del Pezzo surface is a smooth and projective algebraic variety of dimension two such that its anticanonical class is ample. The degree of a Del Pezzo surface S is the self intersection number of its canonical class, $K_S^2$.

Given seven points $P=(P_1, \ldots , P_7)$ in general position in $\mathbb {P}^2$, the blow-up $X=\mathrm {Bl}_P\mathbb {P}^2$ is a Del Pezzo surface of degree 2. Moreover, every Del Pezzo surface of degree 2 can be realized as such a blow-up, see [21]. We denote the blow-up map by $\pi : X \rightarrow \mathbb {P}^2$. However, the points $P_1, \ldots , P_7$ do not only give us the Del Pezzo surface X - we also get the seven exceptional curves $E_1, \ldots , E_7$. Together with the strict transform L of a line in $\mathbb {P}^2$ they determine a basis for the Picard group of X

$$\begin{aligned} \mathrm {Pic}(X) = \mathbb {Z}L \oplus \mathbb {Z}E_1 \oplus \cdots \oplus \mathbb {Z}E_7. \end{aligned}$$

The intersection theory is given by

$$\begin{aligned} L^2=1, \quad E_i^2=-1, \quad L \cdot E_i = E_i \cdot E_j =0, \quad i\ne j. \end{aligned}$$

Not every ordered basis of $\mathrm {Pic}(X)$ comes from a blow-up as above. Bases which do arise in this way are called geometric markings. Two geometrically marked Del Pezzo surfaces $(X,E_1, \ldots , E_7)$ and $(X',E'_1, \ldots , E'_7)$ are isomorphic if there is an isomorphism of surfaces $\phi :X \rightarrow X'$ such that $\phi ^*(E'_i)=E_i$ for all i. We denote the moduli space of geometrically marked Del Pezzo surfaces of degree 2 by ${\mathcal {DP}}_2^{\mathrm {gm}}$.

Given a quartic $C \subset \mathbb {P}^2$ we can obtain a Del Pezzo surface X of degree 2 as the double cover of $\mathbb {P}^2$ ramified along C. Moreover, every Del Pezzo surface of degree 2 can be realized as such a double cover, see [17], Theorem 3.5. We let $p:X \rightarrow \mathbb {P}^2$ denote the covering map and let $\iota$ denote the involution exchanging the two sheets. If $E_1, \ldots , E_7$ is a geometric marking of X then $p(E_1), \ldots , p(E_7)$ is an ordered Aronhold set of bitangents of C.

We have thus seen how to obtain a geometrically marked Del Pezzo surface of degree 2 both from seven ordered points in general position and from a plane quartic curve with level 2 structure and we have also seen how to obtain the quartic curve directly from the seven points. We summarize the situation in the diagram below.

Here $\sigma ^{\vee }$ denotes the composition of $\sigma$ and the duality map. In each of the spaces we have a copy of the curve C: in $\mathbb {P}^2_{\mathrm {curve}}$ we have the actual curve C, in X we obtain an isomorphic copy of C by taking the fixed locus of the involution $\iota$ and in $\mathbb {P}^2_{\mathrm {pts}}$ we have a sextic model S of C with seven double points.

Theorem 2

(van Geemen [7]) The above construction yields $\mathrm {Sp}(6,\mathbb {F}_2)$-equivariant isomorphisms

3 Curves and surfaces with marked points

3.1 Genus three curves with marked points

We now turn our attention to the moduli space $\mathcal {M}_{3,1}[2]$ of genus 3 curves with level 2 structure and one marked point. Also in this case we have a decomposition

into a quartic locus and a hyperelliptic locus. However, in this case there is also a natural decomposition of the quartic locus in terms of the behaviour of the tangent line at the marked point.

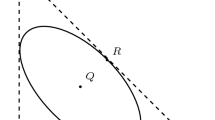
Let C be a plane quartic curve, let P be a point on C and let $T_P \subset \mathbb {P}^{2}$ denote the tangent line of C at P. Since C is of degree 4, Bézout’s theorem tells us that the intersection product $C \cdot T_P$ will consist of 4 points. There are four possibilities:

(i):

$T_P \cdot C = 2P + Q + R$ where Q and R are two distinct points on C, both different from P. In this case, $T_P$ is called an ordinary tangent line of C and P is called an ordinary point of C.

(ii):

$T_P \cdot C = 2P + 2Q$ where $Q \ne P$ is a point on C. In this case, $T_P$ is called a bitangent of C and P is called a bitangent point of C.

(iii):

$T_P \cdot C = 3P +Q$ where $Q \ne P$ is a point on C. In this case, $T_P$ is called a flex line of C and P is called a flex point of C.

(iv):

$T_P \cdot C = 4P$. In this case, $T_P$ is called a hyperflex line of C and P is called a hyperflex point of C.

This yields a decomposition of $\mathcal {Q}_1[2]$

$$\begin{aligned} \mathcal {Q}_1[2]= \mathcal {Q}_{\mathrm {ord}}[2]\sqcup \mathcal {Q}_{\mathrm {flx}}[2]\sqcup \mathcal {Q}_{\mathrm {btg}}[2] \sqcup \mathcal {Q}_{\mathrm {hfl}}[2]\end{aligned}$$

into a locus of curves marked with an ordinary, flex, bitangent and hyperflex point, respectively.

3.2 Del Pezzo surfaces of degree two with marked points

Let X be a Del Pezzo surface of degree 2. Recall that we can realize S both as a double cover $p:S \rightarrow \mathbb {P}^2$ ramified over a plane quartic C and as the blow-up $\pi :X \rightarrow \mathbb {P}^2$ in seven points $P_1, \ldots , P_7$ in general position. Also recall that there is an involution $\iota$ of X and that we can identify the fixed points of $\iota$ in X with $p^{-1}(C)$. We shall now give another characterization of the fixed points of $\iota$.

A curve $A \subset X$ in the anticanonical linear system $|-K_X|$ is called an anticanonical curve. The anticanonical class $-K_X=3L-E_1-\cdots -E_7$ corresponds to the linear system $\mathcal {C}$ of cubics in $\mathbb {P}^{2}$ passing through $P_1, \ldots , P_7$. The curve $B=\pi (p^{-1}(C))$ consists of all the singular points of members of $\mathcal {C}$. We thus see that a point $Q \in X$ is a point of $p^{-1}(C)$ if and only if there is a unique anticanonical curve A with a singularity at Q. Note that since A is isomorphic to a singular plane cubic, its irreducible components will be rational.

By the above construction we have that if (C, P) is a plane quartic with a marked point, the double cover $p:X \rightarrow \mathbb {P}^2$ ramified along C naturally becomes equipped with an anticanonical curve A with a singularity at the inverse image of P. Thus, if we introduce the moduli space ${\mathcal {DP}}_{2,\mathrm {a}}^{\mathrm {gm}}$ of geometrically marked Del Pezzo surfaces of degree 2 marked with a singular point of an anticanonical curve we have an isomorphism $\mathcal {Q}_1[2]\cong {\mathcal {DP}}_{2,\mathrm {a}}^{\mathrm {gm}}$.

Since $p^{-1}(C) \sim -2K_X$ it follows that

$$\begin{aligned} A.p^{-1}(C)=(-K_X).(-2K_X)=4. \end{aligned}$$

We have that A intersects $p^{-1}(C)$ with multiplicity at least 2 so p(A) is a tangent to C. The anticanonical curve A can be of the following types.

(i):

The anticanonical curve A can be an irreducible curve with a node. Then p(A) intersects C with multiplicity 2 at P so p(A) is either an ordinary tangent line or a bitangent. But we have shown that the inverse image of a bitangent under p consists of two exceptional curves which are conjugate under $\iota$ and we conclude that p(A) is an ordinary tangent line. We may thus identify the locus ${\mathcal {DP}}_{2,\mathrm {n}}^{\mathrm {gm}}\subset {\mathcal {DP}}_{2,\mathrm {a}}^{\mathrm {gm}}$ consisting of surfaces such that the anticanonical curve through the marked point is irreducible and nodal with the locus $\mathcal {Q}_{\mathrm {ord}[2]} \subset \mathcal {Q}_1[2]$ consisting of curves whose marked point is ordinary.

(ii):

The anticanonical curve A can be an irreducible curve with a cusp. Then p(A) intersects C with multiplicity 3 at P so p(A) must be a flex line. We may thus identify the locus ${\mathcal {DP}}_{2,\mathrm {c}}^{\mathrm {gm}}\subset {\mathcal {DP}}_{2,\mathrm {a}}^{\mathrm {gm}}$ consisting of surfaces such that the anticanonical curve through the marked point is irreducible and cuspidal with the locus $\mathcal {Q}_{\mathrm {flx}}[2]\subset \mathcal {Q}_1[2]$ consisting of curves whose marked point is a genuine flex point.

(iii):

The anticanonical curve A can consist of two rational curves intersecting with multiplicity one at P. Thus, the cubic $\pi (A)$ must be the product of a conic through five of the points $P_1, \ldots ,P_7$ with a line through the remaining two. Hence, A consists of two conjugate exceptional curves and p(A) is a genuine bitangent. We may thus identify the locus ${\mathcal {DP}}_{2,\mathrm {t}}^{\mathrm {gm}}\subset {\mathcal {DP}}_{2,\mathrm {a}}^{\mathrm {gm}}$ consisting of surfaces such that the anticanonical curve through the marked point consists of two rational curves intersecting transversally in two distinct points with the locus $\mathcal {Q}_{\mathrm {btg}}[2] \subset \mathcal {Q}_1[2]$ consisting of curves whose marked point is a genuine bitangent point.

(iv):

The anticanonical curve A can consist of two rational curves intersecting with multiplicity two at P. An analysis similar to the one above shows that p(A) is then a hyperflex line. We may thus identify the locus ${\mathcal {DP}}_{2,\mathrm {d}}^{\mathrm {gm}}\subset {\mathcal {DP}}_{2,\mathrm {a}}^{\mathrm {gm}}$ consisting of surfaces such that the anticanonical curve through the marked point consists of two rational curves with a double intersection with the locus $\mathcal {Q}_{\mathrm {hfl}}[2]\subset \mathcal {Q}_1[2]$ consisting of curves whose marked point is a hyperflex point.

In [19], Looijenga gave descriptions of each of these loci in terms of arrangements. In order to give his results, we need to investigate the Picard group of X in a bit more detail.

The Del Pezzo surface X has exactly 56 exceptional curves which can be described as follows.

(i):

The 7 exceptional curves $E_i$.

(ii):

The 21 strict transforms of lines between two points $P_i$ and $P_j$. The classes of these curves are given by $L-E_i-E_j$.

(iii):

The 21 strict transforms of conics through all but two points $P_i$ and $P_j$. The classes of these curves are given by $2L-E_1-\cdots -E_7+E_i+E_j$.

(iv):

The 7 cubics through $P_1, \ldots , P_7$ with a singularity in one of the points $P_i$. The classes of these curves are given by $3L-E_1-\cdots -E_7-E_i$.

We denote the set of these classes by $\mathscr {E}$.

The involution $\iota$ fixes the anticanonical class $K_X$. We denote the orthogonal complement of $K_X$ in $\mathrm {Pic}(X)$ by $K_X^{\perp }$. The involution $\iota$ acts as $-1$ on $K_X^{\perp }$. The elements $\alpha$ in $K_X^{\perp }$ such that $\alpha ^2=-2$ form a root system $\Phi$ of type $E_7$. We denote the Weyl group of $E_7$ by $W(E_7)$. The group $W(E_7)$ is isomorphic to $\mathrm {Sp} \left( 6, \mathbb {F}_2 \right) \times \mathbb {Z}/2\mathbb {Z}$ where $\mathbb {Z}/2\mathbb {Z}$ is the group of two elements generated by $\iota$. We denote the quotient $W(E_7)/\langle \iota \rangle$ by $W(E_7)^+$.

3.2.1 The irreducible nodal case

Let X be a geometrically marked Del Pezzo surface of degree 2 and let P be a point of X such that there is a unique rational anticanonical curve A on X which is nodal at P. The Jacobian $\mathrm {Jac}(A)$ is isomorphic to $k^*$ as a group, see Chapter II.6 of [16], and the restriction homomorphism

$$\begin{aligned} \mathrm {Pic}(X) \rightarrow \mathrm {Pic}(A), \end{aligned}$$

induces a homomorphism

$$\begin{aligned} r: K_X^{\perp } \rightarrow \mathrm {Jac}(A). \end{aligned}$$

Recall that $K_S^{\perp }$ is a lattice isometric to the $E_7$-lattice $L_{E_7}$. We thus see that r is an element of the 7-dimensional algebraic torus $T=\mathrm {Hom}(K_S^{\perp },\mathrm {Jac}(A)) \cong (k^*)^7$ and we have a natural action of $W(E_7)$ on T via its action on $K_S^{\perp }$.

Every root $\alpha$ in $\Phi$ determines a multiplicative character on T by evaluation, i.e. by sending an element $\chi \in T$ to $\chi (\alpha ) \in k^*$. Let

$$\begin{aligned} T_{\alpha } = \{\chi \in T | \chi (\alpha )=1\} \end{aligned}$$

and define

$$\begin{aligned} D_{E_7} = \bigcup _{\alpha \in \Phi (E_7)} T_{\alpha }, \end{aligned}$$

and let $T_{E_7}$ be the complement $T {\setminus } D_{E_7}$. We remark that $D_{E_7}$ is the toric arrangement associated to the root system $E_7$.

Theorem 3

[19] There is a $W(E_7)^+$-equivariant isomorphism

$$\begin{aligned} {\mathcal {DP}}_{2,\mathrm {n}}^{\mathrm {gm}}\rightarrow \{\pm 1 \} {\setminus } T_{E_7}. \end{aligned}$$

Since $\mathcal {Q}_{\mathrm {ord}}[2]$ is isomorphic to ${\mathcal {DP}}_{2,\mathrm {n}}^{\mathrm {gm}}$ and $W(E_7)^+$ is isomorphic to $\mathrm {Sp} \left( 6, \mathbb {F}_2 \right)$, it follows that there is a $\mathrm {Sp} \left( 6, \mathbb {F}_2 \right)$-equivariant isomorphism $\mathcal {Q}_{\mathrm {ord}}[2]\cong \{\pm 1 \} {\setminus } T_{E_7}$.

3.2.2 The other cases

The three other cases have similar descriptions. For instance, if we let $V_{E_7}$ denote the complement of the hyperplane arrangement associated to $E_7$ we have the following.

Theorem 4

[19] There is a $W(E_7)^+$-equivariant isomorphism

$$\begin{aligned} {\mathcal {DP}}_{2,\mathrm {c}}^{\mathrm {gm}}\rightarrow \mathbb {P}\left( V_{E_7} \right) . \end{aligned}$$

It follows that there is a $\mathrm {Sp} \left( 6, \mathbb {F}_2 \right)$-equivariant isomorphism $\mathcal {Q}_{\mathrm {flx}}[2]\cong \mathbb {P}(V_{E_7})$.

In order to state the results for the remaining two cases we need to introduce a little bit of notation. Let E be an exceptional curve. Then $E+\iota (E) = K_X$. We denote the orthogonal complement of $\langle E, \iota (E) \rangle$ in $\mathrm {Pic}(X)$ by $\langle E, \iota (E) \rangle ^{\perp }$. Since $K_X \in \langle E, \iota (E) \rangle$ we have $\langle E, \iota (E) \rangle ^{\perp } \subset K_X^{\perp }$ and $\Phi _E=\Phi \cap \mathrm {Pic}^{\perp }_{\langle E, \iota (E) \rangle }(S)$ is a subrootsystem of type $E_6$. We denote the Weyl group of $E_6$ by $W(E_6)$. We denote the complement of the toric arrangement associated to $E_6$ by $T_{E_6}$ and we denote the complement of the hyperplane arrangement associated to $E_6$ by $V_{E_6}$. The elements of $\mathscr {E}$ are in bijective correspondence with the cosets in the quotient $W(E_7)/W(E_6)$ and for each $e \in \mathscr {E}$ we let $T_{E_6}(e)$ be an isomorphic copy of $T_{E_6}$. similarly, we let $\mathbb {P}(V_{E_6})(e)$ be an isomorphic copy of $\mathbb {P}(V_{E_6})$. We then have the following two results.

Theorem 5

[19] There are $W(E_7)^+$-equivariant isomorphisms

$$\begin{aligned} {\mathcal {DP}}_{2,\mathrm {t}}^{\mathrm {gm}}\rightarrow \{\pm 1 \} {\setminus } \coprod _{e \in \mathscr {E}} T_{E_6}(e) \end{aligned}$$

and

$$\begin{aligned} {\mathcal {DP}}_{2,\mathrm {d}}^{\mathrm {gm}}\rightarrow \{\pm 1 \} {\setminus } \coprod _{e \in \mathscr {E}} \mathbb {P}(V_{E_6})(e). \end{aligned}$$

It follows that $\mathcal {Q}_{\mathrm {btg}}[2]$ is $\mathrm {Sp} \left( 6, \mathbb {F}_2 \right)$-equivariantly isomorphic to the quotient $\{\pm 1 \} {\setminus } \coprod _{e \in \mathscr {E}} T_{E_6}(e)$ and that $\mathcal {Q}_{\mathrm {hfl}}[2]$ is $\mathrm {Sp} \left( 6, \mathbb {F}_2 \right)$-equivariantly isomorphic to $\{\pm 1 \} {\setminus } \coprod _{e \in \mathscr {E}} \mathbb {P}(V_{E_6})(e)$.

3.3 Cohomological computations

We have thus seen how each of the four strata of $\mathcal {Q}_1[2]$ either can be described in terms of complements of toric arrangements or in terms of complements of hyperplane arrangements. In the affine hyperplane case, the necessary computations were carried out by Fleischmann and Janiszczak, see [9]. They present their results in terms of equivariant Poincaré polynomials and one goes from the affine to the projective case by dividing their results by $1+t$. In the toric case, the necessary computations were carried out by the author in [2].

Since $W(E_7)=\mathrm {Sp} \left( 6, \mathbb {F}_2 \right) \times \{\pm 1\}$ we have that each representation of $W(E_7)$ either is a representation of $\mathrm {Sp} \left( 6, \mathbb {F}_2 \right)$ times the trivial representation of $\{\pm 1\}$ or a representation of $\mathrm {Sp} \left( 6, \mathbb {F}_2 \right)$ times the alternating representation of $\{\pm 1\}$. Thus, to go from the cohomology of the complement of an arrangement associated to $E_7$ one simply takes the $\{\pm 1\}$-invariant part. This explains how we obtained the cohomology of $\mathcal {Q}_{\mathrm {ord}}[2]$ and $\mathcal {Q}_{\mathrm {flx}}[2]$ given in Table 1 and Table 2, respectively. If one is only interested in the dimensions of the various cohomology groups, these are more conveniently given as Poincaré polynomials.

Theorem 6

The cohomology groups $H^i(\mathcal {Q}_{\mathrm {ord}}[2])$ and $H^i(\mathcal {Q}_{\mathrm {flx}}[2])$ are both pure of type (i, i). The Poincaré polynomial of $\mathcal {Q}_{\mathrm {ord}}[2]$ is

$$\begin{aligned} P(\mathcal {Q}_{\mathrm {ord}}[2],t)= & {} 1 + 63t + 1638t^2 + 22680t^3 + 180089t^4 \\&+\, 820827t^5 + 2004512t^6 + 2064430t^7 \end{aligned}$$

and the Poincaré polynomial of $\mathcal {Q}_{\mathrm {flx}}[2]$ is

$$\begin{aligned} P(\mathcal {Q}_{\mathrm {flx}}[2],t)= & {} 1 + 62t + 1555t^2+ 20180t^3 + 142739t^4 \\&+\, 521198t^5 + 765765t^6. \end{aligned}$$

The structure of the cohomology of $H^i(\mathcal {Q}_{\mathrm {ord}}[2])$ (resp. $H^i(\mathcal {Q}_{\mathrm {flx}}[2])$) as a $\mathrm {Sp} \left( 6,\mathbb {F}_2 \right)$-representation is as given in Table 1 (resp. Table 2).

Table 1 The cohomology of $\mathcal {Q}_{\mathrm {ord}}[2]$ as a representation of $\mathrm {Sp} \left( 6,\mathbb {F}_2 \right)$

Table 2 The cohomology of $\mathcal {Q}_{\mathrm {flx}}[2]$ as a representation of $\mathrm {Sp} \left( 6,\mathbb {F}_2 \right)$

Table 3 The cohomology of $\mathcal {Q}_{\mathrm {btg}}[2]$ as a representation of $\mathrm {Sp} \left( 6,\mathbb {F}_2 \right)$

To obtain the cohomology of $\mathcal {Q}_{\mathrm {btg}}[2]$ from the cohomology of $T_{E_6}$ we first have to induce from $W(E_6)$ and then take $\{\pm 1\}$-invariants. Thus

$$\begin{aligned} H^i(\mathcal {Q}_{\mathrm {btg}}[2]) = \mathrm {Ind}_{W(E_6)}^{W(E_7)} \left( H^i(T_{E_7}) \right) ^{\{\pm 1\}}. \end{aligned}$$

The results are given in Table 3. In an entirely analogous way one obtains the cohomology of $\mathcal {Q}_{\mathrm {hfl}}[2]$ from the cohomology of $\mathbb {P}(V_{E_7})$. The results are given in Table 4.

Table 4 The cohomology of $\mathcal {Q}_{\mathrm {hfl}}[2]$ as a representation of $\mathrm {Sp} \left( 6,\mathbb {F}_2 \right)$

Theorem 7

The cohomology groups $H^i\mathcal {Q}_{\mathrm {btg}}[2])$ and $H^i(\mathcal {Q}_{\mathrm {hfl}}[2])$ are both pure of type (i, i). The Poincaré polynomial of $\mathcal {Q}_{\mathrm {btg}}[2]$ is

$$\begin{aligned} P(\mathcal {Q}_{\mathrm {btg}}[2],t)= & {} 28 + 1176t + 19740t^2 + 168560t^3 + 768852t^4 \\&+\, 1774584t^5 + 1639540t^6 \end{aligned}$$

and the Poincaré polynomial of $\mathcal {Q}_{\mathrm {hfl}}[2]$ is

$$\begin{aligned} P(\mathcal {Q}_{\mathrm {hfl}}[2],t)= & {} 28 + 980t + 13300t^2 + 87500t^3 + 278992t^4 \\&+\, 344960t^5. \end{aligned}$$

The structure of the cohomology of $H^i(\mathcal {Q}_{\mathrm {btg}}[2])$ (resp. $H^i(\mathcal {Q}_{\mathrm {hfl}}[2])$) as a $\mathrm {Sp} \left( 6,\mathbb {F}_2 \right)$-representation is as given in Table 3 (resp. Table 4).

Let $\mathcal {Q}_{\overline{\mathrm {ord}}}[2]$ be the union of $\mathcal {Q}_{\mathrm {ord}}[2]$ and $\mathcal {Q}_{\mathrm {flx}}[2]$ inside $\mathcal {Q}_1[2]$. By Lemma 3.6 of [19] we have that there is a $\mathrm {Sp} \left( 6, \mathbb {F}_2 \right)$-equivariant short exact sequence of mixed Hodge structures

$$\begin{aligned} 0 \rightarrow H^i(\mathcal {Q}_{\overline{\mathrm {ord}}}[2]) \rightarrow H^i(\mathcal {Q}_{\mathrm {ord}}[2]) \rightarrow H^{i-1}(\mathcal {Q}_{\mathrm {flx}}[2])(-1) \rightarrow 0. \end{aligned}$$

Thus, $H^i(\mathcal {Q}_{\overline{\mathrm {ord}}}[2])$ is pure of type (i, i) and we may easily deduce the structure as a $\mathrm {Sp} \left( 6, \mathbb {F}_2 \right)$-representation from Tables 1 and 2. The result is given in Table 5.

Theorem 8

The cohomology group $H^i(\mathcal {Q}_{\overline{\mathrm {ord}}}[2])$ is pure of type (i, i) and the Poincaré polynomial of $\mathcal {Q}_{\overline{\mathrm {ord}}}[2]$ is

$$\begin{aligned} P(\mathcal {Q}_{\mathrm {ord}}[2],t)= & {} 1 + 62t + 1576t^2 + 21125t^3 + 159909t^4 \\&+\, 678068t^5 + 1483314t^6 + 1302665t^7. \end{aligned}$$

The structure of the cohomology of $H^i(\mathcal {Q}_{\overline{\mathrm {ord}}}[2])$ as a $\mathrm {Sp} \left( 6,\mathbb {F}_2 \right)$-representation is as given in Table 5.

Similarly, let $\mathcal {Q}_{\overline{\mathrm {btg}}}[2]$ be the union of $\mathcal {Q}_{\mathrm {btg}}[2]$ and $\mathcal {Q}_{\mathrm {hfl}}[2]$ inside $\mathcal {Q}_1[2]$. Again, by Lemma 3.6 of [19] we have that there is a $\mathrm {Sp} \left( 6, \mathbb {F}_2 \right)$-equivariant short exact sequence of mixed Hodge structures

$$\begin{aligned} 0 \rightarrow H^i(\mathcal {Q}_{\overline{\mathrm {btg}}}[2]) \rightarrow H^i(\mathcal {Q}_{\mathrm {btg}}[2]) \rightarrow H^{i-1}(\mathcal {Q}_{\mathrm {hfl}}[2])(-1) \rightarrow 0. \end{aligned}$$

Thus, $H^i(\mathcal {Q}_{\overline{\mathrm {btg}}}[2])$ is pure of type (i, i) and we may easily deduce the structure as a $\mathrm {Sp} \left( 6, \mathbb {F}_2 \right)$-representation from Tables 3 and 4. The result is given in Table 6.

Theorem 9

The cohomology group $H^i(\mathcal {Q}_{\overline{\mathrm {btg}}}[2])$ is pure of type (i, i) and the Poincaré polynomial of $\mathcal {Q}_{\overline{\mathrm {btg}}}[2]$ is

$$\begin{aligned} P(\mathcal {Q}_{\overline{\mathrm {btg}}}[2],t)= & {} 28 + 1148t + 18760t^2 + 155260t^3 + 681352t^4 \\&+\, 1495592t^5 + 1294580t^6. \end{aligned}$$

The structure of the cohomology of $H^i(\mathcal {Q}_{\overline{\mathrm {btg}}}[2])$ as a $\mathrm {Sp} \left( 6,\mathbb {F}_2 \right)$-representation is as given in Table 6.

Table 5 The cohomology of $\mathcal {Q}_{\overline{\mathrm {ord}}}[2]$ as a representation of $\mathrm {Sp} \left( 6,\mathbb {F}_2 \right)$

Table 6 The cohomology of $\mathcal {Q}_{\overline{\mathrm {btg}}}[2]$ as a representation of $\mathrm {Sp} \left( 6,\mathbb {F}_2 \right)$

Table 7 The cohomology of $\mathbb {P}(\mathcal {C}_3^{[2,2],\mathrm {q}}[2])$ as a representation of $\mathrm {Sp} \left( 6,\mathbb {F}_2 \right)$

Table 8 The cohomology of $\mathbb {P}(\mathcal {C}_3^{\overline{[2,2]},\mathrm {q}}[2])$ as a representation of $\mathrm {Sp} \left( 6,\mathbb {F}_2 \right)$

4 Hyperelliptic curves

We shall now briefly turn our attention to the moduli spaces of hyperelliptic curves, and .

Let C be a hyperelliptic curve of genus $g \ge 2$. Then C can be realized as a double cover of $\mathbb {P}^{1}$ ramified over $2g+2$ points. Moreover, if we pick $2g+2$ ordered points on $\mathbb {P}^{1}$, the curve C obtained as the double cover ramified over precisely those points is a hyperelliptic curve and the points also determine a level 2 structure on C. However, not all level 2 structures on C arise in this way. Nevertheless, there is an intimate relationship between the moduli space and the moduli space $\mathcal {M}_{0,2g+2}$ of $2g+2$ ordered points on $\mathbb {P}^{1}$.

Theorem 10

[26] Let $\mathfrak {S}$ denote the set of left cosets $\mathrm {Sp} \left( 2g,\mathbb {F}_2 \right) /S_{2g+2}$ and for each $[\sigma ] \in \mathfrak {S}$ let $X_{[\sigma ]}$ denote a copy of $\mathcal {M}_{0,2g+2}$. Then

and $\mathrm {Sp} \left( 2g,\mathbb {F}_2 \right)$ acts transitively on the set of connected components of .

See [7] for a slightly weaker form of the above result. See also [25].

Thus, the cohomology of can be obtained by computing the cohomology of $\mathcal {M}_{0,2g+2}$ as a $S_{2g+2}$-representation and then inducing up to $\mathrm {Sp} \left( 2g,\mathbb {F}_2 \right)$. More precisely, we have

where we consider $H^i(\mathcal {M}_{0,2g+2})$ as a representation of $S_{2g+2}$ and as a representation of $\mathrm {Sp} \left( 2g,\mathbb {F}_2 \right)$. One way to compute the cohomology of $\mathcal {M}_{0,2g+2}$ is to make $S_{2g+2}$-equivariant point counts of $\mathcal {M}_{0,2g+2}$. Since $\mathcal {M}_{0,2g+2}$ is isomorphic to a hyperplane arrangement, this will determine its cohomology, see [5]. Other approaches to the computation of the cohomology of $\mathcal {M}_{0,n}$ are due to Getzler [12], Gaiffi [11], Mathieu [22] and Robinson and Whitehouse [24]. For , these computations were carried out in [3] and the results are given, for convenience, in Table 10. We also mention that is pure of type (k, k).

Theorem 11

The Poincaré polynomial of is

The moduli space (as a coarse moduli space) is a $\mathbb {P}^{1}$-fibration over via the forgetful morphism. The Leray-Serre spectral sequence of this fibration degenerates at the second page and allows us to compute the cohomology of , together with its mixed Hodge structure, as

Thus, the cohomology of is completely determined and easily obtained via Table 10.

5 Moduli of Abelian differentials

Let denote the moduli space of pairs $(C,\omega )$ where C is a curve of genus g and $\omega$ is a nonzero holomorphic 1-form (i.e. an Abelian differential). We let denote the moduli space of triples $(C,\omega ,D)$ where C is a curve of genus g, $\omega$ is an Abelian differential and D is a level 2 structure on C. In [18] a stratification of , according to the multiplicities of the zeros of $\omega$, was given. We follow them in order to obtain a corresponding stratification of . More precisely, let $\lambda =[\lambda _1, \ldots ,\lambda _n]$ be a partition of $2g-2$. Then there is a subspace of consisting of triples $(C,\omega ,D)$ such that $\omega$ has exactly n zeros with multiplicities prescribed by $\lambda$. We now have

Let $P(2g-2)$ denote the set of partitions of $2g-2$. The elements of $P(2g-2)$ are partially ordered by refinement and under this order the partition $[2g-2]$ is the maximal element. Let denote the closure of in . Then

Recall that the interval $[\lambda ,[2g-2]]$ consists of all elements $\lambda '$ in $P(2g-2)$ such that $\lambda \le \lambda '$ and $\lambda ' \le [2g-2]$.

The strata are not connected in general and a complete description of their connected components is given in [18]. In genus 3, the result is exceptionally simple (since there are no effective even theta characteristics in genus 3). More precisely, the strata are connected for all $\lambda$ different from [2, 2] and [4]. In these two cases, strata decomposes as

where $\mathcal {C}_3^{\lambda ,\mathrm {h}}$ is the component whose underlying curves are hyperelliptic and $\mathcal {C}_3^{\lambda ,\mathrm {q}}$ is the component whose underlying curves are not hyperelliptic. For a more detailed discussion, see [20].

We introduce corresponding loci in which we denote by $\mathcal {C}_3^{\lambda ,\mathrm {h}}[2]$ and $\mathcal {C}_3^{\lambda ,\mathrm {q}}[2]$, respectively, and we denote their closures in by $\mathcal {C}_3^{\overline{\lambda },\mathrm {h}}[2]$ and $\mathcal {C}_3^{\overline{\lambda },\mathrm {q}}[2]$. However, these loci are not connected–we shall shortly see that the locus $\mathcal {C}_3^{\overline{\lambda },\mathrm {h}}[2]$ consists of 36 connected components while the locus $\mathcal {C}_3^{\overline{\lambda },\mathrm {q}}[2]$ consists of 28 components. This is in sharp contrast with the strata and which remain connected after adding the level 2 structure.

5.1 Moduli of canonical divisors

There is a close connection between the moduli spaces and $\mathcal {M}_{3,1}[2]$ which we shall now explain. If $\omega$ is a nonzero holomorphic differential on a curve C and c is a nonzero constant, then $c \omega$ also is a nonzero holomorphic differential and $c \omega$ has the same zeros as $\omega$. We may thus projectivize and the stratification of induces a stratification of . The space parametrizes genus 3 curves with level 2 structure marked with a canonical divisor.

Now consider the locus . Let P be the marked point P of a hyperelliptic curve C. There is then a unique canonical divisor containing P in its support. If P is a Weierstrass point, then this divisor is namely 4P and if P is not a Weierstrass point, then this divisor is $2P+2i(P)$ where i denotes the hyperelliptic involution. We thus see that

where $\langle i \rangle$ is the group generated by the hyperelliptic involution.

We now instead consider the locus $\mathcal {Q}_1[2]\subset \mathcal {M}_{3,1}[2]$. If P is the marked point of a plane quartic curve C we may naturally define a canonical divisor on C as $D=T_PC \cdot C$. If P is not a genuine bitangent point (i.e. a bitangent point which is not a hyperflex point), P is the unique point giving the canonical divisor D. We thus have isomorphisms

However, if P is a genuine bitangent point we have that $D=T_PC \cdot C= 2P + 2Q$ for some point $Q \ne P$. Thus both P and Q give the same canonical divisor D. Let $\beta$ be the involution on $\mathcal {Q}_{\mathrm {btg}}[2]$ sending a curve marked with a bitangent point to the same curve marked with the other point sharing the same bitangent line. Then

$$\begin{aligned} \begin{aligned} \langle \beta \rangle {\setminus } \mathcal {Q}_{\mathrm {btg}}[2]&\cong \mathbb {P}(\mathcal {C}_3^{[2,2],\mathrm {q}}[2]), \\ \langle \beta \rangle {\setminus } \mathcal {Q}_{\overline{\mathrm {btg}}}[2]&\cong \mathbb {P}(\mathcal {C}_3^{\overline{[2,2]},\mathrm {q}}[2]), \end{aligned} \end{aligned}$$

where $\langle \beta \rangle$ is the group generated by $\beta$.

We have that

$$\begin{aligned} \mathcal {Q}_{\mathrm {btg}}[2] \cong \{\pm 1 \} {\setminus } \coprod _{e \in \mathscr {E}} T_{E_6}(e) \end{aligned}$$

and $\beta$ acts by sending $\chi \in T_{E_6}(e)$ to $\chi ^{-1} \in T_{E_6}(e)$. Recall that we have an isomorphism $W(E_7) \cong \mathrm {Sp}(6,\mathbb {F}_2) \times \mathbb {Z}/2\mathbb {Z}$. The subgroup $W(E_6) \subset W(E_7)$ is entirely contained in $\mathrm {Sp}(6,\mathbb {F}_2)$ and we may therefore identify the group generated by $W(E_6)$ and $\beta$ with $W(E_6) \times \mathbb {Z}/2\mathbb {Z}$. In order to compute the cohomology of $\mathbb {P}(\mathcal {C}_3^{[2,2],\mathrm {q}}[2])$ we thus want to compute the $W(E_6) \times \mathbb {Z}/2\mathbb {Z}$-equivariant cohomology of $T_{E_6}$, induce up to $W(E_7)$ and then take $\{\pm 1\}$-invariants

$$\begin{aligned} H^i(\mathbb {P}(\mathcal {C}_3^{[2,2],\mathrm {q}}[2])) = \mathrm {Ind}_{W(E_6) \times \mathbb {Z}/2\mathbb {Z}}^{W(E_7)}\left( H^i(T_{E_6}) \right) ^{\{ \pm 1\}}. \end{aligned}$$

Using the results from [2], this computation is straightforward.

In order to obtain the cohomology of $\mathbb {P}(\mathcal {C}_3^{\overline{[2,2]},\mathrm {q}}[2])$ we use the $\mathrm {Sp}(6,\mathbb {F}_2)$-equivariant exact sequence of mixed Hodge structures given by Lemma 3.6 of [19]

$$\begin{aligned} 0 \rightarrow H^i(\mathbb {P}(\mathcal {C}_3^{\overline{[2,2]},\mathrm {q}}[2])) \rightarrow H^i(\mathbb {P}(\mathcal {C}_3^{[2,2],\mathrm {q}}[2])) \rightarrow H^{i-1}(\mathbb {P}(\mathcal {C}_3^{[4],\mathrm {q}}[2]))(-1) \rightarrow 0. \end{aligned}$$

Theorem 12

The cohomology groups $H^i(\mathbb {P}(\mathcal {C}_3^{[2,2],\mathrm {q}}[2]))$ and $H^i(\mathbb {P}(\mathcal {C}_3^{\overline{[2,2]},\mathrm {q}}[2]))$ are pure of type (i, i) and their structure as representations of $\mathrm {Sp}(6,\mathbb {F}_2)$ are given in Tables 7 and  8, respectively.

5.2 Cohomology of moduli spaces of Abelian differentials

Before we conclude this section we explain how to obtain the cohomology of the non-projectivized spaces from the cohomology of their projectivized counterparts.

Proposition 2

The cohomology of is given by

Proof

The moduli space is a $\mathbb {P}^{1}$-fibration over and the corresponding Leray-Serre spectral sequence degenerates at the second page. One then obtains the result by reading off the diagonals.$\square$

Completely analogous arguments give the following result.

Proposition 3

6 Plain plane quartics

We now return to the moduli space $\mathcal {Q}[2]$ and compute its cohomology as a representation of $\mathrm {Sp}(6,\mathbb {F}_2)$. A step in this direction was taken in [3] where the cohomology was computed as a representation of the symmetric group on 7 elements (a subgroup of index 288 in $\mathrm {Sp}(6,\mathbb {F}_2)$ which can be thought of as the stabilizer of an unordered Aronhold set of bitangents). We only reproduce the Poincaré polynomial here and refer to the original article for the full result. We will also later see that $H^{i} (\mathcal {Q}[2])$ is pure of type (i, i).

Proposition 4

[3] The Poincaré polynomial of $\mathcal {Q}[2]$ is

$$\begin{aligned} P(\mathcal {Q}[2],t) = 1 + 35t + 490t^2 + 3485t^3 + 13174t^4 + 24920t^5 + 18375t^6. \end{aligned}$$

In order to continue the pursuit of the full structure of the cohomology as a $\mathrm {Sp}(6,\mathbb {F}_2)$-representation we shall relate $\mathcal {Q}[2]$ to some of the spaces that have occurred elsewhere in the paper.

Lemma 2

There is an $\mathrm {Sp} \left( 6,\mathbb {F}_2 \right)$-equivariant injection of mixed Hodge structures

$$\begin{aligned} H^{i} (\mathcal {Q}[2]) \hookrightarrow H^{i} (\mathcal {Q}_{\overline{\mathrm {btg}}}[2]). \end{aligned}$$

In particular, $H^{i} (\mathcal {Q}[2])$ is pure of type (i, i).

Proof

The forgetful morphism

$$\begin{aligned} f: \mathcal {Q}_{\overline{\mathrm {btg}}}[2]\rightarrow \mathcal {Q}[2], \end{aligned}$$

is finite so the map

$$\begin{aligned} f_{!} \circ f^* : H^i(\mathcal {Q}_{\overline{\mathrm {btg}}}[2]) \rightarrow H^i(\mathcal {Q}_{\overline{\mathrm {btg}}}[2]), \end{aligned}$$

is multiplication with $\mathrm {deg}(f) = 56$. Thus, since we are using cohomology with rational coefficients, the map

$$\begin{aligned} f^*: H^{i} (\mathcal {Q}[2]) \rightarrow H^{i} (\mathcal {Q}_{\overline{\mathrm {btg}}}[2]) \end{aligned}$$

is injective.

Unfortunately, the cohomology of $\mathcal {Q}_{\overline{\mathrm {btg}}}[2]$ is much too large in comparison with the cohomology of $\mathcal {Q}[2]$ for the above lemma to give any clues as it stands. The cohomology of $\mathcal {Q}_{\mathrm {flx}}[2]$ is however much smaller. To make the comparison, we make use of Lemma 1.

Proposition 5

There is an $\mathrm {Sp} \left( 6,\mathbb {F}_2 \right)$-equivariant injection of mixed Hodge structures

$$\begin{aligned} H^{i} (\mathcal {Q}[2]) \hookrightarrow H^{i} (\mathcal {Q}_{\mathrm {flx}}[2]). \end{aligned}$$

Proof

Let $X=\mathcal {Q}_{\mathrm {flx}}[2]\sqcup \mathcal {Q}_{\mathrm {hfl}}[2]$ and let $Y=\mathcal {Q}_{\mathrm {hfl}}[2]$ and apply Lemma 1 to see that $H^i(X)$ consists of one part of type (i, i) coming from $H^i(\mathcal {Q}_{\mathrm {flx}}[2])$ and one part of type $(i-1,i-1)$ coming from $\mathcal {Q}_{\mathrm {hfl}}[2]$.

The morphism $f: X \rightarrow \mathcal {Q}[2]$ forgetting the marked point is finite of degree 24 so the map

$$\begin{aligned} f_{!} \circ f^* : H^i(X) \rightarrow H^i(\mathcal {Q}_{\overline{\mathrm {btg}}}[2]), \end{aligned}$$

is multiplication with 24. In particular

$$\begin{aligned} f^*: H^{i} (\mathcal {Q}[2]) \rightarrow H^{i} (X) \end{aligned}$$

is injective. But $H^{i} (\mathcal {Q}[2])$ is pure of type (i, i) so the image of $f^*$ must lie inside the (i, i)-part of $H^i(X)$ which we can identify with a subspace of $H^i(\mathcal {Q}_{\mathrm {flx}}[2])$ by the above.

One could now hope that knowing that $H^i(\mathcal {Q}[2])$ is a subrepresentation of $H^i(\mathcal {Q}_{\mathrm {flx}}[2])$ together with the information about how this representation restricts to $S_7$ from [3] would determine $H^i(\mathcal {Q}[2])$ as a representation of $\mathrm {Sp}(6,\mathbb {F}_2)$. This is the case for $i=0,1,2$ and 3 but not for $i=4,5$ and 6. For instance, in the case $i=4$ there are 1039 representations that satisfy these conditions.

Observe that the space $\mathbb {P}(\mathcal {C}_3^{\overline{[2,2]},\mathrm {q}}[2])$ parametrizes plane quartics with level 2 structure marked with a bitangent line (here we also allow hyperflex lines as bitangent lines). We consider a level 2 structure on a quartic C as an ordered Aronhold set $(\theta _1, \ldots , \theta _7)$ of odd theta characteristics. The odd theta characteristics not in the Aronhold set are of the form

$$\begin{aligned} \theta _{i,j}:=\sum _{k=1}^7 \theta _k-\theta _i-\theta _j, \quad 1 \le i < j \le 7. \end{aligned}$$

We define

$$\begin{aligned} \mathcal {B}_{i} \subset \mathbb {P}(\mathcal {C}_3^{\overline{[2,2]},\mathrm {q}}[2]) \end{aligned}$$

as the subset of points such that the marked bitangent induces the i’th theta characteristic of the ordered Aronhold set. Similarly, we define $\mathcal {B}_{i,j}$ as the subset where the marked bitangent induces the theta characteristic $\theta _{i,j}$.

Let I be any subset of $\{1, \ldots , 7\}$ of size 1 or 2. The spaces $\mathcal {B}_{I}$ are all isomorphic and

$$\begin{aligned} \mathbb {P}(\mathcal {C}_3^{\overline{[2,2]},\mathrm {q}}[2]) = \coprod _I \mathcal {B}_I \end{aligned}$$

where the union is over all such subsets I. Moreover, we have an isomorphism

$$\begin{aligned} \mathcal {Q}[2]\rightarrow \mathcal {B}_1 \end{aligned}$$

sending the class of a plane quartic with level 2 structure, where we think of the level structure as an ordered Aronhold set of bitangent lines, to the class of the same curve with the same level 2 structure marked with the first bitangent of the Aronhold set.

We now rephrase the above slightly. It is well-known that the stabilizer $\mathrm {Stab}(b)\subset \mathrm {Sp}(6,\mathbb {F}_2)$ of a bitangent line b is isomorphic to $W(E_6)$. Let $\mathscr {S}$ denote the quotient set $\mathrm {Sp}(6,\mathbb {F}_2)/W(E_6)$ and let $[\sigma ]$ denote the class of $\sigma \in \mathrm {Sp}(6,\mathbb {F}_2)$ in $\mathscr {S}$. If we now let $X_{[\sigma ]}=\mathcal {Q}[2]$ we have

$$\begin{aligned} \mathbb {P}(\mathcal {C}_3^{\overline{[2,2]},\mathrm {q}}[2]) \cong \coprod _{\sigma \in \mathscr {S}} X_{[\sigma ]} \end{aligned}$$

and $\mathrm {Sp}(6,\mathbb {F}_2)$ acts transitively on the set of connected components of $\mathbb {P}(\mathcal {C}_3^{\overline{[2,2]},\mathrm {q}}[2])$. In particular, we find that

$$\begin{aligned} H^i(\mathbb {P}(\mathcal {C}_3^{\overline{[2,2]},\mathrm {q}}[2])) = \mathrm {Ind}_{W(E_6)}^{\mathrm {Sp}(6,\mathbb {F}_2)} \mathrm {Res}_{W(E_6)}^{\mathrm {Sp}(6,\mathbb {F}_2)} \left( H^i(\mathcal {Q}[2]) \right) . \end{aligned}$$

(1)

We now know how the cohomology groups of $\mathcal {Q}[2]$ restricts to $S_7$, and we know how they relate both to the cohomology groups of $\mathcal {Q}_{\mathrm {flx}}[2]$ and the cohomology groups of $\mathbb {P}(\mathcal {C}_3^{\overline{[2,2]},\mathrm {q}}[2])$. This information is enough to finally determine $H^i(\mathcal {Q}[2])$ in all degrees. The results are presented in Table 9. We remark that even though it may seem plausible at first glance, Equation 1 does not by itself determine the cohomology of $\mathcal {Q}[2]$.

Table 9 The cohomology of $\mathcal {Q}[2]$ as a representation of $\mathrm {Sp} \left( 6,\mathbb {F}_2 \right)$

Table 10 The cohomology of as a representation of $\mathrm {Sp} \left( 6,\mathbb {F}_2 \right)$

7 The moduli space $\mathcal {M}_3[2]$

We now consider the cohomology of the moduli space $\mathcal {M}_3[2]$ of genus 3 curves with level 2 structure. By applying Lemma 1 to the decomposition we obtain the exact sequence of mixed Hodge structures

Since both and $H^{k} (\mathcal {Q}[2])(-1)$ are pure of type (k, k), the above sequence decomposes into sequences

(2)

where $W_{2k}H^{k} (\mathcal {M}_3[2])$ denotes the weight 2k part of $H^{k} (\mathcal {M}_3[2])$. Taking $k=0$ we obtain that $H^{0} (\mathcal {M}_3[2]) = H^{0} (\mathcal {Q}[2]) = \mathbb {Q}$ which is not very surprising.

For $k=1$ and $k=2$ we have the results of Hain [15] and Putman [23] that $H^k(\mathcal {M}_3[2])$ is isomorphic to $H^k(\mathcal {M}_3)$. Combined with the results of Looijenga [19] we have that $H^1(\mathcal {M}_3[2])=0$ and $H^2(\mathcal {M}_3[2])=\mathbb {Q}$ with type (1, 1) and it is reassuring to see that this is indeed compatible with the above sequence.

Given the complexity of the cohomology of $\mathcal {Q}[2]$ and , the cohomology of $\mathcal {M}_3[2]$ is surprisingly simple in low degrees. This phenomenon will not prevail in all degrees though. For instance, taking $k=7$ the above sequence gives that $\mathrm {dim}(H^7(\mathcal {M}_3[2]))$ is at least 7680. This bound is in fact far from optimal, as Fullarton and Putman [10] recently have shown that $\mathrm {dim}(H^7(\mathcal {M}_3[2]))$ is at least 11520 via completely different methods. In particular, we see that the cohomology of $\mathcal {M}_3[2]$ is not the smallest possible fitting in a four term exact sequence of the above type. We also remark that we get an upper bound .

7.1 The weighted Euler characteristic

Let G be a finite group and let $K^G_0(\mathrm {MHS})$ denote the G-equivariant Grothendieck ring of mixed Hodge structures. A variety X on which G acts defines an element $P(X) \in K^G_0(\mathrm {MHS})$ via

$$\begin{aligned} P(X) = \sum _{i,j \ge 0} W_jH^i(X). \end{aligned}$$

Let R(G) denote the complex representation ring of G. There is a homomorphism of rings $\mathrm {Eul}: K^G_0(\mathrm {MHS}) \rightarrow R(G)[u]$ defined by sending an element $V \in K^G_0(\mathrm {MHS})$ of type (i, j) to $(-1)^i\mathrm {dim}(V)u^j$ and extending linearly. By applying $\mathrm {Eul}$ to P(X) we obtain the so-called G-equivariant weighted Euler characteristic of X. The G-equivariant weighted Euler characteristic of X remembers the Hodge weight of $W_jH^i(X)$ but forgets the cohomological degree. Because of the auxiliary role played by P(X), we denote it by $\mathrm {Eul}(X,u)$ instead of $\mathrm {Eul}(P(X),u)$.

Using the exact sequence 2 above the $\mathrm {Sp} \left( 6,\mathbb {F}_2 \right)$-equivariant weighted Euler characteristic of $\mathcal {M}_3[2]$ is easily deduced from Tables 9 and 10. The result is presented in Theorem 1.