Zeros of the Selberg zeta function for symmetric infinite area hyperbolic surfaces

Abstract

In the present paper we give a simple mathematical foundation for describing the zeros of the Selberg zeta functions $Z_X$ for certain very symmetric infinite area surfaces X. For definiteness, we consider the case of three funneled surfaces. We show that the zeta function is a complex almost periodic function which can be approximated by complex trigonometric polynomials on large domains (in Theorem 4.2). As our main application, we provide an explanation of the striking empirical results of Borthwick (Exp Math 23(1):25–45, 2014) (in Theorem 1.5) in terms of convergence of the affinely scaled zero sets to standard curves ${\mathscr {C}}$.

1 Introduction

The Selberg zeta function $Z_X$ associated to a compact Riemann surface X with negative Euler characteristic and without boundary is a well known and much studied complex function. It is a function of a single complex variable defined in terms of the lengths $\ell (\gamma )$ of the primitive closed geodesics $\gamma$ on the surface by analogy with the Riemann zeta function in number theory.

Definition 1.1

We can formally define the Selberg zeta function by

$$\begin{aligned} Z_X(s) = \prod _{n=0}^\infty \prod _{{\mathop { \text{ closed } \text{ geodesics } }\limits ^{\gamma = \text{ prime }}}} \left( 1- e^{-(s+n)\ell (\gamma )}\right) , \qquad s \in {\mathbb {C}}, \end{aligned}$$

(1.1)

where the product is taken over all primitive closed geodesics $\gamma$ on X.

It was shown by A. Selberg in 1956 that for such surfaces the zeta function $Z_X$ has an analytic extension to the entire complex plane and that the non-trivial zeros can be described in terms of the spectrum of the Laplace–Beltrami operator [29] and the Selberg trace formula.

Theorem 1.2

(Selberg) Let X be a compact Riemann surface with negative Euler characteristic and without boundary. Then the function $Z_X$ has a simple zero at $s=1$ and for any zero s in the critical strip $0< \mathfrak {R}(s) <1$ we have that either $s \in [0,1]$ is real, or $\mathfrak {R}(s) = \frac{1}{2}$.

A good reference for this standard result is Chapter 2 of the book of Hejhal [14].

In the case of infinite area surfaces the situation is somewhat different, since the original trace formulae approach of Selberg no longer applies. However, it still follows from the dynamical method of Ruelle that providing the surface X appears as a quotient space of the upper half-plane ${\mathbb {H}}^2$ by a convex cocompact Fuchsian group $\Gamma$ then the analogous zeta function $Z_X$ still has an analytic extension to the entire complex plane [26, 28]. Unfortunately, this approach provides little effective information on the location of the zeros, other than that the first zero at $s=\delta \in (0,1)$, the Hausdorff dimension of the limit set (of the Fuchsian group).

Fig. 1

An artist’s impression of a symmetric three funnelled surface. The three dashed closed geodesics are assumed to be of equal length 2b

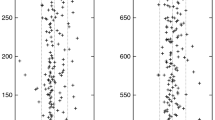
In pioneering experimental work, D. Borthwick has studied the location of the zeros for the zeta function in specific examples of infinite area surfaces [6]. The plot in Fig. 2 is fairly typical for the distribution of zeros in the critical strip for a symmetric three funnelled surface $X_b$, for large b, where each of the three simple closed geodesics corresponding to a funnel has the same length 2b.¹

Fig. 2

The zeros of the associated zeta function $Z_X$ in a critical strip. The individual zeros are so close in the plot that it creates the illusion that they lie on well defined smooth curves

The analysis of the Selberg zeta function is via the action of the Fuchsian group on the boundary of hyperbolic space and the basic method dates back to work of the first author over twenty five years ago [27]. However, it is only with the advent of superior computational resources, and the ingenuity of those that employ them, that the striking features seen in Fig. 2, for example, have been revealed. A contemporary personal computer allows one to study symmetric three funneled surface with the length of the three defining closed geodesics at least 8 without much difficulty, and this turns out to be a sufficiently general case. We refer the reader to [33] for more references to the existing literature.

The main object of study in the present work is the zero set of the function $Z_X$:

$$\begin{aligned} {\mathscr {S}}_X:= \{s \in \mathord {{\mathbb {C}}}\mid Z_X(s)=0\}. \end{aligned}$$

(1.2)

Carefully studying plots of a few thousands zeros of zeta functions associated to symmetric 3-funnelled surfaces in a domain $|s| \le 3000$ and $\mathfrak {R}(s)>0$ for example, one observes that there are certain similarities in a way the zeros are arranged. We formulate our observations in terms of the theory of almost periodic functions.

Definition 1.3

We say that $\tau \in i{\mathbb {R}}$ is a $\varepsilon$-translation of a discrete set $\{A\} \subset {\mathbb {C}}$ if there is a bijection $\{A\} {\mathop {\longrightarrow }\limits ^{\varphi }} \{A + \tau \}$ such that $d(a,\varphi (a))\le \varepsilon$ for all $a\in \{A\}$. We say that a discrete set is almost periodic in the sense of Krein–Levin, if for any $\varepsilon >0$ there exists a relatively dense² set of $\varepsilon$-translations.

Informal qualitative observations Let $X_b$ be the three funnelled surface defined by three simple closed geodesics of equal length³ 2b. Then for a sufficiently large b.

• O1 : The set of zeros ${\mathscr {S}}_{X_b}$appears to be an almost periodic set in the sense of Krein–Levin, with relatively dense set of translations $\tau = \{i( \pi k e^b + \varepsilon _k) \mid k \in {\mathbb {N}} \}$, where $\varepsilon _k = o(e^{-b/2})$ as $b \rightarrow +\infty$.

• O2 : The set of zeros ${\mathscr {S}}_{X_b}$appears to lie on a few distinct curves, which seem to have a common intersection point at $\frac{\delta }{2} + i \frac{\pi }{2}e^b$, as $b \rightarrow +\infty$.

It is well known that the zeta-function can be well approximated by a sequence of finite exponential sums [17, 28], and therefore the first property is to be expected: the zero set of a finite exponential sum is almost periodic (cf. [19], Appendix 1). The main difficulty here is to identify the set of translations.

The second property is more mysterious, and this will follow from a specific approximation of the zeta function by an exponential sum of 12 terms on a large, but bounded, domain, which grows with b exponentially quickly.

In order to provide a rigorous proof, we need to estimate the error term of approximation of the zeta function by exponential sums as $b \rightarrow +\infty$. This is done in Theorem 4.2. Subsequently using properties of the zeta function we simplify the exponential sum, which gives the best approximation, and obtain a function whose zero set belongs to four sinusoids.

According to an old result by McMullen [21] the largest real zero $\delta$ asymptotically behaves like $\frac{\ln 2}{b}$ as $b \rightarrow +\infty$, and it defines the width of the critical strip. Therefore, in the limit $b\rightarrow +\infty$ the zero set converes to imaginry axis. However, a suitable affine rescaling allows one to see the pattern of zeros for large values of b. A natural choice for rescaling factors is the approximate period of the pattern (in the imaginary direction) and approximate reciprocal of the width of the critical strip (in the real direction) (Fig. 3).

Notation 1.4

We will be using the following.

• (a) A compact part of the critical strip of height $T>0$ which we denote by

  $$\begin{aligned} {{\mathscr {R}}}(T) = \{ s \in {\mathbb {C}} \mid 0 \le \mathfrak {R}(s) \le \delta \text{ and } |\mathfrak {I}(s)| \le T\}; \end{aligned}$$

  and a compact part of the normalized critical strip of height $S>0$ which we denote by

  $$\begin{aligned} \widehat{{\mathscr {R}}}(S) = \{ s \in {\mathbb {C}} \mid 0 \le \mathfrak {R}(s) \le \ln 2 \text{ and } |\mathfrak {I}(s)| \le S\}. \end{aligned}$$

• (b) We denote the rescaled set of zeros by

  $$\begin{aligned} \widehat{{\mathscr {S}}}_{X_b} := \left\{ \sigma b+i e^{-b} t \Bigl | \sigma +it \in {{\mathscr {S}}}_X \right\} . \end{aligned}$$

  where evidently, $0< \mathfrak {R}(\widehat{{\mathscr {S}}}_{X_b}) \le \ln 2$. We now introduce a family of four sinusoidal curves approximating $\widehat{{\mathscr {S}}}_{X_b}$ as $b \rightarrow +\infty$.

• (c) Let ${\mathscr {C}}=\cup _{j=1}^4 {\mathscr {C}}_j$, where

  $$\begin{aligned} \begin{aligned} {\mathscr {C}}_1&= \left\{ \frac{1}{2}\ln |2-2\cos (t)| + it \mid t \in {\mathbb {R}} \right\} ; \\{\mathscr {C}}_2&= \left\{ \frac{1}{2} \ln |2+2\cos (t)| + it \mid t \in {\mathbb {R}} \right\} ; \\{\mathscr {C}}_3&= \left\{ \frac{1}{2} \ln \left| 1 - \frac{1}{2} e^{2it} - \frac{1}{2} e^{it} \sqrt{4 - 3 e^{2i t}} \right| + it \mid t \in {\mathbb {R}} \right\} ; \\{\mathscr {C}}_4&= \left\{ \frac{1}{2} \ln \left| 1 - \frac{1}{2} e^{2it} + \frac{1}{2} e^{it} \sqrt{4 - 3 e^{2i t}} \right| + it \mid t \in {\mathbb {R}} \right\} . \end{aligned} \end{aligned}$$

  Note that the curve ${\mathscr {C}}$ in Fig. 4 looks similar to empirical plots in Fig. 5. The apparent intersections in Fig. 2 correspond to the intersections of ${\mathscr {C}}_j$:

  $$\begin{aligned} \bigcap _{j=1}^4 {\mathscr {C}}_j = \Bigl \{ \frac{\ln 2}{2}+i\pi \Bigl (\frac{1}{2} + k\Bigr )\Bigr \}, \quad k\in \mathord {{\mathbb {Z}}}. \end{aligned}$$

Fig. 3

a The strips ${{\mathscr {R}}}(T)$ and $\widehat{{\mathscr {R}}}(S)$; b By renormalizing the strip ${{\mathscr {R}}}(\pi e^b)$ to $\widehat{{\mathscr {R}}}(\pi )$ we can compare the zeros of zeta functions for different b, as b tends to infinity

Fig. 4

Plots of the curves ${\mathscr {C}}_1$, ${\mathscr {C}}_2$, ${\mathscr {C}}_3$, ${\mathscr {C}}_4$ and their union ${\mathscr {C}}$

We can now formally state the approximation result, which provides an explanation for the Observations.

Theorem 1.5

The sets $\widehat{{\mathscr {S}}}_{X_b}$ and $\mathscr {C}$ are close in the Hausdorff metric $\mathrm{dist}_H$ on a large part of the strip $0<\mathfrak {R}(s)<\log 2$. More precisely, there exists $\varkappa > 0$ such that

$$\begin{aligned} \mathrm{dist}_H ( \widehat{{\mathscr {S}}}_{X_b} \cap \widehat{\mathscr {R}}(e^{\varkappa b}) ,{\mathscr {C}} \cap \widehat{\mathscr {R}}(e^{\varkappa b}) )=O\Bigl (\frac{1}{\sqrt{b}}\Bigr ), \text{ as } b \rightarrow +\infty . \end{aligned}$$

The theorem implies that every rescaled zero $s\in \widehat{\mathscr {S}}_{X_b} \cap \widehat{{\mathscr {R}}}(e^{\varkappa b})$ belongs to a neighbourhood of ${\mathscr {C}}$ which is shrinking as $b \rightarrow \infty$. On the other hand, the rescaled zeros are so close, that the union of their shrinking neighbourhoods contains ${\mathscr {C}}$.

Remark 1.6

Although an explicit estimate on the distance between zeros and curves $O\Bigl (\frac{1}{\sqrt{b}}\Bigr )$ is a bonus, the most significant feature of this result is that the height $e^{\varkappa b}$ of the rescaled strip $\widehat{{\mathscr {R}}}(e^{\varkappa b})$ is larger than the period of the curves ${\mathscr {C}}$, and it corresponds to a part of the original strip of height $e^{(1+\varkappa )b}$ which allows us to find a set of $\varepsilon$-translations.

Fig. 5

a The zeros of the $Z_{14}$ (see §4 for definition) approximating $Z_{X_6}$; b A zoomed version in a neighbourhood of $\delta$ showing indvidual zeros. The distance between imaginary parts of consecutive zeros is approximately $\frac{\pi }{6}$

Remark 1.7

A similar analysis can be carried out for a punctured torus and for less symmetric surfaces. However, in most cases the modul⁴ of the exponential sum, approximating the zeta function with suitable accuracy, has more generators, the curves containing zero set can be defined only implicitly, and the set of $\varepsilon$-translations doesn’t have such a simple form.

There is an interesting conjecture due to Jakobson and Naud which we include here for context (see [15], Conjecture 1.1, p. 354).

Conjecture 1.8

(Jakobson–Naud). There are only finitely many zeros in the half plane $\mathfrak {R}(s) > \frac{\delta }{2}$ and this is the largest half-plane with this property (i.e., for any $\varepsilon > 0$ there are infinitely many zeros in the half-plane $\mathfrak {R}(s) > \frac{\delta }{2} - \varepsilon$).

We also note that there are interesting empirical investigations on the (Ruelle) zeta function in the case of Sinai billiards [31].

This project has had a long gestation period, having begun after the first author heard the original empirical results of D. Borthwick presented at a conference on Quantum Chaos in Roscoff in June of 2013. We are grateful to him for sharing his original Matlab code with us. We are grateful to F. Bykov for writing a new program. A preliminary announcement of these results was made by the first author at the conference “Spectral problems for hyperbolic dynamical systems” held in Bordeaux in May of 2014. A preliminary version of this paper was written during authors’ visit to ICERM, Brown University. We would like to thank ICERM for the hospitality.

2 The zeta function and closed geodesics

We begin this section with the some basic background on the surface $X_b$. Any surface with constant curvature $\kappa =-1$ has universal covering space the unit disc ${\mathbb {D}}^2 = \{z = x+iy :|z| < 1\}$ equipped with the usual Poincaré metric $ds^2 = 4\frac{dx^2 + dy^2}{(1- x^2 - y^2)^2}$. In particular, $(\mathbb D^2, ds)$ is a simply connected Riemann surface with constant negative curvature $-1$ and $X_b$ can be viewed as a double oriented cover of a quotient ${\mathbb {D}}^2/\Gamma$ by a discrete subgroup of isometries $\Gamma$ (i.e., a Fuchsian group).

There are many different choices of generators for $\Gamma$. Because of the natural symmetries of $X_b$, it is convenient to choose a presentation of the associated Fuchsian group in terms of three reflections (as in [21], for example). More precisely, we can fix a value $0<\theta \le \frac{\pi }{3}$ and consider the Fuchsian group $\Gamma = \Gamma _\theta := \langle R_1, R_2, R_3\rangle$ generated by reflections $R_1, R_2, R_3$ in three disjoint equidistant geodesics $\beta _1,\beta _2,\beta _3$, with end points $e^{(\frac{2\pi }{3}j\pm \theta )i}\in \partial \mathord {{\mathbb {D}}}^2$, $j=1,2,3$, respectively (cf. Fig. 6).

Fig. 6

Three geodesics of reflection in Poincaré disk with pairwise distance b. The compact connected subset $K_b$ of $X_b$ bounded by the three simple closed geodesics is a double cover for the hyperbolic hexagon illustrated

Although the three individual generators are orientation reversing the resulting quotient surface $X_b = {\mathbb {D}}^2/\Gamma$ is an oriented infinite area surface. Both the infinite area surface and the corresponding compact surface $K_b$ with boundary consisting of three geodesics of the length 2b, share the same closed geodesics, and thus have the same zeta function. Furthermore, the compact surface $K_b$ (sometimes known as a pair of pants) is precisely the double cover for the hyperbolic hexagon in Fig. 6, (see Exposé 3, [10]).⁵ The values b and $\alpha$ can be related using a simple hyperbolic geometry calculation.

Moreover, since $X_b$ is a negatively curved surface it is a classical result of E. Cartan that we can associate a unique closed geodesic $\gamma$ to each conjugacy class in the fundamental group $\pi _1(X_b)$ (see Theorem 2.2 of Chapter of [8]; or Chapter 6 of [4]).

Notation 2.1

We shall denote by $\ell (\gamma )$ length of $\gamma$ in the hyperbolic metric of the surface. We denote by $\omega (\gamma )\in 2{\mathbb {N}}$ the word length, that is the (even) number of generators $R_1, R_2, R_3$ required to represent the conjugacy class corresponding to $\gamma$ in $\Gamma$. Geometrically, the word length corresponds to the period of the associated cutting sequence, i.e, the sequence of reflections corresponding to the sides of the hexagons crossed consecutively by the geodesic [30] and whose period corresponds to the total number of edges crossed.

Remark 2.2

Therefore, since $K_b$ is a double cover for a hyperbolic hexagon (cf. Fig. 6) every closed geodesic must traverse each of the two copies of the hexagon consecutively the same number of times and thus the word length is necessarily even.

2.1 Analytic approximation

Our starting point for understanding the properties of the zeta function is the following important result of D. Ruelle from 1976, stating that the infinite product (1.1) defines an analytic function.

Theorem 2.3

(after Ruelle) Let $\delta >0$ be the largest real zero for $Z_{X_b}$. In the notation introduced above, the infinite product (1.1) converges to a non-zero analytic function for $\mathfrak {R}(s) > \delta$ and extends as an analytic function to ${\mathbb {C}}$.

Proof

The convergence follows from more general results on Axiom A flows which we can apply to the geodesic flow restricted to the recurrent part [25]. The analyticity follows from applying ideas from the work of Ruelle [28], see also [25] for more details. $\square$

The Selberg zeta function, initially defined by (1.1) in terms of lengths of infinitely many closed geodesics, is not an object which can be easily computed numerically. A computer can only deal with a finite set of geodesics. Naturally, a fundamental question arises: how to choose the geodesics to obtain a good approximation to the infinite product?

The approach of Ruelle provides an approximation of the zeta function $Z_{X_b}$ by finite exponential sums, whose multipliers and coefficients depend on all geodesics corresponding to the word length less than n, which make it suitable for numerical experiments.

We begin by considering a more general function in two complex variables

$$\begin{aligned} Z_{X_b}(s,z)= \prod _{n=0}^\infty \prod _{{\mathop {\text{ closed } \text{ geodesic }}\limits ^{\gamma = \text{ primitive }}} } \left( 1- z^{\omega (\gamma )}e^{-(s+n)\ell (\gamma )}\right) , \end{aligned}$$

(2.1)

which converges for |z| sufficiently small and $\mathfrak {R}(s)$ sufficiently large. Taking $z=1$ we recover the original zeta function $Z_{X_b}(s) = Z_{X_b}(s,1)$. We follow Ruelle [28] in re-writing the infinite product as a series

$$\begin{aligned} Z_{X_b}(s,z) = 1 + \sum \limits _{n=1}^\infty a_n(s) z^n, \end{aligned}$$

(2.2)

by taking the Taylor expansion in z about 0. It is then easy to see that $a_n(s)$ is defined in terms of finitely many closed geodesics with word lengths at most n. In fact this series converges to a bianalytic function for both $z,s \in {\mathbb {C}}$ as shown by the next Theorem (which is stronger than Theorem 2.3).

Theorem 2.4

(Ruelle [28]) Using the notation introduced above, there exists $C = C(s) > 0$ and $0< \alpha < 1$ such that $|a_n| \le C \alpha ^{n^2}$ and thus the series (2.2) converges. In particular, we can deduce that $Z_{X_b}(s,z)$ is analytic in both variables.

Theorem 2.3 is a corollary of the stonger Theorem 2.4. We next make an easy observation.

Lemma 2.5

The odd coefficients vanish i.e., $a_1= a_3 = \cdots =0$.

Proof

It was observed in Remark 2.2 that $\omega (\gamma ) \in 2 {\mathbb {N}}$ in the infinite product (2.1) and thus only the even terms $a_2, a_4, \ldots$ can be non-zero in (2.2). $\square$

We can formally rewrite the zeta function (2.1) as

$$\begin{aligned} Z_{X_b}(s,z) = \exp \left( - \sum \limits _{m=1}^\infty \frac{z^m}{m} \sum \limits _{\omega (\gamma )=m} \frac{e^{-s\ell (\gamma )}}{1- e^{-\ell (\gamma )}} \right) =\exp \left( - \sum \limits _{m=1}^\infty \frac{b_m(s)}{m} z^m \right) \end{aligned}$$

(2.3)

where

$$\begin{aligned} b_m(s) = {\left\{ \begin{array}{ll} \sum \limits \limits _{\omega (\gamma )=m} \frac{e^{-s\ell (\gamma )}}{1- e^{-\ell (\gamma )}} &{} \text{ if } m \text{ is } \text{ even; } \\ 0 &{} \text{ if } m \text{ is } \text{ odd; } \end{array}\right. } \end{aligned}$$

(2.4)

and then expand the exponential as a power series and obtain coefficients $a_n$ comparing (2.2) with (2.3), since these series converge provided $\mathfrak {R}(s)>1$. In particular, we can easily check that the first three non-zero terms are:

$$\begin{aligned} \begin{aligned} a_2(s)&= -\frac{1}{2} b_2(s);\\a_4(s)&= - \frac{1}{4}\left( b_4(s) - \frac{b_2^2(s)}{2}\right) ; \\a_6(s)&= - \frac{1}{6} \left( b_6(s) + \frac{1}{4}b_2(s) b_4(s) - \frac{b_2^3(s)}{8}\right) ; \end{aligned} \end{aligned}$$

and in general,

$$\begin{aligned} a_n(s) = -\frac{1}{n}\sum _{j=0}^{n-2} a_j(s) b_{n-j}(s). \end{aligned}$$

Combining the latter with (2.4), we deduce that each of the coefficients $a_n(s)$ is an exponential sum whose multipliers are sums of the lengths of several closed geodesics of the total word length n.

Remark 2.6

It is important to know the number of closed geodesics of word length 2n for practical applications. We can count them by counting periodic cutting sequences. It’s easy to see that the number of cutting sequences of period 2n, associated to closed geodesics, i.e. satisfying the additional condition $\xi _1 \ne \xi _{2n}$, satisfies the reccurence relation $p_n = 3\cdot 4^{n-1} + p_{n-1}$, $p_1=6$. Hence there are exactly $p_n=4^{n}+2$ closed geodesics of the word length $\omega (\gamma )=2n$.

Straightforward approximations to $Z_{X_b}$ obtained by evaluating the series (2.2) at $z=1$ allow one to compute zeros one-by-one numerically using the Newton method. In order to find explicit curves, we need a further simplification. Another approximation to $Z_{X_b}$ can be obtained by replacing the lengths of closed geodesics $\ell (\gamma )$ in (1.1) by suitable close approximations. This will result in a function with zero set on ${\mathscr {C}}$. Afterwards, we shall show that both approximations are sufficiently close to each other.

Remark 2.7

Applying general results cf. [19] Appendix 1, on zeros of exponential sums we also deduce that the zero set of a finite sum $1+\sum \nolimits _{k=1}^n a_k(s)$ belongs to a strip parallel to the imaginary axis, and that the difference between imaginary parts of consecutive zeros is approximately $\frac{\pi }{b}$. This was proved by Weich [33] for small values of $s\in {\mathscr {S}}_{X_b}$, without relying on the theory of almost periodic functions, but instead using “symmetry reduction” first suggested in [9].

2.2 Geometric approximation

The following simple trick allows us to reduce the problem of locating zeros of the double infinite product (1.1) to a problem of locating zeros of a single infinite product. Namely, consider the related Ruelle zeta function $\zeta (s)$ defined by

$$\begin{aligned} \zeta (s) = \prod _{{\mathop { \text{ closed } \text{ geodesic } }\limits ^{ \gamma = \text{ primitive }}}} \left( 1- e^{-s\ell (\gamma )}\right) ^{-1} = \frac{Z_{X_b}(s+1)}{Z_{X_b}(s)}, \end{aligned}$$

(2.5)

where $\gamma$ again denotes a primitive closed geodesic of length $\ell (\gamma )$. Since $Z_{X_b}$ is real analytic and non-zero for $\mathfrak {R}(s)>1$, it has poles corresponding to the zeros $Z_{X_b}(s)$ in the strip $0< \mathfrak {R}(s) < \delta$. The function $\zeta$ is the exact form of the zeta function studied by Ruelle [28] and is better suited to geometric approximation.

We will be following the approach in [25], a similar argument can be found in [32].

Let $\Sigma$ be the set of infinite cutting sequences corresponding to geodesics on the 3-funnelled surface $X_b$. We consider a function

$$\begin{aligned} {\tilde{r}}_n :\Sigma \rightarrow {\mathbb {R}} \qquad {\tilde{r}}_n(\xi ) = \ell (\gamma _{\xi _{[n/2]} \xi _{[n/2]+1}}), \end{aligned}$$

(2.6)

where $\gamma _\xi$ is a closed geodesic corresponding to the cutting sequence $\xi$ and $\gamma _{\xi _{[n/2]} \xi _{[n/2]+1}}$ is the shortest geodesic segment between the intersections with the sides corresponding to $R_{\xi _{[n/2]}}$ and $R_{\xi _{[n/2]+1}}$ which lies on a longer segment passing consecutively through the sides corresponding to the reflections $R_{\xi _1}, \ldots ,R_{\xi _{n+1}}$. In particular, any geodesic is uniquely defined by its cutting sequence and therefore if the word length $\omega (\gamma _\xi )\le 2n$ we have

$$\begin{aligned} \ell (\gamma _\xi ) = \sum _{j=0}^{\omega (\gamma )-1} {\tilde{r}}_n(\sigma ^j \xi ); \text{ and } \end{aligned}$$

(2.7)

in general, we have that

$$\begin{aligned} \ell (\gamma _\xi ) = \lim _{n \rightarrow \infty } \sum _{j=0}^{\omega (\gamma )-1} {\tilde{r}}_n (\sigma ^j \xi ), \end{aligned}$$

(2.8)

where $\sigma :\Sigma \rightarrow \Sigma$ is a shift given by $\sigma (\xi _n) = (\xi _{n+1})$.

We know that periodic sequences in $\Sigma$ are periodic orbits of a subshift of finite type (cf. [23], pp. 11–12). We denote by A the transition matrix of the subshift corresponding to the encoding by subsequences of length n. Let $\xi ^1,\ldots ,\xi ^N$ be all subsequences of the sequences in $\Sigma$ of the length n. (In the case of $X_b$ we have that $N=3\cdot 2^{n-1}$.) We define an $N \times N$ matrix

$$\begin{aligned} A^n_{i,j} = {\left\{ \begin{array}{ll} 1, &{} \text{ if } \xi ^i_{k+1} = \xi ^j_{k}; \text{ for } k=1,\ldots ,n-1 \\ 0, &{} \text{ otherwise. } \end{array}\right. } \end{aligned}$$

(2.9)

We use the transition matrix $A^n$ for the subshift to define a family of matrices A(s) whose elements depend on the length of geodesics segments corresponding to transitions. Namely, we introduce a matrix-valued complex function A(s) by

$$\begin{aligned} A :{\mathbb {C}} \rightarrow Mat(N,N) \qquad A_{i,j}(s) = \exp (-s {\tilde{r}}_n(\xi ))\cdot A^n_{i,j}, \end{aligned}$$

(2.10)

where $\xi = \xi _1^i \ldots \xi _n^i \xi _n^j$. Note that A(s) depends on n but we omit this.

The following fact is very useful and relatively well-known cf. [23, 25, 32].

Lemma 2.8

Using the notation introduced above the following equality holds

$$\begin{aligned} \prod _{{\mathop {\text{ closed } \text{ geodesic }}\limits ^{\gamma = \text{ primitive } }}} \left( 1-e^{-s \ell (\gamma )}\right) ^2 = \lim _{n \rightarrow \infty } \det \left( I_N - A^2(s)\right) ; \end{aligned}$$

(2.11)

where $I_N$ is the $N\times N$ identity matrix.

Proof

Observe that on the domain of convergence the right hand side

$$\begin{aligned} \log \left( \det \left( I_N - A^2(s)\right) \right)&= - \sum _{j=1}^\infty \frac{1}{j} \mathrm{tr}\left( A^{2j}(s)\right) = -\sum _{j=1}^\infty \frac{1}{j} \sum _{\sigma ^{2j} \xi = \xi } e^{- s ({\tilde{r}}_n(\xi )+\tilde{r}_n(\sigma \xi )+\cdots +{\tilde{r}}_n(\sigma ^{2j-1} \xi ))} \end{aligned}$$

we may rewrite the latter term as

$$\begin{aligned}&=-\sum _{j=1}^\infty \sum _{m=1}^\infty \frac{1}{jm} \sum _{{\mathop {\xi \text{ primitive }}\limits ^{\sigma ^{2j} \xi = \xi }} } e^{- s m (\tilde{r}_n(\xi )+\tilde{r}_n(\sigma \xi )+\cdots +{\tilde{r}}_n(\sigma ^{2j-1} \xi ))}, \end{aligned}$$

where the inner summation is taken over primitive fixed points for $\sigma ^{2j}$

$$\begin{aligned}&=-2\sum _{j=1}^\infty \sum _{m=1}^\infty \frac{1}{m} \sum _{{\mathop { \text{ primitive }}\limits ^{\{\xi , \sigma \xi , \sigma ^2\xi ,\cdots ,\sigma ^{2j-1}\xi \}}}} e^{- s m ({\tilde{r}}_n(\xi )+{\tilde{r}}_n(\sigma \xi )+\cdots +{\tilde{r}}_n(\sigma ^{2j-1} \xi ))}, \end{aligned}$$

where the inner summation is taken over primitive closed orbits of period 2j

$$\begin{aligned}&=-2\sum _{j=1}^\infty \sum _{{\mathop { \text{ primitive }}\limits ^{\{\xi , \sigma \xi , \sigma ^2\xi ,\cdots ,\sigma ^{2j-1}\xi \}}} } \log \left( 1 - e^{- s ({\tilde{r}}_n(\xi )+\tilde{r}_n(\sigma \xi )+\cdots +{\tilde{r}}_n(\sigma ^{2j-1} \xi ))}\right) , \\&=-2 \log \prod _{j=1}^\infty \prod _{{\mathop { \text{ primitive }}\limits ^{\{\xi , \sigma \xi , \sigma ^2\xi ,\cdots ,\sigma ^{2j-1}\xi \}}}} \left( 1 - e^{- s ({\tilde{r}}_n(\xi )+{\tilde{r}}_n(\sigma \xi )+\cdots +{\tilde{r}}_n(\sigma ^{2j-1} \xi ))}\right) . \end{aligned}$$

Using (2.8) and swapping the limits, we get the result, since there is a bijection between oriented primitive closed geodesics and primitive periodic cutting sequences. $\square$

The last lemma establishes a connection between the Ruelle zeta function and the determinant of certain matrices. It follows from definition (2.10) that $\det (I_N - A^2(s))$ is a finite exponential sum as a function of s. It turns out that in the particular case of $X_b$, the zero set of $\det (I_N - A^2(s))$ for $N=6$ is easy to describe and that for b large this exponential sum is close to $1+\sum \nolimits _{j=1}^{\infty } a_n(s)$, where $a_n(s)$ are the coefficients in (2.2).

2.3 Computing a geometric approximation

We apply the method described in the previous paragraph in a simple case $n=2$. In other words, we will be computing the length of segments of closed geodsics taking into account only $n+1=3$ consecutive elements of the cutting sequences, and computing the total length by summing up the length of the pieces. We will show afterwards that this approximation is good enough.

In order to compute ${\tilde{r}}_2$ as defined by (2.6), we observe the following simple fact:

Lemma 2.9

Consider a regular hyperbolic hexagon whose even sides are of length $b>1$ and whose odd sides are of length $\varepsilon _b$ then

$$\begin{aligned} \varepsilon _b = 2 e^{-b/2} + e^{-b} + O(e^{-3b/2})\quad \text{ as } b\rightarrow +\infty . \end{aligned}$$

Proof

We recall that (cf. [3], Theorem 7.19.2)

$$\begin{aligned} \cosh \varepsilon _b (\sinh b)^2 = \cosh b + (\cosh b)^2 . \end{aligned}$$

The result follows by expanding the both sides in $e^{-b}$ as $b \rightarrow +\infty$ and comparing the expansions. $\square$

Now we are ready to describe ${\tilde{r}}_2 :\Sigma \rightarrow \mathbb R^+$.

Lemma 2.10

Assume that $\xi \in \Sigma$ is a cutting sequence of period 2n given by

$$\begin{aligned} \xi = \xi _1 \xi _2 \xi _3 \cdots \xi _{2n-1} \xi _{2n} \xi _1 \cdots , \end{aligned}$$

where $\xi _k \ne \xi _{k+1}$ for $1 \le k \le 2n$ and $\xi _{2n} \ne \xi _1$. Then ${\tilde{r}}_2(\xi ) = b + c(\xi ) e^{-b} + O(e^{-2b})$ as $b\rightarrow + \infty$, where

$$\begin{aligned} c(\xi ) = {\left\{ \begin{array}{ll} 0, &{} \text{ if } \xi _{1}=\xi _{3}; \\ 1, &{} \text{ otherwise } . \end{array}\right. } \end{aligned}$$

Proof

We need to estimate the length of the shortest of the segments of closed geodesics passing through $\beta _{\xi _1}$, $\beta _{\xi _2}$, and $\beta _{\xi _3}$ enclosed between the intersections with $\beta _{\xi _1}$ and $\beta _{\xi _2}$.

Let us first consider the case when $\xi _1 = \xi _3$, see geodesic segment $\gamma _{1 3 1}$ in Fig. 7 for example. It is evident that the shortest geodesic whose cutting sequence has a subsequence $\xi _1 \xi _2 \xi _1$ is the boundary one. Therefore, we conclude that ${\tilde{r}}_2(\xi ) = b$.

Fig. 7

A geodesic segment $\gamma _{131}$, running along the side of two hexagons when $R_{\xi _{1}} = R_{\xi _{3}}$; and a geodesic segment $\gamma _{132}$, traversing two hexagons when $R_{ \xi _{n-1}} \ne R_{\xi _{n+1}}$

Now we consider the case $\xi _{1} \ne \xi _{3}$, see the geodesic segment $\gamma _{1 3 2}$ in Fig. 7 for example.

We may denote the point of intersection of the geodesic $\gamma _\xi$ with the side $R_{\xi _k}$ by $A_k$. We may assume that $A_k$ divides the side of reflection in proportions $x_k:(1-x_k)$, for $k=1,\ldots ,3$. Then the geodesic segment $\gamma _{\xi _1\xi _{2}}$ is a side of a right hyperbolic trapezoid with one side of the length b, and two parallel sides of the length $x_1 \varepsilon _b$ and $x_{2} \varepsilon _b$. Similarly, the geodesic segment $\gamma _{\xi _2\xi _{3}}$ is a side of a right hyperbolic trapezoid with one side of the length b, and two parallel sides of the length $(1-x_2) \varepsilon _b$ and $x_3 \varepsilon _b$.

Using hyperbolic sine and cosine laws, we deduce the formula for length of the fourth side of the trapezoid:

$$\begin{aligned} f_1(x_1,x_2) :&= \ell (\gamma _{\xi _1\xi _2})\\&=\mathrm{Arcosh}\left( \cosh b \cdot \cosh ( x_1 \varepsilon _b ) \cdot \cosh \left( x_2 \varepsilon _b \right) - \sinh ( x_1\varepsilon _b) \cdot \sinh \left( x_2 \varepsilon _b \right) \right) . \end{aligned}$$

Similarly, for another segment:

$$\begin{aligned} f_2(x_2,x_3) :&= \ell (\gamma _{\xi _2\xi _3}) = \\&=\mathrm{Arcosh}\left( \cosh b \cdot \cosh ( (1-x_2) \varepsilon _b ) \cdot \cosh \left( x_3 \varepsilon _b \right) - \sinh ( (1- x_2)\varepsilon _b) \cdot \sinh \left( x_3 \varepsilon _b \right) \right) . \end{aligned}$$

Consider the function $f_\xi (x_1,x_2,x_3) = f_1(x_1,x_2) + f_2(x_2,x_3)$. By definition, ${\tilde{r}}_2(\xi ) = f_1(x_1^\prime ,x_2^\prime )$, where $x_1^\prime$ and $x_2^\prime$ are chosen so that

$$\begin{aligned} f_\xi (x_1^\prime ,x_2^\prime ,x_3) = \inf _\xi \inf _{x_1,x_2,x_3} f_\xi (x_1,x_2,x_3). \end{aligned}$$

(2.12)

Analysing this function we obtain that $x_1^\prime = 0$ and $x_2^\prime = 0.5$. We see that

$$\begin{aligned} f_1(0,0.5) = \mathrm{Arcosh}\left( \cosh b \cdot \cosh \left( 0.5 \varepsilon _b \right) \right) . \end{aligned}$$

Finally by a straightforward calculation we can write

$$\begin{aligned} {\tilde{r}}_2(\xi )&= \ln \left( \cosh b \cosh \frac{\varepsilon _b}{2} + \sqrt{\cosh ^2 b \cosh ^2 \frac{\varepsilon _b}{2} -1} \right) \nonumber \\&= \ln \left( 2 \cosh b \cosh \frac{\varepsilon _b}{2} + \frac{1}{2} e^{-b} + O(e^{-2b}) \right) \nonumber \\&= \ln ( 2 \cosh b) + 2 \ln \left( \cosh \frac{\varepsilon _b}{2}\right) + 2\ln \left( 1 + \frac{1}{2} e^{-2b} + O(e^{-3b})\right) . \end{aligned}$$

(2.13)

We have asymptotic expansions

$$\begin{aligned} \ln (2 \cosh b) = b + \ln (1 + e^{-2b}) = b + e^{-2b} + O(e^{-4b}) \end{aligned}$$

(2.14)

and

$$\begin{aligned} \ln \left( \cosh \frac{\varepsilon _b}{2}\right) \!= \!\ln \left( \frac{e^{ e^{-b/2} \!+\! O(e^{-b})} \!+\! e^{ \!-\! e^{-b/2} \!+\! O(e^{-b})}}{2} \right) = \ln \left( 1 + \frac{e^{-b}}{2} + O(e^{-2b})\right) .\qquad \end{aligned}$$

(2.15)

Substituting (2.14) and (2.15) into (2.13), we conclude ${\tilde{r}}_2(\xi ) = b + e^{-b} + O(e^{-2b})$ as $b\rightarrow +\infty$. This completes the case $\xi _1\ne \xi _3$ and proves the Lemma. $\square$

In “Appendix A” we obtain estimates for the length of closed geodesics of the word length 2, 4, 6, and 8; illustrating Lemma 2.10 and formula (2.8).

Now we can use Lemma 2.10 to compute the matrix A(s) defined by (2.10) in the case $n=2$. We write the transition matrix A defined by (2.9), corresponding to 6 subsequences of cutting sequences of length two: $\xi ^1=\{1,2\}$; $\xi ^2=\{1,3\}$; $\xi ^3=\{2,1\}$; $\xi ^4=\{2,3\}$; $\xi ^5=\{3,1\}$; $\xi ^6 = \{3,2\}$:

$$\begin{aligned} A = \left( \begin{matrix} 0&{}\quad 0&{}\quad 1&{}\quad 1&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 1 \\ 1&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 1 \\ 1&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad 1&{}\quad 1&{}\quad 0&{}\quad 0 \\ \end{matrix}\right) . \end{aligned}$$

Substituting ${\tilde{r}}_2(s)$ into (2.10), we get the matrix function:

$$\begin{aligned} A(s) = \left( \begin{matrix} 0&{} 0&{} e^{-sb} &{} e^{-s(b + e^{-b})} &{} 0 &{} 0 \\ 0&{} 0&{} 0&{} 0&{} e^{-sb} &{} e^{-s(b + e^{-b})} \\ e^{-sb} &{} e^{-s(b + e^{-b})}&{} 0&{} 0&{} 0 &{} 0 \\ 0&{} 0&{} 0&{} 0&{} e^{-s(b + e^{-b})} &{} e^{-sb} \\ e^{-s(b + e^{-b})}&{} e^{-sb} &{} 0&{} 0&{} 0 &{} 0 \\ 0&{} 0&{} e^{-s(b + e^{-b})}&{} e^{-sb}&{} 0 &{} 0 \\ \end{matrix}\right) + O\left( e^{-2b}\right) . \end{aligned}$$

Introducing a shorthand notation $z=e^{- s e^{-b}}$ we rewrite the main term of A(s) as

$$\begin{aligned} A(s) = e^{-sb} \left( \begin{matrix} 0&{}\quad 0&{}\quad 1 &{}\quad z &{}\quad 0 &{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 1 &{}\quad z \\ 1 &{}\quad z &{}\quad 0&{}\quad 0&{}\quad 0 &{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad z &{}\quad 1 \\ z &{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0 &{}\quad 0 \\ 0&{}\quad 0&{}\quad z &{}\quad 1 &{}\quad 0 &{}\quad 0 \\ \end{matrix}\right) . \end{aligned}$$

(2.16)

The simplicity of the matrix A(s) allows us to study the zero set of the analytic function

$$\begin{aligned} g(s) = \det (I_6 - A^2(s)) = \det (I_6 -A(s)) \cdot \det (I_6 + A(s)). \end{aligned}$$

Since $\exp (-sb)$ doesn’t vanish, we see that $g(s)=0$ if and only if

$$\begin{aligned} \det (\exp (2 sb) I_6 - \exp (2sb) A^2(s)) =0 \end{aligned}$$

and this inequality holds true if and only if $\exp (2 s b)$ is an eigenvalue of $\exp (2sb)\cdot A^2(s)$.

The eigenvalues of the matrix

$$\begin{aligned} B(z) := \left( \begin{matrix} 0&{}\quad 0&{}\quad 1 &{}\quad z &{}\quad 0 &{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 1 &{}\quad z \\ 1 &{}\quad z &{}\quad 0&{}\quad 0&{}\quad 0 &{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad z &{}\quad 1 \\ z &{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0 &{}\quad 0 \\ 0&{}\quad 0&{}\quad z &{}\quad 1 &{}\quad 0 &{}\quad 0 \\ \end{matrix}\right) ^2 \end{aligned}$$

(2.17)

can be computed explicitly:

$$\begin{aligned} \mu _1(z)&=(z - 1)^2, \\ \mu _2(z)&= (z + 1)^2,\\ \mu _3(z)&=1 - \frac{z^2}{2} + z\frac{\sqrt{4 - 3z^2}}{2}, \\ \mu _4(z)&= 1 - \frac{z^2}{2} - z\frac{\sqrt{4 - 3z^2}}{2}. \end{aligned}$$

We summarise our finding in the following Lemma.

Lemma 2.11

The determinant $\det (I_6 - A^2(s))$ vanishes if and only if $\exp (2bs) = \mu _k(\exp \left( -se^{-b}\right) )$ for some $k=1,2,3,4$ where $\mu _k$ as defined above.

We will show how this Lemma leads to the construction of the four curves containing zeros after computing the errors in approximations of the zeta function by an exponential sum and the exponential sum by the determinant $\det \left( I_6 - A^2(s)\right)$. We would like to finish this section with the following remark on properties of the matrix B.

Remark 2.12

Let us consider the matrix B(z) defined by (2.17). Then the coefficients of the polynomial

$$\begin{aligned} \frac{1}{2n}\mathrm{tr}(B^{n}(z)) = d_{2n} z^{2n} + d_{2n-1} z^{2n-1} + \cdots + d_{1} z + d_0 \end{aligned}$$

are given by

$$\begin{aligned} d_{k } = \#\left\{ \gamma _\xi :\omega (\gamma _\xi ) = 2n \text{ and } \sum _{j=0}^{2n-1} c(\sigma ^j \xi ) = k \right\} . \end{aligned}$$

In particular, $\frac{1}{2n} \mathrm{tr}B^{2n}(1)$ is equal to the number of closed geodesics of the word length 2n.

3 Nuclear operators and analytic functions

Error estimates for approximations of the function $Z_{X_b}$ are based on the original approach in [28] (and the interpretation in [27]). We begin by recalling some abstract results, essentially due to Grothendieck, on nuclear operators. We then complete the section by relating the length of the boundary geodesics to the contraction on the boundary corresponding to reflections, generating the group $\Gamma _\theta$.

3.1 Nuclear operators

The convergence of the series (2.2) in Theorem 2.4 will follow from estimates of Ruelle [28], after Grothendieck [11]. We summarize below the general theory.

Let ${\mathscr {B}}$ be a Banach space.

Definition 3.1

We say that a linear operator $T: {\mathscr {B}} \rightarrow {\mathscr {B}}$ is nuclear if there exist for each $n\ge 1$

• 1. $w_n \in {\mathscr {B}}$, with $\Vert w_n\Vert _{{\mathscr {B}}}=1$;

• 2. $\nu _n \in {\mathscr {B}}^*$, with $\Vert \nu _n\Vert _{{\mathscr {B}}^*}=1$;

• 3. $\lambda _n \in \mathord {{\mathbb {R}}}$, with $0< \lambda < 1$, $C>0$ satisfying $|\lambda _n| \le C \lambda ^n$

such that

$$\begin{aligned} T f= \sum \limits _{n=1}^\infty \lambda _n w_n\nu _n(f). \end{aligned}$$

(3.1)

Lemma 3.2

(after Grothendieck) A nuclear operator on a Banach space is trace class, and we can write

$$\begin{aligned} \det (I-zT) = \exp \Bigl (-\sum _{n=1}^\infty \frac{z^n}{n} \mathrm{tr}T^n\Bigr ). \end{aligned}$$

where the infinite series on the right hand side converges in a small disk $|z|<\varepsilon$ and the equality between analytic continuations then holds on ${\mathbb {C}}$.

As the left hand side is an analytic function we may expand it in a power series at $z=0$:

$$\begin{aligned} \det (I-zT) = 1 + \sum _{n=1}^\infty a_n z^n, \end{aligned}$$

where

$$\begin{aligned} a_n = \sum \limits _{j_1< \cdots < j_n}\det \left( [\nu _{j_k}(w_{j_l})]_{k,l = 1}^n\right) \lambda _{j_1} \ldots \lambda _{j_n}. \end{aligned}$$

(3.2)

Applying estimates of Grothendieck and Ruelle, we obtain an explicit bound.

$$\begin{aligned} |a_n| \le C^n n^{n/2} \lambda ^{n(n+1)/2}, \end{aligned}$$

(3.3)

where $n^{n/2}$ bounds the supremum norm of the matrix⁶$[\nu _{j_k}(w_{j_l})]_{k,l = 1}^n$ and $C\in {\mathbb {R}}$ is a constant.

3.2 Constructing the Banach space

In computations it will prove more useful to use the equivalent representation of hyperbolic space by the upper half-plane $\mathbb H^2 = \{x+i y :y > 0\}$ with the metric $ds^2 = \frac{dx^2 + dy^2}{y^2}$.

Given four points $z_1< w_1< w_2 < z_2$ on the boundary $\partial \mathord {{\mathbb {H}}}^2$, we define the cross ratio by

$$\begin{aligned} {[}z_1,w_1,w_2,z_2]= \frac{(z_1-w_2)}{( z_1 - w_1 )} \frac{(w_1-z_2)}{( w_2 - z_2)}. \end{aligned}$$

We recall the following classical formula (cf. [3] §7.23).

Lemma 3.3

Let $L_1, L_2$ be two disjoint geodesics in $\mathord {{\mathbb {H}}}^2$ with end points $z_1, z_2$ and $w_1, w_2$. The distance $d(L_1,L_2)$ between $L_1$ and $L_2$ satisfies $[z_1,w_1,w_2,z_2] = \tanh ^2(d(L_1,L_2)/2)$.

By assumption, the group $\Gamma =\langle R_1,R_2,R_3\rangle$ is generated by reflections with respect to three disjoint geodesics, which we denote by $\beta _1$, $\beta _2$, and $\beta _3$, respectively. Without loss of generality, we may assume that the geodesic $\beta _j$ has end points $e^{\bigl (\frac{2\pi j}{3} \pm \theta \bigr ) i}$, for $j =1,2,3$ and a small real number $\theta$. More precisely, by straightforward calculation using Lemma 3.3 we get

Lemma 3.4

Let $\beta _1$ and $\beta _2$ be two disjoint geodesics in ${\mathbb {D}}^2$ with end points $e^{\bigl (\pm \frac{2\pi }{3} \pm \theta \bigr ) i}$. Then $\sin \theta =\frac{1}{2\cosh b}$.

Proof

We can apply Lemma 3.3 with $z_1 = e^{\bigl ( \frac{2\pi }{3} + \theta \bigr ) i}$, $z_2 = e^{\bigl ( \frac{2\pi }{3} - \theta \bigr ) i}$, $w_1 = e^{\bigl (- \frac{2\pi }{3} + \theta \bigr ) i}$, $w_2 = e^{\bigl (- \frac{2\pi }{3} - \theta \bigr ) i}$ and $b = d(L_1, L_2)$. $\square$

Remark 3.5

In the notation and under the hypothesis of the last lemma, we have an asymptotic relation

$$\begin{aligned} \theta = \frac{1}{2}e^{-b}\left( 1+e^{-2b}+o(e^{-3b})\right) \text{ as } b\rightarrow \infty . \end{aligned}$$

To define the Banach space, we fix a small $\varphi <\theta$ and introduce three additional geodesics $\upsilon _j$ with end points $e^{\bigl (\frac{2\pi j}{3}\pm \varphi \bigr )i}$, $j=1,2,3$. We may consider the disk $\mathord {{\mathbb {D}}}^2$ as a subset of $\mathord {{\mathbb {C}}}$ and formally extend the geodesics $\upsilon _j$ to circles $\overline{\upsilon }_j \subset \mathord {{\mathbb {C}}}$. Furthermore, let $\{U_j\}_{j=1}^3$ be three disks in $\mathord {{\mathbb {C}}}$ such that $\partial U_j = \overline{\upsilon }_j$ cf. Fig. 8.

Fig. 8

Three geodesics $\beta _j$ in $\mathord {{\mathbb {D}}}^2$ giving rise to the reflections $R_j$; and three additional geodesics $\upsilon _j$ which are used to define domain of the analytic functions in ${\mathscr {B}}$. The disks $U_j$ are the shaded regions

The Banach space of bounded analytic functions $f: \sqcup _{j=1}^3 U_j \rightarrow {\mathbb {C}}$ on the union $\sqcup _{i=1}^3 U_i$ we denote by ${\mathscr {B}}$. We supply it with the supremum norm $\Vert f\Vert _{{\mathscr {B}}} := \Vert f\Vert _\infty$.

3.3 Transfer operators

We can now define transfer operators ${\mathscr {L}}_s$, acting on the Banach space ${\mathscr {B}}$ of bounded analytic functions on $\sqcup _{j=1}^3 U_j$.

Definition 3.6

For each $s \in \mathord {{\mathbb {C}}}$ we can define

$$\begin{aligned} ({\mathscr {L}}_s f)(z) = \sum _{k=1}^3 \chi _{U_k}(z) \sum \limits _{j\ne k}(R_j'(z))^s f(R_j(z)) \qquad \text{ for } f \in {\mathscr {B}}, \end{aligned}$$

(3.4)

where $\chi _{U_k}$ is the indicator function of $U_k$.

We can apply the general theory of nuclear operators to the transfer operators by virtue of the following (compare with [17]).

Lemma 3.7

The operator ${\mathscr {L}}_s :{\mathscr {B}} \rightarrow {\mathscr {B}}$ is nuclear.

Proof

We observe that the operators $f \mapsto f\circ R_j$ are nuclear and $R_j^\prime (z)^s$ are analytic [28]. Thus ${\mathscr {L}}_s$ is nuclear, too. $\square$

Applying Lemma 3.2 to $T_s: {\mathscr {B}} \times \{\pm 1\} \rightarrow {\mathscr {B}} \times \{\pm 1\}$ defined by $T_s(w, \epsilon ) = ({\mathscr {L}}_s w, -\epsilon )$ we recover Theorem 2.4, see [28] for details. In particular, by equation 2.4 we can write

$$\begin{aligned} Z_{X_b}(s,z) = \exp \left( -\sum _{m=1}^\infty \frac{z^{2m}}{2m} \text{ tr }{\mathscr {L}}_s^{2m} \right) = \det (I - T_s) \end{aligned}$$

where

$$\begin{aligned} \text{ tr } {\mathscr {L}}_s^{2m} = \sum _{k_1, \ldots , k_{2m}} \frac{|(R_{k_1} \cdots R_{k_{2n}})'(x_{k_1, \ldots , k_{2m}})|^{-s}}{1-\left| (R_{k_1} \cdots R_{k_{2m}})'(x_{k_1, \ldots , k_{2m}})\right| ^{-1}} \end{aligned}$$

where $x_{k_1, \ldots , k_{2m}}$ is the expanding fixed point for $R_{k_1} \cdots R_{k_{2m}}$. This is completely analogous to the approach to transfer operators associated to modular surface in [20].

4 Estimating aproximation errors

Notation 4.1

We denote a partial sum of the series (2.2) by $Z_n$ ($n\ge 1$):

$$\begin{aligned} Z_n(s) := 1 + \sum _{k=1}^n a_k(s). \end{aligned}$$

(4.1)

Note that it is an exponential sum of $\left[ \frac{n}{2}\right]$ terms, since odd terms vanish $a_{2k+1}=0$.

Our main approximation result is the following.

Theorem 4.2

Let $X_b$ be a symmetric 3-funnelled surface with defining geodesics of length 2b. Then the finite partial sums $Z_n$ give approximations to $Z_{X_b}$ on the domain ${\mathscr {R}}(T)$ and the remainder is bounded as follows: $\sup _{{\mathscr {R}}(T)} |Z_{X_b} - Z_{n}| \le \eta (b,n,T)$ where $T=T(b)=e^{\varkappa b}$ for some constant $\varkappa >1$ independent of b and n, such that

• 1. for any $n \ge 14$ we have $\eta (b,n,T(b)) = O\Bigl ( \frac{1}{\sqrt{b}} \Bigr )$ as $b \rightarrow \infty$

• 2. for any $b \ge 20$ we have $\eta (b,n,T(b)) = O\bigl ( e^{-bk_1n^2} \bigr )$ as $n \rightarrow \infty$

for some $k_1>0$ which is independent of b and n.

For a fixed b this theorem estimates the number of terms $a_n$ needed to uniformly approximate $Z_{X_b}$ to any given error; at the same time for a given n this theorem estimates the difference between $Z_{X_b}$ and $Z_n$ as $b \rightarrow \infty$ on an exponentially growing domain.

Remark 4.3

The constants $\varkappa$ and $k_1$ in Theorem 4.2 should satisfy the inequality $0<k_1<\frac{2-\varkappa }{60}$, although this bound is not sharp. A sharp bound can be obtained using the same argument, but the formulae will be more complicated.

To illustrate Theorem 4.2, we can fix a surface by choosing the length of boundary geodesics 2b and plot the zeros for the approximating trigonometric polynomials $Z_{2n}=1+a_2 + \cdots + a_{2n}$ for $n=1,2,\cdots ,6$. For instance, in Fig. 9 zeros of polynomials approximating $Z_{X_b}$ with $b=5$ are shown. The apparent “gaps” in the zeros are due to instability of the Newton method.

Fig. 9

Plots of the zeros $Z_{n}(s)$ for $n=2, 4,\ldots , 14$ and $b=6$

Remark 4.4

In practice, Theorem 4.2 shows that numerical results obtained for $Z_{n}$ hold in a domain $\mathscr {R}(e^{k_1b})$ for the Selberg zeta function, too. Since in practice n is bounded above by computational considerations, we may assume that it is fixed. Even with a modern computer, one will not be able to consider $n>16$ in a reasonable time.⁷ Moreover, in practical applications b cannot be chosen too large either due to computer restrictions because of accumulation of errors while dealing with small numbers. The coefficients $b_n$ defined by (2.4) involve a sum of $4^{n}+2$ terms of the order $\exp (-2snb)$ with $0<\mathfrak {R}(s)<0.25$, say. The bound $4^{n}+2$ is equal to number of closed geodesics of the word length 2n, see Remark 2.6.

4.1 Proof of the approximation result

In this section we give a proof of Theorem 4.2. We will need the following simple technical estimate.

Lemma 4.5

Let $x_n$ be a sequence of real numbers satisfying $|x_n|\le \exp \bigl (p n -q n^2\bigr )$ for some constants $p,q>0$. Then for any $n>1$ we have that

$$\begin{aligned} \sum _{k=n}^\infty |x_k| \le \frac{\sqrt{\pi }}{2\sqrt{q}} \exp \Bigl (\frac{p^2}{4q} \Bigr ) \exp \Bigl (-q\Bigl (n - \frac{p}{2q} \Bigr )^2\Bigr ). \end{aligned}$$

Proof

The result follows by straightforward calculation using the classical bound for the error function $\int _{n}^\infty \exp (-t^2) d\,t \le \frac{\sqrt{\pi }}{2} \exp (-n^2)$. $\square$

We now turn to the proof of Theorem 4.2. This follows the same lines as [17]. However, the key new idea is that the disks $U_1$, $U_2$ and $U_3$ used to define ${\mathscr {B}}$ are allowed to depend on b.

Proof of Theorem 4.2

Without loss of generality we may assume that the geodesic $\beta _j$ has end points $e^{(\frac{2\pi }{3}j\pm \theta )i}\in \partial \mathord {{\mathbb {D}}}^2$ for $j=1,2,3$. We choose three additional geodesics $\upsilon _j$ with end points $e^{(\frac{2\pi }{3}j\pm \varphi )i}\in \partial \mathord {{\mathbb {D}}}^2$ for some $0<\varphi <\theta$, that we will specify later, see Fig. 8 for details. We may consider $\mathord {{\mathbb {D}}}^2$ as a subset of $\mathord {{\mathbb {C}}}$ with usual Euclidean metric, and then complete $\upsilon _j$ to full Euclidean circles $\overline{\upsilon }_j\in \mathord {{\mathbb {C}}}$. We define $U_j\in \mathord {{\mathbb {C}}}$ to be compact disks with $\partial U_j=\overline{\upsilon }_j$.

It turns out that the calculations are much easier in the upper half plane model of the hyperbolic space ${\mathbb {H}}^2$. We choose the map $S(z) = i \frac{1-z}{1+z}$ to change the coordinates. Then the geodesic $\beta _j$ has end points $\frac{\sin (\frac{2\pi j}{3}\pm \theta )}{1+\cos (\frac{2\pi j}{3}\pm \theta )} \in \partial \mathord {{\mathbb {H}}}^2$, and its Euclidean radius and centre are given by, respectively

$$\begin{aligned} \varepsilon _j&= \frac{1}{2}\left( \frac{\sin (\frac{2\pi j}{3}+\theta )}{1+\cos (\frac{2\pi j}{3}+\theta )} - \frac{\sin (\frac{2\pi j}{3}-\theta )}{1+\cos (\frac{2\pi j}{3}-\theta )} \right) \end{aligned}$$

(4.2)

$$\begin{aligned} c_j&= \frac{1}{2}\left( \frac{\sin (\frac{2\pi j}{3}+\theta )}{1+\cos (\frac{2\pi j}{3}+\theta )} + \frac{\sin (\frac{2\pi j}{3}-\theta )}{1+\cos (\frac{2\pi j}{3}-\theta )} \right) . \end{aligned}$$

(4.3)

The end points of $\upsilon _j$ are $\frac{\sin (\frac{2\pi j}{3}\pm \varphi )}{1+\cos (\frac{2\pi j}{3}\pm \varphi )} \in \partial \mathord {{\mathbb {H}}}^2$ and the euclidean radius is

$$\begin{aligned} r_j = \frac{1}{2}\left( \frac{\sin (\frac{2\pi j}{3}+\varphi )}{1+\cos (\frac{2\pi j}{3}+\varphi )} - \frac{\sin (\frac{2\pi j}{3}-\varphi )}{1+\cos (\frac{2\pi j}{3}-\varphi )} \right) . \end{aligned}$$

(4.4)

We can consider the Banach space ${\mathscr {B}}$ to be the space of bounded analytic functions on $\sqcup _{j=1}^3 U_j \subset \mathord {{\mathbb {C}}}$ with the supremum norm.

We see that the reflection $R_j$ with respect to the geodesic $\beta _j$ in $\mathord {{\mathbb {H}}}^2$ is given by $R_j(z) = \frac{\varepsilon _j^2}{z-c_j}+c_j$. We deduce that for any distinct j, k, l the image $R_j(U_k \cup U_l) \subset U_j$, provided $\frac{\varepsilon _j^2}{z-c_j}< r_j$ for any $z \in U_k \sqcup U_l$. We know that for all $z \in U_k \sqcup U_l$ we have $|z-c_j|>1$, thus it is sufficient to chose $\theta$ and $\varepsilon _j$ such that $\varepsilon _j^2 < r_j$.

Using (4.2) by a straightforward calculation we may estimate $\frac{1}{2}\theta \le \varepsilon _j \le 2 \theta + O(\theta ^2)$ and similarly from (4.4) we have that $\frac{1}{2} \varphi \le r_j \le 2 \varphi + O(\varphi ^2)$ for small values of $\theta$ and $\varphi$. Hence it is sufficient to choose $\theta$ and $\varphi$ such that $4\theta ^2<\frac{1}{2} \varphi$. Using Lemma 3.4, we see

$$\begin{aligned} \theta = e^{-b}(1+e^{-2b}+o(e^{-3b})). \end{aligned}$$

In particular, it is sufficient to choose

$$\begin{aligned} \varphi = e^{-b \varkappa } \text{ for } \text{ some } 1<\varkappa <2 \text{ and } b \text{ sufficiently } \text{ large }. \end{aligned}$$

(4.5)

Then (4.2) and (4.4) give estimates for the radii of inner and outer circles, respectively,

$$\begin{aligned} \frac{1}{2} e^{-b\varkappa }&\le r_j \le 2 e^{-b \varkappa } + O(e^{-2 b\varkappa }), \end{aligned}$$

(4.6)

$$\begin{aligned} \frac{1}{2} e^{-b}&\le \varepsilon _j \le 2 e^{-b} + O(e^{-2b}) . \end{aligned}$$

(4.7)

Using the Cauchy integral formula for $z \in U_k$ and $R_j(z)\in U_j$ we can write

$$\begin{aligned} f(R_j(z)) = \frac{1}{2\pi i} \int _{\partial U_j } \frac{f(\xi )}{\xi - R_j(z)} d\xi \end{aligned}$$

and thus

$$\begin{aligned} (R_j^\prime (z))^s f(R_j(z)) = \frac{(R_j^\prime (z))^s}{2\pi i} \int _{\partial U_j} \frac{f(\xi )}{\xi - R_j(z)} d\xi . \end{aligned}$$

Since ${\mathscr {L}}_s$ is a nuclear operator, it the identity (3.1) should hold. More precisely, we may write

$$\begin{aligned} ( {\mathscr {L}}_s f)(z)&= \sum _{j=1}^3 (R_j^\prime (z))^s f(R_j(z)) \sum _{k=1, k\ne j}^3\chi _{U_k}(z) \\&= \sum _{j=1}^3 (R_j^\prime (z))^s \cdot \left( \sum _{n=0}^\infty \frac{(R_j(z)-c_j)^n}{2 \pi i} \int _{\partial U_j} \frac{f(\xi )}{(\xi -c_j)^{n+1} } d \xi \right) \cdot \left( \sum _{k=1, k \ne j}^3 \chi _{U_k}(z) \right) \\&= \sum \limits _{n=0}^\infty \lambda _n w_n(z) \nu _n (f), \end{aligned}$$

where, $w_n \in {\mathscr {B}}$, $\nu _n \in {\mathscr {B}}^*$, and $\lambda _n \in \mathord {{\mathbb {R}}}^+$ satisfy conditions of Definition 3.1. We may choose for any $j \in \{1,2,3\}$

$$\begin{aligned} w_{3n+j}(z)&\asymp (R_j^\prime (z))^s \cdot \frac{(R_j(z)-c_j)^n}{2 \pi i}\sum _{k=1, k \ne j}^3 \chi _{U_k}(z) \end{aligned}$$

(4.8)

$$\begin{aligned} \nu _{3n+j}(f)&\asymp \int _{\partial U_j} \frac{f(\xi )}{(\xi -c_j)^{n+1} } d \xi , \end{aligned}$$

(4.9)

with normalization $\Vert w_n\Vert _\infty = \Vert \nu _n\Vert _\infty =1$, and where $c_j$ are given by (4.3). Then for any $j \in \{1,2,3\}$

$$\begin{aligned} |\lambda _{3n+j}| = \left\| (R_j^\prime )^s\mid _{U_k\cup U_l} \Vert _\infty \cdot \Vert (R_j-c_j)^n\mid _{U_k\cup U_l} \right\| _\infty \cdot \left\| \frac{1}{2\pi i} \int _{\partial U_j} \frac{f(\xi )}{(\xi -c_j)^{n+1}}d\xi \right\| _\infty ,\nonumber \\ \end{aligned}$$

(4.10)

where $k\ne j$ and $l \ne j$, and the latter term is the supremum norm of the functional

$$\begin{aligned} f \mapsto \frac{1}{2\pi i} \int _{\partial U_j} \frac{f(\xi )}{(\xi -c_j)^{n+1}}d\xi . \end{aligned}$$

We may observe that for any $\xi \in \partial U_j$ one has that $\xi -c_j=r_j$ and conclude

$$\begin{aligned} |\lambda _{3n+j}| \le \Vert R_j^\prime (z)^s\mid _{U_k\cup U_l} \Vert _\infty \cdot \frac{\varepsilon _j^{2n}}{r_j^{n+1}}. \end{aligned}$$

More precisely, using formulae (4.2) and (4.4), we obtain an upper bound

$$\begin{aligned} |\lambda _n|&\le \max _j \Vert R_j^\prime (z)^s\mid _{U_k\cup U_l} \Vert \cdot \max \left\{ \frac{1}{r_1} \frac{\varepsilon _1^{2n/3}}{r_1^{n/3}}, \, \frac{1}{(\varepsilon _2 r_2)^{2/3}} \frac{\varepsilon _2^{2n/3}}{r_2^{n/3}}, \, \frac{1}{\varepsilon _3^{4/3} r_3^{1/3}} \frac{\varepsilon _3^{2n/3}}{r_3^{n/3}} \right\} \\&\le \max _j \Vert R_j^\prime (z)^s\mid _{U_k\cup U_l} \Vert \cdot \frac{1}{\varepsilon _3^{4/3} r_3^{1/3}} \max _j \frac{\varepsilon _j^{2n/3}}{r_j^{n/3}}. \end{aligned}$$

Comparing this with the definition of the nuclear operator 3.1, we get explicit bounds for parameters $\lambda$ and C(s).

$$\begin{aligned} |\lambda _n| \le \max _k \sup _{z \in U_k} \max _{j\ne k}\left| \frac{\epsilon _j^{2s}}{(z-c_j)^{2s}}\right| \cdot \frac{1}{\varepsilon _3^{4/3} r_3^{1/3}} \cdot \max _j \frac{\epsilon _j^{2n/3}}{r_j^{n/3}} \le C(s) \lambda ^n, \end{aligned}$$

with the choices

$$\begin{aligned} \lambda&= \Bigl ( \max _{j}\frac{\epsilon _j^2}{r_j}\Bigr )^{\frac{1}{3}} \end{aligned}$$

(4.11)

$$\begin{aligned} C(s)&= \max _{k} \sup _{z \in U_k} \max _{j \ne k} \left| \frac{\epsilon _j^{2s}}{(z-c_j)^{2s}} \right| \cdot \frac{1}{\varepsilon _3^{4/3} r_3^{1/3}}. \end{aligned}$$

(4.12)

Using the bounds (4.6) and (4.7) for $\varepsilon _j$ and $r_j$, we conclude

$$\begin{aligned} \lambda =\Bigl (\max \frac{\varepsilon _j^2}{r_j}\Bigr )^{\frac{1}{3}} \le 2 e^{-\frac{2-\varkappa }{3}b}. \end{aligned}$$

(4.13)

Furthermore, we see that for any $j \ne k$ for all $z \in U_k$ we have $|\arg (z-c_j)|\le \arcsin (\frac{r_j}{c_k-c_j}) \le 2\varphi$. Therefore for $s=\sigma +it$,

$$\begin{aligned} |(z-c_j)^{2s}|&=\bigl |\exp \bigl (2 (\ln |z-c_j|+i\arg (z-c_j))\cdot (\sigma +it) \bigr )\bigr | \\&=|z-c_j|^\sigma \cdot \exp (-2\arg (z-c_j)t) \ge \exp (4\varphi t), \end{aligned}$$

since by construction $\inf _{z \in U_k}|z-c_j| > 1$. Using (4.6) and (4.7), we deduce

$$\begin{aligned} C(s)= & {} \max _{k} \sup _{z \in U_k} \max _{j \ne k} \left| \frac{\epsilon _j^{2s}}{(z-c_j)^{2s}}\right| \cdot \frac{1}{\varepsilon _3^{4/3} r_3^{1/3}} \nonumber \\&\le \max _{k} \sup _{z \in U_k} \max _{j \ne k} \left| \frac{\epsilon _j^{2\sigma }}{(z-c_j)^{2s}}\right| \cdot 4 e^{b(\varkappa +4)/3} \nonumber \\&\le 4 \epsilon _j^{2\sigma } e^{4 \varphi t + b(\varkappa +4)/3} \le e^{\ln 4 -2b\sigma + 4\varphi t + b(\varkappa +4)/3}. \end{aligned}$$

(4.14)

Substituting bounds (4.13) and (4.14) into Ruelle’s inequality (3.3) and taking into account $t<T$ for $s = \sigma +it \in {\mathscr {R}}(T)$, we obtain an upper bound

$$\begin{aligned} |a_n(s)|&\le C^n(s) \lambda ^{n(n+1)/2} n^{n/2} \nonumber \\&\le \exp \left( (\ln 4 - 2b\sigma + \frac{b(\varkappa +4)}{3} + 4\varphi t)n - \frac{n(n+1)}{2}\Bigl ( \frac{b (2-\varkappa )}{3} - \ln 2 \Bigr ) + \frac{n \ln n}{2} \right) \nonumber \\&\le \exp \left( (\ln 4 + \frac{b(\varkappa +4)}{3} + 4\varphi T) n - \frac{n(n+1)}{2}\Bigl (\frac{ b (2-\varkappa )}{3}- \ln 2 \Bigr ) + \frac{n \ln n}{2} \right) , \end{aligned}$$

(4.15)

since $\exp (-2bn\sigma )\le 1$.

In order to estimate the tail of the series $\sum \limits _{n=14}^\infty a_n(s)$ using Lemma 4.5, it is sufficient to find a constant $k_2<1$ such that

$$\begin{aligned} n\left( \ln 4 + \frac{b(\varkappa +4)}{3} + \frac{ b (2-\varkappa )}{6}\right) + \frac{(n+1)n}{2} \ln 2 + \frac{n \ln n}{2} < \frac{ b n^2 (2-\varkappa )}{6} k_2 \end{aligned}$$

(4.16)

which is equivalent

$$\begin{aligned} \frac{\frac{15\ln 2}{b}+10+\varkappa }{k_2(2-\varkappa )-\frac{3\ln 2}{b}} < n - \frac{3 \ln n}{b k_2 (2-\varkappa ) - 3 \ln 2}. \end{aligned}$$

(4.17)

It is clear that the last inequality doesn’t hold for any $n \le 10$ but it does hold, for example, for all $b\ge 20$ and $n\ge 14$ with the choices $\varkappa =1.05$ and $0.95\le k_2 < 1$. Therefore we obtain an upper bound

$$\begin{aligned} |a_n(s)| \le \exp \left( 4 \varphi T n - \frac{ b (2-\varkappa )(1-k_2) }{6} n^2 \right) , \quad \text{ for } \text{ all } n\ge 14. \end{aligned}$$

(4.18)

We recall that $\varphi =e^{-\varkappa b}$ by (4.5) and applying Lemma 4.5 with the choices $p=4 e^{-\varkappa b} T$ and $q=\frac{b(2-\varkappa )(1-k_2)}{6}$, we get an estimate $\sum \limits _{k=n}^\infty |a_n(\sigma +it)| \le \eta (b,n,T(b))$, where $T(b) = k_0 e^{\varkappa b}$ for some $k_0>0$, all $b\ge 20$, $n\ge 14$ and

$$\begin{aligned}&\eta (b,n,T(b)) \nonumber \\&= \frac{\sqrt{6\pi }}{2\sqrt{b(2-\varkappa )(1-k_2)}} \exp \left( \frac{24 k_0^2 }{b(2-\varkappa )(1-k_2)}\right) \nonumber \\&\quad \times \,\exp \left( \frac{b(2-\varkappa )(k_2-1)}{6} \left( n-\frac{12 k_0}{b(2-\varkappa )(1-k_2)}\right) ^2\right) . \end{aligned}$$

(4.19)

Therefore we have the desired asymptotic estimates:

• 1. for any $n \ge 14$ we have $\eta (b,n,T(b)) = O\bigl ( \frac{1}{\sqrt{b}} \bigr )$ as $b \rightarrow \infty$;

• 2. for any $b \ge 20$ we have $\eta (b,n,T(b)) = O\bigl ( e^{-bk_1n^2} \bigr )$ as $n \rightarrow \infty$;

hold with the choices, for example, $0<k_1 \le \frac{(2-\varkappa )(1-k_2)}{6}$, where $1<\varkappa <2$ and $k_2$ are chosen so that (4.16) holds. $\square$

5 Results on the zero set

We now turn to the problem of describing the distribution of the zeros. In Sect. 2.2 we introduced a matrix function A(s), closely connected to the zeta function. In the following proposition we study the convergence of

$$\begin{aligned} \lim _{n \rightarrow \infty } \det \left( I_N - A^2(s)\right) ; \end{aligned}$$

from Lemma 2.8.

Let us recall the matrix A(s) computed in (2.16) using an approximation to the length of closed geodesics based on the segments of word length 2:

$$\begin{aligned} A^2(s) = e^{-2sb} \left( \begin{matrix} 1 &{}\quad z &{}\quad 0 &{}\quad 0 &{}\quad z^2 &{}\quad z \\ z &{}\quad 1 &{}\quad z^2 &{}\quad z &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1&{}\quad z&{}\quad z &{}\quad z^2 \\ z^2 &{}\quad z &{}\quad z&{}\quad 1&{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad z &{}\quad z^2 &{}\quad 1 &{}\quad z \\ z&{}\quad z^2&{}\quad 0 &{}\quad 0 &{}\quad z &{}\quad 1 \\ \end{matrix}\right) , \qquad \text{ where } z=e^{-se^{-b}}. \end{aligned}$$

As we are looking to study rescaled zeros,

$$\begin{aligned} \left\{ \sigma b+i e^{-b} t \Bigl | Z_{X_b} (\sigma +it) = 0 \right\} = \left\{ \sigma + it \Bigl | Z_{X_b} \left( \frac{\sigma }{b} + it e^b \right) = 0 \right\} , \end{aligned}$$

it is appropriate to consider $A\left( \frac{\sigma }{b} + it e^b \right) = e^{-2\sigma - 2it b e^b} B(z)$, where $z= \exp \left( -\frac{1}{2}\left( \frac{\sigma }{b e^b} + it\right) \right)$ and $B(z) = e^{2bs} A^2(s)$, defined by (2.17). Taking into account that $\exp \left( -\frac{\sigma }{2 b e^b}\right) \rightarrow 1$ as $b \rightarrow + \infty$ for $\sigma >0$, we conclude the following:

Proposition 5.1

Using the notation introduced above, the real analytic function $Z_{12}\bigl (\frac{\sigma }{b} + ite^b\bigr )$ converges uniformly to $\det (I-\exp (-2\sigma -2itbe^b)B(e^{it}))$ on the critical strip, and more precisely,

$$\begin{aligned} \left| Z_{12}\left( \frac{\sigma }{b} + i t e^{b}\right) -\det \left( I-\exp (-2\sigma -2itbe^b)B(e^{it})\right) \right| = O\left( e^{-b}\right) \text{ as } b \rightarrow +\infty . \end{aligned}$$

Proof

This follows by straightforward calculation of the first 12 coefficients and the determinant. Let us introduce dummy variables $x=\exp (-2\sigma -2itbe^b)$ and $y=e^{it}$ with $|x|< 1$ and $|y|=1$. Then

$$\begin{aligned} \det \left( I-\exp (-2\sigma -2itbe^b)B(e^{it})\right) = \det \left( I-xB(y)\right) = \sum _{k=0}^6 x^k P_k(y^2), \end{aligned}$$

(5.1)

where $P_k \in \mathord {{\mathbb {Z}}}[\cdot ]$ are some polynomials with integer coefficients. More precisely, we can compute:

$$\begin{aligned} P_0(y)&\equiv 1, \\ P_1(y)&\equiv 6, \\ P_2(y)&= 15 - 6y^2, \\ P_3(y)&= 20 - 24y^2 + 6y^4 + 2y^6, \\ P_4(y)&= 15 - 36y^2 + 27y^4 - 6y^6, \\ P_5(y)&= -6(y^2-1)^4, \\ P_6(y)&= (y^2-1)^6. \end{aligned}$$

On the other hand

$$\begin{aligned} Z_{12}\left( \frac{\sigma }{b} + i t e^{b}\right) = \sum _{j=0}^{12} a_j\left( \frac{\sigma }{b} + i t e^{b}\right) . \end{aligned}$$

Now one can deduce by comparing coefficients in $x^n$ that $a_{2n}\left( \frac{\sigma }{b} + i t e^{b}\right) = x^n P_n(y) + O(e^{-b})$. $\square$

Remark 5.2

Using the estimates for the hyperbolic length of closed geodesics of the word length $\omega (\gamma )\le 6$, presented in the “Appendix A”, we may explicitly compute the first few non-zero coefficients

$$\begin{aligned} a_2(s)&= - \frac{6 e^{-2bs}}{1-e^{-2b}} \\ a_4(s)&= 15e^{-4bs} - 6 e^{-4bs} \bigl (1+e^{-b} + 2e^{-2b} \bigr )^{2s} + O(e^{-b}) \\ a_6(s)&= - 20e^{-6bs} - 2 e^{-6bs} \bigl (1+3e^{-b}+3e^{-2b}\bigr )^{2s} - 6 e^{-6bs} \bigl (1 + 2 e^{-b} + 3e^{-2b} \bigr )^{2s} + \\&\quad +\, 24e^{-6bs} \bigl (1+e^{-b}+ 2e^{-2b}\bigr )^{2s} + O(e^{-b}). \end{aligned}$$

We shall illustrate Proposition 5.1 using formulae for the coefficients above. We can write

$$\begin{aligned} a_2\left( \frac{\sigma }{b} + i t e^{b}\right)&= -\frac{6\exp \bigl (-2\sigma -2itbe^b\bigr )}{1-e^{-2b}}=\frac{-6x}{1-e^{-2b}} = -6x (1+O(e^{-2b}))= xP_1+O(e^{-b}). \end{aligned}$$

Similarly for $a_4$:

$$\begin{aligned} a_4\left( \frac{\sigma }{b} + i t e^{b}\right)&= 15e^{-4\sigma -4itbe^b} - 6 e^{-4\sigma -4itbe^b} \bigl (1+e^{-b} + 2e^{-2b} \bigr )^{2\sigma /b+2ite^b} + O(e^{-b}) \\&= 15x^2 - 6x^2\bigl (1+e^{-b} + 2e^{-2b} \bigr )^{2\sigma /b}\cdot \bigl (1+e^{-b} + 2e^{-2b} \bigr )^{2ite^b} + O(e^{-b}) \\&= 15x^2 - 6x^2e^{2it}\cdot \bigl (1+O(e^{-b})\bigr )+ O(e^{-b}) \\&= x^2 \bigl (15-6y^2\bigr ) + O(e^{-b})= x^2 P_2(y)+O(e^{-b}), \end{aligned}$$

where we have used the fact that $\bigl (1+e^{-b} + 2e^{-2b} \bigr )^{e^b} = e + O\left( e^{-b}\right)$.

Now we can prove Theorem 1.5.

Proof of Theorem 1.5

We find that the matrix $B(e^{it})$ has exactly four different eigenvalues $\mu _k(t)$, $k=1,\ldots ,4$:

$$\begin{aligned} \mu _1(t)&=(e^{it} - 1)^2 \\ \mu _2(t)&= (e^{it} + 1)^2\\ \mu _3(t)&=1 - \frac{e^{2it}}{2} + e^{it}\frac{\sqrt{4 - 3e^{2it}}}{2} \\ \mu _4(t)&= 1 - \frac{e^{2it}}{2} - e^{it}\frac{\sqrt{4 - 3e^{2it}}}{2}. \end{aligned}$$

By Lemma 2.11, the zero set of the determinant $\det \left( I-\exp (-2\sigma -2itbe^b)B(e^{it})\right)$ belongs to the subset $\left\{ (\sigma ,t)\in \mathord {{\mathbb {R}}}^2 \mid \exists k :|\exp (2\sigma + 2itbe^b)| = |\mu _k| \right\}$. The four equations $\exp (2\sigma )= |\mu _k(t)|$ give us four curves

$$\begin{aligned} \begin{aligned} {\mathscr {C}}_1&= \left\{ \frac{1}{2}\ln |2-2\cos (t)| + it\mid t \in {\mathbb {R}} \right\} ; \\{\mathscr {C}}_2&= \left\{ \frac{1}{2} \ln |2+2\cos (t)| + it \mid t \in {\mathbb {R}} \right\} ; \\\mathscr {C}_3&= \left\{ \frac{1}{2} \ln \left| 1 - \frac{1}{2} e^{2it} - \frac{1}{2} e^{it} \sqrt{4 - 3 e^{2i t}} \right| +it \mid t \in {\mathbb {R}} \right\} ; \\{\mathscr {C}}_4&= \left\{ \frac{1}{2} \ln \left| 1 - \frac{1}{2} e^{2it} + \frac{1}{2} e^{it} \sqrt{4 - 3 e^{2i t}} \right| +it \mid t \in {\mathbb {R}} \right\} . \end{aligned} \end{aligned}$$

Since the curves ${\mathscr {C}}_j$ do not have horizontal tangencies $\sigma \equiv \mathrm {const}$, without loss of generality we may define neighbourhoods as follows:

$$\begin{aligned} V({\mathscr {C}}_j,\varepsilon )\text{: } = \left\{ (\sigma ,t) \mid \left| 2\sigma -\ln |\mu _j(t)|\right| <2\varepsilon \right\} . \end{aligned}$$

To complete the argument we shall show that for all $\varepsilon >0$ and $T>0$ there exists $b_0 > 0$ such that for any $b > b_0$ the zeros of the function $Z\left( \frac{\sigma }{b} + it e^{b}\right)$ with $0 \le \sigma \le 1$ and $|t| \le e^{(2-\varkappa )b}$ belong to a neighbourhood $\cup _k V({\mathscr {C}}_k, \varepsilon )$ of the union of the curves $\cup _k {\mathscr {C}}_k$.

Indeed, given $\varepsilon >0$ and a point $z_0=\sigma _0+it_0$ outside of $\varepsilon$-neighbourhood of $\cup _{j=1}^4 \mathscr {C}_j$ we see that the determinant

$$\begin{aligned} \left| \det \left( I-\exp \left( -2\sigma _0-it_0be^b\right) B(\exp (it_0))\right) \right|>\exp (-6\varepsilon )(\exp \varepsilon -1)^6>0 \end{aligned}$$

is bounded away from zero and the bound is independent of b. Summing up, we see that outside of the neighbourhood $\cup _{j=1}^4 V({\mathscr {C}}_j,\varepsilon )$ the determinant has modulus uniformly bounded away from 0; by Theorem 4.2 for b large we have that the zeta function $Z_{X_b}\left( \frac{\sigma }{b} + it e^b\right)$ can be approximated by $Z_{12}$ arbitrarily closely and by Proposition 5.1$Z_{12}$ can be approximated arbitrarily closely by the determinant. Therefore for b sufficiently large all zeros of the function $Z_{X_b}\left( \frac{\sigma }{b} + it e^b\right)$ belong to the $\varepsilon$-neighbourhood of $\cup _{j=1}^4 {\mathscr {C}}_j$. $\square$

We have concentrated on the particular case of the symmetric 3-funnelled surface (whose defining closed geodesics have the same lengths). However, the same method of combining geometric and analytic approximations works in the case that the boundary curves have different length as well as in the case of symmetric punctured torus, and allows one to explain the nature of the patterns of zeros described in the sections 5.1 and 5.2 of [6].

6 L-functions and covering surfaces

Our results have concentrated on a special class of surfaces, but can be easily adapted to cover a large class of geometrically finite surfaces of infinite area.

There is a fairly simple method for constructing quite complicated surfaces using any (infinite area) surface V without cusps. We can write $V = {\mathbb {D}}^2/\Gamma$ for a convex cocompact group $\Gamma$. Then we can define a (finite) cover ${\widehat{V}} = {\mathbb {H}}^2/\Gamma _0$ for V in terms of a (finite index) normal subgroup $\Gamma _0 < \Gamma$.

Let us denote by $G = \Gamma /\Gamma _0$ the finite quotient group. Let $\gamma$ be a closed geodesic on $X_b$ and then this is covered by the union of closed geodesics $\gamma _1, \ldots , \gamma _n$ on ${\widehat{V}}$.

Let $R_\chi$ be an irreducible representation for G of degree $d_\chi$ with character $\chi = \hbox {tr}(R_\chi )$. The regular representation of G can be written $R = \oplus _\chi d_\chi R_\chi .$ where $|G| = \sum \limits _\chi d_\chi ^2$.

Definition 6.1

Given $s\in {\mathbb {C}}$ we define

$$\begin{aligned} L(z, s, \chi ) = \prod _{\gamma } \det \left( I - z^{|g|}e^{-(s+n)\lambda (g)} R(g\Gamma _0)\right) \end{aligned}$$

where $g\Gamma _0$ is a coset in G.

Lemma 6.2

For characters $\chi _1$ and $\chi _2$ we can write

$$\begin{aligned} L(z, s,\chi _1 + \chi _2) = L(z, s,\chi _1) L(z, s,\chi _2). \end{aligned}$$

If $H < G$ is a subgroup and $\chi$ is a character of H then we can write $G = \cup _{i=1}^m H\alpha _i$ and define the induced character $\chi ^*$ of G by

$$\begin{aligned} \chi ^*(g) = \sum \limits _{\alpha _i g \alpha _i^{-1} \in H} \chi (\alpha _i g \alpha _i^{-1}) \end{aligned}$$

for $g\in G$.

Lemma 6.3

(Brauer–Frobenius) Each non-trivial character $\chi$ is a rational combination of characters $\chi _i^*$ of G induced from non-trivial characters $\chi _i$ of cyclic subgroups $H_i$.

There exist integers $n_1, \ldots , n_k$ with

$$\begin{aligned} n\chi = \sum \limits _{i=1}^k n_i \chi _i^* \end{aligned}$$

and thus

$$\begin{aligned} L(s, z, \chi )^n = \sum \limits _{\alpha _i g \alpha _i^{-1} \in H} \chi (\alpha _i g \alpha _i^{-1}). \end{aligned}$$

Since it is easier to deal with cyclic covering groups. We need the following.

Lemma 6.4

Let $\chi$ be a character of the subgroup $H < G$ and let $\widehat{L}(s,z, \chi ^*)$ be the L-function with respect to the covering ${\widehat{V}}$ of ${\widehat{V}}/H$. Then $L(s, z, \chi ) = {\widehat{L}}(s, z, \chi ^*)$.

The proof is analogous to that of the proof of Proposition 2 in [24].

This leads to the following.

Lemma 6.5

If $\chi$ is an irreducible non-trivial character of G then $L(s, \chi )^n$ is a product of integer powers of L-functions defined with respect to non-trivial characters of cyclic subgroups of G.

Finally this means that we can write the zeta function $Z_{\widehat{V}}(s,z)$ in terms of the L-functions $L(s,z, \chi )$ for V.

Lemma 6.6

We can write

$$\begin{aligned} Z_{{\widehat{V}}}(s,z) = \prod _{\chi \text{ irreducible }} L(s,z, \chi )^{d_\chi }. \end{aligned}$$

where the product is over all irreducible representations of G.

In particular, the zeros for $Z_{{\widehat{V}}}(s,z)$ will be the union of the zeros for the L-functions $L_{V}(s,z, \chi )^{d_\chi }$.

Example 6.7

We can take a double cover ${\widehat{X}}_b$ for a three funnelled surface $X_b$, which corresponds to a 4-funnelled surface. The corresponding covering group is simply ${\mathbb {Z}}_2$ and the zeta function $Z_{{\widehat{X}}_b}(s)$ is then the product of:

• 1. the zeta function $Z_{X_b}(s)$ for the original surface;

• 2. the L-function $L(s,\chi ):= L(s,1,\chi )$ corresponding to the representation $\chi : \pi _1(X_b) \rightarrow {\mathbb {Z}}_2$ where $\chi (g) = (-1)^{n(g)}$ where n(g) counts the number of times the generator a, say, occurs in g.

In particular the zeros for $Z_{{\widehat{X}}_b}(s)$ are a union of the figures for these two functions (see Fig. 10 for a plot).

Fig. 10

(a) Zeros of the zeta function (b) zeros of the L-function in the case $\ell (\gamma _{1,2,3} = 9)$. (c) Superposition of (a) and (b). The apparent gaps are due to instability of the Newton method

Appendices

Appendix A: Examples of the coefficients

In this Appendix we present the asymptotic formulae for the hyperbolic length of the short closed geodesics, which then lead to the asymptotic expressions for the first few non-zero coefficients $a_2$, $a_4$, $a_6$.

Using the identity

$$\begin{aligned} \ell (\gamma _{j_1,j_2,\ldots j_{2n}}) = 2 \mathrm{Arcosh}\left( \frac{1}{2} \mathrm{tr}(R_{j_1} R_{j_2} \ldots R_{j_{2n}} ) \right) , \end{aligned}$$

relating the length of the closed geodesic corresponding to the cutting sequence of period 2n to the matrices defining the reflections, we compute the lengths of the closed geodesics for $n=2,4,6,8$.

The case $n=2$. It has been established in Lemma 2.10, see also Remark 2.6, that there are exactly 6 geodesics of length $\ell (\gamma _{j_1 j_2}) = 2b$.

The case $n=4$. There are 6 geodesics of length 4b and 12 geodesics of length

$$\begin{aligned} \ell (\gamma _{j_1 j_2 j_3 j_2}) = 2\mathrm{Arcosh}\bigl (\cosh (b)+2\cosh ^2(b)\bigr ). \end{aligned}$$

The case $n=6$. There are $4^3+2=66$ homotopy classes of closed geodesics; among which there are 6 geodesics of length 6b and of length

$$\begin{aligned} \ell (\gamma _{j_1 j_2 j_3 j_1 j_2 j_3})&= 2\mathrm{Arcosh}\bigl ( 4\cosh ^3(b) + 6\cosh ^2(b) -1\bigr ) = 6b + 6 e^{-b} + O(e^{-2b}). \end{aligned}$$

There are 18 geodesics of length

$$\begin{aligned} \ell (\gamma _{j_1 j_2 j_1 j_3 j_2 j_3})&= 2\mathrm{Arcosh}\Bigl (8\cosh ^2\Bigl ( \frac{b}{2} \Bigr )\cdot \cosh ^2(b)-1\Bigr ) = 6b + 4 e^{-b} + O(e^{-2b}). \end{aligned}$$

Finally, there are 36 geodesics of length

$$\begin{aligned} \ell (\gamma _{j_3 j_2 j_1 j_2 j_1 j_2})&= 2\mathrm{Arcosh}\bigl ( 4\cosh ^3(b)+ 2\cosh ^2(b)-\cosh (b)\bigr ) = 6b + 2e^{-b} + O(e^{-2b}). \end{aligned}$$

The case $n=8$. There are $4^4+2=258$ homotopy classes of closed geodesics; among which there are 6 geodesics of length 8b. Moreover, there are 24 geodesics of length

$$\begin{aligned} \ell (\gamma _{j_3 j_1 j_3 j_1 j_2 j_1 j_2 j_1 })&= 2\mathrm{Arcosh}(-4\cosh ^2(b)+4\cosh ^3(b)+8\cosh ^4(b)+1)\\&= 8b + 2 e^{-b} + O(e^{-2b}); \end{aligned}$$

and another 48 geodesics of length

$$\begin{aligned} \ell (\gamma _{j_3 j_1 j_2 j_1 j_2 j_1 j_2 j_1} )&= 2\mathrm{Arcosh}(-\cosh (b)-4\cosh ^2(b)+4\cosh ^3(b)+8\cosh ^4(b)) \\&= 8b + 2 e^{-b} + O(e^{-2b}). \end{aligned}$$

In addition, we have 12 geodesics of length

$$\begin{aligned} \ell (\gamma _{j_3 j_1 j_2 j_1 j_3 j_1 j_2 j_1 })&= 2\mathrm{Arcosh}(2\cosh ^2(b)+8\cosh ^3(b)+8\cosh ^4(b)-1) \\&= 8b + 4 e^{-b} + O(e^{-2b}); \end{aligned}$$

and 48 geodesics of length

$$\begin{aligned} \ell (\gamma _{j_3 j_1 j_2 j_3 j_1 j_2 j_1 j_2} )&= 2\mathrm{Arcosh}(\cosh (b)\cdot (4\cosh (2b)+2\cosh (3b)+4\cosh (b)+1)) \\&= 8b + 4 e^{-b} +O(e^{-2b}); \end{aligned}$$

and another 48 geodesics of length

$$\begin{aligned} \ell (\gamma _{j_3 j_2 j_1 j_3 j_1 j_2 j_1 j_2} )&= 2\mathrm{Arcosh}(-\cosh (b)+8\cosh ^3(b)+8\cosh ^4(b)) \\&= 8b + 4 e^{-b} + O(e^{-2b}). \end{aligned}$$

Finally, there are 24 geodesics of length

$$\begin{aligned} \ell (\gamma _{j_3 j_2 j_1 j_2 j_3 j_1 j_2 j_1} )&= 2\mathrm{Arcosh}(\cosh (b)\cdot (6\cosh (2b)+2\cosh (3b)+8\cosh (b)+3)) \\&= 8b + 6 e^{-b} + O(e^{-2b}); \end{aligned}$$

and further more 48 geodesics of length

$$\begin{aligned} \ell (\gamma _{j_3 j_1 j_2 j_3 j_1 j_2 j_1 j_2} )&= 2\mathrm{Arcosh}(-3\cosh (b)+12\cosh ^3(b)+8\cosh ^4(b)) \\&= 8b + 6e^{-b} + O(e^{-2b}). \end{aligned}$$

Appendix B: Non-periodicity

The apparent almost periodicity in the plot can never be exact for a fixed b as we see from the behaviour of the zeros near the vertical line $\mathfrak {R}(s)=\delta$ in Fig. 11. In fact, since the geodesic flow restricted to the non-wandering set is mixing, it is shown in [25] that there is only one zero with $\mathfrak {R}(s)=\delta$. Naud [22] (see also Jacobson & Naud [16]) showed an even stronger result: there exists $\varepsilon > 0$ such that there is only finite number of zeros satisfying $\mathfrak {R}(s)>\delta - \varepsilon$. This is illustrated by the numerical results in Table 1. Namely, we analyze values of zeros closest to the right boundary $\mathfrak {R}(z)=\delta$ of the critical strip:

$$\begin{aligned} {\mathscr {E}}:=\left\{ s_0 \in {\mathscr {S}}_{X_b} \mid \text{ for } \text{ all } s \in {\mathscr {S}}_{X_b} \text{ such } \text{ that } | s-s_0|< \frac{\pi }{2} e^{b} \text{ we } \text{ have } \mathfrak {R}(s) < \mathfrak {R}(s_0) \right\} . \end{aligned}$$

We see that for all $s \in {\mathscr {E}}$ satisfying $\mathfrak {I}(s) < 10^3$ there exist an $s^\prime \in {\mathscr {E}}$ such that⁸

$$\begin{aligned} \bigl |s-s^\prime +\pi e^b\bigr | \le 3. \end{aligned}$$

Apparently, related results have been observed in [7].

Table 1 Empirical estimates on zeros near the right boundary $\mathfrak {R}(z)=\delta$

Fig. 11

a A plot of the zeros in the case $\ell (\gamma _{0})=10$; and b A scaled up version to see the apparent periodicity near $\mathfrak {R}(s)=\delta$

Appendix C: Spacing of zeros

For completeness, in this Appendix we describe a slight strengthening of a particular case of a result of Weich on the spacing of imaginary parts of zeros. The Theorem below asserts that the spacing of the zeros ${\mathscr {S}}_{X_b}$ for the zeta function is approximately $\frac{\pi }{b}$ as $b \rightarrow +\infty$.

Notation C.1

A compact part of the critical strip of width $\delta = \delta (b) > 0$ and height T which we denote by

$$\begin{aligned} {\mathscr {R}}_b(T) = \{ s \in {\mathbb {C}} \mid 0 \le | \mathfrak {R}(s) | \le \delta \text{ and } |\mathfrak {I}(s)| \le T\}. \end{aligned}$$

We denote a set of regularly spaced points on the lines $\mathfrak {R}(s) =0$ and $\mathfrak {R}(s) = \ln 2$ given by ${\mathscr {L}} = (\ln 2 + i\pi )\mathord {{\mathbb {Z}}}\cup i\pi \mathord {{\mathbb {Z}}}$.

Theorem C.2

The sets ${\mathscr {S}}_{X_b}$ and ${\mathscr {L}}$ are close in the Hausdorff metric on a small part of the critical strip. More precisely, there exists $\varkappa > 1$ such that

$$\begin{aligned} \mathrm{dist}_H (b \cdot \left( {\mathscr {S}}_{X_b} \cap \mathscr {R}_b(\varkappa )\right) ,{\mathscr {L}})=O\left( \frac{1}{\sqrt{b}}\right) , \text{ as } b \rightarrow +\infty . \end{aligned}$$

An earlier version of Theorem C.2 was established by Weich [33], where he also considered funnels whose widths are ${\mathbb {Z}}$-multiples of b. On the other hand, his results apply only on a bounded domain and without the error term.

In order to prove Theorem C.2 we need the following approximation Lemma.

Lemma C.3

Given a $\varkappa >1$ as in Theorem 4.2, the complex analytic function $Z_{X_b}\bigl (\frac{s}{b}\bigr )$ converges uniformly to $Z_6\bigl (\frac{s}{b}\bigr )$ on the domain ${\mathscr {R}}(\varkappa b)$, more precisely,

$$\begin{aligned} \sup _{ s\in {\mathscr {R}}(\varkappa b) }\left| Z_{X_b}\left( \frac{s}{b}\right) - Z_6\left( \frac{s}{b}\right) \right| = O\left( \frac{1}{\sqrt{b}}\right) \text{ as } b \rightarrow +\infty . \end{aligned}$$

Proof

By a straightforward manipulation using the lengths of the closed geodesics estimated in Appendix A we show that

$$\begin{aligned} a_n(s)=\exp (-nbs-2b)(1+O(\exp (-2b))^s \text{ for } n=8,10,12 \end{aligned}$$

and therefore

$$\begin{aligned} a_n\left( \frac{s}{b}\right) =\exp (-ns-2b)(1+O(\exp (-2b))^{s/b} \rightarrow 0 \text{ as } b\rightarrow \infty . \end{aligned}$$

The result follows from Theorem 4.2 where the corresponding terms for $n=8,10$, and 12 are of order $\left( \frac{1}{\sqrt{b}}\right)$. $\square$

Now we are ready to prove Theorem C.2, which is easier than Theorem 1.5, because we can use complex analysis.

Proof

We shall show that on the domain ${\mathscr {R}}(\varkappa b)$ we have that the function $Z_{X_b}(s)$ vanishes at $s_n(b)$ such that $\lim \limits _{b\rightarrow \infty } s_n(b)\cdot b = (\ln 2 + i \pi n)$.

The function $\det (I-e^{-2s}A^2)$ vanishes at $\{i\pi n, \ln 2 + i\pi n\}$, for $n \in {\mathbb {Z}}$. For any sufficiently small $\eta > 0$ we have that the closed balls

$$\begin{aligned} \overline{U(\ln 2 + 2i \pi n , \eta )} := \{s \in {\mathbb {C}} :|s - (\ln 2 + 2i \pi n) | \le \eta \} \end{aligned}$$

contains no more zeros. Let us denote $\varepsilon = \inf _{s \in \partial U} |\det (I - e^{-2s}A^2)| >0$. Using Theorem C.3, we can now choose b sufficiently large so that we have

$$\begin{aligned} inf_{s \in \partial U} \left| Z_{X_b}\left( \frac{s}{b} \right) - \det (I - e^{-2s}A^2)\right| < \frac{\epsilon }{2}. \end{aligned}$$

It then follows by Rouché’s Theorem [1] that for any $n \in \mathord {{\mathbb {N}}}$ the function $Z_{X_b}(s)$ has exactly one zero $s_n(b)$, satisfying $\left| s_n(b) - \frac{1}{b} (\ln 2 + i \pi n) \right| < \eta$. $\square$

This implies the asymptotic spacing of imaginary parts of zeros.