Abstract
We consider families of confocal conics and two pencils of Apollonian circles having the same foci. We will show that these families of curves generate trivial 3-webs and find the exact formulas describing them.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The concept of webs was invented by Blaschke [3] and connected with many parts of Geometry. Let us recall, that a trivial 3-web in a planar domain \(\Omega \) are three families of smooth curves such that there is a diffeomorphism \(\varphi :\Omega \rightarrow \Omega ' \subset \mathbb {R}^2\) taking the families to sets of lines parallel to the sides of a fixed triangle. See [7, Lecture 18] as an introduction to the topic. There are several non-trivial 3-webs formed by line- and circle-families, see [10] for history of the problem and new examples of such webs.
In this paper we consider webs in the positive quadrant \(\mathbb {R}^2_+\) formed by confocal conics and pencils of Apollonian circles, which are defined in the following way: Let \(F_1\) and \(F_2\) be two points in the plane called foci. The family of circles passing through \(F_1\) and \(F_2\) is called an elliptic Apollonian pencil. The pencil of circles orthogonal to all the circles of the first family is called a hyperbolic Apollonian pencil. Each circle from the latter family is a locus of points X such that \(|XF_1|/|XF_2|=\mathop {\mathrm {const}}\). We refer to [2, 8] for this and other classical results related with circles and conics.
We construct four trivial webs defined in the positive quadrant \(\mathbb {R}^2_+\). These webs consist of the following families of curves:
- (1) :
-
Both families of Apollonian circles and confocal hyperbolas with foci \(F_1\) and \(F_2\);
- (2) :
-
Both families of Apollonian circles and confocal ellipses with foci \(F_1\) and \(F_2\);
- (3) :
-
Families of confocal ellipses, confocal hyperbolas and the hyperbolic Appolonian pencil with foci \(F_1\) and \(F_2\);
- (4) :
-
Families of confocal ellipses, confocal hyperbolas and the elliptic Appolonian pencil with foci \(F_1\) and \(F_2\).
We prove that these webs are trivial by showing a diffeomorphism from a domain \(\Omega \subset \mathbb {R}^2\) to the positive quadrant \(\mathbb {R}^2_+\) which maps horizontal, vertical and “diagonal” (\(x+y\) or \(x-y\) is a constant) lines to considered curves. For webs 3 and 4 the images of both diagonal direction are remarkable curve: Apollonian circles and lines (vertical or horizontal).
Before going to the proof, let us say how these pencils relate with each other in an algebraic sense. All circles in the plane can be considered as conics passing through two fixed points of the complex infinite line. These points are called circular and have homogeneous coordinates \(I_1=(1,i,0)\) and \(I_2=(1,-i,0)\).
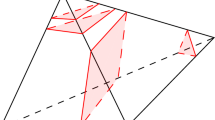
Foci \(F_1\) and \(F_2\) of any conic \(\alpha \) can be described as the intersection of tangent lines to \(\alpha \) from the circular points. The other pair of points of the intersection, denote it by \(F_1'\) and \(F_2'\), can also be considered as foci. On Fig. 1 the projective picture is drawn. Through each point P in the plane pass the four conics: two conics touching sides of the quadrilateral \(F_1F_1'F_2F_2'\) and two passing through its opposite vertices and \(I_1\) and \(I_2\). The lines appearing in webs 3 and 4 can be described as lines passing through intersection of \(I_1I_2\) and \(F_1F_2\) (horizontal lines) and through the intersection of \(I_1I_2\) and \(F_1'F_2'\) (vertical lines). Some triples of these conics have another joint intersections which correspond to points symmetric to P in the axes (Fig. 2). So, in general we describe webs formed by the family of conics tangent to four fixed lines and passing though points of their intersection.
Böhm in [4] constructed a net consisting of lines touching a conic. Quadrilaterals formed by lines of this net can be circumscribed around circles and points of intersection of these lines can be split into families lying on confocal conics. This construction was rediscovered and generalized by the author and Bobenko in [1], where also it was noticed that Böhm’s net is a special case of the Poncelet grid introduced and investigated by Schwarz [11], see also [9] for an additional discussion.
The current constructions were inspired by the work of Edelsbrunner [5, 6], where he invented a new approach for designing smooth surfaces from a set of spheres. His method of connecting spheres by circumscribed hyperboloids is based on the following observation. Let \(k_1\), \(k_2\) satisfy \(k_1^2+k_2^2=1\). If we scale each elliptic Apollonian circle of points \(F_1\) and \(F_2\) \(k_1\) times and each hyperbolic Apollonian circle \(k_2\) with respect to its center, the obtained circles touch a fixed hyperbola with foci \(F_1\) and \(F_2\). Figure 3 shows the case \(k_1=k_2=\frac{1}{\sqrt{2}}\), when the hyperbola is equilateral. Note that if \(k_1>1\), then scaled elliptic Apollonian circles touch an ellipse with foci \(F_1\) and \(F_2\) (Fig. 4). (The touching points may have complex coordinates.)
Let us fix the notation we will use. We suppose that foci of pencils have coordinates \(F_1= (-1, 0)\) and \(F_2=(1, 0)\). Denote by a(P) and b(P) the distances from point P to foci \(F_1\) and \(F_2\). Define the following functions:
-
\(f(P)=\displaystyle \frac{a(P)}{b(P)}\). The locus of points \(f(P)=\mathop {\mathrm {const}}\), is a hyperbolic Apollonian circle corresponding to the points \(F_1\) and \(F_2\). For points \(P\in \mathbb {R}^2_+\) we have \(f(P)>1\).
-
\(g(P)=\displaystyle \frac{a(P)^2+b(P)^2-4}{2a(P)b(P)}\). The locus of points \(g(P)=\mathop {\mathrm {const}}\in (0, 1)\), \(P\in \mathbb {R}^2_+\), is the upper arc of a circle passing through \(F_1\) and \(F_2\) (and the arc symmetric to it in x-axis). Indeed, for any point P on this arc we have \(\cos \angle F_1PF_2=g(P)=\mathop {\mathrm {const}}\).
-
\(h(P)=a(P)-b(P)\). The locus of points \(h(P)=\mathop {\mathrm {const}}\) is a branch of a hyperbola with foci \(F_1\) and \(F_2\). Note that for \(P \in \mathbb {R}^2_+\) we have \(0<h(P)<2\).
-
\(e(P)=a(P)+b(P)\). The locus of points \(e(P)=\mathop {\mathrm {const}}\) is an ellipse with foci \(F_1\) and \(F_2\).
Note that \(P\in \mathbb {R}^2_+\) is uniquely determined by values of any two function from this list. For simplicity in the following sections we denote the values of considered functions at point P by a, b, f, g, h, and e.
2 The web from Apollonian circles and confocal hyperbolas
In this section we prove that two pencils of Apollonian circles with foci at \(F_1\) and \(F_2\), and the family of hyperbolas with foci at \(F_1\) and \(F_2\) form a trivial web in the positive quadrant \(\mathbb {R}_+^2\). Applying the map to vertices of a shifted lattice \(k\mathbb {Z}^2+t\) we obtain a configuration shown on Fig. 5.
Theorem 1
Suppose \(\Omega \) be a set of points \(\mathbb {R}^2\) with positive x-coordinate, and the map \(\varphi : \Omega \rightarrow \mathbb {R}_+^2\) is defined in the following way:
Then \(\varphi \) is surjective and maps lines \(x=\mathop {\mathrm {const}}\) to arcs of circles of the elliptic Apollonian pencil, rays \(y=\mathop {\mathrm {const}}\) to arcs of circles of the hyperbolic Apollonian pencil and rays \(x-y=\mathop {\mathrm {const}}\) to arcs of hyperbolas with foci \(F_1\) and \(F_2\).
Proof
For the proof we need to show that the value of f depends only on y, g only on x, and h only on \(x-y\). We start the calculation from finding values of a and b. Suppose the point P has coordinates (s, t) and it is an image of the point (x, y) under the map \(\varphi \). Then \(a^2=(s+1)^2+t^2\) and \(b^2=(s-1)^2+t^2\). Therefore
Analogously
Now let us compute f, g, and h.
The surjectivity of the map easily follows from the fact that varying x and y we can obtain all circles from Apollonian pencils. \(\square \)
3 The web from Apollonian circles and confocal ellipses
We prove that two pencils of Apollonian circles with foci at \(F_1\) and \(F_2\), and the family of ellipses with foci at \(F_1\) and \(F_2\) form a trivial web in the positive quadrant \(\mathbb {R}_+^2\) (Fig. 6).
Theorem 2
Suppose \(\Omega \) is the forth quadrant, the set of points in the plane with positive x-coordinate and negative y-coordinate. The map \(\varphi : \Omega \rightarrow \mathbb {R}_+^2\) is defined in the following way:
Then \(\varphi \) is surjective and maps rays \(x=\mathop {\mathrm {const}}\) to arcs of circles of the elliptic Apollonian pencil, rays \(y=\mathop {\mathrm {const}}\) to arcs of circles of the hyperbolic Apollonian pencil and rays \(x-y=\mathop {\mathrm {const}}\) to arcs of ellipses with foci \(F_1\) and \(F_2\).
Proof
For the proof we need to show that the value of f depends only on y, g only on x, and e only on \(x-y\). As in the proof of Theorem 1, we start from the calculation of a and b.
Analogously
Now let us compute f, g and e.
Again, the surjectivity of the map easily follows from the fact that varying x and y we can obtain all circles from Apollonian pencils. \(\square \)
4 The web from confocal conics and a hyperbolic Apollonian pencil
In this section we prove that there is a trivial web formed by confocal ellipses and hyperbolas, and the hyperbolic Apollonian pencil. The family of vertical lines can be adjoint to this web in a very natural way (Fig. 7).
Theorem 3
Suppose \(\Omega \) is the forth quadrant and the map \(\varphi : \Omega \rightarrow \mathbb {R}_+^2\) is defined in the following way:
Then \(\varphi \) is surjective and maps rays \(x=\mathop {\mathrm {const}}\) and \(y=\mathop {\mathrm {const}}\) to arcs of ellipses and hyperbolas with foci \(F_1\) and \(F_2\), rays \(x-y=\mathop {\mathrm {const}}\) to arcs of circles of the hyperbolic Apollonian pencil with foci \(F_1\) and \(F_2\), and intervals \(x+y=\mathop {\mathrm {const}}\) to vertical lines.
Proof
In this case a and b have a very nice formulas:
We see that the values \(e=a+b=2\mathrm{e}^x\) and \(h=a-b=2\mathrm{e}^{y}\) defined only by x and y, respectively, it is left to check that the ratio a / b depends only on \(x-y\):
The fact that image of points with \(x+y=\mathop {\mathrm {const}}\) is a vertical lines follows directly form the definition of \(\varphi \). Since varying x and y we can obtain all ellipses and hyperbolas from the confocal family the image of \(\varphi \) is the whole quadrangle \(\mathbb {R}_+^2\). \(\square \)
5 The web from confocal conics and an elliptic Apollonian pencil
The last example of a trivial web is formed by confocal ellipses and hyperbolas, and and elliptic Apollonian pencil, and family of horisontal lines, which can be adjoint to the web as well (Fig. 8).
Theorem 4
Suppose \(\Omega \) is the forth quadrant and the map \(\varphi : \Omega \rightarrow \mathbb {R}_+^2\) is defined in the following way:
Then \(\varphi \) is surjective and maps rays \(x=\mathop {\mathrm {const}}\) and \(y=\mathop {\mathrm {const}}\) to arcs of ellipses and hyperbolas with foci \(F_1\) and \(F_2\), rays \(x-y=\mathop {\mathrm {const}}\) to arcs of circles of the elliptic Apollonian pencil with foci \(F_1\) and \(F_2\), and intervals \(x+y=\mathop {\mathrm {const}}\) to horizontal lines.
Proof
Again, find the formulas for a and b.
Analogously
We have \(e=a+b=2\sqrt{1+\mathrm{e}^x}\) and \(h=a-b=2\sqrt{1+\mathrm{e}^{y}}\). Let us calculate the value of g.
We see, that it depends only on \(x-y\). It is left to notice that from the definition of \(\varphi \), follows that images of intervals \(x+y=const\) are horizontal lines. The map is surjective by the same arguments as in the previous theorem. \(\square \)
References
A. Akopyan and A. Bobenko. Incircular nets and confocal conics. 06 2016, arXiv:1602.04637
A. V. Akopyan and A. A. Zaslavsky. Geometry of conics, volume 26 of Mathematical World. American Mathematical Society, Providence, RI, 2007. Translated from the 2007 Russian original by Alex Martsinkovsky
Blaschke, W.: Einführung in die Geometrie der Waben. Birkhäuser Verlag, Basel und Stuttgart (1955)
Böhm, W.: Verwandte Sätze über Kreisvierseitnetze. Arch. Math. (Basel) 21, 326–330 (1970)
H.-L. Cheng, T. K. Dey, H. Edelsbrunner, and J. Sullivan. Dynamic skin triangulation. Discrete Comput. Geom., 25(4):525–568, 2001. The Micha Sharir birthday issue
Edelsbrunner, H.: Deformable smooth surface design. Discrete Comput. Geom. 21(1), 87–115 (1999)
D. Fuchs and S. Tabachnikov. Mathematical omnibus. American Mathematical Society, Providence, RI, 2007. Thirty lectures on classic mathematics
G. Glaeser, H. Stachel, and B. Odehnal. The Universe of Conics: From the ancient Greeks to 21st century developments. Springer, 2016
Levi, M., Tabachnikov, S.: The Poncelet grid and billiards in ellipses. American Math. Mon. 114(10), 895–908 (2007)
Nilov, F.K.: On new constructions in the Blaschke-Bol problem. Mat. Sb. 205(11), 125–144 (2014)
Schwartz, R.E.: The Poncelet grid. Adv. Geom. 7(2), 157–175 (2007)
Acknowledgements
Open access funding provided by Institute of Science and Technology (IST Austria).
Author information
Authors and Affiliations
Corresponding author
Additional information
Supported by People Programme (Marie Curie Actions) of the European Union’s Seventh Framework Programme (FP7/2007–2013) under REA Grant Agreement No. [291734].
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Akopyan, A. 3-Webs generated by confocal conics and circles. Geom Dedicata 194, 55–64 (2018). https://doi.org/10.1007/s10711-017-0265-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10711-017-0265-6