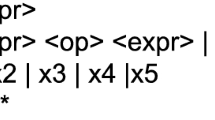Abstract
In this paper we investigate the benefits of applying a multi-objective approach for solving a symbolic regression problem by means of Grammatical Evolution. In particular, we extend previous work, obtaining mathematical expressions to model glucose levels in the blood of diabetic patients. Here we use a multi-objective Grammatical Evolution approach based on the NSGA-II algorithm, considering the root-mean-square error and an ad-hoc fitness function as objectives. This ad-hoc function is based on the Clarke Error Grid analysis, which is useful for showing the potential danger of mispredictions in diabetic patients. In this work, we use two datasets to analyse two different scenarios: What-if and Agnostic, the most common in daily clinical practice. In the What-if scenario, where future events are evaluated, results show that the multi-objective approach improves previous results in terms of Clarke Error Grid analysis by reducing the number of dangerous mispredictions. In the Agnostic situation, with no available information about future events, results suggest that we can obtain good predictions with only information from the previous hour for both Grammatical Evolution and Multi-Objective Grammatical Evolution.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Symbolic Regression (SR) is one of the best-known applications of Genetic Programming (GP) and its variants, such as Grammatical Evolution (GE). The purpose of SR is to obtain closed-form equations that represent a set of data points, i.e., to optimally fit a proper mathematical function to the data. Therefore, SR can be used in many domains like data analysis, modeling, classification and identification.
Healthcare is one of the fields where the above-mentioned domains are becoming more and more important. In this regard, one of the diseases with the highest increase in prevalence is Diabetes Mellitus (DM), or simply Diabetes.Footnote 1 Diabetes is a chronic disease caused by a defect either in the production or in the action of the insulin generated by the pancreatic system, corresponding to the two main types of Diabetes: Type 1 (T1DM) and Type 2 (T2DM). The pancreas in patients with T1DM is not able to generate enough insulin to process the sugar produced after food ingestion. Hence, patients need to inject some additional artificial insulin with each meal, and sometimes between meals, to maintain healthy levels of glucose. In the case of T2DM patients, the insulin generated by the pancreas is not working properly, in a phenomenon known as insulin resistance. In advanced stages of the disease, many T2DM patients also need to inject some insulin.
Insulin injection can be performed following two different alternatives. The first one is through a Continuous Subcutaneous Insulin Infuser (CSII) device, also known as an insulin pump. This device can be programmed and adjusted to administer the desired amount of insulin in different time slots. The alternative is the Multiple Dose of Insulin (MDI) approach which consists of injecting long-acting insulin once or twice daily as a background dose, and rapid-acting insulin injections at each meal time. In both alternatives, the decisions about the amount of insulin to be injected are challenging and many factors have to be considered. Selecting the right amount of insulin is critical. If too much insulin is injected, hypoglycemia may occur, while insufficient injections cause excessively high glucose levels. In both cases, the goal of a Blood Glucose (BG) control system for a patient is to maintain BG levels within the target range most of the time, usually between 70 and 180 mg/dl [44]. It has been shown that when these values are not maintained or there is high variability then both short-term and long-term complications can emerge [13].
Control of BG in insulin-dependent patients requires predicting future glucose values to determine the amount of insulin to inject. This amount depends on many factors, of which four are the most important: (i) the glucose value at the time of the injection; (ii) the estimated amount of ingested food, usually measured in carbohydrate rations; (iii) the previously injected insulin; (iv) the estimated ratio of currently active insulin at the time of the injection. Recently, with the appearance of new smart devices, other variables can also be taken into account. Making all these estimates by hand is a complicated process that must be repeated several times every day. Fortunately, recent advances in both devices and algorithms allow automation of some parts of this control process. Different kinds of BG control strategies have been proposed [24]: manual, semi-automated [52], and automated solutions based on the Artificial Pancreas (AP) [2]. For all of them, it is extremely important to develop mathematical models or artificial intelligence systems to describe the interaction between the glucose system and the insulin control method using current measurements and stored data.
In [37], three different scenarios were defined for BG prediction: What-if, Agnostic and Inertial. The differences among them correspond to the data that are used to produce the models for prognosis. In the What-if scenario the idea is to consider future events for some of the input variables. For instance, the carbohydrates that the patient is going to eat between the current time and the prediction horizon could be used in this case. Models generated under this scenario are very useful for designing insulin or carbohydrate recommendation systems.
The Agnostic scenario only takes into account the values from the input variables that are previous to the current time. Theoretically, under this approach it would be more difficult to achieve accurate predictions, since a model trained under Agnostic conditions needs to implicitly predict events in the future for all possible values of the input variables. Intuitively, Agnostic models will be more appropriate in cases where the number of input variables is small or the number of samples is very large and varied.
Finally, under the Inertial view, models are generated using only samples from the Continuous Glucose Monitoring (CGM) system in the prediction time window. Data from other input variables cannot be used, which is an unrealistic situation since ingestion of food, exercise or stress may occur.
However, as noted by [37], the inertial model can be realistic in the case of nighttime predictions. While the patient sleeps, many of the input variables (such as carbohydrates or exercise) will take a zero value and other variables (such as insulin or stress) will not undergo significant changes. For this reason, Inertial models can be useful for the study of specific situations, such as the study of the Dawn Phenomenon [43], an early morning BG level rise, which is a special situation that appears in some diabetic patients.
In this paper, we focus only on the first two scenarios, excluding the Inertial approach.
The main objective of this work is to investigate the efficiency and benefits of multi-objective GE for BG level prediction using real data collected from patients with T1DM under insulin pump therapy with CGM. We continue with the investigation of a multi-objective approach for modeling glucose and constructing predictive models from the short-term (30 min) to the medium-term (120 min) time horizons. We use GE with two objective functions: Root Mean Squared Error (RMSE) and an adapted fitness, denoted as \(F_{\mathrm {CLARKE}}\), which is based on the Clarke Error Grid (CEG) metric [8]. This paper is an extended version of the work presented at the EvoStar 2020 Conference [10] and the continuation of the machine learning research developed at the Universidad Complutense de Madrid, Adaptive and Bioinspired Systems Research Group since 2013 [18, 21,22,23,24] and [50]. The contribution of this paper in relation to [10] is twofold: on the one hand we have extended the analysis to the Agnostic scenario using a new dataset also coming from real diabetic patients and, on the other hand, we have performed a deeper analysis of the results where we graphically compare the solutions obtained, allowing us to draw medical conclusions.
In particular, we tackle the following research questions: is the multi-objective approach able to improve single-objective predictions?. Does the multi-objective approach obtain solutions that are clinically better?. Is it always better to use more information from the past or can we obtain equivalent predictions with information from the last hour instead of the last two?
As will be seen, the development of a problem-specific fitness function does not only considerably improve the quality and the robustness of the GE algorithm as an SR tool in the What-if scenario, as we show in [10], but also allows us to obtain good Agnostic prediction models using only information from the last hour previous to the time of prediction.
The best single-objective solutions may suffer from a significant number of erroneous predictions that could lead to incorrect treatments that may be dangerous to the patient’s health. Later, we will show that the multi-objective strategy improves this situation by reducing the number of wrong predictions and, therefore, the severity of incorrect treatments.
The rest of the paper is organized as follows. In Sect. 2, we review the previous work. In Sect. 3, we explain the multi-objective approach. Section 4 gives details about the dataset and discusses the results, comparing it with previous work and analyzing the contributions of the multi-objective approach. We finish the paper with the conclusions in Sect. 5.
2 Related work
The problem of modeling and predicting glucose levels and glucose-insulin interaction has been an intensive area of research for the last ten years. We will focus on predicting glucose levels for a forecasting horizon of up to 2 h, as an aid in the daily management of insulin. Two hours is usually the time needed to decide if the dose of insulin after a meal was correct. Hidalgo et al. proposed the application of GE to obtain customized models of patients. The proposal has been tested using in silico patients’ and real patients’ data [24]. The work has been extended recently in [28] and [49], where it has been shown that data augmentation and structured GE increase the quality of the prediction results.
Inspired by Hidalgo’s group, Contreras et al. presented a hybrid model for predicting glucose in the medium term (120 min) for T1DM patients [12]. The system uses synthetic data generated by the UVA/PADOVA simulator [29]. Both the fitness function of the evolutionary grammar and the performance metrics use a penalty factor to take into account the physical damage caused by deviations in BG prediction according to the CEG. The authors generate four models for each patient corresponding to different phases of the day: night, breakfast, lunch, and dinner. The data obtained for the night phase are quite good; however, results with real patients’ data have not been reported. In this work, we use a multi-fitness approach instead of a penalization function, which is more appropriate for a multi-objective problem.
Although more centered on classification, i.e., the prediction of a class instead of a glucose value, there are other interesting approaches. For instance, in [40], the authors developed a method for predicting postprandial hypoglycemia using a classification approach with machine learning techniques personalized for each patient. They described the process of generating a hypoglycemic prediction model by Support Vector Machine (SVM) for binary classification, trained and tested using Scikit-Learn. They use hypoglycemia risk as a feature and as a class-labeling factor. The results demonstrate acceptable performance for all patients (in terms of specificity and sensitivity) and the feasibility of predicting postprandial hypoglycemic events from a classification perspective. In [46], a dual mode adaptive basal-bolus advisor based on reinforcement learning is presented. Authors proposed an Adaptive Basal-Bolus Algorithm (ABBA) which provides a personalized recommendation for the daily insulin doses using information from the previous day. Regarding the level of customization of the models, some proposals provide models for the average case [41], and others provide personalized models for each patient. Several papers apply classical modeling techniques, resulting in models or profiles defined by linear equations with a limited set of inputs [35].
The treatment for subjects with T1DM uses rates of basal insulin delivery, insulin to carbohydrate ratios and individual correction factors, typically from observations by the endocrinologist.
However, the data collected in clinical studies with T1DM patients do not cover sufficiently long periods of time or the different situations of work, stress, etc. that characterize the patient’s life. Therefore, the models generated from these data will be inaccurate [54].
There are also some models, used in AP systems or closed-loop control models, that try to emulate the action of the pancreas [14]. They are based on the assumption that it is possible to reach reasonable control with approximate models, provided that the model is related to the control objective [19]. Experimental results suggest that these approaches, due to the lack of accurate individualized models, have a significant risk of under-administration and thus the possibility of BG levels entering a zone of hyperglycemia with, eventually, long-term complications. Even worse, a major misprediction of BG may lead to the injection of an excessive amount of insulin, causing BG levels to fall into a zone of hypoglycemia which can have immediate fatal consequences for the patient’s health. Our evolutionary models try to avoid both situations.
De Falco et al. [15] presented a work on GP-based induction of a glucose-dynamics model for telemedicine. The work aims to create a regression model that allows the determination of the BG value from interstitial glucose in patients with T1DM with the idea of using it in a telemedicine portal. The work is divided into two parts. In the first part, an imputation of the missing values in the database is carried out using an extrapolation technique based on the Steil-Rebrin model [45]. To make the most accurate estimate, the parameters of this equation are adjusted using an evolutionary algorithm with the RMSE as the fitness function. Since there are many more estimated BG values than actual values, a correction factor must be applied to avoid deviations in the extraction of the model.
Recently, several approaches have solved the prediction problem by using artificial Neural Networks (NNs) with results similar in quality to the solutions based on GP and GE. There are several kinds of NNs and, due to the availability of new high-performance computing architectures, their development and applicability have increased exponentially during the last five years. Long Short-Term Memory (LSTM) networks have achieved very good performance in modeling several time-dependent phenomena. This is why most of the approximations found in the literature for the prediction of BG levels are LSTM since BG data are usually obtained as a time series from CGMs. In [47], the authors make a glucose prediction using a sequential model consisting of an LSTM, a Bi-directional LSTM (Bi-LSTM), each with four units, and three fully connected layers with 8, 64 and 8 units, respectively. The authors of [1] develop a predictive model fpr BG to define future insulin therapy consisting of two stacked LSTMs working in parallel. Meijner and Persson [34] propose to exploit LSTM in a model which takes CGM values, insulin dose and carbohydrate intake as inputs. The proposal tackles only prediction horizons of 30 and 60 min. The training phase experienced initialization problems which led to local optimums. Another interesting work is [32] from an Ohio University group with more than ten years of experience in machine learning for diabetes. In [36], they propose an LSTM architecture and they improve it in [37] by proposing a novel architecture called memLSTM, which is a mixture of LSTM with a type of network called Neuronal Attention Models (NAM) or Augmented Memory Models (AMM). The work presented in [33] analyses 10 machine learning techniques combined with oversampling methods, concluding that the choice of the best algorithm depends on the glycemic range. Convolutional Recurrent Neural Networks (CRNNs) have also been explored to predict the BG level [27] for in silico patients. Almost all of these works use real and in silico patients with short-term prediction horizons (up to 60 min). The proposed architectures obtain a performance similar to the current state of the art.
3 Description of the problem
The work that we present here extends those works based on GE, and explores the use of a multi-objective approach, based on the Non-dominated Sorting Genetic Algorithm (NSGA-II) [16], applied to real data from diabetic patients. We are interested not only in the problem-specific, but also in the performance of the multi-objective implementation. We integrate the different possibilities of using GE for short-term and medium-term glucose prediction in diabetic patients, for the Agnostic and What-if scenarios, and for prediction horizons of 30, 60, 90 and 120 min, using information from 60 and 120 min prior to the time of prediction.
The complete workflow can be seen in Fig. 1. Real data is gathered using different electronic devices such as CGM systems, smart bands and CSII (insulin pump), as well as annotations by the patients. These data are processed to form the different data sets (combining 2 historical windows and 4 prediction horizons) that will be used in the two scenarios studied in this research. In Sects. 3.1 and 3.2 we thoroughly explain the two scenarios but we can summarize that in the What-if case the model predicts future glucose values by taking into account not only past values of the three variables (glucose, carbohydrates and insulin) but also future carbohydrate intake and insulin injections from the present until the prediction horizon. In the Agnostic scenario, the model predicts future glucose values based only on past values. For both scenarios, we train and test, using cross-validation, a GE model and a multi-objective GE model.
One of the advantages of using GE as a modeling approach is that we can tackle the different possibilities mentioned in the paragraph above using the same engine and only making changes in the grammar for each prediction horizon, scenario and information configuration. Each variable, feature or attribute to be used in the model can be easily included in the grammar. In addition, with this procedure we are able to study the contribution of each feature, or group of features, to the quality of the solution.
3.1 What-if scenario or insulin-carbohydrate recommendation
As mentioned in the introduction, the What-if scenario models may have access to input events, so we can predict the BG level after m minutes, supposing that the patient eats a meal with C grams of carbohydrates and I units of insulin are injected in t minutes from the time of prediction. In other words, our objective is to construct an insulin-carbohydrate recommendation tool. Thus, we look for predictive models that help us in evaluating those recommendations. In this scenario, models can use the following data:
-
Interstitial glucose using a Medtronic CGM device that gives us observations every 5 min.
-
Notes of estimated carbohydrate units ingested, taken by each patient.
-
Insulin injected using an insulin infuser device from Medtronic, which registers injections of both basal and bolus insulin every 5 min.
Once all the information has been collected, we process the data to fill in gaps using cubic splines and to match all the events to the closest timestamp in order to construct a set of matched time series, corresponding to glucose, insulin, and carbohydrate values. We also process the set of features available at the time of modeling. The approach of using the cubic spline technique to fill gaps in time series is the most widely used strategy not only in medical literature but also in physical science research [26, 51]. At each time point, t, data from the previous 2 h are available for prediction. We process these data to define a set of new features as we did in [24]. To this aim, we first define two sets: the set of time windows in which we evaluate new features, \(W_{120}=\{0{\text {--}}0,0{\text {--}}30, 31{\text {--}}60, 61{\text {--}}90, 91{\text {--}}120\}\) min, and the set of sample times previous to the current prediction time, \(\mathrm {SP}_{120}=\{0,15,30,45,60,75,90,105,120\}\) min. The new featuresFootnote 2 are:
-
The set of glucose values measured sp minutes previous to prediction time: \(\left\{ G_{sp}(t) \right\} _{\mathrm {SP}_{120}} = \{G(t-sp)\}_{sp \in \mathrm {SP}_{120}}\),
-
The set of the sums (in grams) of the carbohydrates ingested in window w: \(\left\{ C_{w}(t) \right\} _{W_{120}} = \{\sum _{i \in w} C(t-i)\}_{w \in W_{120}}\),
-
The set of the sums of the units of insulin injected in window w: \(\left\{ I_{w}(t) \right\} _{W_{120}}= \{\sum _{i \in w} I(t-i)\}_{w \in W_{120}}\).
Notice that \(G_0(t)=G(t)\), \(C_{0-0}(t)=C(t)\), and \(I_{0-0}(t)=I(t)\) are the actual values at prediction time for glucose, carbohydrates, and insulin, respectively. We also define the set of prediction horizons, i.e., the sample times in future to forecast the BG, \(\mathrm {PH} = \{30,60, 90, 120\}\) min, so that \(\widehat{G}_{ph}(t)\) with \(ph \in PH\) is the predicted BG ph minutes ahead in time, whereas \(I_{ph}(t)\) and \(C_{ph}(t)\) are the values of insulin and carbohydrates ph minutes ahead in time. Hence, our prediction problem can be stated as finding an expression for the predicted BG level, \(\widehat{G}_{sp}(t)\), given by equation (1), that minimizes the objective functions \(\text {RMSE}\) and \(F_{\mathrm {CLARKE}}\).
3.2 Agnostic scenario or glucose prediction in absence of event information
Recently, with the appearance of new smart devices, the possibility of incorporating more predictive variables into models has been raised, in order to improve the accuracy of the models. For example, the activity bracelets on the market provide accurate information on many variables including exercise, sleep, heart rate, body temperature, caloric consumption, and more. When all this information is incorporated to the dataset it becomes much more complicated to make models of the type What-if since the number of possible combinations of the variables and assumptions involved in an event is enormous and its usefulness would be very limited. However, it is possible to produce an Agnostic-type model in which there is no access to information on future events in the prediction phase. This type of model needs to predict those events in an implicit way. For example, the model must identify fasting periods or physical exercise.
Our GE-based model generation engine allows us to make these types of models without substantial changes to our methodology. It only requires adjusting the grammars to reflect access only to the variables available. In the case of Eq. (1), we only need to eliminate access to future values, i.e., \(C_{t+H}(t)\) and \(I_{t+H}(t)\), so the general equation for the models would be expressed by Eq. (2).
In this paper, we solve the Agnostic problem in relationship with the data described in [30]. This dataset includes information on BG levels from a CGM, insulin doses from an insulin pump, self-reported information and data from an activity band. More details can be found in the previous paper. We processed the data in a similar way to that described in Sect. 3.1 in order to obtain aggregated features with information every 15 min, including CGM BG level, insulin doses, carbohydrate estimates, Galvanic Skin Response (GSR), skin temperature, air temperature and acceleration. The influence of these variables in diabetic patients is documented in [9, 25, 48]. However, the analysis of their particular impact is left for future collaborations with medical staff, since it is beyond the scope of the multi-objective analysis made in this paper.
Although the Agnostic scenario may be considered a subset of the What-if scenario, in this paper, we consider them as different problems since we use different data.
In addition to the analysis, we compare two options regarding the information available at the time of prediction. On the one hand, we use the events from the previous 2 h to construct the models as expressed in Eq. (2). On the other hand, we use the information of only the previous hour before the time of prediction. As we will see in the experimental section, this comparison is useful for the applicability of the models, since most of the time the patient has little or no information from the past. Incorporating the information of the variables obtained from the smart devices, we will search for models by applying (3) with window size, \(ws \in \{ 60, 120\}\) min.
Where we incorporate the variables GSR, skin temperature, and magnitude of acceleration to those defined in equation (1):
-
The set of GSR values sp minutes before t: \(\left\{ \mathrm {GSR}_{sp}(t) \right\} _{\mathrm {SP}_{ws}} = \{\mathrm {GSR}(t-sp)\}_{sp \in \mathrm {SP}_{ws}}\),
-
The set of skin temperatures measured sp minutes before t: \(\left\{ \mathrm {K}_{sp}(t) \right\} _{\mathrm {SP}_{ws}} = \{\mathrm {K}(t-sp)\}_{sp \in \mathrm {SP}_{ws}}\),
-
The set of accelerations measured sp minutes before t: \(\left\{ \mathrm {A}_{sp}(t) \right\} _{\mathrm {SP}_{ws}} = \{\mathrm {A}(t-sp)\}_{sp \in \mathrm {SP}_{ws}}\).
3.3 Fitness functions
Again, GE allows us to use the same configuration for both scenarios and both algorithms: single-objective (GE) and multi-objective (MO-GE). GE relies on RMSE to guide the search. RMSE is a common fitness function when adjusting data in SR problems. Equation (4) shows its definition.
In the case of MO-GE, we use a second objective function, denoted as \(F_{\mathrm {CLARKE}}\), which was defined in [21]. This function follows the CEG criterion used to test the clinical significance of differences between a glucose measurement technique and venous BG reference measurements [8]. \(F_{\mathrm {CLARKE}}\) is defined in equation (5).
To compute \(w_i\) we used the next equation:
In this regard, CEG considers a grid divided into five zones (A to E) depending on the severity of the misprediction. The values that fall within zones A and B are clinically exact and/or acceptable and thus the clinical treatment will be correct. We consider A and B as a single category with no contribution to equation (5). Values in zone C can be dangerous in some situations. Although less dangerous than D and E zones, we should also try to minimize predictions in these zones, so predicted points in these zones contribute a value of 1 to equation (5). Finally, zones D and E represent potentially dangerous areas since the prediction is far from being acceptable and the suggested treatment will be different from the correct treatment. Each prediction in zone D adds 10 to equation (5), while predictions in zone E add 100. The inequalities and conditions of Eq. (6) delimit these zones according to [8].
RMSE is a standard linear regression metric that measures the raw quality of a model. Intuitively, it can be expected that the greater the RMSE the greater the \(F_{\mathrm {CLARKE}}\). However, a good model in terms of RMSE can, at the same time, be dangerous from the medical point of view. For instance, an error of 20 mg/dl for an expected value of 50 mg/dl is worse than the same error for 100 mg/dl, since, in the first case, the patient will be in a hypoglycemic situation, whereas in the second case the patient is within the normal glucose range. These kinds of situations are not well identified by RMSE. On the contrary, \(F_{\mathrm {CLARKE}}\) is able to amplify the effect of those dangerous situations. Similarly, a good model in terms of \(F_{\mathrm {CLARKE}}\), with all predictions in zones A and B could reach significant values of RMSE. Therefore, these objective functions are not fully orthogonal, but they help to identify good models in terms of both raw and medical qualities.
Previous experimentation showed poor RMSE results of \(F_{\mathrm {CLARKE}}\) in single-objective GE. Therefore, for the sake of space and the clarity of the discussion, we have discarded these experiments.
3.4 Multi-objective grammatical evolution
In this paper we propose a multi-objective approach to GE [42]. We use the same approach and grammars of [49], where the interested reader can find more details about applying GE for the creation of models in this scenario. As is well known, the GE method is powered by an evolutionary computation algorithm, usually an adapted implementation of a Genetic Algorithm or a Particle Swarm Optimization algorithm. There exist some other multi-objective implementations such as [20]. However, we use our own library, which is publicly available through GitHub.
Here we also use a bi-objective approach, using equations (4) and (5) as fitness functions. As an evolutionary engine, we apply NSGA-II, which is perhaps the most effective way of optimizing and searching for solutions to multi-objective problems with evolutionary computation when dealing with 2 or 3 objectives. One of the important issues for selecting a multi-objective approach is to study the fitness functions, i.e., the objectives. Although the objectives may work in the same direction, it is not desirable that both measure similar features. Fitness functions should guide the algorithm through the search space in different manners, although with a common search. This is the case for Eqs. (4) and (5), where both try to improve the quality of the solution by simultaneously minimizing error and obtaining solutions with 100% of the predictions in zones A and B.
Figure 2 represents an extract of the grammar in Backus-Naur Form (BNF) format designed to find a predictive model for future BG levels. This is a typical grammar for SR adapted to the variables and features for each diabetic patient’s dataset. It is a recursive grammar and the operators are reduced to addition, subtraction and multiplication, based on the conclusions of [38] and our previous experimental experience. Despite the size of the search space being infinite because it is a recursive grammar, the algorithm is able to efficiently explore the search space.
Notice that the grammar is the tool which allows knowledge of the problem to be included in the optimization process. For instance, the grammar proposed sets the particular glucose, carbohydrate and insulin variables to be used, as well as the operands and precision factors available in order to produce model expressions. This way, the search is guided to a certain part of the solutions space.
4 Experimental results
We carry out two types of experiments testing the two scenarios explained in Sects. 3.1 and 3.2 : the What-if and Agnostic scenarios. Hence, we use two different datasets containing the information and variables required by each scenario. In Sect. 4.1, we describe the experiments corresponding to the What-if scenario, which deals with the same dataset of ten real patients, as explained in [10]. In Sect. 4.2, we expand the study to the Agnostic scenario, using a dataset from six new patients with data containing more information that has recently been added by using smart devices that incorporate other variables.
To find the models that will later be tested, we divided the data into two sets, training and test, using the k-fold cross-validation technique. This technique generally results in a less biased estimate of the model’s performance than a simple train/test division. After shuffling the data, the total data set is divided into k subsets (in this article k = 10). Over k iterations, the models are tested on one of the subsets and trained on the other (k-1) subsets. The final results are the union of the k iterations. We could expect that the variance across these small subsets would contribute a biased estimation but, in the literature, we can find research that does not support this idea [3]. It is also interesting to note that here each individual point (value to be predicted) consists of a BG value plus a historical window with glucose, carbohydrate and insulin data. This experimental setup is illustrated in Fig. 3.
We would like to emphasize that obtaining data from real patients is difficult because this is sensitive information that usually requires special authorisation from both the patients and the medical authorities. In addition, patients must be committed to the research since for data completion it is important to wear the devices correctly on a continuous basis, while taking notes and registering any unexpected event that could affect the data. Besides, it is usual to discard part of the data collected because of mistakes made by patients. Therefore, studies usually deal with small datasets, as shown in [7, 17, 31, 53], with 10, 11, 7 and 7 T1DM patients, respectively, with different gender distributions.
The implementation of both GE and MO-GE algorithms is done in Java, and the code is publicly available at the GitHub repository called JECO, which stands for Java Evolutionary COmputation library [23]. As stated above, the multi-objective approach uses the NSGA-II algorithm as an optimization engine. Table 1 summarizes the configuration of the evolutionary engine for the MO-GE approach, which is based on our previous experience, and on a set of preliminary experiments where we studied the convergence of the algorithm as well as the wrapping value. In particular, little use was made of wrapping in the preliminary experiments. On the contrary, the algorithms tended to generate solutions of moderate size. Therefore, we decided to set the maximum number of wrappings to a small value, evolving some complex expressions. In order to maintain a consistent computational effort, the same configuration was used for GE, which only considers RMSE as a fitness function. Finally, for each patient, ten runs were executed with the training data. The best model obtained was later used to calculate its performance on the test data.
In addition to the GE models, we have also fitted Auto-Regressive Integrated Moving Average models, ARIMA(p, d, q), to estimate glucose values. Equation (7) presents the expression of such a model where \(\epsilon (t)\) is the random error at time t, and p, q, and d are integers, called the orders of the model. This model only includes glucose values and does not use exogenous variables such as insulin doses or carbohydrates.
We have tested ARIMA models of different orders in \(0 < p,q \le 12\), with 12 being the number of samples in 1 h for Ohio patients to mimic the same time windows as the GE models. The best results have been for \(p=q=5\). We disregard the integrative component, that is, \(d=0\), because previous experiments show no improvement for \(\phi _i \ne 0\). With every new glucose sample, the 12 model’s coefficients are estimated using maximum likelihood in a 4-h time window using the last 48 samples—including the last one—of the univariate glucose time series, G(t). Once the model is fitted, it is warmed up using the last 24 samples, and then it estimates the glucose prediction for the four prediction horizons in PH.
4.1 What-if scenario
Ten T1DM patients have been selected for the observational study, based on conditions of good glucose control. To be included in the study, three main conditions must be met: (1) at least one year since T1DM diagnosis; (2) absence of diagnosis of major psychiatric disorder; (3) no serious breakthrough disease in the last six months. The study was approved by the Ethics Committee of the Hospital Príncipe de Asturias in Alcalá de Henares, Spain, and all patients signed a prior informed consent. Data acquisition was carried out by two nurses from the Endocrinology and Nutrition Service at the hospital.
Data from patients were acquired over multiple weeks using the devices described in Sect. 3. Log entries were stored in 5-min intervals. In this dataset, we have at least 10 complete days of data for each patient. These days are not necessarily consecutive. Each log entry contains the date and time, the BG value, the amount of insulin (injected via pump), and the amount of carbohydrate intakes estimated by the patients. The population characterization is female (80%), average age 42.30 ± 11.07, years of disease 27.20 ± 10.32, years with insulin pump therapy 10.00 ± 4.98, weight 64.78 ± 13.31 kg and HbA1c average of 7.27 ± 0.50%. The average number of days with data is 44.80 ± 30.73. Figure 4 describes the glucose levels of patients from this dataset. The upper figure shows the percentage of time the patient has a very low glucose level (<54 mg/dl in dark red), low ([54,70) mg/dl in red), in range ([70,180] mg/dl in green), high ((180,250] mg/dl in yellow), and very high (>250 mg/dl in dark yellow). The numbers (from top to bottom) represent the percentage of time the patient has a glucose level >250 mg/dl, in range [70,180] mg/dl and <70 mg/dl. The lower figure shows the interquartile ranges of glucose where the mean values are represented with red dots. This is a common way of evaluating the quality of BG management in diabetics. The greater the time in range ([70–180] mg/dl), the better.
Histograms and boxplots describing the glucose level of the patients from the dataset used in the What-if scenario. The upper figure shows the percentage of time the patient has a very low glucose level (<54 mg/dl in dark red), low ([54,70) mg/dl in red), in range ([70,180] mg/dl in green), high ((180,250] mg/dl in yellow), and very high (>250 mg/dl in dark yellow). The numbers (from top to bottom) represent the percentage of time the patient has a glucose level >250 mg/dl, in range [70,180] mg/dl and <70 mg/dl. The lower figure shows the interquartile ranges of glucose, where the mean values are represented with red dots (Color figure online)
In order to compare the results between the multi-objective (MO-GE) and the single-objective (GE) approaches, we have plotted in Figs. 5, 6, and 7 the RMSE and CDE values for each solution model for several patients under different prediction horizons. CDE is the sum of the number of points in zones C, D, and E for each model. Since \(F_{\mathrm {CLARKE}}\) is a weighted sum of the number of points in those areas, we prefer to represent CDE because it allows us to compare how similar values of RMSE may present different numbers of dangerous mispredictions, accounted for by CDE. This representation allows the comparison of solutions in terms of both the raw quality of a model, given by the RMSE value, and the medical quality of the model, given by the number of points in dangerous regions. It is important to note that a solution with two predictions in the C zone is acceptable and much better than a solution with two prediction points in zones D or E.
RMSE and CDE values for all prediction horizons (30 min in red points, 60 min in green points, 90 min in blue points and 120 min in purple points) for patients 1, 5 and 10 (rows 1, 2 and 3) in the What-if scenario for GE and MO-GE (left and right column) and both historical values (Color figure online)
Figure 5 shows the solutions obtained for patients 4 and 7 with both a single-objective GE evolution approach using the RMSE value as fitness function (red points) and the solutions obtained with the MO-GE approach (green points). As can be seen, the use of \(F_{\mathrm {CLARKE}}\) as an additional objective improves the fitness of the solutions, not only for the new fitness function, but also in terms of RMSE. We can also observe that all the solutions generated by GE are dominated by solutions generated by MO-GE. Moreover, the distribution of the solutions suggests that our MO-GE is more robust than the GE since most solutions it finds are close to the approximation of the Pareto front. This is observed for all four prediction horizons. Similar results were obtained with the rest of the patients in the dataset.Footnote 3 From a medical point of view, this result is a measure of the method’s robustness since patient 4 is very different from patient 7 according to the descriptive statistics. Patient 7 has the worst glucose control since the patient’s glucose values lie within a healthy range only for a very short time (27%) in comparison with medical recommendations (\(\ge 80\%\)). The average glucose level is also poor for this patient since it is the highest in the group (176.33 mg/dl). Nevertheless, we can see in Fig. 5 that GE and MO-GE reach good solutions for the four prediction horizons in both patients, regardless of the a priori difficulty of the dataset.
We would like to highlight that MO-GE is able to reach the optimum solution for patient 1, that is, the solution with both objectives equal to 0 and, hence, with neither error nor dangerous predictions.
It is also important to note that, although there are some non-dominated solutions with a very low number of points in zones CDE, those are not necessarily the best ones. For example, let us analyse the solutions from MO-GE for the 120 min horizon, patient 5, with the lowest value of CDE in the graph (the magenta colored points close to the y axis around point (71 , 7)). This solution is very precise; however, the bad predictions could be very dangerous for the patients since, as the RMSE indicates, the deviation from the correct prediction must be very high. When selecting the final model or predictor, the decision maker should take these characteristics into account. Another interesting feature that can be extracted from Fig. 6 is that the longer the prediction horizon, the worse the RMSE value, which is consistent with the intuitive idea of the difficulty of prediction for long horizons. However, this situation does not happen with CEG. Notice, for instance, that a small set of solutions for the 120 min horizon in patients 5 and 10 are located close to the CDE value of 10, which is quite small. This means that, despite those solutions having a high RMSE value (around 70), the predictions are well located in terms of the grid defined by CEG, which provides a good CDE value.
Figure 6 shows the distribution of the solutions in the multi-objective space with both approaches, GE and MO-GE, for three patients:Footnote 4 1, 5 and 10. As expected, the error and the number of points in dangerous prediction zones increase with the prediction horizon. However, solutions are restricted to a limited area of the graph (maximum RMSE by maximum number of points in zones C, D and E).
In addition, it is observed that the variability of solutions for a prediction horizon of 120 min is the highest, and the variance of the data along the horizontal axis decreases as the prediction horizon gets closer. This means that good CDE values can be reached for every horizon (as well as poor ones), and this variability is reduced with the reduction of the prediction horizon. These facts prove that the two objectives are not correlated and, hence, the multi-objective approach is correct.
Figure 7 presents an additional analysis where we can see the distribution of the solutions in the multi-objective space for patient 6 with both approaches, single-objective (GE) and multi-objective (MO-GE) with the four prediction horizons PH = \(\{\)30, 60, 90, 120\(\}\) min. Each color represents the solutions obtained with one of the folds of the 10-fold cross-validation strategy for a prediction horizon. Two questions arise from them. First, some of the folds are more difficult to solve than others, and a deeper study of the data should be done in order to improve the algorithm, for instance, by detecting some kind of pattern and determining when the MO-GE works better, as proposed in [11].
We performed a quantitative analysis of the solutions by comparing the 40 different instances (10 patients by 4 different time horizons) for both GE and MO-GE methods. For the sake of space we do not include all the plots. However, in all cases, solutions obtained with the MO-GE method dominate solutions obtained with GE.
Table 2 shows the aggregated results for both the single-objective and multi-objective approaches, GE and MO-GE, respectively. It also shows the results obtained with the ARIMA approach. For each time horizon, the percentage of predictions in zones A and B (A + B column), C, D and E are depicted. Since we try to maximize the points in zones A + B and minimize the points in dangerous zones C, D and E, the bold figures highlight the best method. That is, the figures reported in bold in column A + B point out the method that has obtained the maximum value for each time horizon, while the figures reported in bold in columns C, D and E point out the method that has obtained the minimum value for each time horizon. Again, the MO-GE algorithm reaches the best performance, reducing predictions in the most dangerous zones D and E for short-term predictions (30 and 60 min). For medium-term predictions (90 and 120 min), the sum of D and E points are very similar, on average. However, MO-GE finds better solutions considering the distribution of all points in the different zones of the CEG. Results were tested for statistical significance and we found significant differences in the number of points in zones D and E, where the multi-objective approach reduces the most dangerous predictions. With regard to the technique that has a larger percentage of points in the A + B zone, we found that MO-GE is placed first for short-term horizons, whereas GE achieves better results for medium-term horizons. ARIMA gets the worst results in terms of points in zones A + B and in terms of dangerous zones D and E for all horizons except 30 min, where it gets better results than the GE approach.
4.2 Agnostic scenario
The six patients of the dataset used in the Agnostic scenario were selected from the OhioT1DM dataset for Blood Glucose Level Prediction: update 2020 [30]. This dataset contains twelve patients with T1DM and was first released in 2018 with half its current size, containing data for only six patients. We selected the new patients incorporated in this update because the sensor band used in these new patients (Empatica Embrace) registers some of the physiological variables with more precision than the sensor band used in the old dataset (Basic Peak). To protect the data contributors and to ensure that the data be used only for research purposes, we had to sign a Data Use Agreement with the University of Ohio before using the dataset in our research.
Data were acquired over multiple weeks using insulin pump therapy with CGM. Patients wore Medtronic 530G or 630G insulin pumps and used the Medtronic Enlite CGM system. They also wore the Empatica Embrace device, which reported life-event data via a custom smartphone app and provided physiological data from a fitness band. Log entries were stored in 5-min intervals. In this dataset we have at least 53 complete days of data for each patient. These days are not necessarily consecutive nor the same days for all the patients. Each log entry contains the date and time, the BG value, the amount of insulin and the amount of carbohydrate intake as estimated by the patients. Additionally, the dataset includes: self-reported meal times with carbohydrate estimates; self-reported times of exercise, sleep, work, stress, and illness; and data from the Empatica Embrace band, which includes 1-min aggregations of GSR, skin temperature, and magnitude of acceleration. Both bands indicated the time they detected that the wearer was asleep, and this information is included when available. However, not all data contributors wore their sensor bands overnight. The population in this case has 83% of male patients with an average age between 33.33 ± 16.33 and 53.33 ± 16.33 years. The average number of days with data is 56.33 ± 2.06. Figure 8 shows the glucose level of the patients from this dataset in the same way as in the What-if scenario.
Histograms and boxplots describing the glucose level of the patients from the dataset used in the Agnostic scenario. The upper figure shows the percentage of time the patient has a very low glucose level (<54 mg/dl in dark red), low ([54,70) mg/dl in red), in range ([70,180] mg/dl in green), high ((180,250] mg/dl in yellow), and very high (>250 mg/dl in dark yellow). The numbers (from top to bottom) represent the percentage of time the patient has a glucose level >250 mg/dl, in range [70,180] mg/dl and <70 mg/dl. The lower figure shows the interquartile ranges of glucose with mean values as red dots (Color figure online)
For this dataset, we construct models with GE and MO-GE for the four prediction horizons PH = \(\{\)30, 60, 90, 120\(\}\) min. We also compare models with access to the information of WS = \(\{\)60, 120\(\}\) min before the time of predictions (see equation 3). In Figs. 9 and 10 , we analyze the differences in the multi-objective approach (MO-GE) when compared to the single-objective (GE) for patients 567 and 584, taking into account the WS values for each figure. As in the previous section, these figures represent solutions in the multi-objective space, and each point represents a solution referenced by its coordinates (RMSE, CDE).
As can be seen, there are some cases where solutions obtained with historical values of ws = 60 min with GE are dominated by solutions generated with MO-GE, as seen in Fig. 9 for P584 ws = 60 and ph = 30 min. Besides that, there are other cases where solutions obtained with MO-GE are dominated by solutions generated with GE, as seen in Fig. 9 for P567 with ws = 60 and ph = 120 min. The solutions are similar when using historical values of ws = 120 min. Figure 11 shows the results for patient 552 for both historical values. In this case, we find solutions in the Pareto front for both historical values and the different time horizons, so there is no dominance between methods. Similar results were obtained with the rest of the patients in the dataset.
As well as in the What-if scenario, we compare the 24 different instances (6 patients by 4 different time horizons) for both GE and MO-GE methods and for the two historical values. For historical values of ws = 60 min, in 18 out of 24 cases (75%), the solutions obtained with MO-GE dominate the solutions obtained with GE. For historical values of ws = 120 min, in 19 out of 24 cases (79.17%), the solutions obtained with MO-GE dominate the solutions obtained with GE.
Table 3 shows the aggregated results for ws = 120 min for the single-objective (GE), the multi-objective (MO-GE) and the ARIMA approaches. For each time horizon, the percentage of predictions in zones A and B (A + B column), C, D and E are depicted and the bold figures highlight the best method. As in the What-if scenario, the MO-GE algorithm reaches the best performance (in all horizons except for 30 min, where ARIMA gets the best results) and returns the best global solutions.
In a similar fashion, MO-GE achieves the lowest percentage of points in zone E for all horizons. But if we look at the joint zone D + E, we find a different situation: MO-GE is only placed first in the 60 min horizon, GE is the best for the medium-term (90 and 120 min) and the winner for the very short-term (30 min) is ARIMA.
It is interesting to analyze the complexity of the solutions in terms of number of parameters and length of the solutions. Figure 12 shows the results obtained for both the What-if and Agnostic scenarios. The figure represents the average RMSE for each number of parameters found in the solutions for both the GE and MO-GE methods (left-hand side of the figure) and also in relation to the length of the models (right-hand side of the figure). We have observed that solutions obtained with GE have a greater length, a greater number of parameters and a higher RMSE than solutions obtained with MO-GE in both What-if and Agnostic scenarios. GE solutions have a high variability in both the number of parameters and the length of the solutions. The variability is lower for MO-GE. Therefore, solutions obtained with MO-GE are less complex than solutions obtained with GE, and solutions obtained in the What-if scenario are more robust in terms of RMSE.
Analysis of the complexity of the solutions based on two criteria: the number of parameters and the length of the solutions. First row shows RMSE vs the number of parameters (left) and RMSE vs the length of the solutions (right) in the What-if scenario. Second row shows the results in the Agnostic scenario (Color figure online)
In order to study how the different historical values WS = \(\{\)60, 120\(\}\) min contributed to the models, a deeper analysis would be required to assess the statistical significance of the results. To carry out this task, we first created density plots using a Kernel Density Estimation (KDE) for the distribution of the samples. The objective is to visualize whether the data meets the conditions for a parametric test, which is not the case. Figure 13 shows the results obtained with GE and MO-GE for the RMSE objective in the Agnostic scenario results. Using Gaussian distribution, the variance is the same for all the cases. Data distribution is non-unimodal and a non-parametric test is necessary. Similar results have been obtained with CDE, but are not shown for the sake of space. All the plots were obtained following the method explained in [5]. Then, we followed the Bayesian model of [4, 5] based on the Plackett-Luce distribution over historical values and time horizons, taking into account the two methods and objective functions. We used a significance level \(\alpha\) = 0.05, with 20 Monte Carlo chains and 4000 simulations. Figure 14 shows the probability of being the best method, denoted as probability of winning, and its standard deviation for the results obtained with GE and RMSE as objective functions. First, it can be seen that the prediction horizon ph = 30 min is the best, since both configurations with this horizon reach the highest probabilities of winning. Also, it can be seen that the historical value of ws = 60 min has the highest probability. Even so, as the confidence interval overlaps with the results obtained with historical value of ws = 120 min, there is no statistical evidence that one method is better than the other. All the intervals for the rest of the time horizons overlap in the same way, and similar results have been obtained for the rest of the cases.
Bayesian model of [6] to analyse the GE results with RMSE as objective function for the Agnostic scenario
All the experiments were performed on an Intel(R) Core (TM) i7-7700CPU at 3.60 GHz with 16 GB RAM Memory on Windows 10. Experiments were run with 8 threads in parallel to benefit from all the core-threads of the computer without affecting performance and no other task running at the same time. The average time to obtain a model with GE is 6.51 min and 3.10 h for the MO-GE approach, almost 29 times slower.
5 Conclusions
In this paper, which extends the work presented at the EvoStar 2020 Conference [10], we investigate the benefits and drawbacks of a multi-objective implementation of GE in the generation of models for BG prediction in diabetes patients. In particular, we implement a multi-objective GE based on the classic NSGA-II algorithm, which is guided by two fitness functions: RMSE and \(F_{\mathrm {CLARKE}}\), which is a function designed following the CEG metric.
We have produced experimental evidence in two different scenarios: on the one hand, the What-if scenario, which takes into account future input data from the prediction horizon in order to predict glucose values. Data from ten real diabetic patients were studied in this scenario, as in [10]. On the other hand, we have studied the Agnostic scenario, where no information about future events is available. In this case, data from six real patients from the OhioT1DM dataset [30] were studied.
Our results show that the multi-objective approach produces better models, reducing the number of predictions in the most dangerous zones of the CEG metric for both scenarios. These results are achieved due to the fact that the multi-objective approach has a better ability than the single-objective approach to traverse the different areas of the search space defined by the \(F_{\mathrm {CLARKE}}\) objective function. This is an important conclusion, since medical criteria is included in this function, which penalizes the models’ most dangerous mispredictions. In addition, we have also found that GE is able to obtain good results in terms of CEG for both scenarios, despite it not being considered an objective function. However, the multi-objective approach can be considered safer since the CEG metric is explicitly included, and a decision maker could examine non-dominated models and decide which one best fits a patient.
In addition to the new experimental results, we have performed a statistical analysis of the results for the Agnostic scenario. According to our tests, there is no statistical evidence of significant difference between using historical values of 60 and 120 min utes in terms of better models. Hence, Using historical values of 60 min is recommended since the complexity of the model is lower and the execution time of the algorithm is shorter, requiring only half of the data.
We are developing a framework, running in the cloud, to generate and deploy models via glucmodel.ucm.es and glucnet.ucm.es. This way, models generated with the methodology presented in this paper are directly applicable to daily clinical practice since mobile and web apps will have access to the predictions in the cloud, helping the user to decide the dose of insulin and other future actions. As we previously explained, MO-GE generated models for What-if scenarios are practically useful for designing insulin or carbohydrate recommendation systems. Moreover, our models are useful for testing the potential modifications of treatments without risking the patients’ health. Agnostic models are useful when more smart devices are available. In particular we are working on a smart watch application that generates alarm signals when the patient is in at-risk situations.
Our procedures and models have been evaluated by the medical staff collaborating on the project and they have concluded that these can be useful for correcting and improving patients’ lifestyles and therapies. Subject to further clinical validation and regulatory approval, the applications we are developing have the potential to be useful for the daily management of diabetes in order to improve glycaemic control and increase patients’ quality of life and autonomy.
Our technique has the potential to be applied to other areas of medicine where a similar set of physical variables are available for measurement. For example, alerts for potentially dangerous heart rates can be generated by developing models based on the historical values measured by smart devices.
By applying our modelling technique, we can obtain white box models that can potentially be interpreted in terms of the variables used although perhaps not totally explainable in terms of physiological aspects of the body, the advantage being that we do not need an initial model and the search is not limited to previously adopted models.
Our current work is focused on the refinement of the models. Datasets from real patients include many different input variables whose influence on the models changes. Therefore, an analysis of each variable’s contribution could help with the creation of more precise models, even for different times of day (e.g. morning, afternoon and night).
Notes
The International Diabetes Federation estimates around 415 million diabetic patients [39] (rising from 108 million since 1980), which is about 8-10% of prevalence in adults over 18 years of age, and it is the seventh leading cause of death in 2016, with 1.6 million deaths directly caused by diabetes, and 2.2 million additional deaths attributable to high blood glucose levels.
When constructing prediction models that help in the recommendation, we can use variables (features) that include the information involved in the recommendation process and thus be able to use them effectively. This does not mean that we use information from the future.
Similar figures for patients 2 and 10 can be found in [10], since this paper is an extended version of that work.
Figures for all patients can be found in [10].
References
E.M. Aiello, G. Lisanti, L. Magni, M. Musci, C. Toffanin, Therapy-driven deep glucose forecasting. Eng. Appl. Artif. Intell. 87, 103255 (2020)
P.A. Bakhtiani, L.M. Zhao, J. El Youssef, J.R. Castle, W.K. Ward, A review of artificial pancreas technologies with an emphasis on bi-hormonal therapy. Diab. Obes. Metab. 15(12), 1065–1070 (2013)
Y. Bengio, Y. Grandvalet, No unbiased estimator of the variance of k-fold cross-validation. J. Mach. Learn. Res. 5, 1089–1105 (2004)
B. Calvo, J. Ceberio, J.A. Lozano, in Proceedings of the Genetic and Evolutionary Computation Conference Companion. Bayesian inference for algorithm ranking analysis (GECCO’18, Association for Computing Machinery, New York, NY, USA, 2018), p. 324–325
B. Calvo, G. Santafé Rodrigo, scmamp: Statistical comparison of multiple algorithms in multiple problems. R J. 8/1 (2016)
B. Calvo, O.M. Shir, J. Ceberio, C. Doerr, H. Wang, T. Bäck, J.A. Lozan, in Proceedings of the Genetic and Evolutionary Computation Conference Companion. Lozano, Bayesian Performance Analysis for Black-Box Optimization Benchmarking (GECCO’19, Association for Computing Machinery, New York, NY, USA, 2019), p. 1789–1797
I. Capel, M. Rigla, G. García-Sáez, A. Rodríguez-Herrero, B. Pons, D. Subías, F. García-García, M. Gallach, M. Aguilar, C. Pérez-Gandía, E. Gómez Aguilera, A. Caixás, M.E. Hernando, Artificial pancreas using a personalized rule-based controller achieves overnight normoglycemia in patients with type 1 diabetes. Diab. Technol. Therap. 16 (2013)
W. Clarke, D. Cox, L. Gonder-Frederick, W. Carter, S. Pohl, Evaluating clinical accuracy of systems for self-monitoring of blood glucose. Diab. Care 10(5), 622–628 (1987)
S.R. Colberg, R.J. Sigal, J.E. Yardley, M.C. Riddell, D.W. Dunstan, P.C. Dempsey, E.S. Horton, K. Castorino, D.F. Tate, Physical activity/exercise and diabetes: a position statement of the American diabetes association. Diab. Care 39(11), 2065–2079 (2016)
S. Contador, J.M. Colmenar, O. Garnica, J.I. Hidalgo, in International Conference on the Applications of Evolutionary Computation. Short and Medium Term Blood Glucose Prediction Using Multi-Objective Grammatical Evolution (Springer, 2020), p. 494–509
S. Contador, J.I. Hidalgo, O. Garnica, J.M. Velasco, J. Lanchares, in Proceedings of the Genetic and Evolutionary Computation Conference Companion. Can Clustering Improve Glucose Forecasting with Genetic Programming Models? (Association for Computing Machinery, 2019), p. 1829–1836
I. Contreras, S. Oviedo, M. Vettoretti, R. Visentin, J. Vehí, Personalized blood glucose prediction: A hybrid approach using grammatical evolution and physiological models. Public Library of Sci. One 12(11) (2017)
Control, T.D., of Diabetes Interventions, C.T.D., Group, C.E.S.R., Intensive diabetes treatment and cardiovascular outcomes in type 1 diabetes: The dcct/edic study 30-year follow-up. Diabetes Care (2016)
E. Dassau, H. Zisser, R.A. Harvey, M.W. Percival, B. Grosman, W. Bevier, E. Atlas, S. Miller, R. Nimri, L. Jovanovič, F.J. Doyle, Clinical evaluation of a personalized artificial pancreas. Diab. Care 36(4), 801–809 (2013)
I. De Falco, A. Della Cioppa, T. Koutny, M. Krcma, U. Scafuri, E. Tarantino, Genetic programming-based induction of a glucose-dynamics model for telemedicine. J. Netw. Comput. Appl. 119, 1–13 (2018)
K. Deb, D. Kalyanmoy, Multi-Objective Optimization Using Evolutionary Algorithms (John Wiley & Sons Inc, USA, 2001)
E. Donga, M. Dijk, J. van Dijk, N. Biermasz, G.J. Lammers, K. Kralingen, R. Hoogma, E. Corssmit, J. Romijn, Partial sleep restriction decreases insulin sensitivity in type 1 diabetes. Diab. Care 33, 1573–7 (2010)
O. Garnica, J. Lanchares, J. Velasco, J. Hidalgo, M. Botella, Noise spectral analysis and error estimation of continuous glucose monitors under real-life conditions of diabetes patients. Biomed. Sig. Process. Control 61, 101934 (2020)
M. Gevers, Identification for control: From the early achievements to the revival of experiment design. Eur. J. Control 11(4), 335–352 (2005)
E. Hemberg, L. Ho, M. O’Neil, H. Claussen, A comparison of grammatical genetic programming grammars for controlling femtocell network coverage. Genetic Program. Evol. Mach. 14(1), 65–93 (2013)
J.I. Hidalgo, M. Botella, J.M. Velasco, O. Garnica, C. Cervigón, R. Martínez, A. Aramendi, E. Maqueda, J. Lanchares, Glucose forecasting combining markov chain based enrichment of data, random grammatical evolution and bagging. Appl. Soft Comput. 88, 105923 (2020)
J.I. Hidalgo, J.M. Colmenar, J.L. Risco-Martin, A. Cuesta-Infante, E. Maqueda, M. Botella, J.A. Rubio, Modeling glycemia in humans by means of grammatical evolution. Appl. Soft Comput. 20, 40–53 (2014)
J.I. Hidalgo, J.M. Colmenar, J.M. Velasco, G. Kronberger, S.M. Winkler, O. Garnica, J. Lanchares, in Handbook of Grammatical Evolution. Identification of Models for Glucose Blood Values in Diabetics by Grammatical Evolution (Springer, 2018), p. 367–393
J.I. Hidalgo, J.M. Colmenar, G. Kronberger, S.M. Winkler, O. Garnica, J. Lanchares, Data based prediction of blood glucose concentrations using evolutionary methods. J. Med. Syst. 41(9), 142 (2017)
G. Kenny, R. Sigal, R. McGinn, Body temperature regulation in diabetes. Temperature 3, 119–145 (2016)
K.H. Larsen, B.S., Generation of dose calculation data tables using cubic spline interpolation. Med. Dosim. 16 (1991)
K. Li, J. Daniels, C. Liu, P. Herrero, P. Georgiou, Convolutional recurrent neural networks for glucose prediction. IEEE J. Biomed. Health Inform. 24(2), 603–613 (2019)
N. Lourenço, J.M. Colmenar, J.I. Hidalgo, O. Garnica, in Proceedings of the Genetic and Evolutionary Computation Conference. Structured Grammatical Evolution for Glucose Prediction in Diabetic Patients (Association for Computing Machinery, 2019), p. 1250–1257
C.D. Man, F. Micheletto, D. Lv, M. Breton, B. Kovatchev, C. Cobelli, The uva/padova type 1 diabetes simulator: new features. J. Diab. Sci. Technol. 8(1), 26–34 (2014)
C. Marling, R. Bunescu, The ohiot1dm dataset for blood glucose level prediction: update 2020. CEUR Workshop Proceedings (2020)
C. Marling, J. Shubrook, S. Vernier, M. Wiley, F. Schwartz, Characterizing blood glucose variability using new metrics with continuous glucose monitoring data. J. Diab. Sci. Technol. 5, 871–8 (2011)
J. Martinsson, A. Schliep, B. Eliasson, C. Meijner, S. Persson, O. Mogren, in 3rd International Workshop on Knowledge Discovery in Healthcare Data, 13 July 2018. Automatic Blood Glucose Prediction with Confidence Using Recurrent Neural Networks (2018), p. 64–68
M. Mayo, L. Chepulis, R.G. Paul, Glycemic-aware metrics and oversampling techniques for predicting blood glucose levels using machine learning. Public Library Sci. One 14(12) (2019)
C. Meijner, S. Persson, Blood Glucose Prediction for Type 1 Diabetes using Machine Learning Long Short-term Memory Based Models for Blood Glucose Prediction. Master’s thesis (University of Gothenburg, 2017)
M. Messori, C. Toffanin, S.D. Favero, G.D. Nicolao, C. Cobelli, L. Magni, Model individualization for artificial pancreas. Comput. Methods Program. Biomed. (2016)
S. Mirshekarian, R. Bunescu, C. Marling, F. Schwartz, in 2017 39th Annual International Conference of the IEEE Engineering in Medicine and Biology Society. Using lstms to Learn Physiological Models of Blood Glucose Behavior (IEEE, 2017), p. 2887–2891
S. Mirshekarian, H. Shen, R. Bunescu, C. Marling, in 2019 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society. Lstms and Neural Attention Models for Blood Glucose Prediction: Comparative Experiments on Real and Synthetic Data (IEEE, 2019), p. 706–712
D. Moreno-Salinas, E. Besada-Portas, J. López-Orozco, D. Chaos, J. de la Cruz, J. Aranda, Symbolic regression for marine vehicles identification. Int. Fed. Autom. Control Papers Line 48(16), 210–216 (2015)
K. Ogurtsova, J. da Rocha Fernandes, Y. Huang, U. Linnenkamp, L. Guariguata, N. Cho, D. Cavan, J. Shaw, L. Makaroff, Idf diabetes atlas: Global estimates for the prevalence of diabetes for 2015 and 2040. Diab. Res. Clin. Prac. 128, 40–50 (2017)
S. Oviedo, I. Contreras, C. Quirós, M. Giménez, I. Conget, J. Vehi, Risk-based postprandial hypoglycemia forecasting using supervised learning. Int. J. Med. Inform. 126, 1–8 (2019)
L.C. Parsons, M.A. Revell, Pathophysiology and care protocols for nursing management. Nurs. Clin. North Am. 50(4) (2015)
C. Ryan, J. Collins, M. Neill, Grammatical Evolution: Evolving Programs for an Arbitrary Language, in Genetic Programming, Lecture Notes in Computer Science, vol. 1391, ed. by W. Banzhaf, R. Poli, M. Schoenauer, T. Fogarty (Springer, Berlin, 1998), pp. 83–96
M.I. Schmidt, A. Hadji-Georgopoulos, M. Rendell, S. Margolis, A. Kowarski, The dawn phenomenon, an early morning glucose rise: implications for diabetic intraday blood glucose variation. Diab. Care 4(6), 579–585 (1981)
G. Sparacino, F. Zanderigo, S. Corazza, A. Maran, A. Facchinetti, C. Cobelli, Glucose concentration can be predicted ahead in time from continuous glucose monitoring sensor time-series. IEEE Trans. Biomed. Eng. 54(5), 931–937 (2007)
G. Steil, K. Rebrin, F. Hariri, S. Jinagonda, S. Tadros, C. Darwin, M. Saad, Interstitial fluid glucose dynamics during insulin-induced hypoglycaemia. Diabetologia 48(9), 1833–1840 (2005)
Q. Sun, M. Jankovic, J. Budzinski, B. Moore, P. Diem, C. Stettler, S.G. Mougiakakou, A dual mode adaptive basal-bolus advisor based on reinforcement learning. IEEE J. Biomed. Health Inform. (2018)
Q. Sun, M.V. Jankovic, L. Bally, S.G. Mougiakakou, in 2018 14th Symposium on Neural Networks and Applications. Predicting Blood Glucose with an lstm and Bi-lstm Based Deep Neural Network (IEEE, 2018), pp. 1–5
S. Umapathy, T. Rajalakshmi, C. Sri, G. Balachander, K. Shankar, Non-invasive blood glucose analysis based on galvanic skin response for diabetic patients. Biomed. Eng. Appl. Basis Commun. 30, 1850009 (2018)
J.M. Velasco, O. Garnica, S. Contador, J.M. Colmenar, E. Maqueda, M. Botella, J. Lanchares, J.I. Hidalgo, in European Conference on the Applications of Evolutionary Computation. Enhancing Grammatical Evolution Through Data Augmentation: Application to Blood Glucose Forecasting (Springer, 2017), pp. 142–157
J.M. Velasco, O. Garnica, J. Lanchares, M. Botella, J.I. Hidalgo, Combining data augmentation, edas and grammatical evolution for blood glucose forecasting. Memetic Comput. 10(3), 267–277 (2018)
G. Wahba, Spline models for observational data. Reg. Conf. Ser. Appl. Math. 59 (1990)
J. Weissberg-Benchell, J. Antisdel-Lomaglio, R. Seshadri, Insulin pump therapy. Diab. Care 26(4), 1079–1087 (2003)
M. Wilinska, L. Chassin, H. Schaller, L. Schaupp, T. Pieber, R. Hovorka, Insulin kinetics in type-1 diabetes: continuous and bolus delivery of rapid acting insulin. IEEE Trans. Biomed. Eng. 52, 3–12 (2005)
C. Yu, C. Zhao, Rapid model identification for online glucose prediction of new subjects with type 1 diabetes using model migration method. Int. Fed. Autom. Control Proc. Vol. 47(3), 2094–2099 (2014)
Acknowledgements
This work is supported by: Fundación Eugenio Rodriguez Pascual 2019 grant—Desarrollo de sistemas adaptativos y bioinspirados para el control glucémico con infusores subcutáneos continuos de insulina y monitores continuos de glucosa (Development of adaptive and bioinspired systems for glycaemic control with continuous subcutaneous insulin infusors and continuous glucose monitors); Spanish Ministerio de Ciencia, Innovación y Universidades (MCIU/AEI/FEDER, UE) under grant refs. RTI2018-095180-B-I00 and PGC2018-095322-B-C22; Madrid Regional Goverment-FEDER grants B2017/BMD3773 (GenObIA-CM); Y2018/NMT-4668 (Micro-Stress-MAP-CM); and P2018/TCS-4566 (CYNAMON-CM).
Funding
Open Access funding provided thanks to the CRUE-CSIC agreement with Springer Nature.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Area Editor: Una-May O'Reilly.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Contador, S., Colmenar, J.M., Garnica, O. et al. Blood glucose prediction using multi-objective grammatical evolution: analysis of the “agnostic” and “what-if” scenarios. Genet Program Evolvable Mach 23, 161–192 (2022). https://doi.org/10.1007/s10710-021-09424-6
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10710-021-09424-6