Illuminating the Nile: estimating subnational GDP in Egypt using nighttime lights and machine learning

Abstract

Egypt has been reporting several subnational socioeconomic indicators for more than three decades. However, utilizing these valuable datasets for monitoring long temporal trends in local development and inequalities has been hindered by the lack of a key indicator, the Gross Domestic Product (GDP), which was only reported subnationally starting 2013. This paper aims to address this data gap, by employing satellite-generated nighttime lights (NTL) and machine learning, to estimate subnational GDP in Egypt from 1992 to 2012. The paper relies on the harmonized global nighttime lights dataset that extends from 1992 to 2021, to carry out a twofold process. First, it validates NTL as a useful proxy for subnational economic activity in Egypt using econometric methods; then it estimates missing GDP using machine learning algorithms. Results show that the concentration of nearly the entire Egyptian population densely around the Nile River is challenging to nighttime lights accuracy; however, upon accounting for population density and agricultural activity, NTL could serve as a valuable proxy for subnational GDP in Egypt, and consequently a coherent GDP dataset is constructed since 1992.

Introduction

Local development efforts require understanding spatiotemporal differences on a subnational level within a given country. Regional inequalities in development and socioeconomic performance are often evident in developing countries, and offer a rich opportunity for informed policy-making and research. Such efforts in turn need subnational data with extended time-series coverage, for better understanding of trends and correlations across subnational units. Nevertheless, for numerous developing countries, such data is either unavailable, or has been recently produced with short temporal coverage, often due to the limited capacities of developing countries to produce this level of data periodically across several indicators, which is usually through costly surveys and censuses.

In Egypt, decades-long subnational data is available for some indicators, including mostly labour market indicators from labour surveys, some agricultural indicators, population-related measures, and others. However, these indicators are insufficient to understand trends in regional disparities within Egypt, which require data on subnational economic activity, income, inequality, etc. In recent years, Egypt has finally started producing official provincial-level Gross Domestic Product (GDP) data, starting from 2013; this short dataset would be more valuable if it could be extended to match other decades-long subnational indicators, to improve our understanding of spatiotemporal trends in regional development in Egypt.

Over the last decade, there has been a surge in using satellite-generated data to estimate economic indicators globally, especially on the more-scarce subnational level. Since the two seminal papers by Chen & Nordhaus (2011) and Henderson et al. (2012) tested the use of data on nighttime lights (NTL) as a measure for economic output and growth, the utilization of NTL and other satellite data has become well-established in economic literature. Numerous papers have been employing NTL directly based on literature findings, or validating how well of a proxy NTL can be for economic activity in different countries, on different administrative levels, or using different datasets of NTL (Zhang & Gibson, 2022). Simultaneously, recent findings have also pointed to the flaws of NTL data, especially from older satellites, and criticised the use of nighttime lights as an economic proxy in some specific circumstances (Gibson et al., 2021), which make validating NTL as a proxy for economic indicators an important step, prior to empirical utilization of it.

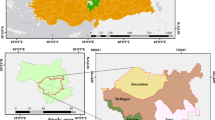
In this paper, I build on the growing nighttime lights literature to estimate provincial GDP in Egypt since 1992, using the dataset with largest temporal coverage, the harmonized global nighttime lights dataset that extends from 1992 to 2021. Satellite night images of the brightly-lit valley and delta of the Nile River in Egypt, such as in Fig. 1 are in fact quite popular; they are frequently used as poster images for nighttime lights by NASA¹ (The National Aeronautics and Space Administration), and Google Earth Engine² among others, to display how fascinating and perceptive NTL is. Hence, it is surprising that such images have not been put to use yet.

To use the harmonized NTL data for estimation, I first validate whether it is a good proxy for subnational GDP in Egypt, by measuring GDP elasticity to NTL econometrically using the official dataset from 2013 to 2021. Then, following a recent but growing literature, I test several machine learning algorithms, to choose which has the best predictive potential, using cross-validation; the best algorithm is then used for out-of-sample prediction of provincial GDP, after performing hyperparameters tuning to improve the algorithm’s performance. In this context, “predict” is used to refer to estimation of non-observed values in past years, rather than forecasting values in the future, as it is commonly used.

Fig. 1

Nighttime lights in Egypt, DMSP-OLS, 2013

Materials and methods

Related literature

Early research prior to Chen & Nordhaus (2011) and Henderson et al. (2012) did use nighttime lights data as a proxy for socioeconomic development in countries with low-quality official data, since light emissions at night are associated with human economic activity. However, it was the contribution of these two papers, by developing optimal weighting of NTL and official GDP, that ushered in a wider use of NTL in economic literature (Gibson et al., 2021).

These two papers, and a significant part of the literature that followed, used NTL data from the Defense Meteorological Satellite Program Operational Linescan System (DMSP-OLS) of the United States Air Force. These satellites measured lights between 8:30 and 10:00 pm, and the final product made available for the public after adjustments and corrections is a grid of digital numbers from 0 (no light) to a maximum of 63, for each 30 arc-second output pixel, which is approximately 0.86 square Kilometres (at the equator) (Lessmann & Seidel, 2017). This dataset has been made available from 1992 until 2013, and was discontinued afterwards.

A new NTL dataset was released in 2013 from the Visible Infrared Imaging Radiometer Suite (VIIRS) on the Suomi National Polar-orbiting Partnership satellite. The VIIRS dataset has been found to offer higher accuracy NTL data compared to the DMSP dataset that suffers from blurring, as the former has higher spatial resolution, on-board calibration, and wider dynamic range to prevent sensor saturation, and hence the VIIRS NTL has been found to provide a better proxy for economic activity (McCord & Rodriguez-Heredia, 2022).

Simultaneously, literature has challenged the accuracy of DMSP NTL as a proxy for economic output, and highlighted some circumstances where it seems to underperform. For example, it was found using DMSP data in a study on a few developing and developed countries, that the GDP NTL relation was unstable within these countries (Bickenbach et al., 2016); other findings using DMSP highlighted that time-series estimates of GDP from NTL were less-reliable than cross-section estimates (Nordhaus & Chen, 2015); more criticism highlighted that this data is also less-reliable as a proxy of economic activity in low population density areas, small scale administrative units, or rural regions (Nordhaus & Chen, 2015; Gibson & Boe-Gibson, 2021).

In fact, both the DMSP and VIIRS nighttime lights datasets were not found to be a good proxy of economic output in low density/rural areas, since agricultural activities emit less lights at night, regardless of the accuracy of the satellites in use (Gibson et al., 2021). This has motivated a strand of literature to augment the utilization of NTL with employing daytime satellite-generated data that capture land use and land cover as a proxy for agricultural output, when relevant official data is unavailable or incomplete, particularly by using the Landsat and MODIS satellite imagery (Keola et al., 2015; Chen et al., 2020; Goldblatt et al., 2020).

However, despite challenges, the DMSP dataset still holds an advantage that makes it a valuable tool to date, which is its long time-series coverage since 1992, compared to the recent short availability of the VIIRS dataset. Nevertheless, caution is required when using it to address its main shortcomings; and validating its goodness of fit as a proxy in different countries or administrative levels remains a valuable step prior to utilizing it for GDP estimation, which is why this research is first validating the relation between GDP and NTL in Egypt using available official GDP, as there has been no previous research that tested this, to the best of my knowledge.

While relevant literature traditionally used econometric methods both to validate the GDP elasticity to NTL and to estimate missing GDP, in recent years machine-learning (ML) has been increasingly employed for prediction of socioeconomic indicators using nighttime lights. Machine learning and NTL are being used to estimate GDP on various sub-national levels (Basihos, 2016; Dasgupta, 2022; Puttanapong et al., 2023), to estimate poverty (Jean et al., 2016; Head et al., 2017; Subash et al., 2018), urbanization (Pandey et al., 2013), industrial development (Otchia & Asongu, 2021), and human development indicators (Bansal et al., 2020). This recent surge in utilization of ML algorithms for out-of-sample-prediction is the result of evidence that ML significantly improves the predictive power compared to conventional econometric methods, hence offering higher accuracy of indicators estimation from NTL (Dasgupta, 2022; Puttanapong et al., 2023).

Data

This paper uses various datasets from both official and remote-sensing sources, extending from 1992 to 2021, except for total GDP, the indicator of interest whose available dataset extends from 2013 to 2021. All datasets utilized for this research are for the first subnational administrative level in Egypt, with 27 provinces. the administrative borders map used in this research is the map released by the official department for data and statistics in Egypt, the Central Agency for Public Mobilization and Statistics (CAPMAS), in 2017 as a part of a census. The map was obtained from the Humanitarian Data Exchange portal, provided by the United Nations Office for the Coordination of Humanitarian Affairs (OCHA). The author does not recommend using other administrative maps for Egypt provided by most open portals used in related literature, as several of them were tested for this research. These maps are inaccurate in some provinces, with seemingly slight border changes resulting in significant differences in mapping of remote-sensing data, due to the sharp contrast of neighbouring high/low density provinces in Egypt, as will be explained later.

A. Nighttime Lights

To benefit from the longest possible temporal coverage of NTL, this research uses the harmonized global nighttime lights annual dataset constructed by Li et al. (2020), which is updated annually and now extends from 1992 to 2021 by combining both the DMSP and VIIRS datasets. In this dataset, first the raw DMSP NTL data was improved using a stepwise calibration approach, generating a temporally consistent data that outperforms those using traditional approaches. Then the VIIRS data was processed and corrected as well, and then harmonized into simulated DMSP-like observations, by first quantifying the DMSP-VIIRS relationship in the overlapping year 2013, then evaluating the generated time-series, thus constructing an integrated and consistent NTL dataset at the global scale (Li et al., 2020).

Distribution of the sum of NTL in Egypt in 1992 and 2021 is shown in Fig. 2, with the administrative borders as well. It is obvious from the maps the concentration of Egyptian population in the narrow valley and delta of the Nile River with high population density, in sharp contrast with the remaining area of the country that is scarcely populated desert. This is a main reason why the utilized administrative borders should be accurate, since slightly moving borders of the peripheral low-density provinces closer to the Nile, especially in the southwest, mistakenly grants them a disproportionately larger share of the NTL observations, compared to their actual population or economic output, which distorts the GDP-NTL relation.

Fig. 2

Harmonized nighttime lights and administrative borders in Egypt, 1992 and 2021

B. Gross domestic product

Annual total GDP in Egyptian Pound (EGP) is obtained from the Egyptian Ministry of Planning for the provincial-level. This dataset, as most economic data in Egypt, is reported for fiscal years not calendar years, and is available from the fiscal year 2012/2013 to 2020/2021. Following the World Bank’s methodology,³ I assign fiscal year data to the calendar year containing the larger share of the fiscal year period. Thus, since the fiscal year in Egypt ends on June 30, the data of the fiscal year is assigned to the second calendar year of the period. For example, data for the fiscal year 2012/2013 is assigned to the calendar year 2013, and so on. Accordingly, official provincial-level GDP dataset utilized in this research extends from 2013 to 2021.

Furthermore, annual GDP in million EGP for the national level is also obtained from the same source, the Ministry of Planning, for the full period 1992–2021. National-level GDP is obtained both at current and constant prices, and is used for training the machine learning models, to improve their predictive performance.

C. Population density

Province-level population data from official sources (CAPMAS) is utilized. This dataset extends from 1992 to 2021, and is reported annually as a population count in mid-year. This population count data is used to calculate annual population density based on the area of each province from CAPMAS. A map of population density distribution across provinces in Egypt for 2021 is shown in the appendix in Fig. 6.

D. Crop area

To control for agricultural output in line with relevant literature, I use an annual unique dataset on crop area in Egypt that extends from 1992 to 2021, and was digitized for this research from CAPMAS archival annual reports. The unit of crop area in this dataset is in Feddan, which is an Egyptian unit of area, equal to 1.038 acres. The way this official crop area measure reports agricultural land area in a given province, is that since the same land plot could be used to grow and harvest more than one crop in a given year, each time a crop is grown and harvested per plot, the plot’s area will be added to the crop area in the province. Thus, this measure captures physical agricultural land area, and to some extent productivity as well, and could be used as an official proxy for agricultural output, in the same sense that the remote-sensing land use and land cover data are used. Figure 10 in the appendix shows a distribution map of crop area as a percentage of total provincial area in Egypt for 2021; the map shows several provinces with a percentage that exceeds 100%, which is a result of how the crop area measure is calculated as discussed above.

E. Climate data

To Improve the predictive power of the machine learning algorithms for the out-of-sample prediction, climate data is also employed, in line with relevant literature (Dasgupta, 2022; Puttanapong et al., 2023), on the provincial-level from 1992 to 2021. Data on precipitation, minimum, and maximum temperature, was obtained from the TerraClimate dataset in Google Earth Engine Data Catalog. TerraClimate is a high-resolution global dataset of monthly climate and climatic water balance from 1958 that uses climatically aided interpolation based on data from multiple sources including satellites and weather stations (Abatzoglou et al., 2018). Monthly data from TerraClimate was downloaded for the same administrative border map mentioned earlier, from Google Earth Engine Code Editor, using JavaScript programming language. The data was then aggregated on the annual level as a sum value for the precipitation, and a mean value for the minimum and maximum temperature.

Adding climate variables, such as temperature and precipitation, to improve prediction of GDP is based on evidence that climate changes do affect economic growth, mainly through impact on agriculture and productivity. Literature has shown that increases in temperature are associated with a decrease in economic growth, while the effect of changes in precipitation has been more mixed, depending on the spatial level, income, and dominant sectors, among other factors (Damania et al., 2020; Kotz et al., 2022; Meyghani et al., 2023; Song et al., 2023).

Table 1 shows descriptive statistics for the variables used in both the econometric models and the machine learning algorithms. As the table shows, data for all variables is complete whether the independent variables that are available from 1992, or the GDP that is available from 2013, except for the crop area. Dataset for crop area has some missing values, resulting either from unavailable annual report(s) from CAPMAS, or missing data in existing reports. Missing values have been imputed using machine learning to complete the crop area dataset, for which more details are provided in the appendix, alongside details concerning other issues related to the utilized datasets.

Table 1 Descriptive statistics of utilized variables

Empirical framework

To validate NTL as a proxy for subnational GDP in Egypt, I employ an empirical strategy based on recent validation literature, in order to examine the elasticity of GDP with respect to nighttime lights, in terms of cross-sectional GDP differences between areas, and annual time-series fluctuations in GDP within areas as well (Zhang & Gibson, 2022; Mendez & Patnaik, 2023). The strategy relies on the following basic panel-data model:

$$\begin{aligned} \log ({GDP})_{{it}}=\alpha +\beta \log ({NTL})_{{it}}+\mu _i+\varphi _t+\varepsilon _{{it}} \end{aligned}$$

(1)

Where NTL is the sum of nighttime lights, GDP the Gross Domestic Product, i indexes the provinces, t the years, $\mu _i$ denotes the provinces fixed effects which capture the influence of unobserved features of each province that are constant over-time, $\varphi _t$ the years fixed effects which capture the unobserved features of each year that are common between provinces, and $\varepsilon _{ it }$ the term for random disturbance. In this model $\beta$ is the parameter of interest, which shows the elasticity of GDP to nighttime lights; and since it is a log-log model, this parameter shows the percentage change in GDP for each one percentage change in the sum of nighttime lights.

From the basic model, three different elasticities could be estimated based on the equations below, in which a vector of controls X is added with a vector of parameters $\delta$.

$$\begin{aligned} \log ({GDP})_{{it}}=\beta _{{Pooled}}\log ({NTL})_{{it}}+\delta _{{Pooled}}X_{{it}}+\mu +\varepsilon _{{it}} \end{aligned}$$

(2)

The first model in Eq. (2) above estimates the elasticity $\beta$ using pooled Ordinary Least Squares (OLS). This parameter shows the percentage change in GDP per one percentage change in NTL without disentangling the relationship either based on cross-sectional differences, or temporal changes.

The second model in Eq. (3) estimates elasticity $\beta$ as the between estimator. In this model, Equation (1) is averaged over-time to estimate a cross-sectional regression with OLS; Thus, elasticity here shows the effect of long-run NTL differences between provinces.

$$\begin{aligned} \overline{\log ({GDP})_i}=\beta _{{Between}}\overline{\log ({NTL})_i}+\delta _{{Between}}\overline{X_i}+\mu _i+\overline{\varepsilon _{{it}}} \end{aligned}$$

(3)

The third model in Eq. 4 estimates the within estimator, by subtracting Eq. (3) from Eq. (1) thus removing unobserved provinces fixed effects. Elasticity $\beta$ in this equation shows the effect of NTL changes within provinces over-time.

$$\begin{aligned} \log ({GDP})_{{it}}\text {-}\;\overline{\log ({GDP})_i}=&\beta _{{Within}}[\log ({NTL})_{{it}}\text {-}\overline{\log ({NTL})_i}]\nonumber \\ +\;\delta _{{Within}}[X_{{it}}\text {-}\overline{X_i}]&+\varphi _t+\varepsilon _{{it}}\text {-}\overline{\varepsilon _{{it}}} \end{aligned}$$

(4)

Models (3) and (4) allow disentangling the GDP-NTL relation in the sense that we can examine from the between estimator the cross-sectional GDP differences between provinces, while the within estimator allows the examination of annual temporal fluctuations in GDP within provinces, which is a level of analysis that Eq. (2) alone does not offer (Zhang & Gibson, 2022; Mendez & Patnaik, 2023).

Machine learning

Conventional regression techniques model the relationship between variables relying on rule-based programming and focusing on unbiasedness. Machine learning regression on the other hand relies on algorithms to flexibly learn from the data, in the sense that they recognize and extract patterns from raw input data, to predict output values (Bishop & Nasrabadi, 2006; Goodfellow et al., 2016). The algorithms account for bias-variance trade-offs in order to handle complex relations and maximize prediction performance, hence yielding better outcomes than conventional methods (Subash et al., 2018).

In order to use machine learning for out-of-sample prediction in this research, several machine learning regression algorithms were trained and tested on the dataset consistently with previous literature (Dasgupta, 2022; Puttanapong et al., 2023), and the one with the best performance was then used for the estimation. Trained ML algorithms were Artificial Neural Network (ANN), Random Forest (RF), Support Vector Machines (SVMs), K-Nearest Neighbours (KNN), Ridge Regression, and eXtreme Gradient Boosting (XGBoost). First, the dataset from 2013 to 2021 that includes official GDP values, was split into a training and a test samples, with ratios of 75% and 25% respectively; then the hyperparameters of each ML algorithm were tuned to improve its accuracy, next the algorithms were trained on the data, and assessed based on 5-fold cross validation to minimize overfitting, using both R² and mean squared error (MSE), where the best model would be the one with the highest R² and the least MSE. Finally, the best model was used on the dataset from 1992 to 2012 to estimate the GDP, after further hyperparameters tuning.

Testing several machine learning algorithms is essential for choosing the best fit one for the data in hand. Flexibility of these algorithms, compared to conventional regression methods, makes a principal choice difficult, especially since each of them has its own advantages and disadvantages. For example, ANN is a powerful algorithm capable of handling complex relations, but it usually requires large datasets to perform well, and could be complicated to tune; regression tree algorithms, such as RF and XGBoost are also quite powerful and capable of understanding non-linear relationships and handling outliers, however they could be prone to overfitting, particularly with smaller datasets, and are computationally demanding; SVMs on the other hand could be more robust to overfitting, but are also challenging to tune due to the reliance on kernel size, and could be problematic with big datasets; regularized regression algorithms such as Ridge are also robust to overfitting and are simple to tune and use, but simultaneously they are more fit for smaller datasets, and cannot handle complex non-linear relations; and finally, KNN is similarly easy to use, but could be computationally demanding for large datasets, and is sensitive to noise and outliers in the data (Juarez-Orozco et al., 2018; Kumar & Sowmya, 2021).

Results

Econometric validation

Visualization of nighttime lights in Egypt in Figs. 1 and 2 highlights a unique characteristic of population and economic activity distribution in Egypt. The sharp contrast of high/low population density regions in the country, which increases with time as population and output grow, is the result of geographic concentration of life in Egypt around the Nile River, with the rest of the country’s area being scarcely populated. Such high/low density contrast could be a challenge to utilization of nighttime lights, particularly the DMSP dataset. High-density regions, particularly urban ones, could be problematic to the top-coded DMSP dataset, and low-density regions are problematic to NTL in general regardless of which dataset is used, as highlighted earlier. Hence, it is expected that the GDP-NTL relation in Egypt could be affected by the density extremes in the country, which is evident from the scatter plot in Fig. 3. The figure plots the logarithm of provincial GDP in Egypt for the 27 provinces from 2013 to 2021, against the logarithm of the sum of nighttime lights.

Fig. 3

Scatterplot and fitted line of NTL and GDP in Egypt in logarithm terms, 2013–2021

As the plot shows, there are two groups of extreme observations at both ends of the GDP-NTL fitted line. At one end are the highly dense urban centres in Egypt: Cairo the capital province, Giza, and Alexandria, while at the other end is the vast mostly desert province El-Wadi El Gedid, which is the least dense province in Egypt with less than one person per square kilometre in 2021.

To account for this issue, population density will be controlled for in the validation tests, in addition to crop area as a proxy for agricultural output, since rural regions do omit less lights at nights on average than urban ones, as discussed earlier. Furthermore, possible non-linearity in the GDP-NTL relationship will be controlled for as well. Non linearity in the relationship is accounted for by adding a quadratic term for nighttime lights - $\log ^2( NTL )$ - as utilized in relevant literature (McCord & Rodriguez-Heredia, 2022). Non-linearity is possible particularly when using the DMSP dataset as it is censored data with a range from zero to 63, while GDP data is uncensored (Bickenbach et al., 2016).

Table 2 shows the results of the three different estimators used for validation from Eqs. (2), (3), and (4), the pooled OLS, the between estimator, and within estimator, with a base model for each using only NTL, and additional models that add the control variables: population density, crop area, and quadratic term for NTL.

Table 2 Pooled OLS, between, and within estimators of GDP-NTL elasticities. Provincial level 2013–2021

Results in Table 2, with all variables in logarithm terms, show a positive and statistically significant association between NTL and GDP using the pooled OLS estimator in the base model (1) of the table. GDP elasticity to NTL increases as population density and crop area are added in models (2) and (3), with R² increasing as well from 0.078 to 0.599. However, for the between and within estimators, that show the cross-sectional and temporal association between GDP and NTL, the elasticities in both are statistically insignificant in the base models (4) and (7), with a negative elasticity in the within base model, which shows that on the subnational level in Egypt, NTL on its own could be a poor proxy for cross-sectional differences in provincial GDP, and for temporal changes within provinces as well.

Nevertheless, for the between estimator, once population density is controlled for in model (5) of the table, GDP elasticity to NTL becomes statistically significant with a value of 0.552; controlling for crop area as well increases the significance level, and the elasticity value which almost doubles in model (6), indicating that a 1% increase in NTL across provinces, is associated with a 1% increase in GDP. R² for the between estimator as well increases significantly from 0.063 for the base model (4) to 0.76 when both population density and crop area are added in model (6).

Finally, for the within estimator models, after controlling for population density and crop area in models (8) and (9) in the table, the elasticity is still negative and statistically insignificant. However, upon controlling for non-linearity in the GDP-NTL relation, by adding the quadratic term in model (10), GDP elasticity to NTL becomes positive and statistically significant, with a considerably high value of 3.941, and an R² of 0.873, thus validating a statistically significant GDP-NTL non-linearity within provinces overtime.

Regarding the two control variables, the coefficients of population density are all statistically significant and positive as expected, with considerably higher elasticity values for the within models compared to the between ones, indicating a higher GDP-population-density association within provinces overtime, compared to across provinces. Crop area coefficients are also statistically significant in all models; however, they are negative in the between model, and positive in the within ones. This result shows that on average, provinces with higher agricultural output, i.e., rural provinces, tend to have less GDP, or be poorer than urban ones, and concurrently as agricultural output increases within these provinces their output increases. Furthermore, GDP-crop-area negative cross-sectional elasticity is almost four times higher than its positive temporal elasticity, which means that the decline in GDP across provinces due to higher agricultural output, i.e., being rural, is much larger than the increase in GDP within these provinces as their agricultural output increases over time.

Furthermore, similar to the four within estimator models in Table 2, which include both region and year fixed effects, in Table 5 of the appendix the same models’ specifications are also estimated, but using regional random effects and year fixed effects, as a robustness check in line with literature that uses subnational observations pooled from multiple countries, instead of observations from the same country as in this research (Lessmann & Seidel, 2017; McCord & Rodriguez-Heredia, 2022). Results from the random effects models with year fixed effects are close to the within models in Table 2, for which the final model corresponding to model (10) showing also positive and statistically significant elasticity of GDP to NTL, with a value of 3.168, but at a lower significance level and R² compared to the within estimator model (10). In the appendix as well, results of the Hausman test for that final model are reported in Table 6, for the choice between fixed or random effects (Hausman, 1978). The test’s results do confirm that the fixed effects (the within estimator) is the model of choice.

In conclusion, results from Table 2 do provide evidence that changes in nighttime lights augmented with crop area and population density, can be used as a proxy for subnational variations in GDP in Egypt, both cross-sectional and temporal. These variables are thus used, in addition to the climate data highlighted earlier, in order to perform out-of-sample prediction of provincial GDP from 1992 to 2012, using machine learning.

Machine learning prediction

As highlighted earlier, six different machine learning algorithms had their hyperparameters tuned, and then were trained using the datasets on variables in model (10) of Table 2, in addition to datasets on national GDP, precipitation, maximum, and minimum temperature, as shown in Table 3 of the algorithms’ variables, i.e., attributes. Machine learning analysis in this paper was executed using the open source scikit-learn library (Pedregosa et al., 2011) in Python programming language. The library offers efficient tools for splitting the data, training various machine learning algorithms, evaluating estimation performance, and tuning the hyperparameters, among other tools.

Table 3 List of attributes for machine learning algorithms

Table 4 shows the results of the R² and MSE of each algorithm using 5-fold cross validation, in addition to the main parameter(s) that produced a best fit.

Table 4 Machine learning algorithms performance using 5-fold cross validation

Results from Table 4 show that Ridge Regression model outperforms other trained machine learning algorithms, with the highest R² of 0.95 and the smallest MSE of 0.01. Hence, Ridge Regression is selected as the prediction algorithm. this result is consistent with previous literature in which Ridge Regression was also found to be the best fitted model for out-of-sample-prediction of GDP from nighttime lights (Dasgupta, 2022), and was also chosen for prediction of poverty using NTL since regularization in Ridge Regression guards against overfitting (Jean et al., 2016). Table 4 shows also that both XGBoost and Random Forest were relatively close in their accuracy to the Ridge Regression model, and did outperform the rest of the trained algorithms.

Figure 4 compares scatterplots of the predicted GDP values by each of the six ML algorithms, against actual test values, both in logarithm terms. The figure also plots 45° lines that represent the highest degree of goodness-of-fit of predictions, to compare the clustering of values along it.

Fig. 4

Scatterplots and $45^{\circ }$ lines of actual and predicted values of log(GDP) from ML models

Following the selection of Ridge algorithm for out-of-sample prediction, its hyperparameters were further tuned for higher accuracy, using the ‘GridSearch Cross Validation’ tool in scikit-learn library, through which all possible hundreds of combinations of a predetermined range of hyperparameters were tried, and the best combination was chosen based on the highest R². Accuracy of the best fitted model was almost identical to the original one, with an R² of 0.955. This best-fitted Ridge model which explains 95.5% of the variation in subnational GDP is then used for the out-of-sample-prediction.

Consistency of prediction is shown in Fig. 5 which plots the overall time-series trend of GDP (in logarithm term) for the 27 provinces in Egypt for the augmented period of 1992 to 2021. For each province the plot shows the predicted values from 1992 to 2012, in the plain area, with the actual values from 2013 to 2021, in the shaded area. We can see for most provinces that the trend of both predicted and actual timer-series is quite consistent, with seemingly more variation within the scarcely populated border provinces, the last five in the figure, which suffer from lower-quality official data gathering. In fact, A break in the trendline is observed for some provinces, not between 2012 and 2013, the transition from predicted to actual values, but around the year 2016 within the range of actual GDP data. This is mostly related to the implementation of a structural adjustment program in Egypt in 2016 with the International Monetary Fund (IMF), which led to an unprecedented shock of more than 50% depreciation of the Egyptian Pound almost overnight, and an inflation that exceeded 20% for two consecutive years. Hence, this break reflects real economic changes rather than measurement or prediction issues.

Fig. 5

Augmented predicted and actual GDP (in logarithm terms) in Egypt by province, 1992–2021

Discussion

This research found that nighttime lights on its own, particularly DMSP, could be a poor proxy for subnational GDP variations in Egypt, whether cross-sectional or temporal. This is likely due to the distribution of population and economic activity in Egypt with a sharp contrast of high-density regions around the Nile, and low-density regions elsewhere, and also due to the fact that several of these high-density regions are also predominantly rural and consequently omit less nighttime lights than equally dense urban regions.

Once these challenges were controlled for, using population density and crop area, this research managed to build a model that is reliable for measuring subnational GDP variations in Egypt, both temporally and cross-sectionally. This model, augmented with climate data, was then employed to estimate unavailable subnational GDP between 1992 and 2012 using machine learning, and the resulting values showed consistency with actual values from 2013 onwards.

An obvious limitation of this research nevertheless, is utilizing official GDP dataset and augmenting it. Egyptian economy is well-known for having a large informal economy, that is usually reflected in labour surveys (ILO, 2018), and is not captured entirely in the official GDP statistics. Hence, predictions in this research that benchmarked NTL and control variables against official GDP, will not be fully capturing the informal economy as well. Another issue on the other hand, is that official GDP data in Egypt might also be inaccurate as its regime is non-democratic, and there has been evidence that non-democratic regimes tend to overstate GDP, in recent literature that also relied on nighttime lights (Martinez, 2022).

Nevertheless, these limitations, that are common for developing economies, might be challenging to overcome. A common practice in predicting GDP in a region without relying on its official GDP data, whether because it is completely missing, or to address the limitations above, is to use official GDP data from neighbouring regions as a benchmark, since these regions are likely to have more similar GDP-NTL elasticities (Ghosh et al., 2009; McCord & Rodriguez-Heredia, 2022). However, for Egypt most neighbouring countries in the Middle East and North Africa (MENA) region suffer from the same limitations concerning their official GDP statistics; informal economy is significantly large across the MENA region (ILO, 2018), and it is also predominantly non-democratic, hence using official data from neighbouring countries is unlikely to solve this issue. Utilizing geographically further countries, with smaller informal economies and democratic regimes as benchmarks, could on the other hand produce GDP-NTL elasticities that are widely different from that of Egypt, for numerous reasons including cultural and economic, related for instance to differences in stages and patterns of development (McCord & Rodriguez-Heredia, 2022).

Conclusion

Constructing a long provincial GDP dataset is bound to benefit research in Egypt that uses subnational data, which despite having several valuable official datasets, has been hindered by the limited availability of one of the most important economic indicators on this administrative level. Admittedly, this dataset has limitations concerning the quality of official benchmark data, which could be an area for future research that aims to test how accurate official GDP in Egypt is. Future extensions of this research could also benefit from employing more diverse data from additional remote sensing and census sources, in order to enhance the spatial and sectoral granularity and accuracy of produced estimates. In the meantime, utilizing official GDP statistics and augmenting them using remotely-sensed imagery as implemented in this research, and further fine-tuning of predictions and methods, remain valuable to monitor and study local development and inequalities. This is a much-needed step to enable informed policy-making in order to better target local development and monitor long temporal trends and relations among socioeconomic indicators, whether in Egypt, or in other developing countries as well, that are in much need of such data.

Appendix

See Figs. 6, 7, 8, 9, 10.

Table 5 Random effects models of GDP-NTL association. Provincial level 2013–2021

Table 6 Results of the Hausman test, for the choice between fixed and random effects

Fig. 6

Population density in people per square kilometres, 2021

Fig. 7

Crop area percentage to total province area, 2021

Fig. 8

Predicted GDP (in logarithm term), 1992

Fig. 9

Actual GDP (in logarithm term), 2021

Fig. 10

Missing values of crop area dataset in number of observations and percentage, 1991–2021

Crop area data is missing for all provinces for 2005 since the annual report is unavailable for this year from CAPMAS. Furthermore, some provinces have missing values in a few of the reports. To impute missing observations, I used the available crop area dataset going back to 1991 instead of 1992, until 2021, for which missing crop area observations are 4.4% of the total; I also augmented the dataset with others on population, marriage rate, birth rate, and rural population rate to improve imputation, which was performed using the missRanger machine learning algorithm, that combines random forest imputation with predictive mean matching.

Nevertheless, six of the missing observations were imputed differently. Luxor province was created in 1997 from Qena province, and hence its data started in 1998. To impute the first six missing years for Luxor, I calculated the average share of crop area in Luxor to the sum of Luxor and Qena in the first five years since Luxor was established 1998–2002, and used it to calculate Luxor’s crop area from Qena’s between 1992 and 1997.

A further issue is that there were two additional provinces, Helwan and 6 October, that were created in 2008 and cancelled in 2011, thus having data only in 2009 and 2010. 6 October province was created from Giza, while Helwan was created mostly from Cairo’s urban areas and Giza’s land. In order to accurately distribute the crop area of Helwan in 2009 and 2010 to Cairo and Giza, the exact areas that were taken from each should be known, which is not the case. Hence, I attributed the crop area of Helwan in 2009 and 2010 to Giza, since the majority of the rural areas were taken from its territories. Nevertheless, for the same issue, but concerning population data, Helwan’s population in 2009 and 2010 was attributed to Cairo not to Giza, since Helwan’s urban dense areas were taken from Cairo’s, which means that the majority of its population were from Cairo province not from Giza, unlike rural land.