A Case Study on Advanced CPT Data Interpretation: From Stratification to Soil Parameters

Abstract

The cone penetration test (CPT) is considered as one of the most reliable in-situ tests and has found numerous applications in the geotechnical engineering field. Traditional CPT interpretation includes, but are not limited to the identification of the soil stratification and the determination of soil parameters. This paper presents a case study concerning a test site located in Salzburg, Austria, in which we focus on the interpretation of CPTs from different perspectives. The manuscript is divided into three main sections dealing with three different aspects of CPT interpretation, namely stratification, ground variability and soil parameters. The first strategy introduces a machine learning based stratification identification strategy to detect soil layer boundaries from CPT measurements. A comparison with reference solutions demonstrates relative merits of this approach to classical filter algorithms based on empirical CPT classifications. The second strategy introduces an intuitive approach to evaluate the ground variability. This is achieved by calculating the level of fluctuation on the basis of CPT measurements and could be used as a data-driven decision-making tool for the improved design of CPT investigation layouts. The third strategy is embedded in an ongoing research project that aims to determine constitutive model parameters from in-situ tests using a graph-based methodology. In the present work, the developed automated parameter determination framework is applied to evaluate the soil parameters of one selected soil layer identified from the CPT interpretations. Potential lines of research in the context of CPT interpretation are explored throughout this work and may serve as valuable reference in future research.

1 Introduction

Since its introduction to the geotechnical engineering field the cone penetration test (CPT) has been applied to numerous engineering tasks, such as the estimation of bearing capacity, design of shallow and deep foundations, walls and embankments, as well as the assessment of ground improvement measures and the site resistance to liquefaction (Umar et al. 2018; Kumar et al. 2021). Nevertheless, estimating soil parameters and site characterization may be regarded as the main purposes for carrying out CPTs (Lunne et al. 1997; Schnaid 2009; Niazi 2022). Essentially, these tasks are non-trivial and often carried out considering empirical interpretation approaches and simplified assumptions that may have limited applicability in engineering practice. Automating these tasks holds promise for enhancing efficiency and transparency.

In this context, this work introduces three different methodologies for the interpretation of CPT data, with particular focus on the soil stratification, fluctuation of CPT readings and soil parameter determination. The applicability of these approaches is demonstrated for a test site located in Salzburg, Austria, detailed in Sect. 2. The core of this paper is divided into three sections, where the different CPT data interpretation strategies are examined. In Sect. 3, machine learning (ML) models are used to automatically determine soil layer boundaries in three-dimensional space. Section 4 introduces an intuitive approach to account for the spatial uncertainty of CPT readings during the design and update, respectively, of CPT investigation layouts. Section 5 illustrates an ongoing research project focusing on the development of a system for automated soil parameter determination. In this section, this framework is used to compute parameters for a fine-grained soil layer identified by one of the performed CPTs. Section 6 closes with the conclusions of this work, discusses advantages and limitations of the developed CPT data interpretation strategies and points out future lines of research.

2 Test Site

The typical soil stratification of valleys in the Alpine region is dominated by postglacial sediments. The Salzburg basin was formed during several glacial periods. During the post-glacial period, the retreat of glaciers led to the formation of a substantial lake within the basin, mainly filled with fine-grained sediments. As a result, these young sediments are often characterized by a high water table and a normally to slightly underconsolidated state (Oberhollenzer et al. 2019, 2021a).

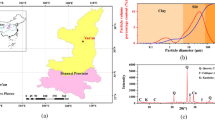
The test site is located in Salzburg, Austria. Over a rectangular area of approximately 90x50 m, several tests were performed. 6 piezocone penetration tests (CPTu), 4 cone penetration tests (CPT), 4 seismic dilatometer tests (SDMT) and 7 core drillings were executed, as shown in Fig. 1. The location of these tests is documented in Fig. 1. The CPTu and CPT tests were conducted using cones with identical cross-sectional areas (10 cm$^2$) and vertical measurement intervals of 1 cm. The SDMT measurements were taken every 20 cm, while the shear wave velocity was measured every 50 cm.

The soil profile can be roughly divided into three main layers (Fig. 2). Adopting the specifications documented in EN ISO 14688-1 (2019), they are classified as: (i) heterogeneous top layer consisting of sand-silt mixtures (from 0 to 4 m) and sandy gravel (from 4 to 7 m); (ii) sand-silt alterations; (iii) clayey silt.

Fig. 1

Test site located in Salzburg, Austria. Note: the position of different tests is measured from point (0,0) located in the lower left corner of the figure

Fig. 2

CPTu 5/12

3 Machine Learning Based Strata Identification

The generation of a site specific ground model that describes the type and extent of the soil layers as well as the subsoil properties is one of the fundamental processes in geotechnical engineering. In traditional approaches to this task, the results of available soil investigations, such as trenches and core drillings, are usually combined with soundings. Subsequently, individual soil layers and their properties are determined based on engineering experience. The minimum number of required core drillings and soundings is specified in respective standards (e.g., ÖNORM 2017). This process requires from the engineers involved not only broad expertise in the interpretation of subsurface investigations, but often also specific knowledge of regional characteristics. In many cases, the latter are only partially substantiated by empirical interpretation schemes, such as Soil Behaviour Type diagrams (e.g., Robertson 2009, 2010, 2016) or analytical correlations. Consequently, the interpretation of CPTs with the aim to generate ground models is frequently bound to the subjective rationale of the engineers involved.

In recent years, numerous ML techniques have been applied to geotechnical engineering problems, such as soil liquefaction, the estimation of ultimate capacity of driven piles and prediction of tunnel boring machine performance (Kumar et al. 2021; Samui 2012; Fattahi and Babanouri 2017); additional geotechnical application cases of ML models are presented in Gomes Correia et al. (2013) and Ebid (2021). To reduce subjective influences on the ground model and ensure a robust and comprehensible basis for the planning and execution of geotechnical structures, a data-driven strategy allowing for the automatic derivation of ground models (that is, solely based on investigation data) is pursued. The underlying database was published by the Institute of Soil Mechanics, Foundation Engineering and Computational Geotechnics at Graz University of Technology (TU Graz) in 2021 (Oberhollenzer et al. 2021b).

3.1 Theoretical Considerations

The main objective of the CPT data interpretation strategy presented in this section is to automatically determine soil layer boundaries in three-dimensional space. For this purpose, the CPT readings are first classified in accordance with the European standard (EN ISO 14688-1 2019) employing a tailor-made ML model that accounts for the dominant grain size (gravel, sand, silt, clay, organics). As a key result of the performed classification, the ground model is subdivided into three categories (fine-grained, coarse-grained, transitional). Empirical thresholds recovered from multiple tests are used to differentiate between the individual classes considering their probability distributions. For example, a data point that is classified as clay with 80% probability is assigned to the category “fine-grained”. Ambiguous points for which no clear distinction can be made (e.g., sand-silt-clay mixtures) are classified as “transitional”. It is pointed out that the reduction from originally five soil classes to three categories smears the CPT data interpretation to a certain degree, that is, similar soil types are grouped together leading to a reduction of fluctuations in the soil layer predictions. Research work concerning this aspect is part of ongoing research.

Since the transition between individual soil layers does not occur at distinct points, but over vertical intervals, it is necessary to define a process which automatically determines distinct points representing the soil layer boundaries. For this task, a Kernel Density Estimation (KDE) (Pedregosa et al. 2021) technique is deployed. Specifically, a KDE graph is created for each predicted soil class (transitional, coarse-grained and fine-grained). Soil layer boundaries are subsequently approximated at the intersections of the dominant graphs. The advantage of this method is, on the one hand, that soil layer boundaries can be described by explicit points, on the other hand, this approach suppresses tedious fluctuations and noise inherent to CPT readings.

In combination with the positional data of the CPT test locations, the classification results can be used to generate 3D ground models, in which the soil layers mark the boundaries of the predicted soil classes that occupy similar properties. In a subsequent step, the ground model may serve as valuable basis for numerical simulations (e.g., FE Model), including reliable soil constitutive parameters. However, the development of a linkage between the derived 3D ground model and finite element codes is part of ongoing research, hence beyond the scope of the present study.

3.2 Data

The database used in the present study was published by the Institute of Soil Mechanics, Foundation Engineering and Computational Geotechnics (Oberhollenzer et al. 2021b) and can be downloaded from the institute’s homepage following the subsequent link:

https://www.tugraz.at/institute/ibg/forschung/numerische-geotechnik/datenbank/

The dataset consists of 1339 CPTs sampled at different test sites in Austria and Germany. 490 tests were additionally supplemented with soil class labels according to EN ISO 14688 that were captured using core drillings. Based on these core drillings, Oberhollenzer et al. (2021b) defined seven classes ranging from coarse to fine-grained soils. In this context, first studies focusing on the soil classification with ML models showed promising results (Rauter and Tschuchnigg 2021). In the next subsection, a novel approach is proposed where the soil domain is classified with regard to the EN classes (EN ISO 14688-1 2019).

3.3 Classification Models

The classification scheme employs the “Oberhollenzer classes” first presented in Rauter and Tschuchnigg (2021). These classes are specified using a random forest classifier built on the well-established scikit-learn Python library (Pedregosa et al. 2011). Table 1 provides selected statistical metrics of the underlying database. The database comprises 1,025,284 samples with grain-size-based soil class labels (“Oberhollenzer classes”) and 2,514,262 samples classified by means of soil behaviour types (SBT, SBTn, Mod. SBTn); for details, the interested reader may refer to Rauter and Tschuchnigg (2021). As a key difference, modified target classes are considered; instead of the original seven "Oberhollenzer_classes", the present classification scheme is based on the dominant soil type (Gravel (Gr), Sand (Sa), Silt (Si), Clay (Cl) and Organic (Or)). The ML model was built using 100 estimators with a maximum depth of 18, which means that there are 100 decision trees in the Random Forest with a maximum of 18 splits. With regard to the classification performance, the ML model achieved a value of 0.81 for accuracy, recall, precision and f1-score, which is slightly higher than the results obtained with the original "Oberhollenzer_classes" (0.75).

Table 1 Selected metrics describing database detailed in Rauter and Tschuchnigg (2021)

3.4 Machine Learning Methodology

In analogy to CPT data interpretation strategies based on “Oberhollenzer classes” or Soil Behaviour Type Charts, noise may have a detrimental effect on the ML-based prediction of EN classes. In order to overcome this problem in the course of the soil layer boundary detection a novel classification approach has been developed. Subsequently, key aspects of the underlying workflow are presented.

As a first step, the CPT measurements are classified using the ML model. Based on the predicted class probabilities, the samples are divided into three categories, namely coarse-grained, fine-grained and transitional. It should be pointed out that the transformation of EN classes into these categories allows for the direct identification of soil layer boundaries. The class probabilities are used to categorize the classified CPT measuring points on the basis of empirical threshold values. In more detail, a sample is classified as “coarse-grained” if the proportional sum of gravel and sand exceeds 80%; inversely, the measuring points are regarded as "fine-grained" if (1) the proportion of clay and silt exceeds 65% and (2) the proportion of gravel and sand is less than 20%. Points for which no distinction can be made are categorized as "transitional". The threshold values were defined on the basis of parametric studies with the aim to ensure practicable classification results. However, it is explicitly stated that the optimization of these parameters is part of ongoing research.

The classification scheme described in the above paragraph serves as basis for the automatic determination of soil layer boundaries. The density distributions of the respective categories are calculated and displayed on a chart using the Kernel Density Estimation (KDE) model employed in the scikit-learn library (Pedregosa et al. 2021). In the present case, a "Gaussian" kernel with a bandwidth of 0.9 was found suitable for this task. The dominant distribution in each case describes the predominant category; a soil layer boundary is therefore recovered at the intersection point of two dominant distribution curves. This approach has the advantage that the noise in the data is considerably suppressed. The disadvantage, however, is that thin layers may be ignored; moreover, a very uneven distribution of categories may lead to inaccurate positions of the predicted soil layer boundaries. The methodological steps can be summarized as follows (Rauter and Tschuchnigg 2022):

• 1. For each EN class, the determinant soil class is evaluated. For example, for siSa (si = silt, Sa = sand), sand would be identified as dominant soil class as well as the corresponding target class with respect to the ML model.

• 2. A classification model based on a random forest algorithm is built and trained using the input features ($q_c$, $R_f$, depth) and the new targets (gravel, sand, silt, clay, organics).

• 3. In the scope of the predicted soil class labels, the class probability is of particular interest as it is used to distinguish between the fine-grained, coarse-grained or transitional soil labels. For example, if the sum of the probabilities for sand and gravel is greater than the sum of the probabilities for clay and silt (e.g., 80/20 ratio), the sample would be classified as coarse-grained, otherwise as fine-grained, and if no clear statement can be made, the sample would be classified as transitional soil.

• 4. The identified soil classes (coarse-grained, fine-grained and transitional) are displayed by means of a binary plot, where each CPT recording is associated with a unique soil class (coarse-grained, fine-grained and transitional). Based on this distribution, a kernel density estimation is performed for each class. It is found that a Gaussian kernel with a bandwidth = 0.9 (that is, a hyperparameter that controls the smoothness of the class probability curves) is reasonable to predict realistic soil layer boundaries.

• 5. The soil class density distributions computed with the KDEs are plotted in one graph, whereas curves with the highest magnitude are locally considered as prevailing soil type. Intersections of the distribution curves represent soil layer boundaries.

The interested reader may refer to Rauter and Tschuchnigg (2022) for more detailed information about the ML-based methodology, in combination with a simple benchmark test.

Figure 3 visualizes the presented workflow. The first plot shows the CPT measurement data ($R_f$ and $q_c$). The second plot indicates the classification according to Robertson’s normalized Soil Behaviour Type chart (Robertson 2009), which serves as reference basis for comparison with the EN-based classification. The third plot yields the probability distribution of the EN classes. The fourth plot shows the binary plot with distinct soil class labels in vertical direction (coarse-grained, fine-grained and transitional). The fifth plot depicts the probability density distribution of the three soil classes. In the present case, two intersections corresponding to two soil layer boundaries can be identified (black dash-dotted lines).

Fig. 3

Example for the presented workflow. Plot of the CPT data, SBT classification, class probabilities of EN-classification, classification in the three newly introduced categories and density distribution (f.l.t.r.)

In the next subsection, the presented workflow is applied to seven different CPTs to identify the soil layer boundaries of the test site described in Sect. 2. For validation purposes, a comparison with the engineering ground model generated in the course of the construction project is provided as well.

3.5 Results

The ground model under study follows the dimensions of the rectangular test site (approximately 90x50 m and a depth of 40 m). The arrangement of the CPTs in the ground model corresponds to the actual arrangement of the soundings in the field (see Fig. 1). The sections used for comparison were defined by engineers in the course of a construction project. In addition to the CPTs, core drillings and seismic dilatometer tests (SDMT) served as a basis for soil layer determination in the reference model, which will be referred to as reference solution or reference boundaries.

Figures 4b and 5b show the spatial distribution of the predicted soil layers from two different perspectives, in which the black vertical lines show the position of the individual CPTs, the red surfaces mark the top of the ground model, the green surfaces indicate the layer boundaries between coarse-grained and transitional soil, and the blue surfaces illustrate the transition from transitional to fine-grained soil. The surfaces were recovered employing the widely-applied surface triangulation interpolation technique; compare Felic (2023).

In the next step, the predicted soil layers are compared to the reference solution along two selected vertical cross-sections. For the purpose of comparison, the locations of these cross-sections are based on the sectioning originally established during the design of the original construction project. The first cross-section extends along CPTu 1/12, 2/12 and 3/12, and is illustrated in Fig. 4a. The coloured areas represent the individual layers according to the three categories, i.e., coarse-grained, fine-grained and transitional. The dashed lines mark the soil layer boundaries of the reference solution (as used for the design). As can be observed from the results, a very good agreement of the predicted soil layer boundaries and the reference solution is achieved. The maximum deviation from the reference solution is around 1 m.

Fig. 4

Cross-section A-A. Comparison between predicted soil layer boundaries and reference solution (dashed line)

The second cross-section used for comparison extends along CPTu 2/12, 5/12 and CPT 1/15. (Note: CPT 1/15 and CPTu x/12 were executed at different times and from non-identical levels). Results concerning cross-section B-B are shown in Fig. 5a. Similar to cross-section A-A, the soil layer boundary at the interface between “transitional” and “fine-grained” agrees reasonably well with the reference solution. However, the soil layer boundary at the interface between “coarse-grained” and “transitional” shows considerable deviations from the reference solution, especially close to CPT 1/15.

Fig. 5

Cross-section B-B. Comparison between predicted soil layer boundaries and reference solution (dashed line)

3.6 Applicability in Engineering Practice

The presented methodology for data-driven and automatic identification of soil layer boundaries based on CPT measurement data represents an attractive alternative to classical filter algorithms that are currently used for the determination of soil layers boundaries. Comparative analyses presented in this section indicate a good agreement of the predicted soil layer boundaries with the reference solutions. However, several open research aspects deserve attention. First, the performance of ML models used for geotechnical problems is significantly controlled by the quality of training samples. In addition, it relies on the amount of data and does not extrapolate well beyond the scope of provided training patterns. There is also a need to develop tailored machine learning methods that can account for uncertainty in the global data, variability between sites, and realistic sample sizes (Phoon and Zhang 2023). It is therefore crucial to utilize an appropriate database that shall be continuously maintained to ensure a satisfactory performance of the presented strategy in future applications. Furthermore, the hyperparameter set employed in the ML and KDE models have to be evaluated and updated as soon as the database is extended with new samples. This aspect is part of ongoing research at the Institute of Soil Mechanics, Foundation Engineering and Computational Geotechnics.

4 Dynamic Updating Strategy for CPT Layouts

The spatial interpretation of CPT measurements, for example, on the basis of ML techniques as discussed in Sect. 3, is sensitive to the CPT investigation layout (Jaksa et al. 2005b). Since the spatial interpretation is deterministic at measured locations, it is unknown at unmeasured locations and needs to be assessed based on predictions from the available limited number of measurements (Kulatilake and Um 2003). In many instances, the accuracy of predictions increases as the scope of investigations and available data increases. However, narrow-spaced CPT layouts parallel both high costs spent in carrying out the investigations and redundant information. Moreover, since every CPT leaves a zone of permanently disturbed soil where soil properties could be considerably different from the original in-situ state, there is need to account for a minimum spacing between adjacent CPT locations (Al-Sammarraie et al. 2022). Consequently, the selection of the optimal location and number of CPT tests represents a multivariate optimization problem that may be regarded as trade-off between stratigraphic uncertainty and site investigation costs; cf. Kahlström et al. (2021).

In common practice, the scope of the geotechnical site investigations rarely addresses the anticipated variability of the ground, but it is rather chosen to reduce initial costs. It is widely accepted that this cost-driven approach is likely to result in cost-overruns, for example, due to construction delays invoked by unforeseen conditions or uneconomic designs resulting from inadequate stratigraphic models (Mazzoccola et al. 1997; Goldsworthy et al. 2004; Jaksa et al. 2005b). The above discussion inevitably raises the following question (Xie et al. 2022): How to use a limited budget to estimate the ground variability with the lowermost uncertainty? This section aims to contribute towards answering this question by means of an intuitive strategy that allows for an increase of the ratio between gained understanding of the spatial subsoil variability and costs spent for carrying out CPTs. The applicability of this method is demonstrated based on both synthetic and real test cases.

4.1 Methodology

Unlike conventional methods that traditionally concern the ground variability solely based on the distance between CPTs, such as kriging-based (Krige 1951) or distance-from-nearest-information (Weil 2020) sources, the presented framework combines geotechnical and spatial sampling information to reduce the stratigraphic uncertainty in the field where CPT measurements are conducted. In more detail, the proposed strategy characterizes the 3D stratigraphic model based on the dimensionless scalar-valued field quantity termed level of fluctuation $\phi (\varvec{x})\in [0,1]$ (not be confused with the scale of fluctuation occupying the unit m (Vanmarcke 1977)). In this respect, $\phi (\varvec{x})$ embodies an unbiased estimator capable of characterizing the spatial variability of the CPT measurements.

As indicated by Fig. 6a, $\phi (\varvec{x})$-values close to 1 signify a high degree of spatial variability in related soil profiles (for example, due to the nugget effect (Jaksa et al. 2005a)), whereas $\phi (\varvec{x})$-values slightly above 0 indicate regions of nominally homogeneous soil properties. In simple terms, $\phi (\varvec{x})$ allows to identify spatial regions of low correlation between neighbouring CPT datasets, thereby taking into account the proximity of unsampled points to available CPT locations by means of a deterministic spatial weighting approach. To prevent the execution of CPTs that result in redundant information being obtained, the CPT layout should be sequentially densified in regions with high $\phi (\varvec{x})$-values. With reference to 6a, carrying out a new CPT at $\varvec{x_1}$ would yield valuable insight to the soil stratification, whereas additional information gained from placing an additional CPT at $\varvec{x_2}$ is expected to be relatively limited. From a practical perspective, this enables to gain maximum insight to the 3D stratigraphic model at minimum costs. Nevertheless, it must be noted that $\phi (\varvec{x})$ introduces a relative measure that helps to detect local regions of high spatial variability on a site-specific level only; as a consequence, quantifying generally applicable $\phi (\varvec{x})$-limits that can readily be adopted to any site investigation lies beyond its current capabilities.

Fig. 6

(a) Schematic description of scalar-valued field quantity termed level of fluctuation $\phi (\varvec{x})$ and (b) framework of proposed model

Figure 6b illustrates the process of generating the level of fluctuation which has been implemented in an object-oriented framework using the programming language Python. It is worth mentioning that the presented framework is theoretically applicable to any continuously sampled 1D quantity, such as the sleeve friction $f_s$, friction ratio $R_f$ or cone tip resistance $q_c$. For the sake of clarity, subsequent considerations are restricted to $q_c$-samplings since the latter is frequently used as critical parameter in the CPT-based pile design (Bustamante and Gianesselli 1982; Hamza and Bellis 2016; Abu-Farsakh and Shoaib 2024). The details of this procedure can be summarized as follows:

Step 1: Loading and pre-processing of CPT data

The one-dimensional $q_c$-profiles obtained from CPT field tests are simultaneously loaded and cleaned. The latter is realized by means of the 1D Gaussian filter technique, similar to Liu et al. (2021). This allows to minimize spurious contributions to the calculation of $\phi (\varvec{x})$ originating from noise and outliers.

Step 2: $L_2$-norm matrix

The inverse degrees of correlation between individual pairs of $q_c$-profiles, $q_c^{(CPTi)}(z)$ and $q_c^{(CPTj)}(z)$, are quantified through the scalar-valued entries $\varvec{A}^{(i,j)}$ of the symmetric L2-norm matrix $\varvec{A}\in \mathbb {R}^{n\times n}$:

$$\begin{aligned} \varvec{A}^{(i,j)}= & {} \Vert q_c^{(CPT_i)}(z)-q_c^{(CPT_j)}(z)\Vert _{L^2(z_{min},z_{max})} \nonumber \\= & {} \sqrt{\int _{z_{min}}^{z_{max}} [q_c^{(CPT_i)}(z)-q_c^{(CPT_j)}(z)]^2 dz} \end{aligned}$$

(1)

In Eq. 1, $i,j\in [1,n]$ denote CPT index numbers, such as considered in Fig. 7b, where n is the total number of CPTs considered, the vertical coordinates z, $z_{min}$ and $z_{max}$ are described in Fig. 6a. Equation 1 is numerically integrated using the trapezoidal Newton-Cotes rule with a step size equal to the CPT penetration interval, traditionally h = 0.01 m. According to this nomenclature, $L_2$-norm matrix entries $\varvec{A}^{(i,j)}$ describe the deviation of $q_c$-profiles obtained from the $i^{th}$ and $j^{th}$ CPT recording, respectively. As diagonal terms ($i=j$) concern the inverse correlation between identical $q_c$-profiles, the corresponding diagonal fill-ins reduce to zero (i.e., they are perfectly correlated; see Fig. 7a).

Fig. 7

(a) Numbering system of L2-norm matrix $\varvec{A}$ and (b) corresponding CPT layout

Step 3: Partition of stratigraphic model

As indicated in Fig. 7b, a regular tessellation pattern is used to generate a quadratic grid. The level of fluctuation $\phi$ is evaluated at cell-centered discrete points $\varvec{x_p} \in \mathbb {R}^2$. As suggested by previous researchers in view of similar problems (Jaksa et al. 2005b; Xie et al. 2022), it is recommended to select a minimum grid size of 0.5 x 0.5 m. This ensures a convenient resolution of the continuous field quantity by means of discrete $\phi (\varvec{x_p})$-values, as well as a high level of computational efficiency considering the large scope of many geotechnical fields.

Step 4: Level of fluctuation

The discrete evaluation of $\phi$ at all cell-centered grid points $\varvec{x_p}$ forms the core of the multi-step procedure and comprises several sub-steps; see Fig. 8a. The first sub-step concerns the evaluation of the distance vector $\varvec{d}\in \mathbb {R}^n$ which contains the horizontal length between $\varvec{x_p}$ and all CPT positions; see Fig. 8b. The calculated values are stored in the form of an attribute table at all $\varvec{x_p}$, similar to Fig. 7a. In the next sub-step, $\varvec{d}$ is used for a point-wise evaluation of the weight matrix $\varvec{W}(\varvec{x_p})\in \mathbb {R}^{n\times n}$, formally written as:

$$\begin{aligned} \varvec{W}(\varvec{x_p})^{(i,j)} = \frac{1/[d_i(\varvec{x_p}) \cdot d_j(\varvec{x_p})]^2}{ \sum \nolimits _{i=1}^{n}\sum \nolimits _{j=1}^{n} 1/[d_i(\varvec{x_p}) \cdot d_j(\varvec{x_p})]^2} \end{aligned}$$

(2)

In Eq. 2, the weight matrix entries $\varvec{W}(\varvec{x_p})^{(i,j)}$ account for the proximity of $\varvec{x_p}$ to the locations of considered CPT pairs, and satisfy the condition of an unbiased estimator $\sum \nolimits _{i=1}^{n}\sum \nolimits _{j=1}^{n}\varvec{W}^{(i,j)}=\varvec{1}$. As formulated in Eq. 3, the final sub-step links contributions originating from geotechnical data $\varvec{A}^{(i,j)}$ with spatial sample information $\varvec{W_p}^{(i,j)}$ in the form of the level of fluctuation $\phi (\varvec{x_p})$:

$$\begin{aligned} \phi (\varvec{x_p}) = \frac{\sum \nolimits _{i=1}^{n}\sum \nolimits _{j=1}^{n} \varvec{A}^{(i,j)} \cdot \varvec{W}^{(i,j)}}{\max \left( \sum \nolimits _{i=1}^{n}\sum \nolimits _{j=1}^{n}\varvec{A}^{(i,j)} \cdot \varvec{W}^{(i,j)}\right) } \end{aligned}$$

(3)

Fig. 8

(a) Sub-steps required to evaluate $\phi (\varvec{x_i})$ and (b) point-wise evaluation of distance vector $\varvec{d}$

The normalizing denominator component involves a loop over all discrete points and facilitates a systematic quantification of the sought field quantity in a range between 0 and 1.

Step 5: Visualization and interpretation

The level of flucation at discrete data points $\phi (\varvec{x_p})$ is effectively visualized using standard triangular irregular networks in combination with 2D filled contours. On a site-specific scale, this allows to anticipate regions with high spatial variability inside the 3D stratigraphic model, which can be mathematically described by $\phi (\varvec{x_p}) \rightarrow 1^-$. Inversely, $\phi (\varvec{x_p}) \rightarrow 0^+$ characterize areas of homogeneously distributed soil properties where further investigation is supposed to yield redundant information; cf. Fig. 6.

It should be pointed out that the CPT layout optimization procedure presented in this subsection can readily be extended to analyse the ground variability in the third dimension (vertical z-direction) as well; for this purpose, the level of fluctuation is alternatively computed at voxel-centered discrete points $\varvec{x_p} \in \mathbb {R}^3$. This allows, for example, to anticipate potential consequences of a CPT investigation depth reduction, or to cross-check whether FE subdomains experiencing high pile load concentrations are circumscribed by reliable site investigation data. From a computational point of view, this requires the consecutive application of the model framework described in Fig. 6b on multiple equally spaced layers with constant depth interval, instead of a single formation spanning the entire CPT investigation depth, see Fig. 6a. As a consequence, the integration limits ($z_{min}, z_{max}$) in Eq. 1 have to be replaced by corresponding pairs of interval boundaries, whereas the mean value representing the z-coordinate is additionally stored at all $\varvec{x_p}$. Moreover, since the normalization is now enforced on $\varvec{x_p}$ occupied by different layers, the normalizing denominator component in Eq. 3 has to be equipped with an additional loop over all layers, each of which incorporates a set of $\varvec{x_p}$ where the three-dimensional level of fluctuation $\phi ^{3D}(\varvec{x_p})\in [0,1]$ is explicitly computed. For the sake of clarity, corresponding figures explaining both strategies ($\phi$, $\phi ^{3D}$) are reported in the subsequent Sects. 4.2 and 4.3.

4.2 Synthetic Case Application

To demonstrate the capabilities of the procedure described in Sect. 4.1, a total of three synthetic CPT layouts have been examined; see Fig. 9a−c. The latter incorporate the measurements of four CPTs (Fig. 9d) which are located at the corners of a squared 100 m x 100 m site, and adopted from the test site described in Sect. 2. The CPT configurations comply in terms of spatial arrangements, but differ with regard to the distribution of $q_c$-profiles. It is evident from Fig. 9a that the homogeneous case (i.e., identical $q_c$-profiles at all four corner points) yields $\phi =0$ $\forall$ $\varvec{x_p}$, indicating a homogeneous distribution of $q_c$ across the test site; hence, carrying out additional CPTs is likely to result in redundant information being obtained. In this context, the zero-valued L2-norm matrix listed in Fig. 10a confirms the implementational fidelity of the code.

Fig. 9

Site investigation schemes and corresponding $\phi (\varvec{x_p})$-distributions obtained with (a) homogeneous, (b) cross-symmetric and (c) heterogeneous case; (d) CPT data considered

Fig. 10

L2-norm matrices obtained with (a) homogeneous and (b) heterogeneous CPT layout

Unlike the homogeneous case, the cross-symmetric as well as the heterogeneous CPT layout yield non-uniform estimates of the $q_c$-variability across the synthetic test sites. In both cases, the CPT corner points are circumscribed by $\phi (\varvec{x_p})$-regions close to 0, which could be expected due to the close proximity to at least one CPT position. However, considerable deviations between both synthetic cases are observed at greater distances to the corners: While the cross-symmetric layout results in a radial-symmetric pattern, where the peak values are aligned with the vertical and horizontal site axis, peak-valued $\phi (\varvec{x_p})$-areas evaluated for the heterogeneous test case are (as expected) non-symmetric. Obviously, they are shifted towards the site edge connecting CPT 4 and CPT 1, or more specifically, the site edge between the CPT pair occupying the maximum L2-norm matrix entry, see Fig. 10b. Again, this observation replicates the anticipated pattern, and confirms the reliability of the implemented workflow.

4.3 Real Case Application

In this subsection, the proposed strategy is employed to identify both the optimal CPT location and a reasonable investigation depth to supplement CPT sampling data described in Sect. 2. The corresponding $q_c$-recordings obtained from 10 CPTs are plotted in Fig. 11b. In accordance with Sect. 3.5, the adopted local coordinates comprise a vertical z-axis starting at the basement level. In this respect, the investigation area includes the subsoil formation extending between 0 m and -30 m of the test site, with at least two relevant soil layer boundaries; cf. Sect. 3.

Unlike the synthetic test cases investigated in Sect. 4.2, $\phi$-values are also calculated at spatial points $\varvec{x_p}$ that are located outside the convex hull-polygon; i.e., the connection line of outermost CPT samplings (Fig. 11a). At a first glance, the extrapolated $\phi$-regions appear consistent with their interpolated counterparts in close proximity to the convex hull-polygon. However, due to the lack of physical evidence in extrapolated regions the use of related results inherently implies a certain degree of randomness (Henke et al. 2020); hence, care should be taken when using extrapolated $\phi$-values for CPT layout optimization purposes. As expected, minimum $\phi$-values are obtained in close proximity to the position of recorded CPT samplings. This observation follows the same pattern as discussed in Sect. 4.2 and showcases the influence of the weight matrix $\varvec{W}$; see Sect. 4.1. On the contrary, Fig. 11a predicts the maximum level of fluctuation at coordinates (x = 20 m, y = 36 m); in turn, the latter represents the optimal position for the execution of subsequent CPT testing in order to acquire maximum insight to the natural variability of $q_c$, respectively, at minimum costs.

Fig. 11

(a) Site investigation layout and corresponding $\phi (\varvec{x_p})$-contour plot, as well as (b) $\phi ^{3D}(\varvec{x_p})$-contour plots presented in y–z and x–y plane, respectively; (c) CPT data considered

The above observations incorporate information on the horizontal variability of $q_c$, but only limited information on its vertical distribution. Nevertheless, soil properties are typically distributed with greater variation in the vertical than in the horizontal direction, primarily due to geological processes that form soils (Jaksa et al. 2005b); for example, this tendency can be triggered by changes in the porewater chemistry and groundwater levels, the influence of climatic effects or the diagenesis; cf. Graham and Shields (1985). Consequently, it may be important to account for the vertical ground variability when updating the CPT layout. The incorporation of this aspect also facilitates a data-driven determination of the CPT investigation depth on the basic premise of uncertainty reduction, rather than randomness.

As theoretically explained at Sect. 4.1, the methodical framework can readily be extended to allow for a three-dimensional analysis of the test site soil domain on the basis of $\phi ^{3D}(\varvec{x_p})$. From a geometrical point of view, the only modification in the presented workflow for calculating the level of fluctuation concerns the partition of the stratigraphic model into cubic voxels, instead of two-dimensional quadratic grid elements; see step 3 in Sect. 4.1. Consequently, $\phi ^{3D}$-values are calculated at voxel-centered discrete points $\varvec{x_p} \in \mathbb {R}^3$ which are defined in all three spatial dimensions. As depicted in Fig. 11a, the abundant data is effectively visualized by means of perpendicular cross-sections presented in both the x–z and y–z-plane, respectively. Obviously, peak $\phi ^{3D}$-values indicating a high vertical variability occur in the near-surface whereas soil regions at vertical distances greater than 6 m below the basement are dominated by fairly homogeneous geotechnical conditions. From a practical point of view, subsequent site investigation effort should therefore focus on the near-surface subsoil instead of deep soil locations. In some instances, this could encourage the application of low-cost CPT-alternatives, which could be a conceivable alternative for site investigation in near-surface regions, cf. Palla et al. (2008).

4.4 Generalisation and Employment in Practice

It is widely acknowledged that, in building projects and civil engineering, the main source of financial and technical risk lies in the ground (Jaksa et al. 2005b; Rana et al. 2023). In particular during the early design phase, the ability to effectively communicate geotechnical information and risk associated with the 3D stratigraphic model to all project stakeholders including authorities, architects, clients, contractors and engineers is a central challenge for geotechnical engineers (Kahlström et al. 2021). In this context, the proposed strategy may help geotechnical engineers to meet this demand. In principal, the authors have identified three use cases where the presented strategy may extend the toolbox of geotechnical engineers: (1) objectification and prioritisation of CPT layout design, (2) effective communication of geo-spatial uncertainty to project stakeholders through the power of visualization and (3) quality assurance of CPT measurements (note that peak $\phi$/$\phi ^{3D}$-values may also be triggered by measurement errors).

In view of the current trend to integrate 3D stratigraphic models to the Building Information Modeling (BIM) process (Henke and Lerch 2020; Giangiulio et al. 2022), $\phi$/$\phi ^{3D}$-values may be stored as soil volume attribute. In this way, they can be readily used as relative measure that link the level of uncertainty with geotechnical parameters listed in respective soil volume attribute tables. Moreover, $\phi$/$\phi ^{3D}$-attributes may be dynamically updated as new CPT samplings are performed using the framework documented in Fig. 6b.

For the sake of clarity, the demonstration cases presented above assess the geotechnical contribution to $\phi$/$\phi ^{3D}$-quantities solely based on $q_c$-recordings (single-factor approach). Depending on the site investigation objectives and the soil properties, it may be beneficial to replace Eq. 1 by a weighted-averaging scheme, in which the $L_2-$norm matrix entries $\varvec{A}^{(i,j)}$ subsume contributions stemming from the cone tip resistance $\varvec{A}_{q_c}^{(i,j)}$, the sleeve friction $\varvec{A}_{f_s}^{(i,j)}$ and the friction ratio $\varvec{A}_{R_f}^{(i,j)}$. A validation of the multi-factor approach, however, is beyond the scope of this paper, and subject of ongoing research.

5 An Automated System for Determining Constitutive Model Parameters

Numerical analyses have several advantages compared to traditional methods. One of the main advantages is the level of detail that could be obtained in several geotechnical engineering problems, such as soil-structure interaction (Brinkgreve 2019). The success of numerical analysis is influenced by many factors. One of the key factors is determining the constitutive model parameters properly. It is usually the case that these parameters are determined based on limited soil data. Most often, these parameters need to be assessed based on experimental tests (e.g., triaxial and oedometer tests) that are not always available in projects (especially not in an early design phase).

In-situ tests offer an alternative method to determine soil parameters. The cone penetration test (CPT) is one of the most popular in-situ tests as it is quick and can be used in soil profiling and determining soil parameters (Lunne et al. 1997; Ricceri et al. 2002; Anagnostopoulos et al. 2003; Schnaid 2009). Furthermore, compared to laboratory tests, CPT has other advantages, including lower cost and minimal disturbance of the soil. Contrary to laboratory tests, it is not possible to determine soil parameters directly from the results of in-situ tests. However, soil parameters can be obtained from in-situ test results based on empirical relationships. It is often the case that several relationships exist to determine the same parameter, presumably leading to a (wide) range of values for the parameters of interest. This variation is attributed to the applicability of these relationships, as they are not suitable for all situations (e.g., specific soil types). In literature, there are some guidelines focusing on the interpretation of soil parameters from CPTs (e.g., Kulhawy and Mayne 1990; Lunne et al. 1997; Mayne 2014; Robertson 2015).

An ongoing research project aims to create an automated parameter determination (APD) framework to determine constitutive model parameters from in-situ tests. This system is based on a graph-based approach that relies on graph theory principals, as will be detailed in Sect. 5.1. The main motivation of this project is to create a transparent and an adaptable parameter determination framework. Transparency is ensured by describing how available information is used to reach a certain solution, while adaptability is achieved by allowing the users of the system to incorporate their knowledge and experience into the system. Van Berkom et al. (2022) illustrated the graph-based approach and presented an example of the determination of parameters for coarse-grained soils based on CPT data. Marzouk et al. (2022) extended the framework by including parameters and empirical relationships for fine-grained soils. The extension of the system to include other in-situ tests is in progress, where the dilatometer (DMT) has been added to the framework.

This section presents a case study where the APD system is used to determine soil parameters based on CPT data that were obtained from the test site described in Sect. 2. Section 5.1 briefly describes the APD framework, while Sect. 5.2 presents selected empirical relationships used to determine soil parameters. In Sect. 5.3, the output of the APD for a CPT is illustrated. The conclusions of the study are summarized in Sect. 5.4.

5.1 Automated Parameter Determination (APD) Framework

5.1.1 Framework

Five connected modules form the framework. A schematic representation of the modules is shown in Fig. 12. The first module (GEF reader) imports CPT raw data in Geotechnical Exchange Format (GEF). In the next step, the CPT measurements (cone resistance $q_c$, sleeve friction $f_s$ and porewater pressure readings $u_2$) are transferred to the second module (CPT layer interpretation). In this module, the soil behaviour type (SBT) is determined based on Robertson’s modified non-normalized SBT chart (Robertson 2010). Nevertheless, other SBT charts (such as Robertson’s normalized chart (Robertson 2009) and Robertson’s updated normalized chart (Robertson 2016)) could be used as well. Afterwards, the CPT profile is stratified into several layers sharing the same SBT. At the moment APD does not use any ML based strata identification (as discussed in Sect. 3). However, the possibility of using ML for the soil layer detection (with SBT charts) will be added to the framework. For each layer, the CPT measurements ($q_c$, $f_s$ and $u_2$) are averaged in a layer-wise manner. The third module (Layer state) uses the averaged CPT measurements to determine the state of the layers (overconsolidation ratio OCR and coefficient of earth pressure $K_0$). The fourth module (Graph-based approach) uses the output of modules 2 and 3 to connect parameters to equations (correlations) and calculates the parameters. The final module (Constitutive model parameters) converts parameters calculated in module 4 to constitutive model parameters. The system is built in the programming language Python.

Fig. 12

Schematic representation of the parameter determination modules

The layering process and determination of the "Layer state" are not considered (modules 2 and 3) in this contribution. It has to be pointed out that the layering used in this case study is based on the stratification obtained from the ML models presented in Sect. 3, thus, the implemented layering algorithms have not been used. Furthermore, this section only illustrates the determination of soil parameters (output of module 4) without the transition to constitutive model parameters (module 5).

5.1.2 SBT Interpretation

In the present study, the CPT profile is classified according to Robertson’s modified non-normalized SBT chart (Robertson 2010). The chart is based on the dimensionless cone resistance ($q_c/p_a$, where $p_a$ is the atmospheric pressure) and friction ratio ($R_f$ in percent, $R_f=f_s/q_c \ 100 \%$). The chart is divided into nine different zones corresponding to different soil behaviour types (Table 2). Therefore, fine and coarse-grained soils are distinguished by this module. Nevertheless, the classification is not limited to Robertson’s modified non-normalized SBT chart, as other charts are already implemented in the system (e.g., Robertson’s normalized SBT chart (Robertson 2009) and Robertson’s updated normalized SBT chart (Robertson 2016)).

Table 2 SBT zones Robertson (2010)

5.1.3 Graph-Based Approach

Graph theory is a branch of discrete mathematics where relationships between different objects within a network are studied. The network is described by two different objects, namely nodes and edges. Nodes describe the entities of the graph, while edges illustrate the relationship between two nodes. One of the main advantages of graphs is their ability to represent complex systems (e.g., transportation network (Likaj et al. 2013) and social media (Chakraborty et al. 2018)). The APD framework uses a weighted directed graph, where the direction between two nodes (sharing a relationship) in the graph is defined (Van Berkom et al. 2022). In addition, weights could be assigned to the edges between the nodes. One-way roads are an example of weighted directed graphs, where roads could have an assigned weight representing distance or travel time.

Van Berkom et al. (2022) illustrated the concept of the graph-based approach employed in APD in detail. Figure 13 summarizes the graph-based approach, where source parameters (CPT raw data) are linked via intermediate parameters to destination parameters (soil or constitutive model parameters). By using a given set of correlations, the system creates all paths (chains of correlations) that link source parameters to the destinations parameters, and calculates the values of the destination parameters from the input values of the source parameters (CPT raw data). Within the framework of APD, the terms ‘correlation’, ‘formula’, ‘equation’, ‘rule of thumb’ are replaced by the term ‘method’. Parameters could be determined based on several ways (e.g., tables and charts), therefore this general term is used (Van Berkom et al. 2022).

Searching for a path in a network from one node to another is a well-known problem, which is widely used in several applications (Shu-Xi 2012). Several graph algorithms exist which allow for solving the shortest path problem (finding the shortest path between two nodes in a graph). Nevertheless, graph algorithms do not apply to branching paths. Within the parameter determination framework, a path to the destination node can have more than one source node as the parameters in the path can be obtained from multivariable formulas, which depend on multiple input parameters (branching paths occur in the framework). Consequently, the existing graph algorithms cannot be applied to the parameter determination framework (Van Berkom et al. 2022).

To deal with branching paths, two types of nodes are implemented, namely parameters (green nodes in Fig. 14) and methods (blue nodes in Fig. 14). Most often method nodes are empirical correlations that depend on more than one parameter. As a result, method nodes have several incoming edges which indicate all the required parameters for this method (Van Berkom et al. 2022). Methods and parameters that share a relationship must be linked. For example, a method to compute the coefficient of earth pressure according to Jaky (1944) considers the well-known relationship $K_0 = 1 - \sin (\varphi ')$, where $K_0$ is the coefficient of earth pressure at rest and $\varphi '$ denotes the effective internal friction angle of the soil. The system must determine the input and output for this method ($\varphi '$ and $K_0$ respectively) and generate links connecting these parameters.

Fig. 13

Graph-based approach implemented in APD

5.1.4 Generating the Graph

As discussed in Sect. 5.1.3, the relationships between parameters and methods are defined based on the output and input(s) of different methods. Parameters and methods are considered as external inputs to the system. Two input files are required, namely, "methods" and "parameters". Due to the adaptability of the framework, users may extend the standard database of methods and parameters provided by the current version of the system. The system generates links between the methods and parameters and calculates the intermediate and destination parameters. The two different input files used to generate the graph are provided in comma-separate values (CSV) format (corresponding to parameters and methods).

Each CSV file is characterised by special properties. With regard to the methods CSV file, it is required to define the several properties, namely method_to, formula, parameters_in, parameters_out, validity and reference. The latter should be provided by the user in the methods CSV file. Following the above example concerning the earth pressure at rest coefficient, method_to presents the name of the method; in this case it could be method_to_K0. In the formula’s field, the corresponding equation should be provided, i.e., $1 - \sin (\phi ')$. Parameters_in implicitly defines the input(s) for this method, i.e., $\phi '$. Following the same definition, parameters_out states the output of the method, i.e., $K_0$. The applicability of different methods is defined in the validity field. As some methods are suitable for all types of soils, other methods are only valid for coarse-grained soils, while others are only applicable for fine-grained soils.

As presented in Table 2, the SBT is based on Robertson’s modified non normalized SBT chart (Robertson 2010). Consequently, the validity is (mainly) defined in terms of SBT. If the method is only applicable to silt, the validity would be SBT(4). Concerning the method of coefficient of earth pressure at rest, the validity would be SBT(1234567). Reference is an optional field, where the user could mention the author of the method (e.g., Jaky_1944).

Moving to the parameters CSV file, the following properties need to be defined: symbol, value, unit, constraints and description. Any parameter that has been defined in the methods CSV file (in the fields of formula, parameters_in and parameters_out) must be defined in the parameters CSV file. In the symbol field, the notation of the parameter (that has been used in the methods CSV file) is stated (e.g., u for porewater pressure). In the value field, the user could specify a value for a parameter (e.g., unit weight of water). It could also be used by the user to provide "known" values as direct "input" for some parameters. Unit is an optional field, where the user could provide the unit for all parameters. In order to avoid problems originating from unit conversion (e.g., using $q_c$ in MPa in a method that requires $q_c$ in kPa), it is recommended to define the units of all parameters. The Constraints field is used to apply lower and upper bounds to the parameters. If the calculated value is lower than the lower bound or higher than the upper bound, it would be discarded. This allows to neglect unrealistically high or low values for parameters. Similar to the reference field in the methods CSV file, the description field is an optional argument, where the user could describe the parameter (e.g., OCR is the overconsolidation ratio).

By defining these two CSV files (methods & parameters), the system imports the two files and creates links between related methods and parameters (parameters_in and parameters_out). The output of module 4 (Graph-based approach) is a graph presenting all the links between all the defined parameters and methods as well as the calculated values for different parameters (e.g., see Fig. 14).

5.2 CPT Interpretation

A standard validated database for methods and parameters has been compiled and is continuously updated and improved. The current version of the database consists of more than 100 methods and parameters. Nevertheless, users are responsible for validating the outcome of the system, even if they used the provided standard database. They still need to apply their experience and knowledge to the output of the system. However, with limited geotechnical knowledge, the system should provide reasonable values for different parameters. However, using all of the methods in the database could lead to a scatter in the obtained values, which will make the representation of the results challenging. To circumvent this problem in the present study, graphs are only created based on a selected number of methods and parameters that are presented as follows:

5.2.1 Initial Parameters

An initial estimate of the total ($\sigma _v$) and effective ($\sigma {_v}^{\prime }$) stress is required to compute some of the CPT parameters (e.g., normalized cone resistance). Consequently, the unit weight needs to be assessed at the beginning of the analysis. In the considered case study the initial unit weight is computed according to Robertson and Cabal (2010):

$$\begin{aligned} \gamma _t = \gamma _w[0.27[\log {R_f}]+0.36[\log {(q_t/p_a)}]+1.236] \end{aligned}$$

(4)

where $\gamma _w$ is the unit weight of water and $q_t$ is the corrected cone resistance, i.e., defined as $q_t=q_c+(1-a)\times u_2$, where a is the cone tip net area ratio.

The porewater pressure ($u_0$) is calculated based on the ground water level (GWL). The GWL is provided in the CPT GEF file, otherwise it could be specified by the user. Based on the previous information, the total and effective stress are computed. As a key result, the following “CPT parameters” are computed:

• Normalized cone resistance

  $$\begin{aligned} Q_t=\frac{q_t-\sigma _v}{\sigma _{v}^{\prime }} \end{aligned}$$

  (5)

• Normalized porewater pressure

  $$\begin{aligned} B_q=\frac{(u_2-u_0)}{(q_t-\sigma _v)} \end{aligned}$$

  (6)

• Normalized cone parameter with variable stress exponent n that varies with soil behaviour type index ($I_{cn}$) and is calculated in an iterative manner:

  $$\begin{aligned} Q_{tn}= & {} \frac{q_t-\sigma _v}{p_a}\Big /\Big(\frac{p_a}{\sigma _{v}^{\prime }}\Big)^n \end{aligned}$$

  (7)
  $$\begin{aligned} n= & {} 0.381(I_c)+0.05 \Big (\frac{\sigma _{v}^{\prime }}{p_a}\Big)-0.15 \le 1.0 \end{aligned}$$

  (8)
  $$\begin{aligned} I_{cn}= & {} \sqrt{(3.47-\log Q_{tn})^2+(\log F_r+1.22)^2} \end{aligned}$$

  (9)

  where $F_r$ is the normalized friction ratio, defined as $F_r = f_s / (q_t - \sigma _v) \ 100\%$.

The parameters circumscribed by Eqs. (4)–(9) are internally calculated in module 2 (cf. Fig. 12) before invoking module 4 (cf. Fig. 12). In other words, these parameters could be treated as source parameters (similar to the CPT raw data) in the generated graphs. This also highlights the importance of selecting an adequate method for assessing the unit weight as it influences the total and effective stress, which in turn influences the calculated “CPT parameters”.

In the following Sects. 5.2.1, 5.2.2, 5.2.3 and 5.2.4, the selected methods and parameters are presented. These methods and parameters serve as basis for generating the graphs in module 4, as will be shown in Sect. 5.3. As mentioned above, in total more than 100 methods are implemented in the APD framework.

5.2.2 Stress History

Stress history is often represented by the overconsolidation ratio defined as $OCR=\frac{\sigma _p^{\prime }}{\sigma _v^{\prime }}$, where $\sigma _{p}^{\prime }$ is the vertical preconsolidation stress. Numerous methods are available in the database to compute OCR. In this study, two methods were selected to determine OCR as follows:

• 1.
  $$\begin{aligned} OCR = \frac{\sigma _{p}^{\prime }}{\sigma _{v}^{\prime }} = \frac{0.33(q_t-\sigma _v)^{m^{\prime }}}{\sigma _{v}^{\prime }} \end{aligned}$$

  (10)

  by Mayne et al. (2009), where $m^{\prime }$ is the yield stress exponent that increases with fines content and decreases with mean grain size. This correlation is valid for different types of soils. Mayne (2017) proposed determining $m^{\prime }$ from CPT material index $I_{cn}$ (Eq. 9) as follows:

  $$\begin{aligned} m^{\prime } =1-\frac{0.28}{1+(\frac{I_{cn}}{2.65})^{25}} \end{aligned}$$

  (11)
• 2.
  $$\begin{aligned} OCR= 0.33 \times Q_{tn} \end{aligned}$$

  (12)

  by Kulhawy and Mayne (1990) and Robertson (2009), where $Q_{tn}$ is defined in Eq. 7. This correlation is only valid for fine-grained soils.

5.2.3 Strength Parameters

Similar to OCR, several methods are provided in the database to derive the effective friction angle ($\varphi ^{\prime }$). In this study, the following method is selected:

$$\begin{aligned} \varphi ^{\prime }=29.5^\circ B_{q}^{0.121} [0.256+0.336B_q+\log (Q_t)] \end{aligned}$$

(13)

by Mayne et al. (2009), where $Q_t$ and $B_q$ are defined in Eqs. 5 and 6, respectively. The valid range for this correlation is $0.1\le B_q \le 1.0$ and $20^\circ \le \phi ^{\prime } \le 45^\circ$ and it is only applicable for fine-grained soils.

5.2.4 Shear Wave Velocity

The small-strain shear modulus ($G_0$) is determined from in-situ $V_s$ measurements. In case the shear wave velocity measurements are not available, correlations relating the shear wave velocity to CPT results could be used to estimate $V_s$. The methods database consists of 15 methods to assess $V_s$, however, in this contribution the following four methods are selected:

• 1.
  $$\begin{aligned} V_s = 3.18q_c^{0.549}f_s^{0.025} \end{aligned}$$

  (14)

  by Hegazy and Mayne (1995); this correlation is only valid for clays.

• 2.
  $$\begin{aligned} V_s = (10.1 \log {q_c}-11.4)^{1.67}(f_s/q_c \times 100)^{0.3} \end{aligned}$$

  (15)

  by Hegazy and Mayne (1995); this correlation is valid for different types of soils.

• 3.
  $$\begin{aligned} V_s = 1.75(q_c)^{0.627} \end{aligned}$$

  (16)

  by Mayne and Rix (1995); this correlation is only valid for clays.

• 4.
  $$\begin{aligned} V_s = [ \alpha _{vs}(q_t-\sigma _v)/p_a]^{0.5} \end{aligned}$$

  (17)

  by Robertson (2015), where $\alpha _{vs} = 10^{(0.55I_{cn}+1.68)}$; this correlation is valid for different types of soils.

5.2.5 Stiffness Parameters

The small strain shear modulus ($G_0$) is deduced from the shear wave velocity as follows:

$$\begin{aligned} G_0 = \rho V_s^2 \end{aligned}$$

(18)

where $\rho$ is the mass density of the soil, defined as $\rho = \gamma _t / g$, in which g is the gravitational acceleration. Similar to the other parameters, a considerable number of additional methods for computing $G_0$ can be selected from the database. Two of these methods are herein considered:

• 1.
  
  $$\begin{aligned} G_0 = 2.78q_c^{1.335} \end{aligned}$$

  (19)

  by Mayne and Rix (1993); this correlation is only valid for clays.

• 2.
  
  $$\begin{aligned} G_0 = 50p_a(q_t-\sigma _v)^{m^*} \end{aligned}$$

  (20)

  by Mayne (2007), where $m^* =$ 0.6 for clean quartz sands, 0.8 for silts and 1.0 for intact clays of low to medium sensitivity.

The 1-D constrained tangent modulus M is generally used to compute settlements. The following correlation is used to determine the constrained modulus:

$$\begin{aligned} M=\alpha _M(q_t-\sigma _v) \end{aligned}$$

(21)

Robertson (2009) suggested an approach based on $I_{cn}$ (Eq. 9) to determine $\alpha _M$:

• If $I_{cn} > 2.2$:

  $\alpha _M = Q_{tn}$ (if $Q_{tn} < 14$)

  $\alpha _M = 14$ (if $Q_{tn} > 14$)

• Otherwise if $I_{cn} < 2.2$:

  $\alpha _M= 0.03[10^{(0.55I_{cn}+1.68)}]$

It has to be pointed out that compared to the methods and parameters presented in Sects. 5.2.1, 5.2.2, 5.2.3 and 5.2.4, the current version of the database consists of numerous additional methods and parameters not considered in this work. The main reason for selecting a limited number of methods and parameters in this contribution is motivated by a reduction of complexity and increase of clarity; generating the graphs with the current version of the database would lead to overloaded graphs involving an unpractical number nodes and edges that would, in turn, make the task of tracing different paths cumbersome to the readers. Inversely, generating the graphs with a limited number of methods and parameters leads to comprehensible graphs (e.g, Fig. 14) that allow to trace back different paths. This is demonstrated by Fig. 15, which presents the output of module 4 in case the number of methods and parameters is increased (e.g., 21 different values were computed for $G_0$ located at the lower left corner of the figure). As the main purpose of Sect. 5 is to present the graph-based approach implemented in APD in an illustrative way, simpler graphs were generated by using a limited number of methods and parameters.

5.3 Determination of Soil Parameters

This subsection demonstrates the output of the APD. The two CSV files (imported by the system as inputs) include the parameters and methods presented in Sects. 5.2.1, 5.2.2, 5.2.3 and 5.2.4.

The CPT data processed in this study is derived from the test site described in Sects. 2, namely CPTu 5/12 (Fig. 2). The CPTu soundings collected for this study revealed issues with the $u_2$ measurements, particularly in Layer 1 (coarse-grained material) and Layer 2 (sand-silt alteration). However, $u_2$ measurements were only used in Layer 3 (fine-grained material) to determine the friction angle (Eq. 13). Consequently, these issues did not affect the results of the other sections.

The ML-based stratification of this CPT is presented in Sect. 3.5 and Fig. 5a. The first steps within APD were as follows: The system imported the CPT GEF file, whereas the layers were provided manually according to Table 3. For each layer, a SBT (according to Table 2) was assigned. Focusing on the 3$^{rd}$ layer, SBT(3) (clay) was selected for this layer as estimated by the ML-based stratification. Knowing the boundaries of the layer, the CPT raw data ($q_c$, $f_s$ and $u_2$) as well as the parameters calculated from Eqs. (4)–(9) were averaged. The average values of these parameters were used as input parameters for the selected methods presented in Sects. 5.2.1, 5.2.2, 5.2.3 and 5.2.4. For each layer, the first and last measurements are filtered out. This procedure reduces the effects of the neighbouring layers. For layer 3 the averaged CPT data yield $q_c = 1392.8 \ kPa$, $f_s = 29.4 \ kPa$ and $u_2 = 1008.7 \ kPa$ at 30.95 m depth. The groundwater level (GWL) is located at 3 m below the ground level. The cone tip net area ratio is provided in the CPT GEF file as 0.85 ($a = 0.85$). The unit weight of water is defined as $10 \ kN/m^3$. The atmospheric pressure ($p_a$) corresponds to $100 \ kPa$. Figure 14 shows the generated graph for layer 3.

Table 3 Machine learning based stratification of CPT 5/12

Two types of nodes are presented in the graph. Parameters are represented by green nodes, while blue nodes correspond to methods. The links between parameters and methods within the system are illustrated by the arrows. These arrows have a defined direction, either going from a parameter to a method or from a method to a parameter. The graph displays the selected parameters and methods, while Table 4 describes the parameters. Table 4 also illustrates the values of the source parameters. These source parameters are either averaged CPT measurements or averaged initial parameters that were computed before generating the graph (e.g., total and effective stress). In this case study, Eq. 4 was used to calculate the unit weight. As the system is created in an adaptable way, the user could select other correlations for computing the initial unit weight. The output of each method is presented on the link connecting this method to the intermediate / destination parameter (e.g., output of method_to_OCR_2 is 1.11). The value of intermediate / destination parameter is shown next to the node (e.g., 2 values were computed for OCR, 1.09 and 1.11).

Fig. 14

Output of module 4 for selected methods

Table 4 Parameters represented in graph (Fig. 14)

It should be pointed out that it was not possible to compare the obtained values (for different parameters) to reference values, as no laboratory tests could be adopted from the test site under study. Nonetheless, the main aim of this case study is to present proof of concept of the parameter determination framework. Starting with the OCR located at the lower left corner in Fig. 14, the selected two methods used to calculate OCR resulted in values of 1.09 and 1.11, respectively. Moving to the friction angle located at the upper right corner in Fig. 14, the selected method resulted in a friction angle of 29.68$^\circ$.

The constrained modulus was obtained from the selected method defined by Eq. 21, which resulted in a value of 3263.63 kPa. As a side note, the prediction of the constrained modulus could be improved by using other in-situ tests; to this end, the DMT (Marchetti 1980) is currently incorporated in the APD framework. Generally, the incorporation of a higher number of in-situ tests to derive the parameters (and compare the outcome of the different in-situ tests) leads to an increase of confidence in the derived parameters.

The shear wave velocity (located at the right side in Fig. 14) is computed by four selected methods. These methods resulted in values of 191.78, 187.26, 163.78 and 184.14 m/s, respectively. The shear modulus at small strains is located at the lower right side in Fig. 14. Selected methods_to_G0_2 and 3 resulted in 48,555 and 45,184 kPa, respectively. As four different values of $V_s$ were computed, method_to_G0_1 results in four different values, 64962.54, 61932.96, 47377.17 and 59885.99 kPa. Ongoing validation studies (not shown here) indicated that the reliability of methods used to determine $V_s$ is highly site dependent. Moreover, as could be expected, using more accurate values of $V_s$ will result in a more accurate prediction of $G_0$, which underlines the necessity of creating a shear wave velocity module that is able to import in-situ $V_s$ measurements. This planned module will be incorporated in module 1 (Fig. 12), where in-situ $V_s$ will be imported and used in further analyses.

Fig. 15

Output of module 4 in case more methods and parameters are used

5.4 Final Comments Related to APD

Figure 14 presents the generated graph for a clay layer using a limited number of methods. In case more methods are used (e.g., all of the methods in the standard database of methods), this will lead to a considerable scatter in some of the derived parameters; cf. Fig. 15. Evaluating the scatter and selecting a suitable approach for choosing a specific value from the range of the calculated values is part of ongoing research; the same applies to the process of validating and updating the correlations database. This is done by comparing the output of different correlations to available laboratory tests; cf. Marzouk et al. (2023a).

The uncertainties associated with using CPT data for parameter determination are not currently taken into account. In the current version of APD, the system can only process one CPT at a time. The consideration of several CPTs at the same time (e.g., executed close to each other or from the same project) would help to investigate whether the uncertainties due to the execution of the CPTs influence the obtained value(s) for the parameters or not.

In this study, the transition from soil parameters to constitutive model parameters was not considered in detail. Several correlations between soil parameters and some constitutive models, such as the Hardening Soil model with small-strain stiffness (HSsmall) (Benz 2007), are already available in the methods database. The transition from the CPT measurements to constitutive model parameters is considered as one of the key aspects of the research project.

Currently, APD is able to interpret CPT and DMT (Marzouk et al. 2023b) data; an extension of the framework (by including additional in-situ tests and measured in-situ shear wave velocity), validation of the output (by comparing the output of APD to interpreted values from laboratory tests) and update and improvement of the database is part of ongoing research.

6 Conclusions

This work examines three different CPT data interpretation strategies, with particular focus on the identification of soil layer boundaries, spatial variability of CPT readings and soil parameter determination. Theoretical aspects and relevant use cases of the underlying workflows, as well as relative merits and limitations compared to related approaches documented in the literature are discussed throughout this manuscript. The applicability and capabilities of the CPT data interpretation strategies are demonstrated considering in-situ CPT recordings recovered from a test site in Salzburg, Austria. The primary objective of this work is to advance towards an automated approach for layer detection, parameter determination, and evaluation of fluctuation degree, and to connect it with numerical analysis.

In Sect. 3, it is demonstrated that the suggested ML-based framework for the automatic identification of soil layers predicts soil boundary distributions that are well in agreement with the reference solution; hence, it offers a powerful alternative to classical filter algorithms based on classification charts. Moreover, the main motivation of automating the layer detection process is to integrate it with other analyses, such as numerical analysis. Additionally, a ground model approach adapted for "real-time" updates by modifying the soil stratification when new information becomes available is being planned. Nevertheless, it is also highlighted that the accuracy of this approach is considerably influenced by the quality and quantity of the database employed; in this respect, parameters of the ML and KDE models should be updated and evaluated whenever the database is extended with additional samples. Furthermore, there is still a lack of studies regarding interpolation strategies between different soundings. Related work is currently under consideration.

Section 4 showcases a data-driven strategy for dynamically updating the CPT investigation layout. Unlike conventional decision-making tools for gaining maximum insight to the stratigraphic model at minimum costs that mainly invoke Tobler’s First Law of spatial analysis (Miller 2004) (i.e., all positions are related but nearby positions are more related than distant positions), the presented procedure involves geotechnical sampling information as well. As a key outcome, a scalar-valued field variable termed "level of fluctuation" is calculated which allows for a systematic reduction of stratigraphic uncertainty in test fields where CPT data is available. The efficacy is demonstrated by means of both synthetic and real case test sites, in combination with a comprehensive discussion of potential application scenarios. The latter include (but in not limited to) the employment as intuitive tool in the communication of geo-spatial uncertainty to project stakeholders or the objectification of the CPT layout design. It is believed that the level of fluctuation is a good starting point for any sensitivity analysis. In the present work, this CPT data interpretation strategy is solely deployed to cone resistance recordings (single-factor approach). The simultaneous consideration of multiple in-situ data types (multi-factor approach), including the sleeve friction, is beyond the capabilities of the current version and will be addressed in future work.

Section 5 highlights a parameter determination framework (APD) that relies on a graph-based approach to determine parameters based on in-situ tests. This is extremely useful in the early stages of projects when limited soil data is available. At this stage, (relatively inexpensive) field tests such as CPT and DMT are carried out prior to a full laboratory test campaign. However, by using APD in the early design phase of the project, users can efficiently obtain much more detail. The motivation is not to replace laboratory tests with in-situ tests. They will still be needed to improve the soil and constitutive model parameters for the final design. Furthermore, APD aims to automatically connect determined parameters to finite element (FE) software for numerical analysis. The system has two key features, transparency and adaptability. This means that users can add their knowledge and experience to the system by extending the standard database of methods and parameters currently provided by the system. However, identifying the representative value for different parameters is the biggest challenge due to the wide range of values obtained from the various correlations (methods) used. Therefore, a statistical module is currently being developed to aid in selecting the representative value. Moreover, APD is currently undergoing expansion and validation.