1 Introduction

Slope stability is often improved by using passive piles. In recent decades there have been several reports in the literature on successful use of piles to stabilize a slope (e.g. Sommer 1977; Fukuoka 1977; Reese et al. 1992; Poulos 1995; Smethrust and Powrie 2007).

Different methods have been proposed to evaluate the performance and design of reinforcing piles in slopes, as well as to evaluate the safety factor of a reinforced slope (Ito et al. 1979, 1981, 1982; Chow 1996, Hassiotis et al. 1997, Cai and Ugai 2000, 2011; Ausilio et al. 2001; Jeong et al. 2003, Won et al. 2005, Wei and Cheng 2009, Ellis et al. 2010, Yamin and Liang 2010; Kourkoulis et al. 2011, 2012; Ashour and Ardalan 2012; Galli et al. 2017; Di Laora and Fioravante 2018). However a widely accepted design procedure is still lacking (Di Laora et al. 2017). As an example, the effect of stabilizing piles on slope stability is considered somewhere as an additional resistance (e.g. Poulos 1995) and elsewhere as a negative action (e.g.Yamin and Liang 2010). Moreover a clear distinction should be made between piles installed to arrest an active landslide and piles used as a preventive measure in stable slopes. In the former case the pile design can be reasonably based on the assumption that the critical slip surface, on which residual strength is mobilized, does not change after the pile installation. In the latter case the pile response must be evaluated for different locations of the potential slip surface and it is likely that the critical slip surface varies respect to the unreinforced slope (Hassiotis et al. 1997).

Although numerical three-dimensional analyses are in principle the most rigorous approach to analyze the problem, they are computationally intensive and time-consuming. Therefore in the practice the so-called decoupled methods are widely used, in which the behavior of slope and piles is analyzed separately (Viggiani 1981; Poulos 1995). This design approach may be simplified in three main steps: (a) computing the lateral force needed to increase the factor of safety of the slope to the target value using the traditional limit equilibrium methods; (b) evaluating the shear force that each pile can offer as a consequence of soil sliding; (c) selecting a pile configuration able to provide this required force without structural damage. The available approaches in the literature (Viggiani 1981; Di Laora et al. 2017; Bellezza and Caferri 2018) are mainly based on the assumption that soil strength is fully mobilized along the Soil–pile interface and, at varying the depth of sliding respect to pile length, a set of analytical expressions is provided for the shear and moment which have to be included in the computation of the safety factor of the reinforced slope (Lee et al. 1995). These procedures refer to the ultimate state only, giving no indication on pile response at intermediate states prior to the ultimate state and on pile and soil movement required to achieve the ultimate state. Alternatively, some analytical methods assume a soil response fully elastic (e.g. Chen and Poulos 1997; Cai and Ugai 2003, 2011; Guo 2014) whereas the elastic–plastic condition is rarely investigated. To overcome these drawbacks, Poulos (1995) proposed a valuable displacement-based design procedure for a passive pile embedded on a continuum elastic, but even for simplified soil profiles the solution is not given in closed-form and the application to real cases requires the use of a specific computer program.

Nowadays the general trend in engineering practice is to install stabilizing piles with a center to center spacing of three/four pile diameter which is the most effective solution to assure the development of soil arching (Ellis et al. 2010). To increase the structural capacity, the use of large pile diameters with a high reinforcement ratio is recommended (Kourkoulis et al. 2011). Therefore, in certain circumstances, the assumption of rigid deformation for the pile can be reasonable.

Bellezza et al. (2017) presented an example of elastic–plastic analysis of rigid passive piles embedded in a single layer with modulus of subgrade reaction and strength linearly increasing with depth providing design charts for pile displacement and maximum bending moment at varying the shear force at the sliding surface. More recently, Lei et al. (2022) proposed an analysis for flexible piles embedded in cohesive layered soils assuming both strength and modulus of subgrade reaction constant with depth.

In this paper a similar analysis is extended to a more realistic two-layer soil profile with soil strength linearly increasing with depth in both layers. The purpose of this study is to provide an effective tool to analyze the pile response at varying the soil movement, so that the pile contribution in terms of stability can be evaluated not only at the ultimate state but also at intermediate states.

2 Method of Analyis

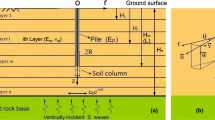
Figure 1 shows a passive pile of length L and diameter D embedded for a length L1 a layer subjected to a lateral soil movement ys and for a length L2 in a stable layer.

Fig. 1
figure 1

Basic assumptions of the proposed method: a soil movement; b rigid pile deformation; c variation of Pu with depth and d variation of ES with depth

Full size image

The rigid displacement of the pile, yp, at any depth z can be written as

$$y_{p} = y_{0} - \tan \omega \cdot z$$
(1)

where y0 is the pile head displacement and ω is the rotation angle.

Similarly to previous studies (e.g. Hassiotis et al. 1997; Cai and Ugai 2000; Gou 2014) the elastic soil reaction [FL−1] is calculated by modeling the soil as a series of independent springs:

$$P_{e} = - E_{s} \left( {y_{p} - y_{s} } \right)$$
(2)

where Es is the modulus of subgrade reaction [FL−2].

According to Poulos (1995) a uniform distribution of soil movement is assumed in the unstable layer:

$$y_{s} = \left\{ {\begin{array}{*{20}c} {y_{s0} } & {0 \le z \le L_{1} } \\ 0 & {L_{1} < z \le L} \\ \end{array} } \right.$$
(3)

In the unstable layer the modulus of horizontal subgrade reaction ES1 and the ultimate lateral soil resistance Pu1 [FL−1] vary linearly with depth:

$$E_{S1} = n \cdot z$$
(4)
$$P_{u1} = m_{1} \cdot z$$
(5)

where n [FL−3] and m1 [FL−2] are the gradient of Es and Pu1, respectively.

In the stable layer the horizontal subgrade reaction is assumed to be constant (ES2), whereas the ultimate soil strength is assumed to linearly increase with depth (Fig. 1d–e):

$$P_{u2} = P_{u20} + m_{2} \left( {z - L_{1} } \right)$$
(6)

where Pu20 is the ultimate soil resistance at the top of the stable layer and m2 is the gradient of Pu2.

The assumption of a uniform Es is generally acceptable for overconsolidated clays (Terzaghi 1955; Viggiani et al. 2012; Zhang & Ahmari 2013).

The appropriate selection of the horizontal modulus of subgrade and limiting lateral soil pressure, although fundamental for the analysis, will not be discussed in this paper. Some suggestions for the choice of Pu values for both isolated pile and pile group can be found in Ito and Matsui 1975; De Beer and Carpentier 1977; Poulos (1995), Georgiadis et al. (2013). A comprehensive discussion on the selection of Es for isolated piles is given by Zhang (2009) and Zhang and Ahmari (2013).

The method does not consider the formation of plastic hinge along the pile shaft; the absence of plastic hinges can be achieved by a proper design of the pile section and reinforcement based on the maximum moment provided by the analysis.

Finally, the assumption of a rigid deformation of the pile holds for particular combinations of pile flexural stiffness, mechanical properties of both unstable and stable layers and relative embedment lengths (L1 and L2). However, for practical purpose, the following condition can be used for a rough, but conservative, check of pile rigidity:

$$L < 2 \cdot \sqrt[4]{{\frac{{E_{P} J_{P} }}{{E_{s2} }}}}$$
(7)

where Ep is the pile elastic modulus of pile and JP is the moment of inertia of pile cross sectional area.

Numerical analyses performed by the author confirm that when the condition (7) is met the pile behaves as a rigid one.

2.1 Dimensionless Parameters

The results of the present study are expressed in terms of dimensionless parameters.

The pile length L is defined by the embedment ratio λ:

$$\lambda = {{L_{2} } \mathord{\left/ {\vphantom {{L_{2} } {L_{1} }}} \right. \kern-0pt} {L_{1} }}$$
(8a)
$$L_{n} = {L \mathord{\left/ {\vphantom {L {L_{1} }}} \right. \kern-0pt} {L_{1} }} = 1 + \lambda$$
(8b)

The distributions of Es and Pu with depth are described by RE, RU and ρ, defined as:

$$R_{E} = {{E_{S2} } \mathord{\left/ {\vphantom {{E_{S2} } {nL_{1} }}} \right. \kern-0pt} {nL_{1} }}$$
(9a)
$$R_{U} = {{P_{u20} } \mathord{\left/ {\vphantom {{P_{u20} } {m_{1} L_{1} }}} \right. \kern-0pt} {m_{1} L_{1} }}$$
(9b)
$$\rho = {{m_{2} } \mathord{\left/ {\vphantom {{m_{2} } {m_{1} }}} \right. \kern-0pt} {m_{1} }}$$
(9c)

As shown in Fig. 1c-d, the parameters RU and RE are the ratio of Es and Pu at the layer interface, respectively.

The shear force mobilized at the sliding depth (which essentially gives the main contribution of a row of passive piles in slope stability) is expressed by:

$$T_{sn} = \frac{{T_{s} }}{{m_{1} L_{1}^{2} }}$$
(10)

In such a way Tsn = 0.5 when the horizontal soil resistance of the unstable layer is fully mobilized.

Similarly, the maximum bending moment along the pile shaft (useful for structural design of passive piles) is normalized as:

$$M_{\max n} = \frac{{M_{\max } }}{{m_{1} L_{1}^{3} }}$$
(11)

Finally, the soil movement, pile head displacement and pile rotation (useful for serviceability limit state analysis) are conveniently expressed by:

$$y_{s0n} = y_{s0} \frac{{R_{E} n}}{{m_{1} }} = y_{s0} \frac{{E_{s2} }}{{m_{1} L_{1} }}$$
(12)
$$y_{0n} = y_{0} \frac{{R_{E} n}}{{m_{1} }} = y_{0} \frac{{E_{s2} }}{{m_{1} L_{1} }}$$
(13)
$$\omega_{n} = \tan \omega \frac{{R_{E} nL_{1} }}{{m_{1} }} = \tan \omega \frac{{E_{s2} }}{{m_{1} }}$$
(14)

3 Results and Discussion

A passive pile is gradually loaded for increase of the soil movement. Referring to Soil–pile interaction three different conditions can be generally distinguished: (1) initially, for relatively small soil displacement an elastic condition is achieved for the entire length; (2) then, for soil movement exceeding a first threshold value, ys0ne, an elastic–plastic condition is achieved with the soil at the ultimate state only in limited zones whose extent increases at increasing soil movements; (3) finally, for soil movement exceeding a second threshold value, ys0np, a plastic condition can be achieved corresponding to the full plasticization of soil above and/or below the sliding depth. For the assumed distributions of soil movement and soil properties (Fig. 1), the extent of the elastic and elastic–plastic zones (i.e. the values of ys0ne and ys0np) depends on λ, RE, RU and ρ.

In the following paragraphs the above-mentioned cases (elastic, elastic–plastic and plastic) are analyzed separately with the aim to obtain, whenever possible, closed-form expressions useful for design purposes.

3.1 Elastic Case

On the basis of (1)-(4), the normalized elastic soil reaction versus depth can be expressed as:

$$P_{en} = \frac{{P_{e} }}{{m_{1} L_{1} }} = \left\{ {\begin{array}{*{20}l} {{{\left( {\omega_{n} z_{n}^{2} - \Delta y_{0n} \cdot z_{n} } \right)} \mathord{\left/ {\vphantom {{\left( {\omega_{n} z_{n}^{2} - \Delta y_{0n} \cdot z_{n} } \right)} {R_{E} }}} \right. \kern-0pt} {R_{E} }}} \hfill & {0 \le z_{n} \le 1} \hfill \\ {\omega_{n} z_{n} - y_{0n} } \hfill & {1 \le z_{n} \le L_{n} } \hfill \\ \end{array} } \right.$$
(15)

where \(\Delta y_{0n} = \left( {y_{0n} - y_{s0n} } \right)\) and zn = z/L1.

Imposing the horizontal force equilibrium and the moment equilibrium about the pile head, a linear system of two variables is obtained:

$$\frac{1}{2}\left( {y_{0n} - y_{s0n} } \right) - \frac{1}{3}\omega_{n} + y_{0n} \left( {L_{n} - 1} \right)R_{E} - \frac{1}{2}\omega_{n} \left( {L_{n}^{2} - 1} \right)R_{E} = 0$$
(16)
$$\frac{1}{3}\left( {y_{0n} - y_{s0n} } \right) - \frac{1}{4}\omega_{n} + \frac{1}{2}y_{0n} \left( {L_{n}^{2} - 1} \right)R_{E} - \frac{1}{3}\omega_{n} \left( {L_{n}^{3} - 1} \right)R_{E} = 0$$
(17)

The analytical solution in dimensionless form is found to be:

$$y_{0n} = \frac{{1 + 12R_{E} \lambda \left( {1 + \lambda } \right)^{2} }}{{1 + 6R_{E}^{2} \lambda^{4} + 6R_{E} \lambda \left( {1 + 2\lambda + 2\lambda^{2} } \right)}}y_{s0n}$$
(18)
$$\omega_{n} = \frac{{6R_{E} \lambda \left( {2 + 3\lambda } \right)}}{{1 + 6R_{E}^{2} \lambda^{4} + 6R_{E} \lambda \left( {1 + 2\lambda + 2\lambda^{2} } \right)}}y_{s0n}$$
(19)

Once y0n and ωn have been obtained, the internal forces at any depth can be calculated by the expressions listed in Table 1. An example of the distribution of the soil reaction, shear force and bending moment is shown in Fig. 2.

Table 1 Internal forces for the elastic case
Full size table
Fig. 2
figure 2

Example of the elastic response of a rigid passive pile subjected to a uniform soil movement: a pile and soil displacement; b soil reaction; c shear force d bending moment

Full size image

In the presence of a uniform soil movement the shear force (Fig. 2c) achieves a relative maximum at the depth of sliding (zn = 1) and it can be calculated as:

$$T_{sn} = y_{0n} \lambda - \frac{1}{2}\omega_{n} \lambda \left( {2 + \lambda } \right)$$
(20)

After rearranging the terms, taking into account Eqs. (18)-(19), the following linear relationships can be derived:

$$T_{sn} = f_{Tys} \cdot y_{s0n}$$
(21)
$$y_{0n}^{{}} = f_{yT} \cdot T_{sn}^{{}}$$
(22)

where \(f_{Tys} = \frac{{\lambda + 3R_{E} \lambda^{4} }}{{1 + 6R_{E}^{2} \lambda^{4} + 6R_{E} \lambda \left( {1 + 2\lambda + 2\lambda^{2} } \right)}}\) and \(f_{yT} = \frac{{1 + 12R_{E} \lambda \left( {1 + \lambda } \right)^{2} }}{{\lambda + 3R_{E} \lambda^{4} }}\).

The bending moment can peak both above and below the sliding surface depending on the combinations of the values of λ and RE. Then, the maximum bending moment is obtained as

$$M_{\max ,n} = \max \left\{ {\left| {M_{1n} } \right|;M_{2n} } \right\} = \max \left\{ {\frac{{9\Delta y_{0n}^{4} }}{{64R_{E} \omega_{n}^{3} }};\frac{{2\omega_{n} }}{3}\left( {L_{n} - \frac{{y_{0n} }}{{\omega_{n} }}} \right)^{3} } \right\}$$
(23)

where M1n and M2n are the maximum bending moment above and below the sliding surface, respectively (Fig. 2d).

For values of the embedment ratio of practical interest the maximum moment is always achieved in the stable zone (see Fig. 2d). Then, rearranging (23) taking into account of (18), (19) and (20), a linear correlation between Mmaxn and Tsn can be obtained:

$$M_{\max n} = f_{MT} \cdot T_{sn}$$
(24)

where \(f_{MT} = \frac{{\left[ {1 + \lambda - \left( {6R_{E} \lambda^{2} } \right)^{ - 1} } \right]^{3} }}{{\left( {1 + 1.5\lambda } \right)^{2} \left[ {3 + \left( {R_{E} \lambda^{3} } \right)^{ - 1} } \right]}}\)

3.2 Elastic–Plastic Cases

By combining different values of ys, λ, RE, RU and ρ various elastic–plastic (EP) cases can occur. The simplest cases are those in which soil reaction reaches its ultimate value only in one zone (Fig. 3a, b). For increasing soil movement more complex cases can develop, where two, three or four zones are simultaneously in plastic state (Fig. 3c, d, e).

Fig. 3
figure 3

Soil reaction in some elastic–plastic cases: a one plastic zone above the sliding surface; b one plastic zone below the sliding surface; c two plastic zones above and below the sliding surface; d three plastic zones above and below the sliding surface and on tip; e generalized case with four plastic zones

Full size image

A generalized EP-case is here comprehensively analyzed assuming a combination of the input parameters ys, λ, RE, RU and ρ for which the soil reaches the ultimate value in four zones, as shown in Fig. 3e.

Horizontal and rotational equilibrium are assured when:

$$\begin{gathered} - \frac{1}{2}b_{n}^{2} - \frac{1}{{2R_{E} }}\left( {y_{0n} - y_{s0n} } \right)\left( {c_{n}^{2} - b_{n}^{2} } \right) + \frac{1}{{3R_{E} }}\omega_{n} \left( {c_{n}^{3} - b_{n}^{3} } \right) + \frac{1}{2}\left( {1 - c_{n}^{2} } \right) - R_{U} \left( {f_{n} - 1} \right) - \frac{1}{2}\rho \left( {f_{n} - 1} \right)^{2} \hfill \\ - y_{0n} \left( {g_{n} - f_{n} } \right) + \frac{1}{2}\omega_{n} \left( {g_{n}^{2} - f_{n}^{2} } \right) + R_{U} \left( {L_{n} - g_{n} } \right) + \frac{1}{2}\rho \left( {L_{n} - 1} \right)^{2} - \frac{1}{2}\rho \left( {g_{n} - 1} \right)^{2} = 0 \hfill \\ \end{gathered}$$
(25)
$$\begin{gathered} - \frac{1}{3}b_{n}^{3} - \frac{1}{{3R_{E} }}\left( {y_{0n} - y_{s0n} } \right)\left( {c_{n}^{3} - b_{n}^{3} } \right) + \frac{1}{{4R_{E} }}\omega_{n} \left( {c_{n}^{4} - b_{n}^{4} } \right) + \frac{1}{3}\left( {1 - c_{n}^{3} } \right) - \frac{1}{2}R_{U} \left( {f_{n}^{2} - 1} \right) - \frac{1}{3}\rho \left( {f_{n}^{3} - 1} \right) \hfill \\ + \frac{1}{2}\rho \left( {f_{n}^{2} - 1} \right) - \frac{1}{2}y_{0n} \left( {g_{n}^{2} - f_{n}^{2} } \right) + \frac{1}{3}\omega_{n} \left( {g_{n}^{3} - f_{n}^{3} } \right) + \frac{1}{2}R_{U} \left( {L_{n}^{2} - g_{n}^{2} } \right) + \frac{1}{3}\rho \left( {L_{n}^{3} - g_{n}^{3} } \right) - \frac{1}{2}\rho \left( {L_{n}^{2} - g_{n}^{2} } \right) = 0 \hfill \\ \end{gathered}$$
(26)

where bn, cn, fn and gn are the normalized depths that define the extent of the plastic zones (Fig. 3e).

By equalizing elastic soil reaction (Pe) and ultimate resistance per unit length (Pu) the following expressions can be derived:

$$b_{n} = \frac{b}{{L_{1} }} = \frac{{y_{0n} - y_{s0n} - R_{E} }}{{\omega_{n} }}$$
(27)
$$c_{n} = \frac{c}{{L_{1} }} = \frac{{y_{0n} - y_{s0n} + R_{E} }}{{\omega_{n} }}$$
(28)
$$f_{n} = \frac{f}{{L_{1} }} = \frac{{y_{0n} - R_{U} + \rho }}{{\omega_{n} + \rho }}$$
(29)
$$g_{n} = \frac{g}{{L_{1} }} = \frac{{y_{0n} + R_{U} - \rho }}{{\omega_{n} - \rho }}$$
(30)

Equations (25–30) represent a nonlinear system of 6 equations in 6 variables (y0n, ωn, bn, cn, fn and gn). The solution of this system cannot be obtained in closed form, but it can be readily accomplished by simple spreadsheet software (e.g. the tool Solver of Microsoft Excel).

On the basis of y0n and ωn, the shear force and bending moment can be computed by the expressions listed in Table 2. The normalized shear force at the sliding depth can be obtained as:

$$T_{sn} = R_{U} \left( {f_{n} + g_{n} - \lambda - 2} \right) - \frac{1}{2}\rho \left[ {\lambda^{2} - \left( {g_{n} - 1} \right)^{2} - \left( {f_{n} - 1} \right)^{2} } \right] + y_{0n} \left( {g_{n} - f_{n} } \right) - \frac{1}{2}\omega_{n} \left( {g_{n}^{2} - f_{n}^{2} } \right)$$
(31)
Table 2 Internal forces for the generalized elastic–plastic case
Full size table

It is worth to note that all possible elastic–plastic cases can be viewed as special cases of that described above. For example, the case with two yielded zones above and below L1 (Fig. 3c) can be analyzed simplifying (25) and (26), as well as the expressions of Table 2, by putting bn = 0 and gn = Ln and solving a nonlinear system with 4 variables (y0n, ωn, cn, and fn).

3.3 Elastic Thresholds

For the assumed distributions of Pu, Es and ys the zone of first plasticization is found to generally occur immediately above (Fig. 3a) or below (Fig. 3b); only for very low embedment ratios the first plasticization can occur at the pile head. The relevant limiting soil displacement (ys0nA, ys0nB and ys0nH) can be obtained by imposing cn = 1 in (28), fn = 1 in (29) and bn = 0 in (27), respectively. Taking into account of (18) and (19), the following values are computed:

$$y_{s0n,A} = \frac{{1 + 6R_{E}^{2} \lambda^{4} + 6R_{E} \lambda \left( {1 + 2\lambda + 2\lambda^{2} } \right)}}{{6R_{E} \lambda^{4} + 6\lambda \left( {1 + \lambda } \right)}}$$
(32a)
$$y_{s0n,B} = \frac{{1 + 6R_{E}^{2} \lambda^{4} + 6R_{E} \lambda \left( {1 + 2\lambda + 2\lambda^{2} } \right)}}{{1 + 6R_{E} \lambda^{2} \left( {1 + 2\lambda } \right)}}R_{U}$$
(32b)
$$y_{s0n,H} = \frac{{1 + 6R_{E}^{2} \lambda^{4} + 6R_{E} \lambda \left( {1 + 2\lambda + 2\lambda^{2} } \right)}}{{6\lambda \left( {1 + 2\lambda } \right) - 6R_{E} \lambda^{4} }}$$
(32c)

The elastic threshold is taken as the minimum (positive) among the above values.

$$y_{s0ne} = \min \left\{ {y_{s0nA} ;y_{s0nB} ;y_{s0nH} } \right\}$$
(33)

The pile head deflection, shear force at the sliding surface Tsne and the maximum bending moment Mmaxne relevant to the elastic threshold can be obtained by substituting ys0ne into (18), (20) and (24), respectively.

In Fig. 4 the values of the normalized shear force at the elastic threshold Tsne are plotted against the embedment ratio for various combinations of RE and RU. It is evident that Tsne monotonically increases with λ regardless of the value of RE and RU. For an assigned value of RU a limiting value of λ (= λ*) exists beyond which Tsne depends only on RE because the elastic threshold is governed by (32a) that does not include RU. The value of λ* decreases for increasing RU. For λ > λ* Tsne increases with RE (solid lines in Fig. 6); as an example, for RE = 5 and λ = 1.6, Tsne is high as 0.45, i.e. the pile response is fully elastic until it reaches 90% of its maximum response. On the other hand for λ < λ* the elastic threshold is governed by (32b) and different curves of Tsne versus λ can be drawn at varying RU (dashed lines in Fig. 4).

Fig. 4
figure 4

Influence of λ, RE and RU on the shear force at the sliding surface at the elastic threshold

Full size image

3.4 Plastic Cases

It is well recognized that, for a free head pile, all elastic–plastic cases converge in one of three failure mechanisms indicates as: short-pile mode or mode A, intermediate mode or mode B and flow mode or mode C (e.g. Viggiani 1981; Poulos 1995; Kanagasabai et al. 2011; Di Laora et al. 2017; Bellezza and Caferri 2018).

In mode A the slide is relatively deep (Fig. 5a) and there is full mobilization of strength in the stable soil (i.e. fn = gn = Ln in eqs. 22 and 23), so that Tsnp = RU λ +0.5 ρλ2. Mode A is of little practical interest in design and therefore it is marginally investigated in this paper.

Fig. 5
figure 5

Soil reaction distribution for plastic cases: a mode A; b mode B; c mode C1; d mode C2; e mode C3

Full size image

In mode B the soil strength is fully mobilized both in the stable and unstable soil (Fig. 5b). This case can be analytically treated as a special case of the generalized EP case putting bn = cn and gn = fn in Eq. (25) and (26). The computation of the maximum shear force (Tsnp = 0.5—cn2) is not straightforward, as the values of cn and fn must be numerically obtained by imposing horizontal and rotational equilibrium. The numerical solution has a practical meaning only when 0 < bn < 1 and 1 < fn < Ln and these conditions are met only for particular combinations of λ, RU and ρ as detailed in Table 3.

Table 3 Analytical equations for failure mode B
Full size table

Finally, in mode C the slide depth is relatively shallow and there is a full strength mobilization of the soil in the unstable layer, so that Tsnp = 0.5 (Fig. 5c, d, e). The equilibrium equations are obtained by putting bn = cn = 0 in (22) and (23).

For an assigned combination of λ, RU and ρ the normalized shear force at the sliding surface, Tsn, is the minimum value among those relevant to mode A, mode B and mode C.

$$T_{snp} = \frac{{T_{s} }}{{m_{1} L_{1}^{2} }} = \min \left\{ {R_{U} \lambda + 0.5\rho \lambda^{2} ;0.5 - c_{n}^{2} ;0.5} \right\}$$
(34)

Figure 6 shows the trend of the normalized shear Tsnp as a function of the embedment ratio λ for different values of RU and ρ. For low values of λ mode A develops and Tsnp increases linearly with λ; then, for λ greater than a first threshold value (λAB), mode B starts to govern the problem and the increase of Tsnp is no more linear; finally, a second threshold value of λ (λBC) exists beyond which Tsnp becomes independent of λ and RU (mode C). The values of λAB and λBC are found to decrease with increasing RU and ρ. The effect of ρ is appreciable only to low values of RU.

Fig. 6
figure 6

Influence of λ, RU and ρ on the normalized shear force at the sliding depth in plastic conditions

Full size image

Bellezza (2020) showed that within mode C three distinct sub-cases can be identified (C1, C2 and C3) which differ for the distribution of soil reaction in the stable layer. In mode C1 the soil is in the plastic state both below the sliding surface and near the tip (Fig. 6c); in mode C2 there is only a plastic zone below the sliding surface (Fig. 6d), whereas in mode C3 the soil remains elastic in the stable zone (Fig. 6e).

For each case (C1, C2 or C3) the governing equations can be algebraically manipulated to obtain closed-form expressions for normalized pile head displacement (y0n), rotation (ωn), limiting soil movement (ys0np) and maximum bending moment (Mmaxn), as well as the extent of the eventual plastic zone below the sliding surface (fn and gn). Tables 4–6 contain the governing expressions for mode C1, C2 and C3, respectively.

Table 4 Analytical equations and closed-form solutions for failure mode C1
Full size table

3.5 Thresholds Values of the Embedment Ratio

For the investigated soil profile, the transition value between mode A and mode B cannot be derived in closed form, but the value of λAB for ρ = 0 can be obtained by interpolating the numerical results as:

$$\lambda_{AB} \cong 0.211 \cdot R_{U}^{ - 0.918}$$
(35)

For ρ > 0 the values of λAB slightly decrease.

Also the ranges of occurrence of case C1 and C2 for ρ > 0 can be obtained only numerically on the basis of the expressions listed at the top of Tables 4–5. Only for ρ = 0 it is possible to obtain a set of closed-form expressions of the threshold values of λ for a given value of RU (Bellezza 2020):

$$\lambda_{C1} = \lambda_{BC} = \frac{{3 + \sqrt {18 + 24R_{U} } }}{{6R_{U} }}$$
(36a)
$$\lambda_{C2} = \frac{{1 + \sqrt {3 + 4R_{U} } }}{{2R_{U} }}$$
(36b)
$$\lambda_{C3} = \frac{{1 + \sqrt {1 + R_{U} } }}{{R_{U} }}$$
(36c)
Table 5 Analytical equations and closed-form solutions for failure mode C2
Full size table

The last threshold value (λC3) is found to be independent of ρ, so that (36c) is valid also for ρ  > 0.

Figure 7 shows the threshold values of λ plotted against RU for two different values of ρ. It can be observed that λC1 significantly decreases with RU and consequently the range of existence of mode C greatly increases. As an example, for RU = 2.5 and ρ = 0, λAB = 0.091, λC1 = λBC ≈ 0.789, λC2 ≈ 0.921 and λC3 ≈ 1.148. As expected, at increasing ρ, λAB, λC1 and λC2 decrease: for RU = 2.5 and ρ = 1 λAB ≈0.090, λC1 ≈ 0.732 and λC2 ≈ 0.822, whereas λC3 remains unchanged, as the first plasticization occurs immediately below the sliding surface.

Fig. 7
figure 7

Ranges of existence of different soil failure modes

Full size image

In Fig. 8 the values of the normalized pile head displacement y0n are plotted as a function of the embedment ratio λ for different values of the strength ratio RU and ρ = 0. For combinations of λ and RU which implies the development of mode B, y0n does not have a finite value and therefore all curves have a vertical asymptote in correspondence of λC1. Then, for λ  > λBC, y0n starts to decrease with λ. The rate of decrease of y0n versus λ is initially very high and decreases at increasing λ according to the expression of Table 4; in the range of occurrence of mode C1 and C2, y0n depends on λ, RU and ρ (Tables 4–5). Finally, for λ  > λC3 the normalized pile head displacement becomes independent of the plastic parameters RU and ρ (see Table 6).

Fig. 8
figure 8

Effect of λ and RU on the normalized pile head deflection for failure mode C

Full size image
Table 6 Analytical equations and closed-form solutions for failure mode C3
Full size table

For a uniform distribution of ys, the limiting soil movement required to reach the plastic case C can be obtained considering cn = 0 in (25), i.e.

$$y_{s0np} = y_{0n} + R_{E}$$
(37)

Obviously, the value of y0n in (37) is that pertaining to the case of occurrence (C1, C2 or C3).

Figure 9 shows the values of the normalized maximum bending moment Mmaxn as a function of the embedment ratio λ for different value of RU. In the investigated range of λ, for a given value of RU, Mmaxn first significantly increases with λ for mode B (dashed curves in Fig. 9); then, there is a small range of in which Mmaxn is constant (mode C1) and finally Mmaxn starts again to increase with λ at the occurrence of mode C2 and C3. For mode C3 the law of variation of Mmaxn versus λ is the same, regardless of the value of RU (see Table 6 for details).

Fig. 9
figure 9

Effect of λ and RU on the normalized maximum bending moment

Full size image

4 Mobilization Curves

On the basis of the analysis developed in the previous sections, the shear force at the sliding depth Tsn, the maximum bending moment, Mmaxn, and the pile head displacement, y0n, can be calculated for any value of the soil movement, obtaining the so-called mobilization curves generally subdivided in elastic, elastic–plastic and plastic part. Figure 10 shows typical examples of mobilization curves relevant to three different combinations of λ, RU and ρ which implies the final development of mode A, mode B and mode C, respectively. Note that for mode A (Fig. 10a) the plastic threshold of soil movement, ys0np, exists; it is possible to demonstrate that for ys0n > ys0np, Tsn and Mmaxn remain constant, but y0n continues to increase with ys0n, maintaining the same difference between y0n and ys0n. For mode B the plastic threshold does not exist; Tsn and Mmaxn tend asymptotically to the plastic values of Table 3, whereas y0n continue to increase monotonically with ys0n (Fig. 10b). The final part of the curves can be obtained by numerically solving the generalized EP case (Fig. 5e). For mode C the pile head displacement and maximum bending moment remain constant after the plastic threshold and the pile response in terms of shear force at the sliding surface reaches its maximum (Fig. 10c). In such a case closed-form expressions are available also to evaluate both y0n and Mmaxn at the plastic threshold (Tables 4–6).

Fig. 10
figure 10

Effect of the soil movement on the normalized shear force at the sliding depth (Tsn), maximum bending moment (Mmaxn) and pile head deflection (y0n) for three different combinations of λ, RE,RU and ρ: a λ = 0.12, RU = RE = 1.5, ρ = 0; b λ = 0.7 RU = RE = 2, ρ = 0; c λ = 1.2 RU = RE = 2 ρ = 0

Full size image

In design procedure the passive piles are requested to provide a stabilizing force needed to increase the factor of safety to the target value (Viggiani 1981; Poulos 1995). When the requested force for a single pile is less than the maximum one (i.e. TsnR < 0.5), pile response can fall in the elastic or in the elastic–plastic range and pile head deflection and the maximum bending moment are obviously less than those calculated in plastic conditions by the expressions obtained for mode C. For a fully elastic pile response (i.e. TsnR < Tsne) the closed-form expressions derived in this paper can be used for ready and accurate evaluations of the y0n and Mmaxn values. Conversely, in the elastic–plastic range (i.e. Tsne < TsnR < 0.5), closed-form expressions are not available and y0n and Mmaxn can be determined on the basis of the mobilization curves similar to those of Fig. 10. Considering that in design process more attention is focused on pile displacement and internal forces instead of soil movement, the mobilization curves of Fig. 11 can be conveniently drawn only in terms of y0n, Tsn and Mmaxn.

Fig. 11
figure 11

Relationship between normalized shear force and pile head deflection for different combinations of λ, RU RE and ρ

Full size image

Figure 11 shows the values of Tsn as a function of y0n for different combinations of λ and RU with RE = RU and ρ = 0.

It is evident that the mobilization curve is mainly influenced by the embedment ratio λ and slightly by RU. The effect of RU is appreciable only for low embedment ratios and when Tsn approaches its maximum value. For λ = 1 the curve for RU = 2 is distinct from other ones; the difference is due to the different failure mode, i.e. for RU = 2 mode C1 occurs, whereas for RU > 2.5 mode C3 develops, at which a smaller pile head displacement occurs (see Table 4 and Table 6 for details). A similar trend is observed for λ = 1.2, but in this case the difference in the final values of y0n is smaller because for RU = 2 mode C2 develops (see Fig. 8). For higher embedment ratios (λ = 1.5 or λ = 2) mode C3 is always activated and all curves converge to the same final value of \(y_{0n}\) for all the investigated values of RU. For higher embedment ratios the mobilization curves are practically superimposed, although the elastic thresholds are slightly different. On the other hand, for increasing embedment ratios it is always more difficult to satisfy the condition of pile rigidity.

Figure 12 shows the values of Mmaxn as a function of Tsn for different combinations of λ and RU with RE = RU and ρ = 0.

Fig. 12
figure 12

Relationship between normalized shear force and maximum bending moment for different combinations of λ, RU, RE and ρ

Full size image

The trend of the curves is similar: in the elastic range Mmaxn linearly increases with Tsn (Eq. 24), whereas beyond the elastic threshold Mmaxn increases nonlinearly, at increasing rates, with increasing Tsn. The slope of the curves in the elastic range, given by (24), significantly increases with the embedment ratio, whereas the effect of RE is appreciable only for low values of λ. In the elastic–plastic range a crossover is evident for λ = 1 because the maximum bending moment for RE = RU = 2 is higher than that for RU ≥ 3 owing the different plastic mechanism (C1 and C3, respectively). On the contrary, for λ = 1.5 and λ = 2 all curves converge to the same final value of Mmaxn relevant to case C3.

To obtain more accurate numerical values, Table 7 and Table 8 list the values of the normalized pile head deflection y0n and maximum bending moment Mmaxn calculated for some intermediate values of the normalized shear force (Tsn < 0.5) for different combinations of λ, RE, RU and ρ. As expected, for increasing values of the embedment ratio λ, y0n decreases whereas Mmaxn increases. At increasing λ the effect of RE and RU tends to be negligible.

Table 7 Values of the normalized pile head displacement y0n × 102 for intermediate values of Tsn
Full size table
Table 8 Values of the normalized maximum bending moment × 103 for intermediate values of Tsn
Full size table

Finally, it can be observed that the effect of ρ is slightly appreciable only for the lower investigated values of λ and RU and for high value of Tsn when soil plasticization occurs also below the sliding surface (see Fig. 3c, d, e); otherwise, when soil plasticization occurs only above the sliding surface (Fig. 3a) the values of y0n and Mmaxn obtained for ρ = 1 are perfectly coincident with those obtained for ρ = 0. Therefore the values of y0n and Mmaxn calculated for ρ = 1 and λ  > 1.2 are not included in Tables 7–8.

4.1 Effect of RU

Tables 7, 8 and Figs. 11, 12 are obtained by assuming RE = RU. While the effect of RU is null below the elastic threshold, it can be potentially appreciable in the elastic–plastic zone. As an example, Fig. 13 shows the curves Tsn-y0n and Mmaxn-Tsn for λ = 1.2, RE = 3 and ρ = 0 at varying RU. As expected, the curves are perfectly superimposed in the elastic range. Note that for RU > 1.68 the elastic threshold is independent of RU, as the soil plasticization first occurs above the sliding surface and Eq. 32a—which does not include RU—determines the beginning of the elastic–plastic part of the mobilization curve. For RU = 1.5 the elastic threshold is slightly lower, as for this combination of RE and RU the elastic threshold is governed by the soil plasticization below the sliding surface (Eq. 32b). Only for Tsn greater than about 0.4 the curves are clearly distinct as the final values of y0n and Mmaxn depend on which plastic mode is reached (C1, C2 or C3) and this on turn depends on RU and ρ. For λ = 1.2 mode C3 always develops when RU > 2.36 and the final values of y0n and Mmaxn become independent of RU. This implies that the mobilization curve relevant to RU = 3—or in general for RU > 2.37—is perfectly coincident with that for RU = 2.37.

Fig. 13
figure 13

Effect of RU on the mobilization curve for λ = 1.2, RE = 3 and ρ = 0: a Tsn vs y0n b Mmaxn vs Tsn

Full size image

4.2 Effect of RE

Figure 14 shows different mobilization curves Tsn-y0n and Mmaxn-Tsn obtained by varying RE for an assigned combination of λ, /RU and ρ (λ =1; RU = 2; ρ = 0). In this case the final values of y0n and Mmaxn are the same, as they depend only on RU and ρ. The elastic thresholds and the extent of the elastic–plastic zone depends on RE. For a given value of Tsn (< 0.5) both y0n and Mmaxn slightly increase with RE. The effect of RE becomes negligible approaching the plastic condition.

Fig. 14
figure 14

Effect of RE on the mobilization curve for λ = 1 RU = 2 and ρ = 0: a Tsn vs y0n b Mmaxn vs Tsn

Full size image

5 Numerical Example

The procedure for designing a stabilizing pile is illustrated by a numerical example.

The soil profile includes an unstable cohesionless layer (γ = 18 kN/m3; ϕ = 30°; n = 2000 kN/m3) of thickness 3.75 m overlying a stable layer of OC clay. Let us assume that a traditional two-dimensional stability analysis requires an additional resistant force of 245 kN/m to achieve the desired safety factor.

Consider a row of stabilizing bored concrete piles (Ep = 32 GPa) with D = 1.5 m and L = 8.4 m, so that the condition of rigidity of Eq. (7) is satisfied. Moreover consider a center to center spacing of 6 m (i.e. 4D), which implies that each pile must support 1470 kN. For this spacing it is reasonable to calculate the value of m1 using the relationship suggested by Fleming et al. (2009) for isolated piles in sand, i.e. \(m_{1} = DK_{P}^{2} \;\gamma\) = 243 kN/m2. Assuming for the stable layer the lateral resistance per unit length, Pu2, equal to 1950 kN/m and subgrade modulus Es2 = 20 MPa, the dimensionless parameters TsnR, λ, RE, RU and ρ can be computed as 0.43, 1.24, 2.67, 2.14 and 0, respectively.

With this input the normalized shear force at the elastic threshold Tsne is computed as 0.37; then, for the required resistant force, the pile response falls in the elastic–plastic range.

Using the values of Table 7 a first linear interpolation is made to compute y0n for λ = 1.24 and RU = 2, obtaining 3.966 and 4.582 for Tsn = 0.40 and Tsn = 0.45, respectively. Repeating the interpolation for RU = 3 gives y0n = 4.026 for Tsn = 0.40 and y0n = 4.602 for Tsn = 0.45.

Starting from these values, a second interpolation is performed to calculate the values of y0n relevant to Tsn = 0.43 which are equal to 4.3356 for RU = 2 and 4.3716 for RU = 3. Finally, a third linear interpolation is required to compute the value of y0n for RU = 2.14 obtaining y0n = 4.34, which corresponds to y0 = 4.34∙ m1/(nRE) = 19.8 cm.

The same procedure can be applied to evaluate the maximum bending moment by the data of Table 8. Specifically, by triple linear interpolation a value of Mmaxn = 0.1817 is obtained, i.e. Mmax = 0.1817∙m1L13 = 2328 kNm.

The pile head deflection and the maximum bending moment are 82% and 79%, respectively, of those calculated at the plastic threshold using the closed-form equations of case C2 listed in Table 5 which gives y0n = 5.284 and Mmaxn = 0.2295.

Note that the previous elastic–plastic computations are strictly valid for RE = RU = 2.14; by performing a specific numerical analysis with RE = 2.67 and RU = 2.14 the normalized pile head deflection and the maximum bending moment are computed as 4.325 and 0.1797, with a difference percentage of about 1% in comparison with the values obtained by the simplified procedure based on Tables 7, 8.

6 Conclusions

An approach based on the modulus of subgrade reaction has been proposed to analyze the response of a rigid unrestrained passive pile subjected to a uniform horizontal soil movement in two-layered soil. The investigated soil profile includes an unstable layer with the modulus of subgrade reaction and the ultimate strength that vary linearly with depth, whereas both are assumed to be constant in the stable layer. In the investigated soil profile the ultimate strength vary linearly with depth in both unstable and stable layer, and the modulus of subgrade reaction is assumed to increase with depth in the unstable layer, whereas is assumed to be constant in the stable layer.

Using dimensionless parameters, the pile response has been analyzed in terms of the shear force developed at the sliding surface, maximum bending moment and pile head deflection.

Unlike some previous studies, the analysis has been focused not only to the soil ultimate state but also to the intermediate soil response, when soil reaction is fully elastic or locally plastic along the pile shaft. The analysis described in this paper allows obtaining the mobilization curves, i.e. the relationships between soil movement, pile head deflection, maximum bending moment and shear force at the sliding depth. For the elastic part of the mobilization curves, analytical expressions have been derived to calculate internal forces, pile deformation and limiting soil movement beyond which the soil response ceases to be elastic. For usual pile embedment the extent of the elastic zone increases with the pile embedment (λ) and with the strength and modulus ratio at the layer interface (RU and RE) and in certain circumstances the pile response remains fully elastic until it reaches 90% of the maximum shear force at the sliding surface.

For the elastic–plastic part of the mobilization curves, a general case has been discussed and the governing equations have been also provided. In such a case the numerical solution of a nonlinear system is needed and closed-form solutions are not available. All the mobilization curves reach one of the possible three failure mechanisms already known in the literature (short pile, intermediate and flow mode). For the investigated soil profile, the occurrence of such failure modes is found to depend on the combined values of the embedment ratio (λ) and the strength ratio at the soil interface (RU), as well as the ratio of the gradients of soil strength (ρ).

The results of a parametric study shows that the mobilization curves is strongly influenced by the embedment ratio (λ) while the effect of the soil properties (RE, RU and ρ) is minor.

Tabulated values of the normalized pile head deflection and maximum bending moment as a function of the required stabilizing force are provided for different combination of λ, RE, RU and ρ for a quick assessment of pile response. A simplified procedure has been described by a numerical example, to check the pile performance even in the elastic–plastic range without the need to solve the nonlinear system governing the problem. The accuracy of this design methodology was demonstrated to be very high, especially if compared with the intrinsic uncertainties involved in the choice of deformability and strength parameters of the soil layers.