1 Introduction

The use of finite element analyses (FEA) in geotechnical engineering has seen a significant increase over the last decades, particularly regarding the calculation of deformations under serviceability limit state (SLS) conditions. The new generation of Eurocode 7 will additionally regulate the use of FEA in determining the performance of geotechnical structures under ultimate limit state (ULS) conditions (Lees 2017, 2019). This is due to the advantages of numerical methods over traditional analytical techniques, such as the capability to simulate:

  • near-realistic soil-structure interaction behaviour,

  • loading–unloading–reloading cycles of the soil and

  • construction-induced loading.

Dimensioning by means of numerical analyses using FEA in geotechnical construction projects, such as excavation pit design, has been state of the art for years and is gradually finding its way into practice. Numerous studies have been conducted to investigate the proper implementation of numerical simulations and the effects of utilizing various constitutive models (Potts et al. 2002; Schweiger et al. 2009; Katsigiannis et al. 2015). Furthermore, research has been carried out on analysing the design of excavation pits using FEA (Schweiger 2014; Lees 2017) and on identifying an optimal workflow for its implementation (Brinkgreve and Post 2013). However, in each case, only existing systems or academic examples were evaluated. Therefore, the question arises whether the systems studied are already optimised by means of stress analysis or dimensioning of the minimum embedment depth. Furthermore, it is necessary to investigate whether or not FEA can be used for the optimisation and dimensioning of excavation pits.

Therefore, in the first part of the paper, the focus lies on investigating the minimum embedment depth using FEA by means of a stepwise embedment depth reduction. Two different methods are feasible and will be examined to achieve this goal. On the one hand, the embedment depth is modelled in sections up to the maximum length such that the wall is then gradually shortened in additional calculation phases until the minimum possible embedment depth is found. On the other hand, the wall’s bottom edge is adjusted and shortened by re-entering the construction phase in the software. Following, the model is re-discretised, and all analysis phases are recalculated such that the excavation process is simulated with the current embedment depth.

Numerical simulations generally require more computational resources and computing time than conventional analytical methods. Therefore, in the framework of pre-planning for excavation pits, comprehensive studies are often carried out using analytical methods like the limit equilibrium analysis methods (LEM). This allows to investigate various options, such as different embedment depths, number of supports or sheet pile profiles in the shortest possible time. The “optimal” solution is then transferred to a numerical model for further analysis (Kinzler and Grabe 2009; Meier 2019). While LEM is valuable for an expeditious evaluation, the method exhibits some certain limitations, such as linear calculation, unrealistic calculated wall displacements and inappropriate soil-structure behaviour. Consequently, for a more accurate and realistic simulation of excavation pits, the adoption of FEA is used in the present studies.

Therefore, in the second part of this paper, mathematical optimisation algorithms (Particle SwarmOptimisation—PSO and Differential Evolution—DE) are utilized to determine the optimal dimensions of a single supported excavation pit. The strut’s position and the embedment depth are varied with five different sheet pile walls and three different strut profiles. The optimisation is carried out regarding the Factor of Safety (FoS) as a result of the stress analysis for the retaining wall.

The aim of this study is to prove the concept of design optimisation by using the advantages of numerical methods compared to analytical methods using the example of a simple excavation pit. With an increasing number of components in the excavation pit, the optimisation effort rises due to the large number of additional parameters. Therefore, a simple example is used to better understand the results. The use of FEA instead of classical analytical methods is justified by the more realistic simulation of the soil as well as soil-structure interaction behaviour and the possibility of considering the stiffness of the excavation components. Therefore, a comprehensive understanding of the optimal design of a single supported excavation pit is provided by investigating different sheet pile walls and strut profiles. Furthermore, it is studied if both PSO and DE are capable to find the “optimal” dimensions of the geotechnical structure and it is discussed if this workflow is useful for practical application. Based on the results, it is possible to investigate whether more complex constructions can also be dimensioned using mathematical optimisation algorithms.

2 Theoretical Background

2.1 Optimisation Algorithms

Optimisation algorithms are powerful tools for identifying optimal solutions for various problems. In geotechnical engineering, this involves, for example, inverse parameter identification (Levasseur et al. 2008; Rechea et al. 2008; Hashash et al. 2010; Yin et al. 2018) and updating parameters during staged excavations (Jin et al. 2019, 2020), safety analysis of slopes (Cheng et al. 2007; Mishra et al. 2020) or structural topology optimisation (Pucker and Grabe 2011; Seitz and Grabe 2016). Furthermore, the design of geotechnical structures necessitates a multitude of decisions to find the optimal solution concerning both serviceability and stability. Several studies have directed towards enhancing the optimum of retaining wall designs, employing classical LEM. Thus, heuristic algorithms are used to optimize economic costs and the design of concrete retaining walls while maintaining the geotechnical stability in stress and deformation conditions (Ghazavi and Bazzazian Bonab 2011; Gandomi et al. 2017a). In the study by Kinzler and Grabe 2009, a multi-criterial optimisation is employed, utilizing an evolutionary algorithm (EA) to find the most economic design of a pile foundation while complying all static analyses. In terms of excavation pit optimisation, Meier 2019 delves into the investigation of the optimal location and geometry of the strand anchors for a quadruple tie-back bored pile wall with respect to construction costs. Therefore, the optimisation process is coupled with commercially available software to apply LEM. With increasing computational capabilities and due to the advantages of numerical methods compared to LEM, it is possible to optimise the design of geotechnical constructions with mathematical optimisation approaches using FEA.

The most commonly used optimisation algorithms in geotechnical engineering are presented in Yin et al. (2018) and Ebid (2021) as part of comparative studies. The present study employs the use of the Particle Swarm Optimisation (PSO) and the Differential Evolution (DE) in order to determine the optimal dimension of an excavation pit with respect to the stress analysis of a sheet pile wall. The use of stochastic optimisation techniques, such as PSO and DE, is mainly justified by occurrence of large uncertainties in the subsoil, hence the need to optimise the geotechnical designs by, for example, varying parameters or boundary conditions. Both PSO and DE are evolutionary algorithms which can be characterized as follows (Grabe et al. 2010):

  • group of particles or individuals is utilized to search the optimal solution (population-based);

  • gradient free method;

  • imitation of an evolutionary process and

  • use of stochastic elements.

Additionally, EA are global-searching algorithms which have a robust performance (Yin et al. 2018). After initialisation of a set of samples (population) in the search space, an exploration or evolution takes place based on the previously calculated population and additional criteria (e.g. the objective function). In the following, the principles of the two optimisation strategies (PSO and DE) are presented and examples of their application in the framework of geotechnical engineering are given. The implementation of the optimisation algorithms in the numerical model is done using the programming language python using the library pyswarms (Miranda 2018) for PSO and the scipy library (Virtanen et al. 2020) for DE.

2.1.1 Particle Swarm Optimisation

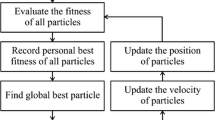
The PSO, suggested by Kennedy and Eberhart 1995, attempts to simulate the behaviour of birds as a group of particles moving in a search space of an objective function \(\epsilon (z)\). In this method, each point-shaped, collision free particle \(n\) is randomly placed with the aim of searching for a set of \({N}_{\mathrm{p}}\) unknown parameters. The new position \({{\varvec{x}}}_{\mathrm{i}}\left(t\right)\) for every particle is calculated according to Eq. 1.

$${{\varvec{x}}}_{\mathrm{i}}\left(t\right)={{\varvec{x}}}_{\mathrm{i}}\left(t-1\right)+{{\varvec{V}}}_{\mathrm{i}}\left(t\right)\times 1,\quad i=\mathrm{1,2},\dots ,{N}_{\mathrm{p}}$$
(1)

For the following generations, the velocity \({{\varvec{V}}}_{\mathrm{i}}\left(t\right)\) of each particle is stochastically updated (see Eq. 2) using a combination of the personal best position (\({{\varvec{x}}}_{\mathrm{i}}^{L}\in X\subseteq {\mathbb{R}}^{m}\)) and the best solution of the group (global best: \({{\varvec{x}}}^{G}\in X\subseteq {\mathbb{R}}^{m}\)). Therefore, the inertia coefficient \(\omega\) is set to 1 to facilitate an exploration around the best solution found so far and cognitive and social coefficients are defined to: \({\mathrm{c}}_{1}={\mathrm{c}}_{2}=2\) as supposed by Knabe et al. 2013. The parameters r1 and r2 are random numbers that are used to update the velocity of particles in the swarm.

$${{\varvec{V}}}_{\mathrm{i}}\left(t\right)=\upomega \left(\mathrm{t}\right){\mathbf{V}}_{\mathrm{i}}\left(\mathrm{t}-1\right)+{\mathrm{c}}_{1}{\mathrm{r}}_{1}\left({{\varvec{x}}}_{\mathrm{i}}^{L}-{{\varvec{x}}}_{\mathrm{i}}\left(t-1\right)\right)+{c}_{2}{r}_{2}\left({{\varvec{x}}}^{G}-{{\varvec{x}}}_{\mathrm{i}}\left(t-1\right)\right)$$
(2)

In geotechnical engineering, the PSO has been applied for several different applications, which are summarized in comprehensive reviews by Hajihassani et al. (2018) and Kashani et al. (2021). For example, in Cheng et al. (2007) and Himanshu et al. (2020), modified PSO algorithms are used to minimize the Factor of Safety (FoS) for a stability analysis of a slope. Furthermore, in Taiyari et al. (2022), the design of a pile wall retaining system in a deep excavation with an objective function, which defines the total structural costs, is optimised by using PSO in combination with a numerical simulation. Another scope of application is the inverse soil parameter calibration based on measured data. Therefore, it is the aim to minimize the difference between the measured and calculated data. Meier et al. (2009) optimised the parameters for a constitutive model comprising linear elasticity and Mohr–Coulomb plasticity of a slope based on inclinometer readings. Furthermore, PSO can be used to identify soil parameters by means of inverse calibration of laboratory tests such as oedometer and drained triaxial compressions tests (Knabe et al. 2013) as well as field pressuremeter tests (Zhang et al. 2013).

2.1.2 Differential Evolution

The DE, originally mentioned by Storn and Price (1997) and evolved by Wormington et al. (1999), optimises a problem by creating a population which is iteratively improved based on an evolutionary process. Therefore, \(n\) adjustable parameters are formed by a vector \({\varvec{x}}=\left[{x}_{1},{x}_{2},\dots ,{x}_{\mathrm{n}}\right]\) which is defined as a candidate solution in the search space. At the beginning of the process to optimise the candidate solution \({\varvec{x}}\), a random initial population \({\varvec{p}}=\left[{{\varvec{x}}}_{0},{{\varvec{x}}}_{1},\dots ,{{\varvec{x}}}_{{\mathrm{\varvec{m}}}-1}\right]\) is created. The population size is defined as \(m = D\times n\), where \(D\) is the dimension of the search space. Within the initial population, the size is doubled to guarantee that there are enough candidate solutions for the following mutations and cross overs. To evaluate the initial value, the Latin Hypercube sampling (McKay et al. 1979) is used to ensure that each parameter \(n\) is uniformly sampled over the bounded search space. The bounds for every parameter \(n\) are user-defined and remain the same for the entire optimisation.

For the iteration process, several different mutation strategies are available (best/1/bin or rand/1/bin). The first word stands for the vector which is used for the mutation: the best fit vector from the previous population (“best”) or a randomly generated new vector (“rand”). The number means that only one vector different from the current population is selected (“1”). The last word “bin” refers to the mathematical crossover operation. In this paper, the best/1/bin strategy (see Eq. 3) is used such that only this approach is further discussed.

$${{\varvec{b}}}^{\boldsymbol{^{\prime}}}={\varvec{b}}+{k}_{\mathrm{m}}\left({{\varvec{p}}}_{{\varvec{a}}}-{{\varvec{p}}}_{{\varvec{b}}}\right)$$
(3)

After the calculation of all candidate solutions \({x}_{\mathrm{n}}\) for the initial population \({\varvec{p}}\), the vector with the most minimized value (“best fit”) is stored as \({\varvec{b}}\) for the current population. For the following mutation, the “best fit” vector \({\varvec{b}}\) is only updated if a better solution is found to track the progress of the optimisation. In addition, the difference between two randomly chosen vectors \({{\varvec{p}}}_{{\mathrm{\varvec{a}}}}\) and \({{\varvec{p}}}_{{\mathrm{\varvec{b}}}}\) from the current population is considered by a mutation constant \({k}_{\mathrm{m}}\), that is selected by the user (standard value: \({k}_{\mathrm{m}}=0.7\)).

In geotechnical engineering, DE is mainly used for inverse analyses, as it achieves an optimal result with relatively few iteration steps. Furthermore, it is insensitive to the choice of initial parameters and is therefore also able to find a solution in wide search space. In Zhao et al. (2015), the optimisation of soil parameters for the Modified Cam-clay constitutive model is performed using measured data (pressuremeter test data) from an excavation pit with good agreement. Yang and Li (2019) introduced a hybrid algorithm which combines DE with a simulated annealing to overcome local minima during the optimisation process of determining creep parameters of rock under complex stress state correctly. Furthermore, both algorithms (DE and PSO) were used for automatic parameter calibration of a hypoplastic constitutive soil model on the basis of laboratory tests in Machaček et al. (2022). Based on oedometric compression and drained monotonic triaxial tests the soil parameters for two different sands are calibrated and optimised with a good agreement using both optimisation strategies, although DE shows a better performance. Another application case is the design of geotechnical constructions, e.g. slopes or cantilever retaining walls as shown in Gandomi et al. (2017a) and Gandomi et al. (2017b). Here, the DE is used for various purposes, such as optimising the FoS or minimising costs. Furthermore, Schmüdderich et al. (2022) employ machine learning algorithms utilizing DE as an optimisation technique to calculate FoS for an opencast mine slope subjected to earthquake loading. This approach results in a reduction of computational costs by two to three orders of magnitude.

3 Numerical Model of the Excavation Pit

The subject of the present study is the single supported retaining wall shown in Fig. 1. The model is the basis for the studies presented in Sects. 4 and 5. At this point, the boundary conditions of the model are presented. Further conditions, such as the profile of the sheet pile wall, are described within the boundary conditions of the respective studies.

Fig. 1
figure 1

Numerical model of the investigated single supported excavation pit

Full size image

The base of the excavation lies at a depth of \(H=8 \mathrm{m}\). The embedment depth \(t\) and the length between the ground surface and the strut \(s\) are varied during the following studies. A 2 m wide excavator load of \({q}_{\mathrm{k}}=40 \mathrm{kN}/{\mathrm{m}}^{2}\) and an infinitely extended uniform line load of \({g}_{\mathrm{k}}=10 \mathrm{kN}/{\mathrm{m}}^{2}\) form the loading conditions at the ground surface. Groundwater is not considered in the simulations. The following phases to simulate the construction states are considered:

  • Phase 0: Initial phase

  • Phase 1: Installation of the retaining wall (wished-in-place)

  • Phase 2: Installation of the strut and first excavation to 0.5 m below the strut

  • Phase 3: Second excavation to − 4.75 m

  • Phase 4: Third excavation to reach the final state (see Fig. 1)

For the discretization a mesh including a local refinement with 5300 generated soil elements (15-noded triangles) with a mean nodal distance in the excavation area of \(0.135\) m and at the boundaries of \(0.500\)  m used. The distance to the model boundaries is selected according to the recommendations of the working group “Numerics in Geotechnics” (EANG 2014) with three times of the excavation depth \(H\) so that an influence on the calculation results can be excluded.

The subsoil is considered constant in all analyses. It contains one layer of filling at the top, a layer of cohesive soil beneath and a layer of sand at the bottom (see Table 1). In the following studies, the Hardening Soil constitutive model with a Mohr–Coulomb failure criterion is employed (Schanz et al. 1999) to consider the stress-dependent stiffness as well as double hardening yield surfaces. As retaining wall, a sheet pile wall is chosen, and the wall friction is selected to be \(\delta =2/3\varphi\).

Table 1 Soil properties for the subsoil of the retaining wall
Full size table

4 Automatic Reduction of the Embedment Depth

4.1 Methods

The reduction of the embedment depth can be done in two ways in a numerical simulation, which are both investigated in the following studies. It is necessary that the excavation pit is successfully calculated with a suitable embedment depth up to the final state and thus system reserves are still available. Therefore, the strut is located at \(s=1 \mathrm{m}\) beneath the ground surface and \(t=6 \mathrm{m}\) is chosen as the initial value for the reduction of the embedment depth.

4.1.1 Reduction Using Additional Phases (Method 1)

The proposed procedure for sequentially reducing the embedment depth in the final state of the numerical simulation requires a sectional modelling of the retaining wall. This means that, initially, an embedment depth with adequate system reserves is modelled. Subsequently, the embedment depth is gradually reduced in a series of phases (method 1), with a specified decrement of e.g. 0.5 m per phase. The value was chosen in this case because it is sufficiently small to show the basic applicability of the method. Thus, only the final phase is calculated with the adjusted embedment depth. The rest of the construction process is examined with an embedment depth that exceeds the final value. This could lead to an overestimation of safety margins and prevent an identification of failure modes, e.g. during excavation. Therefore, it is necessary to recalculate all load and construction phases after the optimal embedment depth has been determined. An advantage, however, is the computational efficiency, as it eliminates the need for re-discretization of the model. In Fig. 2a, the method is depicted in a scheme.

Fig. 2
figure 2

Methods for reducing the embedment depth: Reduction using additional phases (a) and by updating the entire model (b)

Full size image

4.1.2 Reduction by Updating the Entire Model (Method 2)

For this method, the wall’s bottom edge is adjusted (e.g., 0.5 m per step—method 2). Therefore, it is necessary to iteratively navigate back to the modelling stage for updating the embedment depth. Afterwards, the model is discretized again and all phases, starting from the initial stress state, are recalculated. As a result, the entire construction process is calculated considering the adjusted embedment depth. Obviously, this procedure leads to increased computational time compared to the first method proposed, especially for complex models. Figure 2b shows a schematic representation of this method.

4.2 Results

The results for both procedures, reducing the embedment depth stepwise in the calculation phase or adjusting the embedment depth in the modelling stage, yield the same minimum required embedment depth, \({t}_{\mathrm{required}}=4.5 {\text{m}}\), for the investigated excavation pit. Figure 3 shows that method 1 (dashed line) and 2 (dotted line) yield nearly identical results when comparing the distribution of bending moments and earth pressure over the wall length \(z\) for the configuration with minimum required embedment depth. In addition, both bending moment distributions show no restraint effect at the base, suggesting that the wall is near its limit state and further reduction of the embedment depth is not feasible. The only notable difference is a slightly higher deformation in the bottom area regarding the wall's horizontal displacement \({u}_{\mathrm{x}}\) for the simulation with stepwise reduced embedment depth using additional calculation phases (method 1). This is due to a cumulative effect of the additionally simulated phases on the horizontal wall deformation.

Fig. 3
figure 3

Comparison of the bending moment M, horizontal displacements ux and active and passive earth pressure eh for the investigated reduction schemes in the case of minimum required embedment depth

Full size image

It is important to note that characteristic parameters are considered in these investigations. Finally, method 2 for gradual reduction of the embedment depth is recommended due to its ability to account for any potential failure mechanisms during construction, even though it requires a higher computational effort.

5 Numerical Optimisation of Excavation Pits

5.1 Boundary Condition of the Optimisation Problem

The objective of the present study is to optimise the dimension of the excavation pit described in Chapter 3 by means of stress analysis for the sheet pile wall. The optimum solution will be obtained by varying several options. Three distinct pipe profiles (910 × 20, 610 × 20 and 324 × 16) have been selected for the strut, whereas five Z-section profiles (AZ 12-700, AZ 24-700, AZ 36-700N, AZ 42-700N and AZ 48-700) are evaluated for the sheet pile wall. In the numerical model, elastoplastic material behaviour is considered for both structural elements. The relevant geometrical parameters of the sheet pile and strut profiles considered are shown in Tables 2 and 3 respectively. Additionally, the embedment depth is varied from \(t=3\div 8 \mathrm{m}\) and the distance between ground level and strut from \(s=0\div 2.4 \mathrm{m}\). The boundaries of the distances are determined based on the recommendations of the German Working Group “Excavation Pits” (EAB 2021) for load redistribution of earth pressure in single-propped sheet pile excavation pits.

Table 2 Geometrical parameters for the sheet pile wall profiles considered in the present study
Full size table
Table 3 Sectional area parameters for the pipe profiles considered in the present study
Full size table

To find the optimal solution, the optimisation algorithms (PSO and DE) described in Chapter 2.1 are applied. Both algorithms are used to optimise the embedment depth \(t\) as well as the distance between ground level and strut \(s\) for all selected struts and sheet pile walls. As a result, the moment distributions are compared and a stress analysis for the sheet pile wall is performed by means of Eq. 4 considering the calculated bending moment \({M}_{\mathrm{char}}\). The yield strength of the sheet pile wall is selected as \({f}_{\mathrm{y}}=355 \mathrm{N}/{\mathrm{mm}}^{2}\) and the plastic section modulus \({W}_{\mathrm{pl}}\) is considered.

$${\upsigma }_{\mathrm{E, char}}={M}_{\mathrm{char}}/{W}_{\mathrm{pl}}\ge {f}_{\mathrm{y},\mathrm{char}}={\sigma }_{\mathrm{R}}$$
(4)

For any optimisation problem an objective function \(\epsilon\) is required as mathematical representation of the problem being solved. Since the aim of this study is to optimise the results of the stress analysis, a Factor of Safety (\(FoS\)) for the sheet pile wall is used which represents the objective function \(\epsilon\) in the optimisation process following Eq. 5.

$$\epsilon =FoS={\sigma }_{\mathrm{R}}/{\sigma }_{\mathrm{E, char}}=\mathrm{min}!$$
(5)

To implement PSO, \(n=30\) particles and a maximum of 6 iterations (\(\mathrm{max} iter=6\)) for each combination of strut and sheet pile wall are used. To cover the entire search space, a high number of particles \(n\) is chosen. This means that \(n\times \mathrm{max}iter=6\times 30=180\) calculations are performed for each combination.

For implementation of DE, \(n=2\) adjustable parameters and a Dimension of \(D=15\) for the search space, resulting in a population size of \(m = D\times n=15\times 2=30\) are used. In the first Iteration, the population size is doubled to secure results for the first mutation of the candidates. Therefore, a maximum of 5 iterations (\(\mathrm{max} iter=5\)) is defined to get the same amount of 180 calculations as considered in the PSO method. Overall, a total of 2700 calculations are performed for every combination of strut and sheet pile wall using both optimisation algorithms.

It should be noted that no further adjustments or adaptions are conducted after the optimisation algorithms were performed. This could affect the validity of the results regarding the quality of the algorithms. The aim of this study is to evaluate whether PSO or DE is suitable finding the optimum dimension of an excavation pit.

In practical engineering applications, the analysis of single-supported excavation pits typically relies on LEM. To evaluate the feasibility of the optimisation process, a comparative calculation with LEM following Blum’s method has been conducted. For this, it is necessary to select a degree of fixity for the embedment. Due to the optimisation of wall stresses (see Eqs. 4 and 5), a full fixity is chosen resulting in the lowest bending moment \({M}_{\mathrm{char}}\) and the highest embedment depth \(t\). The optimum embedment depth \(t\) is then calculated. In the following, the strut position \(s\) is adjusted iteratively, such that the lower and upper bounds of the parameters are not exceeded. Regarding sheet pile and strut profiles, no distinction is applied as the choice of profile has no influence on the calculation result.

5.2 Results Comparing PSO and DE

The optimised Factors of Safety \(FoS\) as well as the associated distance between ground level and strut \(s\) and embedment depth \(t\) are shown in Table 4. The sheet pile profiles and struts are numbered in ascending order of flexural- and axial rigidity (see Tables 2 and 3). The results indicate that for all combinations investigated, the PSO and DE algorithms give similar \(FoS\) values in case of sheet pile stress analysis. However, in some cases, the excavation pit dimensions (\(s\) and \(t\)) differ even though \({FoS}_{\mathrm{PSO}}\) and \({FoS}_{\mathrm{DE}}\) are almost identical. This is because stiffer sheet pile walls allow a greater redistribution of stresses along the wall. Consequently, changing the embedment depth does not significantly affect the stress analysis. This is observed for the combination AZ 48-700 and 914 × 20, where the \(FoS\) differs only slightly (\({FoS}_{\mathrm{PSO}}=3.43\) and \({FoS}_{\mathrm{DE}}=3.41\)), and the delta of the calculated embedment depths is \(\Delta t={t}_{\mathrm{DE}}-{t}_{\mathrm{PSO}}=4.14-3.77=0.37 \mathrm{m}\).

Table 4 Optimised dimensions of the excavation pit using PSO and DE for the stress analysis of the sheet pile wall
Full size table

In addition, horizontal wall deformations are limited to \({u}_{\mathrm{x}}\le 4 \mathrm{mm}\) due to serviceability reasons. Consequently, calculation steps that result in failure of the limit state or in horizontal wall deformations greater than \({u}_{\mathrm{x}}>4 \mathrm{mm}\) are eliminated and not considered. Analysis of the results for the different sheet pile walls examined in this study reveals that lower stiffness of the wall leads to a deeper strut position \(s\). Therefore, it can be concluded that the strut position \(s\) significantly contributes to limiting the maximum horizontal deformation \({u}_{\mathrm{x}}\). Moreover, for the more flexible sheet pile profiles (AZ 12-700 and AZ 24-700), the strut position is essential not only for stress analysis results but also for maintaining the maximum horizontal deformations. Lower strut positions can reduce the embedment depth while maintaining the maximum deflections, allowing for an economic design for the investigated excavation pit while using less material.

Furthermore, the results show that the choice of the strut only has minimum effect on the stress analysis of sheet pile walls.

Regarding LEM, the strut position \({s}_{\mathrm{LEM}}=2.27 \mathrm{m}\) at full fixity of the embedment is chosen, as this value leads to the upper bound of the embedment depth with \({t}_{\mathrm{LEM}}=3.00 \mathrm{m}\). Based on this, a maximum bending moment \({M}_{\mathrm{char,LEM}}=73.8 \mathrm{kNm}\) is calculated, which leads to a \({FoS}_{\mathrm{LEM}}=\mathrm{4,60}\) for an AZ 12-700 sheet pile wall. Compared to the results of FEA, the calculated embedment depth is lower (\({t}_{\mathrm{LEM}}=3.00 \mathrm{m}<{t}_{\mathrm{FEA}}=3.28\mathrm{m}\)) with a higher Factor of Safety (\({FoS}_{\mathrm{LEM}}=\mathrm{4,60}>{FoS}_{\mathrm{PSO}}=\mathrm{2,16}\)). Therefore, a statement regarding the optimum design for the excavation pit is not possible without considering additional optimisation criteria such as economic costs in the optimisation process.

In Fig. 4 the calculated Factors of Safety \(FoS\) over the search space are displayed as 3D and 2D plots for PSO (a and b) and DE (c and d) representative for all combinations investigated. As expected, the samples of the optimisation algorithms do not explore the entire search space. Regarding the 3D plots in Fig. 4a and c (circled areas), it is noticeable that DE does not investigate higher values of embedment depth \(t\) and strut position \(s\) because an acceptable minimum \(FoS\) was already found in early stages of the stochastic optimisation process. This seems to be an advantage of DE compared to PSO as it leads to acceptable results faster. Additionally, PSO does not investigate minimal values (compare circles in Fig. 4b and d) in a detail compared to DE. Therefore, it can be concluded that PSO may come to rest at a local minimum, not searching for more results around the minimal values, revealing the decisive disadvantage of stochastic optimisation algorithms. This raises the question how many calculations are required to achieve a satisfactory result. This topic will be further investigated in Sect. 5.3.

Fig. 4
figure 4

Factors of Safety FoS for the investigated optimisation algorithms: PSO (a and b) and DE (c and d) depending on the depth of the strut s and the embedment depth t (sheet pile wall: AZ 48-700 and strut: 914 × 20)

Full size image

In Fig. 5 the search spaces of PSO (a) and DE (b) are compared for the combination of sheet pile AZ 24-700N and strut 610 × 20. As previously mentioned, only those steps with successful simulation of excavation and which met the maximum horizontal deformation of the sheet pile wall \({u}_{\mathrm{x}}\le 4 \mathrm{mm}\) are shown. This implies that 125 out of 180 successful calculation steps for PSO and 107 out of 180 for DE are plotted in Fig. 5.

Fig. 5
figure 5

Factors of Safety FoS for the investigated optimisation algorithms: PSO (a) and DE (b) depending on the depth of the strut s and the embedment depth t (sheet pile wall: AZ 24-700N and strut: 610 × 20)

Full size image

Additionally, the boundary of the search space investigated by the other optimisation is plotted as a dashed line. The plot of the boundary line reveals that the search space of PSO is slightly larger than that of DE. Nonetheless, DE obtains the optimal Factor of Safety (\({FoS}_{\mathrm{DE}}=3.41\)) compared to PSO (\({FoS}_{\mathrm{PSO}}=3.43\)) for the combination of AZ 24-700N and 610 × 20, which leads to the already mentioned assumption that DE operates more efficiently.

5.3 Investigation of Optimisation Parameters

In the following, the value for maximum iterations as well as for the population size (DE) or the number of particles (PSO) are varied in order to examine the previously mentioned thesis of higher computational efficiency using DE compared to PSO in more detail. The objective is to compare the performance of the algorithms in the context of feasible and practical design of excavation pits. Due to high computational costs associated with the numerical models during the optimisation process, it is difficult to repeat the iteration several times. In particular, stochastic optimisation algorithms do not always guarantee that the global minimum has been reached. Therefore, the focus in this research is on achieving a satisfactory balance between number of calculation steps and convergence to the global minimum.

Therefore, the excavation pit described in Sect. 3 with a sheet pile wall AZ 24-700N and a strut 610 × 20 is investigated. The maximum number of iterations is varied from 2 to 6, and the population size (DE) or particle numbers (PSO) are varied from 10 to 30. The results with a population size/particle number of 30 and a maximum of 6 iterations are already shown in Table 4 and Fig. 5.

It should be noted that the initialisation of the optimisation algorithms examined is stochastic and results could change with multiple repetitions. In addition, there is a possibility that the optimal result of the optimisation problem may be a local minimum. However, for this study, the primary goal is to determine the applicability of the optimisation algorithms in geotechnical practice. Therefore, the aim is to achieve an optimal result in the first attempt with as few calculation steps as possible.

Based on the results obtained in Sect. 5.2 and to check whether the global minimum has been reached, an acceptable Factor of Safety \(FoS\) is defined in a range of 5% of the optimal \(FoS\) from Table 4: \(\mathrm{max}FoS=\mathrm{1.05}\times \mathrm{2.36}=\mathrm{2.48}\) for the sheet pile wall AZ 24-700N in combination with the strut 610 × 20.

The reached Factor of Safety \(FoS\) regarding the stress analysis of the sheet pile wall for PSO and DE and different optimisation parameters are shown in Table 5. Additionally, the calculation step achieving the minimum \(FoS\), as well as the maximum number of calculation steps, are plotted in brackets for every combination investigated. Furthermore, Fig. 6 displays the results of Table 5. The 3D plot shows the investigated number of samples (particles \(n\) or population size \(m\)) and maximum iterations related to the calculated safety factors depending on the respective optimization algorithms. Based on this, the initialisation in DE leads to a better coverage of the search space compared to PSO. This advantage arises from the fact that an acceptable \(FoS\) is achieved with fewer computational steps. This outcome is attributed to the utilization of Latin Hypercube Sampling, which is employed to initialise the population size \(m\) in DE, as opposed to PSO where particles \(n\) are placed randomly.

Table 5 Factor of Safety \({FoS}_{\mathrm{PSO}}\) and \({FoS}_{\mathrm{DE}}\) for different numbers of iterations and population size or particle numbers using PSO (top) and DE (bottom). In brackets: (step number with the minimum \({FoS}\)/maximum number of calculation steps)
Full size table
Fig. 6
figure 6

Factors of Safety \(FoS\) for the investigated optimisation algorithms: PSO (a) and DE (b) depending on the Particles n / Population size m and the maximum iterations (sheet pile wall: AZ 24-700N and strut: 610 × 20)

Full size image

The comparison of the number of particles \(n\) for PSO and the population size \(m\) for DE against the maximum number of iterations (see Table 5) shows that, in most cases, the number of iterations have a higher priority for the optimisation process than the population. This is because both algorithms store values with better solutions (velocity \({\mathbf{V}}_{\mathrm{i}}\left(\mathrm{t}-1\right)\) for PSO and “best fit” vector \({\varvec{b}}\) for DE) during the optimisation process. Therefore, a higher number of iterations leads to more frequent examinations of the populations (see Eqs. 2 and 3) and the best solution in the entire search space is optimised more frequently.

The investigation of maximum calculation steps in Table 5 shows that with DE all, except for one optimisation process, are lower than the \(\mathrm{max}FoS\). Even the iteration with the lowest number of calculation steps of 20 results in an acceptable \(FoS\). For PSO, the results show that depending on the maximum number of iterations, 40 to 60 calculation steps are required to stay below \(\mathrm{max}FoS\). Therefore, it can be stated that for the selected application case of design optimisation for a single supported excavation pit, the DE converges faster towards a satisfactory solution.

6 Conclusions

The present paper investigates design optimisation for a single supported excavation pit using FEA. In the first part of the paper, two methods for automated reduction of retaining wall embedment depth are presented. These methods are a reduction using additional calculation phase and a reduction by updating the entire model. The results show that for a model considering the minimum embedment depth out of the reduction approaches, the moments and earth pressure curves are identical for both investigated methods. Only the horizontal deformations considering the stepwise reduction method using additional calculation phases are slightly increased. In principle, both methods are considered to be applicable.

In the second part of the paper, Particle Swarm Optimisation (PSO) and Differential Evolution (DE) are applied to optimise the dimensions of the single supported excavation pit. For this purpose, the embedment depth \(t\) and the position of the strut \(s\) are optimised considering five different sheet pile wall and three different strut profiles. As an objective function, the Factor of Safety \(FoS\) out of the stress analysis of the sheet pile wall is minimised. The results show that both algorithms perform similarly well with a high number of calculation steps (180 per optimisation process). In addition, the chosen sheet pile wall influences the position of the strut \(s\) and the embedment depth \(t\).

Further investigations regarding the efficiency of the algorithms have shown that the Latin Hypercube Sampling of the DE used to initialise the population leads to better coverage of the search area compared to the PSO. Therefore, DE is more suitable to converge towards an acceptable Factor of Safety \(FoS\) with fewer calculation steps. In future, the knowledge gained will be extended to more complex excavations in order to generate a conclusive recommendation for practical use.