1 Introduction

The assessment of the sudden transition of a stable ground from a drained state to a fully undrained/unstable one is required for a realistic evaluation of the ground’s overall stability and factor of safety recommendations during designs in geotechnical engineering practices. The potential for a sudden transition of apparently stable ground in a drained state to an unstable one in a fully undrained state may result in a ‘flow failure’ (also referred to as ‘classic’ or ‘static’ liquefaction, as named after Casagrande). A flow failure may be triggered by unstable loading under apparently stable static ground conditions or the result of a sudden temporary load such as vibration or earthquake. The most common consequences of inadequate assessment of the ground’s stability may include but are not limited to failures due to landslides in natural slopes, static liquefaction of earth dams/tailing dams, hydraulically deposited artificial fills, and reclaimed lands near coastlines (Verdugo & Ishihara 1996). In general, soil liquefaction is a major threat to engineering facilities/infrastructures built with or on saturated sandy soils (Robertson 2010). According to Robertson (2010), the two well-known types of liquefaction failures include cyclic liquefaction and flow/static liquefaction. A typical characteristic of the former scenario results in rapid shear strength failure of the soil due to buildup caused by the induced cyclic/dynamic/earthquake loadings and the consequential loss of the soil’s effective stress whose principal function is to hold the soil grains together. A sudden and high-magnitude strain-softening typifies the latter type of liquefaction failure with immediate loss of soils’ shear strength and it is also often referred to as flow liquefaction (e.g., Jefferies & Shuttle 2020).

A review of the subject literature indicated that several hybrids of proxies have been proposed in the past to analyze flow liquefaction mechanisms. However, it turns out that the concept of steady-state (SS) authored by Poulos (1981), and the critical state (CS) developed by Schofield and Wroth (1968) are the two most synchronized frameworks for such purposes, and both theories have been concluded mostly in the literature as the same (Jefferies 1993). The key identifiable difference between the two theories as mentioned by Jefferies and Been (2015) is that the SS has no computable model while the CS has. Additional details of the differences between the two theories have been elaborated elsewhere and not repeated here e.g., Kang (2019). The similarity between the two is that during undrained compression loadings, a continuous steady state of soil deformation is experienced at a constant specific volume \((\upsilon )\), constant mean effective stress \(({p}{\prime})\), and deviatoric stress \((q)\) (Jefferies & Been 2015). Theoretically, the CS framework is a robust and well-established concept in the literature, correlating both the soil’s consolidation and strength characteristics. Other school of thought e.g., Kang (2019) according to their recent review work concluded that the SS was the product modification of the CS. Overall, the critical state soil mechanics (CSSM) is popular and acceptable for modeling typical behavior of sand and clay type of soil under a macroscopic scale (Gu, 2020; Kang, 2019; Rahman & Sitharam 2020).

Several other applications of the CSSM framework are available in the literature. For instance, studies on effects of frictional angle, particle breakage, and deformation on the CS properties of soils (De Bono, 2018; Kang, 2019; Nie, 2022; Taiba, 2023; Wang, 2020; Yang, 2018; Yu 2017); effects of fabric anisotropy vs isotropy (Kazem, 2022; Kolapalli et al. 2023; Papadimitriou, 2019; Rahman & Dafalias 2022); the role of principal stress rotation on the critical state line (Jefferies & Been 2015; Jefferies et al. 2015; Kazem, 2022); the influence of polymer on the critical state of sand (Liu, 2020), and the impact of plastic and non-plastic fines on the critical state of sand (e.g., Mahmoudi et al. 2018; Papadopoulou & Tika 2008, 2016; Rahman & Dafalias 2022; Talamkhani & Naeini 2018). In the domain of numerical modeling of soils, the CSSM has also proved to be accurate in predicting a wide range of soil engineering characteristics. Over the years, the CSSM has been successfully utilized for the calibration of soil parameters that were directly applied with finite difference method (FDM), finite element method (FEM), and discrete element method (DEM) to simulate a wide varieties of soil behaviors at both macroscopic and microscopic scales (e.g., Gu, 2020; Jefferies & Been 2015; Papadimitriou, 2019; Rahman & Dafalias 2022).

The East Coast Sand (ECS) sand considered in this study is a typical coastal sand deposits encountered in the East Coast of the upper North Island of New Zealand, including the important economic region of Auckland. Although seismic hazards for the Auckland and Northland regions are considered to be relatively low within the New Zealand context, typical ECS deposits when deposited loose and saturated were highly susceptible to cyclic liquefaction and flow failures, and present a moderate risk of liquefaction induced ground damage, requiring consideration and mitigation for the engineering design of important infrastructures such as bridges, wharves and marinas, and assessment of the hazard posed to existing coastal reclamations. The source of the studied sand sample, ECS was obtained from near the shore of Pakiri Beach, Mangawhai, north of Auckland, on the North Island of New Zealand, as indicated in Fig. 1 (a) showing its location map. The ECS has been continuously mined for decades to date, yet it has no published information on its basic and advanced intrinsic geotechnical properties. ECS is available in large commercial quantities and routinely utilized for local earthworks construction applications around the Auckland and Northland regions of New Zealand. The sand is an alluvial product of the mechanical weathering of the Pakiri Group sandstone refer Fig. 1 (b), and the reference legend in Fig. 1 (c).

Fig. 1
figure 1

Location and geological map of ECS

Full size image

The formulated research objectives to help achieve the overall aim of the current study were to:

  1. (i)

    determine the relevant basic, advanced geomechanical, and critical state characteristics of the remolded ECS soil, and

  2. (ii)

    analytically compare the experimentally measured undrained behavior of ECS soil with the outputs of a selected critical state-compatible advanced soil constitutive model (Norsand).

The findings in the current work are expected to provide useful insights to practicing engineers working with ECS locally or looking to develop model calibration for similar sandy soil. A simplified calibration process of the advanced soil parameters of Norsand was presented herein since they mostly appear like daunting tasks and the relevance of the applications of the CSSM is shown with the quality of the match between the obtained experimentally measured results and simulated output characteristic plots. The current paper examined the undrained strength behavior specific to ECS including its susceptibilities to static or flow liquefaction with the application of the advanced critical state framework (after Jefferies 1993). The additional contribution of this paper was to establish an information database, which consisted of the basic and advanced geomechanical properties that were specific to ECS, and comparisons made with other well-researched sands such as Toyoura sand (e.g., Verdugo & Ishihara 1996; Yoshimine & Ishihara 1998). Despite the wide applications of ECS in construction, a thorough literature search indicated that there was no available data on its intrinsic engineering properties. Furthermore, this study showcased a simplified and comprehensive calibration process for the Norsand constitutive soil model soil parameters, which was compatible with the state concepts and suitable for the modeling of flow liquefaction phenomena/issues.

2 Experimental and Other Research Methods

2.1 Basic Soil Index Characteristic Tests

The executed laboratory work on the ECS herein included the basic soil index characteristics tests, scanning electron microscopy (SEM), permeability tests, drained and undrained monotonic triaxial compression tests. The particle size distribution (PSD) of ECS executed as per ASTM (2017) – D6913/D6913M indicated that ECS was composed of about 99.81% sand particles and 0.19% fines, which appeared as either impurities or silt (i.e., non-plastic fines), see Fig. 2 for the ECS PSD—chart. The 99.81% content of sand grains suggested that the ECS sand sample can be confirmed as typical clean sand with a negligible quantity of fines content (i.e., 0.19%). The average mean grain size, \({D}_{50}\) was about 0.25 mm; the effective particle size, \({D}_{10}\) was 0.16 mm; the particle size at which 30% was finer, \({D}_{30}\) was 0.20 mm; and the particle size at which 60% are finer, \({D}_{60}\) was 0.26 mm. Table 1 summarizes the derived soil classification as per the unified soil classification system (USC), specific gravity test as per ASTM-D854-14 (2014), the minimum, and maximum density of the sand as per ASTM-D4253-16 (2016).

Fig. 2
figure 2

Particle size distribution and embedded SEM micrographs of ECS

Full size image
Table 1 Basic soil index characteristics of ECS samples
Full size table

Further examination of ECS under the scanning electron microscope (SEM) for identification of its grain shape, angularity, and possible mineralogy indicated its shape to be angular to subangular grains – see the embedded SEM in Fig. 2, ECS was fine in texture. Constant head permeability tests obtained as per AS 1289.6.7.1 (2001) showed that ECS’s permeability was within the range of 4.76*10−4 to 6.66*104 cm/s, which were consistent with typical values provided for sands by Towhata (2008).

2.2 Soil Geomechanical (Strength) Characteristic tests

The universally established and recognized test method for determining the CS of soils is the conventional monotonic triaxial compression testing (e.g., Jefferies & Been 2015; Rahman & Dafalias 2022; Viana da Fonseca et al. 2021), by specifically applying the isotropically consolidated undrained (CIU) triaxial testing in accordance with ASTM D4767 and isotropically consolidated drained (CID) triaxial testing following ASTM D7181. In the current study, four CIU shear tests were executed on loosely prepared specimens to determine the corresponding CS characteristics of the ECS sand; seven CID shear tests were carried out, consisting of 4 tests on loosely prepared and 3 tests on densely prepared ECS specimens, respectively to determine the stress-dilatancy parameters. CIU testing was undertaken at mean effective stresses \(p{\prime}\) (MES) of 50 kPa, 100 kPa, 200 kPa, and 300 kPa. The above-specified stress levels were chosen to enable the effective characterization of the critical state line and other soil model parameters over the range of mean effective stresses of engineering interest and applications. The typical consolidation \(p{\prime}\) levels of the executed CID tests on the loosely prepared specimens were 100 kPa, 200 kPa, 300 kPa, 400 kPa, and 600 kPa, while the dense specimens were sheared after isotropic consolidation of about 50 kPa, 80 kPa, and 100 kPa MES levels, respectively. Table 2 summarizes the initial soil condition properties of the tested ECS sand specimens. As can be seen in Table 2, the remoulded sand specimens were prepared to approximately similar initial densities, thereby providing a similar initial soil states for subsequent comparisons of obtained soil engineering properties.

Table 2 The initial soil testing conditions of ECS sand samples
Full size table

The utilized testing equipment was the Alfa automated triaxial tester (T-333/A), manufactured by Alfa testing equipment, Turkey, and supplied by CMT-Australia. The device's available features included an incorporated state-of-the-art automated data capturing mechanism, computer software for easy data acquisition, and post-data processing. A schematic picture showing the major components of the device is shown in Fig. 3. Comprehensive details of the procedures for executing the conventional monotonic triaxial compression test are available elsewhere and not repeated here, for instance, Donaghe et al. (1988) and Head (2014). A summary of the soil CS testing methods is subsequently provided through the sample preparation to the shear stage herein.

Fig. 3
figure 3

The Alfa triaxial test equipment

Full size image

The adopted soil sample preparation method for the triaxial specimens was the moist tamping (MT) coupled with the undercompaction technique. The MT and undercompaction combination have been reported many times in similar studies of the literature as the best technique for achieving suitably loose specimens for characterizing the soil's critical state parameters (Jefferies & Been 2015; Jefferies & Shuttle 2020; Viana da Fonseca et al. 2021). Carbon dioxide (CO2) was bubbled through prepared soil samples to aid the faster saturation process, much of the saturation processes were achieved at lower back pressures in the range of 50-300 kPa. The Skempton's B-value achieved herein was in the range of 0.98 to 1.00, which were above the 0.95 as set by ASTM D4767 for the attainment of full-saturation status of soil samples under triaxial conditions. Shearing were initiated after the completion of the respective consolidation stages. Typically, the CID specimens were sheared at the rate of 0.1 mm/min to ensure that the generated pore pressure's equilibration in the entire specimen’s mass and the CIU specimens were sheared at a shearing rate of 1.5 mm/min based on Head (2014).

2.2.1 Post-Processing and Calculation Methodology of the Monotonic Triaxial Test Data

In this paper, the conventional Cambridge nomenclature has been adopted for the computation of the stress invariants where:

$$q= {\sigma }_{1}-{\sigma }_{3}$$
(1)
$${p}{\prime}=({{{\sigma }_{1}}^{\prime}}+2{{{\sigma }_{3}}^{\prime}})/3$$
(2)

in which \({\sigma }_{1}\) is the major principal stress equivalent to the applicable axial stress in triaxial conditions, \({\sigma }_{3}\) is the minor principal stress, equivalent to the radial stress (cell-pressure) on the sample in the triaxial apparatus, and effective stresses are denoted with a dash \(({\prime})\) being the total stress less by the pore water pressure u. The stress invariants expressed in Eqs. (1) and (2) are the deviatoric stress \((q)\) and the mean effective stress \(\left({p}{\prime}\right).\) The corresponding strain invariants, namely the deviatoric (shear) strain, \({\varepsilon }_{q}\) and volumetric strain, \({\varepsilon }_{v}\) were computed by Eqs. (3) and (4), respectively, where \({\varepsilon }_{1}\) and \({\varepsilon }_{3}\) are the corresponding respective major and minor principal strains and equivalent to the axial and radial strains, respectively in triaxial conditions:

$${\varepsilon }_{q}=2/3({\varepsilon }_{1}-{\varepsilon }_{3})$$
(3)
$${\varepsilon }_{v}= {\varepsilon }_{1}+2{\varepsilon }_{3}$$
(4)

The specified \(\frac{2}{3}\) factor in Eq. (3) was to allow the stress and strain invariants as work conjugates (Jefferies & Shuttle 2020), with incremental work expressed in Eq. (5).

$$\delta W=q\delta {\varepsilon }_{q}+{p^{\prime}}\delta {\varepsilon }_{v}$$
(5)

2.2.2 The Calculation Process of Post-consolidation Void Ratios

One important factor to consider when establishing the critical state line (CSL) in the \(e-log {p^{\prime}}\) stress-space is the accurate measurement of a sample's void ratio, \(e\) at failure, which was highly sensitive to measurement inaccuracies at the end of the test. In the ‘forward estimation’ procedure, accurate estimation of \(e\) from the pre-test measurement of sample dimensions is hampered because of volume change that occurs during the saturation phase of triaxial testing, prior to the consolidation and shearing phases, which cannot be readily measured. Several methods have been published in the literature for the accurate determination of the post-consolidation void ratio \((e)\) and initial void ratio (\({e}_{0}\)). The freezing technique appears to have been reported as the most accurate method (Jefferies & Been 2015), but it required special facilities that were not available to the authors. For this study, the ‘backward calculation’ method to measure \(e\) as proposed and successfully implemented by Verdugo and Ishihara (1996) was adopted. In this method, the drainage valves were closed after completion of the shearing stages, and the cell pressure was increased to the maximum capacity of the triaxial device in order to squeeze out the excess volume of water from the soil pores and record same, while the remaining moisture content in the soil specimen was determined by the usual oven-drying method. This removes the need for measurements of sample dimensions prior to testing to establish void ratio which were prone to measurement errors and changes during the saturation phase. It is furthermore logical to determine the void ratios that were based on moisture content since both were directly related. The evolution of void ratios \((e)\) during drained shearing was computed from Eq. 6 from the estimated post-consolidation void ratios \(({e}_{0})\) and the volumetric strain.

$$e={e}_{0}-\left(1+{e}_{0}\right)*{\varepsilon }_{v}$$
(6)

2.2.3 The Norsand Numerical Soil Constitutive Model

The Norsand numerical soil model, chosen as the applicable state-based framework in this study and reviewed along with other critical-state compatible models is summarized in Table 3.

Table 3 A critical review of UBCSAND, PM4SAND, DM04, P2P, NORSAND CS-compatible numerical soil liquefaction models
Full size table

The Norsand model soil properties typically include mainly those of the critical state, stress-dilatancy, stiffness properties, and state-dilatancy parameters. Apart from the CS, the physics of the Norsand model is governed by the principles/theories of plasticity, elasticity, hardening/softening rule, flow rule, and soil state. The Norsand is a critical state-compatible and stress-dependent geomechanical advanced constitutive soil model (Been & Jefferies 2004; Itasca 2021; Jefferies & Been 2015), and already implemented in several commercial numerical model codes (e.g., FLAC; PLAXIS, RS2 and several other commercial software), enabling applications to model real-world engineering problems.

A detailed presentation of the model was provided by Jefferies and Been (2015) and a cursory summary of the main governing equations is provided herein to define the key input soil parameters and focus on calibration as applied in the current study. The model is an improved and advanced invariant of the conventional CamClay model (Jefferies & Been 2015). It incorporated two major postulates of the CamClay model, namely: 1) the existence of a critical state, and 2) the tendency towards the so-called CS with rising shear deformation, dependent on confining stress. A recent and additional established third postulate was the softening of the yield surface due to the principal stress rotation (PSR), Jefferies et al. (2015), and this was mostly applicable to situations under cyclic loading. A quick breakdown of the incorporated theories in the Norsand model are enumerated in the following subsections:

The theory of elasticity: The presumed elasticity depends on the shear modulus of the form expressed in Eq. (7)

$$G = G_{{ref}} \left( {\frac{{p^{\prime } }}{{p_{{ref}} }}} \right)^{m}$$
(7)

where \(p^{\prime }\) is the present mean effective stress. \({G}_{ref}\) and \(m\) are material property constants. A logical and acceptable recommended range of \(m\) is 0 ≤ \(m\)  ≤ 1. The reference atmospheric pressure, \({p}_{ref}\), is usually taken as approximated with a value of 100 kPa (Jefferies & Been 2015).

The critical state: A major requirement for the critical state is that following sufficient shear strain acting on a soil undergoing shear, the volume change tends towards zero. This may be represented when the ‘dilatancy’ \({{\varvec{D}}}^{{\varvec{p}}}\), defined as the change in volumetric strain with shear strain (i.e.\({{\varvec{D}}}^{{\varvec{p}}}=\frac{{\dot{{\varvec{e}}}}_{{\varvec{v}}}^{{\varvec{p}}}}{{\dot{{\varvec{e}}}}_{{\varvec{q}}}^{{\varvec{p}}}}\); where \({\dot{{\varvec{e}}}}_{{\varvec{v}}}^{{\varvec{p}}}\) and \({\dot{{\varvec{e}}}}_{{\varvec{q}}}^{{\varvec{p}}}\) denotes the respective plastic volumetric and deviatoric strain), tends to zero and the change in dilatancy with shear strain is also zero, i.e \(D^{p} = 0;(\dot{D}^{p} )/(\dot{e}_{q}^{p} ) = 0,.\)

In the Norsand model, the CSL is expressed by Eq. 8, a semi-logarithmic straight-line idealization in \(e-\mathrm{logp^{\prime }}\) space.

$${e}_{c}\left(p\right)=\Gamma - \lambda \mathrm{ln}\left(\frac{100p}{{p}_{ref}}\right)$$
(8)

where \(\Gamma\) and \(\lambda\) are the intercept at p’0 and the slope of the CSL respectively and are material property constants.

Alternatively, the critical state void ratio, \({e}_{c},\) may be represented by a three-parameter power model in Eq. 9, where \({C}_{1}, {C}_{2},\) and \({C}_{3}\) are material property constant.

$${e}_{c}\left(p\right)={C}_{1}-{C}_{2}{\left(\frac{p}{{p}_{ref}}\right)}^{C3}$$
(9)

3 The State Parameter

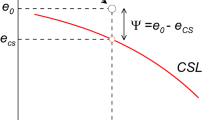
The state parameter is explained as the difference between the present void ratio \(\left(e\right)\) and the critical state void ratio (\({e}_{c}\)) at a given mean effective stress \((p^{\prime }).\) The state parameter is simply represented in the form as shown in Eq. 10 and succinctly captures the current state of the soil in relation to the critical state for any confining pressure, \((p^{\prime })\):

$$\psi =e-{e}_{c}\left(p^{\prime }\right)$$
(10)

3.1 The Failure Yield Surface

The adopted outer yield surface in the Norsand model is likened to the bullet-shaped surface of the well-known CamClay model (Roscoe & Schofield 1963; Schofield & Wroth 1968), expressed in Eq. 11 as:

$$\frac{\eta }{{M}_{i}}=1-\mathrm{ln}\left(\frac{p}{{P}_{i}}\right)$$
(11)

where \({p}_{i},\) known as image stress, determines the magnitude of the outer yield, \(\eta =\frac{q}{p}, q=\sqrt{3{J}_{2}}\), \({J}_{2}\) is a second invariant of the deviator, and \({M}_{i}\) is expressed in Eq. 12:

$${M}_{i}=M\left(1-\frac{{N}_{\chi i}\left|{\psi }_{i}\right|}{{M}_{tc}}\right).$$
(12)

Where \({M}_{tc}\) denotes a strength parameter corresponding to \(q/p^{\prime }\) at critical state in the compressive triaxial (TC) scenario, \(N\) a material constant is known as volumetric coupling coefficient, \(M\) the friction ratio at critical state with an account of the Lode’s angle \(\left(\theta \right)\) influence. Equation 13

$$M={M}_{tc}-\frac{{M}_{tc}^{2}}{3+{M}_{tc}}\mathrm{cos}\left(\frac{3\theta }{2}+\frac{\pi }{4}\right)$$
(13)

The derived parameter \({M}_{i}\) for triaxial compression and extension are shown in Eq. 14 and (15), respectively:

$$M_{i,tc} = M_{tc} - N_{\chi i} \left| {\psi_{i} } \right|,at \theta = {\raise0.7ex\hbox{$\pi $} \!\mathord{\left/ {\vphantom {\pi 6}}\right.\kern-0pt} \!\lower0.7ex\hbox{$6$}}$$
(14)
$$M_{i,tc} = M_{i,tc} - \frac{{3M_{tc} }}{{3 + M_{tc} }},\theta = - {\raise0.7ex\hbox{$\pi $} \!\mathord{\left/ {\vphantom {\pi 6}}\right.\kern-0pt} \!\lower0.7ex\hbox{$6$}},$$
(15)

Where \({\chi }_{i}\) may be approximated according to Eq. (16):

$${\chi }_{i}= \frac{{M}_{tc}{\chi }_{tc}}{{M}_{tc}-\lambda {\chi }_{tc}}$$
(16)

And \({\chi }_{tc}\) is a material constant.

3.2 The Stress-Dilatancy Theory

According to Jefferies and Been (2015), the stress-dilatancy with the associated flow rule can be represented in Eq. 17:

$${D}^{p}=\frac{{\dot{e}}_{v}^{p}}{{\dot{e}}_{q}^{p}}={M}_{i}- \eta$$
(17)

where \({\dot{e}}_{v}^{p}\) and \({\dot{e}}_{q}^{p}\) are the plastic volumetric and deviatoric strain rate, respectively.

The derivations of the complex plastic strain rate ratios are detailed in Jefferies and Shuttle (2002) and not repeated here.

3.3 The Hardening Rule

Norsand’s hardening theory is directly related to the second postulate, and expressed in Eq. 18:

$$\frac{\dot{{p}_{i}}}{{P}_{i}}=H\frac{{M}_{i}}{{M}_{i,tc}}{\left(\frac{p}{{p}_{i}}\right)}^{2}\left(\frac{{p}_{i,max}}{p}-\frac{{p}_{i}}{p}\right){\dot{\varepsilon }}_{q}^{p}+S{T}_{s}+{T}_{PSR}$$
(18)

where \(H\), the hardening modulus is expressed in Eq. 19 as:

$$H={H}_{0}+{H}_{y\psi }$$
(19)

\({H}_{0}\) and \({H}_{y\psi }\) are material constants. \({p}_{i,max}\) is expressed in Eq. 20 as:

$${p}_{i,max}=pexp\left(-\frac{{\chi }_{i}{\psi }_{i}}{{M}_{i,tc}}\right)$$
(20)

The input of \(S=0\) will nullify the effect of the optional cap softening term \({T}_{s}\). \(S\) is zero by default, and its permissible range is \(0\le S\le 1\). A high \(S\) value will lead to quicker softening of sand in typical undrained shear loading. \(S\) > 0 is not recommended for drained loading. The last term in Eq. 20 captures the effects of principal stress rotation according to Jefferies et al. (2015) and expressed in Eq. 21 as:

$${T}_{PSR}=\left[-z\left(\frac{{p}_{i}}{p}-\frac{1}{r}\right)\left|\frac{\dot{\alpha }}{\pi }\right|+\frac{1}{r}\right]\left|{\psi }_{i}\right|$$
(21)

where \(z\) is a material property, \(r=\mathrm{exp}(1)\approx 2.718\) is the fixed value for the yield surface spacing ratio, \(\alpha\) is the angle between the major principal stress direction and the referenced y-coordinate.

3.4 The Calibration of Soil Parameters for the Norsand Model

The software tool that was used for the calibration of the advanced Norsand soil parameters was the NorTxl2, an open-source visual basic (VBA) program within a Microsoft®Excel® spreadsheet provided by Jefferies and Been (2015) for the calibration of soil properties with the Norsand model. The NorTxl2 implements the Norsand governing equations for a single element model under triaxial loading conditions, where new stresses and strains in response to the applied triaxial stress-path loading were computed by the Euler integration method. The NorTxl2 itself simulates four different aspects of the soil behavior but does not simulate the generated excess porewater pressures (PWP). The simulation of the excess PWP is a boundary value problem that required comprehensive numerical simulation of the stress conditions as provided typically within the finite element (FEM) or finite difference method (FDM)—software.

The Fast Lagrangian Analysis of Continua (FLAC) developed by Itasca (2021) is a well-known commercial numerical software for advanced geotechnical analyses in two-dimensions and uses the FDM approach.

The soil undrained shear strength was determined by stress and strain invariants, and not by the principal stresses (Jefferies & Been 2015). To derive the strain invariants, the actual triaxial data was first transformed from the laboratory-measured results to reflect the so-called strain invariants. The strain invariants, i.e., the volumetric strain \(({\varepsilon }_{v})\) was correlated with the corresponding shear strain \(({\varepsilon }_{q})\) based on Eq. 22, where \({\varepsilon }_{1}\) is the current strain state.

$${\varepsilon }_{q}={\varepsilon }_{1}-{\varepsilon }_{v}/3$$
(22)

From the fundamentals of the stress-dilatancy theory, the shear and volumetric strains from the original drained test data were converted as a ratio of strain increments by the central difference method of differentiation in NorTxl2. The parameter of particular interest here is the maximum stress ratio \({(\eta }_{max})\), and the corresponding magnitude of dilatancy known as minimum dilatancy \({(D}_{min})\). In theory, it was said that stress dilatancy would have \({\eta }_{max}\) corresponding with \({D}_{min}\) (Jefferies & Shuttle 2020). The primary reason for focusing on \({D}_{min}\) was because the frictional ratio at the critical state \((M)\) varies with the soil fabric.

In addition, the evolution of void ratios \((e)\) during drained shearing is required, and it was computed from Eq. 6 from the estimated post-consolidation void ratios \(({e}_{0})\) and the volumetric strain.

Lastly, from the drained data, the state parameter corresponding to \({D}_{min}\) was computed from Eq. 23 as

$${D}_{min}= {\rm X}*\Psi$$
(23)

The transformation of stress invariants utilizes \(q\) and \(p^{\prime }\), (refer Eqs. 1 and 2). A breakdown of the calibration procedures for Norsand model parameters is enumerated subsequently.

3.5 The Critical State Line (CSL) Soil Parameters

The two key soil critical state parameters for defining the CSL, gamma \((\Gamma )\) and lambda (\({\lambda }_{10}\)) were determined mainly from the undrained test data as fitted in the \(e-\mathrm{log} p^{\prime }\) stress-space. \(\Gamma\) is the altitude of the CSL at a reference \(p^{\prime }\) corresponding to 1 kPa and \({\lambda }_{10}\) is the corresponding slope of the CSL in the void ratio- MES \((e-\mathrm{log} p^{\prime })\) space (Been et al. 1991), the critical state parameters were considered as intrinsic soil properties. First, the undrained tests were carefully examined to select the MES at the onset of the critical state. Overall, both the drained and undrained \(e-\mathrm{log} p^{\prime }\) were plotted and fitted with Eq. 8 to obtain the best-fit linear relationship. The corresponding derived critical state line (CSL) for the ECS is shown in Fig. 4.

Fig. 4
figure 4

The calibrated critical state line of ECS

Full size image

3.6 The Soil Elasticity-Based Parameters

The relevant soil elastic properties herein included the maximum shear elastic modulus at a reference initial effective stress (\({G}_{max} @ {p}_{0}\)), the elastic exponent (\({G}_{exp})\), and the Poisson’s ratio (\(\upsilon )\). The \({G}_{max}\) may be determined in the laboratory by measuring the shear wave velocities using bender element tests, or in the field by seismic testing (SCPT, downhole or crosshole methods) for example. Alternatively, it may be estimated from empirical relationships to field geotechnical test data (typically CPT or SPT), or laboratory test data as a function of void ratio and confining stress (e.g., Hardin & Richart 1963). In this paper, a forward iterative modeling (FIM) method was applied to estimate \({G}_{max}\), and comparisons made with data of similar soils from the elastic model in NorTxl2 and deriving the best-fit value for the various soil models, refer to Fig. 5 for the elastic modulus check of ECS. From Fig. 5, it can be observed that the elastic modulus linearly increased with the corresponding mean effective stress increase. In other words, the elastic modulus was the function of \(p^{\prime }\) in the soil. Experiments for the determination of Poisson's ratio are extremely difficult to execute in the laboratory, however, typical values in geotechnical engineering practice ranges between 0.15 to 0.3 for soils, a value of about 0.15 was adopted in the current study.

Fig. 5
figure 5

The applicable elastic modulus of numerical simulations

Full size image

3.7 The Soil Plasticity-Based Parameters

The soil plasticity parameters include \({M}_{tc}\), \({N}_{tc}\), \({\rm X}_{tc}\), \({H}_{0}\), and \({H}_{\Psi }\). The subscript tc in the parameters simply indicates the triaxial condition. The properties \({M}_{tc}\) and \({N}_{tc}\) are intrinsic stress-dilatancy properties, referred to as critical friction ratio and volumetric coupling coefficients, respectively. The initially computed dilatancy rate parameter \(\left(D\right)\) as per Been and Jefferies (2004) was subsequently plotted against the stress ratios (\(\eta =q/p^{\prime }\)). The corresponding minimum dilation (\({D}_{min})\) was obtained from Fig. 6 for the derived dilatancy plot for ECS as per Been and Jefferies (2004). Figure 6 alone is not enough to decide the parameters, the plot shown in Fig. 7 is the fitted test data trend for selecting the \({M}_{tc}\) and \({N}_{tc}\) soil parameters. The minimum dilation \(({D}_{min})\) and corresponding maximum stress ratios \({(\eta }_{max})\) for each test are then determined and fitted plots of \({\eta }_{max}\) vs \({D}_{min}\) are created for picking the \({M}_{tc}\) and \({N}_{tc}\) values.

Fig. 6
figure 6

Computed stress–dilatancy plots of ECS

Full size image
Fig. 7
figure 7

Calibration of soil parameters \({M}_{tc}\) and \({N}_{tc}\)

Full size image

The parameter \({\rm X}_{tc}\), is the property defining the state-dilatancy of the soil. The determination of \({\rm X}_{tc}\), similarly, followed the trendline of plotting \({D}_{min}\) versus the state parameter \((\Psi )\). However, the data for the densely prepared samples in this study appeared to be sparse when plotted, hence, engineering judgment was applied in selecting the applicable values used in simulations by using the forward iterative modeling (FIM). Typical values of \({\rm X}_{tc}\) ranges between 2.0—4.0 as found in Jefferies and Shuttle (2020). The parameter \({H}_{0}\) and \({H}_{\Psi }\) are plastic modulus, derived simply by FIM to determine the best fit with the test/experimental data, this soil property is dependent on the soil fabric and consequently, it is a function of the state parameter.

3.8 The Initial Soil State-Based Parameters

The initial soil state parameters included the state parameter (\({\Psi }_{0}),\) post-consolidation void ratio \(({e}_{0})\), initial \({p}_{0}^{\prime }\), and the overconsolidation ratio (\(OCR)\). A positive \({\Psi }_{0}\) indicates a loose soil sample state, while a negative \({\Psi }_{0}\) indicates a dense material state. The best fit of the parameter \({\Psi }_{0}\) will compute the perfect match of all soil engineering properties as obtained from the simulations by iteration. For simplicity, it is assumed that the soil samples are normally consolidated (NCL) under isotropic triaxial conditions, hence, the overconsolidation ratio (\(OCR)\) that was utilized in all simulations ranges between 1.0 to 1.2. In-situ soils in the field would likely exhibit anisotropic behavior (e.g., Papadimitriou, 2019; Rahman & Dafalias 2022; Taiebat & Dafalias 2008), whose analyses are rather considered too complex for simple and quick evaluation in the context of this study, hence simplifying the assumptions is more realistic and convenient.

3.9 Soil Numerical Modeling in VBA and Flac Codes

The calibration tests typically included the consideration of one-zone soil elemental simulation tests based on the conditions of static, loose, undrained triaxial compression conditions (TC) on the studied ECS sand specimens, with further consideration of the so-called conditions that will best-fit with the initial state for static/flow liquefaction modelling, and would mimic the same scenarios as found in the field. The numerical simulations of five different aspects of the soil's undrained behavior under monotonic loads were executed in both VBA and the FLAC codes. In the VBA code, the drainage mode can also be toggled between drained and undrained mode, the CSL idealization can also be toggled between the semi-log and curved CSL idealization. The semi-log CSL idealization was adopted and assumed reasonable for all the executed simulations herein.

The derived soil parameters are summarized in Table 4 and utilized in the subsequent FLAC simulations. The numerical simulation tests were carried out in FLAC by examining a one-zone soil model with an axisymmetric configuration, and a unit dimension in the x- and y-directions. Figure 8 shows the typical configuration of the one-zone soil element boundary conditions and grid system in FLAC.

Table 4 The calibrated Norsand soil parameters and key outputs
Full size table
Fig. 8
figure 8

The specified boundary conditions for a 1-zone soil simulation in FLAC

Full size image

The specified boundary condition in Fig. 8 was such that the base of the model was a roller boundary, the side was subjected to the initial testing MES,\({p}_{0}\), and fixed velocity boundary and strain rate of 1e-6 was applied at the top. A reasonable initial in-situ stress was specified in the FLAC code by a FISH program. FISH is a programming language that is embedded in the FLAC software to write new functions, and assign or obtain model variables and outputs, accordingly. The groundwater configuration was set to a no-flow condition with its fluid properties, the initial fluid tension, and fluid modulus set as constants as -1e20 and 2e6, respectively. In summary, the utilized FLAC code for simulations was written as a batch file in a notepad document and called by the assigned file name into FLAC to run simulations subsequently. The obtained outputs from the FLAC plot histories were further exported into excel.csv files for further post-processing where comparisons of the simulations can be easily made with the VBA and FLAC code for further analytical discussions with the experimental results.

4 Results and discussions

The deviatoric stress – axial strain relationships during flow failure in sandy soils is usually typified by a sharp increase of the deviatoric stress to some peak value, followed by a rapid drop until the steady-state otherwise known as the critical state is attained, and subsequently followed by the so-called constant rate of shear deformation. As shown in Fig. 9, reference to similar studies (e.g., Rahman et al. 2014; Rees 2010) indicated that flow responses are usually identified as strain-softening otherwise known as flow failure (FF), strain-softening changing to strain-hardening (i.e., limited flow, LF), and complete strain-hardening (i.e., no flow, NF). The variation of the soil behavior of the above-mentioned three different stress paths can be directly associated with the difference in soil state which includes relative densities, void ratios, state parameters, OCR, and the existing inter-particle MES between the soil grains/fabric.

Fig. 9
figure 9

Undrained monotonic responses classification types for sands per Rahman et al. (2014)

Full size image

FF was the obtained typical characteristics of the investigated loose ECS specimens, tests were stopped immediately after the observed FF and the consequent collapse of the specimen inside the triaxial cell. From an experimental perspective, SS implies that no change of deviatoric stress must be observed with shearing, meaning a constant rate of soil deformation on the deviatoric stress–strain plots must be attained with no re-gain of deviatoric stress with further shearing (e.g., Rahman et al. 2014). However, the constant rate of deformation did not apply to the studied ECS soil specimens that were tested within 50 kPa to 200 kPa consolidation MES levels as the sample has already collapsed inside the triaxial cell under FF. The typical stress – strain plots and MES paths as obtained from the triaxial tests are shown in Fig. 10 (a and b), respectively. The derived CSL in the MES space was shown in the red line in Fig. 10 (b).

Fig. 10
figure 10

The obtained laboratory stress–strain and MES path of the tested 4 MES levels

Full size image

The experimentally observed soil characteristics plots were directly compared with the simulated results for five (5) different aspects of the soil behaviors under static loads, namely, the deviatoric stresses versus axial strains, the effective stress paths (ESP) showing the stress invariants (i.e., \({p}^{\prime }-q)\) stress space, the volumetric strains versus axial strains, the void ratios versus mean effective stresses showing the CSL in the \(e-logp^{\prime }\) stress space and the excess porewater pressures (PWP) versus axial strains. The first four mentioned aspects above are shown in Fig. 11 for the initial consolidation MES levels of 50 kPa, 100 kPa, 200 kPa, and 300 kPa, respectively. As can be seen in Figs. 10 and 11, the ECS specimens within 50 kPa to 200 kPa MES all experienced the FF mechanism except that LF was the obtained soil response at a higher mean effective stress of 300 kPa.

Fig. 11
figure 11

Comparisons of ECS soil experimental data with the Norsand simulations

Full size image

As noted by Jefferies and Been (2015), most flow failures would usually occur at axial strains that are less than 10% and this fact was consistent with soil specimens tested between the MES of 50 kPa to 200 kPa.

From Figs. 11 and 12, one can see that the simulations were reasonably in good agreement with the experimentally measured soil responses. One striking feature of the Norsand model is that only one set of soil properties is required for numerical simulations. As can be observed in Table 4, only the soil plasticity, elasticity, and the initial state varied as a function of the soil MES, the remaining Norsand properties were the same. The match of the soil model results for the stress-strains relationship and ESPs were identical to the laboratory-measured ones. Although the match of the simulated porewater pressures and the laboratory-measured indicated some minor shoots at the transitioning point between the elastic and plastic part of the axial strain, more iterations of the constant fluid modulus as set in FLAC would produce a perfect match. Hence, at test confining stresses of 50 kPa, 100 kPa, 200 kPa and 300 kPa, the approximate resulting excess PWP were 48 kPa, 98 kPa, 200 kPa, and 240 kPa, respectively. Overall, the simulations results were in good agreement with the experimental measured results for the ECS sand.

Fig. 12
figure 12

Comparisons of the laboratory measured excess PWP versus FLAC model outputs

Full size image

In the current practice, the conventional Mohr–Coulomb (MC) soil model coupled with the limit equilibrium method (LEM) was mostly applied for the computations of the critical factors of safety in global slope stability and landslide issues. The pitfall is that MC model was an over-approximation of the actual transition between the elastic and plastic part of the shear strain of the soil and was unable to capture some notable key features of the soil behavior such as the generated excess PWP, softening, and hardening phenomena. Therefore, it is recommended that suitable models that will capture the significant characteristic soil engineering behavior are applied in 21st-century geotechnical engineering practice. Lastly, the observed slight deviations of the simulated versus laboratory measured post-consolidation void ratios in Fig. 11 (h, l and p) can be attributed to the slightly experienced errors during the computation of the post-consolidation void ratios after shearing. Hence, the freezing method of void ratio estimation is strongly recommended for tests aiming to determine accurate critical state parameters of soils.

5 Conclusions

Summarily, the numerical and laboratory test results were in good agreement for the studied five different aspects of the undrained flow failure behavior of ECS. The investigated ECS within the MES of 50 kPa and 200 kPa in combination with loosely remolded high void ratios exhibited the typical flow failure characteristics. The undrained properties of ECS transformed to a limited flow at a higher testing MES of 300 kPa with the well-known quasi-static steady-state phenomena. The basic soil index properties of ECS indicated that it is predominantly a poorly graded sand (SP) according to the unified soil classification system (USCS). Executed scanning electron microscopy on ECS indicated that its grain shape is angular to subangular and fine in texture. The ECS has a specific gravity of 2.60, minimum and maximum density in the range of 1.43 g/cm3 to 1.67 g/cm3, corresponding minimum and maximum void ratios of 0.561 to 0.820, respectively, permeability in the range of 4.76*10−4 to 6.66*10−4 cm/s, compression index \({C}_{c}\) of 0.0002325 and swelling index \({C}_{s}\) of 0.0000597 as obtained from 1D consolidation test. At 50 kPa, 100 kPa, 200 kPa and 300 kPa test confining stresses, the obtained peak undrained shear strengths just before failure were 29 kPa, 84 kPa, 130 kPa, and 200 kPa, respectively. A linear increase of the soils’ elastic modulus was observed with increase in corresponding testing confining stresses and this is consistent with obtained facts from the literature (e.g., Verdugo & Ishihara 1996).

The advantages and disadvantages of some selected critical state compatible advanced numerical models were summarized while justifying the selection and application of the Norsand soil constitutive framework herein for validating the studied ECS undrained strength characteristics at higher void ratios. The initial calibration of the soil model properties which appear daunting was simplified under the triaxial soil condition, soil model properties may also be calibrated with in-situ tests such as the cone penetrometer tests but are considered out of scope herein. The notable limitations of the application of numerical models may be associated with the soils’ non-linear stress–strain relationships, shear banding during testing, and physical instabilities. The Norsand model can capture the important soil strength characteristics within a combination of a range of void ratios and MES. Hence, the CSSM has proved significant in computing most features of typical undrained soil behavior under static loads.