1 Introduction

Dams are essential infrastructure for water provision and have been serving human societies for 5000 years (ICOLD 2013). Dams are the cornerstone of water resources management by supplying water for irrigation, domestic, and industrial use, flood control, aquaculture, navigation, and recreation activities (Torabi Haghighi et al. 2014). However, dam failure and dam breaks can have catastrophic results. Dam failure gives rise to considerable costs and can result in loss of life and property, particularly in densely populated areas. Overtopping, internal erosion, and seepage problems in dam walls and foundation are reported to have been the main mechanisms behind 111 previous dam failures (ICOLD 1995).

Seepage is a fundamental process in earthfill dam engineering, occurring due to soil permeability and pore pressure in porous media (Hekmatzadeh et al. 2018; Zhou et al. 2015). Uncontrolled flow with high pore pressure in the dam body and foundation leads to internal erosion and piping, which is the reason for 30–50% of earth dam failures (Meehan et al. 2019; Salari et al. 2018). The Hyttejuvet dam in Norway (Ng and Small 1999), the Balderhead dam in the UK (Vaughan et al. 1970), the Viddalsvatn dam in Norway (Vestad 1976), and the Teton dam in the US (Seed et al. 1976) are some examples of earthfill dams that failed due to uncontrolled seepage and hydraulic fracturing.

Although dam builders attempt to use the specified material in the dam embankment, available construction materials are not identical in different layers. One of the main challenges in designing and constructing earthfill dams is the variation in foundation type and available construction materials, which make it impossible to construct a seepage-free structure (Athani et al. 2019). Flow pathways and quantity of seepage from an earthfill dam and its foundations directly and indirectly influence dam safety and reservoir operation. Earthfill dams are designed to be sufficiently safe in different phases of construction, impounding, rapid drawdown, and operation. In this regard, seepage in the dam body and foundation poses a major challenge to the stability of the upstream and downstream slope. Generally, dams and their foundation are equipped with several design features to control and reduce the amount of seepage. Depending on the purpose and expected performance of an earthfill dam, seepage control measures (SCMs) can be constructed in the dam body (e.g., horizontal and vertical drains) or in the foundations (e.g., cutoff wall and grouting diaphragm). Acceptable efficiency of these SCMs could guarantee the required safety of the dam.

Malfunction of SCMs can occur due to shortcomings in design, construction, and operation, or to natural hazards, e.g., earthquakes or intensive rain events. Shortcomings in the design of earthfill dams could be due to misunderstanding about the exact soil characteristics because of insufficient geological and geotechnical investigations, or unpredicted changes in soil characteristics. In the construction process, carrying out soil compaction and placing a transition layer (e.g., filter) between coarse and fine material may be inadequate to meet the design specifications, and can lead to unexpected problems (Zomorodian et al. 2006).

The main aim of this study was to develop a framework for assessing the efficiency of SCMs in earthfill dams. The framework was designed based on comparisons of expected and observed values of seepage magnitude and pore pressure. The main parameters considered in comparisons were seepage quantity from dam and foundation, and piezometric head before and after seepage control features. Expected seepage values were obtained from simulations of seepage using the finite element method, while observed values were obtained directly from dam monitoring systems. There are different methods for monitoring seepage, e.g., using triangle wires, geophysical surveys, temperature measurements, resistivity measurements, and radar technologies (Panthulu et al. 2001). In addition, different type of piezometers can be used to measure the piezometric head in different cross-sections and points. The framework developed here was tested in a case study, by using it to assess the efficiency of Doroudzan dam on the Kor River in Iran.

2 Material and Methods

2.1 Case Study, Doroudzan Dam

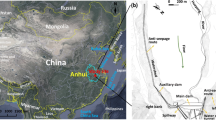
Doroudzan dam is a multipurpose earthfill dam constructed on the Kor River in southern Iran (Fig. 1). It was commissioned in 1972 to control flooding, generate hydropower, supply potable water, and irrigate around 110,000 ha (Pour et al. 2009). The dam is classified as homogeneous, with a layer of riprap protection. The volume of the dam body is 4.8 × 106 m3, the height is 57 m, the crest length is 710 m, the crest width is 10 m, and the maximum width at the base of the dam is 375 m. Total reservoir volume is estimated to be 993 × 106 m3, covering an area of 55 km2 at normal water level (Moayedi et al. 2010; Torabi Haghighi 2003).

Fig. 1
figure 1

Doroudzan dam (a) location in Iran, b plan view (Jalali 2005), and c cross-section of dam structure (Jalali 2005)

Full size image

The Doroudzan dam is constructed on an alluvial foundation that comprises two main layers (Fig. 1). The upper layer is approximately 25–28 m thick and consists of alluvial sediment, including a thick layer of sand, silt, and clay on the top, and gravel and sand in the lower parts. The lower layer is 7–12 m thick and consists of fine-grained material of clay and silt. The lower layer extends 250 m upstream and plays an important role in seepage control in the dam’s alluvial foundation. The main bedrock type in both abutments is limestone, but there are weathered and fractured zones in the left abutment. Lugeon tests performed in the pilot phase of the present study confirmed the possibility of seepage from the left abutment. There was no reported spring flow in that abutment in the study period, but two springs have appeared in the left abutment since dam impounding and spring flow is reported to fluctuate in discharge with reservoir water level (Torabi Haghighi 2003).

2.2 Seepage Control Measures in Earthfill Dams

Piping or internal erosion is one of the major problems in earthfill dams (Fell et al. 2003; Flores-Berrones et al. 2010; Richards and Reddy 2007). In general, internal erosion is the result of uncontrolled seepage in the body or foundation of the earthfill dam, which is initiated from the downstream toe toward the upstream face of geotechnical structures. In order to avoid piping in earthfill, it is important to select suitable materials for construction and to install a transition material (filter) between the coarse and fine materials. In addition, seepage control structures, such as vertical, chimney, horizontal drains, upstream clay blanket, and impermeable cores, can be installed in the dam cross-section to convey or minimize seepage flow. Regarding the fluvial foundation, a cutoff wall, cutoff trench, and relief wells may be constructed to control seepage flow. In terms of rock foundation or abutments, a grouting diaphragm is a common method of seepage control. However, a seepage monitor system should be installed in the dam embankment, foundation, and abutments to record seepage flow and pore water pressure.

In Doroudzan dam, seepage flow and pore water pressure are controlled by a grouting diaphragm in the abutments (Fig. 1b), a cutoff wall (Fig. 1c), a chimney drain and horizontal drain in the body of dam (Fig. 1c), and relief wells in the alluvial foundation (Fig. 2). The chimney drain collects seepage water in the upstream part of the dam body and conveys it to the horizontal drain for transfer to the downstream part of the dam (Fig. 1c). These two drains are connected to the dam body with suitable filtering and water-conducting materials. The cutoff wall, which serves to control seepage in the foundation of the dam, consists of two parallel clay-concrete walls, with a space in between filled with grouting bentonite clay, embedded in the underlying impervious layer (Fig. 1c). It is worth mentioning that the relief walls are placed in left sides of dam’s downstream. In the right abutment, there are two plunge pools as a stilling basin for outflow from hydropower and outflow to the river (Fig. 2). Both plunge pools were constructed on natural bed and armored with riprap. These two free seepage surfaces allow the high-pressure seepage flow from the foundation to be released freely (same function as relief walls in left part), but these flows are not measured by the dam monitoring system.

Fig. 2
figure 2

The seepage monitoring system in Doroudzan dam (background imagery from Google Earth Accessed 05.02.2019)

Full size image

2.3 Doroudzan Dam Monitoring System

The original monitoring system for Doroudzan dam was simple due to available technology at the time of construction (1968–1972). It included 29 hydraulic and nine standpipe piezometers installed in the dam body and foundations. All hydraulic piezometers were damaged during early dam operation and unfortunately did not provide any reliable information. In 1998, 14 new standpipe piezometers were installed in dam body (Fig. 2). Of these, 12 piezometers (NP1–NP12) were installed in the four longitudinal cross-sections in parallel with the dam axis (L sections in Fig. 2) and in three cross-sections in parallel with the dam center line (C sections in Fig. 2). In the first parallel cross-section (C1), four piezometers were placed in the upstream slope of the dam embankment (NP1, NP4, NP7, and NP8), at 14.0 m distance from the dam center line. In the second and third parallel cross-sections, the new piezometers were installed in the downstream slope of embankment at a distance of 10.0 (C2: NP2, NP5, NP8 and NP11) and 100.0 m (C3: NP3, NP6, NP9 and NP12) from the dam center line (Fig. 2). For the assess the efficiency of SCMs we used the observed data of 12 new piezometers (NP1-NP12) and one of old piezometer (OP1). The magnitude of seepage flow from drains, relief walls is measured by nine triangular weirs. total seepage from dam, foundation and the two springs which appeared at the left abutment, near the dam toe, is measured by a Parshall flumes (Fig. 2). The seepage flow from springs are estimated by deducting the magnitude of seepage of dam and foundation (triangular weirs) from total seepage (Parshall flume). The monitoring schedule is two times per month.

2.4 Seepage Analysis

The seepage flow in an earthfill dam is described using the mass balance relation. Assuming Darcy’s law, the seepage flow in the dam cross section may be simulated in two dimensions according to Eq. 1, considering steady-state condition (Hekmatzadeh et al. 2018).

$$\frac{\partial }{\partial x}\left( {K_{x} \frac{\partial h}{{\partial x}}} \right) + \frac{\partial }{\partial z}\left( {K_{z} \frac{\partial h}{{\partial z}}} \right) = 0$$
(1)

where \(K_{x}\) and \(K_{z}\) stand for the hydraulic conductivity of dam materials along x and z direction, respectively; and \(h\) is the water head. This equation was solved numerically using the finite element method (FEM) in the SEEP/W software. In this study, we assumed equal values for both kx and ky.

Regarding boundary conditions, a constant water head (lake water surface level) was considered for the upstream boundary, while seepage face was defined for downstream part since the zero pressure in not known before the seepage analysis.

Of note, the SEEP/W software consider seepage flow in both saturated and unsaturated zone, which need to definition of hydraulic conductivity as a function of soil saturation.

2.5 Assessing the Efficiency of Seepage Control Measures

To assess the efficiency of SCMs, we compared expected and observed values of seepage flow and piezometric head in the standpipe piezometers in the dam embankment. Comparisons were performed based on four reservoir water levels (1661, 1665, 1671, 1676.5 masl) as upstream boundary conditions. The linear correlation between the reservoir water level and the water level in piezometers was analyzed to estimate the observed value of piezometric head and seepage flow at the four reservoir water levels:

$$P_{WL} = m \times R_{wl} + b$$
(2)

where PWL is observed water level (masl) in piezometer, RWL is water level in the reservoir, and m and b are the slope and intercept of the linear regression.

The linear correlation between the reservoir water level and observed seepage flow was analyzed to estimate the observed value of seepage flow at the four reservoir water levels:

$$Q_{seep} = m \times R_{wl} + b$$
(3)

where Qseep is measured seepage flow on the downstream side (measured flow from Parshall flume and triangular weirs), Rwl is water level in the reservoir, and m and b are the slope and intercept of the linear regression.

Overall performance (efficiency, eff) of SCMs was calculated based on the difference between expected and observed total seepage flow from the dam body and foundations:

$$eff = 1 - \frac{{Q_{Obs} - Q_{Exp} }}{{Q_{Exp} }}$$
(4)

where QObs and QExp are observed (from monitoring system) and expected (from seepage numerical simulation) amount of seepage flow from the dam embankment, foundation and springs. To evaluate the expected values, we used the Seep/W software for 2D seepage analysis. We applied the Seep/W model for three cross-sections of the dam (type I, II, and III in Fig. 3a), which were obtained from the geometry of the dam (Fig. 3b). Based on the soil permeability of dam components (Jalali 2005; Torabi Haghighi 2003), we defined eight layers in the Seep/W model (Fig. 3d). Due to the dam geometry, about 300 m of dam valley is filled by the main cross-section (type I in Fig. 3). The rest of the dam body was constructed in smaller cross-sections (types II and III in Fig. 3). By considering the distance between the cross-sections (Fig. 3b) and the seepage flow from each cross-section, the total amount of seepage flow (Doroudzan dam) from the whole dam and foundation (Q, m3 s−1) was estimated as:

$$Q = \left( {l_{1} + l_{7} } \right)\frac{{q_{3} }}{2} + \left( {l_{2} + l_{6} } \right)\left( {\frac{{q_{3} + q_{2} }}{2}} \right) + \left( {l_{3} + l_{5} } \right)\left( {\frac{{q_{1} + q_{2} }}{2}} \right) + \left( {l_{4} )(q_{1} } \right)$$
(5)

where l1–l7 (m) are the distances between different cross-sections (Fig. 3) and q1–q3 (m3 s−1) are the calculated flows per meter of width in the three different cross-sections. The Eq. 5 could be simplified by substituting the values of l1–l7 into Eq. 5 as follow:

$$Q = 400q_{1} + 175q_{2} + 125q_{3}$$
(6)
Fig. 3
figure 3

a, b, c Dam cross-section at different distances from the right and left abutment regarding bedrock and fluvial condition of the geological cross-section of Doroudzan dam and d Permeability of different layer used in modeling

Full size image

The seepage was modeled for the three cross-sections (types I–III) and considering the four different water levels (1661, 1665, 1671, and 1676.5 masl) for the reservoir as upstream boundary condition.

To estimate the magnitude of seepage from the left abutment, the seepage model has been run for a cross-section of left abutment based on a hemogenic system with considering the broken rock chartrestics for the modeling. Then we added a grouting diaphragm with 1 lu (Lugen: unit for hydraulic conductivity of the rock and is about 1.30 × 10–7 ms−1) permeability to left abutment cross section and run the model to estimate the expected value for seepage from left abutment or active spring in this area.

SCM efficiency (cutoff wall, chimney drain) was quantified based on piezometric head before and after the SCM as:

$$Eff_{{SCM}} = 1 - \frac{{\Delta H_{{Obs}} - \Delta H_{{Exp}} }}{{\Delta H_{{Obs}} }}$$
(7)

where ∆HObs and ∆HExp are observed and expected value of the difference in piezometric head before and after the cutoff wall or chimney drain.

3 Results and Discussion

3.1 Observed Value of Water Level and Seepage Flow

3.1.1 Observed Water Level in Piezometers

Monitoring data from the piezometers (two times per month since 1998) clearly showed the performance of the different SCMs (Fig. 4). The water level in piezometers in the first cross-section upstream (C1; piezometers, NP1, NP4, NP7, and NP10) (Fig. 2) showed a strong correlation (R2 > 0.95) with the water level in the reservoir (Fig. 4, Table 1). In this cross-section, the lowest water level was observed in NP10, which is the piezometer nearest the left abutment (Fig. 4). For example, at normal water level in the reservoir (1676.5 masl), the water level in the piezometer nearest the right abutment (NP1) was 2.80 m higher than that in NP10 (Fig. 5a2). This indicates possible seepage flow from the body of the dam to the left abutment. The reason may be insufficiency of the grouting diaphragm in the left abutment since, according to construction reports, this diaphragm was not completed properly in the construction period (Jalali 2005). The water level in piezometers in the second and third cross-sections downstream (C2 and C3) showed a weak correlation (R2 < 0.20) with the water level in the reservoir except in two piezometers (NP11, R2 = 0.33; NP12, R2 = 0.52). These piezometers are installed in the closest longitudinal cross-section (L4) to the left abutment (Fig. 4, Table 1). The observed water level in NP11 and NP12 was higher than in other piezometers installed at the same distance from the dam center line in other longitudinal cross-sections (L1–L3). The water level in NP11 and NP12 was 3.29 and 1.88 m higher than in NP2 and NP3, respectively, at normal water level in the reservoir (1676.5 masl) (Fig. 5 b2, b3). This indicates possible seepage of water back from the left abutment to the dam body, with the appearance of the two springs confirming the presence of uncontrolled flow in this area. Of 9 old piezometers, piezometer OP2 and OP9 does not work, OP1 and OP4 have strong correlation with water level in the reservoir, OP3 and OP5 shows low fluctuation in piezometric heads and weak correlation with water level in the reservoir and seem to have problem, Finally piezometric head in OP6, OP7 and OP8 have correlation with water level in reservoir (Table 1 and Fig. 4).

Fig. 4
figure 4

Correlation between observed water level in the reservoir and in piezometers in Doroudzan dam

Full size image
Table 1 Linear correlation (R2 value) between water level in the reservoir and in piezometers
Full size table
Fig. 5
figure 5

Observed water level in (1) the reservoir and piezometers and (2) piezometers from right abutment to left at normal water level in the reservoir (1676.5 masl). a upstream piezometers (C Sec1), b and c downstream piezometers (C Sec2 and C Sec3)

Full size image

Monitoring of new piezometers clearly shows specific conditions of the left abutment (Fig. 5a2, b2 and c2). In the upper face of dam, the piezometric head near the left abutment is lower than other parts and it indicates possible flow from dam body into the abutment (Fig. 5a1, a2). While in lower part of dam’s body, the piezometric head in the left is higher than right side (Fig. 5b2, c2) and it shows the possibility of flow from left abutment to dam body. Appearing the springs in the left abutment could confirm this possibility as these springs has been activated after filling the reservoir in 1972 and their discharge have correlation with reservoir water level (Fig. 6b).

Fig. 6
figure 6

Correlation between reservoir water level and seepage flow from a total outflow, b springs, and c dam and foundation

Full size image

Based on observed data from piezometers, the performance of the chimney drain and cutoff wall is acceptable, considering the significant drop in piezometric head between upstream and downstream of these SCMs (e.g., NP1 and NP2; Fig. 4) and the weak correlation between water level in the reservoir and downstream piezometers (e.g., NP2, NP5, NP8; Fig. 4).

3.1.2 Observed Seepage Flow

Seepage from the dam and its foundation showed a strong linear correlation (R2 = 0.89) with reservoir water level (Fig. 6). Observed seepage flow from dam and foundation was 32.95, 41.27, 49.58, and 58.75 L s−1 at a reservoir water levels of 1661, 1666, 1671, and 1676.5 masl, respectively (Fig. 6c). Total seepage outflow and spring flow also showed a good correlation with reservoir water level (Fig. 6a, b). At normal water level in the reservoir (1676.5 masl), total seepage outflow was 327.2 L s−1 and spring flow was 273.04 L s−1 (Table 2).

Table 2 Amount of seepage from dam and foundation and abutment, and efficiency of seepage control measures (B: body, F: foundation, qI-III refer to cross-sections shown in Fig. 3)
Full size table

3.2 Expected Value of Water Level and Seepage Flow

Seepage simulations using the Seep/W model of the dam and left abutment were carried out for the three cross-sections shown in Fig. 3 (types I–III) and the four different reservoir water levels (1661, 1666, 1671, 1676.5 masl). The amount of seepage flow from the dam and foundation and from the left abutment was calculated based on the different cross-sections and desired water levels upstream (Fig. 3). The expected water level before and after the chimney drain and two sides of the cutoff wall was calculated based on the piezometric head in the seepage model for the main cross-section of the dam (Fig. 1c; type I in Fig. 3).

3.3 Efficiency of Seepage Control Measures

Comparisons of expected and observed seepage flow values revealed that the overall efficiency of the seepage control system varied between 51 and 70% at different reservoir water levels (Table 2). Both expected and observed values for seepage flow could be affected by several uncertainties, e.g., applying a 2D model to calculate seepage flow, uncertainty in material properties, and human error in measurement. In addition, due to the layout downstream, some parts of seepage flow could be missed by the dam monitoring system, the discharged flow into two plunge pools in the right (Fig. 2). These two free seepage surfaces allow the high-pressure seepage flow from the foundation to be released freely (same function as relief walls in left part), but these flows are not measured by the dam monitoring system. Although the measured seepage from dam and foundation was significantly higher than the expected value, it must still be acceptable since: (1) there is no serious evidence or report of instability of the upstream and downstream slopes of the dam and (2) the amount does not influence reservoir operation (less than 2% of inflow to the reservoir and less than evaporation from the reservoir).

The results indicate good performance of the chimney drain. The maximum piezometric head in all piezometers in the downstream slope (except NP11) was less than the higher elevation of the horizontal drain (1630) in the dam body (Fig. 4). This indicates that the downstream slope is mainly dry and placed below the seepage path flow in the body. Comparisons of expected and observed piezometric head revealed that the efficiency of the chimney drain was more than 92% in the three longitudinal sections (L1–L3) (Table 3). The efficiency of the chimney drain in L4 in the dam body was lower, however, varying between 76 and 82% (Table 3). As mentioned, the piezometric head after the chimney drain (which is the closest section to the left abutment) was higher than in the other cross-sections (Fig. 5b1, c1). Higher piezometric head in this part of dam body could be due to malfunction of the grouting diaphragm in the left abutment, as indicated by the appearance of two springs after the first reservoir impounding in 1972 (Jalali 2005; Torabi Haghighi 2003). The seepage flow from these springs showed good correlation with the water level in the reservoir, which indicates that they are fed by reservoir water (Fig. 6b). A tracing test also showed that water in the reservoir is the source of the spring flow in the left abutment (Water Research Center 1994). These two pieces of evidence confirm our suggestion of possible diversion of water from the dam body to the left abutment before the chimney drain (based on piezometer monitoring, e.g., NP7 and NP10; Fig. 5a2) and back from the left abutment to the dam body below the chimney drain (based on the piezometer monitoring, e.g., NP8 and NP11 or NP9 and NP12; Fig. 5b2, c2). Based on the expected (model results) and observed (monitoring data) seepage flow from the left abutment, the efficiency of the grouting diaphragm was estimated to be less than 20%, clearly reducing expected performance (Table 2).

Table 3 Observed and expected piezometric head before and after the chimney drain and its efficiency in different longitudinal sections
Full size table

In evaluating the performance of the cutoff wall, only two piezometers (NP1 and OP1) were in an eligible position (similar elevation in the foundation before and after the cutoff wall). The significant decrease in piezometric head in these two piezometers indicated acceptable performance of the cutoff wall, the efficiency of which varied between 68 and 74% (Table 4).

Table 4 Observed and expected piezometric head before and after the cutoff wall and its efficiency
Full size table

The importance of dam safety is beyond of the other infra structure. Beside of the considerable direct economic costs of dam failure as construction investment or failing in the operational purposes e.g. supply water for irrigation, municipal and industrial or power generation, it might be led to a natural catastrophe loss of life and. They have potential for destruction greatly beyond of their constructed area. Among different types of dams, the earthfill dams are highly sensitive in term of safety. Usually the soil characteristics of constructed structure is not entirely complying with designed criteria, as the large volume of the soil is used for construction. This heterogeneity in supplied material, lead to increase the uncertainty in dam safety. Here we focused on the efficiency of seepage control measures in earthfill dams which are play a major role in dam safety in different conditions e.g. during construction, end of construction, first impounding, rapid drawdown, rapid impounding and steady state of operation. In addition of assessing the efficiency of seepage control measures, the presented framework would be used as warning system to predict the potential of dam failure. To our knowledge, the method we present in this work is new in the field, and applicable for earthfill dams in other regions and cases.

4 Conclusions

In this paper, we present a framework for evaluating the efficiency of seepage control measures in earthfill dams, which is an important step in addressing seepage problems in existing dams or preventing future problems during the dam design phase. Our novel framework combines dam monitoring data with the results of 2D seepage modeling to quantify the efficiency of seepage control measures in earthfill dams. We applied the method to Doroudzan dam in southern Iran. The results showed that the overall efficiency of seepage control measures at the dam (based on the magnitude of seepage flow) varied between 51 and 70%. For the three major seepage control measures in the case dam, the chimney drain, cutoff wall, and grouting diaphragm in the left abutment, the efficiency was estimated to be 76–82%, 68–74%, and 16–19%, respectively. These values indicate acceptable performance of the chimney drain and cutoff wall, but inadequate function of the grouting diaphragm in Doroudzan dam.