Void growth and coalescence in sigmoidal hardening porous plastic solids under tensile and shear loading

Abstract

This work examines the void growth and coalescence in isotropic porous elastoplastic solids with sigmoidal material hardening via finite element three-dimensional unit cell calculations. The investigations are carried out for various combinations of stress triaxiality ratio (${\mathcal {T}}$) and Lode parameter (${\mathcal {L}}$) and consider a wide range of sigmoidal hardening behaviors with nominal hardening rates spanning two decades. The effect of ${\mathcal {L}}$ is considered in the presence and in the absence of imposed shear stress. Our findings reveal that depending on the nature of sigmoidal hardening the cell stress-strain responses may exhibit two distinct transitions with increasing stress triaxiality (${\mathcal {T}}$). Below a certain lower threshold triaxiality the stress-strain responses are sigmoidal, while above a certain higher triaxiality they exhibit softening immediately following the yield. Between these threshold levels, the responses exhibit an apparent classical rather than sigmoidal strain hardening. The sigmoidal hardening characteristics also influence porosity evolution, which may stagnate before a runaway growth up to final failure. For a given ${\mathcal {L}}$, an imposed shear stress adversely affects the material ductility at moderate ${\mathcal {T}}$ whereas at high ${\mathcal {T}}$ it improves the ductility. Finally, we discuss the role of material hardening and stress state on the residual cell ductility defined as strain to final failure beyond the onset of coalescence.

Implementation of kinematic periodicity and constant stress ratios

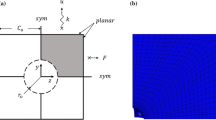
The computational implementation for the kinematic periodic boundary conditions and constant stress ratios closely follows Ref. Tekoglu (2014). For completeness, the procedure is briefly described in the following sections.

1.1 No shear stress ($\rho _{\textrm{xy}} = 0$)

1.1.1 Kinematic periodic boundary conditions

Referring to Fig. 2, five pairs of dummy nodes $(T, T')$, $(R, R')$, $(L, L')$, $(F, F')$, and $(B, B')$ are defined respectively for the top, right, left, front, and the back faces. Each pair is connected by a linear spring element $T-T'$, $L-L'$, $R-R'$, $F-F'$ and $B-B'$, of stiffness k which is taken to be equal to 60, 000 N/mm. The node in the center of the bottom face is fixed to avoid rigid body movement. The force in the springs is transferred to the unit cell. For equilibrium, the forces in the $L-L'$ and $F-F'$ are equal to $R-R'$ and $B-B'$ respectively. With u, v,  and w as the displacement components along the X, Y, and Z directions, the displacement of one end of the spring is coupled with that of the faces as follows:

$$\begin{aligned}{} & {} u_{\textrm{left}}^i - u_{\textrm{right}}^i = u_{L'} - u_{R'} ; \hspace{3ex} v_{\textrm{top}}^i - v_{\textrm{bottom}}^i = v_{T'}; \nonumber \\{} & {} w_{\textrm{front}}^i - w_{\textrm{back}}^i = w_{F'} - w_{B'} \end{aligned}$$

(3)

where the superscript i represents the nodes on the face indicated in the subscript. Note that $v^i_{bottom} = 0$. The nodes L and R (similarly F and B) act as master nodes for the left and right (similarly front and back faces). Eq. (3) ensures periodicity along the three coordinate directions.

1.1.2 Imposing constant axial stress ratios ($\rho _{\textrm{xx}}, \rho _{\textrm{zz}}$)

The volume-averaged macroscopic stresses can be defined in terms of the spring forces as:

$$\begin{aligned}{} & {} \varSigma _{\textrm{xx}} = \dfrac{F_{\textrm{right}}}{A_{\textrm{right}}} = \dfrac{k (u_R - u_{R'})}{L_yL_z} \nonumber \\{} & {} \quad = \dfrac{F_{\textrm{left}}}{A_{\textrm{left}}} = \dfrac{-k (u_L - u_{L'})}{L_yL_z} \end{aligned}$$

(4a)

$$\begin{aligned}{} & {} \varSigma _{\textrm{yy}} = \dfrac{F_{\textrm{top}}}{A_{\textrm{top}}} = \dfrac{k (v_T - v_{T'})}{L_xL_z} \end{aligned}$$

(4b)

$$\begin{aligned}{} & {} \varSigma _{\textrm{zz}} = \dfrac{F_{\textrm{front}}}{A_{\textrm{front}}} = \dfrac{k (w_F - w_{F'})}{L_xL_y} \nonumber \\{} & {} \quad = \dfrac{F_{\textrm{back}}}{A_{\textrm{back}}} = \dfrac{-k (w_B - w_{B'})}{L_xL_y} \end{aligned}$$

(4c)

where $F_i$ and $A_i$ are the force in the spring applied normal to the face i with area $A_i$. From there, the stress ratios $\rho _{\textrm{xx}}$ and $\rho _{\textrm{zz}}$ are written as:

$$\begin{aligned}{} & {} \rho _{\textrm{xx}} = \dfrac{\varSigma _{\textrm{xx}}}{\varSigma _{\textrm{yy}}} = \dfrac{(u_R - u_{R'})}{(L_{0y} + v_{T})}\dfrac{(L_{0x} + u_{R} - u_{L})}{(v_{T} - v_{T'})} \nonumber \\{} & {} \quad = \dfrac{-(u_L - u_{L'})}{(L_{0y} + v_{T})}\dfrac{(L_{0x} + u_{R} - u_{L})}{(v_{T} - v_{T'})} \end{aligned}$$

(5a)

$$\begin{aligned}{} & {} \rho _{zz} = \dfrac{\varSigma _{\textrm{zz}}}{\varSigma _{\textrm{yy}}} = \dfrac{(w_F - w_{F'})}{(L_{0y} + v_{T})}\dfrac{(L_{0z} + w_{F} - w_{B})}{(v_{T} - v_{T'})} \nonumber \\{} & {} \quad = \dfrac{-(w_B - w_{B'})}{(L_{0y} + v_{T})}\dfrac{(L_{0z} + w_{F} - w_{B})}{(v_{T} - v_{T'})} \end{aligned}$$

(5b)

The stress ratios are kept constant by introducing Eq. 5a and 5b as multi-point constraints using an MPC user subroutine in ABAQUS/STANDARD^®.

Note that, $v_{T'}$ is the only prescribed input, which is prescribed via the user-prescribed boundary condition. From that, ABAQUS/STANDARD^® computes the displacements $u_R$, $u_{R'}$, $u_L$, $u_{L'}$, $v_T$, $w_{F}$, $w_{F'}$, $w_{B}$, and $w_{B'}$ at each time increment.

1.2 Imposed shear stress ($\rho _{\textrm{xy}} \ne 0$)

To apply a shear stress along with the axial stresses, an additional pair of dummy nodes $(S, S')$ is defined to which a linear spring element $S-S'$ of the same stiffness k is connected, Fig. 2. For brevity, here we describe the procedure to maintain constant $\rho _{\textrm{xx}}$ and $\rho _{\textrm{xy}}$.

1.2.1 Kinematic periodic boundary conditions

The displacement of the node S is coupled to the unit cell such that periodicity is ensured in the presence of an imposed shear stress. For this, the boundary conditions adopted are as follows:

$$\begin{aligned}&\text {top-mid edge:} \quad u(0,L_y,z) = u_{S}; \quad v(0,L_y,z) = v_{T} \end{aligned}$$

(6a)

$$\begin{aligned}&\text {bottom-mid edge:} \quad u(0,0,z) = v(0,0,z) = 0 \end{aligned}$$

(6b)

$$\begin{aligned}&\text {top-right edge:}\quad u\left( \dfrac{L_x}{2},L_y,z\right) = u_R + u_S \end{aligned}$$

(6c)

$$\begin{aligned}&\text {top-left edge:} \quad u\left( -\dfrac{L_x}{2},L_y,z\right) = u_L + u_S \end{aligned}$$

(6d)

$$\begin{aligned}&\text {bottom-right edge:}\quad v\left( \dfrac{L_x}{2},0,z\right) = 0 \end{aligned}$$

(6e)

$$\begin{aligned}&\text {bottom-left edge:} \quad v\left( -\dfrac{L_x}{2},0,z\right) = 0 \end{aligned}$$

(6f)

$$\begin{aligned}&\text {top and bottom faces except mid-edges:}\nonumber \\&\quad v_{\textrm{top}}^i - v_{\textrm{bottom}}^i = v_{T'} \end{aligned}$$

(6g)

$$\begin{aligned}&\text {right and left faces except top right and left edges:} \nonumber \\&\quad u_{\textrm{left}}^i - u_{\textrm{right}}^i = u_{L'} - u_{R'} \end{aligned}$$

(6h)

$$\begin{aligned}&\text {front and back faces:}\nonumber \\&\quad w_{\textrm{front}}^i - w_{\textrm{back}}^i = w_{F'} - w_{B'} \end{aligned}$$

(6i)

1.2.2 Imposing constant shear stress ratio ($\rho _{\textrm{xy}}$)

The macroscopic shear stress is given in terms of the spring force by:

$$\begin{aligned} \varSigma _{\textrm{xy}} = \dfrac{F_{\textrm{shear}}}{A_{\textrm{top}}} = \dfrac{k(u_S - u_{S'})}{L_xL_z} \end{aligned}$$

(7)

where $F_{\textrm{shear}}$ is the force in the spring S-S’ (Fig. 2). Then, the shear stress ratio is:

$$\begin{aligned} \rho _{xy} = \dfrac{\varSigma _{\textrm{xy}}}{\varSigma _{\textrm{yy}}} = \dfrac{k(u_S - u_{S'})}{L_xL_z}\dfrac{L_xL_z}{k(v_T - v_{T'})} = \dfrac{(u_S - u_{S'})}{(v_T - v_{T'})} \end{aligned}$$

(8)

As the current framework considers a finite deformation setting, the foregoing description accounts for the normal stress that arises due to the imposition of the shear stress (referred to as the Poynting effect).

Consider the case of simple shear with a shear constant $\gamma$. The total deformation gradient ${\textbf{F}}$ is:

$$\begin{aligned} {\textbf{F}} = \begin{bmatrix} 1 &{} \gamma &{} 0\\ 0 &{} 1 &{} 0\\ 0 &{} 0 &{} 1 \end{bmatrix} \end{aligned}$$

(9)

The velocity gradient (L = D + W) is:

$$\begin{aligned} {\textbf{L}} = \begin{bmatrix} 0 &{} {\dot{\gamma }} &{} 0\\ 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 \end{bmatrix} = \underbrace{\begin{bmatrix} 0 &{} \dfrac{{\dot{\gamma }}}{2} &{} 0\\ \dfrac{{\dot{\gamma }}}{2} &{} 0 &{} 0\\ 0 &{} 0 &{} 0 \end{bmatrix}}_{\mathrm{rate \ of \ deformation}} + \underbrace{\begin{bmatrix} 0 &{} \dfrac{{\dot{\gamma }}}{2} &{} 0\\ -\dfrac{{\dot{\gamma }}}{2} &{} 0 &{} 0\\ 0 &{} 0 &{} 0 \end{bmatrix}}_{\textrm{spin}}\nonumber \\ \end{aligned}$$

(10)

The Jaumann rate of Cauchy stress ($\mathbf {{\bar{\sigma }}}$) is expressed as:

$$\begin{aligned}{} & {} {\bar{\sigma }} = {\dot{\sigma }} - {\textbf{W}}.\mathbf {\sigma } + \sigma . {\textbf{W}} \end{aligned}$$

(11a)

$$\begin{aligned}{} & {} C_{ijkl}: D_{kl}^e = {\dot{\sigma }}_{ij} - \sigma _{\textrm{xy}} {\dot{\gamma }} \end{aligned}$$

(11b)

where C is the elasticity tensor and ${\textbf{D}}^e$ is the elastic rate-of-deformation.

In a more general setting where axial stresses are imposed in addition to the shear stress the additional axial stress caused by shear straining must be included. For example, the total axial stress along the X-direction is given by:

$$\begin{aligned} \varSigma _{\textrm{xx}} = \dfrac{F_{\textrm{right}}}{A_{\textrm{right}}} + \underbrace{\int _{0}^{t} (\sigma _{\textrm{xy}} {\dot{\gamma }} + C_{ijkl}: D_{kl}^e) \ \textrm{d} t}_{\approx \dfrac{F_{\textrm{shear}}}{A_\textrm{top}}\gamma } \end{aligned}$$

(12)

From this, we obtain $\rho _{xx}$ on the right face as:

$$\begin{aligned} (\rho _{xx})_{\textrm{right}}{} & {} = \left[ \dfrac{k (u_R - u_{R'})}{L_yL_z} + \dfrac{k (u_S - u_{S'})}{L_xL_z} \dfrac{u_S}{L_y}\right] \nonumber \\{} & {} \quad \times \dfrac{L_xL_z}{k(v_T - v_{T'})} \nonumber \\{} & {} = \dfrac{(u_R - u_{R'})(L_{0x} + u_{R} - u_{L})}{(L_{0y} + v_{T})(v_{T} - v_{T'})}\nonumber \\{} & {} \quad + \dfrac{(u_S - u_{S'})u_{S}}{(v_T - v_{T'})(L_{0y} + v_{T})} \end{aligned}$$

(13a)

and on the left face,

$$\begin{aligned} (\rho _{xx})_{\textrm{left}}{} & {} = \left[ \dfrac{-k (u_L - u_{L'})}{L_yL_z} + \dfrac{k (u_S - u_{S'})}{L_xL_z} \dfrac{u_S}{L_y}\right] \nonumber \\{} & {} \quad \times \dfrac{L_xL_z}{k(v_T - v_{T'})} \nonumber \\{} & {} = \dfrac{(u_{L'} - u_{L})(L_{0x} + u_{R} - u_{L})}{(L_{0y} + v_{T})(v_{T} - v_{T'})} \nonumber \\{} & {} \quad + \dfrac{(u_S - u_{S'})u_{S}}{(v_T - v_{T'})(L_{0y} + v_{T})} \end{aligned}$$

(13b)

Similar expressions can also be derived for $\rho _{\textrm{zz}}$ on the front and back faces. These stress ratios are maintained by introducing 8 and 13a, 13b in addition to 5b as a constraint in the MPC subroutine.