1 Introduction

Numerical modeling of nonlinear crack propagation and fracture behavior of solids is one of the challenging topics in computational mechanics because of the need to describe arbitrary discontinuities in space and time. Various models have been proposed and utilized to simulate crack initiation and propagation, which are generally categorized into two approaches, i.e., smeared crack models and discrete crack models. In the smeared crack approach, the discontinuities are represented within continuum elements, i.e., no explicit representation of the fracture surface, and thus the fracture behavior is directly associated with the stress–strain relationship of a material, i.e., material degradation. For example, a phase-field fracture model (Francfort and Marigo 1998; Bourdin et al. 2000, 2008) has been successfully applied to brittle and ductile fracture (Borden et al. 2012, 2014; Ambati et al. 2015, 2016). Schlüter et al. (2014) extended the phase-field formulation for the quasi-static brittle fracture to the dynamic case. Proserpio et al. (2021) combined the phase-field model with the isogeometric formulation to simulate ductile fracture in shell structures. Additionally, much research has been conducted on cohesive fracture, which is related to the softening behavior during the fracture process, using the phase-field approach. Verhoosel and de Borst (2013) introduced a secondary auxiliary field that represents the displacement jump along the crack surface. Wu (2017) proposed a phase-field regularized cohesive zone model (CZM) to investigate quasi-brittle fracture by introducing the energetic degradation function in terms of length scale parameter. Note that although several phase-field-based approaches have been utilized for cohesive fracture, an internal length scale parameter should be calibrated and provided as an input parameter, while a sufficient mesh resolution is required to achieve numerical solution with reasonable accuracy.

Alternatively, the discrete crack approach also has been widely utilized to investigate crack propagation problems. In the discrete crack models, such as enrichment method, cohesive surface element, etc., the topology of fracture surface is explicitly represented in a discretized domain. A discrete crack is represented by discontinuous enrichment functions, which is named as generalized/extended finite element methods, G/XFEM (Wells and Sluys 2001; Moës and Belytschko 2002; Duarte et al. 2000). Liu and Zhang (2019) proposed an XFEM-based cohesive fracture model to predict the fracture behavior of fiber reinforced concrete in conjunction with a nonlocal slip model. Wang and Waisman (2018) proposed an arc-length method to model the cohesive fracture of quasi-brittle materials using high-order XFEM and Irwin’s crack closure integral. However, when a crack propagates close to the element node, a convergence problem arises in the standard G/XFEM because ill-conditioned or singular systems of equations could be expected (Fries and Belytschko 2010; Dolbow et al. 2000). To improve the condition number, the stable GFEM was proposed by Babuška and Banerjee (2012) and the improved stable XFEM was developed by Wu and Li (2015), through modifying the Heaviside enrichment function. Additionally, Lang et al. (2014) proposed a geometric preconditioner while Agathos et al. (2019) introduced the enrichment quasi-orthogonalization.

For the cohesive surface element approach (Xu and Needleman 1994; Camacho and Ortiz 1996; Ortiz and Pandolfi 1999), the crack surface is represented by inserting crack surface elements along boundaries between continuum elements. In other words, the crack path is restricted according to the shape and arrangement of continuum elements, and thus this limitation results in mesh bias and dependency issues. To alleviate such mesh dependence in the cohesive surface element approach, mesh modification techniques and topological operators have been proposed. For example, a nodal perturbation operator is employed in a structured mesh to reduce mesh bias in the crack path representation (Paulino et al. 2010; Baek et al. 2020; Spring and Paulino 2018). Uribe-Suárez et al. (2020) utilized a local remeshing strategy for 2D crack growth simulation of brittle materials to improve a crack path representation. Choi and Park (2019) successfully eliminated mesh bias in quasi-static cohesive fracture simulation using the element split and domain integral. However, the element split results in relatively large number of low-quality elements because the shape of continuum elements is restricted to triangular or quadrilateral elements in the standard finite element method.

Recently, the virtual element method (VEM) is developed to consistently handle arbitrary polygonal and polyhedral elements (Beirão da Veiga et al. 2013). Because of the flexibility on the element shape, VEM has been utilized to solve various engineering problems (Choi et al. 2021; Park et al. 2019; Chi et al. 2020; Wriggers et al. 2017, 2021). For the application to brittle crack propagation problems, a cutting technique is employed on a polygonal mesh (Hussein et al. 2019), while some of computational results demonstrated the oscillation in a predicted crack path. Recently, Hussein et al. (2020) utilized the phase-field method in conjunction with the adaptive mesh refinement to estimate a crack path while an oscillating behavior is observed in a load–displacement curve. Additionally, Artioli et al. (2020) and Marfia et al. (2022) employed the cutting element scheme on a rectangular mesh for the cohesive fracture simulation, and Benvenuti et al. (2022) introduced additional enrichment functions to the standard virtual element space for the discontinuity representation, similar to the XFEM approach.

The present work proposes an integrated framework of VEM and CZM, which accurately captures nonlinear crack propagation without oscillation in a polygonal mesh. An arbitrary crack path is represented on a polygonal mesh using the element split and nodal relocation operators. For the accurate evaluations of the stress field and crack propagation direction, the virtual grid-based stress recovery (VGSR) is utilized in conjunction with the domain integral. The proposed computational framework is validated through solving three mixed-mode fracture problems.

The remainder of the article is organized as follows. Section 2 introduces the basic formulations of VEM and CZM. Section 3 presents the element splitting procedure to describe an arbitrary crack path on a polygonal mesh. Section 4 explains the crack initiation and growth criteria in relation with a stress recovery scheme and a domain integral method. Then, the proposed computational framework is validated by investigating mixed-mode fracture examples in Sect. 5. Finally, the key findings of the present article are summarized in Sect. 6.

2 Basic formulations

This section presents the weak form of the governing equation for quasi-static cohesive fracture mechanics and introduces a discretization method coupling VEM and cohesive elements.

2.1 Variational form for cohesive fracture

The weak form of the governing equation for a quasi-static cohesive fracture problem is derived using the principle of virtual work. Consider a solid \(\Omega \) in equilibrium under prescribed traction \({{\varvec{T}}}_{ext}\) and displacement fields \({{\varvec{u}}}_{0}\) on traction boundary \({\Gamma }_{{\varvec{T}}}\) and displacement boundary \({\Gamma }_{{\varvec{u}}}\), respectively. The sum of the virtual strain energy in the bulk and the virtual cohesive fracture energy on the fracture surface \(\left({\Gamma }_{c}\right)\) is equal to the virtual work done by the external traction field, namely,

$${\int }_{\Omega }\nabla (\delta {\varvec{u}}):{\varvec{\sigma}}({\varvec{u}})d\Omega +{\int }_{{\Gamma }_{c}}\delta{\varvec{\Delta}}\cdot {{\varvec{T}}}_{c}({\varvec{u}})d{\Gamma }_{c}={\int }_{{\Gamma }_{{\varvec{T}}}}\delta {\varvec{u}}\cdot {{\varvec{T}}}_{ext}d{\Gamma_{{\varvec{T}}}} , \forall \delta {\varvec{u}}\in {\mathcal{K}}_{0},$$
(1)

where \({\varvec{u}}\) and \(\delta {\varvec{u}}\) are the actual and virtual displacement fields, respectively, \({\varvec{\sigma}}\) is the stress tensor, \(\delta{\varvec{\Delta}}\) is the virtual cohesive separation (as a function of \(\delta {\varvec{u}}\)), \({{\varvec{T}}}_{c}\) is the cohesive traction along the fracture surface, and \({\mathcal{K}}_{0}\) stands for the space of admissible displacements that vanishes on the displacement boundary \({\Gamma }_{{\varvec{u}}}\). Small-strain kinematics is assumed in Eq. (1). The terms on left side of Eq. (1) are related to the internal virtual works of the bulk and cohesive surface, respectively, while the term on the right side is associated with the external virtual work.

We utilize the VEM coupled with the CZM to simulate nonlinear crack propagation. Virtual elements of arbitrary polygonal shape are used to discretize the bulk of material and the cohesive surface elements are adaptively inserted to represent the fracture surface. The adaptive insertion of surface elements is consistently handled using the topology-based data structure, named TopS (Celes et al. 2005a, b).

2.2 Virtual element discretization for continuum elements

To leverage the great geometric flexibility offered by VEM, this work adopts a lower-order virtual element approximation of both the bulk part of the internal virtual work and the external virtual work. Given a virtual element tessellation of the bulk of the solid denoted by \({\Omega }_{h}\), we define the corresponding global displacement space \({\mathcal{K}}_{h}\) as

$${\mathcal{K}}_{h}\doteq \left\{{{\varvec{v}}}_{h}\in \mathcal{K}:{{\varvec{v}}}_{h}{\left.\right|}_{E}\in \mathcal{V}\left(E\right),\forall E\in {\Omega }_{h}\right\},$$
(2)

where \(E\) stands for a generic element of the tessellation \({\Omega }_{h}\). In the above definition, \(\mathcal{V}(E)\) is the local (i.e., element-level) virtual displacement space following the definition (Beirão da Veiga et al. 2013) of

$$\mathcal{V}\left(E\right)\doteq \left\{{\varvec{v}}\in {\mathcal{H}}^{1}\left(E\right):\Delta {\varvec{v}}=0 \, \mathrm{in} \, E,{\varvec{v}}{\left.\right|}_{e}\in {\left[{\mathcal{P}}_{1}\left(e\right)\right]}^{2} \forall e\in \partial E\right\},$$
(3)

where \(\Delta \) stands for the Laplacian operator for vectors, \(e\) denotes a generic edge of an element \(E\), and \({\mathcal{P}}_{1}\left(\cdot \right)\) is the space of linear functions. According to such definition, the local displacement field has zero Laplacian in the interior and possesses linear variations on the edges of each element. Then, the displacement degrees of freedom (DoFs) for each element contain the value of \({\varvec{v}}\) on every vertex of \(E\).

Distinguished from the finite element method, the displacement field is only known implicitly within each element in VEM. Thus, local projections are needed to construct a virtual element approximation. Denoted by \({\Pi }_{E}^{\nabla }:\mathcal{V}\left(E\right)\to {\left[{\mathcal{P}}_{1}\left(e\right)\right]}^{2}\), the local projection is formally defined by the following two conditions (Beirão da Veiga et al. 2013):

$${\int }_{E}\nabla \left({\Pi }_{E}^{\nabla }{\varvec{v}}\right)\cdot \nabla {{\varvec{p}}}_{1}d{\varvec{x}}={\int }_{E}\nabla \left({\varvec{v}}\right)\cdot \nabla {{\varvec{p}}}_{1}d{\varvec{x}}\forall {\varvec{v}}\in \mathcal{V}\left(E\right) \,\mathrm{and}\, {{\varvec{p}}}_{1}\in {\left[{\mathcal{P}}_{1}\left(E\right)\right]}^{2}$$
(4)

and

$${\sum }_{{{\varvec{x}}}_{v}\in E}{\Pi }_{E}^{\nabla }{\varvec{v}}{\left.\right|}_{{{\varvec{x}}}_{v}}={\sum }_{{{\varvec{x}}}_{v}\in E}{\varvec{v}}({{\varvec{x}}}_{v}),$$
(5)

with \({{\varvec{x}}}_{v}\) denoting a generic vertex of \(E\).

It can be shown that, for any local displacement field \({\varvec{v}}\in \mathcal{V}\left(E\right)\), its projection \({\Pi }_{E}^{\nabla }{\varvec{v}}\) can always be exactly computed using the DoFs of \({\varvec{v}}\) and without explicitly knowing the form of \({\varvec{v}}\) in the interior of \(E\). This is made clear by applying integration by parts to the right-hand-side expression of Eq. (4), which gives (by noticing that \({\Delta {\varvec{p}}}_{1}=0\) \(\forall {{\varvec{p}}}_{1}\in {\left[{\mathcal{P}}_{1}\left(E\right)\right]}^{2}\)):

$${\int }_{E}\nabla \left({\varvec{v}}\right)\cdot \nabla {{\varvec{p}}}_{1}d{\varvec{x}}={\int }_{\partial E}{\varvec{v}}\cdot (\nabla {{\varvec{p}}}_{1}\cdot {\varvec{n}})ds,$$
(6)

where \({\varvec{n}}\) is the unit outward normal vector of the boundary of \(E.\) Because \({\varvec{v}}\) is explicitly known on \(\partial E\) when given its DoFs, the quantity \({\int }_{E}\nabla \left({\varvec{v}}\right)\cdot \nabla {{\varvec{p}}}_{1}d{\varvec{x}}\) can be exactly calculated using the DoFs of \({\varvec{v}}\) and geometric information of \(E\), and therefore, so as the local projection \({\Pi }_{E}^{\nabla }{\varvec{v}}\) (the implementation details can be found in Beirão da Veiga et al. 2014).

With the definitions of the local displacement spaces \(\mathcal{V}\left(E\right)\) and the associated projection operator \({\Pi }_{E}^{\nabla }\), we are ready to construct the virtual element approximation of the element-level internal virtual work in the bulk part as:

$${\int }_{E}\nabla {\delta {\varvec{v}}}_{h}:{\varvec{\sigma}}({{\varvec{v}}}_{h})d{\varvec{x}}\approx \left|E\right|\nabla \left({\Pi }_{E}^{\nabla }{\delta {\varvec{v}}}_{h}\right):{\varvec{\sigma}}\left({\Pi }_{E}^{\nabla }{{\varvec{v}}}_{h}\right)+\frac{{\alpha }_{E}}{2}{S}_{h,E}\left({\delta {\varvec{v}}}_{h}-{\Pi }_{E}^{\nabla }{\delta {\varvec{v}}}_{h},{{\varvec{v}}}_{h}-{\Pi }_{E}^{\nabla }{{\varvec{v}}}_{h}\right),$$
(7)

where the stability parameter \({\alpha }_{E}\) is taken as 1/2 \(\mathrm{tr}({{\varvec{K}}}_{e}^{\mathrm{cons}})\) (Artioli et al. 2017), and \({S}_{h,E}\left({{\varvec{v}}}_{h},{{\varvec{u}}}_{h}\right)=\sum_{{{\varvec{x}}}_{v}\in E}{{\varvec{v}}}_{h}\left({{\varvec{x}}}_{v}\right)\cdot {{\varvec{u}}}_{h}({{\varvec{x}}}_{v})\) is the bilinear form associated with the stabilization term (Beirão da Veiga et al. 2013). The above approximation gives rises to the consistency and stability parts of the local stiffness matrix, the latter of which is introduced to suppress the non-physical spurious modes in the consistency part due to the usage of local projection operator. Once the local stiffness matrix associated with the virtual element approximation is obtained, the global stiffness matrix can be obtained via the standard assembly procedure as in the finite element method. On the other hand, the virtual element approximation of the external virtual work is done in the standard manner as described in Chi et al. (2017).

2.3 Cohesive elements along fracture surface

In the approximation of the virtual cohesive fracture energy, the separation along the cohesive surface \({\varvec{\Delta}}\) is approximated using the nodal displacements of cohesive surface element, while the normal and tangential cohesive tractions \({{\varvec{T}}}_{c}={\left[{T}_{n},{T}_{t}\right]}^{\mathrm{T}}\) are evaluated according to the cohesive traction–separation relationship. For the normal cohesive interaction (see Fig. 1a), the bilinear softening model (Park et al. 2008) is employed, which is widely utilized to describe the tensile fracture of plain concrete, given as

$${T}_{n}=\left\{\begin{array}{ll}\frac{-{\sigma }_{\mathrm{max}} }{{\Delta }_{1}}{\Delta }_{n}+{\sigma }_{\mathrm{max}}, & 0\le {\Delta }_{n}\le {\Delta }_{k},\\ \frac{-\psi {\sigma }_{\mathrm{max}} }{\Delta_f-\Delta_k}({\Delta }_{n}-{\Delta }_{f}),& {\Delta }_{k}\le {\Delta }_{n}\le {\Delta }_{f},\end{array}\right.$$
(8)

where \({\Delta }_{n}\) and \({\sigma }_{\mathrm{max}}\) are the normal separation and the cohesive strength, respectively. Additionally, \({\Delta }_{1}\), \({\Delta }_{k}\), and \({\Delta }_{f}\) are calculated based on fracture parameters as follows,

$${\Delta }_{1}=\frac{2{G}_{f}}{{\sigma }_{\mathrm{max}}},$$
(9)
$${\Delta }_{k}=(1-\psi)\Delta_1,$$
(10)
$${\Delta }_{f}=\frac{2\left({G}_{F}-{G}_{f}\right)}{\psi {\sigma }_{\mathrm{max}}}+{\Delta }_{1},$$
(11)

where \({G}_{F}\) is the total fracture energy, \({G}_{f}\) is the initial fracture energy, and \(\psi \) is the kink point ratio in the bilinear softening model. The total fracture energy is determined using the total work of fracture method (Guinea et al. 1992; Planas et al. 1992) and the cohesive strength can be selected as the indirect tensile strength of the material (Roesler et al. 2007). For the evaluation of other fracture parameters, i.e., initial fracture energy and kink point ratio, the size effect method or the two parameter fracture model can be used (Bažant 2000; Jenq and Shah 1985). For the tangential cohesive interaction, a linear relation is used without softening behavior, i.e., \({T}_{t}={D}_{tt}{\Delta }_{t}\). To minimize the effects of the tangential cohesive interaction on the global responses, a small value of the tangent stiffness \({D}_{tt}\) is selected in this study, i.e., \({D}_{tt}=1\,\mathrm{ N}/{\mathrm{mm}}^{3}\).

Fig. 1
figure 1

Cohesive constitutive models: a the bilinear softening model for the normal cohesive interaction and b the linear relation for the tangential cohesive interaction

Full size image

3 Arbitrary crack path representation on a polygonal mesh

This section presents an element splitting scheme that describes an arbitrary crack path on the polygonal mesh discretization. Based on the original concept of the element splitting using a triangular mesh, proposed by Choi and Park (2019), we extend the algorithm to handle arbitrary polygonal meshes. First, the crack path representation procedure is introduced on the basis of the polygonal mesh with the element split. Next, we discuss the advantages of the VEM approach (using a polygonal mesh) compared to the FEM approach (using a triangular mesh) in the element splitting procedure.

3.1 Element splitting scheme in VEM

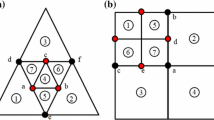
For the arbitrary crack path representation, the element splitting scheme consists of three steps, i.e., (i) checking crack initiation and growth criteria, (ii) splitting a polygon element, and (iii) inserting a cohesive surface element, as illustrated in Fig. 2. At a crack tip, one examines whether the criteria for the crack initiation and growth are satisfied or not. Note that, in this study, the crack propagates along the direction which maximizes the strain energy release rate, and the crack initiates when the normal stress in the orthogonal direction of the calculated path exceeds the cohesive strength of a material. The details of the crack growth criterion are discussed in Sect. 4.2. When one evaluates the potential crack direction and judges the crack initiates at the crack tip, one searches for a polygonal element that lies on the evaluated crack propagation direction. Then, three scenarios are possible for the crack propagation in a polygonal element (see the dashed lines in Fig. 2a). First, if the crack propagates along an existing edge which shares the crack tip, one inserts a cohesive element at the edge without any modification to the polygonal element. Second, if the crack propagates toward an existing node of the polygonal element, one divides the polygonal element into two new elements along the calculated crack direction. The last scenario is that the crack propagates to a position on an edge of the polygonal element. Then, the element is split into two new elements with the creation of a new node. As shown in Fig. 2b, for example, the light-gray element is split into two elements while a new (crack tip) node is created on an edge shared by the light- and dark-gray elements. To keep the topological consistency of the mesh, one updates the element connectivity of the dark gray element. Then, one represents a new crack surface by inserting a cohesive surface element along a newly created edge.

Fig. 2
figure 2

Schematics of the element splitting procedure to represent an arbitrary crack path on the polygonal mesh: a identification of a crack propagation direction, b element split, and c insertion of a cohesive surface element along the calculated crack path direction

Full size image

During the element splitting process, polygonal elements with small edges could be generated if the location of a potential crack tip is very close to an existing element node. The presence of small edges on polygonal elements may result in an ill-conditioned stiffness matrix and/or decrease the accuracy of the VEM solutions (Mascotto 2018; Berrone and Borio 2017). Note that the ill-conditioning issue also has been reported in other computational methods for the crack path representation, as discussed previously (Fries and Belytschko 2010; Dolbow et al. 2000; Babuška and Banerjee 2012; Wu and Li 2015; Lang et al. 2014; Agathos et al. 2019). In this study, to alleviate the creation of the small edges on polygonal elements, a nodal relocation process is introduced during the element split, as illustrated in Fig. 3. When a new crack tip is close to an existing node (Fig. 3a), one relocates the existing node to the location corresponding to the new crack tip position (Fig. 3b). Then, one can represent the calculated crack path without the creation of the small edge, as shown in Fig. 3c. In this study, the node relocation procedure is conducted when the distance between a new node and an existing node is less than 5% of the element edge length. Additionally, flat triangular elements are searched based on the element area and the smallest angle after the crack path representation because these elements can adversely affect the accuracy and convergence of the computational results. Then, these elements are eliminated by removing an existing node or merging a flat triangular element with an adjacent element. To calculate nodal quantities, like displacements of newly inserted or relocated nodes, one uses linear interpolation along an edge where new or relocated nodes are positioned. Then, the target quantity is interpolated from quantities of edge nodes.

Fig. 3
figure 3

Schematics of the node relocation procedure: a identification of a potential edge having small length, b node relocation, and c insertion of a cohesive surface element with the element split

Full size image

3.2 Comparison between VEM and FEM

The main difference between FEM and VEM in the element splitting schemes is that all the elements need to be a specific shape (triangle, rectangle, tetrahedron, etc.) in the standard FEM, whereas a specific shape is not required in a polygonal element approach like VEM. Therefore, in FEM, more numbers of the element splitting occur, and thus a larger number of split elements are generated than in the case of the VEM approach. For example, all elements, which share an edge having a new node, need to be split to describe the crack surface according to a given direction in the FEM approach (see Fig. 4a and b). However, in the VEM approach, only an element located in the crack propagation direction requires a splitting (see Fig. 2b). Since the generation of the low-quality elements having small edges is related to the element splitting process, the use of the polygonal element approach can reduce the number of occurrences of the elements with small edges, which can adversely affect the accuracy of the numerical solution.

Fig. 4
figure 4

Schematics of the element splitting procedure to represent an arbitrary crack path on the triangular mesh: a identification of a crack path direction, b element split, and c insertion of a cohesive surface element along the calculated crack path direction

Full size image

To quantitatively compare VEM with FEM in the crack path representation, a geometrical example is employed with a specified crack path, as shown in Fig. 5. In the square domain, one describes the spiral path using the element splitting scheme, expressed as,

$$\begin{aligned}{x}_{\mathrm{spr}}&=\frac{\theta }{18}\mathrm{sin}\left(\theta \right)+1 \,\mathrm{and }\\{y}_{\mathrm{spr}}&=2.05-\left(\frac{\theta }{18}\mathrm{cos}\left(\theta \right)+1\right)\end{aligned},$$
(12)

where \({x}_{\mathrm{spr}}\) and \({y}_{\mathrm{spr}}\) are the x- and y- coordinates of the spiral path, and \(\theta \) is the coefficient varies from \(1.6\pi \) to \(6.0\pi \). For initial meshes of VEM and FEM, the centroid Voronoi tessellation (CVT) and the triangular meshes are employed, as shown in Fig. 5b and c, respectively. The initial CVT mesh has 1995 nodes and 1000 elements, and the initial triangular mesh has 542 nodes and 994 elements, respectively. During the element split in both meshes, the node relocation procedure is applied to reduce number of occurrences of elements with small edges. Additionally, all the elements of the triangular mesh are maintained as triangular elements during the element splitting procedure, that is the FEM approach.

Fig. 5
figure 5

a Geometry of the square domain with the potential spiral path, b the initial CVT mesh, and c the initial triangular mesh

Full size image

Figure 6 shows the described spiral paths using the element splitting scheme on the CVT and triangular meshes. On both meshes, accurate and smooth spiral paths are observed. After the path representation, larger numbers of the nodes and elements are newly created in the triangular mesh than in the case of the CVT mesh. Specifically, the numbers of the nodes and elements increase by 281 (14.1%) and 149 (14.9%) in the CVT mesh while new 409 nodes (75.5%) and 387 elements (38.9%) are generated in the triangular mesh. Moreover, many elongated elements are generated around the represented path in the triangular mesh. To quantify the quality of meshes before and after the path representation, mesh statistics according to the element area, the interior angle, and the edge length are illustrated in Figs. 7, 8, and 9. In case of the triangular mesh, more elements having small area and/or large aspect ratio are observed than the CVT mesh, after the path representation. Additionally, many short-length edges are generated in the triangular mesh while the distributions of the edge length are almost identical in the CVT mesh, before and after the path representation.

Fig. 6
figure 6

Representation of the spiral path using the element splitting scheme on a the CVT mesh and b the triangular mesh

Full size image
Fig. 7
figure 7

Comparison of the element area distributions before and after the representation of the spiral path: a the CVT mesh and b the triangular mesh

Full size image
Fig. 8
figure 8

Comparison of the interior angle distributions before and after the representation of the spiral path: a the CVT mesh and b the triangular mesh

Full size image
Fig. 9
figure 9

Comparison of the edge length distributions before and after the representation of the spiral path: a the CVT mesh and b the triangular mesh

Full size image

One should note that VEM is identical to FEM if an element shape is limited to triangular for the crack path representation. Yet, the split of a triangular element may result in non-triangular elements, and thus additional splits of non-triangular elements are needed for the triangularization, as discussed previously. Therefore, the use of polygonal elements results in the flexibility on the crack path representation even when the original mesh is triangular. In conclusion, by using the polygonal mesh with the element splitting scheme, one can represent smooth and accurate crack path while preserving the high mesh quality as compared to the standard FEM approach.

4 Stress recovery and evaluation of crack path direction

In quasi-static fracture analysis, it is essential to represent the crack path precisely because inaccurate crack growth leads to locking phenomena and also affects the global load–displacement relationship corresponds to the equilibrium state (Unger et al. 2007). To compute the crack propagation direction, one should accurately compute the gradient of the displacement field around a crack-tip region. However, element quality could be degenerated during the element split, which results in an inaccurate stress field around a crack-tip region. To tackle this issue, we extend the original VGSR scheme, developed by Choi and Park (2019), by tailoring the reconstruction procedure of the displacement field within the VEM framework. In the remainder of this section, we present the basic concept of original VGSR and the details of the extended approach to reconstruct a displacement field of the virtual grid. Then, the maximum strain energy release rate (MSERR) criterion is explained in conjunction with VGSR, which is the choice in this work as a crack growth criterion.

4.1 Virtual grid-based stress recovery (VGSR) in VEM

The basic idea of VGSR is to use a well-structured virtual grid instead of the original mesh for the numerical differentiation such as strain and stress (Choi and Park 2019). By using the virtual grid, one can alleviate the effects of the low-quality elements, e.g., elongated or small elements (shaded elements in Fig. 10a), on the stress evaluation. As the first step of the stress field evaluation using VGSR, one generates a virtual grid of \(6\times 6\) around a crack tip using the quadrilateral elements (see Fig. 10b). The size of a single virtual grid is selected as the average size of original virtual elements around a crack tip region. The center of the virtual grid is located at the crack tip, while the front and rear parts of the virtual grid are positioned according to a calculated crack path direction and a crack trajectory. After the generation of the virtual grid, one evaluates nodal displacements of the virtual grid nodes as the next step. In the original VGSR scheme, the displacement quantities of the virtual grid are computed using a linear Lagrange shape function and the nodal displacement of the finite (triangular) element, e.g., \({{\varvec{u}}}_{vg}({\varvec{x}})={\sum }_{i=1}^{3}{{\varvec{N}}}_{i}({\varvec{x}}){{\varvec{u}}}_{i}\), where \({{\varvec{u}}}_{vg}\) is the displacement of the virtual grid, \({{\varvec{N}}}_{i}\) is the shape function, and \({{\varvec{u}}}_{i}\) is the nodal displacement of the finite element. However, this approach is not applicable in the VEM framework because the local basis functions in VEM are unknown in element interior (Chi et al. 2019). Therefore, in this study, we propose a least-square projection approach based on the coordinates and the nodal displacement of the virtual element to evaluate the displacement field of the virtual grid. As illustrated in Fig. 11, if a certain node of the virtual grid, i.e., the solid square marker, is located inside of a virtual element, i.e., the gray element, one first defines a set of linear basis functions as

$$\mathbf{m}\left({\varvec{x}}\right)=\left[\begin{array}{ccc}1,& \frac{x-{x}_{c}}{{h}_{e}},& \frac{y-{y}_{c}}{{h}_{e}}\end{array}\right],$$
(13)

where \({{\varvec{x}}}_{c}={\left[{x}_{c}, {y}_{c}\right]}^{\mathrm{T}}\) and \({h}_{e}=\sqrt{{A}_{e}}\) are the centroid and the characteristic size of that virtual element, respectively, with \({A}_{e}\) being its area. Then, the nodal displacement of the virtual grid \({{\varvec{u}}}_{vg}={\left[{u}_{x,vg}, {u}_{y,vg}\right]}^{\mathrm{T}}\) is interpolated as a linear combination of basis functions \(\mathbf{m}({\varvec{x}})\) of the form

$${u}_{x,vg}=\mathbf{m}\left({\varvec{x}}\right){\mathbf{q}}^{x}\,\mathrm{and}\, {{u}}_{y,vg}=\mathbf{m}\left({\varvec{x}}\right){\mathbf{q}}^{y},$$
(14)

where \({\mathbf{q}}^{x}={\left[{q}_{1}^{x}, {q}_{2}^{x},{q}_{3}^{x}\right]}^{\mathrm{T}}\) and \({\mathbf{q}}^{y}={\left[{q}_{1}^{y}, {q}_{2}^{y},{q}_{3}^{y}\right]}^{\mathrm{T}}\) are vectors of unknown coefficients. To obtain those coefficients, one solves least-square problems, aiming to minimize residual vectors \({\mathbf{r}}_{x}\) and \({\mathbf{r}}_{y}\) defined by:

$${\mathbf{r}}_{x}=\mathbf{P}{\mathbf{q}}^{x}-{\mathbf{b}}^{x}\,\mathrm{and}\,{\mathbf{r}}_{y}=\mathbf{P}{\mathbf{q}}^{y}-{\mathbf{b}}^{y},$$
(15)

where \({\mathbf{b}}^{x}\) and \({\mathbf{b}}^{y}\) are vectors collecting the x- and y-VEM displacement solutions at the vertices of the element, respectively, and \(\mathbf{P}\) is a matrix collecting the values of the basis functions evaluated at the vertices of that virtual element, namely, the ith row of P is \(\mathbf{m}\left({{\varvec{x}}}_{i}\right)\), where \({{\varvec{x}}}_{1},\dots , {{\varvec{x}}}_{{n}_{v}}\) denote the position vectors of the vertices. Then, the unknown coefficients \({\mathbf{q}}^{x}\) and \({\mathbf{q}}^{y}\) are calculated by using the normal equations of Eq. (15), which are given by,

Fig. 10
figure 10

Schematics of the virtual grid-based stress recovery (VGSR): a an example of the curved crack path representation using the element split, and b generation of the virtual grid

Full size image
Fig. 11
figure 11

Calculation procedure for nodal displacements of the virtual grid

Full size image
$${\mathbf{q}}^{x}={\left({\mathbf{P}}^{\mathrm{T}}\mathbf{P}\right)}^{-1}{\mathbf{P}}^{\mathrm{T}}{\mathbf{b}}^{x}\,\mathrm{and}\,{\mathbf{q}}^{y}={\left({\mathbf{P}}^{\mathrm{T}}\mathbf{P}\right)}^{-1}\,{\mathbf{P}}^{\mathrm{T}}{\mathbf{b}}^{y}.$$
(16)

After the calculation of the coefficients, the nodal displacements of the virtual grid \({{\varvec{u}}}_{vg}\) can be evaluated using Eq. (14). Finally, stresses at the Gauss points of each single virtual grid are obtained using the shape functions of the bilinear quadrilateral element. We remark that the patch-based gradient recovery scheme (Choi et al. 2021; Chi et al. 2019) may be an alternative choice to evaluate the stress field around the crack-tip region, which can provide a more accurate gradient field than the original VEM solutions. A further comparative study of various stress recovery schemes on VEM for fracture modeling is subjected to future investigation.

4.2 Maximum strain energy release rate (MSERR) criterion

Once the displacement and stress fields around the crack tip region are reconstructed using VGSR, the crack propagation direction is evaluated based on the crack growth criterion. In this study, the MSERR criterion is considered, which is originally proposed by Hussain et al. (1974). According to this criterion, a crack propagates in the direction where the strain energy release rate is maximized. The strain energy release rate G can be expressed using the relationship with J-integral (Nishioka and Atluri 1983), given as

$$G={J}_{1}\mathrm{cos}(\theta )+{J}_{2}\mathrm{sin}(\theta ),$$
(17)

where \({J}_{1}\) and \({J}_{2}\) are the components of J-integral, and \(\theta \) is an angle of the local crack tip coordinate system (see Fig. 12). Then, we calculate the crack propagation angle \({\theta }_{c}\) by taking a derivative of Eq. (17) with respect to \(\theta \), expressed as

Fig. 12
figure 12

Schematics of the domain integral to evaluate J-integral

Full size image
$${\theta }_{c}={\mathrm{tan}}^{-1}\left(\frac{{J}_{2}}{{J}_{1}}\right).$$
(18)

To evaluate J-integral, the domain integral method (Gu et al. 1999) is employed in conjunction with the proposed stress recovery scheme. That is to say, the integration domain for J-integral is set as the virtual grid. The domain integral expression for J-integral is given as

$${J}_{k}={\int }_{A}\left({\sigma }_{ij}\frac{{\partial u}_{j}}{\partial {x}_{k}}-W{\delta }_{ki}\right)\frac{\partial q}{\partial {x}_{i}}dA-{\int }_{{C}^{+}+{C}^{-}}{t}_{i}\frac{{\partial u}_{i}}{\partial {x}_{k}}qdC,$$
(19)

where \({\sigma }_{ij}\), \({t}_{i}\) and \({u}_{i}\) are the stress, traction, and displacement components, respectively; W is the strain energy density; \({\delta }_{ij}\) is the Kronecker delta; \(q=q({x}_{1},{x}_{2})\) is an arbitrary smooth function which is zero on the boundary and unity at the crack tip. On the virtual grid generated around the crack-tip region, all the variables are calculated and numerical integration is performed to evaluate J-integral. Because the VGSR process is only employed to evaluate the stress field and J-integral, it can be considered as a post-processing technique which complements VEM (Choi et al. 2022).

5 Mixed-mode examples

In this section, three computational examples are provided to validate the proposed computational framework on the mixed-mode concrete fracture. For the material parameters which are not provided in the experimental data, i.e., initial fracture energy and kink point ratio, we assume them within a reasonable range (Bažant 2002). Additionally, to track post-peak softening behaviors of concrete, the generalized displacement control method (Yang and Shieh 1990) is utilized which is one of incremental-iterative methods to solve a system of nonlinear equations (Leon et al. 2011).

5.1 Four-point shear test

A four-point shear test is investigated as the classical benchmark problem for mixed-mode fracture simulation. The original experiment was performed by Schlangen (1993). The geometry and boundary conditions of the test specimen are illustrated in Fig. 13a. The specimen size is \(440\times 100\times 100\) mm with an initial notch of \(5\times 20\times 100\) mm located at the center of the top surface. Four steel plates are placed at the loading points and the supporting points to alleviate stress concentration. The size of the plates is \(20\times 5\times 100\) mm. Then, the vertical loads are applied at the two bottom plates with the ratio of one to ten, and the relative horizontal displacement is measured at the mouth of the initial notch, i.e., crack mouth opening displacement (CMOD). The domain is discretized using two types of meshes, i.e., a CVT mesh (Fig. 13b), and a low-quality triangular mesh (Fig. 13c). For the CVT and triangular meshes, the number of nodes is 13,482 and 8010, while the number of elements is 6675 and 15,400, respectively. Note that elements with average size of 1 \(\mathrm{mm}\) are distributed around the potential crack path. The material properties measured in the experiments (Schlangen 1993) are given as: Young’s modulus \(E=30\,\mathrm{ GPa}\), Poisson’s ratio \(\nu =0.2\), the tensile strength (corresponding to the cohesive strength) \({\sigma }_{\mathrm{max}}=3 \,\mathrm{MPa}\), and the fracture energy \({G}_{F}=100\,\mathrm{ N}/\mathrm{m}\). For the steel plates, the elastic modulus of \(210\,\mathrm{ GPa}\) and Poisson’s ratio of \(0.3\) are assumed, respectively. All the materials are modeled as isotropic linear elastic materials and the plane strain condition is employed for the computational simulation. Additionally, the initial fracture energy is selected as \(40\,\mathrm{ N}/\mathrm{m}\) having the ratio of 2.5 to the total fracture energy and the kink point ratio is assumed as 0.33 for the bilinear softening model (Bažant 2002).

Fig. 13
figure 13

a Geometry and boundary conditions, b the CVT mesh, and c the low-quality triangular mesh for the four-point shear test

Full size image

The computed crack paths for the CVT and low-quality triangular meshes are illustrated in Fig. 14a and b, respectively. For the both cases, the proposed computational scheme represents the smooth and curved crack patterns (red solid lines) well, and the computed results are within the range of experimental results (black solid and dashed lines). Next, the predicted load P and CMOD relationships are compared to the results from the experiments and the FEM approach (Choi and Park 2019). As shown in Fig. 15, the predicted results are within the range of experimental results, and they also agree with the ones of the FEM approach. Note that the 4k structured mesh is employed for the computation using the FEM approach, consists of 9256 nodes and 18,207 elements.

Fig. 14
figure 14

Computed crack patterns for the four-point shear test using a the CVT mesh and b the low-quality triangular mesh

Full size image
Fig. 15
figure 15

Comparison between computational and experimental results for the load–CMOD relationship

Full size image

5.2 L-shaped panel test

For a second mixed-mode example, an L-shaped panel test is considered which was investigated experimentally by Winkler (2001). The geometry and boundary conditions of the panel are shown in Fig. 16. A vertical load is applied with a distance of 30 mm from the right surface of the panel while the bottom surface is fully constrained. The material properties are taken as Young’s modulus \(E=20\,\mathrm{ GPa}\), Poisson’s ratio \(\nu =0.18\), the tensile strength \({\sigma }_{\mathrm{max}}=2.5 \,\mathrm{MPa}\), and the fracture energy \({G}_{F}=130\,\mathrm{ N}/\mathrm{m}\) (Unger et al. 2007). Note that those material parameters are calibrated to attain the better approximation of experimental results. For the bilinear softening model, we choose the initial fracture energy of 93 N/m and the kink point ratio of 0.2. For the mesh discretization, the CVT mesh is utilized which consists of 15,920 nodes and 8018 elements assuming plane stress condition. In this example, two types of the crack growth criteria, i.e., maximum principal stress and MSERR, are tested to investigate the effects of the biaxial stress state on each criterion and corresponding crack patterns.

Fig. 16
figure 16

Geometry and boundary conditions of a L-shaped panel test

Full size image

The computed crack trajectories and the range of experimental results are shown in Fig. 17a. When the maximum principal stress criterion is utilized as the crack growth criterion, the oscillated crack pattern is observed which is caused by the almost equal biaxial stress state around the crack tip region. Note that similar results are also reported in the literature (Wang and Waisman 2018). When the MSERR criterion is employed, the smooth and curved crack path is represented because it does not suffer from the biaxial stress state (see Fig. 17b). Also, the computed crack path shows a good agreement with the experimental results. Figure 18 shows the computational load–displacement curves obtained using the MSERR criterion. As can be seen, the presented method reproduces the experimental results well, and shows the accuracy as much as the other computational methods, i.e., XFEM and the phase-field method (Wang and Waisman 2016; Mandal et al. 2019).

Fig. 17
figure 17

a Computed crack patterns according to the crack growth criteria and comparisons with experimental data, and b the virtual element mesh obtained using the maximum strain energy release rate criterion

Full size image
Fig. 18
figure 18

Load–displacement relationship for the L-shaped panel test

Full size image

5.3 Off-center notch specimen test

As the last example, an off-center notch specimen test is employed. The original experiment was performed by Jenq and Shah (1988). The test setup of the specimen including the geometry and boundary conditions is illustrated in Fig. 19. The specimen size is \(304.8\times 76.2\) mm with a thickness of 28.6 mm. The length of the initial notch is 25.4 mm. Then, two specimen configurations are considered to investigate the effects of the location of the initial notch, i.e., e = 50.8 and 76.2 mm, on the crack pattern and load–displacement relationship. The elastic modulus and Poisson’s ratio are taken from the experiment (Jenq and Shah 1988), given as 32.8 GPa and 0.18, respectively. To calculate the total fracture energy for each test configuration, we employ the total work of fracture method based on the experimental load–crack opening displacement (COD) data (see Fig. 20). Then, the total fracture energies of 102.5 N/m and 172.7 N/m are used for the specimens with e = 50.8 mm and 76.2 mm, respectively. The cohesive strength (tensile strength) is assumed as 4 MPa based on the experimental compressive strength \({f}_{\mathrm{c}}=34.3\,\mathrm{ MPa}\) and approximated relationships between the tensile and compressive strengths of the plain concrete (Chhorn et al. 2018; Carneiro and Barcellos 1953; Raphael 1984). The initial fracture energy of 41 N/m and the kink point ratio of 0.33 are selected for the specimen with e = 50.8 mm, while the initial fracture energy of 86.4 N/m and the kink point ratio of 0.24 are employed for the specimen with e = 76.2 mm. The material properties used in each specimen are summarized in Table 1.

Fig. 19
figure 19

Geometry and boundary conditions of an off-center notch specimen test

Full size image
Fig. 20
figure 20

Experimental results for load–COD relationship (Jenq and Shah 1988)

Full size image
Table 1 Geometry information and material properties for an off-center notch specimen test
Full size table

The computed load versus COD relationships are illustrated in Fig. 21. For the both cases, the predicted computational results capture the load–displacement relation of the experimental results well, including the peak load. The predicted crack patterns and the experimental results are illustrated as red and black lines in Fig. 22, respectively. For both test configuration cases, the computational results are within the range of experimental results.

Fig. 21
figure 21

Computational results for load–COD relationship and those comparisons with the experimental result: a \(e=50.8 \,\mathrm{mm}\), and b \(e=76.2 \,\mathrm{mm}\)

Full size image
Fig. 22
figure 22

Computed crack patterns for the off-center notch specimen test: a \(e=50.8 \,\mathrm{mm}\), and b \(e=76.2 \,\mathrm{mm}\)

Full size image

6 Concluding remarks

In this paper, we present an integrated VEM–CZM framework to capture nonlinear crack propagation and mixed-mode fracture behavior in conjunction with the element splitting and domain integral. The crack propagation direction is calculated using the domain integral with VGSR; the crack path is accurately represented on a polygonal mesh with the element splitting. To validate the proposed computational framework, three mixed-mode fracture examples are investigated. The main contributions of the present paper are summarized as follows:

  • To represent an arbitrary crack path on a polygonal mesh, the element splitting strategy is employed. During the element split, the node relocation operator decreases the number of possible occurrences of additional elements with small edges that may degrade the quality of the VEM solution.

  • For the crack path representation using the element splitting, the element quality in a polygonal mesh (VEM) is generally higher than that in a triangular mesh (FEM). In the meantime, a larger number of elements are created in a triangular mesh (FEM) than in a polygonal mesh (VEM).

  • For the evaluation of the crack propagation direction, the MSERR criterion is employed in conjunction with VGSR. Then, the oscillation of a crack path is successfully eliminated under the biaxial stress state. When the maximum principal stress criterion is employed, the zigzag crack path is observed under the biaxial stress state in this study.

  • To validate the proposed computational framework, three mixed-mode fracture examples are investigated, i.e., four-point shear test, L-shaped panel test, and off-center notch specimen test. The computational results agree well with experimental results in terms of both crack paths and load–displacement relationships.