The revisited phase-field approach to brittle fracture: application to indentation and notch problems

Abstract

In a recent contribution, Kumar et al. (J Mech Phys Solids 142:104027, 2020) have introduced a comprehensive macroscopic phase-field theory for the nucleation and propagation of fracture in linear elastic brittle materials under arbitrary quasistatic loading conditions. The theory can be viewed as a natural generalization of the phase-field approximation of the variational theory of brittle fracture of Francfort and Marigo (J Mech Phys Solids 46:1319–1342, 1998) to account for the material strength at large. This is accomplished by the addition of an external driving force—which physically represents the macroscopic manifestation of the presence of inherent microscopic defects in the material—in the equation governing the evolution of the phase field. The main purpose of this paper is to continue providing validation results for the theory by confronting its predictions with direct measurements from three representative types of experimentally common yet technically challenging problems: (i) the indentation of glass plates with flat-ended cylindrical indenters and the three-point bending of (ii) U-notched and (iii) V-notched PMMA beams.

Appendix: sample results showcasing the independence of the phase-field theory (4)–(5) on the localization length \(\varepsilon \)

In this appendix, as a complement to the results reported in Section 4.3 in (Kumar et al. 2020), we report sample results for each of the three classes of boundary-value problems investigated in the main body of the text that showcase the independence of the phase-field theory (4)–(5) on the localization length $\varepsilon$.

Fig. 14

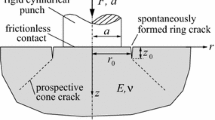
Contour plot of the phase field v predicted by the phase-field theory (4)–(5) for one of the indentation experiments of Mouginot and Maugis (1985). Part a reproduces the result in Fig. 4a for localization length (13), while part b shows the corresponding result for the different localization length (20)

Figure 14 provides a comparison between the result presented in Fig. 4a for the phase field v predicted by the theory for localization length (13) and that obtained for the different localization length

$$\begin{aligned} \varepsilon =\left\{ \begin{array}{ll} 15\, \mu \mathrm{m}, &{}\; \mathbf{X}\in {\mathcal {B}}^\varepsilon \\ \\ 4.75\, \mu \mathrm{m}, &{}\; \mathbf{X}\in {\mathrm \Omega }\setminus {\mathcal {B}}^\varepsilon \end{array}\right. . \end{aligned}$$

(20)

The calibration of the coefficient $\delta ^\varepsilon$ for the values (20) renders $\delta ^\varepsilon =60$ and $\delta ^\varepsilon =6$, respectively, which result in an actual regularized size of the cracks given by $\varepsilon ^\star =\varepsilon /\sqrt{1+\delta ^\varepsilon }=1.9$ $\mu$m. This is about three times smaller than the size of the cracks obtained for the localization length (13). Yet, it is evident that the results in Figs. 14a and b are essentially the same.

Next, Fig. 15 presents a comparison between the critical force $P_{cr}$ in Fig. 9 predicted by the theory for notch depth $A=5$ mm when using a localization length $\varepsilon =12.5$ $\mu$m (solid line) and the corresponding result (dashed line) when using the smaller localization length $\varepsilon =5$ $\mu$m. In the latter case, the calibrated value of the coefficient $\delta ^\varepsilon$ turns out to be $\delta ^\varepsilon =1.15$, which results in a regularized crack size of $\varepsilon ^\star =\varepsilon /\sqrt{1+\delta ^\varepsilon }=3.4$ $\mu$m. This is about two times smaller than the regularized crack size that ensues from $\varepsilon =12.5$ $\mu$m. Clearly, the results in Fig. 15 for the two different localization lengths are largely similar to one another.

Fig. 15

Critical force $P_{cr}$ predicted by the phase-field theory (4)–(5) for one of the U-notched beam experiments of Gómez et al. (2005). The solid line reproduces the result for notch depth $A=5$ mm in Fig. 9 for localization length $\varepsilon =12.5$ $\mu$m, while the dashed line corresponds to the result for localization length $\varepsilon =5$ $\mu$m

Fig. 16

Critical force $P_{cr}$ predicted by the phase-field theory (4)–(5) for one of the V-notched beam experiments of Dunn et al. (1997). The solid line reproduces the result for notch angle $\gamma =90^{\circ }$ in Fig. 13b for localization length $\varepsilon =12.5$ $\mu$m, while the dashed line corresponds to the result for localization length $\varepsilon =9$ $\mu$m

Finally, Fig. 16 presents a comparison between the critical force $P_{cr}$ in Fig. 13b predicted by the theory for notch angle $\gamma =90^{\circ }$ when using a localization length $\varepsilon =12.5$ $\mu$m (solid line) and the corresponding result (dashed line) when using the smaller localization length $\varepsilon =9$ $\mu$m. The calibrated value of the coefficient $\delta ^\varepsilon$ for the latter case is $\delta ^\varepsilon =35$, which results in a regularized crack size $\varepsilon ^\star =\varepsilon /\sqrt{1+\delta ^\varepsilon }=1.5$ $\mu$m that is about six times smaller than the regularized crack size that is obtained for $\varepsilon =12.5$ $\mu$m. Consistent with the two preceding comparisons, a quick glance at Fig. 16 suffices to recognize that the two theoretical predictions based on different localization lengths are practically the same.