Planar cracks of arbitrary shapes in elastic media with ellipsoidal anisotropy: efficient numerical solution

Abstract

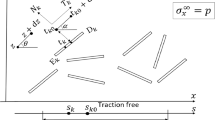
The elasticity problem for planar cracks in infinite homogeneous anisotropic media subjected to arbitrary external stress fields is considered. The problem is reduced to solving the integral equation for the displacement jump on the crack surface. An efficient numerical method of solution of this equation is proposed for media with ellipsoidal anisotropy. In the method, Gaussian radial functions shifted at the nodes of a regular grid on the crack surface are used to approximate the solution. The problem is reduces to a linear algebraic system for the coefficients of the approximation (the discretized problem). For Gaussian approximating functions, the elements the matrix of this system are presented in the forms of standard 1D-integrals. These integrals can be tabulated for small values of the arguments, and they have simple analytical asymptotics for large arguments. As the result, the matrix of the discretized problem is calculated fast. For regular grids of approximating nodes, this matrix has Toeplitz’ structure, and fast Fourier transform algorithm can be used for calculating matrix-vector products by iterative solution of the discretized problem. It substantially accelerates the construction of the numerical solutions. Examples of the solutions for circular, annular and square cracks of various orientations in a strongly anisotropic elastic medium are presented.

Appendix

The function $\Phi ^{0}(\varsigma )$ in Eq. (60) is the integral over the entire 3D-space ($\varsigma =(\varsigma _{1},\varsigma _{2} ,\varsigma _{3}))$

$$\begin{aligned} \Phi ^{0}(\varsigma )&=\int g_{0}(\varsigma -\varsigma ^{\prime } ){\widehat{\varphi }}(\varsigma ^{\prime })d\varsigma ^{\prime },{ \ \ }{\widehat{\varphi }}(\varsigma _{1},\varsigma _{2},\varsigma _{3})\nonumber \\&=\frac{1}{\pi H}\exp \left( -\frac{\varsigma _{1}^{2}+\varsigma _{2}^{2}}{H}\right) \delta (\varsigma _{3}), \end{aligned}$$

(A.1)

$$\begin{aligned} g_{0}(\varsigma )&=\frac{1}{4\pi {\overline{r}}(\varsigma )},{ \ } {\overline{r}}(\varsigma )=\sqrt{\varsigma _{i}D_{ij}^{-1}\varsigma _{j}}. \end{aligned}$$

(A.2)

It follows from Eq. (57) that $\Phi _{0}(\varsigma )$ satisfies the differential equation

$$\begin{aligned} D_{ij}\partial _{i}\partial _{j}\Phi ^{0}(\varsigma )=-{\ }\widehat{\varphi }(\varsigma ). \end{aligned}$$

(A.3)

For construction of $\Phi ^{0}(\varsigma )$, following to Maz’ya and Schmidt (2007), we consider the Cauchy problem for the parabolic equation

$$\begin{aligned} \frac{\partial v(\varsigma ,t)}{\partial t}-D_{ij}\partial _{i}\partial _{j}v(\varsigma ,t)=0,{ \ }v(\varsigma ,t)|_{t=0}=\widehat{\varphi }(\varsigma ).\nonumber \\ \end{aligned}$$

(A.4)

Application to these equations Fourier transform with respect to $\varsigma$-variables yields

$$\begin{aligned}&\frac{\partial v^{*}(k,t)}{\partial t}+\left( D_{ij}k_{i} k_{j}\right) v^{*}(k,t)=0,\text { }v^{*}(k,t)|_{t=0}\nonumber \\&\quad =\exp \left( -\frac{H}{4}(k_{1}^{2}+k_{2}^{2})\right) , \end{aligned}$$

(A.5)

$$\begin{aligned}&\left. v^{*}(k,t)=\int v(\varsigma ,t)\exp \left( ik_{m}\varsigma _{m}\right) d\varsigma ,\text { }i=\sqrt{-1}.\right. \end{aligned}$$

(A.6)

The solution of this problem has the form

$$\begin{aligned}&v^{*}(k,t)=\exp \left( -\frac{1}{4}k_{i}B_{ij}(t)k_{j}\right) ,\nonumber \\&B_{ij}(t)=H{\overline{\delta }}_{ij}+4tD_{ij},\nonumber \\&\overline{\delta }_{ij}=\delta _{ij}-\delta _{i3}\delta _{j3}. \end{aligned}$$

(A.7)

After application of the inverse Fourier transform we obtain the solution of the problem in Eqs. (A.4)

$$\begin{aligned} v(\varsigma ,t)=\frac{1}{\pi ^{3/2}\sqrt{\det B(t)}}\exp \left( -\varsigma _{i}B_{ij}^{-1}(t)\varsigma _{j}\right) . \end{aligned}$$

(A.8)

Then, from the first equation (A.4) we have

$$\begin{aligned}&D_{ij}\partial _{i}\partial _{j}\lim _{T\rightarrow \infty }\int \limits _{0} ^{T}v(\varsigma ,t)dt=\lim _{T\rightarrow \infty }\int \limits _{0}^{T} \frac{\partial v(\varsigma ,t)}{\partial t}dt\nonumber \\&\quad =\lim _{T\rightarrow \infty }v(\varsigma ,T)-v(\varsigma ,0)=-{\widehat{\varphi }}(\varsigma ). \end{aligned}$$

(A.9)

It is taken into account that when $T\rightarrow \infty$, $v(\varsigma ,T)\rightarrow 0$ as $T^{-1/2}$. As a result, we obtain the identity

$$\begin{aligned} D_{ij}\partial _{i}\partial _{j}\int \limits _{0}^{\infty }v(\varsigma ,t)dt=-{\widehat{\varphi }}(\varsigma ). \end{aligned}$$

(A.10)

Comparison with Eq. (A.3) yields the integral presentation of the function $\Phi ^{0}(\varsigma )$

$$\begin{aligned} \Phi ^{0}(\varsigma )&=\int \limits _{0}^{\infty }v(\varsigma ,t)dt=\frac{1}{4\pi ^{3/2}}\int \limits _{0}^{\infty }\frac{\exp \left[ -\varsigma _{i} A_{ij}^{-1}(t)\varsigma _{j}\right] }{\sqrt{\det A(t)}}dt, \end{aligned}$$

(A.11)

$$\begin{aligned} A_{ij}(t)&=H{\overline{\delta }}_{ij}+tD_{ij}. \end{aligned}$$

(A.12)

The asymptotic of this function for large values of $|\varsigma |$ follows from Eq. (A.1) in the form

$$\begin{aligned} \Phi ^{0}(\varsigma )=\frac{1}{4\pi {\overline{r}}(\varsigma )}+O\left( |\varsigma |^{-3/2}\right) . \end{aligned}$$

(A.13)

For calculating the function $\Phi _{ij}^{2}(\varsigma )$ in Eq. (60), we consider the integral over 3D-space

$$\begin{aligned} \Phi ^{2}(\varsigma )=\int g_{2}(\varsigma -\varsigma ^{\prime })\widehat{\varphi }(\varsigma ^{\prime })d\varsigma ^{\prime },{ \ \ }g_{2}(\varsigma )=-\frac{{\overline{r}}(\varsigma )}{8\pi }.\nonumber \\ \end{aligned}$$

(A.14)

Here, the function ${\widehat{\varphi }}(\varsigma )$ is defined in Eq. (A.1). It follows from Eq. (57) that the function $\Phi ^{2}(\varsigma )$ satisfies the equation

$$\begin{aligned} \left( D_{ij}\partial _{i}\partial _{j}\right) ^{2}\Phi ^{2}(\varsigma )={\ }{\widehat{\varphi }}(\varsigma ). \end{aligned}$$

(A.15)

For construction of $\Phi ^{2}(\varsigma )$, following to a method proposed in Maz’ya and Schmidt (2007), we consider the Cauchy problem for the hyperbolic equation

$$\begin{aligned}&\frac{\partial ^{2}w(\varsigma ,t)}{\partial t^{2}}+\left( D_{ij}\partial _{i}\partial _{j}\right) ^{2}w(\varsigma ,t)=0,{ \ }w(\varsigma ,t)|_{t=0}\nonumber \\&={\widehat{\varphi }}(\varsigma ),{ \ }\frac{\partial }{\partial t}w(\varsigma ,t)|_{t=0}=0. \end{aligned}$$

(A.16)

Application of Fourier transform operator with respect to $\varsigma$-variables to these systems yields the solution of this problem in the form

$$\begin{aligned} w(\varsigma ,t)&=\frac{1}{2\pi ^{3/2}}\left[ \frac{\exp \left[ -\varsigma _{i}\left( B^{+}\right) _{ij}^{-1}(t)\varsigma _{j}\right] }{\sqrt{\det B^{+}(t)}}\right. \nonumber \\&\quad \left. +\frac{\exp \left[ -\varsigma _{i}\left( B^{-}\right) _{ij}^{-1}(t)\varsigma _{j}\right] }{\sqrt{\det B^{-}(t)}}\right] , \end{aligned}$$

(A.17)

$$\begin{aligned} B_{ij}^{\pm }(t)&=H{\overline{\delta }}_{ij}\pm i4tD_{ij},\text { }i=\sqrt{-1}. \end{aligned}$$

(A.18)

The function $\Phi _{ij}^{2}(\varsigma )=\partial _{i}\partial _{j}\Phi ^{2}(\varsigma )$ satisfies the equation

$$\begin{aligned} \left( D_{kl}\partial _{k}\partial _{l}\right) ^{2}\Phi _{ij}^{2} (\varsigma )={\ }\partial _{i}\partial _{j}{\widehat{\varphi }}(\varsigma ). \end{aligned}$$

(A.19)

It follows from Eqs. (A.16) that the function $W_{ij}(\varsigma ,t)=\partial _{i}\partial _{j}w(\varsigma ,t)$ is the solution of the following Cauchy problem

$$\begin{aligned}&\frac{\partial ^{2}W_{ij}(\varsigma ,t)}{\partial t^{2}}+\left( D_{kl} \partial _{k}\partial _{l}\right) ^{2}W_{ij}(\varsigma ,t)=0,\nonumber \\&W_{ij}(\varsigma ,t)|_{t=0}=\partial _{i}\partial _{j}{\widehat{\varphi }} (\varsigma ),{ \ }\frac{\partial }{\partial t}W_{ij}(\varsigma ,t)|_{t=0}=0.\nonumber \\ \end{aligned}$$

(A.20)

Multiplying the first of these equations with t and integrating from 0 to T, we obtain

$$\begin{aligned}&-\left( D_{kl}\partial _{k}\partial _{l}\right) ^{2}\int \limits _{0}^{T} tW_{ij}(\varsigma ,t)dt\nonumber \\&\quad =\int \limits _{0}^{T}t\frac{\partial ^{2} W_{ij}(\varsigma ,t)}{\partial t^{2}}dt={\ }\left. t\frac{\partial W_{ij}(\varsigma ,t)}{\partial t}\right| _{t=0}^{t=T}\nonumber \\&\qquad -\int \limits _{0} ^{T}\frac{\partial W_{ij}(\varsigma ,t)}{\partial t}dt\nonumber \\&\quad =T\frac{\partial W_{ij}(\varsigma ,T)}{\partial t}-W_{ij}(\varsigma ,T)+\partial _{i}\partial _{j}{\widehat{\varphi }}(\varsigma ). \end{aligned}$$

(A.21)

Because $W_{ij}(\varsigma ,T)=O(T^{-1/2})$ and $\frac{\partial W_{ij} (\varsigma ,T)}{\partial t}=O(T^{-3/2})$ when $T\rightarrow \infty ,$ we have the identity

$$\begin{aligned} \left( D_{kl}\partial _{k}\partial _{l}\right) ^{2}\left( -\int \limits _{0}^{\infty }tW_{ij}(\varsigma ,t)dt\right) ={\ }\partial _{i}\partial _{j}{\widehat{\varphi }}(\varsigma ).\nonumber \\ \end{aligned}$$

(A.22)

Comparison with Eq. (A.15) yields presentation of $\Phi _{ij}^{2}(\varsigma )$ in the integral form

$$\begin{aligned}&\Phi _{ij}^{2}(\varsigma )=-\int \limits _{0}^{\infty }tW_{ij}(\varsigma ,t)dt,\nonumber \\&{ \ }W_{ij}(\varsigma ,t)=\partial _{i}\partial _{j}w(\varsigma ,t), \end{aligned}$$

(A.23)

where the function $w(\varsigma ,t)$ is defined in Eq. (A.17). After application of Cauchy theorem, the integral in this equation can be transformed to the following one (see Maz’ya and Schmidt 2007, page 132)

$$\begin{aligned}&\Phi _{ij}^{2}(\varsigma )=\frac{1}{16\pi ^{3/2}}\int \limits _{0}^{\infty } \partial _{i}\partial _{j}\exp \left[ -\varsigma _{i}A_{ij}^{-1}(t)\varsigma _{j}\right] \nonumber \\&\quad \frac{tdt}{\sqrt{\det A(t)}},\text { }A_{ij}(t)=H\overline{\delta }_{ij}+tD_{ij}. \end{aligned}$$

(A.24)

This equation coincides with Eq. (63) of the paper.

The asymptotic of the function $\Phi _{ij}^{2}(\varsigma )$ for large $|\varsigma |$ follows from Eq. (A.14) in the form

$$\begin{aligned} \Phi _{ij}^{2}(\varsigma )=\partial _{i}\partial _{j}\left( -\frac{\overline{r}(\varsigma )}{8\pi }\right) +O\left( |\varsigma |^{-3/2}\right) . \end{aligned}$$

(A.25)