Study on the cohesive edge crack in a square plate with the cohesive element method

Abstract

The size of the fully developed process zone (FDPZ) is needed for the arrangement of displacement sensors in fracture experiments and choosing element size in numerical models using the cohesive element method (CEM). However, the FDPZ size is generally not known beforehand. Analytical solutions for the exact FDPZ size only exist for highly idealised bodies, e.g. semi-infinite plates. With respect to fracture testing, the CEM is also a potential tool to extrapolate laboratory test results to full-scale while considering the size effect. A numerical CEM-based model is built to compute the FDPZ size for an edge crack in a finite square plate of different lengths spanning several magnitudes. It is validated against existing analytical solutions. After successful validation, the FDPZ size of finite plates is calculated with the same numerical scheme. The (FDPZ) size for finite plates is influenced by the cracked plate size and physical crack length. Maximum cohesive zone sizes are given for rectangular and linear softening. Further, for this setup, the CEM-based numerical model captures the size effect and can be used to extrapolate small-scale test results to full-scale.

1 Introduction

In cohesive zone theory, the fully developed process zone (FDPZ) is the region in which material degradation is activated. The size of this zone is needed in experiments for measuring purposes, e.g. the arrangement of displacement sensors in ice fracture experiments (Dempsey et al. 1999a, b, 2004; Lu et al. 2015a, 2019), and in numerical models based on the Cohesive Element Method (CEM), where a size estimate is required for appropriate discretisation. However, the FDPZ size is generally not known beforehand. There are formulas for rough estimates (Turon et al. 2007), but it is nontrivial to obtain its exact length. Analytical solutions only exist for highly idealised cracked bodies, e.g. an edge crack in a semi-infinite plate. A closely related problem is the scaling of laboratory fracture tests to full-scale considering the size effect, i.e. the nominal strength depending on structure size, which can theoretically be done with the CEM (Bažant and Yavari 2005). To tackle these issues, a CEM-based model for an edge crack in finite square plates of different sizes is built, where several magnitudes lie between the smallest and the largest plate. FDPZ sizes and crack-opening loads are computed and the ability of the CEM to capture the size effect is investigated.

To be more specific, the CEM is popular in many fields concerning material or structural failure, e.g. (Miller et al. 1999; Xu and Needleman 1994; Wang et al. 2019a; Feng et al. 2016; Konuk et al. 2009a, b; Konuk and Yu 2010; Pandolfi et al. 2000), due to its straightforward incorporation in FEM models. It is implemented in commercial software, such as Abaqus and LS-Dyna, to simulate fracture problems e.g. crack propagation and fragmentation. Here, it is used for its ability to resolve the Fracture Process Zone (FPZ). Yet, for CEM-based models, it is not straightforward to choose a consistent set of parameters, e.g. the maximum cohesive traction, due to their mutual influence (Turon et al. 2007; Blal et al. 2013). The cohesive element size in particular is critical (Foulk 2010; Seagraves and Radovitzky 2010). Too large elements cannot accurately resolve the fracture process, whereas smaller elements increase computational effort. However, choosing an appropriate element size requires knowing the maximum size of the FPZ for a given scenario, the FDPZ. More precisely, the FDPZ is the zone when the half crack opening displacement at the traction-free crack tip reaches the critical separation of the cohesive model. Currently, the FDPZ size has to be computed and is rarely known. An exception is the work by Ha et al. (2015) who estimated its size for bending- and compact tension tests, for which however no analytical solutions exist.

Fig. 1

An example showing the arrangement of displacement sensors within the FPZ ahead of the physical crack tip

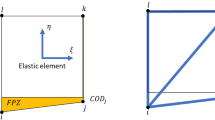
Furthermore, a cohesive law is required. It describes the traction-separation relationship within the FPZ and is considered a material property, which needs to be identified with either lab- or field-measurements. For such measurements, an initial estimate about the size of the FDPZ is needed for sufficient sensor deployment around the fracture process zone. Figure 1 shows an example of a large-scale sea ice fracture experiment to measure the fracture properties, and the related displacement sensors arrangement ahead of the physical crack tip (see the physical crack size B in Fig. 1). This is also required for measurements of cohesive fracture properties for other quasi-brittle materials, e.g. concrete, rock, or ceramics (Bažant and Planas 1998). Moreover, because most of the test samples are of limited size, it is important to know the dependence of the cohesive properties (e.g. the FDPZ size) on the test sample size.

A third and related issue is the scaling of small-scale fracture test results to full-scale while respecting the size effect, i.e. the dependence of the nominal strength of geometrically similar structures on size. For an in-depth discussion of the size effect and different underlying theories see e.g. (Bažant 2005). Testing of full-scale geometries such as large ice floes or concrete structures is often not possible due to the required effort. Most tests are done with much smaller specimens. Hence computations, e.g. for the design of large structures, must rely on extrapolation of test results, see e.g. the discussion for concrete testing by Bažant (2002). The CEM should be able to capture the size effect and is a potential tool for this extrapolation (Lu et al. 2015b; Bažant and Yavari 2005; Elices et al. 2002). This was for instance confirmed by Morel and Dourado (2011) and Ha et al. (2018), though for beam tests and a limited range of specimen sizes.

Hence the first objective is creating and validating a CEM-based numerical model for finite plates. Analytical solutions based on Linear Elastic Fracture Mechanics (LEFM) are used to validate the force required to achieve crack propagation in a finite plate (Lu et al. 2015b). More importantly, both force and the FDPZ size for large plates are compared to the work by Wang et al. (2019b), who studied a cohesive edge crack in a semi-infinite plate. The authors derived the length of the FDPZ (R) and its evolution with the physical crack size (B) under a pair of concentrated forces (P) at the crack mouth. Their solutions can be seen as an analytical benchmark to the application of any Cohesive Zone Method based numerical method, e.g. (Lu et al. 2012; Turon et al. 2007; Park et al. 2012; de Borst 2003; Elices et al. 2002; Falk et al. 2001; Remmers et al. 2003; Kuutti et al. 2013; Paulino et al. 2008; Molinari et al. 2007; Unger et al. 2007; Zi and Belytschko 2003; Moës and Belytschko 2002).

After the validation, the second objective is to extend the results of Wang et al. (2019b) to that of a finite square plate as well as identify the unknown FDPZ size and its dependence on plate size and crack tip position. The third aim is to investigate the ability of the CEM model to capture the size effect with respect to the material strength and plate size.

2 Methods

2.1 Cohesive edge crack in a square plate

Consider an Edge-Cracked Square Plate (ECSP) (see Fig. 2) with finite width $W=L$, length L and thickness t. The cohesive law results in Eq. (1), which theoretically eliminates the stress singularity at the cohesive crack tip A.

$$\begin{aligned} \begin{aligned} K&= \int _0^A \Sigma (X) H_{\mathrm {r}}(A,X) \mathrm {d}X \\&\quad -\int _0^A \Sigma _{\mathrm {coh}}(A,B,S) H_{\mathrm {r}}(A,S) \mathrm {d}S = 0 \end{aligned} \end{aligned}$$

(1)

Where K is the stress intensity factor and $\Sigma _{\mathrm {coh}}$ the normal tensile traction in the cohesive zone. $H_{\mathrm {r}}(A,X)$ is a weight function for the ECSP of related width to length ratios W/L and given by Dempsey and Mu (2014). Detailed information on the weight function is given in the Appendix.

Fig. 2

Illustration of the cohesive ECSP and its dimensions. For the simulation with intrinsic cohesive elements, the stress profile resembles the one in Fig. 6

Following the notation of Wang et al. (2019b), two cohesive stress profiles $\Sigma _{\mathrm {coh}} (A,B,X)$ are considered, the rectangular softening in Eq. (2) and linear softening in Eq. (3).

$$\begin{aligned} \Sigma _{\mathrm {coh}} (A,B,X) {=} {\left\{ \begin{array}{ll} 0 ;&{} 0< X < B \\ \Sigma _{\mathrm {0}} ;&{} B \le X \le A \end{array}\right. } \end{aligned}$$

(2)

$$\begin{aligned} \Sigma _{\mathrm {coh}} (A,B,X) = {\left\{ \begin{array}{ll} 0 ;&{} 0< X < B \\ \Sigma _{\mathrm {0}}(1{-}\frac{U(A,B,X)}{U_{\mathrm {cr}}}); &{} B {\le } X \le A \end{array}\right. } \end{aligned}$$

(3)

$\Sigma _{\mathrm {0}}$ is the local tensile strength, U is half of the crack opening displacement (COD) and $U_{\mathrm {cr}}$ half of the critical separation at which the traction in the cohesive zone becomes zero, B is the physical crack length. When the cohesive size $R=A-B$ is much smaller than the cracked body, i.e. $R\ll L$, small scale yielding can be assumed and the cohesive crack model yields the same results (in terms of peak external force $\Sigma (X) |_{\mathrm {Peak}}$ and crack profiles U(A, B, X)) as those predicted by Linear Elastic Fracture Mechanics (LEFM). However, when the size L becomes comparable to the cohesive size R, the cohesive crack model deviates from the LEFM prediction.

For an edge cracked semi-infinite plate under a concentrated force P at the crack mouth, i.e. $\Sigma (X)=P/t \delta (X)=P_{*} \delta (X)$, Wang et al. (2019b) defined that the Fully Developed Process Zone (FDPZ) takes shape when $U(A,B,B)=U_{\mathrm {cr}}$; and solved the FDPZ’s evaluation with the physical crack length B.

Here, we extend the work to studying the finite ECSP by numerical simulations under the same $P_{*} \delta (X)$ at the crack mouth (Fig. 2). For generality, a characteristic length $\lambda =\pi E'U_{\mathrm {cr}}/(2\Sigma _0)$ is introduced to normalise all the spatial terms, where $E'=E$ for plane stress and $E'=\frac{E}{1-\nu ^2}$ for plane strain, $\nu$ is Poisson’s ratio. The plate sizes are multiples of $\lambda _{\mathrm {L}}$, i.e. $L=n\lambda _{\mathrm {L}}$, where $\lambda _{\mathrm {L}}=G_{\mathrm {c}}E'/\Sigma _0^2$ and $G_{\mathrm {c}}$ the energy release rate¹. The definition of $\lambda _{\mathrm {L}}$ is more general such that its numerical value does not change for different shapes of traction-separation laws (TSL) for a given material (albeit with the same $G_{\mathrm {c}}, E'$ and $\Sigma _0$). In this regard it differs from the previous $\lambda =\pi E'U_{\mathrm {cr}}/(2\Sigma _0)$, which depends on TSL shape. Nonetheless they have the same meaning: they are both characteristic lengths depending solely on material properties. In this paper, for simplicity, we use $\lambda _{\mathrm {L}}$ to normalise the size of the ECSP but express the FDPZ size in terms of $\lambda$; the results are interchangeable. See also corresponding section in the Appendix.

With $\alpha =A/\lambda$, $\beta =B/\lambda$, and $x=X/\lambda$, Eqs. (1) to (3) become Eqs. (4) to (6), respectively. Furthermore, by Eqs. (38) and (39), $l=L/\lambda$ with $l=2n/\pi$ for linear- and $l=4n/\pi$ for rectangular softening.

$$\begin{aligned}&K = \frac{P_*h_{\mathrm {r}}(\alpha ,0)}{\sqrt{\lambda }} - \int _0^a \frac{\Sigma _{\mathrm {coh}}(\alpha , \beta , s)h_{\mathrm {r}}(\alpha , s)\,\lambda \mathrm {d}s}{\sqrt{\lambda }} = 0\nonumber \\ \end{aligned}$$

(4)

$$\begin{aligned}&\Sigma _{\mathrm {coh}} (\alpha ,\beta ,x) = {\left\{ \begin{array}{ll} 0; &{} 0< x < \beta \\ \Sigma _{\mathrm {t}}; &{} \beta \le x \le \alpha \end{array}\right. } \end{aligned}$$

(5)

$$\begin{aligned}&\Sigma _{\mathrm {coh}} (\alpha ,\beta ,x) = {\left\{ \begin{array}{ll} 0; &{} 0< x < \beta \\ \Sigma _{\mathrm {t}}(1-\frac{U(\alpha ,\beta ,x)}{U_{\mathrm {cr}}}); &{} \beta \le x \le \alpha \end{array}\right. } \end{aligned}$$

(6)

When the plate size $L/\lambda _{\mathrm {L}}$ gets very large, the solution of the ECSP will converge to that predicted by Wang et al. (2019b). This is the benchmark of the current numerical simulation before new results concerning finite size ECSP are presented.

2.2 Cohesive element method

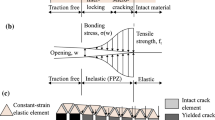
The cohesive zone model (or the fictitious crack model) was initially proposed by Hillerborg et al. (1976), who examined available fracture mechanics theories (the stress intensity factor, the energy balance approach, and the Dugdale and Barenblatt approaches) to describe crack initiation and propagation by means of the FEM. It models accumulated, localized damage as effective behaviour in the Fracture Process Zone (FPZ) ahead of the crack tip. In the process zone, also called cohesive zone, fracture is represented as a gradual process of separation of two virtual surfaces, resisted by tractions between these surfaces.

It is a rather simple phenomenological model to generalize the Fracture Process Zone behaviour with different types of material bonding (Bažant 2008). It assumes a traction-separation relationship (cohesive law) to describe the line-like (2D) or surface-like (3D) cohesive zone (see Fig. 3). The benefit of this method is the elimination of the stress singularity at the crack tip (Eq. (1)) which makes its integration with existing numerical methods (e.g., the Finite Element Method, FEM) rather straightforward.

The cohesive zone theory, i.e. Eq. (1), can be integrated into the Finite Element Method through the so-called Cohesive Elements (CE). The constitutive behaviour of the CEs is described by the traction-separation law (TSL), i.e., $\Sigma _{\mathrm {coh}}(x)$ versus U(x) in the FPZ (i.e. $\alpha -\beta$). Various shapes of TSL exist for different purposes, e.g. ductile or brittle fracture. Eqs. (5) and (6) are two common traction and separation laws. In the numerical model these are slightly modified and used as intrinsic TSL, see Fig. 3. Intrinsic indicates a finite initial stiffness or slope of the TSL $K_{\mathrm {coh}}$. This is required to maintain compatibility and momentum transfer across elements because cohesive elements exist in the simulation model prior to fracture. By contrast, an extrinsic approach assumes an initially rigid response. This would require a dynamical insertion of cohesive elements during computation (Seagraves and Radovitzky 2010).

Here, to directly utilise the CEM framework in existing software and with little deviation from the theoretical requirement, we adopt the intrinsic CEMs and set the initial stiffness $K_{\mathrm {coh}}$ to be as large as numerically admissible. Prior to reaching the peak traction $\Sigma _0$, the cohesive elements have a reversible elastic response.

Fig. 3

The constitutive relationship of the cohesive elements. Left: linear softening and right: rectangular softening

Fig. 4

Normalised displacement over time

For linear softening, passing the peak traction $\Sigma _0$ initiates a damage process which decreases the element’s stiffness, see left-hand side of Fig. 3. This model is based on (Dávila and Camanho 2001). For rectangular softening, the traction plateaus at the peak traction, see right-hand side of Fig. 3. This model is based on the work by Tvergaard and Hutchinson (1992) and its implementation as described in (Sandia National Laboratory 2003). The original model is a trapezoid with finite slopes on both sides. Here, there is no right-hand finite slope which is a better approximation of the TSL from the analytical solution in (Wang et al. 2019b). The conversion from the variables of the original Tvergaard–Hutchinson model to the material properties used here is given in the Appendix.

Fig. 5

Exemplary mesh for $D\ne L$ case. On the left is the complete mesh, on the top side one node in the middle of the plate is fixed. Middle: a magnification of the black area in left picture around the crack, D is the length along which cohesive elements are inserted. Right: a further magnification where the thick black solid line indicates where cohesive elements are inserted, the dashed line indicates the pre-crack which exists to symmetrically apply the force P to several nodes

Table 1 Geometries of the simulated ECSP models. $\lambda _{\mathrm {L}}={1.111}{\mathrm{m}}$, values are approximate

After reaching the critical separation $2U_{\mathrm {cr}}$ the element is deleted. The area under the curve is the energy release rate $G_{\mathrm {c}}$. Cohesive models are usually defined in three directions, here only mode I is activated, i.e. separation normal to cohesive surfaces.

The size of the FDPZ is usually not known beforehand and needs to be solved in accordance to the equilibrium stated in Eq. (1). Practically, we insert cohesive elements along the centre line of the ECSP (see Fig. 5) and obtain its size by identifying the spatial locations of $\alpha$ and $\beta$ at the critical moment of $2U(\alpha , \beta , \beta )=2U_{\mathrm {cr}}$, i.e. when the leading element at the physical crack tip (at $\beta$) reaches the predefined critical separation $2U_{\mathrm {cr}}$.

3 CEM-based numerical modeling

3.1 Numerical model

To achieve the two objectives of this paper, a square plate with different sizes is simulated. The cases are listed in Table 1. The numerical model maps the cohesive edge crack in a square plate (ECSP) with finite- and cohesive elements. The software LS-Dyna with an explicit time integration was used because future applications of similar models seek to simulate dynamic scenarios, e.g. a collision between an ice floe and a ship. Nevertheless, implicit solving should also be possible.

The plate consists of Belytschko–Lin–Tsay shell elements with unit thickness, one through-thickness integration point, and a Poisson’s ratio of zero. The to-be-calculated FDPZ size R is scaled with the characteristic length $\lambda _{\mathrm {L}}$; and the numerical accuracy of the calculated FDPZ is largely dependent on the cohesive element size. The cohesive element size should be small to capture the stress gradients along the crack, see Fig. 6. Through trial and error, a cohesive element size of smaller or equal to $\approx 0.007\lambda _{\mathrm {L}}$ was chosen, which balances accuracy and computational effort. This also indicates the spatial resolution of the results. The cohesive elements are inserted along the prescribed crack path and connect the edges of the shell elements. See (Livermore Software Technology Corporation 2019) for element formulations.

In the following, the length over which cohesive elements are inserted is termed D, see Fig. 5. A small initial crack of a length equal to 6–11 cohesive elements is prescribed in the model to apply the crack mouth opening displacement (CMOD). The displacement is applied to one element less than initial crack length, i.e. over the length of 5–10 cohesive elements, see Table 1. This mimics the loading condition of $\Sigma (X)=P/t\,\delta (X)=P_*\delta (X)$ at the crack mouth. The splitting process is displacement controlled for numerical stability. The displacement is applied with an almost zero initial slope to avoid potential dynamic behaviour, see Fig. 4. Global mass weighted nodal damping is applied for the same reason but turned out to not influence the results. See (Livermore Software Technology Corporation 2019) for a description of the damping mechanism. The force required to achieve this displacement is the splitting load. One node in the middle of the far end of the plate is fixed.

Fig. 6

Exemplary normalised cohesive stress along crack with indication of $\alpha , \beta$ and cohesive zone size $R/\lambda$

An exemplary mesh is shown in Fig. 5. The first rows of elements around the crack path are rectangular shells. All other elements are triangular shells which allows for a rapid increase of element size away from the crack and keeps the total number of elements within a reasonable range. For plates of sizes $L\le 30\lambda _{\mathrm {L}}$ cohesive elements are inserted throughout the whole plate, i.e. $D=L$. For larger plates D is capped at $30\lambda _{\mathrm {L}}$. This is because the number of cohesive elements drives the total number of elements due to their small size and the small size of surrounding elements.

A simple elastic material model is used for the shell elements. Its parameters are $E=10^{10}\,\mathrm {Pa}$, $\nu =0$, and a density of $900\,\mathrm {kg\cdot m^{-3}}$. User-defined material models are used for the cohesive elements based on the above-mentioned TSLs, see (Dávila and Camanho 2001; Tvergaard and Hutchinson 1992; Sandia National Laboratory 2003). The fracture energy $G_{\mathrm {c}}$ and the initial stiffness $K_{\mathrm {coh}}$ is the same for both TSLs. $K_{\mathrm {coh}}$ is several magnitudes larger than the Young’s modulus of the bulk material. Both user-defined material models were validated against material models from the LS-Dyna library, see Appendix. Values for parameters and properties are given in Table 2.

3.2 Simulation results processing

We capture the potential dynamics of crack propagation through explicit time integration. When a cohesive element reaches the peak traction or the maximum separation (points $\alpha$ and $\beta$ in Fig. 6) an output with the time, position and its element id is generated. For every point in time where an element failed, the closest point in time where any other element reached peak stress is identified with a bisection algorithm. The X-coordinates of the element that reached peak traction and the element that reached maximum separation are used to compute $\alpha$ and $\beta$, respectively. Then the cohesive zone size is²$R/\lambda =\alpha - \beta$. All results are normalised with $\lambda$ or $\lambda _{\mathrm {L}}$, where $\lambda$ is not the same for the different TSL, but $\lambda _{\mathrm {L}}$ is. Non-normalised parameters are given in the Appendix Table. 2.

This yields our results of interest, i.e. R and $P_*$ versus the varying physical crack length B. Fig. 7 illustrates the cohesive stress profile $\Sigma _{\mathrm {coh}}$’s distribution with varying $\beta$ values (i.e. a running crack). The stress progresses as expected. Once the crack tip is close to D, the lack of additionally inserted cohesive elements along the “future” crack path distorts the stress distribution $(\beta \ge 8)$.

Fig. 7

Exemplary progression of stress distribution along crack path x for different crack tip positions $\beta$

4 Validation with LEFM

First, the simulated splitting load is compared to an analytical solution for finite plates. When the size $L/\lambda _{\mathrm {L}}$ of an ECSP gets large, the CEM-based simulation should yield the same results as those by LEFM. Based on LEFM theory, which basically means $\Sigma _{\mathrm {coh}}=0$ in Eq. (4), this leads to the formulation for the normalised peak force in Eq. (7).

$$\begin{aligned} \frac{P}{tK\sqrt{\lambda }}=\frac{1}{h_{\mathrm {r}}(\alpha ,0)} \end{aligned}$$

(7)

As an example, the normalised weight function $h_{\mathrm {r}}(\alpha ,0)$ for an edge cracked semi-infinite plate is given by Wang and Dempsey (2011) and repeated in Eq. (8).

$$\begin{aligned} h_{\mathrm {r}}(\alpha , x) =&\sqrt{\frac{2}{\pi }}\frac{1}{\sqrt{\alpha -x}}\bigg [ 1 + 0.7867\left( 1- \frac{x}{\alpha } \right) \nonumber \\&- 1.424\left( 1- \frac{x}{\alpha } \right) ^2 + 3.995\left( 1- \frac{x}{\alpha } \right) ^3 \nonumber \\&-3.611\left( 1- \frac{x}{\alpha } \right) ^4 + 1.087\left( 1- \frac{x}{\alpha } \right) ^5 \bigg ] \end{aligned}$$

(8)

In Fig. 8, a normalised splitting force $P/tK\sqrt{L}$ is plotted over a normalised crack tip position. Analytical solutions are given for a finite plate and it is natural to choose the physical crack tip position as the crack length. In contrast to LEFM, the fracture process in the CZM is not concentrated in one point. Theoretically, as the size of the plate gets large, the CZM model and LEFM model should yield the same results. The larger the FPZ size compared to the plate size, the more the solutions are expected to diverge from the analytical solution.

Simulated and analytical solutions are given in Fig. 8. The analytical solutions for the semi-infinite and finite plate diverge after $B/L\cong 0.1$. The larger the plate, the better the match between LEFM and CZM solutions. However, if the tail from the stress distribution (right hand side in Fig. 6) approaches D, the length along with cohesive elements are inserted, the results are distorted, see D in Fig. 5 and the stress distribution along the crack for $\beta =14$ in Fig. 7. Hence for plates larger than $30\lambda _{\mathrm {L}}$ solutions are not independent of D anymore and therefore not shown in Fig. 8. Results for $L\ge 30\lambda _{\mathrm {L}}$, and with $D\ne L$, are only used for computing the cohesive zone size until it reaches a plateau (Figs. 11 and 17). The plateau is reached before the stress distribution reaches D. On the lower end, the solution for the $1\lambda _{\mathrm {L}}$ plate does not match the LEFM solution. Further, close to $B/L=1$ at the right-hand side of the plot, we can also see a small distortion due to the stress distribution reaching D.

Fig. 8

Comparison of splitting load for simulation with linear softening to analytical LEFM model, Eq. (7), horizontal axis is the normalised crack tip position

5 Results

After the validation of the numerical model, the major results are presented in this section.

5.1 Size effects simulated by the CEM

According to the cohesive zone theory, there is a nonlinear size effect regarding the strength of the cracked body (Elices et al. 2002). The comparison made between the CEM and LEFM in the preceding section only makes sense when the sample size is large. For an ECSP of arbitrary size it is convenient to compare the CEM-based results with an available cohesive zone theory based analytical solution concerning the crack initiation force $P/tK\sqrt{L}$.

In cohesive zone theory, for the linear softening case (i.e., Eq. (6)), the solution to the peak splitting force can be reduced to an eigen-value problem in Eq. (9), where ${\mathcal {U}}(\alpha , x, 0)$ is the normalised Green’s function defined in Eq. (10). Equation (9) is derived in the Appendix.

$$\begin{aligned}&\frac{P}{t}= U_{\mathrm {cr}}E'\frac{\int _{A}^{B} \Sigma (X) \mathrm {d}X}{\int _{A}^{B}\Sigma (X) \,{\mathcal {U}}(A, X, 0) \mathrm {d}X} \end{aligned}$$

(9)

$$\begin{aligned}&{\mathcal {U}}(A,X,S)=\int _{\mathrm {max}(X,S)}^A H_{\mathrm {r}}(A,X)H_{\mathrm {r}}(A,S)\,\mathrm {d}A \end{aligned}$$

(10)

The material strength is defined as P/tL in accordance with (Bažant 2005). The solutions of Eqs. (9) and (10) are compared with the CEM-based simulation results in Fig. 9 illustrating the size effect, i.e. the material strength’s variation with the size of geometrically similar structures (i.e., $L/\lambda _{\mathrm {L}}$).

Fig. 9

Splitting force over plate length for a fixed ratio of $B/L=0.043$ for linear softening. CZM curves are both normalised with $\lambda _{\mathrm {L}}$ for comparability. Analytical solutions are from Eqs. (7) and (9)

The results presented in Fig. 9 are only for the case with a physical crack length of $B=0.043L$. However, the same trend can be found for other physical crack lengths as well, e.g. see reference (Lu et al. 2015b) for the case with $B=0.3L$ (see also Fig. 17 in that reference).

Fig. 10

Normalised splitting force (left axis) vs normalised separation of leading cohesive element (right axis) over time for a plate size $0.1\lambda _{\mathrm {L}}$ for linear softening. The dashed black line indicates time of failure of the element

Generally, when the plate size $L\rightarrow \infty$, the structural strength P/tL is scaled with $\sqrt{L}$ according to the LEFM scaling, thus the 2 : 1 slope for all curves at the lower-right end of Fig. 9. In this case, with $B=0.043L$, we see the convergence from CZM to LEFM starts from around $L=20\lambda$. For the case with $B=0.3L$, the convergence appears to take place from $L=12\lambda$ according to (Lu et al. 2015b).

When the size gets smaller, the predictions by CZM-based methods start to deviate from the LEFM-based results (black dashed line). In Fig. 9, three CZM-based methods are presented. These are (1) the CEM-simulated CZM with linear softening (blue solid line with triangular symbols), (2) the CEM-simulated CZM with rectangular softening (green dotted line with rectangular symbols), and (3) the CZM-based analytical solution with linear softening (dashed red line). All in all, the CEM-simulated linear softening result and its corresponding analytical solution coincide, signifying the correctness of the CEM-based implementation. Additionally, to the very left, we see that the rectangular softening based results predict a stronger material strength over those based on linear softening. This is an expected outcome as the rectangular softening characterises a stronger material compared to its linear softening counterpart.

Fig. 11

Normalised cohesive zone size for different plate sizes and linear softening. Analytical solution including limiting case from Wang et al. (2019b)

For smaller ECSP sizes $L\le 0.3\lambda _{\mathrm {L}}$ the behaviour is different. The external force already decreases when the leading cohesive element reaches critical separation, see Fig. 10. With increasing CMOD, the FPZ size increases until it spans the entire crack line (i.e. the D region in Fig. 5). The external force at the CM also increases, but at its maximum the leading cohesive element has not failed yet. Instead, when the critical separation is reached, the external force is already in a downward slope. From the point where maximum external force is reached (between 2 and 3 s), the separation accelerates, a “catastrophical failure”. Achieving a stable crack growth in the simulation is challenging when the fractured sample is too small. Hence in Fig. 9 the maximum for P/Lt is taken instead of the value at $B/L= 0.043$ for the three leftmost points, i.e. the three smallest plates.

5.2 Cohesive zone size

Plots of the cohesive zone size versus the physical crack tip position are given in Figs. 11 and 17. The dashed black line is the analytical solution for semi-infinite plates, as derived in (Wang et al. 2019b). The horizontal dashed black line is the limiting case of a fully developed process zone as $A\rightarrow \infty$. Other coloured curves are numerical model results. For plates with $L\ge 30\lambda _{\mathrm {L}}$, the results are cut off when B is close to D for reasons given above (Sect. 3.2).

In the case of linear softening (Fig. 11) the curves for the larger plates with $L\ge 80\lambda _{\mathrm {L}}$ appear to approach the limiting case from the analytical solution for the range of $B/\lambda$ simulated here. For the smaller plates, the cohesive zone size increases, reaches a maximum, and then decreases as the physical crack tip approaches the end of the plate. The curves for plates $L\ge 30\lambda _{\mathrm {L}}$ follow the analytical solution. The smaller plates deviate earlier from the analytical solution due to their size. The results for rectangular softening are very similar (see Appendix, Fig. 17).

Maximum cohesive zone sizes (the plateau values, $R_{\mathrm {max}}$) are given in Fig. 12 for both traction-separation relationships. The larger the plate, the closer the maximum cohesive size to the analytical limit case for semi-infinite plates. The $R_{\mathrm {max}}$ values are larger for rectangular softening. This is in line with theory, as they represent an upper boundary compared to the linear softening case. The values for the smallest plates should be treated with caution as these model sizes are very small in the context of the applied methodology.

Two opposite cases, indicated in Fig. 12a, b, are schematically shown in Fig. 13. Figure 13a illustrates $R_{\mathrm {max}}$ for a smaller plate, where the FDPZ almost covers the whole plate, whereas Fig. 13b shows what happens if $R_{\mathrm {max}}$ approaches its limit case for large plates.

Fig. 12

Maximum cohesive zone size vs plate length, linear and rectangular softening. For better comparison to the analytical solutions from Wang et al. (2019b) $R_{\mathrm {max}}$ is normalised with $\lambda$ for linear or rectangular softening, respectively, the plate length L is normalised with $\lambda _{\mathrm {L}}$ for both cases. Therefore the sizes of $R_{\mathrm {max}}$ are not as appears with this normalisation and should not be compared between the two TSLs, see also Fig. 13. The points (a) and (b) are further illustrated in Fig. 14

Fig. 13

Visualization of the maximum fully developed process zone for a very small (a) and very large (b) cracked body. The thick grey line indicates the maximum FDPZ, numbers are approximate

5.3 Splitting force

A different plot of the splitting load over crack tip position is given in Figs. 14 and 18 for linear and rectangular softening. These plots contain the same information as in the LEFM comparison plot, Fig. 8, but with a different normalisation, in line with the analytical solution. The dashed black line is the analytical solution for an edge crack semi-infinite plate (Wang et al. 2019b). The forces for the larger plates follow the analytical solution until $\approx 3-4 \beta$, whereas the forces for the smaller plates reach their maxima quickly and slowly decrease after. The forces for the small plates with $L\le 1\lambda _{\mathrm {L}}$ don’t plateau and decrease immediately. Overall, the forces are as expected for finite plates. The behaviour is similar for linear and rectangular softening.

Fig. 14

Normalised P force for linear softening over normalised crack tip position $\beta$. Analytical solution from Wang et al. (2019b)

6 Application

6.1 Cohesive zone size for ice

Coming back to the motivation of this work, the first major contribution is the maximum cohesive zone size presented in Fig. 12. The results should be valid for all types of quasi-brittle materials, e.g., rock, cement concrete, ceramics and ice. Nonetheless, owing to the authors’ background, this section uses ice as a practical example of applying Fig. 12, for which material properties are given in Table 3.

For lab ice, for linear softening, and using Eq. (38), we have $\lambda = {0.0565}{\mathrm{m}}$ and $\lambda _{\mathrm {L}}={0.036}{\mathrm{m}}$. From the plot in Fig. 12 we take point $(L/\lambda _L = 5.0;\,R_{\mathrm {max}}/\lambda =0.358)$, so $L = 5.0\cdot 0.036 = {0.18}{\mathrm{m}}$. Then, $R_{\mathrm {max}}=0.358\cdot 0.0565={0.02}{\mathrm{m}}$, or about 11% of the specimen length L. The same calculation for sea ice with $\lambda = {0.377}{\mathrm{m}}$ and $\lambda _{\mathrm {L}}={0.24}{\mathrm{m}}$ gives $R_{\mathrm {max}}={0.135}{\mathrm{m}}$.

The same applies to rectangular softening. Take the same point as before $(L/\lambda _{\mathrm {L}} = 5.0;\,R_{\mathrm {max}}/\lambda =0.4105)$. Then, $L = {0.18}{\mathrm{m}}$. Now, due to the different $\lambda$ we have $R_{\mathrm {max}}=0.4105\lambda =0.4105\cdot 0.0283={0.0116}{\mathrm{m}}$, or about 6% of the specimen length L.

As $\lambda$ is material-specific, estimating $R_{\mathrm {max}}$ like this can help to design experiments similar to the model setup (Fig. 2). Exemplary tables for $R_{\mathrm {max}}$ for laboratory and sea ice are given in the Appendix.

6.2 Cohesive element size

In any CEM-based simulation, the cohesive element size must be smaller than the FPZ size (Falk et al. 2001; Turon et al. 2007). How much smaller is subject of ongoing research and was not the focus of this work, but some remarks can be given.

As the cohesive zone size varies, any element size criteria based on its maximum (see exemplary calculations in above section) is an upper bound. That is, it is likely necessary to use smaller elements to capture the cases when $B\rightarrow 0$ and $B\rightarrow L$ and the cohesive zone size R is small. Plots of the cohesive zone size, e.g. Fig. 11, as well as cohesive stress profiles along the crack such as Fig. 6 can help choosing the element size for simulating cracks in plates similar to our model (Fig. 2).

7 Discussion

7.1 Splitting force and size effect

The splitting force versus the physical crack length is compared between the analytical solution and CEM-based numerical simulations. Two sets of analytical solutions are adopted: (1) the splitting force of a finite ECSP in Fig. 8; (2) the splitting force for a semi-infinite plate in Figs. 14 and 18.

In both scenarios, the analytical solutions are a manifestation of LEFM solutions. This is because firstly, the analytical solution in Fig. 8 is based on LEFM theory (see Eq. (7)); and secondly, in Figs. 14 and 18, the corresponding cohesive zone sizes are rather small in comparison to the plate size. Theoretically, we expect in the CEM-based simulations, as the size of the cracked plate increases, that the normalised splitting force (either $P/tK\sqrt{L}$ or $P/t\lambda \Sigma _0$) converges to those analytical solutions. This is confirmed in the comparisons, showing our CEM-based numerical model works as intended.

Moreover, the CEM-based numerical model captures the size effect, at least in this setup, see Sect. 5.1 (Fig. 9 is strictly valid only for $B/L=0.043$ and the given TSLs). It is another potential tool to extrapolate lab-scale measurements to field scale in addition to the “CZM + weight function” approach developed in (Lu et al. 2015b). This includes the parameters of the traction separation law, which are the same for all model sizes used here, similar to results by Ha et al. (2015). The discretization around the crack line (D in Fig. 5) is the same for sizes $\ge 1\lambda _{\mathrm {L}}$. Below $1\lambda _{\mathrm {L}}$ element length must change to accustom the small geometries. The element sizes used here are too small for simulations of full-scale scenarios, also considering that only a single crack was simulated. Nevertheless it should be possible to also capture the size effect with a coarser mesh, especially if the aim is not to calculate accurate cohesive zone sizes, see also (Turon et al. 2007). Overall, it seems that the size effect is captured as long as the FPZ is sufficiently resolved by the element size. These results are encouraging, despite known problems of numerical CEM-based models (Seagraves and Radovitzky 2010; Rimoli and Rojas 2015; Lu et al. 2014).

7.2 Fully developed cohesive zone

The fully developed cohesive zone is defined as the size of $\beta -\alpha$ as in Fig. 6 when the leading cohesive element’s separation reaches the critical separation $2U=2U_{\mathrm {cr}}$. From the size effect validation case in Fig. 9, for a large ECSP, we can extract the maximum splitting force reached so far before the leading cohesive element’s failure right when its separation $2U=2U_{\mathrm {cr}}$ (and the traction-free crack opening is at $B/L =0.043$). This is before the peak splitting force is reached, since splitting force is increasing monotonically, even after the failure of the first cohesive element.

However, for the small cracked plate, e.g. $L=0.1\lambda _{\mathrm {L}}$, the maximum splitting force (during the lifetime of the leading cohesive element) does not occur when the cohesive zone is fully developed (i.e., see Fig. 10, the peak force is reached before the failure of the leading cohesive element). Instead, when the cohesive zone is fully developed, the splitting force is already decreasing. This means that a crack would propagate in a small ECSP even with a decreasing splitting force, leading to an unstable crack propagation scenario. This indicates that it can be rather challenging to obtain a stable crack growth in an experiment when the fractured sample is too small (e.g., lab-scale experiments).

7.3 Static and running cracks

The cohesive zone size is extracted from a running physical crack (B) shown in Fig. 7 but it is compared to analytical solutions that are based on static analyses.

In the simulation, a slow application of prescribed displacement was applied to reduce dynamic effects. Yet this approach is limited since a slower displacement does not reduce the minimum time step but increases the number of time steps needed to achieve the same displacement, which in turn increases computation time. So although a rather slow displacement controlled loading scenario is simulated, a running crack will potentially bring in inertia effects (Seagraves and Radovitzky 2010).

However, given the satisfactory agreement of the cohesive zone size in the limiting scenario (i.e., favourable agreement in Figs. 11 and 17), we expect the presented results for other plate sizes are not far from their corresponding static solutions. Moreover, the kinetic energy was close to zero in all simulations.

So, for the time being, it is unknown what the exact difference between a static and a running crack’s cohesive zone size is. Nevertheless, we expect the numerical results presented in Figs. 11 and 12 to be of practical interest for most lab experiments.

7.4 Numerical errors

The mapping from the analytical to the numerical model introduces sources of error. Despite the agreement between the numerical results and the analytical solutions in limiting scenarios, potential error sources are emphasized.

Generally, the analytical model is essentially a static 2D model, whereas the numerical model is solved as a dynamic quasi-2D (see Sect. above and 3.1) model with explicit time integration. The numerical results are also affected by discretization and element formulations. This was checked with a mesh convergence study and different element configurations, which did not change the outcome. If $R_{\mathrm {max}}$ is compared to the cohesive element size, there are mostly 40 to 50 cohesive elements or more in the process zone, but not less than 26. This should be sufficient for accurately resolving the cohesive zone (see also Sect. 7.1), but more research is needed for general element size recommendations.

Also, the analytical solutions are based on a concentrated force at the crack mouth. This is not the case in the numerical model as a point force often leads to numerical errors, e.g. a distorted stress field near the corresponding node. Nonetheless, the area over which the force was applied is magnitudes smaller than the plate size, see Table 1.

Lastly, the numerical material models deviate slightly from the analytical behaviour due to the issue of initial stiffness, as described in Sect. 3. The plateau in the traction-separation law for the rectangular softening material model, see Fig. 3, leads to some oscillations in force and cohesive zone size R in the numerical results. Also, R sizes can be slightly bigger than for the semi-infinite analytical solution, which should not happen for the finite plate numerical model.

8 Conclusions

In a nutshell, the numerical CEM model works as expected. Several points can be derived from the results:

• For this setup, the CEM-based numerical model captures the size effect. Like the CZM + weight function method (Lu et al. 2015b), it is a potential tool to extrapolate laboratory scale measurements to field scale.

• For finite plate sizes of practical interest, Fig. 12 presents the maximum cohesive zone sizes $R_{\mathrm {max}}$ in dependence of plate size. This is the major contribution of this paper and the results presented have an accuracy of about $0.0072\lambda _{\mathrm {L}}$. $\lambda _{\mathrm {L}}$ is a characteristic length and depends only on material properties.

• In general, the fully developed process zone (FDPZ) size for finite plates is influenced by the cracked plate size and physical crack length.

• With increasing physical crack length within a finite edge cracked plate, the FDPZ first increases, then plateaus to a maximum value $R_{\mathrm {max}}$, before it decreases as the physical crack reaches the far end boundary of the finite plate. This is illustrated in Figs. 11 and 17.

• The plateaued FDPZ size $R_{\mathrm {max}}$ increases with the plate size and with $L\rightarrow \infty$ converges to $0.5\lambda$ and $0.465\lambda$ for the rectangular and linear softening traction and separation law, respectively. $\lambda$ is a characteristic length and a material property, similar to $\lambda _{\mathrm {L}}$.

• The presented CEM-based numerical model can be implemented to evaluate the cohesive zone size evolution for other cracked geometries.

Appendix

1.1 Weight function method

In this paper, the weight function method, which is independent of external loading profiles, is adopted to calculate the Stress Intensity Factor (SIF). The weight function method developed by Bueckner (1970) and Rice (1972) characterizes the SIF for a cracked symmetric body with a crack length of A under a unit loading at a location X. For an arbitrary loading profile, its corresponding SIF K(A) can be calculated with

$$\begin{aligned} K(A) = \int _0^A \Sigma (X) H_{\mathrm {r}}(A,X) \mathrm {d}X \end{aligned}$$

(11)

Different cracked geometries have different weight functions $H_{\mathrm {r}}(A, X)$. Here, we adopt the weight function developed by Dempsey and Mu (2014) for the considered centrally cracked square plate. The weight function $H_{\mathrm {r}}(A, X)$ has the general form in the following equation in which the function needs to be separately established for specific cracked geometries, see e.g. (Wu and Carlsson 1991).

$$\begin{aligned} H_{\mathrm {r}}(A, X) = \frac{1}{\sqrt{2\pi A}}\sum _{i=1}^{5}G_i\left( \frac{A}{L}\right) \left( 1-\frac{X}{A}\right) ^{i-3/2}\qquad \end{aligned}$$

(12)

Note with A/L and $l/\lambda$, also $A/L=\alpha /l$. For this paper, the explicit form of $G_i$ (expressed as a collection of other functions involving the characterization of crack surface displacement and crack surface area) can be found in the work by Dempsey and Mu (2014) and is not repeated.

One of the important properties of the weight function is that, if we introduce a scaling $\alpha =A/\lambda$, $\beta = B/\lambda$ and $x = X/\lambda$, we have $h_{\mathrm {r}}(\alpha , x)=\sqrt{\lambda }H_{\mathrm {r}}(A, X)$. When we have a concentrated force acting at the crack mouth $x=0$, the weight function reduces to $h_{\mathrm {r}}(\alpha , 0)$. For example, one simple form of the weight function for the cracked semi-infinite plate is expressed in Eq. (8). When it is under a pair of splitting forces acting at the crack mouth, we simply need to introduce $x=0$ to obtain its corresponding weight function.

1.2 Derivation of Eq. (9)

The derivation of Eq. (9) follows the procedures in the original works of Li and Bažant (1994) and Li and Liang (1993). Similar derivations can also be found in (Bažant and Planas 1998) and (Wang and Dempsey 2011). A detailed derivation of Eq. (9) is presented in Appendix A in (Lu et al. 2015b). For completeness, these derivations are repeated below.

According to the concept of cohesive zone theory, we have

$$\begin{aligned}&\int _0^{A}\Sigma (X)H_{\mathrm {r}}(A,X)\mathrm {d}X\nonumber \\&\quad -\int _0^{A}\Sigma _{\mathrm {coh}}(A,B,S)H_{\mathrm {r}}(A,S)\mathrm {d}S=0 \end{aligned}$$

(13)

Additionally, the half COD U(A, B, X) can be written as the linear summation of half COD $U_{\Sigma }(A, B, X)$ induced by external loading and half COD of $U_{\Sigma _{\mathrm {coh}}}(A, B, X)$ induced by the cohesive stress $-\Sigma _{\mathrm {coh}}(A,B,S)$ in Eq. (14)

$$\begin{aligned} U(A,B,X) = U_{\Sigma }(A,B,X)+U_{\Sigma _{\mathrm {coh}}}(A,B,X) \end{aligned}$$

(14)

The general expression for the half COD can be written as

$$\begin{aligned} U(A,X)= & {} \frac{1}{E'}\int _0^{A}K(A)H_{\mathrm {r}}(A,X)\mathrm {d}A \nonumber \\= & {} \frac{1}{E'}\int _0^{A}\int _0^{A} \Sigma (S)H_{\mathrm {r}}(A,S)\mathrm {d}S \,H_{\mathrm {r}}(A,X)\mathrm {d}A\qquad \end{aligned}$$

(15)

Rearranging Eq. (15) leads to

$$\begin{aligned} U(A,X) = \frac{1}{E'}\int _0^A \Sigma (S){\mathcal {U}}(A, X, S)\mathrm {d}S \end{aligned}$$

(16)

The Green function ${\mathcal {U}}(A,X,S)$ is defined as

$$\begin{aligned} {\mathcal {U}}(A,X,S)=\int _{\mathrm {max}(X,S)}^A H_{\mathrm {r}}(A,X)H_{\mathrm {r}}(A,S)\mathrm {d}A \end{aligned}$$

(17)

For a linear softening cohesive crack, we have

$$\begin{aligned} \begin{aligned} \Sigma _{\mathrm {coh}}(X)&= \Sigma _0\left( 1-\frac{U(A,X)}{U_{\mathrm {cr}}}\right) \quad \mathrm {or} \\ U(A,X)&= U_{\mathrm {cr}}\left( 1 - \frac{\Sigma _{\mathrm {coh}}(X)}{\Sigma _0} \right) \end{aligned} \end{aligned}$$

(18)

Inserting the right-hand side of Eq. (18) into the left-hand side of Eq. (14), we have

$$\begin{aligned} U_{\mathrm {cr}}\left( 1-\frac{\Sigma _{\mathrm {coh}}(X)}{\Sigma _0}\right) = U_{\Sigma }(A,B,X) + U_{\Sigma _{\mathrm {coh}}}(A,B,X) \end{aligned}$$

(19)

The two terms on the right-hand side of Eq. (19) can be expressed according to the weight function method following Eq. (16). This transforms Eq. (19) into Eq. (20).

$$\begin{aligned}&U_{\mathrm {cr}}\left( 1-\frac{\Sigma _{\mathrm {coh}}(X)}{\Sigma _0}\right) \nonumber \\&\quad =\frac{1}{E'}\bigg [\int _0^A\Sigma (S){\mathcal {U}}(A,X,S)\mathrm {d}S\nonumber \\&\qquad -\int _0^A\Sigma _{\mathrm {coh}}(S){\mathcal {U}}(A,X,S)\mathrm {d}S\bigg ] \end{aligned}$$

(20)

Introducing the concentrated point load pairs acting at the crack mouth in Eq. (21), and realising the cohesive stress $\Sigma _{\mathrm {coh}}(S)$ exists only in the cohesive zone ($B\rightarrow A$, i.e., $\Sigma _{\mathrm {coh}}(S)=0$ for $S\le B$), this simplifies Eqs. (20) to  (22)

$$\begin{aligned}&\Sigma (X) = \frac{P}{t}\delta (X) \end{aligned}$$

(21)

$$\begin{aligned}&U_{\mathrm {cr}}\left( 1 - \frac{\Sigma _{\mathrm {coh}}(X)}{\Sigma _0}\right) \nonumber \\&\quad =\frac{1}{E'}\bigg [\frac{P}{t}{\mathcal {U}}(A,X,0) -\int _B^A\Sigma _{\mathrm {coh}}(S){\mathcal {U}}(A,X,S)\mathrm {d}S\bigg ]\nonumber \\ \end{aligned}$$

(22)

According to the Leibniz integral rule, taking variations over A upon Eq. (22) leads to

$$\begin{aligned}&-\frac{U_{\mathrm {cr}}}{\Sigma _0}\delta \Sigma _{\mathrm {coh}}(X) \nonumber \\&= \frac{1}{E'}\frac{\delta P}{t}{\mathcal {U}}(A,X,0)+\frac{1}{E'}\frac{P}{t}\delta {\mathcal {U}}(A,X,0) \nonumber \\&\quad -\frac{1}{E'}\bigg [\frac{\delta A}{\delta A}\Sigma _{\mathrm {coh}}(A){\mathcal {U}}(A,X,A)\nonumber \\&\quad -\frac{\delta B}{\delta A}\Sigma _{\mathrm {coh}}(B){\mathcal {U}}(A,X,B) \nonumber \\&\quad + \int _B^A \delta \Sigma _{\mathrm {coh}}(S){\mathcal {U}}(A,X,S)\mathrm {d}S \nonumber \\&\quad + \int _B^A \Sigma _{\mathrm {coh}}(S)\delta {\mathcal {U}}(A,X,S)\mathrm {d}S\bigg ] \end{aligned}$$

(23)

By definition, at peak value, $\delta P = 0$ (Bažant and Planas 1998). Therefore, the first term on the right hand side of Eq. (23) vanishes. In addition, due to symmetry, ${\mathcal {U}}(A,X,A)={\mathcal {U}}(A,A,X)=0$ in the third term. The fourth term also vanishes as $\delta B / \delta A =0$.

Because of the relationship in Eq. (24), which can be introduced to the second and sixth term in Eq. (23), these two terms cancel each other by virtue of Eq. (13).

$$\begin{aligned} \delta {\mathcal {U}}(A,X,S)&=\frac{\partial }{\partial A} \bigg [\int _{\mathrm {max}(X,S)}^A H_{\mathrm {r}}(A,X)H_{\mathrm {r}}(A,S)\mathrm {d}A \bigg ] \nonumber \\&= H_{\mathrm {r}}(A,X)H_{\mathrm {r}}(A,S) \end{aligned}$$

(24)

Eventually, Eq. (23) is simplified into Eq. (25).

$$\begin{aligned} \delta \Sigma _{\mathrm {coh}}(X)=\frac{\Sigma _0}{U_{\mathrm {cr}}E'}\int _B^A\delta \Sigma _{\mathrm {coh}}(S){\mathcal {U}}(A,X,S)\mathrm {d}S \end{aligned}$$

(25)

Replacing $\delta \Sigma _{\mathrm {coh}}(X)$ with a proportional cohesive stress profile $\Sigma (X)$, we can obtain Eq. (26), which is a typical eigenvalue problem to solve. After identifying the eigenvector $\Sigma (X)$, we can begin to calculate the peak splitting force $P/t\delta (X)$.

$$\begin{aligned} \Sigma (X)=\frac{\Sigma _0}{U_{\mathrm {cr}}E'}\int _B^A \Sigma (S){\mathcal {U}}(A,X,S)\mathrm {d}S \end{aligned}$$

(26)

Recalling that for linear softening the cohesive stress could be written as in the left-hand side version of Eq. (18). Multiplying both sides of this formula with the obtained eigenvector $\Sigma (X)$ and integrating within the cohesive zone (i.e., $B\rightarrow A$) lead to Eq. (27).

$$\begin{aligned}&\int _B^A \Sigma (X)\Sigma _{\mathrm {coh}}(X)\mathrm {d}X\nonumber \\&\quad =\Sigma _0\int _B^A\Sigma (X)\mathrm {d}X - \frac{\Sigma _0}{U_{\mathrm {cr}}}\int _B^A\Sigma (X)U(X)\mathrm {d}X \end{aligned}$$

(27)

According to Eqs. (14) and (16), U(X) in Eq. (27) can be written as in Eq. (28).

$$\begin{aligned} U(X)=\frac{1}{E'}\bigg [\frac{P}{t}{\mathcal {U}}(A,X,0)-\int _B^A\Sigma (S){\mathcal {U}}(A,X,S)\mathrm {d}S\bigg ] \end{aligned}$$

(28)

Inserting Eq. (28) into Eq. (27) leads to Eq. (29).

$$\begin{aligned}&\int _B^A\Sigma (X)\Sigma _{\mathrm {coh}}(X)\mathrm {d}X = \Sigma _0\int _B^A\Sigma (X)\mathrm {d}X \nonumber \\&\quad -\frac{\Sigma _0}{U_{\mathrm {cr}}}\frac{1}{E'}\int _B^A\Sigma (X)\bigg [\frac{P}{t}{\mathcal {U}}(A,X,0) \nonumber \\&\quad -\int _B^A\Sigma _{\mathrm {coh}}(S){\mathcal {U}}(A,X,S)\mathrm {d}S\bigg ]\mathrm {d}X \nonumber \\&=\Sigma _0\int _B^A\Sigma (X)\mathrm {d}X \nonumber \\&\quad -\frac{\Sigma _0}{U_{\mathrm {cr}}E'}\int _B^A\Sigma (X)\frac{P}{t}{\mathcal {U}}(A,X,0)\mathrm {d}X \nonumber \\&\quad +\frac{\Sigma _0}{U_{\mathrm {cr}}E'}\int _B^A\Sigma (X)\int _B^A\Sigma _{\mathrm {coh}}(S){\mathcal {U}}(A,X,S)\mathrm {d}S\,\mathrm {d}X \end{aligned}$$

(29)

Using Eq. (26), the last term in Eq. (29) can be written as Eq. (30), which cancels out the left-hand side of Eq. (29).

$$\begin{aligned} \begin{aligned} \frac{\Sigma _0}{U_{\mathrm {cr}}E'}\int _B^A\Sigma (X)\int _B^A\Sigma _{\mathrm {coh}}(S){\mathcal {U}}(A,X,S)\mathrm {d}S\,\mathrm {d}X\\ =\frac{\Sigma _0}{U_{\mathrm {cr}}E'}\frac{U_{\mathrm {cr}}E'}{\Sigma _0}\int _B^A\Sigma (X)\Sigma _{\mathrm {coh}}(X)\mathrm {d}X \end{aligned}\nonumber \\ \end{aligned}$$

(30)

Eq. (29) is simplified into Eq. (31),

$$\begin{aligned} \Sigma _0\int _B^A\Sigma (X)\mathrm {d}X = \frac{\Sigma _0}{U_{\mathrm {cr}}E'}\int _B^A\Sigma (X)\frac{P}{t}{\mathcal {U}}(A,X,0)\mathrm {d}X\nonumber \\ \end{aligned}$$

(31)

which finally leads to

$$\begin{aligned} \frac{P}{t}=U_{\mathrm {cr}}E'\frac{\int _B^A \Sigma (X)\mathrm {d}X}{\int _B^A\Sigma (X){\mathcal {U}}(A,X,0)\mathrm {d}X} \end{aligned}$$

(32)

1.3 Validation of user material models

User material models must be used to obtain element information at the points of peak stress and failure $(\alpha$ and $\beta )$. They were programmed as LS-Dyna subroutines (Erhart 2011). The user material models were validated against standard material models which are available from the LS-Dyna library. The linear softening model was validated against the cohesive mixed mode model (nr. 138 in the library), based on (Dávila and Camanho 2001). The rectangular softening was validated against the Tvergaard–Hutchinson model (nr. 185 in the library) based on (Sandia National Laboratory 2003).

The Tvergaard–Hutchinson model characterises separation with a dimensionless gap vector $\Lambda$. The separation for the initial and final peak tractions are $\Lambda _1$ and $\Lambda _2$, the critical separation is $\Lambda _{\mathrm {fail}}$. These are related to the material properties based on the area of a trapezoid without right-hand side slope, i.e. $\Lambda _2 = \Lambda _{\mathrm {fail}}$ (Fig. 3). Both separations are normalised with $u_{\mathrm {fail}}$ such that $\Lambda /\Lambda _{\mathrm {fail}}=1$ for the critical separation.

$$\begin{aligned}&u_1 = \frac{\Sigma _0}{ K_{\mathrm {coh}}} \end{aligned}$$

(33)

$$\begin{aligned}&\Lambda _1 = \frac{u_1}{ u_{\mathrm {fail}}} \end{aligned}$$

(34)

$$\begin{aligned}&u_2 = u_{\mathrm {fail}} = \frac{G_{\mathrm {c}}}{\Sigma _0} + \frac{\Sigma _0}{2 K_{\mathrm {coh}}} \end{aligned}$$

(35)

$$\begin{aligned}&\Lambda _2 = \Lambda _{\mathrm {fail}} = 1 \end{aligned}$$

(36)

The forces were compared for the same model with user defined and reference material model. Models with plate sizes of $5\lambda$ and $1\lambda$ were used. The comparison for the linear softening model is shown in Fig. 15. The curves match. The comparison of the splitting forces for rectangular softening and the Tvergaard–Hutchinson model is shown in Fig. 16. Again, due to the zigzag behaviour the curves were smoothed. The curves for the rectangular user- and reference material model also match.

Fig. 15

Splitting force vs. time for the linear softening user material model and the reference ‘mat_138’ material model for plate sizes $1\lambda _{\mathrm {L}}$ and $5\lambda _{\mathrm {L}}$

Fig. 16

Splitting force vs. time for the rectangular softening user material model and the reference Tvergaard–Hutchinson material model for plates sizes $1\lambda _{\mathrm {L}}$ and $5\lambda _{\mathrm {L}}$

1.4 Relation between $\lambda$ and $\lambda _{\mathrm {L}}$

Two definitions are used for the characteristic length, one for normalising results $\lambda$, and a more generally defined one for describing lengths $\lambda _{\mathrm {L}}$. They are related as follows:

$$\begin{aligned} \lambda _{\mathrm {L}} = \frac{E' G_{\mathrm {c}}}{\Sigma _0^2} \end{aligned}$$

(37)

For the linear case, since the fracture energy is $G_{\mathrm {c}} = 0.5 \Sigma _0 2 U_{\mathrm {cr}} = \Sigma _0 U_{\mathrm {cr}}$,

$$\begin{aligned} \lambda = \pi \frac{E' U_{\mathrm {cr}}}{2\Sigma _0} = \frac{\pi }{2}\frac{E'}{\Sigma _0}\frac{G_{\mathrm {c}}}{\Sigma _0} = \frac{\pi }{2}\frac{E' G_{\mathrm {c}}}{\Sigma _0^2} = \frac{\pi }{2}\lambda _{\mathrm {L}} \end{aligned}$$

(38)

and for the rectangular case, because the fracture energy is $G_{\mathrm {c}} = \Sigma _0 2 U_{\mathrm {cr}} = 2 \Sigma _0 U_{\mathrm {cr}}$,

$$\begin{aligned} \lambda = \pi \frac{E' U_{\mathrm {cr}}}{2\Sigma _0} = \frac{\pi }{2} \frac{E'}{\Sigma _0} \frac{G_{\mathrm {c}}}{2\Sigma _0} = \frac{\pi }{4} \frac{E' G_{\mathrm {c}}}{\Sigma _0^2} = \frac{\pi }{4} \lambda _{\mathrm {L}} \end{aligned}$$

(39)

Fig. 17

Cohesive zone size for different plate sizes and rectangular softening, analytical solution including limiting case from Wang et al. (2019b). The cohesive size of the large plates ($100\lambda _{\mathrm {L}}$ and $80\lambda _{\mathrm {L}}$) plateaus towards the limiting case of the semi-infinite plate’s scenario. The range of $\beta$ values is different compared to Fig. 11 due to $\lambda$ being different for linear and rectangular softening. The plateau in the traction separation law for the rectangular softening material model (see Fig. 3) leads to some oscillations in force and cohesive zone size R in the numerical results. Hence curves are smoothed. Raw data is given in lighter colours

Fig. 18

Normalised P force for rectangular softening over normalised crack tip position $\beta$. The range of $\beta$ values is different compared to Fig. 14 due to $\lambda$ being different for linear and rectangular softening. Analytical solution from Wang et al. (2019b)

Fig. 19

Maximum cohesive zone size vs plate length for linear and rectangular softening. To illustrate the difference in TSL, everything (L and $R_{\mathrm {max}}$) is now normalised with the same $\lambda _{\mathrm {L}}$. The limiting cases from the analytical solutions (Wang et al. 2019b) are scaled accordingly

Table 2 Non-normalised values of model parameters

1.5 Additional plots

The plots in Figs. 17 and 18 are analogous to Figs. 11 and 14 but for rectangular softening.

1.6 Additional tables

Table 2 gives non-normalised parameter values used for the elastic material model surrounding the crack as well as the cohesive models. $K_{\mathrm {Ic}}$ is used for the ‘LEFM + weight function’ curve in Fig. 9 and calculated with $\sqrt{G_{\mathrm {c}}E'}$. Table 3 gives ice material properties for the scaling in Sect. 6. Values for laboratory ice are from Schulson and Duval (2009) and for sea ice from Dempsey et al. (1999a). Table 4 gives exemplary cohesive zone sizes, see Sect. 6.

Table 3 Ice material properties for scaling example

Table 4 Exemplary cohesive zone sizes for lab- and sea ice