Theoretical assessment of ELS test data reduction technique using virtual testing

Abstract

In this paper a theoretical analysis of crack initiation and propagation conditions in a bonded specimen loaded under pure mode II condition is proposed. The end-loaded-split (ELS) test response is evaluated using a semi-analytical model where the adherends are modeled as two deformable Timoshenko beams and considering non-linear behaviour of the adhesive. Bi-linear elastic-plastic, elastic-softening and trapezoidal adhesive layer shear behaviours (ALSBs) have been implemented and studied. From the results we observed that the load–displacement curve does not permit accurate evaluation of the adhesive layer shear behaviour. An alternative procedure consisting of analyzing the strain energy release rate versus shear displacement at the crack tip is proposed for data reduction of ELS test results.

Appendices

Appendix A: Compliance assessment

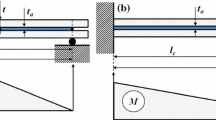
The classical beam theory does not take into account the adhesive layer compliance. The specimen is seen as Timoshenko beams under flexure caused by applied load P. Specimen dimensions are seen in Fig. 1.

The Griffith’s energy balance gives the Strain Energy Release Rate $\mu$ (SERR) as:

$$\begin{aligned} \mu =\frac{1}{2w}\frac{\partial C(a)}{\partial a}P^2 \end{aligned}$$

(20)

To obtain the compliance C(a), the whole specimen potential energy $W_e$ is integrated:

$$\begin{aligned} W_e= & {} \frac{1}{2}C(a)P^2 \end{aligned}$$

(21)

$$\begin{aligned} \delta W_e= & {} \frac{1}{2}\frac{T^2}{\kappa GS_{eff}}+\frac{1}{2}\frac{M^2}{EI_{eff}} \end{aligned}$$

(22)

T is the transverse force and M the bending moment. $S_{eff}$ and $I_{eff}$ are respectively effective area and effective quadratic bending moment of the part of the specimen concerned. $\kappa$ is the beam shear correction factor $\kappa =5/6$, E and G are respectively Young’s and Coulomb’s modulus of the adherends. Considering the specimen as a 2t thickness beam along the bonded length $l_c$ connected to two t thickness beams in parallel along the crack length a (all beams width is w), we have:

$$\begin{aligned}&T(x) = P \ \ for\ \ 0\le x \le L \end{aligned}$$

(23)

$$\begin{aligned}&M(x) = P(L-x) \ \ for\ \ 0\le x \le L \end{aligned}$$

(24)

$$\begin{aligned}&S_{eff}=2S=2wt \end{aligned}$$

(25)

$$\begin{aligned}&I_{eff} = 8I \ for \ 0< x< L-a, \nonumber \\&I_{eff} = 2I \ for \ L-a< x < L, \ I = \frac{wt^3}{12}\nonumber \\ \end{aligned}$$

(26)

We then find the whole specimen compliance as a function of the crack length a and the expression for the SERR:

$$\begin{aligned} C(a)= & {} \frac{L}{2\kappa GS}+\frac{1}{2EI}\left( \frac{a^3}{4}+\frac{L^3}{12}\right) \end{aligned}$$

(27)

$$\begin{aligned} \mu= & {} \frac{3a^2P^2}{16wEI} = \frac{9a^2P^2}{4w^2t^3E} \end{aligned}$$

(28)

Appendix B: Full derivation of constitutive equations

According to Timoshenko beam theory, the constitutive equations linking local forces to the displacements are:

$$\begin{aligned} M(x)= & {} EI\frac{d\varphi (x)}{d(x)} \end{aligned}$$

(29)

$$\begin{aligned} T(x)= & {} \kappa GS\left[ \frac{dv(x)}{dx}-\varphi (x)\right] \end{aligned}$$

(30)

$$\begin{aligned} N(x)= & {} ES\frac{du(x)}{dx} \end{aligned}$$

(31)

where $I = wt^3/12$ is the quadratic bending moment of one adherend cross section, $\kappa$ is the beam shear correction factor $\kappa =5/6$, G is the shear modulus of the adherends, $S=wt$ is the area of one adherend cross section. The local static equilibrium (see Fig. 4) is described with the following equations:

$$\begin{aligned} \frac{dM(x)}{dx}+T(x)-w\frac{t}{2}\uptau (x)= & {} 0 \end{aligned}$$

(32)

$$\begin{aligned} \frac{dT(x)}{dx}= & {} 0 \end{aligned}$$

(33)

$$\begin{aligned} \frac{dN(x)}{dx}-w\uptau (x)= & {} 0 \end{aligned}$$

(34)

where $\uptau (x)$ is the shear stress along the adhesive. The shear strain $\gamma$ is (see Fig. 4):

$$\begin{aligned} \gamma (x)=\frac{1}{t_a}\left( 2u(x)+2\frac{t}{2}\varphi (x)\right) \end{aligned}$$

(35)

We obtain the shear stress distribution from Eqs. (29) to (35) depending on the Adhesive Layer Shear Behaviour (ALSB).

Shear stress for the elastic regime can be defined as:

$$\begin{aligned} \uptau (x)=\frac{G_a}{t_a}\left[ 2u(x)+2\frac{t}{2}\varphi (x)\right] \end{aligned}$$

(36)

Combining Eqs. (29) to (36) leads to a third order differential equation:

$$\begin{aligned} \frac{d^3\uptau }{dx}-\frac{2wG_a}{t_a}\left[ \frac{1}{EI}\left( \frac{t}{2}\right) ^2+\frac{1}{ES}\right] \frac{d\uptau }{dx} = 0 \end{aligned}$$

(37)

The solution to this equation in $\uptau (x)$ is:

$$\begin{aligned} \uptau (x)=Ae^{\lambda _{\uptau }X}+Be^{-\lambda _{\uptau }(X+l_e+l_1+l_2)}+\uptau _m \end{aligned}$$

(38)

with

$$\begin{aligned} \lambda _{\tau } = \sqrt{2\frac{G_a}{t_a}w\left[ \frac{1}{EI}\left( \frac{t}{2}\right) ^2+\frac{1}{ES}\right] } \end{aligned}$$

(39)

where X varies in the interval $[-l_e;-(l_1+l_2)]$. X, $l_1$, $l_2$ are defined in Fig. 6. $\uptau _m$ is the mean shear stress. To obtain general expression for the local forces N(x), T(x), M(x) and the displacements u(x), v(x) and the rotation $\varphi (x)$, $\uptau (x)$ is replaced by its expression in Eqs. (29) to (34) finding:

$$\begin{aligned} N(x)= & {} w\uptau _mX + A\frac{w}{\lambda _{\uptau }}e^{\lambda _{\uptau }X} \nonumber \\&-B\frac{w}{\lambda _{\uptau }}e^{-\lambda _{\uptau }(X+l_e+l_1+l_2)}+N_0 \end{aligned}$$

(40)

$$\begin{aligned} M(x)= & {} -\frac{P}{2}X + \frac{wt}{2} \left[ w\uptau _mX + \frac{A}{\lambda _{\uptau }}e^{\lambda _{\uptau }X}\nonumber \right. \\&\left. -\frac{B}{\lambda _{\uptau }}e^{-\lambda _{\uptau }(X+l_e+l_1+l_2)}\right] + M_0 \end{aligned}$$

(41)

$$\begin{aligned} T(x)= & {} -\frac{P}{2} \end{aligned}$$

(42)

$$\begin{aligned} u(x)= & {} \frac{1}{ES} \left[ w\uptau _m\frac{X^2}{2} + \frac{Aw}{\lambda _{\uptau }^2}e^{\lambda _{\uptau }X}\nonumber \right. \\&\left. +\frac{Bw}{\lambda _{\uptau }^2}e^{-\lambda _{\uptau }(X+l_e+l_1+l_2)} + N_0X\right] + u_0 \end{aligned}$$

(43)

$$\begin{aligned} \varphi (x)= & {} \frac{1}{EI} \left[ -\frac{P}{2} \frac{X^2}{2} + \frac{wt}{2} \left[ \frac{\uptau _m}{2}X^2 + \frac{A}{\lambda _{\uptau }^2}e^{\lambda _{\uptau }X} \right. \right. \nonumber \\&+\left. \left. \frac{B}{\lambda _{\uptau }^2}e^{-\lambda _{\uptau }(X+l_e+l_1+l_2)} \right] + M_0X \right] + \varphi _0 \end{aligned}$$

(44)

$$\begin{aligned} v(x)= & {} \frac{1}{\kappa GS}\frac{P}{2}X +\frac{1}{EI} \left[ -\frac{P}{4} \frac{X^3}{3} \nonumber \right. \\&+ \frac{wt}{2} \left[ \frac{\uptau _m}{2}\frac{X^3}{3} + \frac{A}{\lambda _{\uptau }^3}e^{\lambda _{\uptau }X}\right. \nonumber \\&\left. -\frac{B}{\lambda _{\uptau }^3}e^{-\lambda _{\uptau }(X+l_e+l_1+l_2)} \right] \nonumber \\&\left. + \frac{M_0}{2}X^2 \right] +\varphi _0X + v_0 \end{aligned}$$

(45)

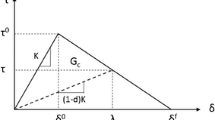
where $N_0$, $M_0$, $u_0$, $\varphi _0$ and $v_0$ are integration constants. In the case of softening or hardening behaviour, shape of the ALSB is defined by a local tangent modulus $G_t^2 \ne 0$. A similar third order differential equation is obtained:

$$\begin{aligned} \frac{d^3\uptau _2}{dx}-\frac{2wG_t^2}{t_a}\left[ \frac{1}{EI}\left( \frac{t}{2}\right) ^2+\frac{1}{ES}\right] \frac{d\uptau _2}{dx} = 0 \end{aligned}$$

(46)

Leading to a similar stress distribution:

$$\begin{aligned} \uptau _2(x)=A_1e^{\lambda _{\uptau }^2X}+B_1e^{-\lambda _{\uptau }^2(X+l_2)}+\uptau _{m2} \end{aligned}$$

(47)

with

$$\begin{aligned} \lambda _{\tau }^2 = \sqrt{2\frac{G_t^2}{t_a}w\left[ \frac{1}{EI}\left( \frac{t}{2}\right) ^2+\frac{1}{ES}\right] } \end{aligned}$$

(48)

where X varies in the interval $[-l_2;0]$. $l_2$ being the length of the damaged zone as described in Fig. 6. $X=0$ corresponds to the crack tip position. $\lambda _{\uptau }^2$ is the characteristic wave number that controls the extent of the process zone. $\uptau _2$ is the shear stress along the damaged region of the adhesive developped during the softening or hardening stage. As for the elastic stage, $\uptau _2$ is replaced by its expression in Eqs. (29) to (34) which gives similar expressions to Eqs. (40) to (45).

In the case of a trapezoidal ALSB, a perfectly plastic behaviour is considered where the local tangent modulus is equal to 0. Shear stress for this regime can be defined as:

$$\begin{aligned} \tau _1=\tau _{max} \end{aligned}$$

(49)

After solving a second order differential equation, local forces and displacements can therefore be described as:

$$\begin{aligned} N_1(x)= & {} w\uptau _{max}X+N_{01} \end{aligned}$$

(50)

$$\begin{aligned} M_1(x)= & {} -\frac{P}{2}X+\frac{wt}{2}\uptau _{max}X+M_{01} \end{aligned}$$

(51)

$$\begin{aligned} u_1(x)= & {} \frac{1}{ES}\left( w\uptau _{max}\frac{X^2}{2}+ N_{01}X\right) +u_{01} \end{aligned}$$

(52)

$$\begin{aligned} \varphi _1(x)= & {} \frac{1}{EI}\left( -\frac{P}{2}\frac{X^2}{2}\nonumber \right. \\&\left. +\frac{wt}{2}\uptau _{max}\frac{X^2}{2}+M_{01}X\right) +\varphi _{01} \end{aligned}$$

(53)

$$\begin{aligned} v_1(x)= & {} \frac{1}{\kappa GS}\frac{P}{2}X+\frac{1}{EI}\left( -\frac{P}{4}\frac{X^3}{3}\nonumber \right. \\&\left. +\frac{wt}{4}\uptau _{max}\frac{X^3}{3}+M_{01}\frac{X^2}{2}\right) \nonumber \\&+\varphi _{01}X+v_{01} \end{aligned}$$

(54)

where in this trapezoidal case, X varies in the interval $[-(l_1+l_2);-l_2]$.

A simple optimisation procedure is used to simulate the mechanical response of an ELS specimen. Indeed, the whole specimen is represented with segments connected together where shear stress distribution are given by relations (38) and (47). Considering displacements and cohesive forces along the adherend, the parameters to be identified are the lengths of each segment ($l_e$,$l_1$,$l_2$). This procedure is illustrated in algorithms 1 in the case of a bilinear ALSB with the following boundary conditions (see Fig. 6):

• Boundary condition considering the specimen clamped at its left end: $u(0) = 0$, $v(0) = 0$ and $\varphi (0) = 0$.

• At crack tip, $N_2(l_e+l_2) = 0$ and $M_2(l_e+l_2) = Pa/2$ since there is no loaded adhesive. The specimen behaves like a simple beam under flexure.

• Continuity conditions between elastic region and damaged region (see Fig. 6): $u(l_e)=u_2(l_e)$, $v(l_e)=v_2(l_e)$, $\varphi (l_e)=\varphi _2(l_e)$, $N(l_e)=N_2(l_e)$, $M(l_e)=M_2(l_e)$.

• Fully developed FPZ condition: $\uptau _2(l_e)=\uptau _{max}$.

• Shear stress condition: $\uptau =\uptau _{max}$.

• Compatibility conditions: u(x) and $\varphi (x)$ are replaced by their expression (Eqs. 43 and 44) in Eq. 36. Then identification between shear stress distribution (see Eq. 38) and shear stress as a function of shear strain (see Eq. 36) gives:

  $$\begin{aligned} \tau _m= & {} cste \end{aligned}$$

  (55)
  $$\begin{aligned} \uptau _m= & {} 2\frac{G_a}{t_a}\left[ \left( \frac{1}{ES}\left[ w\uptau _m\frac{X^2}{2}+N_0 X\right] +u_0\right) \right. \nonumber \\&+\left. \frac{t}{2}\left( \frac{1}{EI}\left[ -\frac{PX^2}{2}+\uptau _m\frac{tw}{2}\frac{X^2}{2}+M_0 X\right] +\varphi _0\right) \right] \nonumber \\ \end{aligned}$$

  (56)

  Polynomial terms in Eq. 56 must be equal to zero because $\uptau _m=cste$, so we obtain:

  $$\begin{aligned} \uptau _m= & {} \frac{P}{wt} \frac{St^2}{4I + St^2} \end{aligned}$$

  (57)
  $$\begin{aligned} M_0= & {} -\frac{2I}{tS} N_0 \end{aligned}$$

  (58)
  $$\begin{aligned} \uptau _m= & {} 2\frac{G_a}{t_a} \left[ u_0 + \frac{t}{2}\varphi _0 \right] \end{aligned}$$

  (59)

Algorithm 1 describes how local forces and displacement are obtained for the elastic, FPZ development and crack propagation regimes for a bilinear ALSB. More over, it describes how the maximum length for the process zone is obtained: multiple lengths are tested until shear strain goes over maximum shear strain ($\gamma _2$). For each length of process zone, local forces and displacements are obtained. Similarly, during crack propagation regime, for each crack length a tested, quantities are calculated, especially shear strain. If shear strain is included in an interval $[\gamma _{max}-\varepsilon ,\gamma _{max}+\varepsilon ]$, crack propagates (crack length a rises). $\varepsilon$ is the precision expected with respect to the ALSB parameters. Moreover, it permits the semi-analytical model to converge to a solution. If shear strain is not in the interval, size of the FPZ $l_{FPZ}$ has to be adjusted. In the case of bi-linear ALSB, $l_{FPZ} = l_2$. In the case of trapezoidal ALSB, $l_{FPZ} = l_1 + l_2$.

Getting the local forces and displacements describes crack propagation along the adhesive layer as a function of the applied load. Shear stress and strain are obtained and can be correlated with the adhesive layer shear behaviour. These quantities depends on the geometrical and ALSB parameters.

Appendix C: Approximate solution

The shear stress distribution is:

$$\begin{aligned} \uptau (x)=\uptau _m+Ae^{\lambda _{\uptau }X}+Be^{-\lambda _{\uptau }(X+l_e+l_1+l_2)} \end{aligned}$$

(60)

$\uptau _m$ is the mean shear stress. X, $l_e$, $l_1$, $l_2$ are described in Fig. 6. Assuming non interacting large gradient regions at both bondline edge, the boundary condition at the crack tip edge $X=0$ reduced to:

$$\begin{aligned} N(X=0)= & {} 0=\frac{Aw}{\lambda _{\uptau }}+N_0 \end{aligned}$$

(61)

$$\begin{aligned} M(X=0)= & {} 0=\frac{wt}{2}\frac{A}{\lambda _{\uptau }}+M_0 \end{aligned}$$

(62)

$N_0$, $M_0$ are integration constants. With compatibility conditions obtained with the method described in Appendix B:

$$\begin{aligned} M_0= & {} -\frac{2I}{St}N_0 \end{aligned}$$

(63)

$$\begin{aligned} \uptau _m= & {} \frac{P}{wt}\frac{St^2}{St^2+4I} \end{aligned}$$

(64)

We obtain:

$$\begin{aligned} A= & {} \frac{\lambda _{\uptau }}{w}\frac{St}{St^2+4I}Pa \end{aligned}$$

(65)

$$\begin{aligned} N_0= & {} -\frac{St}{St^2+4I}Pa \end{aligned}$$

(66)

$$\begin{aligned} M_0= & {} \frac{2I}{St^2+4I}Pa \end{aligned}$$

(67)

So near crack tip region ($B=0$):

$$\begin{aligned} \uptau (x)=\frac{P}{wt}\frac{St^2}{St^2+4I}\left[ 1+\lambda _{\uptau }ae^{\lambda _{\uptau }X}\right] \end{aligned}$$

(68)

and near clamping region with $\uptau (X=-l_e)=0$

$$\begin{aligned} \uptau (x)=\frac{P}{wt}\frac{St^2}{St^2+4I}\left[ 1-e^{-\lambda _{\uptau }(X+l_e+l_1+l_2)}\right] \end{aligned}$$

(69)

Replacing Eq. (69) in classical constitutive equations, we obtain:

$$\begin{aligned} \varphi (x)=&\frac{1}{EI}\left[ -\frac{PX^2}{4}+\frac{wt}{2}\uptau _m\left[ \frac{X^2}{2}+\frac{4I}{St^2}aX \right. \right. \nonumber \\&\left. \left. -\frac{1}{{\lambda _{\uptau }}^2}e^{-\lambda _{\uptau }(X+l_e+l_1+l_2)}\right] \right] +\varphi _0 \end{aligned}$$

(70)

with $\varphi (X=-l_e)=0$

$$\begin{aligned} \varphi _0=-\frac{1}{EI}\left[ -\frac{P{l_e}^2}{4}+\frac{wt}{2}\uptau _m\left[ \frac{{l_e}^2}{2}-\frac{4I}{St^2}al_e-\frac{1}{{\lambda _{\uptau }}^2}\right] \right] \end{aligned}$$

(71)

near crack tip

$$\begin{aligned} \varphi (x)= & {} \frac{1}{EI}\frac{wt}{2}\frac{A}{{\lambda _{\uptau }}^2}+\varphi _0 \end{aligned}$$

(72)

$$\begin{aligned} \varphi (X=0)= & {} \frac{P}{EI}\frac{4I}{St^2+4I}\left[ \frac{{l_e}^2}{2}+al_e\right] \nonumber \\&+\frac{P}{EI}\frac{St^2}{St^2+4I}\left[ \frac{1}{{\lambda _{\uptau }}^2}+\frac{a}{\lambda _{\uptau }}\right] \end{aligned}$$

(73)

$$\begin{aligned} \varphi _r= & {} \frac{P}{EI}\frac{St^2}{St^2+4I}\left[ \frac{1}{{\lambda _{\uptau }}^2}+\frac{a}{\lambda _{\uptau }}\right] \nonumber \\\simeq & {} \frac{P}{EI}\frac{St^2}{St^2+4I}\frac{a}{\lambda _{\uptau }} \end{aligned}$$

(74)

$\varphi _r$ is the root rotation coeeficient.

The same procedure is applied to determine the root deflection coefficient $v_r$:

$$\begin{aligned} \begin{aligned} v(x)=&\frac{P}{2\kappa GS}+\frac{1}{EI}\left[ -\frac{PX^3}{12}+\frac{wt}{2}\uptau _m\left[ \frac{X^3}{6}+\frac{4I}{St^2}a\frac{X^2}{2} \right. \right. \\&+\left. \left. \frac{1}{{\lambda _{\uptau }}^3}e^{-\lambda _{\uptau }(X+l_e+l_1+l_2)}\right] \right] +\varphi _0X+v_0 \end{aligned} \end{aligned}$$

(75)

with $v(X=-l_e)=0$

$$\begin{aligned} v_0=&\frac{Pl_e}{\kappa GS}+ \frac{P}{2EI}\frac{4I}{St^2+4I}\left[ \frac{{l_e}^3}{3}+\frac{3}{4}a{l_e}^2\right] \nonumber \\&-\frac{P}{2EI}\frac{St^2}{St^2+4I}\left[ \frac{1}{{\lambda _{\uptau }}^3}-\frac{l_e}{{\lambda _{\uptau }}^2}\right] \end{aligned}$$

(76)

near crack tip

$$\begin{aligned} v(x)= & {} \frac{wt}{2EI}\frac{B}{{\lambda _{\uptau }}^3}+v_0 \end{aligned}$$

(77)

$$\begin{aligned} v(X=0)= & {} \frac{Pl_e}{\kappa GS}+\frac{P}{2EI}\frac{4I}{St^2+4I}\left[ \frac{{l_e}^3}{3}+\frac{3}{4}a{l_e}^2\right] \nonumber \\&+\frac{P}{2EI}\frac{St^2}{St^2+4I}\left[ \frac{l_e}{{\lambda _{\uptau }}^2}-\frac{1}{{\lambda _{\uptau }}^3}+\frac{a}{{\lambda _{\uptau }}^3}\right] \nonumber \\ \end{aligned}$$

(78)

$$\begin{aligned} v_r= & {} \frac{P}{2EI}\frac{St^2}{St^2+4I}\left[ \frac{l_e}{{\lambda _{\uptau }}^2}-\frac{1}{{\lambda _{\uptau }}^3}+\frac{a}{{\lambda _{\uptau }}^3}\right] \end{aligned}$$

(79)